螺栓连接非线性振动特性研究 陈学前
考虑滞回效应的螺栓连接组合结构非线性随机振动分析

考虑滞回效应的螺栓连接组合结构非线性随机振动分析吴鹏辉;王纪磊;毛晨洋;赵岩【期刊名称】《振动与冲击》【年(卷),期】2024(43)5【摘要】针对具有滞回效应的螺栓连接组合结构,结合虚拟激励法和多谐波平衡法实现了随机振动响应频域功率谱分析。
首先,对于随机激励作用下的组合结构,以Jenkins模型进行本构建模。
其次,将随机激励表达为复指数级数,将响应谱分析转化虚拟响应的向量运算,提出了扩展虚拟激励法(extended pseudo excitation method, E-PEM)。
最后,对虚拟响应求解中频域本构的计算困难,引入时频变换处理;将非线性迭代转换为优化问题并利用信赖域方法求解,有效解决了传统牛顿法的收敛困难。
以二自由度和组合梁模型为对象,研究了结构的随机振动响应谱特性,并同蒙特卡罗模拟法对比验证E-PEM的正确性,同时对结构特有的非线性随机振动机制进行了讨论。
结果表明:建立的E-PEM为一般非线性结构随机振动频域分析提供了一个可借鉴的求解思路。
【总页数】8页(P223-230)【作者】吴鹏辉;王纪磊;毛晨洋;赵岩【作者单位】大连理工大学运载工程与力学学部工业装备结构分析优化与CAE软件全国重点实验室;大连理工大学宁波研究院【正文语种】中文【中图分类】O324【相关文献】1.考虑垫片时滞效应的管板-法兰-垫片-螺栓连接系统三维有限元分析--预紧工况和加压工况下密封垫片的压紧应力分析2.考虑弹塑性结构退化和捏拢滑移效应的光滑滞回模型3.考虑几何非线性的Pall型摩擦阻尼器滞回特性分析4.组合楼板效应对带低屈服点钢耗能梁段高强钢框筒结构滞回性能影响分析5.考虑失稳效应的角钢非线性滞回模型研究因版权原因,仅展示原文概要,查看原文内容请购买。
计算机视觉对震动环境下螺丝松动的监测仿真

计算机视觉对震动环境下螺丝松动的监测仿真陈向华;周娟【期刊名称】《计算机仿真》【年(卷),期】2014(31)10【摘要】在频繁震动环境下,高精度设备受到无规则振动、冲击以及高温蠕变的影响,导致螺栓结构产生非固定滑动、分离或者脱落.螺栓结构具有复杂的动态性,脱落过程呈现不明显变化,螺丝帽与杆的相对位置变化过程与振动强度、外部环境呈现复杂关系,无法建立有效关联.传统视觉监控方法在振动条件下,获取的螺栓帽和杆的相对像素位置在无法建立关联的情况下,以静态阀值观测为主,存在较大的偏差,无法获取准确的螺栓松动监测结果.提出震动环境下聚类RBF神经网络的视觉螺丝松动监测方法.提取螺丝松动监控计算机视觉图像的特征,并针对上述螺丝帽与脱离的异常距离进行有效的识别.利用傅里叶变换方法建立螺丝松动监控图像特征矩阵,计算特征脱离聚类目标函数,并建立聚类RBF神经网络模型,完成监控.实验结果表明,利用改进算法可以实现计算机视觉对震动环境下螺丝松动监测,可以提高监测的准确性,防止由于螺丝松动造成的损失.【总页数】4页(P433-436)【作者】陈向华;周娟【作者单位】电子科技大学信息与软件工程学院,四川成都610054;成都工业学院计算机工程系,四川成都611730;电子科技大学信息与软件工程学院,四川成都610054;成都工业学院计算机工程系,四川成都611730【正文语种】中文【中图分类】F127【相关文献】1.复杂环境下洞室开挖的爆破震动监测与控制 [J], 饶杨安;吴立2.复杂环境下浅埋隧道的爆破震动监测与控制技术 [J], 段宝福;朱应磊;吴圣智3.强震动冲击环境下的网络异常信号检测仿真 [J], 朱小刚;陈大可4.基于机器视觉高空飞机螺栓松动监测仿真 [J], 刘超华;林亚军;王述运5.干扰环境下基于计算机视觉的多目标动位移高精度监测方法 [J], 周洲;陈太聪因版权原因,仅展示原文概要,查看原文内容请购买。
螺栓连接对结构模态及传递特性影响研究

明, 忽略接触阻尼的计算值与试验值存在最大误差约 1 5 %; 同一预紧力时 , 随螺栓刚度 的提高 固有 频率呈增 大趋势 , 各阶
c h a n g e s o f s t uc r t ur e mo d e s a n d t r a n s f e r f u n c t i o n we r e a na l y z e d. By u s i ng t h e ANS YS s o f t wa r e,t h e v i b r a t i o n mo d e s a n d
e l e me n t c a l c u l a t i o n d a t a a n d t e s t d a t a o f t h r e e k i n d s o f b o l t s w i t h d i f f e r e n t s t i f f n e s s u n d e r d i f f e r e n t p r e — t i g h t e n i n g f o r c e ,t h e
振 第3 3卷第 2期
动
与
冲
击
J OURNAL OF VI BRATI ON AND S HOCK
螺 栓连 接 对 结构 模态 及 传 递特 性 影 响研 究
陈长盛 ,王 强 ,柳瑞 锋 ,李 国平 ,周
2 0 0 0 3 1 )
高强度螺栓抗拉连接的仿真及实验研究

Key words:high strength bolted connection,prying force,natural strain and stress,
clement contact status nonlinearities,material nonlinearities,firdte
method
section the paper specifies three possible failure modes of the ultimate resistance, depending Oil the ratio between the flexural resistance of the flanges and the axial
II
重庆大学硕士论文
1绪论
1.1引言
钢结构近几年在全国发展势头强劲,钢结构建筑以其适应造型复杂的建筑设 计要求、施工的便捷和建设周期短等特点在建筑市场上成为关注的焦点。钢结构 的体系计算已是较为成熟的理论。理论中关注的重点是结构体系中梁、柱的受压 稳定性问题。在结构和构件稳定性问题方面国内外学术界研究已取得了骄人的成 果,目前研究正朝弹塑性稳定方向进一步深入发展。稳定问题是一个较为复杂的 问题,我们从实际运用和计算理论的结合处考察不难发现节点的受力性能是另一 个关键性问题。节点受力性能是构件约束条件的重要保证,而约束条件则是构件 稳定分析中的基本条件。一位研究钢结构的前辈曾经说过“约束等于刚度”,我们 可以体会出约束对于稳定问题的重要性。本文关注抗拉螺栓连接的受力性能问题, 并进行了分析研究。
△P=F冬屯 kb+k,‘
(1.1)
重庆大学硕士论文
1绪论
N。f。
-f叶
△e
一+一 △e
螺栓连接非线性振动特性研究 陈学前

μ1 、 μ 2 ,辨识结果为:
α 1 = 1.377 × 108 α 2 = −9.201× 10 3 μ1 = 27.626 μ 2 = 0.189
因此非线性方程式(10)可以写成: (16)
⎧& & + (27.626 + 0.189 y 2 ) y & + (1.377 × 10 8 − 9.201 × 10 3 y 2 ) y = h sin ωt y ⎨ 17.375 ≤ y ≤ 39.619 ⎩
THE STUDY ON THE NONLINEAR VIBRATIONAL CHARACTERISTIC OF BOLT-JOINTS CHEN Xueqian,DU Qiang,FENG Jiaquan
(Institute of Systems Engineering, CAEP, Mianyang, Sichuan, 621900)
2. 非线性理论模型
& 的多项式函 在Crawley与O’Donnell的相关研究中,他们将非线性传递力表示为 y 和 y
数 ,根据前面的实验数据分析,下面将系统的振动微分方程表示成如下形式:
[8]
& & + ( μ1 + μ 2 y 2 ) y & + (α 1 + α 2 y 2 ) y = P0ω 2 sin ωt y
0. 引言
螺栓连接广泛应用于工程结构中,如:各电子仪器组件与安装板的连接,两个部组件通 过螺栓法兰连接成为一体。 这类连接由于螺栓预紧力和外界激励不同, 使得螺栓连接的两部 分构件界面的特性(如:接触、干摩擦等)均会发生改变,从而导致产品结构在不同的动载 荷下出现一定的非线性特性。 由于它们连接的动力学特性将直接影响到结构在振动环境下的 响应,因此,国内外众多学者对螺栓连接的特性进行了研究。陈汝训[1]考虑了在拧紧螺栓过 程中螺栓既受拉应力,又受剪应力时研究了螺栓的极限拧矩;李以农[2]建立了在高频情况下 一维构件的波传播模型, 讨论了波在其中传播的特性及能量耗散问题, 提出了一种简化的螺 [3~4] 栓非线性接头模型;Hess 研究了单个螺栓在轴向正弦激励载荷作用下的响应情况,发现
最新螺栓联接静、动态特性实验报告
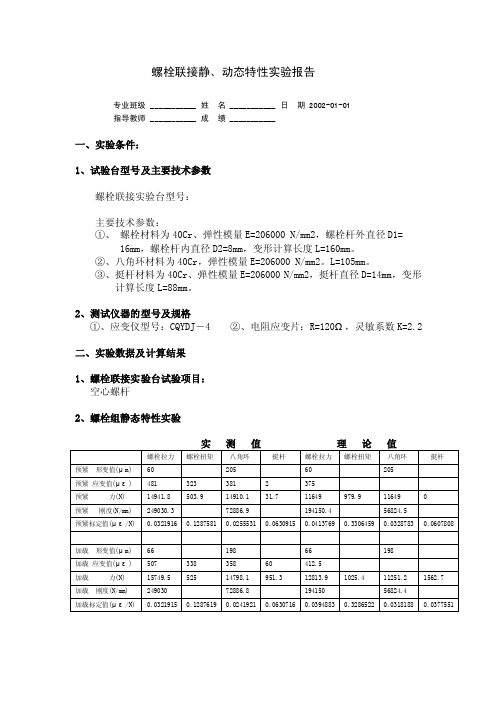
螺栓联接静、动态特性实验报告专业班级 ___________ 姓名 ___________ 日期 2002-01-01指导教师 ___________ 成绩 ___________一、实验条件:1、试验台型号及主要技术参数螺栓联接实验台型号:主要技术参数:①、螺栓材料为40Cr、弹性模量E=206000 N/mm2,螺栓杆外直径D1=16mm,螺栓杆内直径D2=8mm,变形计算长度L=160mm。
②、八角环材料为40Cr,弹性模量E=206000 N/mm2。
L=105mm。
③、挺杆材料为40Cr、弹性模量E=206000 N/mm2,挺杆直径D=14mm,变形计算长度L=88mm。
2、测试仪器的型号及规格①、应变仪型号:CQYDJ-4 ②、电阻应变片:R=120Ω,灵敏系数K=2.2二、实验数据及计算结果1、螺栓联接实验台试验项目:空心螺杆2、螺栓组静态特性实验3、螺栓联接静、动特性应力分布曲线图 (空心螺杆)三、实验结果分析工作总结-财务处长个人工作总结[工作总结-财务处长个人工作总结]工作总结-财务处长个人工作总结(范文)工作总结-财务处长个人工作总结2009-07-06 11:52财务处长个人工作总结光阴似箭、岁月如梭,转眼之间一年过去了,新的一年已经开始,工作总结-财务处长个人工作总结。
回顾一年来的工作,我处在局党组和*局长的正确领导下,在各兄弟处室和同志们的大力支持和积极配合下,全处上下团结奋进,开拓创新,圆满地完成了全年的各项工作任务。
现将主要情况汇报如下:一、加强政治业务学习,努力提高自身素质。
我深知作为财务处长,肩负的任务繁重,责任重大。
为了不辜负领导的重托和大家的信任,更好的履行好职责,就必须不断的学习。
因此我始终把学习放在重要位臵。
一是认真学习党的"十六大"和十六届三中全会精神,特别是重点研读了胡锦涛总书记在"三个代表"重要思想理论研讨会上的讲话。
螺栓连接条件下结构振动模态的时频分析方法

螺栓连接条件下结构振动模态的时频分析方法王强龙;李耀彬;伞晓刚;刘震宇【摘要】在精密光电跟踪设备中,光机结构的振动特性对保持目标跟踪的精度和稳定性具有重要意义.螺栓连接是光机结构的常用连接形式,但其非线性接触特性也使得结构的振动特性变得较为复杂.采用时域激励计算结构位移响应并进行频域分析的方法计算结构的共振频率.相比于弹簧单元模拟螺栓连接等简化方法,此方法不需要对每一个螺栓分别进行弹簧单元刚度等参数的选取和处理.以螺栓连接的悬臂梁为例,先利用接触面固结的模型验证方法的准确性,其后对考虑接触和螺栓预紧力的模型进行仿真计算.仿真的模态结果和试验模态结果对比表明,所提的仿真方法正确且有效.【期刊名称】《机械设计与制造》【年(卷),期】2016(000)007【总页数】5页(P72-76)【关键词】振动模态;接触非线性;时频积分;频域处理【作者】王强龙;李耀彬;伞晓刚;刘震宇【作者单位】中国科学院长春光学精密机械与物理研究所,吉林长春130033;中国科学院大学,北京100039;中国科学院长春光学精密机械与物理研究所,吉林长春130033;中国科学院长春光学精密机械与物理研究所,吉林长春130033;中国科学院长春光学精密机械与物理研究所,吉林长春130033【正文语种】中文【中图分类】TH16;TP391.9对于承受时间依赖载荷的机械结构,螺栓连接处的接触状态将强烈影响整体结构的动态响应特性[1]。
在工程仿真分析中,如何处理连接处的接触非线性是保证仿真结果准确性的一个重要环节。
由于螺栓连接形式的多样性以及预紧力的大小不同,简单的线性模态数值解和试验模态结果相差较大,导致基于模态叠加法的快速结构动态分析在实际工程问题中的使用受到了一定的限制[2-3]。
当螺栓连接面积相比整体结构较小时,接触状态引起的非线性大多表现为接触区域周围有限区域结构刚度的非线性变化,进而影响整体结构的变形和振动特性[4-5]。
对于大多数的工程结构分析问题,虽然大部分的非连接结构区域仍然可以采用线性近似分析方法,但用刚性连接来近似等效螺栓连接已经被证明与实际情况出入较大,不能正确反映螺栓变形和接触区域的变化对结构振动频率的影响。
非线性振动的研究对象、方法及发展简史

非线性振动的研究对象、方法及发展简史在自然界、工程技术、日常生活和社会生活中,普遍存在着物体的往复运动或状态的循环变化,这类现象称为振荡。
例如大海的波涛起伏、花的日开夜闭、钟摆的摆动、心脏的跳动、经济发展的高涨和萧条等形形色色的现象,都具有明显的振荡特性。
振动是一种特殊的振荡,即平衡位置附近微小或有限的振荡。
如声波和超声波、工程技术中的机器和结构物的机械振动、无线电和光学中的电磁振荡等。
从最小的初等粒子到巨大的天体,从简单的摆到复杂的生物体,无处不存在振动现象。
有时人们力图防止或减小振动,有时又力图制造和利用振动。
尽管振动现象的形式多种多样,但有着共同的客观规律和统一的数学表达形式。
因此有可能建立统一的理论来进行研究,即振动力学。
振动力学是力学、声学、无线电电子学、自动控制理论等学科,以及机械、航空、土木、水利等工程学科的理论基础之一。
它应用数学分析、实验量测和数值计算等方法,探讨振动现象的机理和基本规律,为解决与振动有关的实际问题提供理论依据。
根据描述振动的数学模型的不同,振动理论区分为线性振动理论和非线性振动理论。
线性振动理论适用于线性系统,即质量不变、弹性力和阻尼力与运动参数成线性关系的系统,其数学描述为线性常系数常微分方程;不能简化为线性系统的系统为非线性系统,研究非线性系统的振动理论就是非线性振动理论。
线性振动理论是对振动现象的近似描述,在振幅足够小的大多数情况下,线性振动理论可以足够准确地反映振动的客观规律。
频率、振幅、相位、激励、响应、模态等,都是在线性理论中建立起来的基本概念。
实际机械系统中广泛存在着各种非线性因素,如电场力、磁场力、万有引力等作用力非线性,法向加速度、哥氏加速度等运动学非线性,非线性本构关系等材料非线性,弹性大变形等几何非线性等。
因此,工程实际中的振动系统绝大多数都是非线性系统。
由于非线性微分方程尚无普遍有效的精确求解方法,而线性常微分方程的数学理论已十分完善,因此将非线性系统以线性系统代替是工程中常用的有效方法,但仅限于一定的范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
β=
1 (ω − ω ) + (2ξω nω ) 2
2 n 2 2
(2)
β max =
1 2ξ 1 − ξ 2
(3)
式中, ξ 为相对阻尼系数, ω n 为无阻尼系统的固有频率。 对于小阻尼系统,式(3)可以近似写成:
β max ≈
1 2ξ
(4)
通过振幅放大因子曲线的峰值可以确定固有频率,再结合式(4)就可得到系统的相对 阻尼系数 ξ 。表 1 是不同振动量级下系统固有频率及相对阻尼系数的实验结果。 表1
螺栓连接非线性振动特性研究*
陈学前,杜强,冯加权
(中国工程物理研究院总体工程研究所,四川,绵阳,621900)
摘要:在不同的外界激励下,螺栓连接常常表现出一定的非线性。为研究螺栓连接的非线性 特性,设计了一个螺栓连接系统,并对其进行不同基础激励下的正弦扫频实验。通过实验数 据的分析得到了螺栓连接的共振频率和相对阻尼系数, 发现其随着激励量级的不同呈现出较 明显的非线性特性。在理论模型研究中,将系统简化为非线性弹簧、非线性阻尼器、质量块 的单自由度模型,并利用实验数据对非线性方程中的系数进行了识别。利用此非线性模型, 求出系统的主共振频率和相对阻尼系数, 它们与实验结果相比差别较小, 说明文中所给的非 线性方程能较好描述螺栓连接的振动特性。 关键词:螺栓连接;振动;非线性 中图分类号:O324 文献标识码:A
ce (a ) =
aωπ ∫
1
2π
0
[aμ1ω sin φ + a 3 μ 2ω sin φ cos 2 φ ] sin φ dφ
(11)
1 = μ1 + μ 2 a 2 4
将(10) 、 (11)式代入(8)和(9)可以解得:
a= =
{[ω (a) − ω ] + c (a)ω }
2 n 2 2 2 e 2
2. 非线性理论模型
& 的多项式函 在Crawley与O’Donnell的相关研究中,他们将非线性传递力表示为 y 和 y
数 ,根据前面的实验数据分析,下面将系统的振动微分方程表示成如下形式:
[8]
& & + ( μ1 + μ 2 y 2 ) y & + (α 1 + α 2 y 2 ) y = P0ω 2 sin ωt y
μ1 、 μ 2 ,辨识结果为:
α 1 = 1.377 × 108 α 2 = −9.201× 10 3 μ1 = 27.626 μ 2 = 0.189
因此非线性方程式(10)可以写成: (16)
⎧& & + (27.626 + 0.189 y 2 ) y & + (1.377 × 10 8 − 9.201 × 10 3 y 2 ) y = h sin ωt y ⎨ 17.375 ≤ y ≤ 39.619 ⎩
P0ω 2
0.5
{[α + 0.75α a
1 2
2
− ω 2 + ( μ1 + 0.25μ 2 a 2 ) 2 ω 2
]
P0ω 2
(12)
2
}
0.5
tgψ =
− ( μ1 + 0.25μ 2 a 2 ) α + 0.75α 2 a 2 − ω 2
(13)
对于定加速度扫频, (12)式中 P0ω 2 = h(ω ) = 常数 ,只与基础控制加速度值相关。在
& ≡ 0 ,由式(8)可以得出与式(5)相对应的保守系统的一 若取 P0 = 0, ( μ1 + μ 2 y 2 ) y
次谐波的幅频关系:
2 ωn (a ) = α 1 + α 2 a 2
3 4
(10)
对于有阻尼的强迫振动情况(5)式,将表达式 a0 = 0 代入(9)式可以求出等效阻尼 系数 ce ( a ) :
加速度传感器 试件 振动台 A2 A6 电荷放大器 A5 A8 A7 A3
功率放大器 A1 A4
振动控制器
数据采集系统
图 1 实验系统示意图
图 2 实验测点布置图
1.2 实验结果
正弦振动实验采用A1~A4 四点加速度响应平均控制, 控制基准谱采用 800Hz~2000Hz 的定加速度谱曲线, 谱线数为 801 线, 扫频速率为 2Hz/s, 振动量级为 1g、 2g、 …、 5g (g=9.8m/s2, 下同) 。实验数据分析时,将系统简化为弹簧、阻尼器、质量块的单自由度模型(如图 3 所 示) ,设 x (t ) 及 xs (t ) 分别是质量块及基础的位移,得到系统的振动微分方程为: x
0. 引言
螺栓连接广泛应用于工程结构中,如:各电子仪器组件与安装板的连接,两个部组件通 过螺栓法兰连接成为一体。 这类连接由于螺栓预紧力和外界激励不同, 使得螺栓连接的两部 分构件界面的特性(如:接触、干摩擦等)均会发生改变,从而导致产品结构在不同的动载 荷下出现一定的非线性特性。 由于它们连接的动力学特性将直接影响到结构在振动环境下的 响应,因此,国内外众多学者对螺栓连接的特性进行了研究。陈汝训[1]考虑了在拧紧螺栓过 程中螺栓既受拉应力,又受剪应力时研究了螺栓的极限拧矩;李以农[2]建立了在高频情况下 一维构件的波传播模型, 讨论了波在其中传播的特性及能量耗散问题, 提出了一种简化的螺 [3~4] 栓非线性接头模型;Hess 研究了单个螺栓在轴向正弦激励载荷作用下的响应情况,发现
(5)
在 ω ≈ ω n 的基本强迫振动中常数成份 a 0 和一次谐波项 a cos(ωt + ψ ) 占有优势,而高 次谐波项只有很小的振幅,所以方程(5)的近似稳态解可设为 :
[9]
y = a0 + a cos(ωt + ψ ) = a0 + a cos φ
应用谐波平衡法可确定常数分量 a 0 、一次谐波幅值 a 和相位差ψ :
2 (12)式中,当 ω n ( a ) = ω 2 时,振幅取最大值 a max ,再联合(10)式,有:
2 ω 2 (a max ) = α 1 + 0.75α 2 a max
(14)
h(ω ) 2 = μ1 + 0.25μ 2 a max a maxω
(15)
结合实验结果,当系统发生主共振时,可以通过式(14) 、式(15)来辨识系数 α 1 、α 2 、
*中国工程物理研究院面上基金(20060319)资助项目;中国工程物理研究院双百人才基金课题(ZX04002)资助项目
随着振动量级以及振动频率的变化,观察到了螺栓松动与拧紧的试验现象;Hess[5]采用理论 和试验相结合的研究方法,研究了一个由单个螺栓、弹簧、质量块组成的系统,得到影响系 统松弛、压紧的主要因素;EL-ZAHRY[6]把螺栓法兰简化为弹簧、阻尼器、质量块两自由度系 统,研究了螺栓法兰连接结构在正弦激励载荷作用下的响应情况。 本文通过一个螺栓连接系统在预紧力一定和不同量级的正弦基础激励振动实验, 对螺栓 连接的动刚度和动阻尼进行了识别, 根据识别结果选用一种非线性数学模型来描述该螺栓连 接模型。
THE STUDY ON THE NONLINEAR VIBRATIONAL CHARACTERISTIC OF BOLT-JOINTS CHEN Xueqian,DU Qiang,FENG Jiaquan
(Institute of Systems Engineering, CAEP, Mianyang, Sichuan, 621900)
振动量级/g 固有频率/Hz 相对阻尼系数/% 1 1848.62 0.212 2 1835.68 0.254
实验结果
3 1808.64 0.331 4 1797.49 0.415 5 1791.11 0.494
从表 1 可以看出,随着基础激励量级的增大,系统固有频率减小,相对阻尼系数增大, 呈现出较明显的非线性现象。故对此类问题的数学描述不能再用线性方程(1)来描述,有 必要研究其振动的非线性方程。
Abstract: Bolt joints are widely used in many structures, they represent some nonlinearity subjected to different environment exciting generally. In order to study on their nonlinear characteristic, a bolt-joints system is designed, and the sin-sweep vibration tests are done on the system subjected to different base exciting. The resonant frequencies and the relative damping coefficients of the bolt-joints system are obtained by analyzing the test data, they show obvious nonlinear characteristic with the vibration level changing. In theory study, the system is simplified to be a single freedom degree mass-spring-damper model with nonlinear spring and nonlinear damper. The coefficients of the nonlinear equation are identified by the test data. Last, the main resonant frequencies and the relative damping coefficients of the system are obtained by the nonlinear equation. The theory results are coincident with the test results better, as shows that the nonlinear equation in the paper depicts the vibration characteristics of the bolt-joints better. Keywords: Bolt-joints; Vibration; Nonlinearity
