2012年安徽省中考摸底考数学试卷及答案
2012年安徽中考数学试卷(解析版)

2012年安徽省初中毕业学业考试数 学 本试卷共8大题,计23小题,满分150分,考试时间120分钟。
题号 一 二 三 四 五 六 七 八 总分 得分一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出代号为A 、B 、C 、D 的四个选项,其中只有一个是正确的,请把正确选项的代号写在题后的括号内,每一小题选对得4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分.1.(2012安徽,1,4分)下面的数中,与-3的和为0的是 ………………………….( ) A .3 B .-3 C .31D .31 考点解剖:本题考查了有理数的运算,解题的关键掌握有理数的加法法则。
解题思路:方法一:根据有理数的加法法则,互为相反的两个数的和为0,可以做出正确的选择。
方法二:也可以根据有理数的加法与减法互为逆运算来求解。
解答过程:(1)∵互为相反数的两个数的和为0,而-3的相反数是3,,∴这个数是3,故选A .(2)∵所求的数与-3的和为0,∴这个数是0-(-3)=0+3=3,故选A .答案:A .规律总结:有理数加法运算可以根据其法则先确定结果的符号,再确定结果的绝对值;也可以依据有理数加减法互为逆运算,先列出符合题意得算式,再运算。
关键词:相反数 有理数的加法 有理数的减法2. (2012安徽,2,4分)下面的几何体中,主(正)视图为三角形的是( )A. B . C . D .考点解剖:本题考查了三视图的概念,正确理解主视图(正视图)的概念是解题的关键。
解题思路:根据三视图(主视图)的概念,找到各选项的主视图,从而正确选择主视图是三角形的选项。
解答过程:选项A 、B 、D 图形的主视图是矩形,只有选项C 图形的主视图是三角形,故选C . 答案:C .规律总结:我们从不同的方向观察同一个物体,可能看到不同的图形,其中把从正面看到的平面图形叫做主视图。
关键词:画三视图3.(2012安徽,3,4分)计算(-2x 2)3的结果是( )A.-2x 5 B .-8x 6 C .-2x 6 D .-8x 5考点解剖:本题考查了幂的运算性质中的积的乘方和幂的乘方的运算性质,正确掌握幂的运算性质是解题的关键。
2012年安徽中考数学试卷及答案doc

2012年安徽省初中毕业学业考试数学本试卷共8大题,计23小题,满分150分,考试时间120分钟。
题号一 二 三 四 五 六 七 八 总分得分一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出代号为A 、B 、C 、D 的四个选项,其中只有一个是正确的,请把正确选项的代号写在题后的括号内,每一小题选对得4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分.1.下面的数中,与-3的和为0的是………………………….()A.3B.-3C.31D.31-2.下面的几何体中,主(正)视图为三角形的是() A.B.C.D.3.计算32)2(x -的结果是() A.52x - B.68x - C.62x - D.58x -4.下面的多项式中,能因式分解的是() A.n m +2 B.12+-m m C.n m -2 D.122+-m m5.某企业今年3月份产值为a 万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是()A.(a -10%)(a +15%)万元B.a (1-10%)(1+15%)万元C.(a -10%+15%)万元D.a (1-10%+15%)万元6.化简xxx x -+-112的结果是() A.x +1B.x -1C.—x D.x得分 评卷人7.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a ,则阴影部分的面积为() A.22a B.32a C.42a D.52a8.给甲乙丙三人打电话,若打电话的顺序是任意的,则第一个打电话给甲的概率为()A.61B.31C.21D.329.如图,A 点在半径为2的⊙O 上,过线段OA 上的一点P 作直线 ,与⊙O 过A 点的切线交于点B ,且∠APB=60°,设OP=x ,则△PAB 的面积y 关于x 的函数图像大致是()10.在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是()A.10B.54C.10或54D.10或172二、填空题(本大题共4小题,每小题5分,满分20分)11.2011年安徽省棉花产量约378000吨,将378000用科学计数法表示应是______________.12.甲乙丙三组各有7名成员,测得三组成员体重数据的平均数都是58,方差分别为362=甲S ,252=乙S ,162=丙S ,则数据波动最小的一组是___________________.13.如图,点A 、B 、C 、D 在⊙O 上,O 点在∠D 的内部,四边形OABC 为平行四边形,则∠OAD+∠OCD=_______________°. 14.如图,P 是矩形ABCD 内的任意一点,连接PA 、PB 、PC 、PD ,得到△PAB 、△PBC 、△PCD 、△PDA ,设它们的面积分别是S 1、S 2、S 3、S 4,给出如下结论: ①S 1+S 2=S 3+S 4②S 2+S 4=S 1+S 3 ③若S 3=2S 1,则S 4=2S 2④若S 1=S 2,则P 点在矩形的对角线上其中正确的结论的序号是_________________(把所有正确结论的序号都填在横线上).三、(本大题共2小题,每小题8分,满分16分) 15.计算:)2()1)(3(-+-+a a a a 解:16.解方程:1222+=-x x x得分 评卷人解:四、(本大题共2小题,每小题8分,满分16分)17.在由m ×n (m ×n >1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数f ,(1)当m 、n 互质(m 、n 除1外无其他公因数)时,观察下列图形并完成下表: 猜想:当m 、n 互质时,在m ×n 的矩形网格中,一条对角线所穿过的小正方形的个数f 与m 、n 的关系式是______________________________(不需要证明); 解: (2)当m 、n 不互质时,请画图验证你猜想的关系式是否依然成立, 解:18.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC (顶点是网格线的交点)和点A1.(1)画出一个格点△A1B1C1,并使它与△ABC 全等且A 与A1是对应点;(2)画出点B 关于直线AC 的对称点D ,并指出AD 可以看作由AB 绕A 点经过怎样的旋转而得到的. 解:五、(本大题共2小题,每小题10分,满分20分)19.如图,在△ABC 中,∠A=30°,∠B=45°,AC=32,求AB 的长, 解: 20.九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,月均用水量x (t)频数(户) 频率6 0.12 0.24 16 0.32 10 0.20 420.04请解答以下问题:(1)把上面的频数分布表和频数分布直方图补充完整;1 2 3 2 1 3 4 3 2 3 5 4 2 4 73 5 745°30°C BA第19题图第20题图频数(户)月用水量(t)30252015105161284OA 1C B A第18题图(2)若该小区用水量不超过15t 的家庭占被调查家庭总数的百分比; 解:(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t 的家庭大约有多少户? 解:六、(本题满分12分)21.甲、乙两家商场进行促销活动,甲商场采用“慢200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元;……,乙商场按顾客购买商品的总金额打6折促销。
2012安徽中考数学模拟试题

一.选择题(共10小题,满分40分,每小题4分)1.(4分)(2007•自贡)下列各式中,p,q互为相反数的是()A.pq=1 B.pq=﹣1 C.p+q=0 D.p﹣q=02.(4分)(2011•阜新)随着2011年“毒馒头、毒豆芽”等事件的曝光,人们越来越关注健康的话题.关于甲醛污染问题也一直困扰人们.我国质检总局规定:针织内衣、被套、床上用品等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000 075千克以下,将0.000 075用科学记数法表示为()A.0.75×10﹣4B.7.5×10﹣4C.7.5×10﹣5D.75×10﹣63.(4分)(2011•株洲)如图是一个由7个同样的立方体叠成的几何体.请问下列选项中,既是中心对称图形,又是这个几何体的三视图之一的是()A. B. C. D.4.(4分)(2011•重庆)下列调查中,适宜采用抽样方式的是()A.调查我市中学生每天体育锻炼的时间 B.调查某班学生对“五个重庆”的知晓率C.调查一架“歼20”隐形战机各零部件的质量 D.调查广州亚运会100米参赛运动员兴奋剂的使用情况5.(4分)(2011•梧州)如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是()A.△ACE≌△BCD B.△BGC≌△AFC C.△DCG≌△ECFD.△ADB≌△CEA6.(4分)(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A.5 B.25 C.10+5 D.357.(4分)(2003•武汉)已知:如图,AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.以下结论:①AD∥OC;②点E为△CDB的内心;③FC=FE;④CE•FB=AB•CF.其中正确的只有()A.①②B.②③④ C.①③④ D.①②④8.(4分)(2008•南平)有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中平均一个人传染的人数为()A.8人B.9人C.10人D.11人9.(4分)(2003•泰安)如图,菱形纸片ABCD的一内角为60°,边长为2,将它绕O点顺时针旋转90°后到A′B′C′D′位置,则旋转前后两菱形重叠部分多边形的周长是()A.8 B.4(﹣1) C.8(﹣1) D.4(+1)10.(4分)(2009•临沂)矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB 向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的()A. B. C. D.二.填空题(共4小题,满分20分,每小题5分)11.(5分)(2002•河南)m、n满足|m+2|+=0,分解因式:(x2+y2)﹣(mxy+n)=_________.12.(5分)(2010•抚顺)如图所示,已知a∥b,∠1=28°,∠2=25°,则∠3=_________度.13.(5分)(2010•凉山州)如图,如果从半径为3cm的圆形纸片剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的体积是_________cm3.14.(5分)(2006•临沂)判断一个整数能否被7整除,只需看去掉一节尾(这个数的末位数字)后所得到的数与此一节尾的5倍的和能否被7整除.如果这个和能被7整除,则原数就能被7整除.如126,去掉6后得12,12+6×5=42,42能被7整除,则126能被7整除.类似地,还可通过看去掉该数的一节尾后与此一节尾的n倍的差能否被7整除来判断,则n= _________(n是整数,且1≤n<7).三.解答填空题(共1小题,满分8分,每小题8分)15.(8分)(2008•乌鲁木齐)先化简,再求值:当x=﹣1时,=_________.四.解答题(共8小题,满分82分)16.(8分)张老师于2010年9月份在杭州买了一套楼房,当时(即9月份)在建行贷款96万元,贷款期限为20年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%(每月还款数额=平均每月应还的贷款本金+月利息,月利息=上月所剩贷款本金数额×月利率).(1)求张老师借款后第一个月的还款数额.(2)假设贷款月利率不变,请写出张老师借款后第n(n是正整数)个月还款数额p与n之间的函数关系式(不必化简).(3)在(2)的条件下,求张老师2011年10份的还款数额.17.(8分)(2011•锦州)如图所示,在边长为1个单位的正方形网格中建立平面直角坐标系,△ABC的顶点均在格点上.(1)画出△ABC关于y轴对称的△A1B1C1;(2)将△A1B1C1向下平移3个单位,画出平移后的△A2B2C2;(3)将△A2B2C2绕点C2顺时针旋转90°,画出旋转后的△A3B3C2;并直接写出点A3、B3的坐标.18.(8分)挑战自我!下图是由一些火柴棒搭成的图案:(1)摆第①个图案用_________根火柴棒,摆第②个图案用_________根火柴棒,摆第③个图案用_________根火柴棒.(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?(3)计算一下摆121根火柴棒时,是第几个图案?19.(10分)(2011•连云港)如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一条输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A 在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.(1)线段BQ与PQ是否相等?请说明理由;(2)求A,B间的距离.(参考数据cos41°=0.75)20.(10分)(2011•资阳)小国同学的父亲参加旅游团到某地旅游,准备买某种礼物送给小国.据了解,沿旅游线路依次有A、B、C三个地点可以买到此种礼物,其质量相当,价格各不相同,但不知哪家更便宜.由于时间关系,随团旅游车不会掉头行驶.(1)若到A处就购买,写出买到最低价格礼物的概率;(2)小国同学的父亲认为,如果到A处不买,到B处发现比A处便宜就马上购买,否则到C处购买,这样更有希望买到最低价格的礼物.这个想法是否正确?试通过树状图分析说明.21.(12分)(2011•资阳)如图,已知反比例函数y=(x>0)的图象与一次函数y=﹣x+b 的图象分别交于A(1,3)、B两点.(1)求m、b的值;(2)若点M是反比例函数图象上的一动点,直线MC⊥x轴于C,交直线AB于点N,MD⊥y 轴于D,NE⊥y轴于E,设四边形MDOC、NEOC的面积分别为S1、S2,S=S2﹣S1,求S 的最大值.22.(12分)(2011•肇庆)己知:如图.△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC干点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.(1)求证:∠DAC=∠DBA;(2)求证:P是线段AF的中点;(3)若⊙O的半径为5,AF=,求tan∠ABF的值.23.(14分)如图,已知正方形ABCD的边长为4cm,动点P从点B出发,以2cm/s的速度、沿B→C→D方向,向点D运动;动点Q从点A出发,以1cm/s的速度、沿A→B方向,向点B运动.若P、Q两点同时出发,运动时间为t秒.(1)连接PD、PQ、DQ,设△PQD的面积为S,试求S与t之间的函数关系式;(2)当点P在BC上运动时,是否存在这样的t,使得△PQD是等腰三角形?若存在,请求出符合条件的t的值;若不存在,请说明理由;(3)以点P为圆心,作⊙P,使得⊙P与对角线BD相切.问:当点P在CD上运动时,是否存在这样的t,使得⊙P恰好经过正方形ABCD的某一边的中点若存在,请求出符合条件的t的值;若不存在,请说明理由.答案与评分标准一.选择题(共10小题,满分40分,每小题4分)1.(4分)(2007•自贡)下列各式中,p,q互为相反数的是()A.pq=1 B.pq=﹣1 C.p+q=0 D.p﹣q=0考点:相反数。
2012年安徽省中考最新模拟考试数学试卷
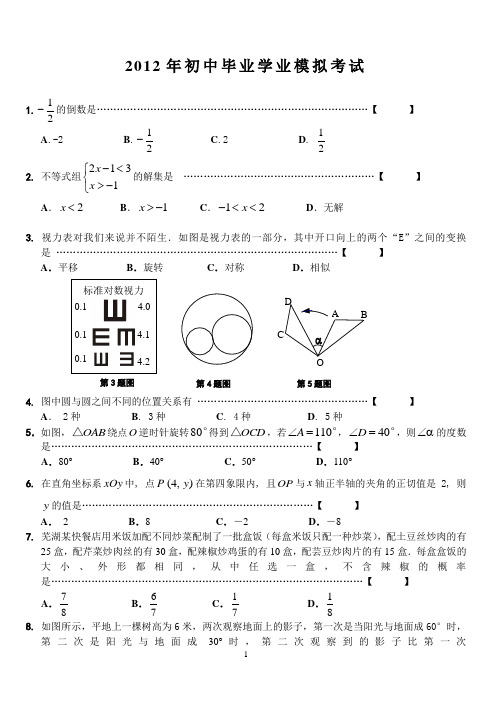
2012年初中毕业学业模拟考试1.21-的倒数是………………………………………………………………………【 】 A .-2 B .21- C .2 D . 212. 不等式组2131x x -<⎧⎨>-⎩的解集是 …………………………………………………【 】A .2x <B .1x >-C .12x -<<D .无解3. 视力表对我们来说并不陌生.如图是视力表的一部分,其中开口向上的两个“E”之间的变换是 …………………………………………………………………………【 】 A .平移 B .旋转 C .对称 D .相似4. 图中圆与圆之间不同的位置关系有 ……………………………………………【 】 A . 2种 B . 3种 C . 4种 D . 5种5.如图,OAB △绕点O 逆时针旋转80°得到OCD △,若110A ∠=°,40D ∠=°,则∠α的度数是……………………………………………………………………【 】 A .80° B .40° C .50° D .110° 6. 在直角坐标系xOy 中, 点),4(y P 在第四象限内, 且OP 与x 轴正半轴的夹角的正切值是2, 则y 的值是……………………………………………………………【 】A . 2B .8C .-2D .-87. 芜湖某快餐店用米饭加配不同炒菜配制了一批盒饭(每盒米饭只配一种炒菜),配土豆丝炒肉的有25盒,配芹菜炒肉丝的有30盒,配辣椒炒鸡蛋的有10盒,配芸豆炒肉片的有15盒.每盒盒饭的大小、外形都相同,从中任选一盒,不含辣椒的概率是…………………………………………………………………………………【 】 A .78B .67 C .17D .188. 如图所示,平地上一棵树高为6米,两次观察地面上的影子,第一次是当阳光与地面成60°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次标准对数视力0.1 4.0 0.1 4.1 0.14.2第3题图第4题图第5题图长…………………………………………………………………………………【 】 A.3 B.C.D.3-9. 由7个大小相同的正方体搭成的几何体如图所示,则关于它的视图说法正确的是…………………………………………………………………………………【 】 A .主视图的面积最大 B .俯视图的面积最大C .左视图的面积最大D .三个视图的面积一样大 10.如图,在Rt ABC △中,90ACB ∠=°,3BC =,4AC =,AB 的垂直平分线DE 交AB 于点D ,交BC 的延长线于点E ,则CE 的长为 ………………………【 】 A .32 B .76 C .256D .2 二、填空题(本题共4小题,每小题5分,满分20分)11.计算:cos 60°+tan 230°= .12.第十一届全国人民代表大会第五次会议于2012年3月5日至14日在北京人民大会堂召开,出席会议的代表为2978人,用科学记数法表示为 _______________人.(保留二位有效数字)13. 在我们刚刚学过的九年级数学下册课本第11页,用“描点法”画某个二次函数图象时,列了如下表格:根据表格上的信息回答问题:该二次函数在x =9时,y = . 14.如图,在扇形纸片AOB 中,OA =10,∠AOB =36︒,OB 在桌面内的直线l 上.现将此扇形沿l 按顺时针方向旋转(旋转过程中无滑动),当OA 落在l 上时,停止旋转.则点O 所经过的路线长为 . 三、(本题共2小题,每小题8分,满分16分)AD BE第8题图第9题图第10题图得分评卷人l第14题图15. 计算:()()︒+--+30sin 41212.【解】16. 用配方法解方程:x 2+x -2=0. 【解】 四、(本题共2小题,每小题8分,满分16分)17. 如图,在△ABC 中,D 是BC 边上的点(不与B ,C 重合),F ,E 分别是AD 及其延长线上的点,CF ∥BE . 请你添加一个条件,使△BDE ≌△CDF (不再添加其它线段,不再标注或使用其它字母),并给出证明.(1)你添加的条件是: ; (2)【证明】:18. 如图,已知四边形ABCD 是平行四边形,以A 为圆心,AB为半径的圆分别交AD 、BC 于F 、G ,•延长BA 交圆于E ,连接EF 、FG .求证:EF =FG .A CB DFE第17题图 FEDA【证】五、(本题共2小题,每小题10分,满分20分)19. 已知二次函数bx ax y +=2的图象经过点(2,0)、(-1,6).(1)求二次函数的解析式; (2)画出它的图象;(3)写出它的对称轴和顶点坐标. 【解】20. 国家一直把“民生工程”作为工作重点.房价问题是“民生工程”之一,由于房价过快增长,直接影响老百姓安居和社会稳定,为此,国家采取了一系列措施稳定房价,让房价进入正常价位.已知弋江区某开发商在2010年出售的平均房价约为7000元/平方米,经过两次调价后现在出售的平均房价约为5670元/平方米,假设每次调价的百分数相同,求该开发商每次下调房价的百分数. 【解】第19题图六、(本题满分12分)21.如图,△ABC中,AB=AC,∠BAC=108°.(1)只用直尺和圆规作图,首先在BC上截取BD=AB,再作BD的中垂线,分别交AB、BD于点E、F,连结AD,DE(保留作图痕迹).(2)请找出上面所画图形中与△BDE相似的所有三角形,并选择其中一对相似三角形进行证明. 【解】第21题图七、(本题满分12分)22. 今年4月4日是清明节.在“清明节”前夕,我区某校决定从九年级(1)班、(2)班中选一个班去芜湖市烈士陵园扫墓,为了公平,有同学设计了一个方法,其规则如下:在一个不透明的盒子里装有形状、大小、质地等完全相同的3个小球,把它们分别标上数字1、2、3,由(1)班班长从中随机摸出一个小球,记下小球上的数字;在另一个不透明口袋中装有形状、大小、质地等完全相同的4个小球,把它们分别标上数字1、2、3、4,由(2)班班长从口袋中随机摸出一个小球,记下小球上的数字,然后计算出这两个数字的和,若两个数字的和为奇数,则选(1)班去;若两个数字的和为偶数,则选(2)班去.⑴用树状图或列表的方法求九年级(1)班被选去扫墓的概率;⑵你认为这个方法公平吗?若公平,请说明理由;若不公平,请设计一个公平的方法. 【解】八、(本题满分14分)23. 几何模型:条件:如图1,A 、B 是直线l 同旁的两个定点.问题:在直线l 上确定一点P ,使PA PB +的值最小.方法:作点A 关于直线l 的对称点A ',连结A B '交l 于点P ,则P A P B AB'+=的值最小(不必证明).模型应用: (1)如图2,正方形ABCD第22题图A B A 'P l A BP R Q O A B C A BEC P P的边长为2,E 为AB 的中点,P 是AC 上一动点.连结BD ,由正方形对称性可知,B 与D 关于直线AC 对称.连结ED 交AC 于P ,则PB PE +的最小值是___________(填具体数值); (2)如图3,O ⊙的半径为2,点A B C 、、在O ⊙上,OA OB ⊥,60AOC ∠=°,P 是OB 上一动点,求PA PC +的最小值;(3)如图4,45AOB ∠=°,P 是AOB ∠内一点,10PO =,Q R 、分别是OA OB 、上的动点,求PQR △周长的最小值. 【解】2012年九年级数学学业模拟考试参考答案一、选择题 二、填空题 6511、12、3.0×10313、7.5 14、π12 三、15、解:原式=2-1-2+21………………………………………………………… 6分 =21-……………………………………………………………… 8分 16、解:配方,得22221221⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛++x x ……………………………………… 3分即 49212=⎪⎭⎫ ⎝⎛+x …………………………………………………… 4分所以 2321=+x 或2321-=+x . …………………………………………… 6分 解得 11=x ,22-=x . ……………………………………………………… 8分 四、17、(1)DC BD =(或点D 是线段BC 的中点),ED FD =,BE CF =中任选一个即可.…………………………………………………………………………………… 3分(2)以DC BD =为例进行证明: ∵ CF ∥BE ,∴ ∠FCD ﹦∠EBD .………………………………………………………… 5分 又∵DC BD =,∠FDC ﹦∠EDB ,∴ △BDE ≌△CDF .………………………………………………………… 8分18、证明:连结AG . ………………………………………………………………… 1分∵ A 为圆心, ∴AB =AG .∴ ∠ABG =∠AGB . ……………………………………………………………… 3分 ∵ 四边形ABCD 为平行四边形. ∴ AD ∥BC .∴ ∠AGB =∠DAG ,∠EAD =∠ABG . …………………………………………… 5分 ∴ ∠DAG =∠EAD . …………………………………………………………… 6分 ∴ EF =FG . ……………………………………………………………………… 8分五、19、(1)依题意,得:⎩⎨⎧=-=+6024b a b a ,解得:⎩⎨⎧-==42b a …………………… 2分所以,二次函数的解析式为:y=2x2-4x…………………………………… 3分(2)∵y=2x2-4x=2(x2-2x+1-1)=2(x-1) 2-2,由对称性列表如下:……………………………………………………………………………… 5分(图略);………………………………………………………………………… 7分(3)由y=2(x-1) 2-2可知对称轴为直线x=1,顶点坐标为(1,-2)………10分20、解:设该开发商每次下调房价的百分数为x,根据题意,得 7000(1-x)2=5670 ……………………………………… 6分解得x1=1.9>1不合题意,舍去,x2=0.1=10%.…………………………… 9分答:该开发商每次下调房价的百分数是10%. ……………………………… 10分六、21、(1)图如下,作出弧AD得1分,作出BD的中垂线得2分,连结AD,DE得1分. ……………………………………………………………………………… 4分(2)与△BDE相似的三角形有:△ADC和△ABC…………………………… 8分选择△BCA∽△BDE.证明如下:………………………………………………… 9分∵EF是BD的垂直平分线,∴EB=ED.∴∠EDB=∠B.…………………………………………………………………… 10分又AB=AC,∴∠B=∠C.∴∠EDB=∠C.…………………………………………………………………… 11分∴△BCA∽△BDE. ……………………………………………………………… 12分(选择△ACD∽△BDE进行证明,可参照上述给分).七、22、⑴解法一:解法二:………… 4分由上可知,共有12种等可能的结果,其中和为奇数的有6种, ∴ P (和为奇数)=126=21. 即九年级(1)班被选去扫墓的概率为21.…………………………………… 6分 (2)答:这个方法公平.理由如下:…………………………………………… 7分 由⑴可知,在12种等可能的结果中,和为偶数的也有6种, ∴ P (和为偶数)=126=21. …………………………………………………… 9分 ∴ P (和为奇数)= P (和为偶数). …………………………………………… 11分 ∴ 该方法公平. …………………………………………………………………… 12分 八、23、(1)5 …………………………………………………………………… 3分 (2)解:延长AO 交⊙O 于点D ,连接CD 交OB 于P . ………………………… 4分则P A =PD ,P A +PC =PC +PD =CD . ………………………………………………… 5分 连接AC ,∵ AD 为⊙O 的直径, ∴ ∠ACD =90°,AD =4. 又 ∠AOC =60°,∴ ∠ADC =30° . …………………………………………… 6分在Rt △AC D 中,CD =cos 30°・AD =23,……………………………………… 7分 即P A +PC 的最小值为23. ……………………………………………………… 8分(3)解:分别作点P关于OA,OB的对称点E,F,连接EF分别交OA、OB于点Q、R,则△PRQ的周长等于EF. ………………………………………………………10分∵OP=OE=OF=10,∠FOB=∠POB,∠POA=∠AOE,∴∠EOF=2∠AOB又∠AOB=45°, ∴∠EOF=90°.……………………………………………………12分在Rt△EOF中,∵OE=O F=10,∴EF=102,即△PRQ的周长最小值为102. ………………………………………………14分11。
安徽省2012年初中毕业数学学业模拟考试
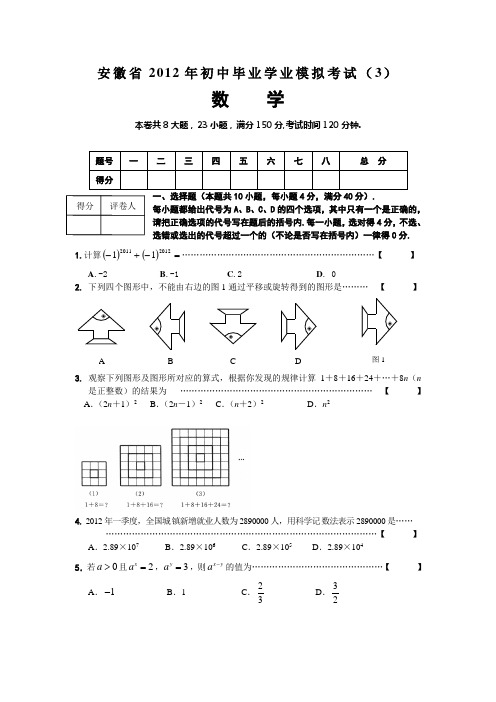
安徽省2012年初中毕业学业模拟考试(3)数学本卷共8大题,23小题,满分150分,考试时间120分钟.题号一二三四五六七八总分得分一、选择题(本题共10小题,每小题4分,满分40分).每小题都给出代号为A、B、C、D的四个选项,其中只有一个是正确的,请把正确选项的代号写在题后的括号内.每一小题,选对得4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分. 1.计算()()=-+-2012201111…………………………………………………………【】A.-2B.-1C.2D. 02.下列四个图形中,不能由右边的图1通过平移或旋转得到的图形是………【】3.观察下列图形及图形所对应的算式,根据你发现的规律计算1+8+16+24+…+8n(n是正整数)的结果为…………………………………………………………【】A.(2n+1)2B.(2n-1)2C.(n+2)2D.n24. 2012年一季度,全国城镇新增就业人数为2890000人,用科学记数法表示2890000是………………………………………………………………………………………【】A.2.89×107B.2.89×106 C.2.89×105 D.2.89×1045.若0a>且2xa=,3ya=,则x ya-的值为………………………………………【】A.1-B.1 C.23D.32得分评卷人A B C D 图16. 如图,△ABC 的三个顶点分别在正方形网格的格点上,则tan ∠C 的值是……【 】 A .34B .43C .45D .547. 已知抛物线y =x 2+x -1经过点P (m ,11),则代数式m 2+m +2000的值为 ………【 】 A .2010B .2011C .2012D .20138. 如图所示,在矩形ABCD 中,垂直于对角线BD 的直线l ,从点B 开始沿着线段BD 匀速平移到D .设直线l 被矩形所截线段EF 的长度为y ,运动时间为t ,则y 关于t 的函数的大致图象是 ……………………………………………………………………【 】9. 如图,将平面直角坐标系中的△AOB 绕点O 顺时针旋转90°得△A ′OB ′.已知∠AOB =60°,∠B =90°,AB =3,则点B ′的坐标是………………………………………………【 】 (A )31,22⎛⎫ ⎪ ⎪⎝⎭ (B )33,22⎛⎫ ⎪ ⎪⎝⎭ (C )33,22⎛⎫ ⎪ ⎪⎝⎭ (D )13,22⎛⎫⎪ ⎪⎝⎭10.如图大正方形中有2个小正方形,如果它们的面积分积是S 1,S 2,那么S 1,S 2的大小关系是…………………………………………………………… 【 】A 、S 1>S 2B 、S 1=S 2C 、S 1>S 2D 、S 1,S 2大小关系不能确定二、填空题(本题共4小题,每小题5分,满分20分)A .OytB .OytC .OytD .Oyt第8题图得分评卷人第10题图′′A B y xABO第9题图 第6题图11.在体育中招考试的跳绳项目考试中,我校两个小组共8位同学的成绩分别如下:(单位:个/分钟)154、187、173、205、197、177、185、188,则这组数据的中位数是 . 12.计算a 22a-8a 3 (a >0)= . 13. 在△ABC 中,AB =6,AC =8,BC=10,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M为EF 中点,则AM 的最小值为 ; 14.数学家们在研究15、12、10这三个数的倒数时发现:111112151012-=-.因此就将具有这样性质的三个数称之为调和数,如6、3、2也是一组调和数.现有一组调和数:x 、5、3(x >5),则x 的值是 .三、(本题共4小题,每小题4分,满分16分)15. 计算或化简:(1)计算21)2011(60tan 3201-+-+--π. (2)化简: 2)1(111-÷⎪⎭⎫ ⎝⎛--+x x x x x 【解】 【解】16. (1)求不等式组1184 1.x x x x --⎧⎨+>-⎩≥,的整数解; 【解】得分评卷人第13题图(2)解一元二次方程:0142=+-x x (配方法) 【解】 四、(本题共2小题,每小题8分,满分16分)17. 某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)25 26 21 17 28 26 20 25 26 30 20 21 20 26 30 25 21 19 28 26 (1)请根据以上信息完成下表:销售额(万元) 17 19 20 21 252628 30 频数(人数)113322(2)上述数据中,众数是 万元,中位数是 万元,平均数是 万元; (3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由. 【解】18. 如图,在菱形ABCD 中,E 是AB 的中点,且DE ⊥AB .(1)求∠ABD 的度数;(2)若菱形的边长为2,求菱形的面积. 【解】五、(本题共2小题,每小题10分,满分20分)得分评卷人得分评卷人ABCDE 第18题图A EDFG19. 如图,已知反比例函数ny x=(n >0)与一次函数(0)y kx b k =+≠相交于A 、B 两点,AC ⊥x 轴于点C .若OC=1,且tan ∠AOC =3.点D 与点C 关于原点O 对称。
安徽省2012年中考数学模拟测试(一)

第3题图αD CBA P第8题2012年安徽省中考数学模拟试题一、选择题(本大题共10小题,每题4分,共40分)1.下列计算正确的是 ( )A .030=B .33-=--C .331-=- D .39±=2. 下列二次根式中属于最简二次根式的是( ) A .44+aB .48C .14D .b a3.如图所示零件的左视图是( )A .B .C .D .4. 一副三角板,如图所示叠放在一起,则图中∠α的度数是( ) A 、 75° B 、60° C 、65° D 、55°5. 若两圆的圆心距等于7,半径分别是R 、r ,且R 、r 是关于x 的方程ax ax 2560-+=的两个根,则这两圆的位置关系是()A. 相离B. 相交C. 内切D. 外切6. 如右图,某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( ) A.7、7 B.8、7.5 C.7、7.5 D. 8、6.57. 如右图,⊙O 中,弦AB 的长为6cm ,圆心O 到AB 的距离为4cm , 则⊙O 的半径长为( )A .3cmB .4cmC .5cmD .6cm8. 如图,矩形ABCD 中,1AB =,2AD =,M 是CD 的中点,点P 在矩形的边上沿A B C M →→→运动,则APM △的面积y 与点P 经过的路程x 之间的函数关系用图象表示大致是下图中的 ( )A. B. C. D. 9. 图①、图②、图③是三种方法将6根钢管用钢丝捆扎的截面图,三种方法所用的钢丝长分别为a,b,c ,则a, b, c,的大小关系为( )。
A 、a=b >c B. a=b=c C. a<b<c D. a>b>c10. 已知二次函数2y ax bx c =++的图象如图所示,有以下结论:①0a b c ++<;②1a b c -+>;③0abc >;④420a b c -+<;⑤1c a ->( )A .①②B . ①③④C .①②③⑤D .①②③④⑤二、填空题 (本大题共4小题,每题5分,共20分)11.一个正n 边形的外角和比内角和小360度,则n=___________. 12.分解因式:322363x x y xy -+=___________________.13. 已知圆锥的底面直径为4,母线长为6,则它的侧面展开图的圆心角为____________ 14. 如图,n +1个边长为2的等边三角形有一条边在同一直线上,设△211B D C 的面积为1S ,△322B D C 的面积为2S ,…,△1n n n B D C +的面积为n S ,则2S = ____;n S =____ ______(用含n 的式子表示).三、(本大题共2小题,每小题8分,共16分)15.计算:60tan 34201031(01--+--16.解方程:212423=+--x x x四(本大题共2小题,每小题8分,满分16分)17. 如图,在网格中有一个四边形图案.(1)请你画出此图案绕点O 顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错; (2)若网格中每个小正方形的边长为l ,旋转后点A 的对应点依次为A 1、A 2、A 3,求四边形AA 1A 2A 3的面积。
2012年安徽省中考数学试卷-答案
安徽省2012年初中毕业学业考试数学答案解析一、选择题 1.【答案】A【解析】设这个数为x ,由题意得:(3)0x +-=30x -=3x =。
【提示】设这个数为x ,根据题意可得方程(3)0x +-=,再解方程即可。
【考点】有理数的加法 2.【答案】C【解析】A .主视图是长方形,故此选项错误;B .主视图是长方形,故此选项错误;C .主视图是三角形,故此选项正确;D .主视图是正方形,中间还有一条线,故此选项错误;【提示】主视图是从几何体的正面看所得到的图形,根据主视图所看的方向,写出每个图形的主视图及可选出答案。
【考点】简单几何体的三视图3.【答案】B【解析】原式3236(2)()8x x =-=-。
【提示】根据积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘;幂的乘方法则:底数不变,指数相乘进行计算即可。
【考点】幂的乘方与积的乘方 4.【答案】D【解析】A .2m n +不能分解因式,故本选项错误;B .21m m -+不能分解因式,故本选项错误;C .2m n -不能分解因式,故本选项错误;D .221m m -+是完全平方式,故本选项正确。
【提示】根据多项式特点和公式的结构特征,对各选项分析判断后利用排除法求解。
【考点】因式分解的意义5.【答案】B【解析】3月份的产值是a 万元,则:4月份的产值是(110%)x a -万元,5月份的产值是(115%)(110%)a +- 万元。
【提示】根据3月份的产值是a 万元,用a 把4月份的产值表示出来(110%)a -,进而得出5月份产值列 出式子(110%)(115%)a -⨯+万元,即可得出选项。
【考点】列代数式【提示】将分母化为同分母,通分,再将分子因式分解,约分即可。
【考点】分式的加减法 ABC S =正八边形中间是边长为a 的正方形,∴阴影部分的面积为:2222a a a +=。
【提示】根据正八边形的性质得出45CAB CBA ∠=∠=︒,进而得出BC AC ==,再利用正八边形周围四个三角形的特殊性得出阴影部分面积即可。
2012年安徽中考数学真题卷含答案解析
2012年安徽省初中毕业学业考试数学7A(满分:150分 时间:120分钟)第Ⅰ卷(选择题,共40分)一、选择题(本大题共10小题,每小题4分,满分40分)1.下面的数中,与-3的和为0的是( ) A.3 B.-3 C.13 D.-132.下面的几何体中,主(正)视图为三角形的是( )3.计算(-2x 2)3的结果是( ) A.-2x 5B.-8x 6C.-2x 6D.-8x 54.下面的多项式中,能因式分解的是( ) A.m 2+n B.m 2-m+1C.m 2-nD.m 2-2m+15.某企业今年3月份产值为a 万元,4月份比3月份减少了10%,5月份比4月份增加了15%.则5月份的产值是( )A.(a-10%)(a+15%)万元B.a(1-10%)(1+15%)万元C.(a-10%+15%)万元D.a(1-10%+15%)万元6.化简x2x -1+x 1-x的结果是( ) A.x+1 B.x-1 C.-x D.x7.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域.设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )A.2a 2B.3a 2C.4a 2D.5a 28.给甲、乙、丙三人打电话,若打电话的顺序是任意的,则第一个打给甲的概率为( )A.16B.13C.12D.239.如图,A 点在半径为2的☉O 上,过线段OA 上的一点P 作直线l,与☉O 过A 点的切线交于点B,且∠APB=60°.设OP=x,则△PAB 的面积y 关于x 的函数图象大致是( )10.在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( )A.10 B .4√5C.10或4√5D.10或2√17第Ⅱ卷(非选择题,共110分)二、填空题(本大题共4小题,每小题5分,满分20分)11.2011年安徽省棉花产量约378 000吨,将378 000用科学记数法表示应是 . 12.甲、乙、丙三组各有7名成员,测得三组成员体重数据的平均数都是58,方差分别为s 甲2=36,s 乙2=25.4,s 丙2=16.则数据波动最小的一组是 .13.如图,点A、B、C、D在☉O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=°.14.如图,P是矩形ABCD内的任意一点,连结PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4.给出如下结论:①S1+S4=S2+S3②S2+S4=S1+S3③若S3=2S1,则S4=2S2④若S1=S2,则P点在矩形的对角线上其中正确结论的序号是(把所有正确结论的序号都填在横线上).三、解答题(本大题共9小题,满分90分)15.(本题满分8分)计算:(a+3)(a-1)+a(a-2).16.(本题满分8分)解方程:x2-2x=2x+1.17.(本题满分8分)在由m×n(m×n>1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数f.(1)当m、n互质(m、n除1外无其他公因数)时,观察下列图形并完成下表:m n m+n f123213432354257347猜想:当m、n互质时,在m×n的矩形网格中,一条对角线所穿过的小正方形的个数f与m、n 的关系式是(不需证明);(2)当m、n不互质时,请画图验证你猜想的关系式是否仍然成立.7B18.(本题满分8分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.(1)画出一个格点△A1B1C1,使它与△ABC全等且A与A1是对应点;(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.19.(本题满分10分)如图,在△ABC中,∠A=30°,∠B=45°,AC=2√3.求AB的长.20.(本题满分10分)九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.月均用水量x(t)频数(户)频率0<x≤560.125<x≤100.2410<x≤15160.3215<x≤20100.2020<x≤25425<x≤3020.04请解答以下问题:(1)把上面的频数分布表和频数分布直方图补充完整;(2)求月均用水量不超过15t的家庭数占被调查家庭总数的百分比;(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?21.(本题满分12分)甲、乙两家商场进行促销活动.甲商场采用“满200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元;…….乙商场按顾客购买商品的总金额打6折促销.(1)若顾客在甲商场购买了510元的商品,付款时应付多少钱?(2)若顾客在甲商场购买商品的总金额为x(400≤x<600)元,优惠后得到商家的优惠率为p(p=优惠金额),写出p与x之间的函数关系式,并说明p随x的变化情况;购买商品的总金额(3)品牌、质量、规格等都相同的某种商品,在甲、乙两商场的标价都是x(200≤x<400)元,你认为选择哪家商场购买该商品花钱较少?请说明理由.22.(本题满分12分)如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等.设BC=a,AC=b,AB=c.(1)求线段BG的长;(2)求证:DG平分∠EDF;(3)连结CG,如图2,若△BDG与△DFG相似,求证:BG⊥CG.23.(本题满分14分)如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围);(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;(3)若球一定能越过球网,又不出边界,求h的取值范围.2012年安徽省初中毕业学业考试一、选择题1.A互为相反数的两数之和为0,-3的相反数是3,故选A.2.C圆柱的主视图是长方形;正方体的主视图是正方形;圆锥的主视图是三角形;三棱柱的主视图是含有实线的长方形.综上所述应选C.3.B(-2x2)3=(-2)3(x2)3=-8x6,故选B.4.D A、B、C三个选项中的多项式既不含有公因式,又不能利用平方差、完全平方公式进行分解,而m2-2m+1=(m-1)2,故选D.5.B4月份的产值可以表示为a×(1-10%)万元,5月份的产值可以表示为a×(1-10%)(1+15%)万元,故选B.6.D x2x-1+x1-x=x2x-1-xx-1=x2-xx-1=x(x-1)x-1=x,故选D.7.A n边形的内角和公式为(n-2)·180°,所以正八边形的每个内角均为(8-2)·180°8=135°,由此易得外围阴影的三角形均为斜边长为a的等腰直角三角形,每个这样的三角形的面积均为12(a×sin45°)2=14a2,所以四个三角形的面积和为4×14a2=a2;中间正方形的面积为a2,所以阴影部分的面积为2a2,故选A.评析本题综合考查正多边形的性质,多边形的内角和,三角函数及三角形、正方形的面积等知识,利用三角函数知识求得等腰直角三角形的直角边长是关键,属中等难度题.8.B第一个电话可以打给甲或乙或丙,事件有三个等可能的结果,所以第一个打给甲的概率为13.9.D因为AB是☉O的切线,所以OA⊥AB,在Rt△APB中,∠APB=60°,AP=2-x,所以AB=√3(2-x),S△PAB=12AP·AB=12·√3·(2-x)2=√32(2-x)2=√32x2-2√3x+2√3(0≤x<2),根据解析式可判断选项D正确.评析本题是圆的切线、三角函数及函数图象的综合应用题,以圆的知识为背景,应用三角函数的知识求得函数解析式,并利用函数解析式及自变量的取值范围找到对应的函数图象,设计巧妙,知识点覆盖面广,属难度较大题.10.C根据题意复原直角三角形可能有以下两种情况:根据题目条件知,点M、N分别是三角形斜边的中点,由相似三角形的性质可以得到如图所示的各线段的长度,从而由勾股定理得到三角形的斜边长是10或4√5.评析本题考查相似三角形的判定及性质,同时考查学生的动手操作,对图形的空间想象等能力,题目难点多,对学生的要求较高,难度大.二、填空题11.答案 3.78×105解析科学记数法即将数字写成a×10n(1≤|a|<10,n为整数)的形式,378000=3.78×105.12.答案丙组解析方差的大小反映一组数据的波动大小,方差越大,波动越大,方差越小,波动越小,因为丙组数据的方差最小,所以丙组数据的波动最小.13.答案60解析四边形OABC是平行四边形,所以∠AOC=∠B;∠AOC和∠D是同弧所对圆心角和圆周角,所以∠D=12∠AOC;由题意得∠D+∠B=180°,所以∠D=60°;连结OD,△AOD和△COD 均为等腰三角形,所以∠CDO=∠DCO,∠ADO=∠DAO.综上所述,∠OAD+∠OCD=∠D=60°.14.答案②④解析因为△APB和△CPD的高线和恰好等于AD的长,△APD和△CBP的高线和恰好等于AB的长,易得S1+S3=12S ABCD,S2+S4=12S ABCD,S1+S3=S2+S4,故②正确,①③错误;若S1=S2,则S1+S3=S2+S3=12S ABCD,所以P点在矩形的对角线上,故④正确.评析本题利用三角形、矩形之间的面积关系考查学生整体代入求值的思想,利用整体求值是解决本题的关键,属中等难度题.三、解答题15.解析原式=a2+2a-3+a2-2a(4分)=2a2-3.(8分)16.解析方程可化为x2-4x-1=0.(2分)∵Δ=(-4)2-4×1×(-1)=20,∴x=4±√202=2±√5,∴x1=2-√5,x2=2+√5.(8分)17.解析(1)表中填6;6.(2分)关系式为f=m+n-1.(4分)注:若猜想出的是其他关系式,只要这个关系式对表中5种情况都成立就可酌情给分.(2)当m、n不互质时,关系式f=m+n-1不成立.例如:当m=2,n=2时,图形如图.(6分)对角线所穿过的小正方形的个数f=2,而m+n=4,等式f=m+n-1不成立.(8分)评析本题属于探究规律问题,通过简单图形总结发现其中的规律是解决问题的关键,考查学生的观察、归纳、分析问题的能力,难度较大.18.解析(1)本题是开放题,答案不唯一.图中给出了两个满足条件的三角形,其他解答只要正确就相应给分.(4分)(2)D点如图所示.(6分)AD是由AB绕A点逆时针旋转90°而得到的,或AD是由AB绕A点顺时针旋转270°而得到的.(8分)19.解析作CD⊥AB于D点(如图).在Rt△ACD中,∠A=30°,AC=2√3,所以AD=ACcos30°=2√3×√3=3,2CD=ACsin30°=√3.(6分)在Rt△BCD中,∠B=45°,所以BD=CD=√3,∴AB=AD+CD=3+√3.(10分)20.解析(1)表中填12;0.08.补全的图形如图.(4分)(2)0.12+0.24+0.32=0.68.即月均用水量不超过15t的家庭数占被调查的家庭总数的68%.(7分)(3)(0.08+0.04)×1000=120.所以根据调查数据估计,该小区月均用水量超过20t的家庭大约有120户.(10分)21.解析(1)510-200=310(元),付款时应付310元.(3分)(2)p与x之间的函数关系式为p=200x.当400≤x<600时,p随x的增大而减小.(6分)(3)设在甲、乙两家商场购买该商品实付款分别为y1、y2元,则y1=x-100,y2=0.6x,y1-y2=0.4x-100=0.4(x-250).(9分)当200≤x<250时,y1<y2,选择甲商场花钱较少;当x=250时,y1=y2,选择两家商场花钱相同;当250<x<400时,y1>y2,选择乙商场花钱较少.(12分)评析本题考查学生构建函数模型,通过函数与方程、不等式的关系对实际问题进行优化设计的能力.22.解析(1)∵△BDG与四边形ACDG的周长相等,且BD=DC,∴BG=AG+AC=12(AB+AC)=12(b+c).(3分)(2)证明:∵点D、F分别是BC、AB的中点,∴DF=12AC=12b.又∵FG=BG-BF=12(b+c)-12c=12b,∴DF=FG,∴∠FDG=∠FGD.(6分)∵点D、E分别是BC、AC的中点,∴DE∥AB,∴∠EDG=∠FGD,∴∠FDG=∠EDG,即DG平分∠EDF.(8分)(3)证明:∵△BDG与△DFG相似,∠DFG>∠B,∠BGD=∠DGF(公共角),∴∠B=∠FDG.由(2)知∠FGD=∠FDG,∴∠FGD=∠B,∴DG=BD.(10分)∵BD=DC,∴DG=BD=DC,∴B、G、C三点在以BC为直径的圆周上,∴∠BGC=90°,即BG⊥CG.(12分)评析本题考查三角形的中位线、平行线的性质及判定以及三角形相似的性质等知识,对学生的逻辑推理能力有较高的要求,属较难题.23.解析(1)h=2.6时,y=a(x-6)2+2.6.由其图象过点(0,2),得36a+2.6=2,解得a=-160.所以y=-160(x-6)2+2.6.(3分)(2)当h=2.6时,由(1)知y=-160(x-6)2+2.6.当x=9时,y=-160(9-6)2+2.6=2.45>2.43,所以球能越过球网;(6分)由-160(x-6)2+2.6=0,x>0,得x=6+√156>18.或当x=18时,y=-160(18-6)2+2.6=0.2>0,所以球落地时会出界.(8分)(3)根据题设知y=a(x-6)2+h.由图象经过点(0,2),得36a+h=2,①由球能越过球网,得9a+h>2.43,②由球不出边界,得144a+h≤0.③(11分)由①②③解得h≥83,所以h的取值范围是h≥83.(14分)评析本题以实际问题为背景,考查二次函数与方程、不等式的综合应用,并应用二次函数的知识解决实际问题,对学生的能力要求较高,题目难度较大.解决本题的关键在于正确理解球是否出界与二次函数的对应关系.。
2012年安徽中考数学模拟试题及参考答案
2012年安徽最新模拟数学试题及答案一.选择题(本大题共10个小题,每小题4分,共40分)在每小题给出的四个选项中,只有一个选项符合题意,把所选项前的标号填在题后的括号内1.-2的相反数是()A、B、-C、-2 D、22.x-(2x-y)的运算结果是()A、-x+yB、-x-yC、x-yD、3x-y3.“神舟”五号载人飞船,绕地球飞行了14圈,共飞行约590200km,这个飞行距离用科学计数法表示为()A、59.02×104kmB、0.5902×106kmC、5.902×105kmD、5.902×104km 4.下列多项式中,能用提公因式法分解因式的是()A、x2-yB、X2+2xC、X2+y2D、x2-xy+y25.方程x2-3x+1=0的根的情况是()A、有两个不相等的实数根B、有两个相等的实数根C、没有实数根D、只有一个实数根6.如图,扇子的圆心角为xº,余下扇形的圆心角是yº,x与y的比通常按黄金比来设计,这样的扇子外形较美观。
若取黄金比为0.6,则x为()A、216B、135C、120D、1087.购某种三年期国债x元,到期后可得本息和y元,已知y=kx,A、kB、k/3C、k-1D、(k-1)/38.如图,某种牙膏上部圆的直径为3cm,下部底边的长度为4.8cm。
现要整理长方体的牙膏盒,牙膏盒的上面是正方形。
以下列数据作为正方形边长整理牙膏盒,既节省材料又方便取放的是(取1.4)()A、2.4cmB、3cmC、3.6cmD、4.8cm8.如图,O是正六边形ABCDE的中心,下列图形中可由△OBC平移得到的是(华东版教材实验区试题)()A 、△OCDB 、△OABC 、△OAFD 、OEF9.圆心都在x 轴上的两圆有一个公共点(1,2),那么这两圆的公切线有 ( ) A 、1条 B 、2条 C 、3条 D 、4条10.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓缓爬行的乌龟,骄傲起来,睡了一觉。
2012年安徽中考数学试题及答案
2012年安徽省中考数学试卷一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出代号为A、B、C、D的四个选项,其中只有一个是正确的,请把正确选项的代号写在题后的括号内,每一小题选对得4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分.1.(2012•安徽)下面的数中,与﹣3的和为0的是()A.3B.﹣3C.D.2.(2012•安徽)下面的几何体中,主(正)视图为三角形的是()A.B.C.D.3.(2012•安徽)计算(﹣2x2)3的结果是()A.﹣2x5B.﹣8x6C.﹣2x6D.﹣8x54.(2012•安徽)下面的多项式中,能因式分解的是()A.m2+n B.m2﹣m+1C.m2﹣n D.m2﹣2m+15.(2012•安徽)某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份的产值是()A.(a﹣10%)(a+15%)万元B.a(1﹣10%)(1+15%)万元C.(a﹣10%+15%)万元D.a(1﹣10%+15%)万元6.(2012•安徽)化简的结果是()A.x+1B.x﹣1C.﹣x D.x7.(2012•安徽)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为()A.2a2B.3a2C.4a2D.5a28.(2012•安徽)给甲乙丙三人打电话,若打电话的顺序是任意的,则第一个打电话给甲的概率为()A.B.C.D.9.(2012•安徽)如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线ℓ,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是()A.B.C.D.10.(2012•安徽)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是()A.10B.C.10或D.10或二、填空题(本大题共4小题,每小题5分,满分20分)11.(2012•安徽)2011年安徽省棉花产量约378000吨,将378000用科学记数法表示应是_________.12.(2012•安徽)甲乙丙三组各有7名成员,测得三组成员体重数据的平均数都是58,方差分别为,,,则数据波动最小的一组是_________.13.(2012•安徽)如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD= _________°.14.(2012•安徽)如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1+S2=S3+S4;②S2+S4=S1+S3;③若S3=2S1,则S4=2S2;④若S1=S2,则P点在矩形的对角线上.其中正确的结论的序号是_________(把所有正确结论的序号都填在横线上).三、(本大题共2小题,每小题8分,满分16分)15.(2012•安徽)计算:(a+3)(a﹣1)+a(a﹣2)16.(2012•安徽)解方程:x2﹣2x=2x+1.四、(本大题共2小题,每小题8分,满分16分)17.(2012•安徽)在由m×n(m×n>1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数f,(1)当m、n互质(m、n除1外无其他公因数)时,观察下列图形并完成下表:m n m+n f1 2 3 21 3 4 32 3 5 42 4 73 5 7猜想:当m、n互质时,在m×n的矩形网格中,一条对角线所穿过的小正方形的个数f与m、n的关系式是_________(不需要证明);(2)当m、n不互质时,请画图验证你猜想的关系式是否依然成立.18.(2012•安徽)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.(1)画出一个格点△A1B1C1,并使它与△ABC全等且A与A1是对应点;(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.五、(本大题共2小题,每小题10分,满分20分)19.(2012•安徽)如图,在△ABC中,∠A=30°,∠B=45°,AC=,求AB的长.20.(2012•安徽)九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.请解答以下问题:月均用水量x(t)频数(户)频率0<x≤5 6 0.125<x≤10 0.2410<x≤15 16 0.3215<x≤20 10 0.2020<x≤25 425<x≤30 2 0.04(1)把上面的频数分布表和频数分布直方图补充完整;(2)若该小区用水量不超过15t的家庭占被调查家庭总数的百分比;(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?六、(本题满分12分)21.(2012•安徽)甲、乙两家商场进行促销活动,甲商场采用“买200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元;…,乙商场按顾客购买商品的总金额打6折促销.(1)若顾客在甲商场购买了510元的商品,付款时应付多少钱?(2)若顾客在甲商场购买商品的总金额为x(400≤x<600)元,优惠后得到商家的优惠率为p(p=),写出p与x之间的函数关系式,并说明p随x的变化情况;(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(200≤x<400)元,你认为选择哪家商场购买商品花钱较少?请说明理由.七、(本题满分12分)22.(2012•安徽)如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG 的周长相等,设BC=a、AC=b、AB=c.(1)求线段BG的长;(2)求证:DG平分∠EDF;(3)连接CG,如图2,若△BDG与△DFG相似,求证:BG⊥CG.八、(本题满分14分)23.(2012•安徽)如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;(3)若球一定能越过球网,又不出边界,求h的取值范围.2012年安徽省中考数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出代号为A、B、C、D的四个选项,其中只有一个是正确的,请把正确选项的代号写在题后的括号内,每一小题选对得4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分.1.(2012•安徽)下面的数中,与﹣3的和为0的是()A.3B.﹣3C.D.考点:有理数的加法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年安徽省中考摸底考试卷数 学 试 题考生注意:本卷共八大题,计23小题,满分150分,考试时间120分钟 一、选择题(本大题共10小题,每小题4分,满分40分)1、2-的相反数是…………………………………………………( )A 、2B 、-2C 、4D 2、2009年我省GDP 突破万亿达到10052.9亿元,这意味着安徽已经成为全国GDP 万亿俱乐部的第14个成员,10052.9亿元用科学记数法表示为(保留三个有效数字)………………( )元 A 、121.0010⨯ B 、121.00510⨯ C 、121.0110⨯ D 、121.0052910⨯3、如图,把矩形直尺沿直线断开并错位,点E 、D 、B 、F 在同一条直线上,若∠ADE=125°,则∠DBC 的度数为……………………………………………………………………( ) A 、55° B 、65° C 、125° D 、135°4、如图是一个几何体的三视图,根据图中标注的数据求出这个几何体的体积为……( ) A 、24π B 、32π C 、36π D 、48π5、小明正在玩飞镖游戏,如果小明将飞镖随意投中如图所示的正方体木框中,那么投中阴影部分的概率为……………………………………………………………………………( ) A 、16 B 、18 C 、19 D 、5186、已知⊙O 1和⊙O 2的半径是方程2560x x -+=两根,且两圆的圆心距等于5,则⊙O 1和⊙O 2的位置是……………………………………………………………………………( ) A 、相交 B 、外离 C 、外切 D 、内切7、将量角器按如图所示的方式放置在三角形纸板上,使点C 在半圆上,点A 、B 的读数分别为86°、30°,则∠ACB 的大小为………………………………………………( )A 、15°B 、28°C 、29°D 、34°8、如图,CD 是平面镜,光线从A 点出发经CD 上点E 反射照到B 点,若入射角为α,AC ⊥CD ,BD ⊥CD ,且AC=3,BD=6,CD=12,则tan α值为…………………( ) A 、35 B 、43 C 、45 D 、349、如图所示是二次函数2y ax bx c =++图象的一部分,图象过A 点(3,0),对称轴为1x =,给出四个结论:①240b ac ->;②20a b +=;③0a b c ++=;④当1x =-或3x =时,函数y的值都等于0。
其中正确结论是…………………………………………………( ) A 、②③④ B 、①③④ C 、①②③ D 、①②④10、如图,在中,AB=6,AD=9,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,BG ⊥AE ,垂足为G ,BG=4,则△CEF 的周长为……………………( ) A 、8 B 、9.5 C 、10 D 、11.5二、填空题(本大题共4小题,每小题5分,满分20分) 11、请将右边的英语翻译成汉语。
____________________12..___________________________13、如图,AB 是⊙O 的直径,∠BAC=30°,点P 在线段OB 上运动(包括O 点、B 点)。
设∠ACP=x ,则x 的取值范围是_____________________。
14、给出下列两条抛物线:221y x x =++,2241y x x =++请尽可能多地找出这两条抛物线的共同点:(至少三条)①___________________②__________________③_________________。
三、(本大题共2小题,每小题8分,满分16分)15、计算:0|3|tan30(2010)π--16、如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到间圆O’,与AB交于点P。
(1)求AP的长。
(2)求图中阴影部分的面积(结果保留π)。
四、(本大题共2小题,每小题8分,满分16分)17、2009年6月1日法航客机失事引起全球高度关注,为调查失事原因,巴西军方派出搜救船在失事海域搜寻飞机残骸和黑匣子(如图)。
在海面A处搜救船测得俯角为30°正前方的海底有黑匣子信号发出,继续直线航行2千米后再次在B处测得俯角为45°正前方的海底有黑匣子信号发出,求海底C处距离≈≈)1.73218、如图所示的网格中,每个小方格都是边长为1的小正方形,B点的坐标为:B(-1,-1)。
(1)把△ABC绕点C按顺时针旋转90°后得到△A1B1C1,请画出这个三角形并写出点B1的坐标;(2)以点A为位似中心放大△ABC,得到△A2B2C2,使放大前后的面积之比为1︰4请在下面网格内画出△A2B2C2。
五、(本大题共2小题,每小题10分,满分20分)19、如图所示,在正方形ABCD 中,AB=2,两条对角线相交于点O ,以OB 、OC 为邻边作第.1.个正方形....OBB 1C ,对角线相交于点A 1;再以A 1B 1、A 1C 为邻边作第.2.个正方形....A 1B 1C 1C 对角线相交于点O 1;再以O 1B 1、O 1C 1为邻边作第.3.个正方形....O 1B 1B 2C 1,……依此类推。
(1)求第1个正方形OBB 1C 的边长1a 和面积S 1;(2)写出第2个正方形A 1B 1C 1C 和第3个正方形的边长2a ,3a 和面积S 2,S 3;(3)猜想第n 个正方形的边长n a 和面积S n 。
(不需证明)20、大家看过中央电视台“购物街”节目吗?其中有一个游戏环节是大转轮比赛,转轮上平均分布着5、10、15、20一直到100共20个数字。
选手依次转动转轮,每个人最多有两次机会。
选手转动的数字之和最大不超过100者为胜出;若超过100则成绩无效,称为“爆掉”。
(1)某选手第一次转到了数字5,再转第二次,则他两次数字之和为100的可能性有多大?(2)现在某选手第一次转到了数字65,若再转第二次了则有可能“爆掉”,请你分析“爆掉”的可能性有多大?六、(本题满分12分)21、某旅游公司取得了2011年上海世博会门票销售权,每张普通票的成本为100元,投放市场进行试销发现:销售票价x(元/张)与每天销售量y(张)之间满足如图所示关系。
(1)求出与之间的函数关系式;(2)写出每天的利润W与销售票价之间的函数关系式,若你是公司负责人,会将票价定为多少,来保证公司每天获得的利润最大,最大利润是多少?七、(本题满意分12分)22、把两个含有45°角的直角三角板如图1放置,点D在BC上,连结BE、AD,AD的延长线交于BE于点F。
(1)问:AD与BE在数量上和位置上分别有何关系?说明理由。
(2)若将45°角换成30°如图2,AD与BE在数量和位置上分别有何关系?说明理由。
(3)若将图2中两个三角板旋转成图3、图4、图5的位置,则(2)中结论是否仍然成立,选择其中一种图形进行说明。
八、(本题满分14分)23、受我国经济刺激政策和全球经济复苏的影响,2009年我国房地产市场开始回暖,下图反映08年7月至09年6月我国70个大城市房价同比增长率变化情况(注:同比增长率是指房价与上一年同时期相比增长的百分比)(1)看图分析:2008年7月房价比2007年7月的房价;2008年8月的房价比2008年7月的房价;(填“高”、“相等”、“低”、“不能确定”。
)(2)从图上可以看出:同比增长率与月份之间折线图可以“近似”的看成一段抛物线,以2008年7月的坐标为(0,7.0)建立平面直角坐标系。
请你根据图中信息求出同比增长率与月份之间“近似”的函数关系式,并据此推算2009年9月同比增长率会达到多少?(3)若从2008年7月到2008年9月房价持平,求从2009年7月开始到2009年9月房价月平均增长率。
(结果精确到0.0122.83≈22.47≈)参考答案及评分标准一、选择题(每小题4分)1、A2、C3、B4、A5、D6、C7、B8、B9、D 10、A 二、填空题(每小题5分)11、我爱我家(意思对即可)12、答案不唯一;13、30°≤x ≤90°14、答案不唯一,例①开口方向②对称轴相同③与y 轴的交点相同④x=1时函数值相同,等等 三、15、解原式=3213--…………………………………6分 =1………………………………………………………8分16、解:(1)由题意可得:∠O ’BA=45°,O ’P=O ’B ,∴△O ’PB 是等腰直角三角形,∴’ ∴AP=AB -BP=20-4分 (2)阴影部分面积为:'''111001010255042O PB O A P S S ππ+=⨯⨯+⨯⨯=+ 扇形………………………………8分四、17、(1)过C 作CD 垂直AB 于D 点,………………………1分设CD 为x ,由图得:在Rt △ACD 与Rt △BCD 中,∠CAD=30°,∠CBD=45°,AC=CD=2x ,AD=AB+CD=2+x ,∴在Rt △ACD 中有:222(2)(2)x x x ++=………………………6分∴1x =(舍去)1 2.732x ≈或答:海底C 处距海面2.732千米。
…………………………………8分 18、解:(1)如图:B (5,5)…………………4分(2)如图所示:……………………………………8分19、解:(1)正方形AABCD 中,AB=2,∴∴112a BO BD ===221S BO ==…………………………3分(2)21a =;3a =,21S =;212S =…………………………………7分(3)n a =;212n n S -=……………………………………10分 20、解:(1)由题可得:则第二次必须转到95,总共有20个数字,∴此时的可能性为120………………………………………………4分 (2)由题可得:转到数字35以上就会“爆掉”,有13种情况,总共有20个数字, ∴此时的可能性为1320…………………………………………………10分 21、解:(1)由图可得:可设(0)y kx b k =+≠图象经过(130,50)和(150,30)代入求得:1,180k b =-= 即:180y x =-+……………………………5分(2)2(180)(100)28018000(140)1600W x x x x x =-+-=-+-=--+当140x =元时,W 最大值为1600元。
