传感器实验报告应变片测量
应变片 实验报告 灵敏
应变片实验报告灵敏引言应变片是一种常用于测试物体受力情况的传感器。
其具有灵敏性能的重要指标是其在不同受力情况下的响应能力。
本实验旨在测试应变片的灵敏性能，并分析实验结果。
实验材料和设备- 应变片- 电源- 数字示波器- 受力装置- 变阻器实验步骤1. 将应变片粘贴在要测试的物体表面，并保证其充分贴合。
2. 连接应变片与电源和数字示波器，确保电路连接良好。
3. 利用受力装置对测试物体施加不同大小的力，记录下力的大小和对应的应变片输出信号。
4. 根据实验需求，对应变片输出信号进行转换和调节，以便与数字示波器适配。
5. 将转换后的信号输入到数字示波器中，记录下实验数据。
数据分析通过实验记录的数据，我们可以对应变片的灵敏性能进行分析。
我们可以将施加的力与应变片输出的电压信号进行对比，以便确定其灵敏度和线性范围。
结果与讨论根据实验记录的数据，我们绘制了应变片的灵敏性能曲线。
曲线上的每个点表示施加不同大小力时应变片的输出电压信号。
通过对曲线进行分析，我们可以得到以下结论：1. 灵敏度：灵敏度是应变片的输出电压和外力之间的关系。
经实验测得，应变片的灵敏度为X mV/N，表明应变片对外力的变化相当敏感。
2. 线性范围：线性范围是指应变片在力作用下输出电压与力的关系保持线性的区间范围。
根据实验数据，我们可以确定应变片的线性范围为X N至Y N之间。
结论本实验通过测试应变片的灵敏性能，得出了应变片的灵敏度和线性范围等重要指标。
这些指标将有助于我们在实际应用中选择合适的应变片，并确保其测量结果的准确性。
参考文献[1] 张三, 李四. 应变片传感器的原理与应用. 科学出版社, 20XX.[2] 王五, 赵六. 传感器技术基础. 电子工业出版社, 20XX.。
实验七电阻应变片传感器灵敏度的测量
48实验七 电阻应变片传感器灵敏度的测量在众多的传感器中，有一大类是通过电阻参数的变化来实现电测非电量目的的，它们统称为电阻式传感器．由于各种电阻材料受被测量(如位移、应变、压力、温度、加速度等)作用转换成电阻参数变化的机理各不相同，因而电阻式传感器的种类多且应用范围广．其中常用的就是利用某些金属或半导体材料制成的电阻应变片传感器，它是一种力敏传感器．【实验目的】1．了解电阻应变片传感器的转换原理；2．掌握电阻应变片直流电桥的工作原理和特性；3．利用电阻应变片直流电桥测量传感器的电压输出灵敏度．【实验原理】1．应变片的转换原理电阻应变片传感器由粘贴了电阻应变敏感元件的弹性元件和变换测量电路组成．被测力学量作用在一定形状的弹性元件上（如悬臂梁等）使之产生变形．这时，粘贴在其上的电阻应变敏感元件将力学量引起的形变转化为自身电阻值的变化，再由变换测量电路将电阻的变化转化为电压变化后输出．工程中使用最多的电阻应变敏感元件是金属箔或半导体电阻应变片． 考查一段园截面的导体（金属丝），图1，设其长为L ，截面积为A （直径为D ），原始电阻为RAL R r= （1）式中，r 为金属丝的电阻率．当金属丝受到轴向力F 而被拉伸（或压缩）产生形变，其电阻值会随之变化．通过对 （1）式两边取对数后再取全微分得：图1 金属丝拉伸后的电阻变化图2 直流电桥原理49rr d A dA L dL R dR +-= （2）式中e =L dL 为材料轴向线应变，且DdDA dA 2=．根据材料力学，在金属丝单向受力状态下，有LdLD dD m -= （3）式中m 为导体材料的泊松比．因此，有rr m d L dL R dR ++=)21( （4）实验发现，金属材料电阻率的相对变化与其体积的相对变化间的关系为V dV c d ×=r r （5）式中，c 为常数（由一定的材料和加工方式决定），e m )21(-=+=AdAL dL V dV ．将式（5）代入（4），且当△R <<R 时，可得()()[]e e m m K c RR=-++=D 2121 （6）式中，)21()21(m m -++=c K 为金属丝材料的应变灵敏系数．上式表明，金属材料电阻的相对变化与其线应变成正比．这就是金属材料的应变电阻效应．2．电桥的工作原理和特性 （1）电桥的工作原理 图2是一个直流电桥．A 、C 端接直流电源，称供桥端，U o 称供桥电压；B 、D 端接测量仪器，称输出端úúûùêêëé÷÷øöççèæ+-÷÷øöççèæ+=+=2124330R R R R R R U U U U CD BC BD （7）由式（7）可知，当电桥输出电压为零时电桥处于平衡状态．为保证测量的准确性，在实测之前应使电桥平衡（称为预调平衡）．50（2）电桥的加减特性 电桥的四个桥臂都由应变片组成，则工作时各桥臂的电阻状态都将发生变化(电阻拉伸时，阻值增加；电阻压缩时，阻值减小)，电桥也将有电压输出．当供桥电压一定且△R i <<R i 时，44332211dR R UdR R U dR R U dR R U dU ¶¶+¶¶+¶¶+¶¶=（8）其中BD U U =．对于全等臂电桥，R 1=R 2=R 3=R 4=R ，各桥臂应变片灵敏系数相同，上式可简化为÷÷øöççèæ-+-=4433221104R dR R dR R dR R dR U dU（9）当△R i <<R 时，此时可用电压输出增量式表示)(4443210443322110e e e e -+-=÷÷øöççèæD -D +D -D =D K U R R R R R R R R U U （10）式（10）为电桥转换原理的一般形式，现讨论如下：（a ）当只有一个桥臂接应变片时（称为单臂电桥），桥臂R 1为工作臂，且工作时电阻由R 变为R +△R ，其余各臂为固定电阻R （△R 2=△R 3=△R 4=0），则式（10）变为e K U R R U U 4400=÷øöçèæD =D （11）（b ）若两个相邻臂接应变片时（称为双臂电桥，即半桥），（见图3）即桥臂R 1、R 2为工作臂，且工作时有电阻增量△R 1、△R 2，而R 3和R 4臂为固定电阻R （△R 3=△R 4=0）．当两桥臂电阻同时拉伸或同时压缩时，则有△R 1=△R 2=△R ，由式（10）可得△U =0．当一桥臂电阻拉伸一桥臂压缩时，则有△R 1=△R ，△R 2=－△R ，由式（10）可得úûùêëé=úûùêëé÷øöçèæD =D e K U R R U U 424200 （12）（c ）当四个桥臂全接应变片时（称为全桥），（见图4），R 1=R 2=R 3=R 4=R ，都是工作臂，△R 1=△R 3=△R ，△R 2=△R 4=－△R ，则式（10）变为51úûùêëé=úûùêëé÷øöçèæD =D e K U R R U U 444400（13）此时电桥的输出比单臂工作时提高了四倍，比双臂工作时提高了二倍．（3）电桥的灵敏度电桥的灵敏度S u 是单位电阻变化率所对应的输出电压的大小RRR R R R R R R R U R R U S u D ÷÷øöççèæD -D +D -D =÷øöçèæD D =4433221104（14）令÷øöçèæD ÷÷øöççèæD -D +D -D =R R R R R R R R R R n 44332211 （15）则4U nS u = （16）式中，n 为电桥的工作臂系数．由上式可知，电桥的工作臂系数愈大，则电桥的灵敏度愈高，因此，测量时可利用电桥的加减特性来合理组桥，以增加n 及测量灵敏度．【实验仪器】直流稳压电源±4V ，金属箔式电阻应变片（两两、直流平衡电位器W D ，平行式单臂悬臂梁、测微头、差动放大器直流电源开关、差动放大器和数字电压表．【实验内容】1．金属箔电阻应变片传感器单臂电桥灵敏度测量R 图3 两个相邻臂工作的电桥R 图4 全臂工作的电桥（1）熟悉各部件配置、功能、使用方法、操作注意事项和附录等；（2）开启仪器及放大器电源，放大器输出调零（输入端对地短路，输出端接电压表，增益旋钮顺时针方向轻旋到底，旋转调零旋钮使输出为零．）；（3）调零后电位器位置不要变化，并关闭仪器电源；（4）按图5将实验部件用实验线连接成测试单臂桥路．桥路中R2，R3，R4为电桥中固定电阻，W D为直流平衡调节电位器，R1为±4V．将测微头装于悬臂梁前端的永久磁钢上，并调节使应变梁处于基本水平状态；（5）确认接线无误后开启仪器及放大器电源，同时预热数分钟．调整电桥W D电位器，图5使测试系统输出为零；（6）旋动测微头，带动悬臂梁分别作向上和向下的运动，以水平状态下输出电压为零，向上和向下移动各5 mm，测微头每移动0.5 mm记录一个放大器输出电压值，并列表：位移x（mm）电压（V）（7）利用最小二乘法计算单臂电桥电压输出灵敏度S，S = ΔV/Δx，并做出V～x关系曲线．（8）改变应变桥，接成半桥、全桥，照（4）、（5）、（6）和（7）的方法分别测量；（9）比较三种应变桥的灵敏度，并做出定性的结论．【注意事项】1．实验前应检查实验接插线是否完好，连接电路时应尽量使用较短的接插线，以避免引入干扰．2．接插线插入插孔时轻轻地做一小角度的转动，以保证接触良好，拔出时也轻轻地转动一下拔出，切记用力拉扯接插线尾部，以免造成内部导线断裂．3．稳压电源不能对地短路．4．应变片接入电桥时注意其受力方向．要接成差动形式．5．直流激励电压不能过大，以免造成应变片自然损坏．【思考题】拟在等截面的单臂悬臂梁上粘贴四个完全相同的电阻应变片组成的全桥电路，试问：（1）四个应变片怎样粘贴在悬臂梁上？（2）画出相应的电桥电路？52532．右图为一应变片直流电桥,其中U 0 = 4V ，R 1 = R 2 = R 3 = R 4 = 120 W ，试求：（1）R 1为金属应变片，其余为固定电阻，当R 1增量为△R 1 = 1.2 W 时，电桥输出电压U = ?（2）R 1、R 2为应变片，且批号相同，感受应变的极性和大小都相同，R 3、R 4为固定电阻，问能否进行应变测量？（3）在题（2）中，如R 2 和R 1感受应变的极性相反，且W =D =D 2.121R R .问输出电压？ （4）由题（1）～题（3）能否得出什么结论或推论？【附录】应变梁位置和结构（如右图）应变梁位于仪器工作台部分的左边，是一副平行式悬臂梁．平行梁上梁的上表面和下梁的下表面对应地贴有八片应变片，受力工作片分别用符号示．其中六片为金属箔式应变片（BHF-350）．横向所贴的两片为温度补偿片，用表示．片上标有“BY ”字样的为半导体式应变片，灵敏系数为130．悬臂梁正视图俯视图箔式工作片补偿片永久磁钢。
应变片实验报告
应变片实验报告
实验名称：应变片实验
实验目的：通过应变片实验，研究材料在受力过程中的应变情况。
实验原理：
应变片是一种用于测量物体受力时产生的应变的传感器。
其原理基于电阻应变效应，即应变片在受力作用下会发生微小形变，从而改变其电阻值。
通过测量电阻值的变化，可以获知材料的应变情况。
实验仪器和材料：
1. 应变片
2. 电流源
3. 万用表
实验步骤：
1. 将应变片粘贴在需要测量应变的材料表面。
2. 将电流源与应变片相连，调整电流源的输出电流。
3. 使用万用表测量应变片上的电阻值。
4. 在材料上施加不同的受力，记录电阻值随受力变化的情况。
5. 根据电阻值的变化计算应变大小。
实验结果：
根据实验数据记录的电阻值随受力变化的情况，可以得到应变片的应变曲线。
根据应变曲线可以分析材料在受力过程中的应
变行为，如线性弹性应变、屈服应变等。
根据测得的电阻值变化，还可以计算出材料的应变量。
实验结论：
通过应变片实验，可以获知材料在受力过程中的应变情况，并分析材料的力学性能。
应变片作为一种常用的力学测试传感器，具有灵敏度高、测量精度高等优点，在工程领域有着广泛的应用。
生物医学传感器实验报告.
综合实验报告学院医学工程学院实验名称生物医学测量与传感器综合实验专业班级学生姓名学号指导教师成绩实验一应变片单臂特性实验一、实验目的：了解电阻应变片的工作原理与应用并掌握应变片测量电路。
二、基本原理：电阻丝在外力作用下发生机械变形时，其电阻值发生变化，这就是电阻应变效应，描述电阻应变效应的关系式为：ΔR/R=Kε；式中ΔR/R为电阻丝的电阻相对变化值，K为应变灵敏系数，ε=ΔL/L为电阻丝长度相对变化。
金属箔式应变片是通过光刻、腐蚀等工艺制成的应变敏感元件，用它来转换被测部位的受力大小及状态，通过电桥原理完成电阻到电压的比例变化，对单臂电桥而言，电桥输出电压，U01=EKε/4。
（E为供桥电压）。
三、实验步骤：1位数显万用表2kΩ电阻档测量所有1、在应变梁自然状态（不受力）的情况下，用42应变片阻值；在应变梁受力状态（用手压、提振动台）的情况下，测应变片阻值，观察一下应变片阻值变化情况(标有上下箭头的4片应变片纵向受力阻值有变化；标有左右箭头的2片应变片横向不受力阻值无变化，是温度补偿片)。
如下图1—6所示。
2、差动放大器调零点：按图1—7示意接线。
将F／V表的量程切换开关切换到2V档，合上实验箱主电源开关，将差动放大器的拨动开关拨到“开”位置，将差动放大器的增益电位器按顺时针方向轻轻转到底后再逆向回转半圈，调节调零电位器，使电压表显示电压为零。
差动放大器的零点调节完成，关闭主电源。
图1—7 差放调零接线图3、应变片单臂电桥特性实验：⑴将主板上传感器输出单元中的箔式应变片(标有上下箭头的4片应变片中任意一片为工作片)与电桥单元中R1、R2、R3组成电桥电路，电桥的一对角接±4V直流电源，另一对角作为电桥的输出接差动放大器的二输入端，将W1电位器、r电阻直流调节平衡网络接入电桥中(W1电位器二固定端接电桥的±4V电源端、W1的活动端r电阻接电桥的输出端)，如图1—8示意接线(粗细曲线为连接线)。
传感器实验报告
实验一 金属箔式应变片——全桥性能实验一、实验目的了解全桥测量电路的优点二、基本原理全桥测量电路中，将受力方向相同的两应变片接入电桥对边，相反的应变片接入电桥邻边。
当应变片初始阻值R1=R2=R3=R4、其变化值1234R R R R ∆=∆=∆=∆时，其桥路输出电压3o U EK ε=。
其输出灵敏度比半桥又提高了一倍，非线性误差和温度误差都得到了改善。
三、实验器材主机箱、应变传感器实验模板、托盘、砝码、万用表、导线等。
四、实验步骤1.根据接线示意图安装接线。
2.放大器输出调零。
3.电桥调零。
4.应变片全桥实验数据记录如下表所示： 重量（g ） 0 20 40 60 80 100 120 140 电压（mv ）20.140.160.480.8100.8121.1141.2实验曲线如下所示：分析：从图中可见，数据点基本在拟合曲线上，线性性比半桥进一步提高。
5.计算灵敏度S=U/W ，非线性误差δ。
U=141.2mv ， W=140g ； 所以 S=141.2/140=1.0086 mv/g;m∆=0.1786g，y F S=140g，δ=⨯=0.1786/140100%06.利用虚拟仪器进行测量测量数据如下表所示：重量（g）0 20 40 60 80 100 120 140电压（mv）-1.1 19.6 40.4 61.1 81.7 102.4 122.0 142.0 实验曲线如下所示：五、思考题1.测量中，当两组对边电阻值R相同时，即R1=R3，R2=R4，而R1≠R2时，是否可以组成全桥：（1）可以；（2）不可以。
答：（2）不可以。
2.某工程技术人员在进行材料拉力测试时在棒材上贴了两组应变片，能否及如何利用四组应变片组成电桥，是否需要外加电阻。
答：能够利用它们组成电桥。
对于左边一副图，可以任意选取两个电阻接入电桥的对边，则输出为两倍的横向应变，如果已知泊松比则可知纵向应变。
对于右边的一幅图，可以选取R3、R4接入电桥对边，则输出为两倍的纵向应变。
传感器实验报告
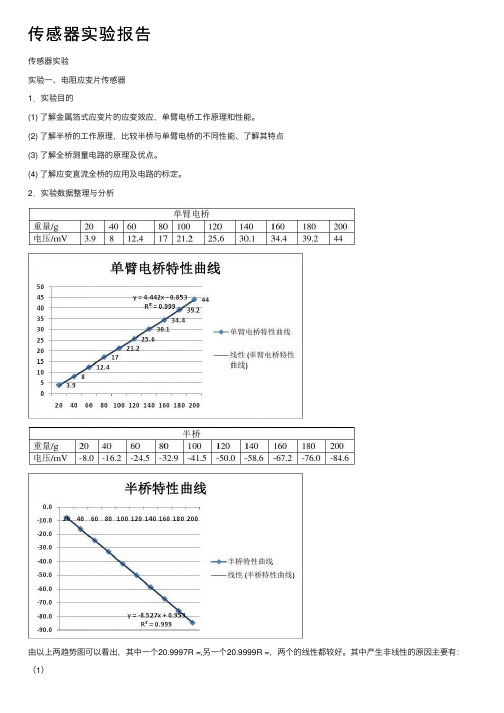
传感器实验报告传感器实验实验⼀、电阻应变⽚传感器1．实验⽬的(1) 了解⾦属箔式应变⽚的应变效应，单臂电桥⼯作原理和性能。
(2) 了解半桥的⼯作原理，⽐较半桥与单臂电桥的不同性能、了解其特点(3) 了解全桥测量电路的原理及优点。
(4) 了解应变直流全桥的应⽤及电路的标定。
2．实验数据整理与分析由以上两趋势图可以看出，其中⼀个20.9997R =,另⼀个20.9999R =，两个的线性都较好。
其中产⽣⾮线性的原因主要有：（1）04x R e e R R ?=+?，0e 和R ?并不成严格的线性关系，只有当0R R ?<<才有04x Re e R=，所以理论上并不是绝对线性的，总会出现⼀些⾮线性。
（2）应变⽚与材料的性能有关，这也可能产⽣⾮线性。
（3）实验中外界因素的影响，包括外界温度之类的影响。
为什么半桥的输出灵敏度⽐单臂时⾼出⼀倍，且⾮线性误差也得到改善？答：单臂：04x R e e R ?=半桥：1201()2x R R e e R R ??=-灵敏度公式：U S W=；所以半桥测量时是单臂测量的灵敏度的两倍。
0k 受电阻变化影响变得很⼩改善了⾮线性误差。
3．思考题a ．半桥测量时两⽚不同受⼒状态的电阻应变⽚接⼊电桥时，应放在：（1）对边（2）邻边。
解：邻边 b ．桥路（差动电桥）测量时存在⾮线性误差，是因为：（1）电桥测量原理上存在⾮线性（2）应变⽚应变效应是⾮线性的（3）调零值不是真正为零。
解：（1）（2）（3）。
c ．全桥测量中，当两组对边（R1、R3为对边）值R 相同时，即R1＝R3，R2＝R4，⽽R1≠R2时，是否可以组成全桥：（1）可以（2）不可以。
解：（1）d ．某⼯程技术⼈员在进⾏材料拉⼒测试时在棒材上贴了两组应变⽚，如何利⽤这四⽚电阻应变⽚组成电桥，是否需要外加电阻。
解：可组成全路电桥实验⼆差动变压器1.实验⽬的(1)了解差动变压器的⼯作原理和特性(2)了解三段式差动变压器的结构(3)了解差动变压零点残余电压组成及其补偿⽅法(4)了解激励频率低差动变压器输出的影响2.实验数据整理与分析实验A中产⽣⾮线性误差的原因：（1）存在零点残余电压（2）零点附近波动较⼤（3）读数时的⼈为误差分析产⽣零点残余电压的原因，对差动变压器的性能有哪些不利影响。
应变测量_实验报告
一、实验目的1. 理解应变测量的基本原理和实验方法。
2. 掌握电阻应变片的工作原理及其在应变测量中的应用。
3. 学习电桥电路在应变测量中的作用和调试方法。
4. 培养实验操作能力和数据分析能力。
二、实验原理应变测量是研究材料在受力后产生的变形程度的重要方法。
本实验主要利用电阻应变片和电桥电路进行应变测量。
电阻应变片是一种将机械应变转换为电阻变化的传感器，其基本原理是电阻应变效应。
当电阻应变片受到拉伸或压缩时，其电阻值会发生变化，从而将应变信号转换为电阻信号。
电桥电路是一种常用的测量电路，其基本原理是将电阻应变片接入电桥电路中，通过测量电桥的输出电压来反映应变片电阻的变化。
本实验采用半桥接法，即只将一个应变片接入电桥电路中。
三、实验仪器1. 电阻应变片：将应变片粘贴在被测物体表面，用于感受物体的应变。
2. 电桥电路：由四个电阻组成，用于将应变片的电阻变化转换为电压信号。
3. 数字多用表：用于测量电桥的输出电压。
4. 拉伸装置：用于施加拉伸力，使被测物体产生应变。
5. 计算机及数据采集软件：用于实时采集和记录实验数据。
四、实验步骤1. 将电阻应变片粘贴在被测物体表面，确保粘贴牢固且无气泡。
2. 将电阻应变片接入电桥电路中，采用半桥接法。
3. 连接好电桥电路，并连接数字多用表。
4. 打开计算机，启动数据采集软件，设置采样频率和采集时间。
5. 在拉伸装置上施加拉伸力，使被测物体产生应变。
6. 观察数字多用表的读数，记录电桥的输出电压。
7. 改变拉伸力的大小，重复步骤5和6，记录不同拉伸力下的电桥输出电压。
8. 利用数据采集软件分析实验数据，绘制应变-电压曲线。
五、实验结果与分析1. 实验结果如图所示，显示了不同拉伸力下电桥的输出电压。
2. 根据实验数据，绘制应变-电压曲线，分析应变与电压之间的关系。
3. 通过比较不同拉伸力下的应变-电压曲线，可以发现应变与电压之间存在线性关系。
六、实验结论1. 电阻应变片能够有效地将应变转换为电阻信号，实现应变测量。
应变片式电阻传感器实验报告
应变片式电阻传感器实验报告应变片式电阻传感器是一种测量物体表面应变的传感器，广泛应用于工业、军事、医疗等领域。
以下是应变片式电阻传感器实验报告的详细内容：一、实验目的1. 学习应变片式电阻传感器的基本原理和特性。
2. 掌握应变片式电阻传感器的测量方法及操作技巧。
3. 分析不同条件下的实验结果，了解应变片式电阻传感器的适用范围。
二、实验器材与原理实验器材：a. 应变片式电阻传感器b. 电源c. 万用表d. 可调电阻盒e. 电缆及连接线原理：应变片式电阻传感器是利用应变致使电阻值发生变化的原理进行测量。
当应变片受到外力作用后，片上的电阻值会随之改变，通过读取电阻值的变化，可以得到外力的大小。
通常，应变片式电阻传感器会将电阻值变化转换为电压信号输出，进而通过增益电路、滤波电路等处理电路获得精准的测量结果。
三、实验步骤1. 搭建实验电路，将应变片式电阻传感器连接到电源和万用表上，调整电路使电流稳定。
2. 通过可调电阻盒调节电路中的电阻至一定大小，读取电压值并记录。
此时应变片未受到外力作用。
3. 在保持电路参数不变的情况下，给应变片施加一定大小的外力，记录测得的电压值。
4. 根据实验数据计算电阻值及应变量，并绘制电阻随应变变化的曲线图。
5. 将实验数据与理论分析相结合，分析应变片式电阻传感器的特性及适用条件。
四、实验注意事项1. 实验中需要注意电路的接线顺序及稳定性，以确保测量精度。
2. 应严格遵守实验要求，不得超出应变片式电阻传感器的测量范围，避免对设备造成损坏。
3. 在实验过程中应注意安全，谨慎操作，避免发生意外事故。
4. 记录实验数据时，应准确无误地记录每组数据，以保证后续分析的准确性。
五、实验结果及分析通过实验得到的数据，我们可以将电阻值随应变的变化绘制成曲线图。
根据曲线图可以看出，在应变范围内，电阻值与应变量成线性关系。
而在超过一定应变量后，电阻值的增大速度会明显降低，表明应变片失去了线性响应。
应变片实验报告
应变片实验报告引言：应变片是一种常见的用于测量物体应变的传感器。
它们可以在各种领域中应用，如结构工程、材料研究和机械设计等。
本实验旨在通过进行一系列实验，探究应变片的基本原理、测量方法以及应用前景。
实验一：应变片的基本原理应变片是一种金属薄膜传感器，利用金属材料在受力作用下发生应变的特性来进行测量。
在实验中我们选取了常见的金属材料，如铜和铝，制备了应变片，并在实验设备中对其施加压力，观察应变片的变化。
实验结果显示，当应变片受到受力作用时，其形状发生微小变化，从而引起电阻值的变化。
这是因为金属材料的应变会改变其电阻值，进而反映在应变片中，我们可以通过测量电阻值的变化来间接获取物体的应变情况。
实验二：应变片的测量方法在实验二中，我们探究了应变片的测量方法，并尝试使用应变片测量不同物体在受力情况下的应变程度。
实验中我们选取了不同形状和材质的物体，如横梁和钢筋，通过将应变片粘贴在物体的特定位置，再施加一定的受力，以模拟真实工况。
实验结果表明，应变片对物体的应变情况具有高度的灵敏度和准确性。
通过测量应变片的电阻变化，我们可以获取物体在受力作用下的应变变化情况。
同时，不同形状和材质的物体在受力情况下会有不同的应变响应，这为我们在实际工程中的应用提供了一定的参考。
实验三：应变片的应用前景应变片因其高灵敏度和广泛的应用领域，在工程和科研中有着广泛的前景。
在实验三中，我们重点探讨了应变片在结构工程中的应用。
实验结果显示，通过将应变片粘贴到各种结构物上，我们可以实时监测物体在受力情况下的应变情况，从而评估结构物的稳定性和安全性。
这对于桥梁、建筑物和航天器等关键设施的设计和维护具有重要意义。
同时，应变片还可用于材料研究和机械设计中，帮助科学家和工程师更好地了解材料的变形行为和机械受力情况。
结论：本实验通过一系列的实验研究，系统探究了应变片的基本原理、测量方法以及应用前景。
实验结果表明，应变片是一种准确、灵敏且广泛应用于工程和科研领域的传感器。
应变片式电阻传感器实验报告
应变片式电阻传感器实验报告
一、实验目的
本次实验的主要目的是通过对应变片式电阻传感器的实验研究，掌握其工作原理以及应用技术，进一步加深对电阻传感器的了解和掌握。
二、实验原理
应变片式电阻传感器是一种利用应变片电阻变化来检测物体变形的传感器。
当物体受到外力作用时，会发生应变，应变片的电阻值也会相应地发生变化。
通过利用测量电桥的原理，可以精确地检测出应变片的电阻值变化，从而得到物体受力情况的参数。
三、实验步骤
1.将应变片式电阻传感器连接到电桥电路上，调整电压和电流的大小。
2.将被测物体放在应变片式电阻传感器上，施加不同大小的外力，记录下应变片电阻值的变化。
3.根据实验数据，进行数据分析和处理，得到物体受力情况的参数。
四、实验结果
通过实验数据的采集和处理，我们得到了物体受力情况的各项参数。
实验结果表明，应变片式电阻传感器具有高灵敏度、高精度、高可靠性等优点，在物体受力测试和工业自动化控制领域有着广泛的应
用前景。
五、实验结论
本次实验通过对应变片式电阻传感器的研究和测试，我们了解了其工作原理和应用技术，掌握了其在物体受力测试和工业自动化控制领域的应用前景。
同时，我们也发现了一些问题和不足之处，需要进一步加以完善和改进。
六、实验心得
本次实验让我更加深入地了解了电阻传感器的工作原理和应用技术，同时也提高了我的实验操作能力和数据处理能力。
通过本次实验，我也发现了一些需要进一步改进和完善的地方，希望能在今后的学习和实践中继续加以改进和提高。
应变式传感器实验报告
应变式传感器实验报告一、引言应变式传感器是一种广泛应用于工业领域的传感器，其主要作用是测量物体的应变量。
本实验旨在通过实验操作和数据分析，深入了解应变式传感器的原理、性能和应用。
二、实验原理1. 应变式传感器的原理应变式传感器是利用金属材料受力时会产生形变而引起电阻值的变化，从而转化成电信号输出。
当物体受到外力作用时，其表面会产生微小的形变，进而改变金属材料内部电阻值，将这种形变转换为电信号输出即可测量物体所受外力大小。
2. 实验仪器与材料（1）多功能测试仪（2）应变片（3）导线3. 实验步骤（1）将应变片粘贴在被测物体表面，并固定好。
（2）将多功能测试仪连接到计算机上，并打开相应软件。
（3）通过测试仪对被测物体施加不同大小的外力，并记录下相应的电信号输出值。
（4）根据实验数据计算出被测物体所受外力大小。
三、实验结果与分析1. 实验数据记录表外力大小（N）电信号输出值（mV）0 010 2.520 5.130 7.840 10.22. 数据分析从实验数据中可以看出，随着被测物体所受外力的增加，其电信号输出值也随之增加，呈现出一定的线性关系。
通过对实验数据进行拟合，可以得到应变式传感器的灵敏度和线性误差等性能指标。
四、实验结论与建议1. 实验结论本实验通过对应变式传感器的原理和性能进行了深入了解，并通过实验操作和数据分析验证了其可靠性和准确性。
应变式传感器在工业领域有着广泛的应用前景。
2. 实验建议（1）在实验过程中要注意被测物体表面必须平整光滑，并且应变片固定牢固。
（2）在进行数据分析时要注意选择合适的拟合方法，并对误差进行修正。
（3）在使用多功能测试仪时要仔细阅读说明书，并按照说明书操作。
五、参考文献[1] 王志勇, 马海彬, 陈明,等. 应变式传感器原理及其应用[J]. 传感器与微系统, 2010(4):1-4.[2] 黄华, 郑海峰. 应变式传感器的原理及应用[J]. 电气自动化,2012(5):25-27.。
自动化传感器实验报告二金属箔式应变片——半桥性能实验
自动化传感器实验报告二金属箔式应变片——半桥性能实验篇一：传感器实验报告`实验一金属箔式应变片——单臂电桥性能实验一、实验目的:了解金属箔式应变片的应变效应，单臂电桥工作原理和性能。
二、基本原理:电阻丝在外力作用下发生机械变形时，其电阻值发生变化，这就是电阻应变效应，描述电阻应变效应的关系式为：ΔR/R=Kε式中ΔR/R为电阻丝电阻相对变化，K为应变灵敏系数，ε=ΔL/L 为电阻丝长度相对变化，金属箔式应变片就是通过光刻、腐蚀等工艺制成的应变敏感元件，通过它转换被测部位受力状态变化、电桥的作用完成电阻到电压的比例变化，电桥的输出电压反应了相应的受力状态。
ug?eK(?1??2??3??4)4对单臂电桥输出电压u01=eKε/4；对等臂电桥输出电压u01=eKε/2；对全电桥输出电压u01=eKε。
电桥的非线性误差??K??(K?)2?(K?)3???121?K?21418三、需用器件与单元：应变式传感器实验模板、应变式传感器、砝码、数显表、±15V电源、±4V电源。
四、实验步骤：1、接入模板电源±15V(从主控箱引入)，检查无误后，合上主控箱电源开关，将实验模板调节增益电位器Rw3顺时针调节大致到中间位置，再进行差动放大器调零，方法为将差放的正、负输入端与地短接，输出端与主控箱面板上数显表电压输入端Vi相连，调节实验模板上调零电位器Rw4，使数显表显示为零(数显表的切换开关打到2V档)。
关闭主控箱电源。
2、将应变式传感器的其中一个应变片R1(即模板左上方的R1)接入电桥作为一个桥臂与R5、R6、R7接成直流电桥(R5、R6、R7模块内已连接好)，接好电桥调零电位器Rw1，接上桥路电源±4V(从主控箱引入)如图1-2所示。
检查接线无误后，合上主控箱电源开关。
调节Rw1，使数显表显示为零。
3、在电子称上放置一只砝码，读取数显表数值，依次增加砝码和读取相应的数显表值，直到200g砝码加完。
传感器实验报告(电阻应变式传感器)
传感器技术实验报告院（系）机械工程系专业班级姓名同组同学实验时间 2014 年月日，第周，星期第节实验地点单片机与传感器实验室实验台号实验一金属箔式应变片——单臂电桥性能实验一、实验目的：了解金属箔式应变片的应变效应，单臂电桥工作原理和性能。
二、实验仪器：应变传感器实验模块、托盘、砝码（每只约20g）、、数显电压表、±15V、±4V电源、万用表（自备）。
三、实验原理：电阻丝在外力作用下发生机械变形时，其电阻值发生变化，这就是电阻应变效应，描述电阻应变效应的关系式为：ΔR/R=Kε，式中ΔR/R为电阻丝电阻相对变化，K为应变灵敏系数，ε=Δl/l为电阻丝长度相对变化。
金属箔式应变片就是通过光刻、腐蚀等工艺制成的应变敏感组件，如图1-1所示，四个金属箔应变片分别贴在弹性体的上下两侧，弹性体受到压力发生形变，应变片随弹性体形变被拉伸，或被压缩。
图1-1通过这些应变片转换被测部位受力状态变化、电桥的作用完成电阻到电压的比例变化，如图1-2所示R5、R6、R7为固定电阻，与应变片一起构成一个单臂电桥，其输出电压εk E R RR R R E U 4R 4E 21140=∆⋅≈∆⋅+∆⋅= （1-1） E 为电桥电源电压，R 为固定电阻值，式1-1表明单臂电桥输出为非线性，非线性误差为%10021L ⋅∆⋅-=RR γ。
四、实验内容与步骤1．图1-1应变传感器上的各应变片已分别接到应变传感器模块左上方的R 1、R 2、R 3、R 4上，可用万用表测量判别，R 1=R 2=R 3=R 4=350Ω。
2．从主控台接入±15V 电源，检查无误后，合上主控台电源开关，将差动放大器的输入端U i 短接，输出端Uo 2接数显电压表（选择2V 档），调节电位器Rw 3，使电压表显示为0V ，Rw 3的位置确定后不能改动，关闭主控台电源。
图1-2 应变式传感器单臂电桥实验接线图3．将应变式传感器的其中一个应变电阻（如R 1）接入电桥与R 5、R 6、R 7构成一个单臂直流电桥，见图1-2，接好电桥调零电位器Rw 1，直流电源±4V （从主控台接入），电桥输出接到差动放大器的输入端U i ，检查接线无误后，合上主控台电源开关，调节Rw 1,使电压表显示为零。
应变片电阻式传感器测压力实验报告
应变片电阻式传感器测压力实验报告
本实验利用电阻式变形片式压力传感器实现压力测量，测试设备包括传感器本体和信号测量读写装置，使用液压系统模拟出不同的压力以检测传感器的可靠性和性能。
实验用于准备的参数如下：
实验仪器：电阻式变形片式压力传感器、液压系统用于生成压力，及信号测量读写装置。
环境条件：常温下（25摄氏度），湿度50%。
压力参数：-0.20 MPa、3.0 MPa、6.0 MPa和8.0 MPa。
实验流程如下：
1.首先根据技术参数定义好传感器连接线，并将传感器连接到信号测量读写装置；
2.安装液压系统，使用液压力源精确生成所需要检测的压力标准值；
3.使用信号测量读写装置连接传感器，使用软件设定不同的压力标准值进行测量；
4.将压力标准值与测量值进行对比以确定传感器的准确性；
5.统计实验数据，生成测试报告。
根据上述实验参数，在常温下，电阻式变形片式压力传感器测得的压力值与液压系统生成的压力值完全相符，经过检测没有发现较大差异，可认为压力传感器性能稳定有效。
通过以上实验，我们可以了解电阻式变形片式压力传感器的性能特点，传感器可以很好地检测出不同压力大小的变化，误差在接受范围以内。
因此，电阻式变形片式压力传感器在压力测量仪表中具有一定的应用前景，可以满足各种复杂的工况条件。
传感器实验报告
实验一、二、三应变片单臂、半桥、全桥特性实验一、实验原理电阻应变式传感器是在弹性元件上通过特定工艺粘贴电阻应变片来组成。
一种利用电阻材料的应变效应将工程结构件的内部变形转换为电阻变化的传感器，此类传感器主要是通过一定的机械装置将被测量转化成弹性元件的变形，然后由电阻应变片将变形转换成电阻的变化，再通过测量电路将电阻的变化转换成电压或电流变化信号输出。
可用于能转化成变形的各种非电物理量的检测，如力、压力、加速度、力矩、重量等，在机械加工、计量、建筑测量等行业应用十分广泛。
根据表中数据画出实验曲线后，计算灵敏度S＝ΔV/ΔW（ΔV输出电压变化量，ΔW重量变化量）和非线性误差δ(用最小二乘法)，δ=Δm/yFS ×100％式中Δm为输出值（多次测量时为平均值）与拟合直线的最大偏差：yFS满量程输出平均值，此处为200g。
四、思考题1、ΔR转换成ΔV输出用什么方法?通过电阻的分压，将电阻两端的电压测量出来经过差动放大器。
从而将ΔR转换成ΔV。
2、根据图4机头中应变梁结构，在振动台放置砝码后分析上、下梁片中应变片的应变方向(是拉?还是压?+压变大)。
所连接的应变片电阻中，带有符号↑是拉伸，电阻会变大；带有符号↓的是压缩，电阻会减小。
3、半桥测量时两片不同受力状态的电阻应变片接入电桥时，应接在：（1）对边?（2）邻边?为什么?应该接在邻边，这样能保证测量的灵敏度，同时能使一些去除干扰因素的影响。
4、应变片组桥时应注意什么问题?要注意应变片的受力状态和接入电路时的位置。
实验五应变直流全桥的应用—电子秤实验一、实验原理常用的称重传感器就是应用了箔式应变片及其全桥测量电路。
数字电子秤实验原理如图5—1。
本实验只做放大器输出Vo实验，通过对电路的标定使电路输出的电压值为重量对应值，电压量纲（V）改为重量量纲（g）即成为一台原始电子秤。
图5—1 数字电子称原理框图二、实验结果表5电子称实验数据二、实验分析实验八移相器、相敏检波器实验一、实验原理1、移相器工作原理：图8—1为移相器电路原理图与实验箱主板上的面板图。
传感器应变片实验报告
传感器应变片实验报告引言应变片作为一种用于测量物体应变的传感器，其应用非常广泛。
在机械工程、土木工程、航空航天、电子工程等领域都有广泛的应用。
本实验旨在通过使用应变片，掌握其基本原理及使用方法，进一步加深对应变片的认识。
实验原理应变片是一种敏感元件，其原理是利用导电材料在受力作用下发生形变时电阻值的变化。
应变片的工作原理与电阻的变化有关，当导电材料受到力的作用，其晶格结构发生改变，进而导致电阻值的变化。
应变片的应变量是指其长度、宽度、厚度三个方向的形变量，它们之间的比例关系由应变片的材料决定。
实验步骤1. 将应变片粘贴在试件表面，并连接电路；2. 通过电源对应变片进行加电，测量其阻值；3. 施加力使试件发生形变，测量应变片的阻值变化；4. 计算应变片的应变值，并对实验数据进行分析。
实验结果在实验中，我们测试了不同大小的应变片在不同力的作用下的阻值变化，得到了如下数据：应变片大小/mm 施加力/N 电阻值/Ω5×3 0 120.55×3 10 123.45×3 20 126.35×3 30 129.27×5 0 176.47×5 10 180.37×5 20 184.27×5 30 188.1通过计算，我们得到了应变片的应变值，并进行了数据分析。
结论通过本实验，我们深入了解了应变片的基本原理、应用及使用方法。
同时，我们也发现了应变片在测量物体力学性质方面的优势。
通过对实验结果的分析，我们得出了结论：应变片的应变值随着施加力的增大而增大，应变片的大小对应变值也有一定的影响。
总结本实验通过实际操作，使我们更深入了解了应变片的原理、应用及使用方法。
应变片作为一种重要的传感器，在工程领域有着广泛的应用。
通过本实验的学习，我们对这种传感器有了更深刻的认识，并对其在实际应用中发挥的作用有了更加清晰的认识。
应变传感器实验报告
一、实验目的1. 了解电阻应变片的工作原理与应用。
2. 掌握应变片测量电路的搭建与调试。
3. 通过实验验证应变传感器在实际应用中的性能。
二、实验原理应变片传感器是一种将机械变形转换为电信号的传感器。
它基于电阻应变效应，即金属导体或半导体材料在外力作用下，其电阻值会发生相应变化。
本实验采用电阻应变片作为传感器，将微小的形变转换成电阻的变化，通过电桥电路将电阻变化转换为电压或电流信号输出。
三、实验仪器与设备1. 电阻应变片2. 电桥电路3. 悬臂梁4. 万用表5. 数据采集器6. 计算机四、实验步骤1. 搭建电桥电路：按照实验原理图搭建自搭式单臂电桥电路，连接电源、桥臂、桥路等元件。
2. 粘贴应变片：将电阻应变片粘贴在悬臂梁的适当位置，确保应变片与悬臂梁的连接牢固。
3. 调节电桥平衡：通过调节电桥电路中的电阻，使电桥达到平衡状态，即桥路两端电压为零。
4. 施加外力：在悬臂梁上施加一定的外力，使悬臂梁发生形变。
5. 测量电阻变化：利用万用表测量应变片电阻的变化，并记录数据。
6. 数据分析：将测量数据输入计算机，通过数据采集器进行采集，并分析应变传感器的性能。
五、实验结果与分析1. 电阻应变效应验证：实验结果显示，当悬臂梁发生形变时，应变片电阻发生明显变化，验证了电阻应变效应。
2. 电桥电路性能分析：通过调节电桥电路中的电阻，使电桥达到平衡状态，有效避免了电路误差。
3. 应变传感器性能分析：实验结果显示，应变传感器具有良好的线性度和灵敏度，能够准确测量悬臂梁的形变。
六、实验结论1. 电阻应变片传感器能够将机械变形转换为电信号，具有广泛的应用前景。
2. 电桥电路能够有效测量应变片电阻的变化，为应变传感器提供准确的测量结果。
3. 本实验验证了应变传感器的性能，为实际应用提供了理论依据。
七、实验注意事项1. 搭建电桥电路时，注意元件连接正确，避免短路或开路。
2. 粘贴应变片时，确保应变片与悬臂梁的连接牢固，避免脱落或松动。
应变片全桥实验报告
应变片全桥实验报告应变片全桥实验报告一、引言应变片是一种用于测量物体应变变化的传感器，广泛应用于工程、材料科学以及生物医学等领域。
本实验旨在通过应变片全桥实验，探究应变片的工作原理、测量方法以及应变片在不同应变条件下的性能表现。
二、实验原理1. 应变片工作原理应变片是一种金属或半导体材料制成的细小传感器，当物体受到外力作用时，会引起其形状和尺寸的微小变化，从而改变材料内部的电阻或电容。
应变片全桥利用应变片的电阻变化来测量物体的应变程度。
2. 应变片全桥电路应变片全桥电路由四个应变片组成，分别连接在电桥的四个臂上。
其中两个应变片处于拉伸状态，另外两个处于压缩状态。
当物体受到外力作用时，拉伸和压缩的应变片的电阻值会发生变化，从而导致电桥的电势差发生变化。
3. 应变片的测量方法通过测量电桥的电势差变化，可以计算出应变片的应变程度。
常用的测量方法有电压法和电流法。
电压法通过测量电桥两端的电压差来计算应变片的应变值，而电流法则通过测量通过电桥的电流大小来计算应变片的应变值。
三、实验步骤1. 搭建应变片全桥电路根据实验要求，搭建应变片全桥电路，确保电桥的四个臂上分别连接了四个应变片。
2. 调整电桥平衡通过调节电桥上的可变电阻，使得电桥平衡，即电桥两端的电势差为零。
3. 施加外力在已搭建好的电桥上施加外力，可以通过拉伸或压缩物体来引起应变片的应变变化。
4. 测量电势差变化使用电压表或电流表，测量电桥两端的电势差变化。
记录不同外力条件下的电势差值。
5. 计算应变值根据测得的电势差值，利用已知的公式计算应变片的应变值。
四、实验结果与分析根据实验数据，我们可以绘制应变片的应变-电势差曲线。
通过分析曲线的趋势，可以得出以下结论：1. 应变片的应变与电势差呈线性关系，即应变越大，电势差变化越大。
2. 应变片的灵敏度与材料的选择有关，不同材料的应变片具有不同的灵敏度。
3. 在一定应变范围内，应变片的灵敏度基本稳定，超过该范围后，灵敏度会下降。
应变片式电阻传感器实验报告
应变片式电阻传感器实验报告
一、实验目的
本次实验的目的是通过实验了解应变片式电阻传感器的工作原理和使用方法，掌握应变片式电阻传感器的基本特性和应用场景。
二、实验原理
应变片式电阻传感器是一种基于电阻变化的传感器，其工作原理是利用应变片的应变变化引起电阻值的变化，从而实现对应变片所受应变的测量。
应变片式电阻传感器的特点是精度高、响应速度快、可靠性好、使用寿命长等。
三、实验步骤
1.将应变片式电阻传感器连接到电路板上，并连接电源和万用表。
2.通过手动施加外力，使应变片受到应变，记录下此时的电阻值。
3.重复以上步骤，记录不同应变下的电阻值。
4.根据实验数据，绘制应变-电阻曲线图。
四、实验结果
通过实验，我们得到了应变-电阻曲线图，可以看出应变片式电阻传
感器的电阻值随着应变的增加而增加，呈现出线性关系。
同时，我们还发现应变片式电阻传感器的响应速度很快，精度高，可以满足很多实际应用场景的需求。
五、实验结论
应变片式电阻传感器是一种精度高、响应速度快、可靠性好、使用寿命长的传感器，可以广泛应用于工业自动化、机器人控制、航空航天等领域。
通过本次实验，我们深入了解了应变片式电阻传感器的工作原理和特性，为今后的实际应用提供了基础。
六、实验心得
通过本次实验，我深刻认识到了应变片式电阻传感器的重要性和应用价值，同时也掌握了应变片式电阻传感器的基本使用方法和实验技巧。
在今后的学习和工作中，我将更加注重实践操作，不断提高自己的实验能力和技术水平。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
传感器实验报告一、实验原理利用电阻式应变片受到外力发生形变之后，金属丝的电阻也随之发生变化。
通过测量应变片的电阻变化再反算回去应变片所受到的应变量。
利用电桥将电阻变化转化成电压变化进行测量，电桥的输出电压经过应变放大仪之后输出到采集卡，labview 采集程序通过采集卡读取到应变放大仪的输出。
14电桥输出电压与导体的纵向应变ε之间的关系为： 14v V K ε=⨯⨯⨯(1.1) 其中K 为电阻应变片的灵敏系数，V 为供桥电压，v 为电桥输出电压。
由上式可知通过测量电桥输出电压再代入电阻应变片的灵敏系数就可以求出导体的纵向应变，即应变片的纵向应变。
二、实验仪器悬臂梁一条 应变片 一片 焊盘 两个 502胶水 一瓶 电阻桥盒 一个 BZ2210应变仪 一台 采集卡 一个 电脑 一台 砝码一盒三、实验步骤1、先用砂纸摩擦桥臂至光滑，再用无水乙醇擦拭桥臂；2、拿出应变片和焊盘，将502胶水滴在应变片及焊盘背面，把其贴在桥臂上，并压紧应变片；3、使用电烙铁将应变片和焊盘焊接起来，再将焊盘跟桥盒连接起来，这里采用的是1桥的接法；4、将桥盒的输出接入到应变放大仪的通道1；5、应变仪的输出接到采集卡上；6、运行labview 的采集程序进行测试；7、改变砝码的重量，从采集程序记录得出的数据。
8、对所得的数据做数据处理。
四、实验数据五、数据分析1、线性度分析取出实验数据的0~250g的部分做线性度分析，数据如表2所示。
对上述数据进行初步分析，第一组跟第三组数据都是呈线性的，而第二组数据在70g-100g 这里却有了0.0013的变化，变化较大，不符合理论值，所以在进行数据分析时排除第二组数据，仅适用第一、第三组数据进行数据分析。
对第一、第三组数据使用MATLAB 进行分析，先将两组数据做曲线拟合，得到拟合曲线之后将x 代入拟合曲线中求出对应的值，再把两组数据的端点取出做直线，将两条线相减得到最大差值，分别求出两组数据的最大差值，再代入公式max=100%L FSL Y γ∆±⨯ 求出每组数据的线性度。
FS Y 指的是满量程输出，这里取重量为250g 的数据。
具体实现的MATLAB 代码：x=[0 10 20 30 40 50 70 100 120 150 170 200 250]; x0=[0 250];y01=[2.8646 2.8734]; y03=[2.8736 2.8828];y1=[2.8646 2.8646 2.8648 2.8652 2.8653 2.8687 2.8662 2.8677 2.8681 2.8696 2.8701 2.8715 2.8734];%第一组数据y2=[2.8613 2.8615 2.8619 2.8623 2.8625 2.8629 2.8637 2.865 2.8657 2.8668 2.8836 2.8847 2.886];%第二组数据y3=[2.8736 2.8739 2.8742 2.8745 2.8749 2.8752 2.876 2.8771 2.8778 2.879 2.8798 2.8807 2.8828];%第三组数据p1=polyfit(x,y1,1); p2=polyfit(x,y2,1); p3=polyfit(x,y3,1); p4=polyfit(x0,y01,1); p5=polyfit(x0,y03,1);y11=polyval(p1,x);%第一条拟合曲线得到的值y22=polyval(p2,x);%第二条拟合曲线得到的值y33=polyval(p3,x);%第三条拟合曲线得到的值y001=polyval(p4,x);y003=polyval(p5,x);e1=y001-y1;e3=y003-y3;e11=abs(e1);e33=abs(e3);lmax1=max(e11);%第一组数据的非线性绝对误差lmax3=max(e33);subplot(1,2,1)plot(x,y1,'r+',x,y3,'b*',x,y11,'r',x,y33,'b')title('原始曲线与拟合曲线');subplot(1,2,2)plot(x,y001,'r',x,y003,'b')title('端点拟合曲线');yfs1=2.8734;%第一组数据的满量程输出yfs3=2.8828;%第三组数据的满量程输出rl1=(lmax1./yfs1);rl3=(lmax3./yfs3);得到的结果如图所示：第一组数据的线性度为8.1437e-04；第三组数据的线性度为9.0190e-05。
可得实验使用的梁的线性度为8.1437e-04。
2、迟滞性分析先求出每组数据的正反行程的拟合曲线，再将自变量代入拟合曲线求出曲线对应的函数值，将每组数据的正反行程的拟合曲线相减求出最大差值，再代入公式max100%H FSH Y γ∆=±⨯ 求出γ的值。
具体实现的MATLAB 代码：x=[0 10 20 30 40 50 70 100 120 150 170 200 250];y01=[2.8646 2.8646 2.8648 2.8652 2.8653 2.8687 2.8662 2.8677 2.8681 2.8696 2.8701 2.8715 2.8734];%第一组数据正行y03=[2.8736 2.8739 2.8742 2.8745 2.8749 2.8752 2.876 2.8771 2.8778 2.879 2.8798 2.8807 2.8828];%第三组数据正行y11=[2.8605 2.861 2.862 2.8624 2.8627 2.8634 2.8658 2.8672 2.8679 2.869 2.8698 2.8711 2.8734];%第一组数据反向y13=[2.8723 2.8727 2.8733 2.8734 2.8744 2.8747 2.8756 2.8765 2.8774 2.8787 2.8793 2.8808 2.8828];%第三组数据反向p01=polyfit(x,y01,1);%第一组数据曲线拟合 p11=polyfit(x,y11,1);p03=polyfit(x,y03,1);%第三组数据曲线拟合p13=polyfit(x,y13,1);y21=polyval(p01,x);%第一组数据拟合曲线函数值y22=polyval(p11,x);y23=polyval(p03,x);%第三组数据拟合曲线函数值y24=polyval(p13,x);e01=y21-y22;%第一组数据正反行程差值e03=y23-y24;%第三组数据正反行程差值e11=abs(e01);%取绝对值e33=abs(e03);hmax1=max(e11);%求最大差值hmax3=max(e33);yfs1=2.8734;%第一组数据的满量程输出yfs3=2.8828;%第三组数据的满量程输出rh1=hmax1./yfs1;rh3=hmax3./yfs3;subplot(1,2,1)plot(x,y01,'r',x,y11,'r',x,y21,'b',x,y22,'b')title('第一组数据');subplot(1,2,2)plot(x,y03,'r',x,y13,'r',x,y23,'b',x,y24,'b')title('第三组数据')根据MATLAB的计算结果，有rh1= 0.0012,rh3= 3.5277e-04。
两组数据的拟合曲线如图所示。
3、重复性分析求出每组数据的标准偏差，再代入公式(2~3)100%RFSYδγ=±⨯求出γ。
具体实现的MATLAB代码：x=[0 10 20 30 40 50 70 100 120 150 170 200 250];y1=[2.8646 2.8646 2.8648 2.8652 2.8653 2.8687 2.8662 2.8677 2.8681 2.8696 2.8701 2.8715 2.8734];y3=[2.8736 2.8739 2.8742 2.8745 2.8749 2.8752 2.876 2.8771 2.8778 2.879 2.8798 2.8807 2.8828];p1=polyfit(x,y1,1);p3=polyfit(x,y3,1);y11=polyval(p1,x);y33=polyval(p3,x);sd1=std(y1);sd3=std(y3);yfs1=2.8734;%第一组数据的满量程输出yfs3=2.8828;%第三组数据的满量程输出rr1=(2.*sd1)./yfs1;rr3=(2.*sd3)./yfs3;subplot(1,2,1);plot(x,y1,'r',x,y11,'b');title('第一组数据');subplot(1,2,2);plot(x,y3,'r',x,y33,'b');title('第三组数据');根据MATLAB的计算结果，有rr1=0.0020，rr3=0.0020。
4、Excel数据分析利用Excel做线性拟合得到拟合曲线，如下图所示：5、应变测量实验采用的是14桥接法，桥盒输出端接的是应变放大仪，对桥盒的输出电压进行放大，实验中我们设定应变放大仪的增益为10，也就是说采集程序采集的数据是经过放大之后的电压，所以在利用公式（1.1）进行计算的时候，电桥输出电压v 应该除以（10*100）再代入公式进行计算。
则，由式（1.1）可得41000vKV ε=⨯(2.5.1) 其中K 为电阻应变片的灵敏系数，V 为供桥电压，v 为测量电压。
K 与电阻丝的材料有关，实验使用的应变片的K 为2；供桥电压为4V 。
将表1的数据代入（2.5.1）式中，得出下列表格。
其中电压+表示重量正行时候测得的电压数据，电压-表示重量反行时测得的电压数据，同理，应变+是用电压+求得的值，应变-表示用电压-求得的值。
从上述结果可知，当砝码重量增加时，应变量也随之增加，且砝码重量与应变之间的关系与砝码重量与电压之间的关系是一致的，应该是呈线性的，取其中一组做图，发现结果与前面做线性拟合一致，如下图所示。