人教版高中数学(理科)选修正态分布(一)
最新人教版高中数学选修2-3《正态分布》知识讲解

2.4 正态分布1.正态曲线(1)函数______________,x ∈(-∞,+∞),其中实数μ和σ(σ>0)为参数.我们称φμ,σ(x )的图象为正态分布密度曲线,简称________.(2)随机变量X 落在区间(a ,b ]的概率为P (a <X ≤b )≈__________,即由正态曲线,过点(a,0)和点(b,0)的两条x 轴的垂线,及x 轴所围成的平面图形的面积,就是X 落在区间(a ,b ]的概率的近似值.预习交流1(1)正态曲线φμ,σ(x )中参数μ,σ的意义是什么?(2)设随机变量X 的正态分布密度函数φμ,σ(x )=12πe -(x +3)24,x ∈(-∞,+∞),则参数μ,σ的值分别是( ).A .μ=3,σ=2B .μ=-3,σ=2C .μ=3,σ= 2D .μ=-3,σ= 22.正态分布一般地,如果对于任何实数a ,b (a <b ),随机变量X 满足P (a <X ≤b )=__________,则称X 服从________.正态分布完全由参数μ和σ确定,因此正态分布常记作________,如果随机变量X 服从正态分布,则记为________.3.正态曲线的特点(1)曲线位于x轴____,与x轴______;(2)曲线是单峰的,它关于直线____对称;(3)曲线在____处达到峰值______;(4)曲线与x轴之间的面积为__;(5)当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移,如图①;(6)当μ一定时,曲线的形状由σ确定,σ越小,曲线越“____”,表示总体的分布越集中;σ越大,曲线越“____”,表示总体的分布越分散,如图②.预习交流2设随机变量X~N(μ,σ2),且P(X≤C)=P(X>C),则C=().A.0B.σC.-μD.μ4.正态总体在三个特殊区间内取值的概率若X~N(μ,σ2),则对于任何实数a>0,概率P(μ-a<X≤μ+a)=__________.特别地有P(μ-σ<X≤μ+σ)=______,P(μ-2σ<X≤μ+2σ)=______,P(μ-3σ<X≤μ+3σ)=______.5.3σ原则正态变量在(-∞,+∞)内的取值的概率为1,正态总体几乎总取值于区间(μ-3σ,μ+3σ)之内,而在此区间以外取值的概率只有0.002 6,通常认为这种情况在一次试验中几乎不可能发生,因此在实际应用中通常认为服从于正态分布N(μ,σ2)的随机变量X只取(μ-3σ,μ+3σ)之间的值,简称为________.预习交流3(1)如何求服从正态分布的随机变量X在某区间内取值的概率?(2)正态总体N(4,4)在区间(2,6]内取值的概率为__________.答案:1.(1)φμ,σ(x)=12πσ22()2exμσ--正态曲线(2)∫b aφμ,σ(x)d x预习交流1:(1)提示:参数μ反映随机变量取值的平均水平的特征数,即若X~N(μ,σ2),则E(X)=μ.同理,参数σ是衡量随机变量总体波动大小的特征数,可以用样本的标准差去估计.(2)提示:写成标准式φμ,σ(x)=12π2 e∴μ=-3,σ= 2.2.∫b aφμ,σ(x)d x正态分布N(μ,σ2)X~N(μ,σ2)3.(1)上方不相交(2)x=μ(3)x=μ1σ2π(4)1(6)瘦高矮胖预习交流2:提示:正态分布在x=μ对称的区间上概率相等,则C=μ.4.∫μ+aμ-aφμ,σ(x)d x0.682 60.954 40.997 45.3σ原则预习交流3:(1)提示:首先找出服从正态分布时μ,σ的值,再利用3σ原则求某一个区间上的概率,最后利用在关于x=μ对称的区间上概率相等求得结果.(2)提示:由题意知μ=4,σ=2,∴P(μ-σ<X≤μ+σ)=P(2<X≤6)=0.682 6.一、正态曲线的图象应用如图所示的是一个正态曲线,试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差.思路分析:给出一个正态曲线就给出了该曲线的对称轴和最大值,从而就能求出总体随机变量的期望、标准差以及解析式.如图是正态分布N(μ,σ21),N(μ,σ22),N(μ,σ23)(σ1,σ2,σ3>0)相应的曲线,那么σ1,σ2,σ3的大小关系是().A.σ1>σ2>σ3 B.σ3>σ2>σ1 C.σ1>σ3>σ2D.σ2>σ1>σ3(1)用待定系数法求正态变量概率密度曲线的函数表达式,关键是确定参数μ和σ的值,并注意函数的形式.(2)当x=μ时,正态分布的概率密度函数取得最大值,即f(μ)=12πσ为最大值,并注意该式在解题中的应用.二、利用正态曲线的对称性求概率已知随机变量X服从正态分布N(2,σ2),P(X<4)=0.84,则P(X≤0)=().A.0.16 B.0.32 C.0.68 D.0.84思路分析:画出正态曲线,结合其意义及特点求解.若随机变量ξ服从正态分布N(0,1),已知P(ξ<-1.96)=0.025,则P(|ξ|<1.96)=().A.0.025 B.0.050 C.0.950 D.0.975充分利用正态曲线的对称性及面积为1的性质求解.①熟记正态曲线关于直线x=μ对称,从而在关于x=μ对称的区间上概率相等.②P(X<a)=1-P(X≥a);P(X<μ-a)=P(X>μ+a).三、正态分布的应用在某次数学考试中,考生的成绩ξ服从一个正态分布,即ξ~N(90,100).(1)试求考试成绩ξ位于区间(70,110]内的概率是多少?(2)若这次考试共有2 000名考生,试估计考试成绩在(80,100]间的考生大约有多少人?思路分析:正态分布已经确定,则总体的期望μ和标准差σ就可以求出,这样就可以根据正态分布在三个常见的区间上取值的概率进行求解.为了了解某地区高三男生的身体发育状况,抽查了该地区1 000名年龄在17.5岁至19岁的高三男生的体重情况,抽查结果表明他们的体重X(kg)服从正态分布N(μ,22),且正态分布密度曲线如图所示.若体重大于58.5 kg小于等于62.5 kg属于正常情况,则这1 000名男生中属于正常情况的人数是().A.997 B.954 C.819 D.683求正态变量X在某区间内取值的概率的基本方法:(1)根据题目中给出的条件确定μ,σ的值;(2)将待求问题向(μ-σ,μ+σ],(μ-2σ,μ+2σ],(μ-3σ,μ+3σ]这三个区间进行转化;(3)利用上述区间求出相应的概率.答案:活动与探究1:解:从给出的正态曲线可知该正态曲线关于直线x=20对称,最大值是12π,所以μ=20,12πσ=12π,则σ= 2.所以概率密度函数的解析式是f(x)=12π2(20)4ex--,x∈(-∞,+∞).总体随机变量的期望是μ=20,方差是σ2=(2)2=2.迁移与应用:A活动与探究2:A解析:由X~N(2,σ2),可知其正态曲线如图所示,对称轴为x=2,则P(X≤0)=P(X≥4)=1-P(X<4)=1-0.84=0.16.迁移与应用:C解析:由已知正态曲线的对称轴为x=μ=0,∴P(ξ<-1.96)=P(ξ>1.96)=0.025.∴P(|ξ|<1.96)=1-P(ξ≥1.96)-P(ξ≤-1.96)=0.950.活动与探究3:解:∵ξ~N(90,100),∴μ=90,σ=100=10.(1)由于正态变量在区间(μ-2σ,μ+2σ]内取值的概率是0.954 4,而该正态分布中,μ-2σ=90-2×10=70,μ+2σ=90+2×10=110,于是考试成绩ξ位于区间(70,110]内的概率就是0.954 4.(2)由μ=90,σ=10得μ-σ=80,μ+σ=100.由于正态变量在区间(μ-σ,μ+σ]内取值的概率是0.682 6,所以考试成绩ξ位于区间(80,100]内的概率是0.682 6.一共有2 000名考生,所以考试成绩在(80,100]间的考生大约有2 000×0.682 6≈1 365(人).迁移与应用:D解析:由题意,可知μ=60.5,σ=2,故P(58.5<X≤62.5)=P(μ-σ<X≤μ+σ)=0.682 6,从而属于正常情况的人数是1 000×0.682 6≈683.1.正态曲线关于y轴对称,则它所对应的正态总体的均值为().A.1 B.-1 C.0 D.不确定2.设随机变量X ~N (1,22),则D ⎝⎛⎭⎫12X =( ).A .4B .2 C.12D .1 3.已知随机变量ξ服从正态分布N (0,σ2),若P (ξ>2)=0.023,则P (-2≤ξ≤2)=( ).A .0.447B .0.628C .0.954D .0.9774.在某项测量中,测量结果ξ服从正态分布N (1,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为__________.5.一批灯泡的使用时间X (单位:小时)服从正态分布N (10 000,4002),则这批灯泡使用时间在(9 200,10 800]内的概率是__________.答案:1.C 解析:由正态曲线关于y 轴对称,∴μ=0,均值为0.2.D 解析:因为X ~N (1,22),所以D (X )=4,所以D ⎝⎛⎭⎫12X =14D (X )=1.3.C 解析:∵随机变量ξ服从标准正态分布N (0,σ2),∴正态曲线关于x =0对称.又P (ξ>2)=0.023,∴P (ξ<-2)=0.023.∴P (-2≤ξ≤2)=1-2×0.023=0.954.4.0.8 解析:易得P (0<ξ<1)=P (1<ξ<2),故P (0<ξ<2)=2P (0<ξ<1)=2×0.4=0.8.5.0.954 4 解析:μ=10 000,σ=400,P (9 200<X ≤10 800)=P (10 000-2×400<X ≤10 000+2×400)=0.954 4.。
新人教版高中数学《正态分布》PPT优秀课件1

式中的实数m、s是参数
1.正态分布定义 y
如果对于任何实数 a<b,随机变量X满足:
P(aXb)abm,s(x0)dx a b
x
则称X 的分布为正态分布. 正态分布由参数m、s
唯一确定, m、s分别表示总体的平均数与标准差.
正态分布记作N( m,s2).其图象称为正态曲线.
如果随机变量X服从正态分布,则记作:
由σ决定.
o
x
3. 3个特殊结论 若 X~: N(m,s2) ,则
区间
ms,ms
m2s,m2s
m3 s,m3 s
取值概率
0.6826 0.9544 0.9974
4. 3σ原则
正态总体几乎总取值于区间 m3s,m3s
之内,而在此区间以外取值的概率只有0.26%,通 常认为这种情况在一次试验中几乎不可能发生.
感谢聆听,欢迎指导!
X~N(m,s2)
y
正态曲线的性质
0
x
m,s(x)
1 e
2s
(xm)2
2s2 x(,)
式中的实数m、s是参数
2.正态曲线的性质
(1)非负性:曲线 m ,s ( x ) 在轴的上方,与x轴
不相交(即x轴是曲线的渐近线).
(2)定值性:曲线 m ,s ( x ) 与x轴围成的面积为1.
(3)对称性:正态曲线关于直线 x=μ对称, 曲线成“钟形”. (4)单调性:在直线 x=μ的左边, 曲线是上升的; 在直线 x=μ的右边, 曲线是下降的.
正态分布
一个随机变量x,受到了众多互不相干的、不分主次 的偶然因素的影响.则x服从或近似服从正态的分布
正态分布
如何才能使拟合度更高.估计更准确
人教版高中数学选修2-3 第二章正态分布 同步教案
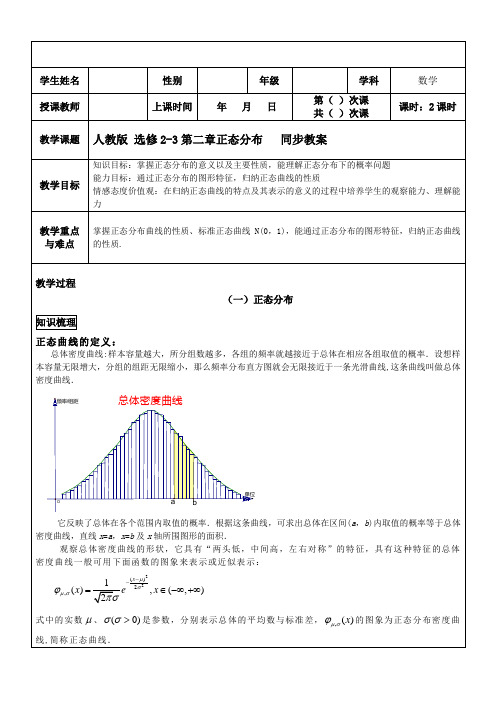
学生姓名 性别 年级 学科 数学 授课教师上课时间 年 月 日第( )次课 共( )次课课时:2课时教学课题 人教版 选修2-3第二章正态分布 同步教案教学目标知识目标:掌握正态分布的意义以及主要性质,能理解正态分布下的概率问题 能力目标:通过正态分布的图形特征,归纳正态曲线的性质情感态度价值观:在归纳正态曲线的特点及其表示的意义的过程中培养学生的观察能力、理解能力教学重点与难点 掌握正态分布曲线的性质、标准正态曲线N(0,1),能通过正态分布的图形特征,归纳正态曲线的性质.教学过程(一)正态分布知识梳理正态曲线的定义:总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线.总体密度曲线b单位O频率/组距a它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a ,b )内取值的概率等于总体密度曲线,直线x =a ,x =b 及x 轴所围图形的面积.观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示:22()2,1(),(,)2x x e x μσμσϕπσ--=∈-∞+∞式中的实数μ、)0(>σσ是参数,分别表示总体的平均数与标准差,,()x μσϕ的图象为正态分布密度曲线,简称正态曲线.正态分布的定义:一般地,如果对于任何实数a b <,随机变量X 满足,()()baP a X B x dx μσϕ<≤=⎰,则称 X 的分布为正态分布(normal distribution ) .正态分布完全由参数μ和σ确定,因此正态分布常记作),(2σμN .如果随机变量 X 服从正态分布,则记为X ~),(2σμN .说明:1参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去佑计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计.2.正态分布),(2σμN )是由均值μ和标准差σ唯一决定的分布通过固定其中一个值,讨论均值与标准差对于正态曲线的影响3.通过对三组正态曲线分析,得出正态曲线具有的基本特征是两头底、中间高、左右对称 正态曲线的作图,书中没有做要求,教师也不必补上 讲课时教师可以应用几何画板,形象、美观地画出三条正态曲线的图形,结合前面均值与标准差对图形的影响,引导学生观察总结正态曲线的性质 4.正态曲线的性质:(1)曲线在x 轴的上方,与x 轴不相交 (2)曲线关于直线x=μ对称(3)当x=μ时,曲线位于最高点πσ21(4)曲线与x 轴之间的面积为1(5)当x <μ时,曲线上升(增函数);当x >μ时,曲线下降(减函数) 并且当曲线向左、右两边无限延伸时,以x 轴为渐近线,向它无限靠近(6)μ一定时,曲线的形状由σ确定σ越大,曲线越“矮胖”,总体分布越分散; σ越小.曲线越“瘦高”.总体分布越集中.若X~N (μ,2σ) ,则对于任何实数a>0,概率()()dx x a a P a a⎰+-=+≤-μμσμϕμμ,X <为如图中的阴影部分的面积,对于固定的μ 和 a 而言,该面积随着σ的减少而变大。
新人教版高中数学选择性必修一课件:7.5 正态分布

如果随机变量X服从正态分布, 则记作: X~N( μ,σ2)
在新人教实A版际高中数遇学精到品教学的课件许多随机现象都服从或近似服从 正态分布: 在生产中:在正常生产条件下各种产品的质量指标; 在测量中:测量结果;
在生物学中:同一群体的某一特征;……; 在气象中:某地每年七月份的平均气温、平均湿度
A. f (x)
1
( x )2
e 2 2 , , ( 0)都是实数
2
B. f (x)
2
x2
e2
2
1
( x1)2
C. f (x) 2
e
2
4
1
x2
D. f (x)
e2
2
概率等 y 新人教A版高中数学精品教学课件 于该曲 边梯形 的面积
平均数
a bc d
x
若用X表示落下的小球第1次与高尔顿板底
以及降雨量等,水文中的水位; 总之,正态分布广泛存在于自然界、生产及科学 技术的许多领域中。
正态分布在概率和统计中占有重要地位。
3、正态曲线的性质 新人教A版高中数学精品教学课件
( x) 21 e ,
( x )2 2 2
, x (, )
y
y
y
μ= -1
σ=0.5
μ=0 σ=1
μ=1 σ=2
-3 -2 -1 0 1 2 x -3 -2 -1 0 1 2 3 x -3 -2 -1 0 1 2 3 4x
新人教A版高中数学精品教学课件
2.设离散型随机变量X~N(0,1),则 P( X 0) = 0.5 .
3.若已知正态总体落在区间(0.3, ) 的概率为0.5,则相 应的正态曲线在x= 0.3 时达到最高点。
人教版高中数学(理科)选修正态分布教案

正态分布2目的要求1.利用标准正态分布表求得标准正态总体在某一区间内取值的概率。
2.掌握正态分布与标准正态分布的转换。
3.了解正态总体的分布情况,简化正态总体的研究问题。
内容分析1.标准正态分布是正态分布研究的重点,各式各样的正态分布可以通过)()(σμ-Φ=x x F 转换成标准正态曲线,转换后正态分布的各项性质保持不变,而标准正态分布的概率又可以通过查表求得,因而标准正态分布表的使用是本节课的重点之一。
2.介绍《标准正态分布表》的查法。
表中每一项有三个相关的量:x 、y 、P ,x 是正态曲线横轴的取值,y 是曲线的高度,P 是阴影部分的面积。
即)()(00x x P x <=Φ。
3.标准正态曲线关于y 轴对称。
因为当00>x 时,)()(00x x P x <=Φ;而当00<x 时,根据正态曲线的性质可得:)(1)(00x x -Φ-=Φ,并且可以求得在任一区间),(21x x 内取值的概率。
)()()(1221x x x x x P Φ-Φ=<<。
4.由例2、例3的讲授,对于任一正态总体),(2σμN 都可以通过)()(σμ-Φ=x x F ,求得其在某一区间内取值的概率。
5.从下列三组数据不难看出,正态总体在(μ-3σ,μ+3σ)以外的概率只有万分之二十六,这是一个很小的概率。
这样,就简化了正态总体中研究的问题。
F (μ-σ,μ+σ)≈0.683,F (μ-2σ,μ+2σ)≈0.954,F (μ-3σ,μ+3σ)≈0.997。
教学过程1.复习提问(1)借助于正态曲线图形,回忆正态曲线的性质。
(2)运用正态曲线的性质,解决实际问题。
2.标准正态总体的概率问题,只要有标准正态分布表即可解决,如何查表是必须解决的问题。
3.对于标准正态总体N (0,1),)(0x Φ是总体取值小于0x 的概率,即:)()(00x x P x <=Φ,其中00>x ,图中阴影部分的面积表示为概率。
高中数学人教版选修正态分布课件系列一

2. 正态分布密度函数的性质
正态分布密度函数满足以下性质:
(1)函数图像关于 直线x=μ对称
;
(2) σ(σ>0)的大小 决定函数图像的“胖”“瘦”;
(3)如下图所示,
P(μ-σ<X<μ+σ)=68.3%, P(μ-2σ<X<μ+2σ)=95.4%, P(μ-3σ<X<μ+3σ)=99.7%.
(4)在分布密度函数图像下方和x轴上方范围内的区域面积为
的.
课前自主学习
1. 正态分布
如果一个连续型随机变量X的分布密度函数为
f(x)=σ 12πexp{-x-2σμ2 2},-∞<x<+∞
,
其中exp{g(x)}=eg(x),那么称X服从参数为μ和σ2的正态分 布,通常记作 X~N(μ,σ2) .
正态分布的两个重要参数:均值μ和方差σ2(σ>0).当μ和σ2 给定后,就是一个具体的正态分布.不同的μ和σ对应着不同的 分布密度曲线,如下图所示.
[思路分析] 由正态曲线的图像可知,该曲线的对称轴为x
=20,最大值为2
1
π,因此,μ=20,由2
1
= πσ
12π可求得σ的
值.
[完美作答] 从给出的正态曲线可知,该正态曲线关于直
线x=20对称,最大值是2 1 π,所以μ=20.
由 σ
1 =1 2π 2
π,解得σ=
2.
于是概率密度函数的解析式是P(x)=2 1 πexp{-
人教版 必修2-3
第二章 随机变量及其分布 2.4 正态分布
课标要求
学法指导
1.利用实际问题的直方图,了解正态分 1.正态分布的小概率事件是一个重要的概
高二数学人选修课件正态分布
概率计算步骤
确定概率类型(单侧或双 侧),查找对应的z值, 利用标准正态分布表计算 概率。
一般正态分布概率计算
一般正态分布定义
均值布转化为标准正态分布进 行计算。z=(x-μ)/σ。
概率计算步骤
确定概率类型,进行z变换 ,查找对应的z值,利用标 准正态分布表计算概率。
THANKS
感谢观看
01
练习题一
已知某次考试的分数服从正态 分布,均分为70分,标准差为 10分。求分数在60分以下的概 率。
02 解题思路
首先根据正态分布的性质,确 定分数在60分以下对应的z值, 然后查找标准正态分布表或使 用相关软件计算对应的概率。
03
练习题二
04
某工厂生产的产品重量服从正态 分布,均重为500克,标准差为 10克。若要保证95%的产品重 量在480克至520克之间,问该 工厂应如何调整生产流程?
04
正态分布在生活中应用
质量控制与六西格玛管理法
质量控制
在制造业中,正态分布被广泛应用于质量控制。通过对生产过程中的数据进行正 态分布拟合,可以判断产品质量的稳定性和一致性,进而采取相应的措施进行改 进。
六西格玛管理法
六西格玛管理法是一种追求卓越的管理哲学,其核心思想是通过减少变异和提高 过程能力来达到更高的质量水平。正态分布在这里扮演着重要角色,它提供了一 种衡量过程变异和确定过程能力的方法。
社会科学领域数据分析与可视化
数据分析
在社会科学领域,正态分布被广泛应用于数据分析。例如,在心理学、教育学等研究中,通过对实验 数据进行正态分布检验,可以判断数据是否符合正态分布假设,进而选择合适的统计方法进行分析。
可视化
正态分布也为数据可视化提供了便利。通过将数据按照正态分布进行拟合和展示,可以更加直观地呈 现数据的分布规律和特点,有助于研究者更好地理解和解释数据。
人教版数学高二-《正态分布》精品课件 新课标
• [题后感悟] 解答此类题目的关键在于将待求 的问题向(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ -3σ,μ+3σ)这三个区间进行转化,然后利用 上述区间的概率求出相应概率,在此过程中依 然会用到化归思想及数形结合思想.
高中数学
• 3.设在一次数学考试中,某班学生的分数服 从X~N(110,202),且知满分150分,这个班 的学生共54人.求这个班在这次数学考试 中及格(不小于90分)的人数和130分以上的 人数.
高中数学
• A.三科总体的标准差及平均数都相同 • B.甲、乙、丙三科的总体的平均数不相同 • C.丙科总体的平均数最小 • D.甲科总体的标准差最小 • 解析: 由题图可得,甲、乙、丙三科的平均
分一样,但它们的标准差大小不同,σ甲<σ乙 <σ丙. • 答案: D
高中数学
(2011湖北高考)已知随机变量ξ服从 正态分布N(2,σ2),且P(ξ<4)=0.8,则 P(0<ξ<2)=( )
(3)曲线在 x=μ
处达到峰值 1 ; σ 2π
高中数学
1
σ
μ
• (4)曲线与x轴之间的面积为 • (5)当 越一大定时,曲线随着
沿x轴平移,如图①;
;
越小
的变化而
• (6)当μ一定时,曲线的形状由σ确定,σ ,曲线越“瘦高”;σ , 曲 线 越
“.正态总体在三个特殊区间内取值的概率值 • P(μ-σ<X≤μ+σ)= 0. ;682 6 • P(μ-2σ<X≤μ+2σ)= 0.954 4 ; • P(μ-3σ<X≤μ+3σ)= 0.997 4 .
越大,曲线越“矮胖”,表示总体越分散;σ 越小,曲线越“高瘦”,表示总体的分布越集 中,这个性质可直接判断.由正态曲线性质知 μ1<μ2,σ1<σ2. • 答案: A
人教版高中数学《正态分布》公开课课件
不能一一列举
可以一一列举
连续型随机变量与离散型分组的组距不断缩小时, 思考:频率分布直方图的轮廓有何特点?
频率 组距
o
时间
y
正态曲线
x O
定义1
正态密度函数:
f(x)
C 解析:由红外线自动测温门测量体温误差服从正态分布 N(0.1,0.32),得 μ=0.1,σ=0.3. 所 以 测 量 体 温 误 差 在 区 间 (0.4,0.7] 内 的 概 率 为:P(0.4<ξ≤0.7)=P(μ+σ<ξ≤μ+2σ)= [P(μ-2σ≤ξ≤μ+2σ)-P(μ-σ≤ξ≤μ+σ)]=0.135 9.
信息技术演示
3σ原则
--------正态分布的实际应用
正态分布中变量X几乎总取值于区间(μ-3σ,μ+3σ]之内,而在此区间 以外取值的概率只有0.27%,通常认为这种情况在一次试验中几乎不可能发生。
故在实际应用中,通常认为正态分布的随机变量X只取[μ-3σ,μ+3σ]之 内的值,简称“3σ”原则.
1
3、曲线在 x=μ 处达到峰值 σ 2π .
y
0
ab
x
思考2:x轴与正态曲线所夹面积为多少? 1
思考3:对称区域面积有何特征?
S(-,-x)
正态曲线下的面积规律: 正态曲线下对称区域的面积相等
S(x,+)=S(-,-x) 对应的概率也相等
应用探究
例 已知随机变量ξ服从正态分布N(2, σ2), 且P(ξ<4)=0.8, 则P(0<ξ<2)=( )C
当堂达标
红外线自动测温门能有效避免测温者与被测温者的近距离接触,降低潜在的 病毒感染风险,为防控新冠肺炎,某厂生产的红外线自动测温门,其测量体温误 差服从正态分布 N(0.1,0.32),从已经生产出的测温门中随机取出一件,则其测 量体温误差在区间(0.4,0.7]内的概率为( ) ( 附 : 若 随 机 变 量 ξ 服 从 正 态 分 布 N(μ,σ). 则 P(μ-σ≤ξ≤μ+σ)=0.682 7,P(μ-2σ≤ξ≤μ+2σ)=0.954 5) A.0.317 4 B.0.271 8 C.0.135 9 D.0.045 6
人教版高中数学选修2-3-正态分布-1完整ppt课件
完整版PPT课件
10
σ一定
μ =-1
μ =0
O
正态曲线的特点
m,s (x)
1
( xm )2
e 2s 2
2 s
μ =1
μ一定
σ=0.5
σ=1
σ=2
x
O
x
(5)当 一定时,曲线随着 的变化而沿x轴平移;
(6)当μ一定时,曲线的形状由σ确定 .
σ越大,曲线越“矮胖”,表示总体的分布越分散;
σ越小,曲线越“瘦高”,表示总体的分布越集中.
唯一确定, m、s分别表示总体的平均数与标准差.
正态分布记作N( m,s2).其图象称为正态曲线.
如果随机变量X服从正态分布,则记作记为
X~N(m,s2)
完整版PPT课件
7
例题探究
例1.给出下列两个正态总体的函数表达式,请找出其
均值m和标准差s
(1)
(x)
1
x2
e2,x(,)
2
m0 , s 1
(2)
m m P ( ax≤ a )m a m a
m,s(x )d x
x=μ
m-a m+a
正态曲线.gsp
完整版PPT课件
14
特别地有
P(msXms)0.6826, P(m2sXm2s)0.9544, P(m3sXm3s)0.9974.
完整版PPT课件
15
例3.商场经营的某种包装的大米质量服从正态分布 N(10,0.12)(单位:kg)任选一袋这种大米质量 在9.8~10.2kg的概率是多少?
变式训练3:
若X~N(μ,σ2),问X位于区域(μ,μ+σ)
内的概率是多少?
解:由正态曲线的对称性可得,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正态分布(一)
教学目的:
1 掌握正态分布在实际生活中的意义和作用
2.结合正态曲线,加深对正态密度函数的理理
3.通过正态分布的图形特征,归纳正态曲线的性质
教学重点:正态分布曲线的性质、标准正态曲线N(0,1)
教学难点:通过正态分布的图形特征,归纳正态曲线的性质
授课类型:新授课
课时安排:1课时
教具:多媒体、实物投影仪
内容分析:
1.在实际遇到的许多随机现象都服从或近似服从正态分布在上一节课我们研究了当样本容量无限增大时,频率分布直方图就无限接近于一条总体密度曲线,总体密度曲线较科学地反映了总体分布但总体密度曲线的相关知识较为抽象,学生不易理解,因此在总体分布研究中我们选择正态分布作为研究的突破口正态分布在统计学中是最基本、最重要的一种分布
2.正态分布是可以用函数形式来表述的其密度函数可写成:
2
()
2
(),(,)
x
f x x
μ
σ
-
-
=∈-∞+∞,(σ>0)
由此可见,正态分布是由它的平均数μ和标准差σ唯一决定的常把它记为)
,
(2
σ
μ
N
3.从形态上看,正态分布是一条单峰、对称呈钟形的曲线,其对称轴为x=μ,并在x=μ时取最大值从x=μ点开始,曲线向正负两个方向递减延伸,不断逼近x轴,但永不与x轴相交,因此说曲线在正负两个方向都是以x轴为渐近线的
4.通过三组正态分布的曲线,可知正态曲线具有两头低、中间高、左右对称的基本特征
5.由于正态分布是由其平均数μ和标准差σ唯一决定的,因此从某种意义上说,正态分布就有好多好多,这给我们深入研究带来一定的困难但我们也发现,许多正态分布中,重点研究N(0,1),其他的正态分布都可以通过)
(
)
(
σ
μ
-
Φ
=
x
x
F转化为N(0,1),我们把N(0,1)称为标准正态分布,其密度函数为
2
2
1
2
1
)
(x
e
x
F-
=
π
,x∈(-∞,+∞),从而使正态分布的研究得以简化
6.结合正态曲线的图形特征,归纳正态曲线的性质正态曲线的作图较难,教科书没做要求,授课时可以借助几何画板作图,学生只要了解大致的情形就行了,关键是能通过正态曲线,引导学生归纳其性质教学过程:
一、复习引入:
总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线.
它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a ,b )内取值的概率等于总体密度曲线,直线x =a ,
x =b 及x 轴所围图形的面积.
观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示: 2()2(),(,)x f x x μσ--=∈-∞+∞
式中的实数μ、)0(>σσ是参数,
分别表示总体的平均数与标准差,函数)(x f 称为正态函数,)(x f 的图象称为正态曲线.
本节课,我们将学习一种在实际生产、生活中常见的总体密度曲线——正态曲线 二、讲解新课:
1.正态分布密度函数:
22()2(),(,)x f x x μσ--=∈-∞+∞,
(σ>0) 其中π是圆周率;e 是自然对数的底;x 是随机变量的取值;μ为正态分布的均值;σ是正态分布的标准差.正态分布一般记为),(2σμN
2.正态分布)
,(2
σμN )是由均值μ和标准差σ唯一决定的分布
通过固定其中一个值,讨论均值与标准差对于正态曲线的影响
3.通过对三组正态曲线分析,得出正态曲线具有的基本特征是两头底、中间高、左右对称正态曲线的作图,书中没有做要求,教师也不必补上讲课时教师可以应用几何画板,形象、美观地画出三条正态曲线的图形,结合前面均值与标准差对图形的影响,引导学生观察总结正态曲线的性质
4.正态曲线的性质:
(1)曲线在x 轴的上方,与x 轴不相交
(2)曲线关于直线x=μ对称
(3)当x=μ时,曲线位于最高点
(4)当x <μ时,曲线上升(增函数);当x >μ时,曲线下降(减函数)并且当曲线向左、右两边无限延伸时,以x 轴为渐近线,向它无限靠近
(5)μ一定时,曲线的形状由σ确定
σ越大,曲线越“矮胖”,总体分布越分散;
σ越小.曲线越“瘦高”.总体分布越集中:
五条性质中前三条学生较易掌握,后两条较难理解,因此在讲授时应运用数形结合的原则,采用对比教学
5.标准正态曲线:当μ=0、σ=l 时,正态总体称为标准正态总体,其相应的函数表示式是22
21
)(x e x f -=π,(-∞<x <+∞)
其相应的曲线称为标准正态曲线
标准正态总体N (0,1)在正态总体的研究中占有重要的地位任何正态分布的概率问题均可转化成标准正态分布的概率问题
三、讲解范例:
例1.给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ
(1)),(,21
)(22+∞-∞∈=-x e x f x π
(2)),(,221)(8)1(2
+∞-∞∈=--x e x f x π (3)22(1)(),(,)
x f x x -+=∈-∞+∞ 答案:(1)0,1;(2)1,2;(3)-1,0.5
四小结 :总体密度曲线——正态曲线——标准正态曲线
五、课后作业:
六、板书设计(略)
七、课后记:。
