初二数学几何类综合题及参考答案
初二几何练习题及答案

初二几何练习题及答案一、选择题1. 下列图形中,边数最多的是:A. 正方形B. 三角形C. 圆形D. 长方形答案:B. 三角形2. 以下哪个选项是一个多边形?A. 圆形B. 长方形C. 椭圆形D. 正方形答案:B. 长方形3. 以下哪个几何图形是三角形的一种?A. 圆B. 梯形C. 正方形D. 椭圆答案:B. 梯形4. 对于一个正方形,边长为a,则它的周长是:A. 2aB. 4aC. a²D. a³答案:B. 4a5. 对于一个圆形,半径为r,则它的周长是:A. 2rB. 4rC. πr²D. 2πr答案:D. 2πr二、填空题1. 一个正方形的边长为5cm,则它的面积是__________。
答案:25cm²2. 一个长方形的长为8cm,宽为4cm,则它的周长是__________。
答案:24cm3. 一个三角形的底边长为7cm,高为4cm,则它的面积是__________。
答案:14cm²4. 一个正方形的周长为12cm,则它的边长是__________。
答案:3cm5. 一个圆形的直径为10cm,则它的半径是__________。
答案:5cm三、解答题1. 如图所示,画出一个正方形,边长为6cm。
(略)2. 如图所示,已知直角三角形的一条直角边长为5cm,斜边长为10cm,求另一条直角边的长度。
解:根据勾股定理,直角三角形的两个直角边的平方和等于斜边的平方。
假设另一条直角边长为a,则有:5² + a² = 10²化简得:25 + a² = 100移项得:a² = 100 - 25计算得:a² = 75开方得:a ≈ 8.66cm答案:约为8.66cm3. 如图所示,计算一个边长为10cm的正方形的面积和周长。
解:面积 = 边长² = 10² = 100cm²周长 = 4 ×边长 = 4 × 10 = 40cm答案:面积为100cm²,周长为40cm4. 如图所示,求一个高为8cm,底边长为6cm的三角形的面积。
初二数学几何题50道,要带答案带过程

初二数学几何题50道,要带答案带过程选择题:1. 若两角互为补角,则它们的差是()。
A.0°B.45°C.60°D.90°2. 在图中,如点S、T分别在边AB的延长线上,且∠ASP=60°,∠BAT=20°,则∠AST为()。
A.40°B.50°C.80°D.110°3. 已知正方形ABCD的边长为5cm,点E、F分别在边AD、AB上,且AE=BF,则三角形CEF的面积为()。
A.(5/8) cm²B.(9/8) cm²C.(13/8) cm²D.(15/8) cm²4. 如果一个圆心角的度数为30°,则它所对的弧度数是()。
A.π/6B.π/3C.π/4D.π/2填空题:1.如图,已知BC平分∠ABD,设∠BAC=a°,∠BCA=b°,则∠CBD=\_\_\_\_°。
2.如图,点A、B、C在同一条直线上,则对于ΔABC来说,以下说法正确的是:①AB=AC;②\angleBAC是钝角;③\angleABC+\angleACB =180^\circ,所以\angleABC=\_\_\_\_°,\angleACB=\_\_\_\_°。
3. 已知直角三角形ABC,其中\angleC=90°,BC=3,AC=4,则AB=\_\_\_\_。
4.如图,长方形ABCD中,点E、F分别为BC、CD上的点,若∠BAE=∠EFD,AB=10cm,则DF=\_\_\_\_cm。
解答题:1.如图,在\triangleABC中,垂足分别为D、E、F。
若AC=6,BD=8,DE=5,EF=9,则BC=()。
2.如图,已知\angleBAC=60°,AD平分\angleBAC,且BD=AD,点E为AD的延长线上的点,且\angleBEC=140°,则\angleACD=\_\_\_\_\_\_°。
几何初二试题及答案

几何初二试题及答案一、选择题1. 已知一个三角形的两边长分别为3和4,第三边的长x满足的不等式是:A. 1 < x < 7B. 4 < x < 7C. 1 < x < 4D. 3 < x < 7答案:D2. 一个圆的半径为5cm,那么这个圆的周长是多少?A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案:D3. 已知一个矩形的长为6cm,宽为4cm,那么这个矩形的面积是多少?A. 20cm²B. 24cm²C. 18cm²D. 16cm²答案:B二、填空题1. 平行四边形的对角线互相______。
答案:平分2. 如果一个角的度数是30°,那么它的余角是______。
答案:60°3. 一个直角三角形的两条直角边分别为3和4,那么它的斜边长是______。
答案:5三、简答题1. 描述如何使用勾股定理来计算直角三角形的斜边长。
答案:首先确定直角三角形的两条直角边的长度,设为a和b。
根据勾股定理,斜边c的长度可以通过公式c = √(a² + b²) 来计算。
2. 解释什么是相似三角形,并给出一个例子。
答案:相似三角形是指两个三角形的对应角相等,对应边的比例相等的三角形。
例如,如果三角形ABC与三角形DEF的角A等于角D,角B等于角E,角C等于角F,并且边AB与边DE、边BC与边EF、边AC与边DF的长度比例相等,那么这两个三角形就是相似的。
四、解答题1. 已知一个等腰三角形的底边长为10cm,两腰的长度为13cm,求这个三角形的面积。
答案:首先,我们可以将等腰三角形分成两个直角三角形,通过底边的中点。
这样,每个直角三角形的底边长度为5cm,斜边为13cm。
根据勾股定理,我们可以计算出高h:h = √(13² - 5²) = √(169 - 25) = √144 = 12cm。
(完整版)八年级数学几何经典题【含答案】
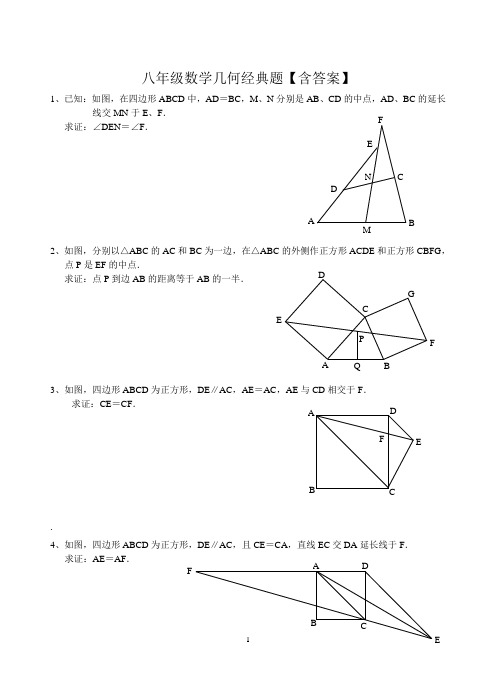
F八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.3、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF ..4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .B5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。
求证:EF=FD 。
8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA,九年级数学【答案】1.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。
2.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
初二几何试题及答案

初二几何试题及答案1. 已知三角形ABC中,AB=AC,D是BC边上的中点。
求证:AD垂直于BC。
答案:因为AB=AC,所以三角形ABC是等腰三角形。
根据等腰三角形的性质,底边的中线、高线和角平分线重合。
因此,AD既是BC边上的中线,也是高线,所以AD垂直于BC。
2. 一个矩形的长是宽的两倍,且对角线长为10cm。
求矩形的长和宽。
答案:设矩形的宽为x cm,则长为2x cm。
根据勾股定理,对角线的长度满足方程x^2 + (2x)^2 = 10^2。
解得x^2 + 4x^2 = 100,即5x^2 = 100,所以x^2 = 20,x = √20。
因此,矩形的宽为√20 cm,长为2√20 cm。
3. 一个圆的直径是10cm,求这个圆的面积。
答案:圆的面积公式为A = πr^2,其中r是圆的半径。
因为直径是10cm,所以半径r = 10/2 = 5cm。
代入公式得A = π * 5^2 = 25π cm^2。
4. 一个梯形的上底是8cm,下底是12cm,高是5cm。
求梯形的面积。
答案:梯形的面积公式为A = (a + b) * h / 2,其中a和b分别是上底和下底的长度,h是高。
代入数据得A = (8 + 12) * 5 / 2 = 20 * 5 / 2 = 50 cm^2。
5. 已知一个直角三角形的两条直角边分别是6cm和8cm,求斜边的长度。
答案:根据勾股定理,斜边的长度c满足方程c^2 = a^2 + b^2,其中a和b分别是两条直角边的长度。
代入数据得c^2 = 6^2 + 8^2 = 36+ 64 = 100,所以c = √100 = 10cm。
6. 一个正六边形的边长是4cm,求它的面积。
答案:正六边形可以被分成6个等边三角形,每个等边三角形的边长都是4cm。
等边三角形的面积公式为A = (√3 / 4) * a^2,其中a是边长。
因此,正六边形的面积为6 * (√3 / 4) * 4^2 = 6 * √3 * 4 = 24√3 cm^2。
初二平面几何考试题及答案

初二平面几何考试题及答案一、选择题(每题2分,共20分)1. 下列哪个图形是轴对称图形?A. 正方形B. 圆C. 长方形D. 等边三角形答案:B2. 一个圆的半径为5cm,那么它的周长是多少?A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案:C3. 一个三角形的内角和是多少度?A. 90°B. 180°C. 360°D. 540°答案:B4. 一个平行四边形的对角线互相平分,那么这个平行四边形是:A. 矩形B. 菱形C. 梯形D. 不规则四边形答案:A5. 如果一个角是直角的补角,那么这个角的度数是多少?A. 45°B. 90°C. 135°D. 180°答案:A6. 一个正六边形的内角是多少度?A. 60°B. 90°C. 120°D. 180°答案:C7. 一个圆的面积公式是:A. πr²B. πdC. π(r+d)²D. πr²/48. 一个三角形的外角等于与它相邻的内角的:A. 补角B. 余角C. 相等D. 两倍答案:A9. 一个矩形的对角线相等,那么这个矩形是:A. 正方形B. 长方形C. 梯形D. 不规则四边形答案:A10. 一个圆的内接四边形的对角线互相垂直,那么这个四边形是:A. 矩形B. 菱形C. 梯形D. 平行四边形答案:B二、填空题(每题2分,共20分)11. 一个直角三角形的两条直角边分别为3cm和4cm,那么它的斜边长是________cm。
答案:512. 一个正五边形的每个内角是________度。
答案:10813. 如果一个三角形的三边长分别为a, b, c,且满足a² + b² = c²,那么这个三角形是________三角形。
答案:直角14. 一个圆的半径增加1cm,那么它的面积增加了________πcm²。
初二数学几何试题及答案
初二数学几何试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项不是三角形的内角和?A. 180°B. 360°C. 540°D. 720°2. 如果一个三角形的两条边长分别为3和4,第三边的长度可能为:A. 1B. 5C. 7D. 93. 一个圆的半径为5厘米,那么它的周长是:A. 10π cmB. 20π cmC. 30π cmD. 40π cm4. 一个正方形的对角线长度为10厘米,那么它的边长是:A. 5 cmB. 7.07 cmC. 10 cmD. 14.14 cm5. 一个长方形的长和宽分别是8厘米和6厘米,那么它的面积是:A. 48 cm²B. 36 cm²C. 24 cm²D. 12 cm²二、填空题(每题2分,共10分)6. 一个等腰三角形的底角是45°,那么它的顶角是________度。
7. 如果一个正多边形的每个内角都是120°,那么它是________边形。
8. 一个圆的直径是14厘米,那么它的半径是________厘米。
9. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的斜边长是________厘米。
10. 如果一个平行四边形的对角线互相平分,那么它是一个________。
三、计算题(每题10分,共20分)11. 一个正六边形的边长为2厘米,求它的周长和面积。
12. 已知一个圆的半径为7厘米,求它的面积和周长。
四、解答题(每题15分,共30分)13. 在一个等边三角形ABC中,点D是边AB上的一点,且AD=2,BD=1。
求∠ADC的度数。
14. 一个圆的半径为10厘米,圆心到一个点P的距离为8厘米,求点P到圆上任意一点的距离的最大值和最小值。
答案:一、选择题1. B2. B3. B4. B5. A二、填空题6. 907. 68. 79. 510. 矩形三、计算题11. 周长:2×6=12厘米;面积:(3√3)×2²=12√3平方厘米。
初二数学几何综合训练题及答案
初二几何难题训练题1,如图矩形ABCD对角线AC、BD交于O,E F分别是OA、OB的中点(1)求证△ADE≌△BCF:(2)若AD=4cm,AB=8cm,求CF的长。
证明:(1)在矩形ABCD中,AC,BD为对角线,∴AO=OD=OB=OC∴∠DAO=∠ADO=∠CBO=∠BCO∵E,F为OA,OB中点∴AE=BF=1/2AO=1/2OB∵AD=BC, ∠DAO=∠CBO,AE=BF∴△ADE≌△BCF(2)过F作MN⊥DC于M,交AB于N∵AD=4cm,AB=8cm∴BD=4根号5∵BF:BD=NF:MN=1:4∴NF=1,MF=3∵EF为△AOB中位线∴EF=1/2AB=4cm∵四边形DCFE为等腰梯形∴MC=2cm∴FC=根号13cm。
2,如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.(1)求证:四边形ABFE是等腰梯形;(2)求AE的长.(1)证明:过点D作DM⊥AB,∵DC∥AB,∠CBA=90°,∴四边形BCDM为矩形.∴DC=MB.∵AB=2DC,∴AM=MB=DC.∵DM⊥AB,∴AD=BD.∴∠DAB=∠DBA.∵EF∥AB,AE与BF交于点D,即AE与FB不平行,∴四边形ABFE是等腰梯形.(2)解:∵DC∥AB,∴△DCF∽△BAF.∴CD AB =CF AF =1 2 .∵CF=4cm,∴AF=8cm.∵AC⊥BD,∠ABC=90°,在△ABF与△BCF中,∵∠ABC=∠BFC=90°,∴∠FAB+∠ABF=90°,∵∠FBC+∠ABF=90°,∴∠FAB=∠FBC,∴△ABF∽△BCF,即BF CF =AF BF ,∴BF2=CF•AF.∴BF=4 2 cm.∴AE=BF=4 2 cm.3,如图,用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接AE与BG、CF分别交于P、Q,(1)若AB=6,求线段BP的长;(2)观察图形,是否有三角形与△ACQ全等?并证明你的结论解:(1)∵菱形ABGH、BCFG、CDEF是全等菱形∴BC=CD=DE=AB=6,BG∥DE∴AD=3AB=3×6=18,∠ABG=∠D,∠APB=∠AED∴△ABP∽△ADE∴BP DE =AB AD∴BP=AB AD •DE=6 18 ×6=2;(2)∵菱形ABGH、BCFG、CDEF是全等的菱形∴AB=BC=EF=FG∴AB+BC=EF+FG∴AC=EG∵AD∥HE∴∠1=∠2∵BG∥CF∴∠3=∠4∴△EGP≌△ACQ.4,已知点E,F在三角形ABC的边AB所在的直线上,且AE=BF,FH//EG//AC,FH、EC分别交边BC所在的直线于点H,G1 如果点E。
初二几何试题及答案
初二几何试题及答案一、选择题(每题2分,共10分)1. 在直角三角形中,如果一个锐角为30°,那么另一个锐角的度数是多少?A. 30°B. 45°C. 60°D. 90°答案:C2. 一个矩形的长是10厘米,宽是5厘米,那么它的周长是多少厘米?A. 20厘米B. 25厘米C. 30厘米D. 50厘米答案:B3. 一个圆的半径是3厘米,那么它的直径是多少厘米?A. 6厘米B. 9厘米C. 12厘米D. 15厘米答案:A4. 在一个平行四边形中,如果对角线互相平分,那么这个平行四边形是:A. 正方形B. 长方形C. 菱形D. 梯形答案:B5. 如果一个三角形的三边长分别为3厘米、4厘米、5厘米,那么这个三角形是:A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形答案:C二、填空题(每题2分,共10分)6. 一个三角形的内角和等于________度。
答案:1807. 如果一个圆的周长是12.56厘米,那么它的半径是________厘米。
答案:28. 在一个直角三角形中,斜边的长度是两直角边长度的________。
答案:平方和的平方根9. 一个矩形的对角线相等,那么这个矩形是________。
答案:正方形10. 一个平行四边形的对角线互相平分,那么这个平行四边形是________。
答案:矩形三、解答题(每题5分,共10分)11. 已知一个直角三角形的两条直角边分别为6厘米和8厘米,求斜边的长度。
答案:根据勾股定理,斜边长度为√(6² + 8²) = √(36 + 64) = √100 = 10厘米。
12. 一个圆的半径是4厘米,求其面积。
答案:圆的面积公式为A = πr²,所以面积为A = π × 4² = 16π ≈ 50.27平方厘米。
结束语:本试题涵盖了初二几何课程的基础知识和一些基本公式的应用,希望同学们通过练习能够加深对几何概念的理解和运用能力。
(完整版)八年级数学几何经典题【含答案】
F八年级数学几何经典题【含答案】1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.3、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF ..4、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .B5、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .6、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .7如图,△ABC 中,∠C 为直角,∠A=30°,分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ,DE 与AB 交于F 。
求证:EF=FD 。
8如图,正方形ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD 。
9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA,九年级数学【答案】1.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。
2.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中几何综合测试题
(时间120分满分100分)
一.填空题(本题共22分,每空2分)
1.一个三角形的两条边长分别为9和2,第三边长为奇数,则第三
边长为 .
2.△ABC三边长分别为3、4、5,与其相似的△A′B′C′的最大边长是
10,则△A′B′C′的面积是 .
4.弦AC,BD在圆相交于E,且,∠BEC=130°,
则∠ACD= .
5.点O是平行四边形ABCD对角线的交点,若平行四边行ABCD的
面
积为8cm,则△AOB的面积为 .
6.直角三角形两直角边的长分别为5cm和12cm,则斜边上的中线
长为
.
7.梯形上底长为2,中位线长为5,则梯形的下底长为 .
9.如图,分别延长四边形ABCD两组对边交于E、F,若DF=2DA,
10.在Rt△ABC中,AD是斜边BC上的高,如果BC=a,∠B=30°,
那么AD等于 .
二.选择题(本题共44分,每小题4分)
1.一个角的余角和它的补角互为补角,则这个角是[ ]
A.30°
B.45°
C.60°
D.75°
2.依次连结等腰梯形的各边中点所得的四边形是[ ]
A.矩形
B.正方形
C.菱形
D.梯形
3.如图,DF∥EG∥BC,AD=DE=EB,△ABC被分成三部分的
面积之比为[ ]
A.1∶2∶3
B.1∶1∶1
C.1∶4∶9
D.1∶3∶5
4.如果两个圆的半径分别为4cm和5cm,圆心距为1cm,那么这
两个圆
的位置关系是[ ]
A.相交
B.切
C.外切
D.外离
5.已知扇形的圆心角为120°,半径为3cm,那么扇形的面积为[ ]
6.已知Rt△ABC的斜边为10,切圆的半径为2,则两条直角边的
长为[ ]
7.和距离为2cm的两条平行线都相切的圆的圆心的轨迹是[ ]
A.和两条平行线都平行的一条直线。
B.在两条平行线之间且与两平行线都平行的一条直线。
C.和两平行线的距离都等于2cm的一条平行线。
D.和这两条平行线的距离都等于1cm的一条平行线。
8.过圆外一点作圆的割线PBC交圆于点B、C,作圆的切线PM,M
为切点,若PB=2,BC=3,那么PM的长为[ ]
9.已知:AB∥CD,EF∥CD,且∠ABC=20°,∠CFE=30°,
则∠BCF的度数是[ ]
A.160°
B.150°
C.70°
D.50°
10.如图OA=OB,点C在OA上,点D在OB上,OC=OD,AD和
BC相交于E,图中全等三角形共有[ ]
A.2对
B.3对
C.4对
D.5对
11.既是轴对称,又是中心对称的图形是[ ]
A.等腰三角形
B.等腰梯形
C.平行四边形
D.线段
三.计算题(本题共14分,每小题7分)
第一次在B处望见该船在B的南偏西30°,半小时后,又望见该
船
在B的南偏西60°,求该船的速度.
2.已知⊙O的半径是2cm,PAB是⊙O的割线,PB=4cm,PA=3cm,PC
是⊙O的切线,C是切点,CD⊥PO,垂足为D,求CD的长.
四.证明题(本题共20分,每小题4分)
1.如图,在△ABC中,BF⊥AC,CG⊥AD,F、G是垂足,D、E分
别是BC、FG的中点,求证:DE⊥FG
2.如图已知在平行四边形ABCD中,AF=CE,FG⊥AD于G,
EH⊥BC于H,求证:GH与EF互相平分
3.如图,AE∥BC,D是BC的中点,ED交AC于Q,ED的延长线交
AB的延长线于P,求证:PD·QE=PE·QD
4.如图,在梯形ABCD中,AB∥DC,AD=BC,以AD为直径的圆
O交AB于点E,圆O的切线EF交BC于点F.
求证:(1)∠DEF=∠B;(2)EF⊥BC
5.如图,⊙O中弦AC,BD交于F,过F点作EF∥AB,交DC延
长线于E,过E点作⊙O切线EG,G为切点,求证:EF=EG
初中几何综合测试题参考答案
一. 填空(本题共22分,每空2分)
1.9
2.24
二. 选择题(本题共44分,每小题4分)
1.B
2.C
3.C
4.B
5.A
6.C
7.D
8.C
9.D10.C
11.D
三.(本题共14分,每小题7分)
解1:
如图:∠ABM=30°,∠ABN=60° ∠A=90°,AB=
∴MN=20(千米),即轮船半小时航20千米,
∴轮船的速度为40千米/时
∵PC是⊙O的切线
又∵CD⊥OP
∴Rt△OCD∽Rt△OPC
四.证明题(本题共20分,每小题4分)
1.证明:
连GD、FD
∵CG⊥AB,BF⊥AC,D是BC中点
∴GD=FD, △GDF是等腰三角形
又∵E是GF的中点
∴DE⊥GF
2.证明:
∵四边形ABCD是平行四边形
∴AD∥BC
∠1=∠2
又AF=CE
∠AGF=∠CHE=Rt∠
Rt△AGF≌Rt△CHE
∴EH=FG,又FG⊥AD,EH⊥BC,AD∥BC
∴FG∥EH
∴四边形FHEG是平行四边形,
而GH,EF是该平行四边形的对角线
∴GH与EF互相平分
3.证明:
∵AE∥BC
∴∠1=∠C, ∠2=∠3
∴△AQE∽△CQD
又∵AE∥BC
又∵BD=CD
∴
即PD·QE=PE·QD
4.证明:
(1)在梯形ABCD中,DC∥AB,AD=BC
∴∠A=∠B
∵EF是⊙O的切线
∴∠DEF=∠A
∴∠DEF=∠B
(2)∵AD是⊙O的直径
∴∠AED=90°,∠DEB=90°
即∠DEF+∠BEF=90°
又∵∠DEF=∠B
∴∠B+∠BEF=90°
∴∠EFB=90°
∴EF⊥BC
5.证明:
-
∵EF∥AB
∴∠EFC=∠A
∵∠D=∠A
∴∠EFC=∠D
又∠FEC=∠DEF
∴△EFC∽△EDF
即EF=EC·ED
又∵EG切⊙O于G
∴EG=EC·ED
∴EF=EG
∴EF=EG
- . - 总结资料-。
