电感元件的伏安特性
电路元件特性曲线的伏安特性测量法 实验报告
实验报告课程名称：_______________________________指导老师：________________成绩：__________________ 实验名称：_______________________________实验类型：________________同组学生姓名：__________ 一、实验目的和要求（必填） 二、实验内容和原理（必填） 三、主要仪器设备（必填） 四、操作方法和实验步骤 五、实验数据记录和处理 六、实验结果与分析（必填） 七、讨论、心得一、实验目的和要求1.熟悉电路元件的特性曲线；2.学习非线性电阻元件特性曲线的伏安测量方法；3掌握伏安测量法中测量样点的选择和绘制曲线的方法； 4.学习非线性电阻元件特性曲线的示波器观测方法。
二、实验内容和原理1、电阻元件、电容元件、电感元件的特性曲线 在电路原理中，元件特性曲线是指特定平面上定义的一条曲线。
例如，白炽灯泡在工作时，灯丝处于高温状态，其灯丝电阻随着温度的改变而改变，并且具有一定的惯性；又因为温度的改变与流过灯泡的电流有关，所以它的伏安特性为一条曲线。
电流越大、温度越高，对应的灯丝电阻也越大。
一般灯泡的“冷电阻”与“热电阻”可相差几倍至十几倍。
该曲线的函数关系式称为电阻元件的伏安特性，电阻元件的特性曲线就是在平面上的一条曲线。
当曲线变为直线时，与其相对应的元件即为线性电阻器，直线的斜率为该电阻器的电阻值。
电容和电感的特性曲线分别为库伏特性和韦安特性，与电阻的伏安特性类似。
线性电阻元件的伏安特性符合欧姆定律，它在u-i 平面上是一条通过原点的直线。
该特性曲线各点斜率与元件电压、电流的大小和方向无关，所以线性电阻元件是双向性元件。
非线性电阻的伏安特性在u-i 平面上是一条曲线。
普通晶体二极管的特点是正向电阻和反向电阻区别很大。
正向压降很小正向电流随正向压降的升高而急骤上升，而反向电压从零一直增加到十几伏至几十伏时，其反向电流增加很小，粗略地可视为零。
元件模拟电路实验报告(3篇)
一、实验目的1. 理解并掌握基本模拟电路元件（电阻、电容、电感）的特性及其在电路中的作用。
2. 掌握模拟电路的测试方法，包括伏安特性曲线的测量、阻抗测量等。
3. 培养实验操作技能，提高分析问题、解决问题的能力。
二、实验原理1. 电阻元件：电阻元件是模拟电路中最基本的元件之一，其特性表现为对电流的阻碍作用。
电阻元件的伏安特性曲线为直线，其斜率即为电阻值。
2. 电容元件：电容元件的特性表现为储存电荷的能力。
电容元件的伏安特性曲线为非线性，其斜率与电容值和电压值有关。
3. 电感元件：电感元件的特性表现为储存磁场能量的能力。
电感元件的伏安特性曲线为非线性，其斜率与电感值和电流值有关。
4. 电路测试方法：伏安特性曲线的测量方法为在电路中施加一定的电压，测量通过电路的电流，然后绘制电压与电流的关系曲线。
阻抗测量方法为测量电路的电压和电流，然后根据欧姆定律计算电路的阻抗。
三、实验器材1. 电阻元件：R1、R2、R3（不同阻值）2. 电容元件：C1、C2、C3（不同容量）3. 电感元件：L1、L2、L3（不同电感值）4. 直流稳压电源5. 电压表6. 电流表7. 示波器8. 电路实验板四、实验步骤1. 测量电阻元件的伏安特性曲线（1）将电阻元件R1、R2、R3分别接入电路，测量通过电阻元件的电流和对应的电压值。
（2）根据测量的电压和电流值，绘制电阻元件的伏安特性曲线。
2. 测量电容元件的伏安特性曲线（1）将电容元件C1、C2、C3分别接入电路，测量通过电容元件的电流和对应的电压值。
（2）根据测量的电压和电流值，绘制电容元件的伏安特性曲线。
3. 测量电感元件的伏安特性曲线（1）将电感元件L1、L2、L3分别接入电路，测量通过电感元件的电流和对应的电压值。
（2）根据测量的电压和电流值，绘制电感元件的伏安特性曲线。
4. 测量电路阻抗（1）将待测电路接入电路实验板，测量电路的电压和电流值。
（2）根据测量的电压和电流值，计算电路的阻抗。
12.元件伏安特性相量形式
U
返回
章目录 上一页 下一页
深圳职业技术学院
电工技术
2. 电容元件的功率
u 2Usi nω t i 2Uω C si n( ω t 90)
i
u
ωt
瞬时功率：
p i u UI si n2 ω t
o平均功率：P =0u Nhomakorabeap+
i
+ u
i
-
u
+
i
u
+
i
无功功率：
Q UI I X C
90
相位差
ψu ψi 90
退出 章目录 上一页 下一页 返回
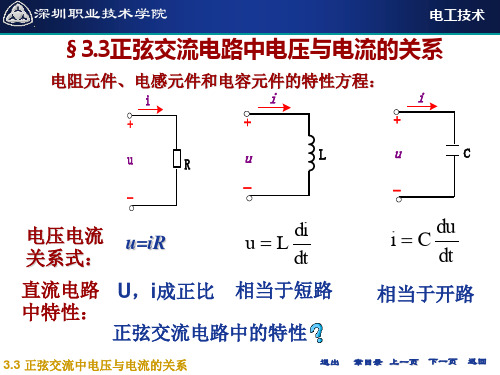
2.1 正弦交流中电压与电流的关系
深圳职业技术学院
电工技术
u 2Usinω t i 2Uω C sin( ω t 90)
有效值
I U ω C 或 1 1 定义： XC 容抗（Ω ） ωC 2 π f C
返回
深圳职业技术学院
电工技术
§3.3.3 纯电容电路
1. 电压电流关系
du 基本关系式： i C dt 设：u 2 U sin ω t
2 U ωC sin( ω t 90) u i
du dt 2 UC ω cos ω t
i
+ u _
C
则： i C
u
i
ωt
1) 频率关系： 频率相同 2)大小关系： I =UC 3)相位关系 ： 电流超前电压90
退出
章目录 上一页 下一页
返回
深圳职业技术学院
电工技术
§ 3.3.1 纯电阻电路
1.电压与电流的关系 根据欧姆定律:
实验1线性和非线性元件伏安特性测定
2． 实验内容和步骤
3.接线图
实验13.异步电动机继电控制的基本电路
2.实验内容和步骤 3.接线图
2． 实验内容和步骤
3.接线图
1.实验原理
测量电容两端电压随时间变化的曲线 （P.22图6-4取消，电路中的电阻用电阻箱）
用示波器只能测电压，不能测电流。
用示波器测量电流曲线的方法：从电阻 上测电压，再换算成电流。
实验7.研究LC元件在直流电路和交流电 路中的特性
1.实验原理 2.实验内容和步骤 3.接线图
1． 实验原理
线性电感元件上的电压、电流关系为 线性电容元件上的电压和电流关系为
解放电过程的微分方程
U c(t)
U e (t t0)/ 0
观测方法：用函数信号发生器输入连续 的方波（包括正负阶跃），通过示波器 观测波形，测量时间常数
实验内容：四个电路，每个电路两组参 数，在坐标纸上绘制8张输出波形图；用 示波器测量第一个电路第一组参数的时 间常数（从充电曲线和放电曲线中任选 一条曲线测量）
（a）含源一端口网络
（b）用戴维南定理等效替代 图3-1等效电源定理
（c）用诺顿定理等效替代
2． 实验内容和步骤
3.接线图
实验4.电压源与电流源的等效变换
1.实验原理 2.实验内容和步骤 3.接线图
1． 实验原理
电流源是除电压源以外的另一种形式的电源，它可以给外电路提供电 流。电流源可分为理想电流源和实际电流源（实际电流源通常简称电流 源），理想电流源可以向外电路提供一个恒值电流，不论外电路电阻的大 小如何。理想电流源具有两个基本性质：第一，它的电流是恒值的，而与 其端电压的大小无关；第二，理想电流源的端电压并不能由它本身决定， 而是由与之相联接的外电路确定的。理想电流源的伏安特性曲线如图4-1所 示。
电路习题附答案
1、 非关联参考方向下电感元件的伏安特性为（ C ）。
A ． di u Ldt = B ．du i L dt= C ． di u L dt =- D ．du i L dt =- 2、 图示电路中，元件伏安特性的关系式为（ D ）。
A ．10i u =B ．10i u =-C ．10u i =D ．10u i =-3、电感元件的特点是（ B ）。
A ．耗能B ．储存磁场能量C ．储存电场能量D ．既储存电场能量又储存磁场能量4、非关联参考方向下电容元件的伏安特性为（ C ）。
A ．di u Cdt = B ．di u C dt=- C ． du i C dt = D ． du i C dt =- 5、电容元件的特点是（ C ）。
A ．无储存能量B ．储存磁场能量C ．储存电场能量D ．既储存电场能量又储存磁场能量6、理想电流源外特性的正确描述是（ B ）。
A ．电流和端电压均恒定B ．电流恒定，端电压由外电路决定C ．端电压恒定，电流由外电路决定D ．电流和端电压均不恒定7、当电流源开路时，该电流源内部（ D ）。
A ．有电流，有功率损耗B ．有电流，无功率损耗C ．无电流，有功率损耗D ．无电流，无功率损耗8、图示电路中，S U 、S I 均为正值，其工作状态是（ B ）。
A ．电压源发出功率B ．电流源发出功率C ．电压源和电流源都发出功率D ．电压源和电流源都不发出功率9、图示电路中，U S =12V 、I S =2A 、Ω=3R ，其工作状态是（ A ）。
A ．电流源I S 发出功率B ．电压源U S 发出功率C ．电压源和电流源都发出功率D ．电压源和电流源都不发出功率图1-6 题1-9图10、图示电路中的电流L I 值为（ A ）。
A ．0.3AB ．0.15AC ．0.1AD ． 0图1-7 题1-10图11、 图示电路中，电容电压的值为（ B ）。
A ．6VB ．4VC ． 2VD ． 012、图示电路中的短路电流SC I 为（ D ）。
电路元件伏安特性的测量实验报告答案
实验一电路元件伏安特性的测量一、实验目的1．学习测量电阻元件伏安特性的方法；2．掌握线性电阻、非线性电阻元件伏安特性的逐点测试法；3．掌握直流稳压电源和直流电压表、直流电流表的使用方法。
二、实验原理在任何时刻，线性电阻元件两端的电压与电流的关系，符合欧姆定律。
任何一个二端电阻元件的特性可用该元件上的端电压U与通过该元件的电流I之间的函数关系式I＝f(U)来表示，即用I－U平面上的一条曲线来表征，这条曲线称为电阻元件的伏安特性曲线。
根据伏安特性的不同，电阻元件分为两大类：线性电阻和非线性电阻。
线性电阻元件的伏安特性曲线是一条通过坐标原点的直线，如图1-1（a）所示。
该直线的斜率只由电阻元件的电阻值R决定，其阻值R为常数，与元件两端的电压U和通过该元件的电流I无关；非线性电阻元件的伏安特性曲线不是一条经过坐标原点的直线，其阻值R不是常数，即在不同的电压作用下，电阻值是不同的。
常见的非线性电阻如白炽灯丝、普通二极管、稳压二极管等，它们的伏安特性曲线如图1-1（b）、（c）、（d）所示。
在图1-1中，U ＞0的部分为正向特性，U＜0的部分为反向特性。
(a)线性电阻(b)白炽灯丝绘制伏安特性曲线通常采用逐点测试法，电阻元件在不同的端电压U 作用下，测量出相应的电流I ，然后逐点绘制出伏安特性曲线I ＝f (U )，根据伏安特性曲线便可计算出电阻元件的阻值。
三、实验设备与器件1 台2.直流电压表 1 块3.直流电流表 1 块4.万用表 1 块5.白炽灯泡 1 只6. 二极管 1 只7.稳压二极管 1 只8.电阻元件 2 只四、实验内容1．测定线性电阻的伏安特性 按图1-2接线。
调节直流稳压电源的输出电压U ，从0伏开始缓慢地增加（不得超过10V ），在表1-1中记下相应的电压表和电流表的读数。
表1-1 测定线性电阻的伏安特性U （V ） 0 1 2 3 4 5 6 7 8 9 10 I （mA ） 012．测定白炽灯泡的伏安特性将图1-2中的1kΩ线性电阻R 换成一只的灯泡，重复1的步骤，在表1-2中记下相应的电压表和电流表的读数。
电路实验报告一(伏安特性的测量)
U
I
U
I
锗二极管
I
硅二极管
稳压管
0.4
0.20.60.81
-5
-10
图1-1 线性电阻的图1-2白炽灯泡的图1-3 二极管、稳压管的伏安特性曲线伏安特性曲线伏安特性曲线
图1-4理想电压源的输出特性曲线图1-5实际电压源的输出特性
图1-6 伏－安特性实验线路
实验电路图
直
流
稳
压
电
源
mA
V
200Ω
+
-
实验步骤
１、测量线性电阻的伏－安特性。
按图1-6接线，调节直流稳压电源的输出（从小到大），分别测出电阻Ｒ的电流和电压。
２、测量白炽灯泡的伏－安特性。
将电阻去掉，接入白炽灯泡，调节直流稳压电源的输出（注意：白炽灯泡的最大电压值），分别测出白炽灯泡的电流和电压。
３、测量二极管的伏－安特性。
将白炽灯泡去掉，接入二极管（注意二极管的导通方向），调节直流稳压电源的输出（注意：锗二极管导通电压0.4V，硅二极管导通电压0.7V），分别测出二极管的电流和电压。
４、测量稳压管的伏－安特性。
将二极管去掉，接入稳压管（注意稳压管的方向），调节直流稳压电源的输出（注意：稳压管最大稳压电压），分别测出稳压管的电流和电压。
（选做）
二、数据分析处理（参照实验教材“实验报告”要求分析处理）
误差分析：误差主要是万用表的内阻
三．思考题（参照实验教材“思考题”要求回答问题）。
伏安特性与电路元件的应用
伏安特性与电路元件的应用一、伏安特性1.定义：伏安特性是指用电压和电流描述导体或半导体在某一温度下的导电性能的图形。
a)金属的伏安特性：线性关系，随着电压的增大，电流也增大。
b)半导体的伏安特性：非线性关系，随着电压的增大，电流的增大速度远远大于电压的增大速度。
2.伏安特性曲线的变化规律：a)在一定电压范围内，电流与电压成正比，表现为线性关系。
b)当电压超过一定值时，电流增大速度明显加快，表现为非线性关系。
二、电路元件的应用a)定义：电阻是阻碍电流流动的物理量。
b)单位：欧姆（Ω）。
c)作用：在电路中起到分压、限流的作用。
d)应用实例：灯泡、电热器等。
e)定义：电容是储存电荷的容器。
f)单位：法拉（F）。
g)作用：在电路中起到滤波、耦合、旁路的作用。
h)应用实例：滤波器、耦合器等。
i)定义：电感是阻碍电流变化的物理量。
j)单位：亨利（H）。
k)作用：在电路中起到滤波、延迟、振荡的作用。
l)应用实例：扼流圈、振荡器等。
4.二极管：a)定义：二极管是一种具有单向导电性的半导体器件。
b)作用：在电路中起到整流、稳压、调制的作用。
c)应用实例：整流器、稳压器等。
5.晶体管：a)定义：晶体管是一种具有放大作用的半导体器件。
b)作用：在电路中起到放大信号、开关控制的作用。
c)应用实例：放大器、开关等。
6.电压源和电流源：a)定义：电压源是提供恒定电压的装置，电流源是提供恒定电流的装置。
b)作用：在电路中提供稳定的电压或电流。
c)应用实例：电源、稳压器等。
通过了解伏安特性和电路元件的应用，我们可以更好地理解和分析电路的运行原理，为电路设计和故障排查提供依据。
习题及方法：1.习题：已知金属导体的电阻率随温度升高而增大，一电阻器由纯金属制成，当电阻器的温度从20℃升高到100℃时，其电阻值变为原来的5倍。
求该电阻器的电阻率。
方法：根据电阻率的定义ρ = R * S / l，其中 R 是电阻值，S 是电阻器的横截面积，l 是电阻器的长度。
伏安特性图
第3节电阻、电容、电感元件及其特性在我们研究的电路中一般含有电阻元件、电容元件、电感元件和电源元件（如图1.11所示），这些元件都属于二端元件，它们都只有两个端钮与其它元件相连接。
其中电阻元件、电容元件、电感元件不产生能量，称为无源元件；电源元件是电路中提供能量的元件，称为有源元件。
上述二端元件两端钮间的电压与通过它的电流之间都有确定的约束关系，这种关系叫作元件的伏安特性。
该特性由元件性质决定，元件不同，其伏安特性不同。
这种由元件的性质给元件中通过的电流、元件两端的电压施加的约束又称为元件约束。
用来表示伏安特性的数学方程式称为该元件的特性方程或约束方程。
1．3．1 电阻元件及欧姆定律1．电阻元件的图形、文字符号电阻器是具有一定电阻值的元器件，在电路中用于控制电流、电压和控制放大了的信号等。
电阻器通常就叫电阻，在电路图中用字母“R”或“r”表示，电路图中常用电阻器的符号如图1．1２所示。
电阻器的SI（国际单位制）单位是欧姆，简称欧，通常用符号“Ω”表示。
常用的单位还有“KΩ”“MΩ”，它们的换算关系如下：1MΩ=1000KΩ=1000000Ω电阻元件是从实际电阻器抽象出来的理想化模型，是代表电路中消耗电能这一物理现象的理想二端元件。
如电灯泡、电炉、电烙铁等这类实际电阻器，当忽略其电感等作用时，可将它们抽象为仅具有消耗电能的电阻元件。
电阻元件的倒数称为电导，用字母G表示，即电导的SI单位为西门子，简称西，通常用符号“S”表示。
电导也是表征电阻元件特性的参数，它反映的是电阻元件的导电能力。
2．电阻元件的特性电阻元件的伏安特性，可以用电流为横坐标，电压为纵坐标的直角坐标平面上的曲线来表示，称为电阻元件的伏安特性曲线。
如果伏安特性曲线是一条过原点的直线，如图1．1３（a）所示，这样的电阻元件称为线性电阻元件，线性电阻元件在电路图中用图1．1３（b）所示的图形符号表示。
在工程上，还有许多电阻元件，其伏安特性曲线是一条过原点的曲线，这样的电阻元件称为非线性电阻元件。
电阻电容电感元件及其特性
一、电阻元件
二端元件： 有两个端钮与外部相连的元件。
二端电阻元件的 u、i 关系可由 u – i 平面的一条
曲线（伏安特性曲线）确定。
f(u,i)0
（电阻元件的电压与电流的约束关系， 简称VCR）
分 时不变电阻 或 线性电阻（过原点的直线）
类 时变电阻
非线性电阻
的值及 t = 2π/300 时的电流。
解： 电压 u 的最大值为60V，所以
+ i
1C 602 18 2
C632063366010 02F
u -
C
i C d u 0 .0d ( 1 6s0 1 in t0 ) 0 6c0 1 otA 0 s 0
d t
d t
t 2π 时 300
u、i、e（电动势）的参考方向为关联参考方向
edLdi
dt
dt
ue Ldi dt
i1
t
udti(0)
L0
i
+
–
uL e
–
+
3. 电感元件储存的能量 （关联参考方向）
电感 L 在任一瞬间吸收的功率：
pui Lidi dt
电感 L 在 dt 时间内吸收的能量：
P > 0 吸收能量 P < 0 释放能量
瓷介电容器系列 主要有：CC1， CC81， CT1，CT81，等
独石电容器 主要有： CC4， CT4. CC42, CT42 等
多层片状陶瓷电容器 （ SMD 贴 片 电 容 全 系 列） 片式钽电解电容 主要有： CC41，CT41.CA45 等
小型电 解电容
金属化聚丙烯 薄膜电容器
实验1线性与非线性元件伏安特性的测定
图4-1 理想电流源及其伏安特性
2． 实验内容和步骤
3.接线图
实验5 一阶电路实验
研究内容
实验电路
正阶跃响应 负阶跃响应 电路参数对阶跃响应的影响 如何测量一阶电路的时间常数
输入正阶跃信号
输出波形？ 输入负阶跃信号
输出波形？
以第一个一阶电路为例，解充电过程的 微分方程，得到
Uc( t) U0 ( 1e
（a）含源一端口网络
（b）用戴维南定理等效替代 图3-1等效电源定理
（c）用诺顿定理等效替代
2． 实验内容和步骤
3.接线图
实验4.电压源与电流源的等效变换
1.实验原理 2.实验内容和步骤 3.接线图
1． 实验原理
电流源是除电压源以外的另一种形式的电源，它可以给外电路提供电 流。电流源可分为理想电流源和实际电流源（实际电流源通常简称电流 源），理想电流源可以向外电路提供一个恒值电流，不论外电路电阻的大 小如何。理想电流源具有两个基本性质：第一，它的电流是恒值的，而与 其端电压的大小无关；第二，理想电流源的端电压并不能由它本身决定， 而是由与之相联接的外电路确定的。理想电流源的伏安特性曲线如图4-1所 示。
星形电路:
三角形电路:
2.实验步骤:
1)线电压、相电压测量，用MC1098直接测量， 测量结果填表. 2)星形电路：按图连接电路，测量对称负载有中 线、对称负载无中线、不对称负载有中线、不 对称负载无中线电路的参数。用二瓦计法测量 三相功率的测量电路. 3)三角形电路：测量对称负载、不对称负载电路 的参数，按连接电路. 4)相序测量
实验11
三相交流电路
1.实验原理: 线电压：端线之间的电压（UAB、UBC、UCA）。标称值 为380V，实际值与负载有关。 相电压：每一相的电压（UA0、UB0、UC0）。标称值为 220V，实际值与负载有关。 线电流：端线中的电流（IA、IB、IC） 相电流：各相电压源中的电流（IAB、IBC、ICA） 电压与电流之间的位相差：φ 功率因数：cosφ 有功功率又称平均功率：P=UIcosφ，单位：w 无功功率：Q=UIsinφ，单位：var 视在功率：S=额定电压×额定电流，单位：V· A 瞬时功率：用普通仪器不易测量 三相电路中负载的接法：星形、三角形
非线性电感
第十二章 非线性电路§12.1 非线性元件12.1.1 非线性电阻电阻元件的特性可以用电压u 和电流i 之间的关系来描述，称之为伏安特性关系。
线性电阻的伏安特性可以用欧姆定律来表示，即Ri u =，在i u -平面上是一条通过坐标原点的直线。
而非线性电阻元件的电压和电流关系不满足欧姆定律，它一般用某种特定的非线性函数来表示。
图12-1（a ）表示非线性电阻元件的电路符号，图12-1（b ）表示某种非线性电阻的伏安特性曲线。
根据非线性电阻元件的伏安特性，可以分为以下几类。
(a) (b)图12-1 非线性电阻及伏安特性曲线 1. 单调型非线性电阻元件单调型非线性电阻元件的伏安特性是单调增加或单调减小的函数。
如图12-2（a ）所示的PN 结二极管是典型的单调增加型非线性电阻，伏安特性如图12-2（b ）所示，从图12-2（b ）可以看出，电流i 随着电压u 的变化单调递增，但是图像过原点而关于原点不对称，其伏安特性可以用下列函数表示：)1(-=kT quS e I i (12-1)其中S I 为反向饱和电流，是常数，C q 19106.1-⨯=，是电子的电荷量，K J k /1038.123-⨯=，是玻尔兹曼常数，T 为热力学温度。
在K T 300=（室温）时，140-=V kTq 则 )1(40-=u S e I i从上式可以看出，电流i 随着电压u 单调增加。
-u(a) (b)图12-2 PN 结二极管及其伏安特性2. 电压控制型非线性电阻元件如果非线性电阻元件两端的电流是其电压的单值函数，这种电阻就称为电压控制型电阻，其伏安特性可以用下列函数关系表示)(u g i = (12-2)其典型的伏安特性曲线如图12-3所示。
从特性曲线可以看出，对于每一个电压值u ，有且只有一个电流值i 与之对应，但是，对于某一个电流值，则可能对应多个电压值。
隧道二极管就具有这样的伏安特性。
图12-3 隧道二极管的伏安特性曲线3. 电流控制型非线性电阻元件如果非线性电阻元件两端的电压是电流的单值函数，这种电阻就称为电流控制型电阻，其伏安特性可以用下列函数关系表示)(i f u = (12-3)其典型的伏安特性曲线如图12-4所示，从特性曲线可以看出，对于每一个电流值i ，有且只有一个电压u 值与之对应，但是，对于某一个电压值，则可能对应多个电流值。
大工15秋《电路理论》辅导资料六
电路理论辅导资料六主 题： 第三章 线性动态电路的时域分析（第1-3节） 学习时间： 2015年11月2日--11月8日 内 容：一、本周知识点及重难点分布表6-1 本周知识点要求掌握程度一览表序号学习知识点要求掌握程度本周难点了解熟悉 理解 掌握 1 电容元件 ★ 2 电感元件★ 3 换路定律与初始值的计算★☆二、知识点详解【知识点1】电容元件电容元件、电感元件称为“动态元件”，包含他们的电路称为动态电路。
动态电路是“有记忆”的。
1、电容器和电容元件电容器：因介质不理想存在导电和损耗。
电容元件：实际电容器的理想化模型。
定义：如果一个二端元件，在任一时刻其存储的电荷与其两端电压之间的关系可用u-q 平面上的一条曲线来确定，则此二端元件称为电容元件。
若该曲线为u-q 平面上的一条过原点的直线，则此电容元件称为线性、非时变电容元件。
2、电容元件的伏安关系qC u= 单位：法拉（F ）-61μF 10F =，121pF 10F -=伏安关系：d d d d q u i C t t== 图6-1 电容元件的库伏特性稳态直流电路中，u 不随时间变化，0I =,电容相当于开路，有隔直作用。
①0d d >tu 时，电流流向电容正极板，电容充电；②0dd<tu时，电流从电容正极板流出，电容放电。
电容的电压不能发生突变。
假设电容电压突变，则电流为无穷大值，即：∞→=tuCidd因实际中电容上存储的电荷量不可能发生突变，图6-2 电容元件的符号故电容的电流恒为限制，电容电压不能突变。
3、电容的储能u i、为关联参考方向下：()()()()()ttutCut i tutpdd==①0>p：电容吸收功率，将电能转换成电场能②0<p：电容释放功率，将电场能转换成电能从t~∞-时间内电容上存储（释放）的能量为：()()()()()()()()()()∞--====⎰⎰⎰-∞-∞-222121ddddd CutCuuuCuCuptWuuttξξξξξξξξξξ若电容从零开始充电，即()0=∞-u，则：()()212W t Cu t=表明：电容在某时刻的储能值，只取决于该时刻的电容电压值，与电流无关。
电子技术基础——电路与模拟电子(第3章)
du(t ) p(t ) = u (t )i (t ) = Cu(t ) dt
(3―6)
对上式从-∞到 进行积分 可得t时刻电容上的储能为 进行积分， 对上式从 到t进行积分，可得 时刻电容上的储能为 计算过程中认为u(-∞)=0。 。 计算过程中认为
ωC (t ) = ∫
t
−∞
p (ξ )d ξ
（3-7）
1 1 1 = + C C1 C2
或写为
C1C2 C= C1 + C2
(3―18)
上式中C为电容 相串联时的等效电容。由式(3―17)画出 上式中 为电容C1与C2相串联时的等效电容。由式 为电容 画出 其等效电路如图3.6(b)所示。同理可得，若有 个电容 k(k=1,2,…,n) 所示。同理可得，若有n个电容 个电容C 其等效电路如图 所示 相串联， 相串联，其等效电容为
第3章 动态电路分析
电容元件及电容电流波形分别如图3.2（ ）、 例3-1 电容元件及电容电流波形分别如图 （a）、 （b）所示，已知 ）所示，已知u(0)=0，试求 ，试求t=1s、t=2s、t=4s时的电 、 、 时的电 容电压u以及 以及t=2s时电容的储能。 时电容的储能。 容电压 以及 时电容的储能
第3章 动态电路分析
电感串并联： 电感串并联：
是电感L 相串联的电路， 图 3.8(a)是电感 1 与 L2 相串联的电路 ， 流过两电感的电流是同一电 是电感 的微分形式和KVL，有 流i。根据电感 。根据电感VAR的微分形式和 的微分形式和 ，
L = L1 + L2
(3―25)
称为电感L1与 L2串联时的等效 称为电感 与 串联时的等效 电感。 由式(3―26)画出相应的等效 电感 。 由式 画出相应的等效 电路如图3.8(b)所示 。 同理 ， 若有 所示。 同理， 若有n 电路如图 所示 个 电感 Lk(k=1,2,…,n) 相 串联 ， 可 推 导其等效电感为
电感元件的伏安特性
A2的模
r2 ( 3) 2 42 5
4 126 .9 3
(在第二象限)
辐角 2 arctan
则A2的极坐标形式为 A2 5 / 126.9
例 写出复数A=100/30°的三角形式和代数形式。
解 三角形式A=100（cos30°+jsin30° 代数形式A=100(cos30°+jsin30°)=86.6+j50 3. 复数的四则运算 (1) 复数的加减法
号, 虚单位常用j表示。 ＋j
3 A
O
4
＋1
复数在复平面上的表示
＋j b P
r
O a ＋1
复数的矢量表示
r A a 2 b2 b arctan ( 2 ) a
a r cos b r sin
2.
(1) 复数的代数形式
A a jb
(2) 复数的三角形式
(1)φ 12=θ 1-θ 2>0且|φ 12|≤π 弧度
(2) φ
(3) φ
12=θ 1-θ 2<0且|φ 12|≤π
弧度
12=θ 1-θ 2=0,称这两个正弦量同相
(4) φ
12=θ 1-θ 2=π
, 称这两个正弦量反相
/2, 称这两个正弦量正交
(5) φ
12=θ 1-θ 2=π
同频率正弦量的几种相位关系
当φ>0，正弦波零点在计时起点之左，其波形相对于φ=0的 左移φ角，
当φ<0，正弦波零点在计时起点之右，其波形相对于φ=0的 波形右移|φ|角， 确定φ角正负的零点均指离计时起点最近的那个零点
i i1＝Imsint
i
i2＝Imsin( t＋ 2)
电路分析基础第06章储能元件
q 的波形与 u 的波形相同。
（ 3）在 0 ~ 2 ms 时， P 2 tmW
10 在 2 ~ 4 ms 时， P （ 8 3 2 t ） mW
i(t) C du(t) dt
Cq u
p u iCud u dt
例：已知电容两端电压波形 如图所示，求 电容 的电流、功率及储能 。
韦安特性
i－电流，单位：安培（A）
L－电感（正常数），单位：亨利（H）
二、电感元件的伏安特性
1、若 u 与 i 取关联参考方向， i ( t ) L
根据电磁感应定律，有
+ u(t) -
u (t) d(t)d (L i) L d i(t)
dt dt
dt
i(t)i(t0)L 1 tt0u()d
由KVL，端口电流
i i1 i2 . .in . (C 1 C 2 . .C .n )d d u tC ed q d
n
式中 CeqC1C2.. .Cn Ck k1
Ceq为n个电容并联的等效电容。
例: 如图所示电路，各个电容器的初始电压均为零，
给定 C 1 1 F ,C 2 2 F ,C 3 3 F ,C 4 4 F 试求ab间的等
思考：在t0-t1时间内，电容吸收(释放)的电场能量？ 释放的能量和储存的能量关系?(W放≤ W吸)
五、线性电容元件吸收的功率
在关联参考方向下： puiCudu dt
非关联参考方向下，电容释放能量
四、电容元件的特点
i (t)
1、电压有变化，才有电流。
C
i(t) C du(t) dt
+ u(t) -
t
i(t)
w L [t0 ,t]t0p (
电路分析基础复习知识点
电路分析基础知识第一章1.参考电压和参考电流的表示方法。
(1)电流参考方向的两种表示：A）用箭头表示：箭头的指向为电流的参考方向。
(图中标出箭头）B）用双下标表示：如i AB , 电流的参考方向由A指向B。
(图中标出A、B）(2) 参考电压方向: 即电压假定的正方向，通常用一个箭头、“+”、”-”极性或“双下标”表示。
（3）电路中两点间的电压降就等于这两点的电位差，即U ab = V a- V b2.关联参考方向和非关联参考方向的定义若二端元件上的电压的参考方向与电流的参考方向一致（即参考电流从参考电压的正极流向负极），则称之为关联参考方向。
否则为非关联参考方向。
3.关联参考方向和非关联参考方向下功率的计算公式：（1）u, i 取关联参考方向：p = u i （2）u, i 取非关联参考方向：p =- ui 按此方法，如果计算结果p>0，表示元件吸收功率或消耗功率；p<0，表示发出功率或产生功率。
关联参考方向和非关联参考方向下欧姆定律的表达式：（1）电压与电流取关联参考方向:u Ri（2）电压与电流取非关联参考方向: u –Ri 。
4．电容元件（1）伏安特性（2）两端的电压与与电路对电容的充电过去状况有关（3）关联参考方向下电容元件吸收的功率（4）电容元件的功率与储能5．电感元件（1）电感元件的电压-电流关系——伏安特性（2）电感两端的电压与流过的电流无关,而与电流的变化率成正比（3）电感元件的功率与储能6．实际电压源随着输出电流的增大，端电压将下降，可以用理想电压源U S和一个内阻R0串联来等效。
7．实际电流源可以用理想电流源与一个电阻并联来等效. 电流源两端电压愈大，流过内阻的电流越大,输出的电流就愈小。
8．基尔霍夫电流定律（KCL）的内容及表达式。
KCL：对于任一集总电路中的任一节点，在任一时刻，流出（或流进）该节点的所有支路电流的代数和为零。
即例：对图示电路有：KCL的推广：KCL不仅适用于电路的节点，也适用于电路中任意假设的封闭面。
电路试验报告一伏安特性的测量
电路A （B）实验报告实验项目:班级姓名学号实验目的:1、掌握电路元件的伏-安特性的测试方法。
2、掌握实际电压源和电流源的使用方法。
3、学习常用电工仪表的使用方法。
4、根据实验数据描绘曲线。
实验原理在电路中，任何一个二端口元件的特性可用该元件上的端电压U与通过元件上的电流I之间的函数关系U = f（I）来表示，即用I-U平面上的一条曲线来表征，这种函数关系称为该元件的伏-安特性。
也称外特性（电源的外特性是指它的输出端电压和输出电流之间的关系）。
其对应的I-U平面上的那条曲线就叫做伏安特性曲线或外特性曲线。
如果元件的伏-安特性曲线在I-U平面内是一条通过坐标原点的直线，则该元件称为线性元件。
如果元件的伏-安特性曲线在I-U平面内不是一条直线而是曲线，则该元件称为非线性元件。
电路的基本元件包括电阻元件、电感元件、电容元件、独立电源元件；晶体二极管、双极性晶体管和绝缘栅型场效应晶体管等。
本实验中用到的元件有线性电阻、白炽灯泡，二极管、稳压管及电源常见电路元件。
其中线性电阻的伏一安特性是一条过原点的直线，即服从欧姆定律（。
=RI），如图1-1所示，该直线的斜率等于该电阻的阻值。
白炽灯泡在工作时灯丝处于高温状态，其灯丝的电阻随着温度的变化而发生变化，并且具有一定的惯性，因此其伏一安特性为一条曲线，如图1-2所示。
可见电流越大，温度越高，对应的电阻也越大，一般灯泡的冷电阻与热电阻可相差几倍到几十倍。
一般半导体二极管和稳压管也是非线性元件，锗二极管两端的电压小于0.4V时，锗二极管基本处于关闭状态，其通过电流很小，当其两端的电压大于）.4丫时，锗二极管基本处于导通状态，其通过电流很大；硅二极管的导通电压为）.7V,其伏一安特性见图1-3所示。
稳压管则是利用二极管的反向特性，当稳压管两端电压达到一定的值以后，其端电压保持恒定不变，即不随外加电压的变化而变化，即稳压，其伏一安特性见图1-3所示。
理想电压源的端电压是固定的常数，无论负载如何变化，端电压保持一定，而与通过它的电流无关。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Q I2RT
Q T i2R dt 0
I 2RT T i2R dt 0
I 1 T i2dt T0
U 1 T u2dt T0
正弦量的有效值
I
1 T
T 0
I
2 m
sin2 tdt
I
2 m
T 1 cos2t
)
4.33mA
3.1.2 相位差
两个同频率正弦量的相位之差, 称为相位差, 用字母“φ” 表示。
u1 U m1 sin(t 1) u2 U m2 sin(t 2 )
相位差:
12 (t 1) (t 2 ) 1 2
当两个同频率正弦量的计时起点改变时，它们之间 的初相也随之改变，但二者的相位差却保持不变。
第3章 正弦交流电路
3.1 正弦量的基本概念 3.2 正弦量的相量表示法 3.3 电容元件和电感元件 3.4 三种元件伏安特性的相量形式 3.5 基尔霍夫定律的相量形式 3.6 RLC串联的交流电路 3.7 RLC并联电路 3.8 用相量法分析正弦交流电路 3.9 正弦交流电路中的功率 3.10 正弦交流电路中的最大功率
例 已知选定参考方向下正弦量的波形图如图4.4所示,
试写出正弦量的解析式。
解
u1
200sin(t
3
)V
u2
250sin(t
6
)V
u/V
250
u2
200 u1
0
3
6
2
t
例 3-1 图3-1-4给出正弦电压uab和正弦电流iab的波形。(1) 写出uab和iab的解析式并求出它们在t=100ms时的值。(2)写 出iab的解析式并求出t=100ms时的值。
确定φ角正负的零点均指离计时起点最近的那个零点
i i1＝Imsint
i i2＝Imsin(t＋ 2)
i i3＝Imsin(t＋ 6)
i
i4＝Imsin(t－
6)
0
t 0
t 0
t 0
t
2
6
6
(a)
(b)
(c)
(d)
几种不同计时起点的正弦电流波形
例 在选定的参考方向下, 已知两正弦量的解析式为 u=200sin (1000t+200°) V, i=-5sin (314t+30°) A, 试求两个 正弦量的三要素。
2. 周期和频率
正弦量变化一周所需的时间称为周期。通常用“T”
表示，单位为秒(s)。正弦量每秒钟变化的周数称为频
率，用“f ” 表示，单位为赫兹(Hz)。周期和频率互成
f 1 T
3.相位、角频率和初相
ωt+φ－－－相位角
在不同的瞬间，正弦量有着不同的相位，因而 有着不同的状态。相位的单位一般为弧度(rad)。
下面分别加以讨论：
(1)φ12=θ1-θ2>0且|φ12|≤π弧度 (2) φ12=θ1-θ2<0且|φ12|≤π弧度
(3) φ12=θ1-θ2=0,称这两个正弦量同相
(4) φ12=θ1-θ2=π, 称这两个正弦量反相 (5) φ12=θ1-θ2=π/2, 称这两个正弦量正交
同频率正弦量的几种相位关系
由波形可知电压和电流的最大值分别为300mV和5mA，频 率都为1kHz，角频率为2000πrad/s，初相分别为π/6和π/3， 它们的解析式分别为:
(1)T =100ms时，
uab
(t)
300sin(2000πt
π 6 )mV,iab
(t)
5sin(2000πt
π 3
)mV
uab (0.1)
解 (1) u=200sin(1000t+200°)=200sin(1000t-160°)V
所以电压的振幅值Um=200V, 角频率ω=1000rad/s, 初相θu=160°。
(2) i=-5sin(314t+30°)=5sin(314t+30°+180°)
=5sin(314t-150°)A
所以电流的振幅值Im=5A, 角频率ω=314rad/s, 初相θi=-150°。
3.1 正弦量的基本概念
3.1.1 正弦交流电的三要素
按正弦规律变化的交流电动势、交流电压、交流电流等物理量统称为 正弦量，如图3-1-1所示。
以正弦电流为例，对于给定的参考方向，正弦量的 一般解析函数式为
i(t) Im sin(t )
1. 正弦量瞬时值中的最大值, 叫振幅值, 也叫峰值。
用大写字母带下标“m”表示, 如Um、Im等。
300sin(2000π 0.1
π) 6
300sin
π 6
150mV
iab (0.1)
5sin(2000π 0.1
π) 3
5 s in
π 3
4.33m
(2)当t＝100ms时
iba
(t)
iab
5sin(2000πt
π 3
π)
5sin(2000πt
2π 3
)mA
iba
(0.1)
5sin(
2π 3
角频率－－－相位角变化的速度。 单位：rad/s或1/s。
相位变化2πrad，经历一个周期T，那么
2π T
2πf
与f成正比
当φ=0时，正弦波的零点就是计时起点 当φ>0，正弦波零点在计时起点之左，其波形相对于φ=0的 左移φ角，
当φ<0，正弦波零点在计时起点之右，其波形相对于φ=0的 波形右移|φ|角，
(b) 由图知θ1=θ2, φ12=θ1-θ2=0, 表明二者同相。
(c) 由图知θ1-θ2=π, 表明二者反相。
(d) 由图知θ1=0,
前于 i2
3ቤተ መጻሕፍቲ ባይዱ
4
2
3
4
,12
1
2
3
4
,
表明i1越
3.1.3
有效值的定义
交流电的有效值。 交流电的有效值是根据它的热效应 确定的。交流电流i通过电阻R在一个周期内所产生的热量 和直流电流I通过同一电阻R在相同时间内所产生的热量相 等, 则这个直流电流I的数值叫做交流电流i的有效值, 用大写 字母表示, 如I、 U等。
例 分别写出下图中各电流i1、 i2的相位差, 并说明i1 与i2
i
i1
i2
3
2
2
2
0
t
i i1
i2
0
2
3
2 t
2
＝
(a)
(b)
i
i1
i2
i
i1
i2
3 2 t
2
2
(c)
3 2
t
2
2
3 4
(d)
解 (a) 由图知θ1=0, θ2=90°, φ12=θ1-θ2=-90°, 表明i1滞后 于i2 90°。
例题:已知: u 220 2 sin(t 235)V , i 10 2 sin(t 45)A 求u和i的初相及两者间的相位关系。
解 : u 220 2 sin(t 235)V 220 2 sin(t 125)V
所以电压u的初相角为125,电流i的初相角为45
ui u i 125 45 170 0 表明电压u滞后电流170。