行政职业能力测验-数量关系(一)
行政职业能力测试-数量关系(一)_真题-无答案

行政职业能力测试-数量关系(一)(总分100,考试时间90分钟)第二部分数量关系一、数学运算1. 的值为______。
A.B.C.D.2. 对分数进行操作,每次分母加15,分子加7,问至少经过几次这样的操作能使得到的分数不小于?______A.46次 B.47次 C.48次 D.49次3. 合唱团成员排练时站在一个五级的台阶上,最上面一级站N个人。
若上面一级比下面一级多站一个人,则多了7个人;若上面一级比下面一级少站一个人,则少多少人?______A.4个 B.7个 C.10个 D.13个4. 某班有56名学生,每人都参加了a、b、c、d、e五个兴趣班中的其中一个。
已知有27人参加a兴趣班,参加b兴趣班的人数第二多,参加c、d兴趣班的人数相同,e兴趣班的参加人数最少,只有6人,问参加b兴趣班的学生有多少个?______A.7个 B.8个 C.9个 D.10个5. 有a、b、c三种浓度不同的溶液,按a与b的质量比为5:3混合,得到的溶液浓度为13.75%;按a与b的质量比为3:5混合,得到的溶液浓度为16.25%;按a、b、c的质量比为1:2:5混合,得到的溶液浓度为31.25%。
问溶液c的浓度为多少?______A.35% B.40% C.45% D.50%6. 两支篮球队打一个系列赛,三场两胜制,第一场和第三场在甲队的主场,第二场在乙队的主场。
已知甲队主场赢球概率为0.7,客场赢球概率为0.5。
问甲队赢得这个系列赛的概率为多少?______A.0.3 B.0.595 C.0.7 D.0.7957. 有30名学生,参加一次满分为100分的考试,已知该次考试的平均分是85分,问不及格(小于60分)的学生最多有几人?______A.9人 B.10人 C.11人 D.12人8. 四对情侣排成一队买演唱会门票,已知每对情侣必须排在一起,问共有多少种不同的排队顺序?______A.24种 B.96种 C.384种 D.40320种9. 甲、乙、丙三人跑步比赛,从跑道起点出发,跑了20分钟,甲超过乙一圈,又跑了10分钟,甲超过丙一圈,问再过多长时间,丙超过乙一圈?______A.30分钟 B.40分钟 C.50分钟 D.60分钟10. 用a、b、c三种不同型号的客车送一批会议代表到火车站,用6辆a型车,5趟可以送完;用5辆a型车和10辆b型车,3趟可以送完;用3辆b型车和8辆c型车,4趟可以送完。
辅警招聘考试行政职业能力测验(数量关系)模拟试卷1(题后含答案及解析)

辅警招聘考试行政职业能力测验(数量关系)模拟试卷1(题后含答案及解析)题型有:1. 单项选择题单项选择题1.完成以下数列:1,2,4,7,( ),16。
A.9B.10C.11D.12正确答案:C。
解析:这一数列的排列规律是相邻两项之差构成一个等差数列1,2,3,4,5,故空缺项应为11。
正确答案为C。
知识模块:数量关系2.完成以下数列:1,2,4,8,16,( )。
A.16B.24C.32D.36正确答案:C。
解析:原数列是一个等比数列,后一项是前一项的2倍,故正确答案为C。
知识模块:数量关系3.完成以下数列:1,3,5,7,( )。
A.8B.9C.11D.13正确答案:B。
解析:本数列为奇数数列,1,3,5,7,9,11,也是公差为2的等差数列。
知识模块:数量关系4.完成以下数列:3,11,13,29,31,( )。
A.52B.53C.54D.55正确答案:D。
解析:数列中每相邻两项的差得出的数观察如下:11-3=8,29-13=16,则括号里的数减去31应等于24或32(等差数列或等比数列),则括号里的数为24+31=55或32+31=63,对照选项,只有D选项符合。
知识模块:数量关系5.完成以下数列:16,8,8,12,24,60,( )。
A.90B.120C.180D.240正确答案:C。
解析:数列中每相邻两项的商为0.5,1,1.5,2,2.5,所以括号里的数除以60应该等于3,故选C。
知识模块:数量关系6.完成以下数列:3,2,5/3,3/2,( )。
A.7/5B.5/6C.3/5D.3/4正确答案:A。
解析:数列进行通分可得:3/1,4/2,5/3,6/4,可推测出下一个数为7/5。
知识模块:数量关系7.完成以下数列:0,2,12,36,( )。
A.80B.82C.84D.86正确答案:A。
解析:题干数列可做如下分解:0=02×1;2=12×2;12=22×3;36=32×4;故第5个数应为:42×5=80。
行政职业能力测试题型(数量关系、阅读理解、判断推理、常识、资料分析)

行政职业能力测试大体分为数量关系、阅读理解、判断推理、常识、资料分析五大部分,这五部分中包含大约1 5个题型,题量在135道题左右,共涉及了从小学到研究生的各类学科知识,知识面涉及之广是其他考试无法比的,而规定的考试时间为120分钟。
行政职业能力测试中的各种题型及其解题技巧、规律,帮助大家以最快的速度找出正确的答案.各题型介绍及技巧第一部分数量关系数量关系体现了一个人抽象思维的发展水平。
在行政职业能力测验中,数量关系测验主要是从数字推理和数学运算两个角度来考查考生对数量关系的理解能力和反应速度。
这部分对考生而言是最需要技巧运用的题型:1、数字推理数字推理题给出一个数列,但其中缺少一项,要求考生仔细观察这个数列各数字之间的关系,找出其中的排列规律,然后从4个供选择的答案中选出自己认为最合适、合理的一个,来填补空缺项,使之符合原数列的排列规律。
近年来数字推理题的趋势是越来越难,即需综合利用两个或者两个以上的规律。
在备考该题型时,大家首先要熟记数字的平方、立方,提高对数字的敏感度,看到某个数字就应感觉到它可能是某个数字的平方或立方,例如看到63、65大家就应该想到它可能是8的平方加减1得来的其次,牢记基本数列如:自然数列、质数列、合数列等。
例如:2,3,5,7,11,13,…… 一看就知道这是一个质数数列牢记以上两点,不仅提高你的作答速度,而且它也是你破解复合数列的良好基础。
数字推理题的解题方法与技巧:a、数列各数项之间差距不大的,就可考虑用加减等规律;b、如果各数项之间差距明显的,就可考虑用平方、立方、倍数等规律;c、如果是分数数列,就要通过通分、约分看变化。
2、数学运算该题型主要是考查考生解决数学问题的能力。
考生要尽量用心算而避免演算,这样才能加快做题的速度。
数学运算中涉及到以下几个问题:a。
四则运算b。
比例分配c。
浓度问题d. 路程问题e。
流水问题f。
工程问题g. 种树问题h. 青蛙跳井问题i. 年龄问题等数学运算的解题方法与技巧:a、认真审题,因为数量关系的题干极其精练,它的每个字每个词都有它存在的价值,尤其注意题中的一些关键信息,只有这样才能将题意化繁为简.b、在平时通过训练和细心总结,尽量掌握一些数学运算的技巧、方法和规则,熟悉常用的基本数学知识。
行政职业能力测验(数量关系)

等差数列a、a+d、a+2d、a+3d、… … 等比数列 a、aq、aq2 、aq3 、… …
周期数列:自某一项开始重复出现前面相同 (相似)项的数列,如:
1,3,7,1,3,7,… 1,7,1,7,1,7,… 1,3,7,-1,-3,-7,…
对称数列 :围绕中间项对称规律(相同或相 似)的数列,如:
4+1,9+1 ,16+1 ,25+1 ,( ) 例:6 , 24, 60, 120,( )
A.186 B.200 C.210 D.220 规律:23-2,33-3,43-4,53-5,63-6
平方数变形型
特征:在平方数的基础上加减乘除同一个常数 例 : 66、83、102、123、( ) A、144 B、145 C、146 D、147 规律:8-12的平方加2
解题指导:寻找数字规律的方法
(1)相邻数之间通过加、减、乘、除、平方、 开方等运算方式发生联系,产生规律。
(2)数列中每一个数字本身的特点形成数字之 间的规律。
数字推理数量关系的规律
(一)等差数列
例:2,5 ,8,11,( )
A.12 B.13 D.15
例:0.5,0.9 ,( ),1.7,2.1
(三)和(差)数列及其变式
1.典型和(差)数列 例题11:2 1 3 4 7 ( ) A.13 B.9 C.11 D.10 解析:C。前两个数之和等于第三个数。 例题14:13 9 4 5 -1 6 ( ) A.7 B.-7 C.5 D.-5 解析:B。前一数减去后一数等于第三个数。
应试对策
1.快速游览已给出的数字,仔细观察和分析各数之 间的关系,尤其是前三个数之间的关系,在此基础 上提出假设,并将这一假设应用到对下一数的检验 上,如成功说明假设正确,就可找出正确答案;如 果不正确,就立即改变思路提出另一个假设,直到 找到该题规律为止。
广东公考行政职业能力测验模拟试题一(1)

第⼀部分数量关系(共15题,参考时间15分钟) 本部分包括两种类型的题⽬。
⼀、数字推理:共5题,每题给你⼀个数列,但其中缺少⼀项,要求你仔细观察数列的排列规律,然后从四个供选择的选项中选出你认为最合理的⼀项,来填补空缺项。
【例题】1,2,4,8,16,()。
A. 32B. 24C. 64D. 20 【解答】A,前⼀个数扩⼤2倍就为后⼀个数,依此规律,本题正确答案是A. 1. ,,3,20,139,()。
A. 972B. 654C. 829D. 354 2. ,,,,,()。
A. B. C. D. 3. 27,14,20,21,24,17,9,()。
A. 32B. 19C. 14D. 24 4. 1,0,8,19,45,()。
A. 24B. 36C. 80D. 114 5. 26,51,86,21,56,81,()。
A. 79B. 56C. 26D. 86 ⼆、数学运算:共10题。
你可以在草稿纸上运算,要求你充分利⽤所给条件,寻找答题的途径。
【例题】88×87-89×86=()。
A. 1B. 2C. 3D. 4 【解答】B,实际上你只要⽤最后⼀位运算⼀下,就会发现最后⼀位数是2,只有B符合要求。
6. 在某⼩学各年级都参加的⼀次朗读⽐赛中,三、四年级共有24⼈获奖,在获奖者中有20⼈不是三年级的,有18⼈不是四年级的,该校朗读⽐赛获奖的总⼈数是多少⼈?()A. 34B. 31C. 26D. 17 7. 从1到400的⾃然数中,不含有数字5的⾃然数有多少个?()A. 414B. 401C. 324D. 296 8. 服装⼚⼆车间⼈数占全⼚⼈数的25%,三车间⼈数⽐⼆车间少,⼀车间⼈数⽐三车间多,⼀车间是156⼈,这个服装⼚共有多少⼈?()A. 640B. 620C. 600D. 540 9. 甲、⼄两个仓库存放⼀批化肥,甲仓库⽐⼄仓库多120袋,如果从⼄仓库搬出25袋放进甲仓库,⼄仓库的化肥的袋数就是甲仓库的,⼄仓库原有化肥多少袋?()A. 280B. 400C. 270D. 300 10. 某校有100名学⽣参加第四届⼩学“祖冲之杯”数学竞赛,平均分是63分,其中参赛男同学平均分为60分,⼥同学平均分为70分,那么该校参赛男同学⽐⼥同学多多少⼈?()A. 10B. 80C. 30D. 40盒,从⼩盒取出10⽀圆珠笔放⼊⼤盒,必须在⼤盒中再添两⽀同样的钢笔,两盒笔的总价才相等。
中职行政专业职业能力测验标准预测试卷(一):数量关系
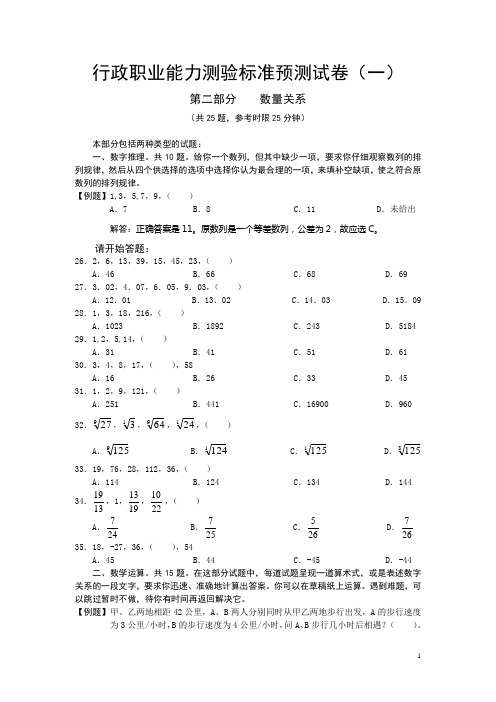
行政职业能力测验标准预测试卷(一)第二部分 数量关系(共25题,参考时限25分钟)本部分包括两种类型的试题:一、数字推理。
共10题。
给你一个数列,但其中缺少一项,要求你仔细观察数列的排列规律,然后从四个供选择的选项中选择你认为最合理的一项,来填补空缺项,使之符合原数列的排列规律。
【例题】1,3,5,7,9,( )A .7B .8C .11D .未给出解答:正确答案是11。
原数列是一个等差数列,公差为2,故应选C 。
请开始答题:26.2,6,13,39,15,45,23,( )A .46B .66C .68D .69 27.3.02,4.07,6.05,9.03,( )A .12.01B .13.02C .14.03D .15.09 28.1,3,18,216,( )A .1023B .1892C .243D .5184 29.1,2,5,14,( )A .31B .41C .51D .61 30.3,4,8,17,( ),58A .16B .26C .33D .45 31.1,2,9,121,( )A .251B .441C .16900D .96032.927,13,964,124,( )A .9125B .1124C .1125D .8125 33.19,76,28,112,36,( )A .114B .124C .134D .14434.1319,1,1913,2210,( ) A .247 B .257 C .265 D .267 35.18,-27,36,( ),54A .45B .44C .-45D .-44二、数学运算。
共15题。
在这部分试题中,每道试题呈现一道算术式,或是表述数字关系的一段文字,要求你迅速、准确地计算出答案。
你可以在草稿纸上运算。
遇到难题,可以跳过暂时不做,待你有时间再返回解决它。
【例题】甲、乙两地相距42公里,A 、B 两人分别同时从甲乙两地步行出发,A 的步行速度为3公里/小时,B 的步行速度为4公里/小时,问A 、B 步行几小时后相遇?( )。
行测的考试题及答案

行测的考试题及答案行政职业能力测验(行测)模拟题一、数量关系题目1:某公司员工总数为100人,其中男性员工占60%,女性员工占40%。
如果公司决定裁员10%,那么裁员后男性员工的比例是多少?答案:首先,公司男性员工数为100人*60%=60人,女性员工数为100人*40%=40人。
裁员10%即裁员10人。
因为男女员工比例为3:2,所以裁员时按照比例裁员,男性裁员6人,女性裁员4人。
裁员后男性员工数为60-6=54人,女性员工数为40-4人=36人。
裁员后总员工数为54+36=90人。
因此,裁员后男性员工的比例为54/90=60%。
二、判断推理题目2:如果所有的苹果都是水果,所有的水果都是植物,那么可以推断出所有的苹果都是植物吗?答案:是的,可以推断出所有的苹果都是植物。
因为苹果是水果,而所有的水果都是植物,所以根据逻辑推理,所有的苹果也必然是植物。
三、资料分析题目3:某市2019年的GDP为1000亿元,2020年的GDP为1100亿元。
请问2020年的GDP增长率是多少?答案: GDP增长率计算公式为:(2020年GDP - 2019年GDP) / 2019年GDP * 100%。
根据题目数据,2020年的GDP增长率为:(1100 - 1000) / 1000 * 100% = 10%。
四、常识判断题目4:以下哪个不是中国的传统节日?A. 春节B. 清明节C. 圣诞节D. 中秋节答案: C. 圣诞节。
春节、清明节、中秋节都是中国的传统重要节日,而圣诞节是西方传统节日。
五、言语理解与表达题目5:以下哪个成语与“画蛇添足”意思相近?A. 多此一举B. 一举两得C. 事半功倍D. 一举成名答案: A. 多此一举。
“画蛇添足”意指做事多余,无益,与“多此一举”意思相近。
六、逻辑填空题目6:他虽然______,但仍然坚持完成了任务。
A. 身体不适B. 精神不振C. 情绪低落D. 状态不佳答案: D. 状态不佳。
山东省公务员行政职业能力测验(数量关系)-试卷1

山东省公务员行政职业能力测验(数量关系)-试卷1(总分:62.00,做题时间:90分钟)一、数量关系(总题数:31,分数:62.00)1.数学运算在这部分试题中,每道试题呈现一道算术式或是表述数字关系的一段文字,要求你迅速、准确地计算出答案。
(分数:2.00)__________________________________________________________________________________________ 解析:2.某市制定了峰谷分时电价方案,峰时电价为原电价的110%,谷时电价为原电价的八折。
小静家六月用电400度,其中峰时用电210度,谷时用电190度。
实行峰谷分时电价调整方案后小静家用电成本为调整前的多少?( )(分数:2.00)A.95.75%√B.87.25%C.90.5%D.85.5%解析:解析:费用问题。
假设原电价为1元/度,则调整后峰时电价为1.1元/度,谷时电价为0.8元×100%=95.75%。
故本题答案为A。
3.某人银行账户今年底余额减去1500元后,正好比去年底余额减少了25%,去年底余额比前年底余额的120%少2000元。
则此人银行账户今年底余额一定比前年底余额( )。
(分数:2.00)A.多1000元B.少1000元C.多10%D.少10%√解析:解析:根据已知条件,设前年底余额为x元,则去年底余额为(1.2x—2000)元,今年底余额为[0.75×(1.2x—2000)+1500]元,化简得今年底余额为0.9x元,即比前年底余额减少10%。
故本题选择D。
4.某单位共有职工72人,年底考核平均分数为85分,根据考核分数,90分以上的职工评为优秀职工。
已知优秀职工的平均分数为92分,其他职工的平均分为80分,问优秀职工的人数是多少?( )(分数:2.00)A.12B.24C.30 √D.42解析:解析:题干中给出总的职工数,让我们求优秀职工数,可看作是求优秀职工和其他职工的比值,可用“十字交叉法”:说明优秀职工共有30人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行政职业能力测验-数量关系(一)(总分:100.00,做题时间:90分钟)一、{{B}}数量关系{{/B}}(总题数:50,分数:100.00)1.3,7,15,31,______∙ A.59∙ B.63∙ C.67∙ D.71(分数:2.00)A.B. √C.D.解析:[解析] 方法一,前一项×2+1=后一项。
3×2+1=7,7×2+1=15,15×2+1=31,31×2+1=(63)。
故答案为B。
方法二,各项分别改写为22-1、23-1、24-1、25-1、(26-1=63)。
故答案为B。
2.3,4,6,8,12,______∙ A.16∙ B.17∙ C.18∙ D.19(分数:2.00)A. √B.C.D.解析:[解析] 奇数项3,6,12是公比为2的等比数列;偶数项4,8,(16)是公比为2的等比数列。
故答案为A。
3.169,192,225,268,______∙ A.301∙ B.311∙ C.320∙ D.321(分数:2.00)A.B.C.D. √解析:[解析] 二级等差数列。
[*]4.29,31,60,______∙ A.71∙ B.83∙ C.91∙ D.95(分数:2.00)A.B.C. √D.解析:[解析] 可以看出,29+31=60,即前两项之和等于第i项,所以最后一项为31+60=(91)。
5.0,3,2,5,4,7,______∙ A.10∙ B.9∙ C.8∙ D.6(分数:2.00)A.B.C.D. √解析:[解析] 方法一,间隔组合数列,奇数项和偶数项分别构成公差为2的等差数列。
方法二,和数列变式。
[*]6.1,3,7,15,______∙ A.25∙ B.29∙ C.31∙ D.35(分数:2.00)A.B.C. √D.解析:[解析] 方法一,二级等差数列变式。
[*]方法二,a n+1=2×a n+1,所求为2×15+1=(31)。
方法三,多次方数列变式。
各项可依次改写为21-1、22-1、23-1、24-1、25-1=(31)。
7.3,2,11,14,27,34,______∙ B.47∙ C.42∙ D.51(分数:2.00)A.B.C.D. √解析:[解析] 方法一,二级等差数列。
[*]方法二,平方数列变式。
各项可依次改写为12+2、22-2、32+2、42-2、52+2、62-2、(72+2=51)。
8.-6,-5,-2,3,10,______∙ A.19∙ B.22∙ C.32∙ D.40(分数:2.00)A. √B.C.D.解析:[解析] 二级等差数列。
[*]9.3,3,6,8,12,13,24,______∙ A.16∙ B.18∙ C.20∙ D.24(分数:2.00)A.B. √C.D.解析:[解析] 间隔组合数列,奇数项3,6,12,24是公比为2的等比数列;偶数项3,8,13,(18)是公差为5的等差数列。
10.68,91,114,137,______∙ A.158∙ B.159∙ C.160(分数:2.00)A.B.C. √D.解析:[解析] 公差为23的等差数列。
11.23,56,1130,5330,______∙ A.111590∙ B.111580∙ C.112430∙ D.121540(分数:2.00)A. √B.C.D.解析:[解析] 可以看出2+3=5,2×3=6;5+6=11,5×6=30;1+1+3+0=5,11×30=330。
可知,每一项都是由前一项的各位数字经过运算拼凑而成的。
5+3+3+0=11,53×30=1590,所以最后一项为111590。
12.0,1,2,2,3,6,4,______∙ A.3∙ B.7∙ C.8∙ D.10(分数:2.00)A.B. √C.D.解析:[解析] 相邻的三项相加,得到3,5,7,11,13,(17),是质数列,选B。
13.1,2,5,10,17,26,______∙ A.29∙ B.32∙ C.35∙ D.37(分数:2.00)A.B.C.D. √解析:[解析] 方法一,二级等差数列。
[*]方法二,各项可依次改写为02+1、12+1、22+1、32+1、42+1、52+1、(62+1=37)。
14.10,19,29,10,39,29,______∙ A.10∙ B.49∙ C.20∙ D.68(分数:2.00)A.B.C.D. √解析:[解析] 10+19=29,29-19=10,29+10=39,39-10=29,39+29=(68),选D。
15.1,18,4,14,7,10,______∙ A.8∙ B.9∙ C.10∙ D.11(分数:2.00)A.B.C. √D.解析:[解析] 间隔组合数列,奇数项1,4,7,(10)是公差为3的等差数列;偶数项18,14,10是公差为-4的等差数列。
16.4,5,13,23,49,______∙ A.6∙ B.84∙ C.95∙ D.99(分数:2.00)A.B.C. √D.解析:[解析] 第一项×2+第二项=第三项,23×2+49=(95)。
17.6,13,29,63,133,______∙ A.212∙ B.235∙ C.269∙ D.275(分数:2.00)A.B.C.D. √解析:[解析] 三级等差数列变式。
[*] 18.2,16,6,40,8,70,10,______∙ A.108∙ B.90∙ C.86∙ D.80(分数:2.00)A. √B.C.D.解析:[解析] 分组组合数列。
[*] 19.1,3,6,10,15,______∙ A.21∙ B.23∙ C.26∙ D.31(分数:2.00)A. √B.C.D.解析:[解析] 二级等差数列。
[*] 20.4,6,10,14,22,26,______∙ A.30∙ B.33∙ C.34∙ D.36(分数:2.00)A.B.C. √D.解析:[解析] 各项除以2得到质数列2、3、5、7、11、13、(17),故应填入17×2=(34)。
21.37,35,32,27,19,______∙ A.4∙ B.6∙ C.9∙ D.13(分数:2.00)A.B. √C.D.解析:[解析] 二级等差数列变式。
[*]22.2,3,6,15,42,______∙ A.98∙ B.117∙ C.123∙ D.135(分数:2.00)A.B.C. √D.解析:[解析] 二级等差数列变式。
[*]23.,,,______ A. B. C. D(分数:2.00)A.B.C. √D.解析:[解析] 各项依次改写为[*]、[*]、[*]、([*]),分子构成公差为7的等差数列,分母构成二级等差数列。
24.4,4,6,12,______,90∙ A.24∙ B.26∙ C.28∙ D.30(分数:2.00)A.B.C.D. √解析:[解析] 4÷4=1,6÷4=1.5,12÷6=2,(30)÷12=2.5,90÷(30)=3。
商构成公差为0.5的等差数列。
25.3,11,27,51,______∙ A.79∙ B.81∙ C.83∙ D.85(分数:2.00)A.B.C. √D.解析:[解析] 方法一,二级等差数列。
[*]方法二,平方数列变式。
各项依次可写为12+2、32+2、52+2、72+2、(92+2=83)。
26.2,2,6,14,34,82,______∙ A.148∙ B.168∙ C.180∙ D.198(分数:2.00)A.B.C.D. √解析:[解析] 第一项+第二项×2=第三项,34+82×2=(198)。
27.1,3,4,6,10,12,22,24,______∙ A.58∙ B.46∙ C.36∙ D.32(分数:2.00)A.B. √C.D.解析:[解析] 1+3=4,4+6=10,10+12=22,22+24=(46)。
28.1,3,5,9,17,31,______∙ A.78∙ B.65∙ C.57∙ D.46(分数:2.00)A.B.C. √D.解析:[解析] 三项和数列,9+17+31=(57)。
29.26,42,68,110,______∙ A.134∙ B.178∙ C.146∙ D.166(分数:2.00)A.B. √C.D.解析:[解析] 第一项+第二项=第三项。
26+42=68,42+68=110,68+110=(178)。
30.1,3,4,8,16,______∙ A.20∙ B.24∙ C.28∙ D.32(分数:2.00)A.B.C.D. √解析:[解析] 1+3=4,1+3+4=8,1+3+4+8=16,1+3+4+8+16=(32)。
31.2,3,5,9,17,33,______∙ A.60∙ B.64∙ C.65∙ D.70(分数:2.00)A.B.C. √D.解析:[解析] [*]32.2,2,5,17,71,______∙ A.288∙ B.316∙ C.359∙ D.381(分数:2.00)A.B.C. √D.解析:[解析] 2×1+0=2,2×2+1=5,5×3+2=17,17×4+3=71,71×5+4=(359)。
33.15,19,23,28,33,______∙ A.38∙ B.39∙ C.40∙ D.41(分数:2.00)A.B. √C.D.解析:[解析] 相邻两项之差分别为4、4、5、5、(6),下一项为33+6=(39)。
34.,,,,______ A. B. C.-3(分数:2.00)A.B.C. √D.解析:[解析] 原数列可以改写为[*],[*],[*],[*],([*]),故所填数应是[*],答案选C。
35.5,6,19,17,______,-55∙ A.15∙ B.344∙ C.343∙ D.11(分数:2.00)A.B. √C.D.解析:[解析] 第一项的平方=第二项+第三项,52=6+19,62=19+17,192=17+(344),172=(344)+(-55)。
答案选B。
36.1.01,2.02,3.04,5.07,______,13.20∙ A.7.09∙ B.7.01∙ C.8.10∙ D.8.12(分数:2.00)A.B.C.D. √解析:[解析] 整数部分1、2、3、5、(8)、13为和数列,小数部分为前一个数整数部分和小数部分数字之和,括号处小数部分为5+7=(12),因此所求数为8.12。
