智慧作业---圆周角定理
圆周角定理一条弧所对圆周角等于它所对圆心角的一半

圆周角定理:一条弧所对圆周角等于它所对圆心角的一半证明:已知在⊙O中,∠BOC与圆周角∠BAC同对弧BC,求证:∠BOC=2∠BAC.证明:情况1:如图1,当圆心O在∠BAC的一边上时,即A、O、B在同一直线上时:图1向左转|向右转∵OA、OC是半径解:∴OA=OC∴∠BAC=∠ACO(等边对等角)∵∠BOC是△AOC的外角∴∠BOC=∠BAC+∠ACO=2∠BAC情况2:如图2,,当圆心O在∠BAC的内部时:连接AO,并延长AO交⊙O于D图2向左转|向右转∵OA、OB、OC是半径解:∴OA=OB=OC∴∠BAD=∠ABO,∠CAD=∠ACO(等边对等角)∵∠BOD、∠COD分别是△AOB、△AOC的外角∴∠BOD=∠BAD+∠ABO=2∠BAD(三角形的外角等于两个不相邻两个内角的和)∠COD=∠CAD+∠ACO=2∠CAD(三角形的外角等于两个不相邻两个内角的和)∴∠BOC=∠BOD+∠COD=2(∠BAD+∠CAD)=2∠BAC情况3:如图3,当圆心O在∠BAC的外部时:图3向左转|向右转连接AO,并延长AO交⊙O于D连接OA,OB。
解:∵OA、OB、OC、是半径∴OA=OB=OC∴∠BAD=∠ABO(等边对等角),∠CAD=∠ACO(OA=OC)∵∠DOB、∠DOC分别是△AOB、△AOC的外角∴∠DOB=∠BAD+∠ABO=2∠BAD(三角形的外角等于两个不相邻两个内角的和)∠DOC=∠CAD+∠ACO=2∠CAD(三角形的外角等于两个不相邻两个内角的和)∴∠BOC=∠DOC-∠DOB=2(∠CAD-∠BAD)=2∠BAC从而得证:∠BOC=2∠BAC.。
圆周角定理及其推论

圆周⾓定理及其推论
圆周⾓定理指的是⼀条弧所对圆周⾓等于它所对圆⼼⾓的⼀半。
这⼀定理叫做圆周⾓定理。
定理推论:在同圆或等圆中,同弧或等弧所对的圆周⾓相等,相等的圆周⾓所对的弧也相等。
定理内容
圆周⾓的度数等于它所对弧上的圆⼼⾓度数的⼀半,同弧或等弧所对的圆周⾓相等。
圆周⾓:顶点在圆上,并且两边都和圆相交的⾓叫做圆周⾓,这⼀定义实质上反映的是圆周⾓所具备的两个特征:①顶点在圆上,②两边都和圆相交。
这两个条件缺⼀不可。
定理推论
1.在同圆或等圆中,同弧或等弧所对的圆周⾓相等,相等的圆周⾓所对的弧也相等。
2.半圆(直径)所对的圆周⾓是直⾓;90°的圆周⾓所对的弦是直径。
3.圆的内接四边形的对⾓互补,并且任何⼀个外⾓都等于它的内对⾓。
2.1圆周角定理

例1:如图:AB,AC是⊙O的两条弦,延长CA到D, 使AD=AB.若∠ADB=40°, 求∠BOC的度数.
B O C
D A
160°
例2.AB是⊙O的直径,BD是⊙O的弦, 延长BD到点C,使CD=BD,连接AC. 判断AB与AC的大小有什么关系?为什么?
C
小结: 圆周角/圆心角定理
圆周角定理:
圆上一条弧所对的圆周角等于它所对的圆心角的一半. 圆心角定理:圆心角的度数等于它所对弧的度数. 推论1:在同圆或等圆中, 同弧或等弧所对的圆周角相等; 相等的圆周角所对的弧也相等. 推论2:半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
小结: 圆周角/圆心角定理
B E · O H D G C
3.如图,BC是半圆的直径,P是半圆上的一点,过 BP 的中点A,作AD⊥BC,垂足为D,BP交AD 于E,交AC于F, 求证:BE=AE=EF
︵
A
2
B
EF D
1
3 4
P
C
4、如图, Δ ABC内接于⊙O,AH⊥BC于点H, 求证:(1)∠OAB=∠HAC (2)OA·AH=1/2AB·AC
(第1题) (第2题) (第3题)
2.如图,圆的直径AB=13cm,C为圆上一点,CD⊥AB,垂 足D,且CD=6cm.求AD的长. ⌒ ⌒ 3.如图,BC是⊙O的直径, AD⊥BC,垂足D.AB=AF,BF 和 AD相交于E.求证:AE=BE.
2、如图,设AD,CF是Δ ABC的两条高, AD,CF的延长线交Δ ABC的外接圆O于G,AE 是⊙O的直径,求证: (1)AB·AC=AD·AE F A (2)DG=DH
初中数学易错题流程化-圆周角定理

初中数学易错题流程化-圆周角定理重庆中考中,有关圆的考点相对比较简单,但正因为比较简单,导致很多学生对圆不太敏感,很多时候看似都做对了,其实逻辑性并不严明,属于蒙对的,所以在考试中并不能保证百分之百做对。
今天我们就先讲其中一个考点—圆周角定理。
知识点:圆周角定理,圆中边角弦的关系流程化讲解例:如图,BC是⊙O的直径,点A在圆上,连接AO,AC,∠AOB=64°,则∠ACB= .(出自2017重庆中考15题)解题过程:1. 标注∠AOB=64°,所求∠ACB的位置(几何计算中,第一步都是读题标注好已知信息)2. ∵∠ACB和∠AOB是均是弧AB所对应的圆周角和圆心角∴∠ACB=1/2∠AOB=32°(这道题解题过程很简单,直接用圆周角定理就能做对,所以圆的内容在重庆中考中不难,大家不要担心自己不会做)总结:这道题很简单,很多同学总觉得没什么可讲的,那么我所表达的流程化到底在哪儿呢,我们来分析一下:第一步:标注已知信息(这一步是所有几何题都都应该先做的,不只是计算题,几何证明题也同样重要)第二步:看问题,分析找所求角对应弧,比如这道题对应的就是弧AB(在几何计算中,我们重要的就是看问题所求的量,角也好,边也好,我们得分析出这个角如何求,边如何求)第三步:找对应弧上的圆周角或圆心角,如果没有,可添加辅助线构造那么这道题简单就简单在这里,弧AB所对应的就只有圆心角AOB第四步:求出对应的圆心角或者圆周角,那么这道题简单就简单在这里,弧AB所对应的就只有圆心角AOB已知其度数,所以利用圆周角定理就求出答案了。
(如果不知道角的度数,我们就要导角,那么导角对于圆的题来说相对比较简单,就是与已知角产生关系)流程化巩固(为了更好地帮助大家理解到这简单三步的好处,我们下面再来看一道题)例:如图,CD 是⊙O的直径,A、B两点在⊙O上,且 AB与CD 交于点E,若∠BAO=30°,AO∥BC,则∠AOD的度数为()A.120° B.100° C.170° D.150°解:第一步:标注已知信息相信大家都做好了第二步:第二步所求∠AOD对应的弧是弧AD第三步:弧AD所对应的圆周角图中没有,可以连接BD构造∠ABD,此时我们知道求出∠ABD乘以2,就求出了∠AOD第四步:求∠ABD,∠ABD挨着∠ABC,∠ABC=∠BAO=30°,且∠ABC+∠ABD=∠BCD(这样就与已知角产生了关系),又因为∠BCD=90°,所以∠ABD=90°-30°=60°所以就求出来∠AOD=120°注:今天给大家讲了一个很简单的几何计算题,并不是说这道题难,而是在给大家提供一个思路,就是几何题的逻辑思路,很多同学在做几何的时候就是没有方向,自己把每个角每条边能算的都算出来,最后来看能否求出答案,很明显就算最后选对了答案,也浪费了很多时间,所以一定要注意,不管多简单的几何题,都能明白解题的方向在哪儿,能理清楚解题的逻辑性,那么才算真的掌握到了几何解题的要点。
圆周角定理的应用

圆周角定理的应用圆周角定理是圆中的一个非常重要的定理,通过它,我们可以在求角度、算线段等方面有所作为。
我们一起来看几例。
一、求出相关角度。
圆周角定理揭示了它和同弧所对的圆心角度数之间的关系。
例1如图,点A、B、C都在⊙O上,若∠C=34°,则∠AOB的度数为多少分析:观察图形,发现∠C和∠AOB都是AB所对的角,一个是圆周角,另一个是圆心角,根据圆周角定理可得出结论。
解:因为∠C和∠AOB都是AB所对,则∠AOB=2∠C,得∠AOB=68°。
评:理解定理,运用定理。
例2如图,点A、B、C、D、E都在⊙O上,若∠A=14°,∠E=12°,则∠DOB的度数为多少分析:观察图形,∠A和∠E这两个圆周角共起来,才和圆心角∠DOB同对一弧,问题可解。
解:∠A和∠E这两个圆周角共起来,才和圆心角∠DOB同对一弧BD,所以∠DOB=2(∠A+∠E)=52°。
评:寻求已知和求知之间的联系。
二、求相关线段之间的关系通过圆周角定理,可找出相关线段所在三角形中角度之间的关系,从而可进一步加以探索。
例3 如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于D,DE∥BA交⊙O于E。
求证:AC=DE。
分析:因为相等的圆周角所对的弦相等,则要证AC=DE,只需证∠DAE =∠ADC。
证:连结AE、DC,因为AD平分∠BAC,所以∠BAD=∠DAC,因为DE∥BA,所以∠BAD=∠EDA,所以∠DAC=∠EDA,因为EC公共,所以∠EAC=∠EDC,所以∠DAC+∠CAE=∠ADE+∠EDC所以∠DAE=∠ADC,所以AC=DE。
评:通过寻求同一圆中,同弧或等弧所对的圆周角与弦等元素之间的对应关系,寻求解题思路。
例4 已知:如图,△ABC是⊙O的内接三角形,AD⊥BC于D,AE是⊙O 的直径,若S△ABC=S,⊙O的半径为R.求证:AB·AC=AD·AE分析:本题要证明的结论是“等积式”,•通常的思路是把等积式转化成比例式,再找相似三角形.上式可改成AB AEAD AC,则寻求△ADC∽△ABE。
圆周角定理及其运用
求证: △ABC 为直角三角形.
C
证明: 以AB为直径作⊙O,
1
∵AO=BO, CO= 2 AB,
A
·
B
O
∴AO=BO=CO.
∴点C在⊙O上.
又∵AB为直径,
∴∠ACB=
1 2
×180°=90°.源自∴ △ABC 为直角三角形.
3. 如图,在直径为AB的半圆中,O为圆心,C、D 为半圆上的两点,∠COD=50°,则
圆周角定理
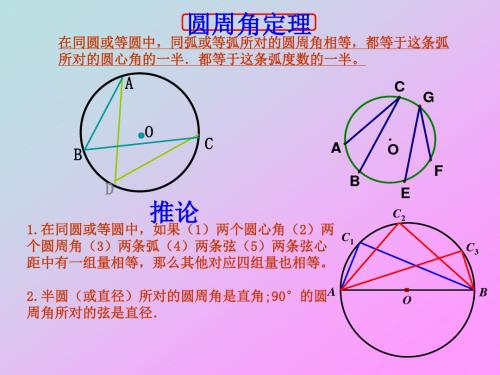
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧 所对的圆心角的一半.都等于这条弧度数的一半。
A
C
G
B
●O
C
A
D
B
推论
1.在同圆或等圆中,如果(1)两个圆心角(2)两 个圆周角(3)两条弧(4)两条弦(5)两条弦心 C1
距中有一组量相等,那么其他对应四组量也相等。
2.半圆(或直径)所对的圆周角是直角;90°的圆A 周角所对的弦是直径.
∠CAD=_2_5__°__;
4、在⊙O中,一条弧所对的圆心角和圆周角分别为
(2x+100)°和(5x-30)°,则x=_20°_;
D
A
O 40° B
C
例题
例 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平
分线交⊙O于D,求BC、AD、BD的长.
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
C
在Rt△ABC中,
BC AB2 AC2 102 62 8
A
O
B
∵CD平分∠ACB,
ACD BCD.
O F
E
C2
C3
·O
圆周角定理的推论2及圆

圆周角定理的推论2及圆
圆周角定理是几何学中的重要定理,它指的是:在任意三角形中,其三个内角的和为180°;而在任意园形内,相应的三角形所有内角的和为园周角,即360°,这就是圆周角定理。
圆周角定理是根据三角形和圆形的基础知识来说明的,其中三角形在几何学中是一种重要的几何体,其有三个角度。
任意三角形中,其三个角度的和是180°,而圆则是一个完整的圆形,因而其一个圈中包含了好多条边缘,所有的角度的和就是360°,这也正好等于园周角。
圆周角定理的推论2是:如果三点不在一条直线上,则这三点可以构成一个三角形,而在三角形内,其三个内角的和为180°;另一方面,一个圆中包含了很多条边缘,而它们如果组成三角形,那么它们的和是360°,因此,三角形内角的和等于园周角的和,就是圆周角定理。
因此,圆周角定理的推论2的意义在于,它使得对于所有的园形,可以很容易构绘出来,也可以更方便地计算出其内部的角度数。
圆周角定理的推论2也可以用来帮助解决许多几何问题,比如求椭圆的长短轴长度等。
总而言之,圆周角定理是一个重要的定理,它反映了三角形和圆形之间的关系,并由此推论出了圆周角定理的推论2,使得求解复杂几何问题更加容易,不仅提高了几何的计算应用,而且也成为了几何学的一大宝贵知识。
圆周角定理

∵∠1=∠2,∴ = ,
∴BF=CG, = ,
∴∠FBD=∠GCE.
又 ∵BD=CE,∴△BFD≌△CGE,
∴∠F=∠G,∴ = ,
∴AB=AC.
题型一
题型二
题型三
题型三
易错辨析
易错点:误认为同弦或等弦所对圆周角相等而致错
【例3】 如图,若∠BAD=75°,则∠BCD=
分成两条弧:优弧和劣弧,若圆周角的顶点同在优弧上或同在劣弧
上,同弦或等弦所对的圆周角相等;若一个圆周角的顶点在优弧上,
另一个圆周角的顶点在劣弧上,则同弦或等弦所对的圆周角不相等,
它们互补(如本题).
(2)在圆周角定理的证明中,运用了数学中分类讨论和化归的思想
以及归纳的证明方法.这个定理是从特殊情况入手研究的,首先研
究当角的一边过圆心时,得到圆周角与同弧所对的圆心角的关系,
然后研究当角的一边不经过圆心时,圆周角与同弧所对的圆心角之
间的关系.当角的一边不经过圆心时,又有两种情况:一是圆心在圆
周角内部;二是圆心在圆周角外部.经过这样不同情况的讨论,最后
第二讲
直线与圆的位置关系
一
圆周角定理
1.了解圆心角定理,并能应用定理解决问题.
2.理解圆周角定理及其两个推论,并能应用定理解决有关问题.
圆周角定理的理解
剖析:(1)应用圆周角定理时,要注意的问题如下:
圆周角定理推论1中,同圆或等圆中,相等的圆周角所对的弧相等.
这一定理成立的前提是同圆或等圆,否则不成立.
角形,从而得到成比例线段,再列方程求得线段长.
题型一
题型二
题型三
【变式训练 1】 如图,已知△ABC 内接于☉O, = , 点是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
智慧作业---圆周角定理
例题
如图,正方形ABCD 的顶点都在⨀O 上,P 是DC
̂上的一点,求∠BPC 的度数. 解:连接BD ,
∵ BD 是直径,
∴△BCD 是等腰直角三角形,
∴∠BDC=45°,
∴∠BPC=∠BDC=45°.
举一反三
1.如图,0A ,0B 是O0的半径,点C 在⊙0上,连接AC ,BC.若∠AOB=120°,则∠ACB= 60 度.
【解析】解:同弧或等弧所对的圆心角是圆周角的2倍,
.∠ACB=12∠AOB=1
2×120=60°.
2.如图,⊙0是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为( )
A.40°
B.30°
C.45°
D.50°
试题分析:根据等边对等角及圆周角定理求角即可.
∵OA=OB
∴∠OAB=∠OBA=50°
∴∠AOB=80°
∴∠ACB=40°.
故选A .
考点: 1.圆周角定理;2.三角形内角和定理. 3.如图,AB 是⊙0的直径,C ,D 是⊙0上的两点,若∠BCD=28°,则∠ABD=_______ ∵AB 是⊙0的直径,
∴∠ACB=90°,
∴∠ACD=90°-∠BCD=62°,
由圆周角定理得,∠ABD=∠ACD=62°,
故选:B .。
