复摆实验 实验报告
物理实验报告复摆

一、实验目的1. 了解复摆的振动规律。
2. 学习使用复摆进行测量,掌握测量摆长、摆角和周期的方法。
3. 通过实验,验证单摆周期公式,加深对单摆理论的理解。
二、实验原理复摆是一种由两个或多个单摆组成的系统,其振动规律与单摆类似。
在理想情况下,复摆的周期仅与摆长和重力加速度有关,与摆角无关。
本实验通过测量复摆的周期,验证单摆周期公式。
单摆周期公式为:\[ T = 2\pi \sqrt{\frac{L}{g}} \]其中,T为周期,L为摆长,g为重力加速度。
三、实验器材1. 复摆装置2. 刻度尺3. 秒表4. 计算器四、实验步骤1. 将复摆装置固定在支架上,确保复摆可以自由摆动。
2. 使用刻度尺测量复摆的摆长,记录数据。
3. 调整复摆的摆角,使其在30°~60°之间。
4. 使用秒表测量复摆摆动n次所需的时间,记录数据。
5. 重复步骤3和4,进行多次测量,取平均值。
6. 根据单摆周期公式,计算理论周期,并与实验周期进行比较。
五、实验数据及处理1. 摆长L = 1.0 m2. 摆角θ = 45°3. n = 104. 实验周期T1 = 1.5 s5. 实验周期T2 = 1.4 s6. 实验周期T3 = 1.6 s7. 平均实验周期T = (T1 + T2 + T3) / 3 = 1.5 s六、实验结果与分析1. 根据单摆周期公式,计算理论周期:\[ T_{理论} = 2\pi \sqrt{\frac{L}{g}} = 2\pi \sqrt{\frac{1.0}{9.8}}\approx 1.97 \text{ s} \]2. 比较实验周期与理论周期:\[ \frac{T_{理论}}{T} = \frac{1.97}{1.5} \approx 1.32 \]3. 分析误差来源:a. 实验误差:由于测量误差、计时误差等因素,导致实验周期与理论周期存在一定偏差。
b. 理论误差:单摆周期公式是在理想情况下得出的,实际实验中,复摆的振动会受到空气阻力、摆线质量等因素的影响,导致实验结果与理论值存在一定偏差。
用复摆测重力加速度实验报告

用复摆测重力加速度实验报告本次实验的主要目的是通过复摆实验来检测地心引力的大小,并确定出地球上的重力加速度。
实验过程中运用基本物理原理,通过实验数据求出重力加速度大小。
二、实验原理复摆,又称双摆,是由英国物理学家牛顿在1700年实验发现的。
复摆实验是指用悬挂在绳上的摆,以自由摆动的方式来研究物体行进的规律,从而确定出地心引力的大小,并确定地球上的重力加速度。
复摆运动,采用受到重力力的作用,由弹性力和摩擦力的作用,摆会由一定的速度一直摆动,并且摆的角度也保持不变。
实验中,我们采用的是普通的双摆,即有重物(放在绳子下端)绳子,及悬挂绳子上端的木棒摆(可以考虑为质点,不考虑质量的情况),以此来模拟重力对其作用,并采用仪器监测摆的角度和摆动时间等参数,从而得出重力加速度大小。
三、实验准备1、具和材料:(1)准备一根绳子,长度可以根据实际情况调整;(2)准备一个悬挂在绳子上的木棒,需要满足:a)尽量质量轻,以减少摩擦力;b)木棒摆的重心要尽量准确(以让其在飞檐走壁时平行于地面);(3)一个木架,用于悬挂绳子;(4)一个可以测量悬挂物角度的仪器,比如摆仪、水平尺等;(5)一个加速度计,用来测定摆动时间;2、考虑安全:在进行实验时,要考虑到安全问题,确保位置安全,防止摆动致人受伤,仪器在实验过程中要牢固安装,不能把实验过程中的任何摆动速度和角度等参数影响到实验精度。
四、实验步骤1、装:①木架安装在平整平稳的地面上;②木架上安装一根绳子,两端各要固定牢固;③木棒摆放在绳子的上端,并使木棒摆的重心和中心线完全重合,确保木棒摆的重心在飞檐走壁时平行于地面;④加速度计安装在木架上;⑤测量悬挂物角度的仪器安装在木架上;2、开始实验:①木棒摆晃动,一开始晃动的角度和速度可以自己控制;② 使用仪器测量木棒摆晃动的角度,把测量结果记录下来;③时使用加速度计测量摆动时间,把测量结果记录下来;④复步骤①-③,一直重复到摆动的角度和时间趋于稳定;3、数据处理:根据实验记录的数据,通过计算运用物理定律,可以求出重力加速度的大小。
大学物理实验报告 复摆法测重力加速度

大学物理实验报告复摆法测重力加速度内容
本实验旨在利用复摆法测量重力加速度。
实验仪器包括72 cm长铝管臂、影线、调整扳手、油流仪、抗干扰模块(磁力仪)等。
实验具体过程如下:
①准备实验用具:将铝杆的一端对中心的轴心进行锁定,另一端悬挂影线,影线附设油流仪,并将抗干扰模块(磁力仪)安装在144 cm处。
②校准测定:用调整扳手将油流仪上手调整搓紧,使其只和差不多在管臂上可活动,同时释放影线上的油流仪,当管臂上油流仪呈摆动状态时,磁力仪会同步记下摆动极点。
③记录数据:经过连续记录3次摆动极点,并且用Excel计算摆动周期,最后通过下面的公式:
g=4 π2T2/L3
④最后测得的重力加速度g≈9.80m/s2
实验最后的结果表明:通过复摆法可以得到准确的重力加速度,实验大多数结果符合物理原理以及数据的要求。
此外,实验者需要注意复摆实验中细节,以便获得更加精确的测量结果。
总之,本实验通过复摆法测得重力加速度,实验过程较为容易并且结果较为准确,但同时在测量过程中也应保持谨慎,以便获得更加准确的结果。
实验报告_复摆实验
1.764
1.764
1.764
4
1.774
1.774
1.774
6
1.537
1.533
1.535
6
1.527
1.527
1.527
8
1.379
1.389
1.384
8
1.406
1.406
1.406
10
1.301
1.306
1.304
10
1.317
1.317
1.317
12
1.265
1.269
1.267
12
1.262
姓名
学号
院系
时间
地点
【实验题目】复摆实验
【实验记录】
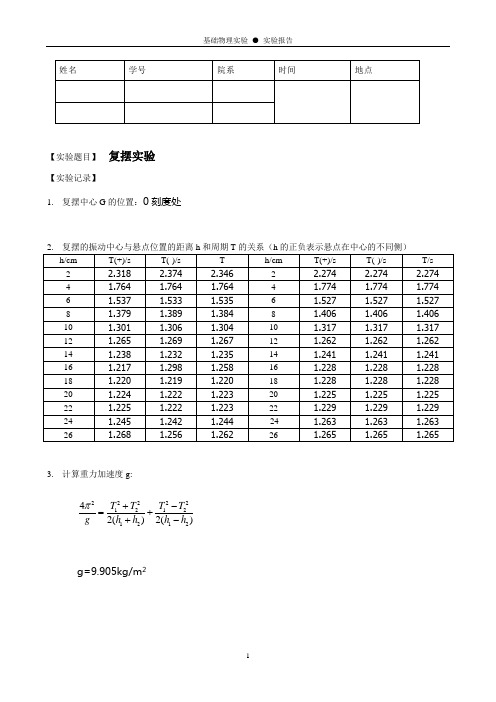
1.复摆中心G的位置:0刻度处
2.复摆的振动中心与悬点位置的距离h和周期T的关系(h的正负表示悬点在中心的不T(-)/s
T
h/cm
T(+)/s
T(-)/s
T/s
2
2.318
2.374
2.346
2
2.274
2.274
2.274
1.262
1.262
14
1.238
1.232
1.235
14
1.241
1.241
1.241
16
1.217
1.298
1.258
16
1.228
1.228
1.228
18
1.220
1.219
1.220
18
1.228
1.228
1.228
20
1.224
1.222
1.223
2018-复摆的实验报告-推荐word版 (6页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==复摆的实验报告篇一:实验报告 _复摆实验【实验题目】复摆实验【实验记录】1. 复摆中心G的位置:0刻度处3. 计算重力加速度g:4?2T12?T22T12?T22??g2(h1?h2)2(h1?h2)g=9.905kg/m214. 作T-h图5. 利用mgT2h?4?2IG?4?2mh2,作T2h~h2关系图,考察其线形关系,由最小二乘法计算g和复摆对重心的转动惯量IG。
IG=0.002536kg*m*m【结论与讨论】误差分析:1 在实验中,复摆的摆动不能很好的控制在同一平面摆动。
2 实验前没有很好的调节复摆对称。
3 复摆摆动可能幅度过大。
结论:利用复摆可以测量重力加速度,同时还可以由这个方法衍生开来测量不规则物体的转动惯量。
成绩(满分30分):????????? 指导教师签名:??????????????????? 日期:???????????????????2篇二:实验报告 _复摆实验【实验题目】复摆实验【实验记录】1. 复摆中心G的位置:3. 计算重力加速度g:4?2T12?T22T12?T22??= g2(h1?h2)2(h1?h2)g=14. 作T-h图5. 利用mgTh?4?IG?4?mh,作Th~h关系图,考察其线形关系,由最小二乘法计222222算g和复摆对重心的转动惯量IG。
【结论与讨论】成绩(满分30分):????????? 指导教师签名:??????????????????? 日期:???????????????????2篇三:复摆振动研究.实验报告复摆振动的研究姓名:黄青中学号:201X02050238摘要:了解用复摆物理模型来测量物体的转动惯量。
通过观测复摆的振动,测定复摆振动的一些参量(重力加速度g,回转半径r,转动惯量IG)。
复摆法测重力加速度实验报告

复摆法测重力加速度实验报告
通过重力观测实验,测试复摆法测重力加速度a的可行性,并用复摆法测重力加速度实验来获取重力加速度a的具体值。
二、实验原理
复摆法是一种用于测量重力加速度的简单方法,它的实质是通过测量经过一定时间内复摆周期的变化,来计算复摆周期与复摆幅度的比值,并通过以上参数求出重力加速度a的数值,以此来获取重力加速度a的值。
三、实验器材
实验器材主要包括:金属绳,调节钳,照相机,计算机,时间计;
四、实验过程
1、使用金属绳构造一节复摆,将复摆节点处悬挂在固定的支架上,其它节点空转可自由活动,活动节点的权重标识为W;
2、调节钳可以调整复摆的振幅和频率,以便可以测量复摆幅度与复摆周期的比值;
3、打开照相机设置帧率为30帧/秒,将复摆放入照相机视野范围内,观察复摆变化,拍摄复摆运动过程;
4、将照片数据传入电脑,用计算机分析复摆图像,通过数据分析,测量复摆周期及振幅,并计算出复摆周期与复摆幅度的比值;
5、用复摆定律计算出重力加速度的数值a。
五、实验结果
通过实验,可得出重力加速度的值为a=9.8 m/s^2,说明复摆法
可以准确测量重力加速度。
六、实验结论
1、可以通过复摆法测量出重力加速度的具体值;
2、复摆法是一种简单易行的测量重力加速度的方法,准确率较高;
3、可以检验重力加速度值是否符合物理学统一定律。
本次实验证明了复摆法可以用来测量重力加速度,取得了理想的效果,实验顺利完成。
复摆的实验报告.doc

复摆的实验报告.doc摘要:本实验通过利用复摆的摆动周期和摆长与摆角度之间的关系,通过多次实验来研究复摆的动力学规律和特性。
实验结果表明,复摆的摆动周期受到重力加速度和摆长的影响,摆长越长,摆臂相对较长,振幅相对小,周期越长。
同时,复摆的摆角度对振幅和周期都产生了影响,当摆角度较小时,振幅较小,周期较长。
关键词:复摆,摆动周期,摆角度,摆长Abstract:In this experiment, the dynamic laws and characteristics of the compound pendulum are studied by utilizing the relationship between the swinging period and the swinging length and swing angle of the compound pendulum. The experimental results show that the swinging period of the compound pendulum is affected by the gravity acceleration and the swinging length. The longer the swinging length, the longer the swinging arm, the smaller the amplitude, andthe longer the period. At the same time, the swinging angle of the compound pendulum affects the amplitude and period. When the swinging angle is small,the amplitude is small and the period is long.Keywords: compound pendulum, swinging period, swinging angle, swinging length实验方案:所用仪器:复摆、计时器、卡尺、直尺、秤。
实验十六(a) 复摆

实验十六(a ) 复摆实验目的1.研究复摆摆动周期与回转轴到重心距离之间的关系。
2.测量重力加速度。
实验仪器复摆,光电计时装置,卷尺等。
实验原理复摆又称为物理摆。
如图16a -1表示一个形状不规则的刚体,挂于过O 点的水平轴(回转轴)上,若刚体离开竖直方向转过θ角度后释放,它在重力力矩的作用下将绕回转轴自由摆动,这就是一个复摆。
当摆动的角度θ较小时,摆动近似为谐振动。
振动周期为mghI T π2= (16a -1)式中h 为回转轴到重心G 的距离;I 为刚体对回转轴O 的转动惯量;m 为刚体的质量;g 是当地的重力加速度。
设刚体对过重心G ,并且平行于水平的回转轴O 的转动惯量为I G ,根据平行轴定理得I =I G +mh 2将此公式代入(16a -1)式,得mghmh I T G 22+=π(16a -2)由此可见,周期T 是重心到回转轴距离h 的函数,且当 h →0或h →∞时,T →∞。
因此,对下面的情况分别进行讨论:(1)h 在零和无穷大之间必存在一个使复摆对该轴周期为最小的值,可将此值叫做复摆的回转半径,用r 表示。
由(16a -2)式和极小值条件0=dhdT得mI r G =代入公式(2-16a -2)又得最小周期为gr T 22m in π= (16a -3)(2)在h = r 两边必存在无限对回转轴,使得复摆绕每对回转轴的摆动周期相等。
而把这样的一对回转轴称为共轭轴,假设某一对共轭轴分别到重心的距离为h 1、h 2(h 1≠h 2),测其对应摆动周期为T 1、T 2。
将此数据分别代入(16a -2)式并利用T 1=T 2得I G =mh 1h 2 (16a -4)gh h T 212+=π(16a -5)把公式(16a -5)与单摆的周期公式gl Tπ2=比较可知,复摆绕距的重心为h 1(或其共轭轴h 2)的回转轴的摆动周期与所有质量集中于离该轴为h 1+h 2点的单摆周期相等,故称h 1+h 2为该轴的等值摆长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复摆实验报告
一、实验数据
复摆质量m=396.71 g
复摆重心位置H G=0.00 cm
铜刀口质量m′=6.30 g
表1 数据记录、计算与列表
h/cm 20T/s T/s h2/m2 T2|h|/(s2m)
28.16 25.0594 1.25297 0.07929856 0.442093364
27.16 24.8624 1.24312 0.07376656 0.419716336
26.12 24.6864 1.23432 0.06822544 0.397950179
25.16 24.5101 1.225505 0.06330256 0.377868606
24.12 24.3415 1.217075 0.05817744 0.357282699
23.12 24.1924 1.20962 0.05345344 0.338287342
22.14 24.0407 1.202035 0.04901796 0.319898234
21.16 23.9264 1.19632 0.04477456 0.302838014
20.14 23.8218 1.19109 0.04056196 0.285725251
19.14 23.7382 1.18691 0.03663396 0.269635774
18.16 23.7012 1.18506 0.03297856 0.255033084
17.14 23.6818 1.18409 0.02937796 0.240314649
16.16 23.72 1.186 0.02611456 0.227305914
15.18 23.7819 1.189095 0.02304324 0.214637142
14.16 23.9204 1.19602 0.02005056 0.20255368
13.16 24.1304 1.20652 0.01731856 0.191568871
12.16 24.4062 1.22031 0.01478656 0.18108143
11.14 24.7928 1.23964 0.01240996 0.171189197
10.14 25.319 1.26595 0.01028196 0.162506621
8.16 26.8804 1.34402 0.00665856 0.147401404
6.16 29.6492 1.48246 0.00379456 0.135377559
4.12 34.6873 1.734365 0.00169744 0.123930504
2.18 46.7125 2.335625 0.00047524 0.118922142
1.12 61.3588 3.06794 0.00012544 0.105417265
-28.28 25.0597 1.252985 0.07997584 0.443987915
-27.28 24.8769 1.243845 0.07441984 0.422062625
-26.26 24.6732 1.23366 0.06895876 0.399655403
-25.28 24.4948 1.22474 0.06390784 0.379196983
-24.28 24.3283 1.216415 0.05895184 0.359262772 -23.28 24.1769 1.208845 0.05419584 0.340192091 -22.29 24.0344 1.20172 0.04968441 0.321896791 -21.28 23.9301 1.196505 0.04528384 0.304649633 -20.28 23.8118 1.19059 0.04112784 0.287469922 -19.29 23.749 1.18745 0.03721041 0.271996234 -18.28 23.71
1.1855
0.03341584
0.256908994 -17.29 23.6919 1.184595 0.02989441 0.242624573 -16.28 23.7116 1.18558 0.02650384 0.22883167 -15.29 23.7244 1.18622 0.02337841 0.215148325 -14.29 23.9142 1.19571 0.02042041 0.204307332 -13.28 24.1227 1.206135 0.01763584 0.193192346 -12.28 24.4301 1.221505 0.01507984 0.183226744 -11.29 24.7789 1.238945 0.01274641 0.173299774 -10.28 25.301
1.26505 0.01056784
0.164516134 -9.29 25.9778 1.29889 0.00863041 0.156733005 -7.29 27.3267 1.366335 0.00531441 0.13609492 -5.29 31.8271 1.591355 0.00279841 0.133964528 -3.29 39.3259 1.966295 0.00108241 0.127201797 -1.28
61.9938 3.09969 0.00016384
0.1229834
法一:直线拟合
分别对左半部分和右半部分的T 2h-h 2关系作图,剔除无效数据,做线性拟合。
左半部分如图1所示:
斜率k 1=4.1123 s 2/m ,截距b 1=0.1182 s 2m ,相关系数R 12=0.999 计算得:
2
1
2
1/600.94)1(g s
m k ==π
右半部分如图2 所示:
斜率k 2=4.037s 2/m ,截距b 2=0.1215s 2m ,相关系数R 22=0.9998 计算得:
22
2
2/779.94)2(g s m k ==π
对以上两次测量求得的g 做加权平均,权重比正比于1
2)-1-R (,得:
2
2
22112112
21/749.9)
1()1()2()1()1()1(g s m R R g R g R =-+--+-=
复摆对重心的转动惯量:
3
2
110994.24b )1(-⨯==
π
G I 3
2
210078.34b )2(-⨯==
π
G I 3
2
221212
2G
10064.3)
1()1()2()1()1()1(I -⨯=-+--+-=R R I R I R G G 310779.2m
-⨯==
G
G I R 法二:近似共轭点法
T-h 关系如图3所示,在图中选择三组近似共轭点,选点具体信息如表2所示:
表2 共轭点选取
所以,
22/737.93
658
.9690.9864.9g s m =++=
法三:共轭点法
从图4上读出T=1.22000 s 除的两对共轭点的横坐标(见表3)
表3 T=1.22000处两对共轭点位置
cm 73.362
2
1=+=
L L L 22
23/742.94g s m T
L ==π。
