捷联惯导姿态算法若干问题的研究
捷联惯导零速修正技术中姿态误差反馈方法的比较研究

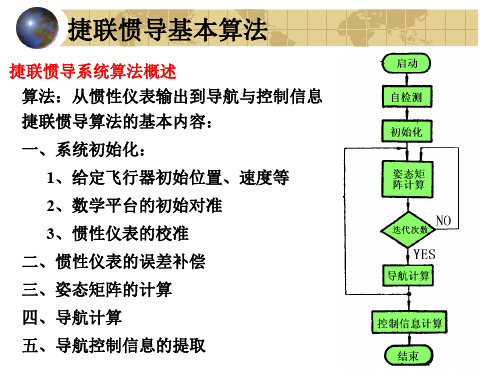
捷联惯导系统算法.ppt
cos
b Ebz
注意事项:当 θ= 90 度时,方程出现奇点
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
其中
C bE
CbE
b Eb
0
b Eb
z
z
0
y
x
y x
0
由于陀螺仪直接测得的是载体 相对惯性空间的角速度,所以:
CbE
b ib
E iE
C
E b
或四元数微分方程:
q(t)
(
b ib
b iE
)q(t)
注意事项: 1、上述两个方程中的角速度表达式不一样 2、方程第二项较小,计算时速度可以低一些
增量算法 矩阵方程精确解
一、角增量算法
角增量:陀螺仪数字脉冲输出,每个脉冲代表一个角增量
一个采样周期内,陀螺输出脉冲数对应的角增量为:
C
0
0
c os
0 0 0 sin
sin
sin
c os
cos cos
求解欧拉角速率得
1 0
0
cos
0 sin
惯性器件的误差补偿
姿态计算 欧拉角微分方程1
姿态矩阵的计算 假设数学坐标系模拟地理坐标系 飞行器姿态的描述:
航向角ψ、俯仰角θ、滚动角γ 一、欧拉微分方程
从地理坐标系到载体坐标系 的旋转顺序:
Ψ →θ →γ
高动态环境下的捷联惯导系统姿态算法的研究

M U Shu z .BU o — hu.LIY o - n —hi Xing z ng xi
( c o l fMe h nclEn ie r g S h o c a ia gn ei .NUS o n T.Na jn 1 0 4. ia n ig 2 0 9 Chn )
捷联式惯性导航积分算法设计(连载)上篇:姿态计算

捷联式惯性导航积分算法设计(连载)上篇:姿态计算
卢军政
【期刊名称】《江南航天科技》
【年(卷),期】2001(000)002
【摘要】本论文分上下两篇,给用于现代捷联惯导系统的主要软件算法设计提供
一个严密的综合方法:将角速率积分成姿态角,将加速度变换或积分成速度以及将速度积分成位置。
该算法是用两速修正法构成的,而两速修正法是具有一定创新程度的新颖算法,是为姿态修正而开发出来的,在姿态修正中,以中速运用精密解析方程去正积分参数(姿态,速度或位置),其输入是由在参数修正(姿态锥化修正,速度遥橹修正以及高分辨率位置螺旋修正)时间间隔内计算运动角速度和加速度的高速算法提供的,该设计方法考虑了通过捷联系统惯性传感器对角速度或比力加速度所进行的测量以及用于姿态其准和矢量速度积分的导航系旋转问题。
本论文上篇定义了捷联惯导积分函数的总体设计要求,并开发出了用于姿态修正算法的方向余弦法和四元数法,下篇着重讨论速度和位置积分算法的设计。
尽管上下两篇讨论中常常涉及到基本的惯性导航概念。
然而,本论文是为那些已对基础惯导概念很熟悉的实际工作者而写的。
【总页数】20页(P14-33)
【作者】卢军政
【作者单位】江南航天集团302所
【正文语种】中文
【中图分类】V249.322
【相关文献】
1.惯性导航系统航向姿态计算算法研究
2.捷联式惯性导航计算机控制系统
3.捷联惯性导航积分算法设计--第一部分:姿态算法
4.捷联惯性导航积分算法设计
5.捷联惯性导航积分算法设计
因版权原因,仅展示原文概要,查看原文内容请购买。
捷联惯导动基座对准新方法及导航误差抑制技术研究

捷联惯导动基座对准新方法及导航误差抑制技术研究一、本文概述随着导航技术的不断发展,捷联惯导系统(Strapdown Inertial Navigation System, SINS)在动基座对准和导航误差抑制方面展现出越来越高的应用价值。
本文旨在探讨一种新型的捷联惯导动基座对准方法,并对导航误差抑制技术进行深入研究。
通过对比分析传统对准方法的不足,本文提出了一种基于多传感器融合的新型对准算法,旨在提高对准精度和效率。
针对导航过程中的误差积累问题,本文还研究了有效的误差抑制策略,以期提高捷联惯导系统的导航精度和可靠性。
本文首先介绍了捷联惯导系统的基本原理和应用背景,阐述了动基座对准和导航误差抑制在惯性导航中的重要性和挑战。
随后,详细介绍了新型对准方法的基本原理和实现过程,包括多传感器数据融合、对准算法设计以及实验验证等方面。
在误差抑制技术研究方面,本文重点探讨了误差来源、误差传播特性和抑制策略,提出了一种基于卡尔曼滤波的误差估计与补偿方法。
本文的研究成果对于提高捷联惯导系统的性能具有重要意义,不仅有助于提升动基座对准的精度和效率,还能有效抑制导航过程中的误差积累,从而提高整个导航系统的可靠性和稳定性。
本文的研究方法和结论也为相关领域的研究人员提供了有益的参考和借鉴。
二、捷联惯导系统概述捷联惯导系统(Strapdown Inertial Navigation System,简称SINS)是一种不依赖外部信息、完全自主式的导航系统。
其核心部件包括陀螺仪和加速度计,分别用于测量载体相对于惯性空间的角速度和线加速度。
通过积分这些测量值,系统能够推算出载体的速度、位置和姿态信息。
捷联惯导系统的最大特点在于它将传统的平台式惯导系统中的实体平台用数学平台来替代,从而大大简化了系统结构,提高了可靠性,并降低了成本。
捷联惯导系统的基本原理是通过载体上安装的陀螺仪和加速度计实时测量载体的角运动和线运动参数,再结合初始对准得到的姿态矩阵,将加速度计测量的比力转换到导航坐标系下,进行积分运算得到速度和位置信息。
机载捷联惯导的导航计算模型与精度分析

文 章 编 号 : 2 33 4 2 1 )21 6—6 0 5 —7 X(0 1 1 —8 50
机 载 捷联 惯导 的导 航 计 算模 型 与精 度 分 析
刘 春 ,周 发 根 。
(. 1 同济大学 测量与国土信 : gT程系 , 上海 2 0 9 ; . 0 0 2 2 现代工程测量 国家测绘局重点实验室 , 上海 20 9 ) 0 0 2
S a g a 0 0 2, ia;2 Ke b r tr fAd a e gie rn h n h i2 0 9 Chn . y La o ao y o v ncd En n e ig S r e fS M , h n h i 0 0 2, ia u v yo BS S a g a 0 9 Chn ) 2
Ab t a t s r c :A t d s ma e o t e n v g t n c lu a i n su y wa d f h a i a i ac lt o o mo e c lfa n e a ld s e s f r s r p o n r il d l n l a me a d d t i t p o ta d wn i e t i o l e a n vg t n s s e ( I a i a i y t m S NS) h n t r o h r c e it s o o .T e h e r r c a a t rs i f e c S NS wa n l z d t r u h n v g t n ac l t n wih h I s a a y e h o g a ia i c lu a i t t e o o
第3 9卷第 1 2期
21 0 1年 1 2月
同 济 大 学 学 报( 然 科 学 版) 自
车载捷联惯导系统定位测姿算法研究

第15卷第l期2007年2月中国惯性技术学报JoumalofChineseInertialTcchnologyVbl.15No.1Feb.2007文章编号:1005-6734(2007)01一0024-04车载捷联惯导系统定位测姿算法研究陈允芳1,叶泽田2,钟若飞3(1.山东科技大学地球信息科学与工程学院,青岛266510;2.中国测绘科学研究院,北京100039;3.首都师范大学,北京100037)摘要:GPs/INs组合精确测定平台的位置和姿态是移动测图系统中的重要模块。
对陀螺仪和加速度计所测角速度和比力进行两次积分得载体姿态、速度和位置即sINs力学机械编排。
目前该过程大多在地理坐标系进行。
这里详细推导了地球坐标系中完整的解算过程,以四元数姿态矩阵更新及重力计算为核心,由IMu原始观测值解算出了载体位置、速度和姿态等参数,可快速高效与GPs输出的位置速度信息进行组合滤波处理,可据此编程进行工程应用数据处理。
关键词:捷联惯导系统;姿态矩阵;坐标转换;力学编排;四元数中图分类号:u666.1文献标识码:APositioningandorientationcomputationonVehicle-borneSINSanddiscussofcalculationerrorcHENYun.‰91,YEze-tian2,zHONGRuo.fei3(1.Geo·info衄ationScience&EngineeringCollege,ShandongUniverSi哆ofScienceaIldTbchnology,Qingdao266510,China;2.SurveyingaTldMappingScienceResearchInStituteofChina,Beijing100039,China;3.C印italNomlalUniverSi劬Beijing100037,China)Abstract:GPSandINSintegratedtoaccuratelydeteminingpositionaIldattitudeofnatI‘oofisVitalmoduleinmobilemappingSystem.Specincforcc行omspeedometer蚰d舭glerate矗om留roareinte铲atedtwicerespectiVelytoachievean沁de,veloc时aIldpositionn锄elySINSmechaIlization.Currentlythistookplacedingeogr印hiccoordinate,whiIeheredemonstratedindetailmewholemechaJlizationineanll-centclrcdearth-fixedcoordinate,mostlyquatemiona钍itudematrixupdating锄dgravit)rcaIculation.Ultimatelyvehiclenavigationpar锄eterssuchaSattitude,veIocity锄dpositionwercgahed丘omIMUorigin“0bservations.Mathematicsplatfo眦isfomlcdinSrNStocarryoutsuⅣeyingaJldcalculatingpreciselythenavigationmoVementpar锄cterS.Theresultsarcpronetointe黟atewitllsimilarpammeters疔omGPStofilterprocessing.Pro可锄minghercbyc锄pmcessdatainengineeringapplicationKeywords:SINS;attitudematrix;coordinatetransfomation;mechanization;quatemion随着惯性技术与卫星导航定位技术的发展,由GPS/INs不同程度组合而成的定位定姿传感器已成为移动测图系统中确定载体轨迹和平台姿态的重要工具,其中GPs多用于定位而INS则用于测姿。
动基座条件下舰载武器捷联惯导系统初始对准研究

动基座条件下舰载武器捷联惯导系统初始对准研究1. 引言1.1 研究背景传统的捷联惯导系统在动基座条件下存在着诸多挑战,如基座的姿态变化、振动等因素会影响系统的捷联性能和初始对准精度。
研究动基座条件下舰载武器捷联惯导系统初始对准成为当前研究领域中的一个重要课题。
为了提高舰载武器系统的精确打击能力和战场生存能力,有必要深入研究动基座条件下捷联惯导系统的初始对准问题,探讨解决方案,优化系统性能。
这不仅对提升我国的军事实力具有重要意义,还对推动捷联惯导技术的发展和应用具有重要意义。
开展动基座条件下舰载武器捷联惯导系统初始对准研究具有重要的实践意义和战略意义。
1.2 研究意义本研究旨在探究动基座条件下舰载武器捷联惯导系统初始对准的问题,具有重要的实际意义和军事价值。
通过对捷联惯导系统的研究,可以提高舰载武器的打击精度和命中率,从而提升海军舰队的作战效能。
研究动基座条件下的挑战和解决方案,对于提升我国军事科技水平具有重要意义。
随着军事技术的不断发展和更新换代,对舰载武器系统的研究和改进势在必行,本研究将为我国海军现代化建设提供重要的技术支持。
本研究具有重要的实际意义和战略意义,对于提高海军舰队的作战效能和保障国家安全具有重要意义。
【内容结束】2. 正文2.1 动基座条件下舰载武器捷联惯导系统简介动基座条件下舰载武器捷联惯导系统是一种集成了捷联惯导技术的舰载武器系统,在对抗复杂环境下能够实现高精度打击目标的能力。
该系统由动基座、惯导系统和传感器组成,可以实现对目标的精确识别、跟踪和打击。
动基座可以根据目标的运动状态和环境变化实时调整武器的姿态,从而提高武器的打击精度和生存能力。
捷联惯导系统则能够利用惯性传感器和GPS等技术实现对目标的精确定位和引导,确保武器能够准确命中目标。
动基座条件下舰载武器捷联惯导系统是一种先进的武器系统,具有高度的精度和灵活性,能够有效应对复杂多变的作战环境,对提高舰载武器的作战效能具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
α cos 2 0 α Q (t ) = sin cos ω t 2 sin α sin ω t 2
Q (t + h) = Q (t )È q( h)
图1
锥运动
设由 t 至 t+h,b 系的更新四元数为 q( h) ,则在 t 和 t+h 时刻 R 系至 b 系的旋转四元数有如下关系:
第 10 卷第 2 期
中国惯性技术学报
2002 年 4 月
・系统研究与分析・
文章编号: 1005-6734(2002)02-0001-06
捷联惯导姿态算法若干问题的研究
张士邈,刘 放,秦永元
(西北工业大学 905 教研室,西安 710072) 摘 要: 研究了捷联系统姿态更新的等效旋动矢量算法,并以锥运动为条件,对等效旋动矢量算 法进行了优化。此外还对四元数、旋动矢量及其优化算法进行了仿真比较,仿真结果表明:等 效转动矢量算法的精度明显优于四元数算法,且等效转动矢量的采样频率越高,姿态更新算法 的精度就越高。 关 键 词: 捷联惯导系统;锥运动;四元数;等效旋动矢量 中图分类号: U666.12 文献标识码: A
_____________________ 收稿日期: 2002-01-02 作者简介: 张士邈(1974—) ,女,西北工业大学在读硕士,从事惯性导航系统技术研究。
2
中国惯性技术学报
2002 年 4 月
2 锥运动
v 设 XYZ 为参考坐标系,记为 R;xyz 为机体坐标系,记为 b; OL 为 YOZ 平面内的一条射线,xyz v v (b 系)是由 XYZ(R 系)绕 OL 旋转 α 后形成的(见图 1) 。当 OL 以角速度 ω 绕原点 O 在 YOZ 平面内 v 旋转时,则 Ox 轴的轨迹形成一个锥面,锥顶位于 O 点,对称轴为 OX 轴。应注意,OL 并不与 b 系固联,
~ Φe ≈ 2∂q
新算法的精度准则。 4 姿态更新算法 4.1 三子样旋转矢量的求解 旋转矢量的微分方程(2)为:
(4)
~ 为 ∂q 的矢量部分,则Φ 表征了计算得到的变换四元数 q 其中 ∂q ˆ 的计算误差,我们把它作为检验姿态更 e
(6)
根据泰勒级数展开得
2 & (t k −1 ) h + h Ö &&(t k −1 ) + L Ö(t k −1 + h) = Ö(t k −1 ) + Ö 2!
(7)
式中, Ö(t k −1 + 0) = 0 。 记
è = ù(t k −1 + ô )dô ∫
(9)
代入(7)式得 Ö(t k −1 + h) = ah + b h 2 + c h 3 + 1 a × b h 3 + 1 a × c h 4 + 1 b × c h5 6 4 10 式中系数 a、 b、 c 可根据(8)式确定:即将时间段 [t k −1 , t k ] 作三等分,记 (10)
而仅与 Ox 轴具有固定的相对角关系。
v v v 根据欧拉定理,b 系可视为由 R 系的一次旋转形成。设该旋转矢量为Ö , Ö 沿 OL 方向,大小为 v v v v v Ö = α 。设 OL 的单位向量为 u L ,并取 OL 与 OY 轴重合时的点为起点(t=0),则 u L 在 R 系内的分量为 0 0 vR v vR vR α cos ω t Ö Ö ( t ) = ⋅ u ( t ) = uL t (t) = cos ω L ,因此: 。 t sin ω α sin ω t v 由 Ö 所形成的四元数,即表征 R 系到 b 系的四元数为:
èi =
i h 3
i −1 h 3
∫ ω(t
k −1
+ τ )dτ
(11)
当 i 分别取 1、2、3 时,可得关于 a、b、c 的三个独立方程,因此可唯一确定出这些系数。将所得系数 代入(10)式,得:
Ö(t k −1 + h) = è + X (è 1 × è 3 ) + Yè 2 × (è 1 − è 3 )
(12)
4
中国惯性技术学报
2002 年 4 月
其中, è = è 1 + è 2 + è 3 ,X=0.412 5,Y =0.712 5。 上述系数是根据角速度为二次抛物线的假设得出的,而实际角速度并非真正如此,所以所得系数并 不能保证算法漂移最小。 4.2 Miller 三子样优化算法 Miller 优化算法的实质是把锥运动作为检验算法优劣的基础, 以使锥误差达到最小为准则, 重新确 定(12)式三子样旋转矢量的系数 X 和 Y。我们在第 2 节中已推导出锥运动的角速度ù(t ) ,代入(11) 式得到 è 、 è 1 、 è 2 、 è 3 ,然后再代入(12)式,则计算得到的旋转矢量为
2 2
(1)
ωh h cos ω ( t + ) sin α sin 2 2
& (t ) , & (t ) = 1 Q (t )È Ω bq (t ) ,有 Ω bq (t ) = 2Q −1 (t )È Q 由四元数微分方程 Q 2
即 ω
α ωh ωh ωh − 2(ωh) sin2 + 8sin2 α sin2 ( ) sin( )[ X cos + Y ] 2 6 3 3 Φ x = − 2sinα sin(ωh ) − 8 (ωh) sin2 α sinα sin(ωh ) sin(ωh ) sinω(t + h ) 。 (13) Ö= Φ y 2 3 2 6 3 2 ωh 8 ωh ωh h Φz 2α 2sinα sin( ) + (ωh) sin sinα sin( ) sin( ) cosω(t + ) 2 3 2 6 3 2
ˆ* ⋅ R n' ⋅ q ˆ ,代入(3)式得 现考虑 q 有误差,设计算得到的变换四元数为 q ˆ ,则有 R b = q
ˆ* ⋅ R n' ⋅ q ˆq* , R n = qq
第2期
张士邈等:捷联惯导姿态算法若干问题的研究
3
令 ∂q = qq ˆ* ,则 R n = ∂q ⋅ R n' ⋅ ∂q * ,即 n 和 n' 之间的误差变换四元数为 ∂q ,即 n' 相对 n 有一个误差等效转 动,我们用Ö表示,Φ = Ö 为其转角,则 ∂q = cos Φ + Ö sin Φ 。考虑到Φ 为小量,取 cos Φ ≈ 1 , sin Φ ≈ Φ , 2 2 Φ 2 2 2 则上式可写为 ∂q ≈ 1 + Ö 。令 2
& = ù + 1 Ö× ù + 1 Ö× (Ö× ù) Ö 2 12
(5)
设 Ö(tk −1 + h) 为 [t k −1 , t k ] 时间段内的等效旋转矢量,机体角速度用二次曲线拟合,即
ù(t k −1 + τ ) = a + 2bτ + 3c τ 2 sin x = 2 ω y − ω sin α sin ω t ω z ω sin α cos ω t 0
(2)
其中矢量 ù(t ) 即为假定的锥运动情况下 b 系相对 R 系的角速度在 b 系内的分量。 3 精度准则 设 R b 和 R n 分别表示同一个固定矢量在 b 坐标系和 n 坐标系的轴向分量构成的四元数。q 是坐标系 b 和坐标系 n 之间的变换四元数 [1] ,则 R n = q ⋅ R b ⋅ q * 式中 q * 为 q 的共轭四元数。 (3)
Study on Some Questions of Attitude Algorithm for Strapdown Inertial Navigation System
ZHANG Shi-miao,LIU Fang,QIN Yong-yuan (Northwestern Polytechnical University, xi’an 710072, China) Abstract: The attitude updating algorithm is an determinant factor in strapdown inertial navigation system(SINS). This paper studies the rotation vector algorithm, and their improved algorithms are discussed under the coning base motion. The simulation results show that when the sample frequency is higher, the accuracy of the rotation vector algorithm is better. Key words : SINS; coning motion; quaternion; rotation vector 1 引 言 在捷联惯导中,姿态更新算法是其算法的核心,也是影响捷联惯导系统精度的主要因素之一,因此 设计和采用合理的姿态更新算法就成为需要研究的课题。在工程实践中常用四元数法,但 由于刚体有限 转动的不可交换性,在四元数算法中不可避免地引入了不可交换误差,特别是作高动态飞行时,误差很 大,必须采取有效措施加以克服。1971 年,Bortz 提出的等效转动矢量概念,有效地解决了不可交换误 差的问题。以后的研究就都集中在等效旋转矢量的求解问题上,其中 Miller 的三子样优化算法最具代 表性。他提出了机体在作锥运动时,即把锥运动作为检验算法的基准,对三子样算法进行了优化,并给 出其算法漂移。 本文主要是对 Miller 优化算法的一些问题进行了研究:首先推导了锥运动的更新四元数和角速率; 然后针对 Miller 优化算法精度准则难以理解的问题,重新进行了阐述,并根据 Miller 的三子样优化算 法推导出二子样优化算法、四子样优化算法及其算法漂移,还对各种算法进行了仿真比较;最后给出一 种推导 Miller 优化算法的简单方法。本文的理论研究对提高捷联惯导算法精度具有很高的参考价值。
