(完整版)同方向同频率简谐振动合成的公式及推导
合集下载
谐振动分析(三)两个同方向同频率简谐运动的合成
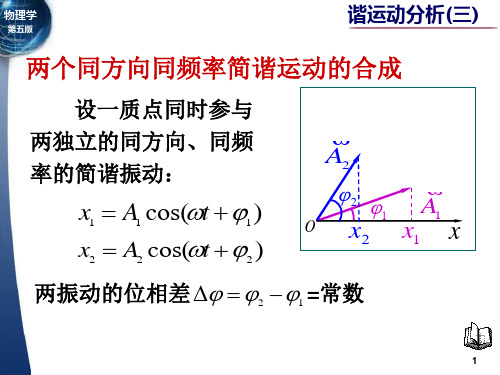
o
o
A1
A2
A
T
t
A A1 A2
x (A A )cos(t )
1
2
2 1 2k π
3
物理学
第五版
谐运动分析(三)
(2)相位差 (2k 1) π(k 0,1, )
2
1
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A2 A1)cos(t )
2
1
(2k
1)π
4
物理学
第五版
小结
(1)相位差
2
1
2k
π
A A1 A2
谐运动分析(三)
(k 0,1, ) 加强
(2)相位差
2
1
(2k 1) π
(k 0,1, )
A A A
1
2
减弱
(3)一般情况
A1 A2 A A1 A2
5
物理学
第五版
谐运动分析(三)
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
x 阻尼振动位移时间曲线
A
Ae t
Aet cost
O
T A
t
( 0)
21
物理学
第五版
三种阻尼的比较
谐运动分析(三)
(a)欠阻尼
2 0
2
(b)过阻尼
2 0
2
(c)临界阻尼
2 0
2
x
b
oc
t
a
22
物理学
第五版
谐运动分析(三)
例 有一单摆在空气(室温为 20C)中来 回摆动. 摆线长l 1.0 m,摆锤是半径r 5.0103 m 的铅球.求(1)摆动周期;(2)振幅减小 10%所需的时间;(3)能量减小10%所需 的时间;(4)从以上所得结果说明空气的 粘性对单摆周期、振幅和能量的影响.
2、简谐振动的合成

A A1 A2
x
x1 A1 cos t x2 A2 cos(ωt π ) x x ( A2 A1 ) cos(ωt π)
o 2
A 2
A1
o
T
t
A
1) 相位相同 φ2 φ1 或 Δφ φ2 φ1 0
A A1 A2
相互加强
x A cos( t 1 ) A cos( t 2 ) 2) 相位相反 Δφ φ2 φ1 π
此结论对讨论各种波的干射、衍射极为有用。
二、 两个同方向不同频率简谐振动的合成 x1 A1 cos 1t A1 cos 2 π 1t
x2 A2 cos 2t A2 cos 2 π 2t
讨论 A1 A2 ,
x x1 x2
2 1 1 2 的情况
x y 2 1 2 A1 A2
π y A2 cos( t ) 2 0 质点沿顺时针方向运动
2 2
y
A1
A2
o
x
A2 y
x A1 cos t
o
A1
x
2 质点沿逆时针方向运动
用 旋 转 矢 量 描 绘 振 动 合 成 图
两 相 互 简 垂 振 直 动 同 的 频 合 率、 成 不 图 同 相 位
1 1 可见 π ( 2 1 )T拍 ∴ T拍 2 1 拍
拍 2 1
拍频(振幅变化的频率)
注意:书上的拍频写成,此处的拍频写成拍
2 1 1 2
( 1 2 ) / 2 1 2 , 1 2
(C)
3k / m /( 2π )
§3.3 简谐振动的合成

2 1 2 2
x
x
o ϕ2
ω A2
A1
A = A1 − A2 ϕ = ϕ2
o
T
t
A
相位差
ϕ 2 − ϕ1 = 2 k π
A = A1 + A2
ϕ 2 − ϕ1 = (2k + 1)π
A = A1 − A2
当A1=A2 时,A=0
(k = 0 , 1, ) ± L
相互加强
相位差
(k = 0 , 1, ) ± L
A1
在任一时刻离开坐标原点位移为: 在任一时刻离开坐标原点位移为: (2) ϕ 2 − ϕ1 = π 两个分运动反相位, 两个分运动反相位, 得
A2 y= x A1
y A2
o
A1
x
(3) φ2−φ1=π/2,得
x y + 2=1 2 A1 A2
2
2
这是坐标轴为主轴的椭圆,质 这是坐标轴为主轴的椭圆, 点的轨迹是顺时针旋转。 点的轨迹是顺时针旋转。 (4) φ2−φ1=3π/2,仍然得
三、相互垂直的简谐振动的合成 1. 频率相同
若质点同时参与两个同频率的相互垂直的分运 动,其位移表达式分别为
x = A1 cos(ωt + ϕ1 ) y = A2 cos(ωt + ϕ 2 )
消去时间参数, 消去时间参数,得
x 2 y 2 2 xy + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 2 A1 A2 A1 A2
x = A1 cos(ω1t + ϕ1 ) y = A2 cos(ω 2t + ϕ 2 )
李 萨 如 图
ϕ1 = 0
π π 3π π ϕ 2 = 0, , , , 8 4 8 2
x
x
o ϕ2
ω A2
A1
A = A1 − A2 ϕ = ϕ2
o
T
t
A
相位差
ϕ 2 − ϕ1 = 2 k π
A = A1 + A2
ϕ 2 − ϕ1 = (2k + 1)π
A = A1 − A2
当A1=A2 时,A=0
(k = 0 , 1, ) ± L
相互加强
相位差
(k = 0 , 1, ) ± L
A1
在任一时刻离开坐标原点位移为: 在任一时刻离开坐标原点位移为: (2) ϕ 2 − ϕ1 = π 两个分运动反相位, 两个分运动反相位, 得
A2 y= x A1
y A2
o
A1
x
(3) φ2−φ1=π/2,得
x y + 2=1 2 A1 A2
2
2
这是坐标轴为主轴的椭圆,质 这是坐标轴为主轴的椭圆, 点的轨迹是顺时针旋转。 点的轨迹是顺时针旋转。 (4) φ2−φ1=3π/2,仍然得
三、相互垂直的简谐振动的合成 1. 频率相同
若质点同时参与两个同频率的相互垂直的分运 动,其位移表达式分别为
x = A1 cos(ωt + ϕ1 ) y = A2 cos(ωt + ϕ 2 )
消去时间参数, 消去时间参数,得
x 2 y 2 2 xy + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 2 A1 A2 A1 A2
x = A1 cos(ω1t + ϕ1 ) y = A2 cos(ω 2t + ϕ 2 )
李 萨 如 图
ϕ1 = 0
π π 3π π ϕ 2 = 0, , , , 8 4 8 2
振动之同方向的简谐振动的合成

x
- (A1sinφ1 + A2sinφ2)sinωt
x
令Acosφ = A1cosφ1 + A2cosφ2,Asinφ = A1sinφ1 + A2sinφ2, 则x = Acosφcosωt – Asinφsinωt =Acos(ωt + φ),
其中
A
A12
A22
2 A1 A2
cos(2
(2)有n个同一直线同频率的简谐振动,它们的振幅都
是ΔA,相差都是Δφ,第一个振动的初相为零。求N个C
简谐振动的振幅和初相。
nΔφ
M Δφ ΔA5
振幅 A A sin(n / 2)
r Δφ A ΔA 4Δφ
sin( / 2)
初相为 1 (π ) 1 (π n) n 1
利用和差化积公式可得合振动为
同频率的简谐振动合
x
x1
x2
2 A cos(2
1
2
t) cos(2
1
2
t
成之后不是简谐振动, )也没有明显的周期性。
当两个分振动的频率比较大而差异比较小时:|ω2 - ω1| << ω2 + ω1,方程就表示了振幅按2Acos[(ω2 - ω1)t/2]变化 的角频率为(ω2 + ω1)/2的“近似”的简谐振动。
矢量的合成如图所示。
终点都在以C为圆心的圆周上。
设圆的半径为r,每个矢量对 A 2r sin
应的圆心角都是Δφ ,因此
2
这是多个 等幅同频
全部矢量对应的圆 心角是nΔφ,因此
A 2r sin n
2
同方向的简谐振动的合成

合振动的振幅随时间作缓慢的周期性的变化, 合振动的振幅随时间作缓慢的周期性的变化,振 动出现时强时弱的拍现象 拍现象。 动出现时强时弱的拍现象。 拍频:单位时间内强弱变化的次数。 拍频:单位时间内强弱变化的次数。 ω2 − ω1 γ= = γ 2 − γ1 2π
同方向不同频率的两个简谐振动的合成 拍
同方向同频率的两个简谐振动的合成
C
r A
O
r a1
r r a3 α a2
α
r a4 α
rα a5
M
X
因各个振动的振幅相同且相差依次恒为 α ,上图 为圆心的圆周上, 中各个矢量的起点和终点都在以 C为圆心的圆周上, 为圆心的圆周上 根据简单的几何关系, 根据简单的几何关系,可得
∠OCM = Nα
同方向同频率的两个简谐振动的合成
x1
t
x2
t
x
t
同方向不同频率的两个简谐振动的合成 拍
反相迭加,合振幅最小。 反相迭加,合振幅最小 当A1=A2 时,A=0。 。 (3)通常情况下,合振幅介于 通常情况下, 通常情况下 和 之间。 之间。
同方向同频率的两个简谐振动的合成
个同方向、同频率的简谐振动,它们的振幅相等, 例15-4 N个同方向、同频率的简谐振动,它们的振幅相等, 15初相分别为0, , 2a, 依次差一个恒量a, 初相分别为0, a, 2 , ..., 依次差一个恒量 ,振动表达式可 写成
求它们的合振动的振幅和初相。 求它们的合振动的振幅和初相。
采用旋转矢量法可使问题得到简化, 解:采用旋转矢量法可使问题得到简化,从而避开 烦琐的三角函数运算。 烦琐的三角函数运算。 根据矢量合成法则, 个简谐振动对应的旋转矢 根据矢量合成法则,N个简谐振动对应的旋转矢 量的合成如下图所示: 量的合成如下图所示:
同方向不同频率的两个简谐振动的合成 拍
同方向同频率的两个简谐振动的合成
C
r A
O
r a1
r r a3 α a2
α
r a4 α
rα a5
M
X
因各个振动的振幅相同且相差依次恒为 α ,上图 为圆心的圆周上, 中各个矢量的起点和终点都在以 C为圆心的圆周上, 为圆心的圆周上 根据简单的几何关系, 根据简单的几何关系,可得
∠OCM = Nα
同方向同频率的两个简谐振动的合成
x1
t
x2
t
x
t
同方向不同频率的两个简谐振动的合成 拍
反相迭加,合振幅最小。 反相迭加,合振幅最小 当A1=A2 时,A=0。 。 (3)通常情况下,合振幅介于 通常情况下, 通常情况下 和 之间。 之间。
同方向同频率的两个简谐振动的合成
个同方向、同频率的简谐振动,它们的振幅相等, 例15-4 N个同方向、同频率的简谐振动,它们的振幅相等, 15初相分别为0, , 2a, 依次差一个恒量a, 初相分别为0, a, 2 , ..., 依次差一个恒量 ,振动表达式可 写成
求它们的合振动的振幅和初相。 求它们的合振动的振幅和初相。
采用旋转矢量法可使问题得到简化, 解:采用旋转矢量法可使问题得到简化,从而避开 烦琐的三角函数运算。 烦琐的三角函数运算。 根据矢量合成法则, 个简谐振动对应的旋转矢 根据矢量合成法则,N个简谐振动对应的旋转矢 量的合成如下图所示: 量的合成如下图所示:
简谐振动的合成

x1 (t ) = a cosωt x2 (t ) = a cos(ωt + δ ) x3 (t ) = a cos(ωt + 2δ )
C
Nδ
R
A
aN
⋮ x N ( t ) = a cos[ ω t + ( N − 1)δ ]
O
δ
a3
a1 P
在∆COM中:A = 2 R sin( N δ / 2 ) 中 上两式相除得: 上两式相除得: 在∆OCP中: a = 2R sin(δ / 2) 中
2
A2 y= x 为直线方程 A1
利用旋转矢量合成
∆ϕ = 0
2 1
y
8 7 6
4 4
y
1 2
3
3 7 6
4Байду номын сангаас
8
x
5
5 3
2 1
播 放 动 画
16
5 6 7
x
8
2. |ϕ 2
− ϕ1 | π =
2 2
反相位
y
x y 2xy =0 + + A1 A2 A1 A2
3
利用旋转矢量法求合振动也可得到相同的结果。 •利用旋转矢量法求合振动也可得到相同的结果。 取质点振动的平衡位置O为 取质点振动的平衡位置 为 坐标原点,振动方向沿OX轴。A 坐标原点,振动方向沿 轴 2 点作两个长度分别为A 从O点作两个长度分别为 1、 点作两个长度分别为 ϕ2 ϕ A2的矢量 A1 , A2 ,它们在 它们在t=0时 时 与X轴的夹角分别为ϕ1、ϕ2。 轴的夹角分别为ϕ 轴的夹角分别为
x1 = 4 cos 3t ,
= A cos(3t + ϕ )
振动合成与分解

从数学上讲 任何形式的周期函数都可通过付里叶级数分解 成一系列不同频率、不同振幅的谐振动之和; 成一系列不同频率、不同振幅的谐振动之和;而非 周期振动可通过傅里叶积分把它展成无数个频率连 续分布的谐振动。 续分布的谐振动。 将任一周期性振动 x(t +T) = x(t) 按付立叶级数展开 a0 ∞ x (t ) = + ∑ (an cos nω t + bn sin nω t ) 2 n=1 2 π 若周期振动的频率为: 若周期振动的频率为:ν ω =2 = πν T 则各分振动的频率为:ν、2ν、3ν、… 则各分振动的频率为: (基频 , 二次谐频 , 三次谐频 , …) ) 由于所包含的频率取分立值,这类频谱称为离散谱。 由于所包含的频率取分立值,这类频谱称为离散谱。
二. 同方向不同频率简谐振动的合成 分振动 合振动
x2 = Acos(ω2t +ϕ2)
x = x + x2 1
1 1 x = 2 A cos [(ω 2 − ω1 )t + (ϕ 2 − ϕ1 )] ⋅ cos [(ω 2 + ω1 )t + (ϕ 2 + ϕ1 )] 2 2
x = Acos(ω t +ϕ1) 1 1
图(a) 中实线所代表的周期性振动可分解为基频 倍频的两个简谐振动的叠加。 和3倍频的两个简谐振动的叠加。 倍频的两个简谐振动的叠加 而图(b)则是一种“方波”振动信号, 而图 则是一种“方波”振动信号,它所包含 则是一种 的简谐振动成分就多了。 的简谐振动成分就多了。 这里用竖直线段在横坐标上的位置代表所包含 简谐振动的频率,竖直线高度代表所对应振幅, 简谐振动的频率,竖直线高度代表所对应振幅,该 称为振动频谱 图(c)称为振动频谱。 称为振动频谱。
两个同方向同频率的简谐运动的合成

2)相位差 2 1 (2k 1)π
(k 0 , 1, )
A A1 A2
合成的振幅最小
合成的振动的初相和振幅大的分振动的初相相同
4 –2 两个同方向同频 1)π (k 0 , 1, )
x1 A1 cost x2 A2 cos(t π ) x ( A2 A1 ) cos(t π)
2 A2 cos 2 A12 cos 2 1 A2 cos 2 2 2 A1 A2 cos 1 cos 2 2 A2 sin 2 A12 sin 2 1 A2 sin 2 2 2 A1 A2 sin 1 sin 2
2 A2 A12 A2 2 A1 A2 cos 1 cos 2 sin 1 sin 2
A2
2
0
A
x2
x A cos(t )
x x1 x2
x2
1
x1
A1
x
x
A1 sin 1 A2 sin 2 tan A1 cos 1 A2 cos 2 2 2 A A1 A2 2 A1 A2 cos( 2 1 )
4 –2 两个同方向同频率振动的合成 根据余弦定理
3)一般情况
A A1 A2
相互削弱
A1 A2 A A1 A2
4 –2 两个同方向同频率振动的合成
本节练习 1 (D) 2. 两个分振动的圆频率相同,所以,合振动 旋转矢量的大小为常量,合振动的圆频率 也和分振动的圆频率相同。
4 –2 两个同方向同频率振动的合成
作业
习题 4-4
x
x
2
o 2
A 2
