§11-3同方向的简谐振动的合成
合集下载
谐振动分析(三)两个同方向同频率简谐运动的合成
o
o
A1
A2
A
T
t
A A1 A2
x (A A )cos(t )
1
2
2 1 2k π
3
物理学
第五版
谐运动分析(三)
（2）相位差 (2k 1) π(k 0，1, )
2
1
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A2 A1)cos(t )
2
1
(2k
1)π
4
物理学
第五版
小结
（1）相位差
2
1
2k
π
A A1 A2
谐运动分析(三)
(k 0，1， ) 加强
（2）相位差
2
1
(2k 1) π
(k 0，1， )
A A A
1
2
减弱
（3）一般情况
A1 A2 A A1 A2
5
物理学
第五版
谐运动分析(三)
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
x 阻尼振动位移时间曲线
A
Ae t
Aet cost
O
T A
t
( 0)
21
物理学
第五版
三种阻尼的比较
谐运动分析(三)
(a)欠阻尼
2 0
2
(b)过阻尼
2 0
2
(c)临界阻尼
2 0
2
x
b
oc
t
a
22
物理学
第五版
谐运动分析(三)
例 有一单摆在空气（室温为 20C）中来 回摆动. 摆线长l 1.0 m，摆锤是半径r 5.0103 m 的铅球.求（1）摆动周期；（2）振幅减小 10％所需的时间；（3）能量减小10％所需 的时间；（4）从以上所得结果说明空气的 粘性对单摆周期、振幅和能量的影响.
简谐振动的合成
0 < ∆ϕ < π
质点沿顺时针方向运动
π < ∆ϕ < 2π 质点沿逆时针方向运动
说明：任何一个直线简谐振动， 说明：任何一个直线简谐振动，椭圆运动或匀速 圆周运动都可分解为两个相互垂直的简谐振动. 圆周运动都可分解为两个相互垂直的简谐振动
上页 下页 返回 结束
第九章 振 动
用旋转矢量描绘振动合成图
(1) ϕ2 − ϕ1 = 0或2π
A2 y= x A1
y
A2
o
A1
x
时刻t 质点离开平衡位置的位移（合振动） 时刻 质点离开平衡位置的位移（合振动）
2 r = x2 + y 2 = A12 + A2 cos(ωt + ϕ )
2 2 A = A1 + A2
——合振动也是谐振动 合振动也是谐振动
上页 下页 返回 结束
上页 下页 返回 结束
第九章 振 动
Acosϕ = A1 cosϕ1 + A2 cosϕ2
令
Asinϕ = A1 sinϕ1 + A2 sinϕ2
A = A12 + A22 + 2A1 A2 cos( 2 −ϕ1 ) ϕ
A1 sin ϕ 1 + A2 sin ϕ 2 tan ϕ = A1 cos ϕ 1 + A2 cos ϕ 2
上页
下页
返回
结束
第九章 振 动
两相 互垂直同 频率不同 相位差简 谐运动的 合成图
上页
下页
返回
结束
第九章 振 动பைடு நூலகம்
§9.4.4 互相垂直不同频率简谐振动的合成·李萨如图形 互相垂直不同频率简谐振动的合成 李萨如图形
同方向同频率简谐振动的合成初相位
同方向同频率简谐振动的合成初相位同方向同频率的简谐振动听起来挺高深的，其实简单得很，就像咱们日常生活中常见的摇摇摆摆，咯吱咯吱的秋千。
你想象一下，两个小伙伴在秋千上并肩而坐，摇摆得十分起劲。
要是他们的节奏一致，频率相同，配合得就像小鸟在枝头上唱和，那真是美得不要不要的。
可要是他们的节奏不一样，那画面可就有点尴尬了。
就像一对恋人在跳舞，一人慢一人快，结果就是扭得稀巴烂。
什么是合成初相位呢？简单来说，就是这两个秋千的小伙伴最开始的起点。
如果他们同时开始摇，那就是同一个起点，一起飞，冲上云霄。
要是其中一个比另一个早一点，那他就提前起跑了。
这样一来，两个秋千的互动就会变得有趣多了。
我们可以想象一下，一个小伙伴先开始，结果另一个还在原地踏步，等他反应过来，已经被甩得老远，真是让人哭笑不得。
在物理学上，合成初相位能影响最终的合成振动。
想想两个秋千相遇的瞬间，波浪涌动的美妙感。
相位差越小，合成振动越强，感觉就像是合唱团里每个人的声音都在同一调上，和谐动人。
而相位差越大，合成振动就像是乐队里每个人都在演奏不同的旋律，结果可想而知，就是一场音乐会的灾难。
有趣的是，合成初相位也常常会出现在我们的日常生活中。
就像朋友聚会时，大家都来得差不多，气氛瞬间就热烈起来，大家一起聊，笑声不断，简直就是欢乐的海洋。
可要是有一个朋友迟到了，刚好打断了大家的欢乐，那气氛就会微妙地变了，像个捣蛋鬼一样。
你看，这个合成初相位的影响力，简直不容小觑。
想象一下你和好友一起打游戏，两个人的配合相当重要。
如果你们都在同一时间攻击敌人，那真是配合默契，像专业战队一样，敌人根本来不及反应。
而要是你总是慢半拍，那可就难了，往往被敌人痛揍一顿。
这时候就能真切感受到合成初相位的重要性，毕竟团队合作离不开每个人的步伐一致嘛。
合成初相位的概念还可以用在爱情中。
想想看，情侣之间的默契有多重要。
就像两个人的心灵感应，若是心有灵犀，瞬间就能理解对方的想法。
而若是两人总是各自为政，彼此心里没谱，那可是要闹出不少笑话的。
10.2 两个简谐振动的合成
2
2
频率都较大且频率差很小的两个同方向简谐
振动，在合成时会产生合振幅时强、时弱的现 象，这称为拍。
拍频 ：单位时间内振动加强或减弱的次数
振幅 2Acos (2 1)t 的频率
2 由于是绝对值，所以
2
2
1
2
2
1
拍频等于两个分振动的频率之差
10.2.3 互相垂直的同频率简谐振动的合成
质点按分振动的周 期作左旋正椭圆运动
A1=A2：左旋圆运动
（5）当 2 1 取其他值时，合振动的轨迹一
般为斜椭圆。 与上述合成过程相反，一个圆运动或椭圆运
动可以分解成两个互相垂直的同频率简谐振动 这在分析光的偏振时要经常用到
*10.2.4 互相垂直的不同频率简谐振动的合成
合振动的轨迹一般是不稳定的。但当两个分 振动的频率比恰好等于简单的整数比时，合振 动的轨迹是稳定的封闭曲线，称为李萨如图。
李萨如图
判定两种频率是否成整数比，据此可由已知 频率确定未知频率。
x1 A1 cos( t 1)
x2 A2 cos( t 2 )
合振动仍是一个角 频率为ω的简谐振动：
x x1 x2 Acos( t )
A A12 A22 2A1 A2 cos(2 1) tan A1 sin 1 A2 sin 2
A1 cos1 A2 cos2
（3）2
1
2
，y 比 x 超前
2
：
x2 y2 1 A12 A22
质点的运动轨迹是以
坐标轴为主轴的正椭圆 （或圆） 不是简谐振动!
谐振动分析(三)两个同方向同频率简谐运动的合成
x A cos( p t )
A
f (02 p2 )2 4 2p2
t
dA 0 d p
x A0 e
cos(t ) A cos( p t )
28
物理学
第五版
谐运动分析(三)
共振频率
r | 2 |
2 0 2
A
共振频率 小阻尼 阻尼 0
3
物理学
第五版
谐运动分析(三)
（2）相位差 2 1 (2k 1) π (k 0 ， 1, )
x
A1
x
2
o
o
T
t
x ( A2 A1 ) cos( t ) A A1 A2 2 1 (2k 1)π
4
A
A2
物理学
第五版
物理学
第五版
谐运动分析(三)
两个同方向同频率简谐运动的合成
设一质点同时参与 两独立的同方向、同频 率的简谐振动：
A2
2
O
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
x2
1
x1
A1
x
两振动的位相差 2 1 =常数
1
物理学
第五版
5
解 （2） 有阻尼时 A' Ae t ln( 1 ) 0 . 9 t t 174 s 3 min 0.9 A Ae 1
1
E 0.9E, t ? （ 3）
E ' A ' （ 3） ( ) 2 e 2t E A 1 ) ln( 2t 0.9 87 s 1.5 min 0.9 e t2 2
A
f (02 p2 )2 4 2p2
t
dA 0 d p
x A0 e
cos(t ) A cos( p t )
28
物理学
第五版
谐运动分析(三)
共振频率
r | 2 |
2 0 2
A
共振频率 小阻尼 阻尼 0
3
物理学
第五版
谐运动分析(三)
（2）相位差 2 1 (2k 1) π (k 0 ， 1, )
x
A1
x
2
o
o
T
t
x ( A2 A1 ) cos( t ) A A1 A2 2 1 (2k 1)π
4
A
A2
物理学
第五版
物理学
第五版
谐运动分析(三)
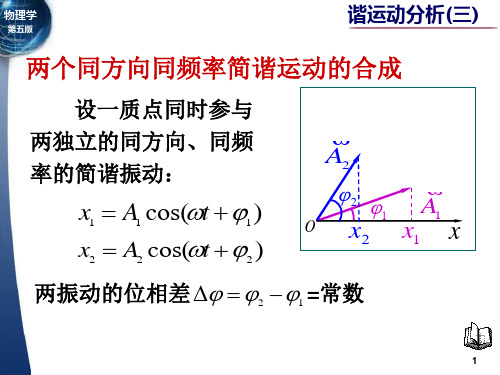
两个同方向同频率简谐运动的合成
设一质点同时参与 两独立的同方向、同频 率的简谐振动：
A2
2
O
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
x2
1
x1
A1
x
两振动的位相差 2 1 =常数
1
物理学
第五版
5
解 （2） 有阻尼时 A' Ae t ln( 1 ) 0 . 9 t t 174 s 3 min 0.9 A Ae 1
1
E 0.9E, t ? （ 3）
E ' A ' （ 3） ( ) 2 e 2t E A 1 ) ln( 2t 0.9 87 s 1.5 min 0.9 e t2 2
简谐振动的合成
x1 (t ) = a cosωt x2 (t ) = a cos(ωt + δ ) x3 (t ) = a cos(ωt + 2δ )
C
Nδ
R
A
aN
⋮ x N ( t ) = a cos[ ω t + ( N − 1)δ ]
O
δ
a3
a1 P
在∆COM中：A = 2 R sin( N δ / 2 ) 中 上两式相除得： 上两式相除得： 在∆OCP中： a = 2R sin(δ / 2) 中
2
A2 y= x 为直线方程 A1
利用旋转矢量合成
∆ϕ = 0
2 1
y
8 7 6
4 4
y
1 2
3
3 7 6
4Байду номын сангаас
8
x
5
5 3
2 1
播 放 动 画
16
5 6 7
x
8
2. |ϕ 2
− ϕ1 | π =
2 2
反相位
y
x y 2xy =0 + + A1 A2 A1 A2
3
利用旋转矢量法求合振动也可得到相同的结果。 •利用旋转矢量法求合振动也可得到相同的结果。 取质点振动的平衡位置O为 取质点振动的平衡位置 为 坐标原点，振动方向沿OX轴。A 坐标原点，振动方向沿 轴 2 点作两个长度分别为A 从O点作两个长度分别为 1、 点作两个长度分别为 ϕ2 ϕ A2的矢量 A1 , A2 ，它们在 它们在t=0时 时 与X轴的夹角分别为ϕ1、ϕ2。 轴的夹角分别为ϕ 轴的夹角分别为
x1 = 4 cos 3t ,
= A cos(3t + ϕ )
一维简谐振动的合成
• 设两个角频率 非常接近，振动方程分别为
x1 Acos(1t ) x2 Acos(2t )
合振动为
x x1 x2 Acos(1t ) Acos(2t )
2
A
cos
2
2
1
t
cos
2
2
1
t
1.2 两个同方向、不同频率 简谐振动的合成 拍现象
• 由于
2 1 2 1
2
2
2k
N
k 为不等于 Nk 的整数。此时
sin k A A0 sin k N 0
• 在振动矢量图中，各个分振幅矢量依次相接构成一个闭合 的正多边形，合振幅当然为零。
1.2 两个同方向、不同频率 简谐振动的合成 拍现象
• 为讨论简单起见，考虑振幅和初相位相同，但角频率不同的 两个振动合成的问题。
2
下面讨论两种特殊情况：
(1)当各个分振动同相，即 2k , k 0, 1, 2,
时，合振动的振幅
sin N 2
A
lim
0
A0
sin
2
NA0
为最大值。在振动矢量图中，此时各分振动矢量相同，因
此也可以得到最大振幅。
1.1 两个同方向、同频率简谐振动的合成
• （2）当各个分振动的初相位差
大学物理
一维简谐振动的合成
• 1.1 两个同方向、同频率简谐振动的合成
• 1.2 两个同方向、不同频率简谐振动的合成
•
拍现象
1.1 两个同方向、同频率简谐振动的合成
• 设两个在同一直线上的同频率的简谐振动，以平衡位置为坐 标原点，在任一时刻 的位移分别为
x1 A1 cos(t 1) x2 A2 cos(t 2 )
x1 Acos(1t ) x2 Acos(2t )
合振动为
x x1 x2 Acos(1t ) Acos(2t )
2
A
cos
2
2
1
t
cos
2
2
1
t
1.2 两个同方向、不同频率 简谐振动的合成 拍现象
• 由于
2 1 2 1
2
2
2k
N
k 为不等于 Nk 的整数。此时
sin k A A0 sin k N 0
• 在振动矢量图中，各个分振幅矢量依次相接构成一个闭合 的正多边形，合振幅当然为零。
1.2 两个同方向、不同频率 简谐振动的合成 拍现象
• 为讨论简单起见，考虑振幅和初相位相同，但角频率不同的 两个振动合成的问题。
2
下面讨论两种特殊情况：
(1)当各个分振动同相，即 2k , k 0, 1, 2,
时，合振动的振幅
sin N 2
A
lim
0
A0
sin
2
NA0
为最大值。在振动矢量图中，此时各分振动矢量相同，因
此也可以得到最大振幅。
1.1 两个同方向、同频率简谐振动的合成
• （2）当各个分振动的初相位差
大学物理
一维简谐振动的合成
• 1.1 两个同方向、同频率简谐振动的合成
• 1.2 两个同方向、不同频率简谐振动的合成
•
拍现象
1.1 两个同方向、同频率简谐振动的合成
• 设两个在同一直线上的同频率的简谐振动，以平衡位置为坐 标原点，在任一时刻 的位移分别为
x1 A1 cos(t 1) x2 A2 cos(t 2 )
大学物理-12第十二讲简谐振动的合成、阻尼、受迫振动（001）
解得 ω = ωr = ω02 − 2β 2
则
A=
2mβ
F0
ω02 − β 2
= Amax
A
β2 β3
β1
ω
β1 > βω2 0> β3
23
2.速度共振—使速度振幅达最大值的状态
v = dx = − Aω sin(ωt − δ )
dt
速度振幅 vm = Aω
而 Aω =
F0ω
m (ω02 − ω2 ) + 4β 2ω2
●合振幅A的大小由两个分振动的初相差决定。
当 Δϕ = ϕ2 − ϕ1 = ±2kπ
(k = 0，1，2") 同相
Y ωK
A2
ωK
A ωK
A = A1 + A2 = Amax
θ2
Δθ θ1
A1
合振动加强
x2 θ x1 x x
4
当 Δϕ = ϕ2 −ϕ1 = ±(2k +1)π 反相
(k = 0，1，2")
ϕ =0
t
19
2. β =ω0（临界阻尼） x = e −βt (C1 + C 2t)
●在临界阻尼时，质点到达平衡位置时速度即减为 零，振动不可能发生。
◆原理常用于阻尼天平等，以减少摆动时间.
3. β >ω0（过阻尼）
x = e − βt (C 1e ω1t + C 2 e −ω1t )
●过阻尼时，质点的速度 x
F强 = F0 cosωt
v = dx = Aω cos ωt v与强迫力同位相。
dt
●在整个周期内外力的方向和物体运动方向一致， 不断对物体作正功，使振动最强。 ◆外力的周期性变化与物体的固有振动“合拍”。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2 1 2 2
x
x
ϕ 0 = ϕ 20
A1
ϕ 20
o
o
T
太原理工大学物理系
t
ω A2
A
两个简谐振动的相位关系 （1）相位差 ϕ 20 − ϕ10 = 2k π ( k = 0 ， 1， ) ± L 两个简谐振动的相位相同， 两个简谐振动的相位相同，合振动的振幅 相位相同
A = A1 + A2
相互加强
§3 同方向简谐振动的合成
当一个物体同时参与几个谐振动时,就需考 当一个物体同时参与几个谐振动时 就需考 虑振动的合成问题。 虑振动的合成问题。本节讨论 的简谐振动的合成, （1）同方向、同频率的简谐振动的合成 它 ）同方向、同频率的简谐振动的合成 是波的干涉的重要基础。 干涉的重要基础 是波的干涉的重要基础。 的简谐振动合成， （2）同方向、不同频率的简谐振动合成，其 ）同方向、不同频率的简谐振动合成 结论可以给出重要的实际应用。 结论可以给出重要的实际应用。
（2）相位差 ϕ 20 − ϕ10 = ( 2k + 1) π ( k = 0 ， 1， ) ± L 两个简谐振动的相位相反，合振动的振幅 两个简谐振动的相位相反， 相位相反
A = A1 − A2
一般情况下 （3）一般情况下
相互削弱
A1 + A2 > A > A1 − A2
太原理工大学物理系
二、两同方向不同频率的简谐振动的合成 设分振动 合振动
x1 = A1 cos ω1t
x2 = A2 cos ω2t
= 2 A cos(
频率相差较小
x = x1 + x2 ω1 − ω2
2
t ) cos(
ω1 + ω2
2
t)
令A(t ) = 2 A cos(
ω1 − ω2
2 ω1 + ω2 cos ωt = cos( t) 2
t)
太原理工大学物理系
合振动特点： 合振动特点： （1）合振动频率 （2）合振幅
ω=
ω1 + ω2
2
≈ ω1 ≈ ω2
2 t)
A(t ) = 2 A cos(
ω1 − ω 2
合振动的振幅在0--2A之间随 周期性变化，时强 之间随t周期性变化 合振动的振幅在 振幅 之间随 周期性变化， 时弱，合振动不是简谐振动。 时弱，合振动不是简谐振动。 合振幅时强时弱的现象称为拍 合振幅时强时弱的现象称为拍。 合振幅在单位时间内变化的次数称拍频 拍频。 合振幅在单位时间内变化的次数称拍频。 拍频
两个同方向、 频率简谐运动合成 合成后 两个同方向、同频率简谐运动合成后，仍然为 简谐运动 振动频率仍为ω 运动， 频率仍为 简谐运动，振动频率仍为ω. 太原理工大学物理系
A、ϕ0 可由旋转矢量法导出，这比用解析法方便。 、 可由旋转矢量法导出，这比用解析法方便 方便。
v A2
0
2 1
ω
v A
ϕ 20 ϕ x2
太原理工大学物理系
一
两个同方向同频率简谐运动的合成 设有两个同频率的谐振动，表达式分别为： 设有两个同频率的谐振动，表达式分别为：
x1 = A1 cos( ω t + ϕ10 ) x2 = A2 cos( ω t + ϕ 20 )
合振动位移 x = x1+ x2 由 三角函数可以证明
x = A cos( ω t + ϕ 0 )
太原理工大学物理系
π
2 2
10
v ϕ 0A
x1
1
x
x
A = A + A + 2 A1 A2 cos(ϕ20 − ϕ10 ) A1 sin ϕ10 + A2 sin ϕ 20 tan ϕ 0 = A1 cos ϕ10 + A2 cos ϕ 20
太原理工大学物理系
讨论两种特殊情况
A = A + A + 2 A1 A2 cos(ϕ20 − ϕ10 ) ± ± 1）同相位 ∆ϕ = ϕ 20 − ϕ10 = 2k π (k = 0 ， 1， 2,L) ）
∆ν = ν 1 − ν 2
太原理工大学物理系
拍现象
太原理工大学物理系
例8 两个同方向的简谐振动曲线如图所示， 两个同方向的简谐振动曲线如图所示，求合 振动方程。 振动方程。
A1
A2
x1
x2
t
太原理工大学物理系
解：由振动曲线得
ϕ10 =
π
2
ϕ 20
3π = 2
A1 > A2
合振动方程
x = ( A1 − A2 ) cos(ωt + ) 2 T π = ( A1 − A2 ) cos( t + ) 2π 2
2 1 2
x
ϕ0
x
o
T
A = A1 + A2 x = ( A1 + A2 ) cos( ω t + ϕ ) ϕ0 = ϕ20 = ϕ10 + 2k π
太原理工大学物理系
A ω
A2
A1
o
t
A = A + A + 2 A1 A2 cos(ϕ20 − ϕ10 ) ∆ ± 2）反相位 ϕ = ϕ 20 − ϕ10 = ( 2k + 1) π( k = 0 ， 1, L) x1 = A1 cos ω t x = ( A2 − A1 ) cos(ωt + π) x 2 = A 2 cos( ω t + π ) A = A1 − A2
x
x
ϕ 0 = ϕ 20
A1
ϕ 20
o
o
T
太原理工大学物理系
t
ω A2
A
两个简谐振动的相位关系 （1）相位差 ϕ 20 − ϕ10 = 2k π ( k = 0 ， 1， ) ± L 两个简谐振动的相位相同， 两个简谐振动的相位相同，合振动的振幅 相位相同
A = A1 + A2
相互加强
§3 同方向简谐振动的合成
当一个物体同时参与几个谐振动时,就需考 当一个物体同时参与几个谐振动时 就需考 虑振动的合成问题。 虑振动的合成问题。本节讨论 的简谐振动的合成, （1）同方向、同频率的简谐振动的合成 它 ）同方向、同频率的简谐振动的合成 是波的干涉的重要基础。 干涉的重要基础 是波的干涉的重要基础。 的简谐振动合成， （2）同方向、不同频率的简谐振动合成，其 ）同方向、不同频率的简谐振动合成 结论可以给出重要的实际应用。 结论可以给出重要的实际应用。
（2）相位差 ϕ 20 − ϕ10 = ( 2k + 1) π ( k = 0 ， 1， ) ± L 两个简谐振动的相位相反，合振动的振幅 两个简谐振动的相位相反， 相位相反
A = A1 − A2
一般情况下 （3）一般情况下
相互削弱
A1 + A2 > A > A1 − A2
太原理工大学物理系
二、两同方向不同频率的简谐振动的合成 设分振动 合振动
x1 = A1 cos ω1t
x2 = A2 cos ω2t
= 2 A cos(
频率相差较小
x = x1 + x2 ω1 − ω2
2
t ) cos(
ω1 + ω2
2
t)
令A(t ) = 2 A cos(
ω1 − ω2
2 ω1 + ω2 cos ωt = cos( t) 2
t)
太原理工大学物理系
合振动特点： 合振动特点： （1）合振动频率 （2）合振幅
ω=
ω1 + ω2
2
≈ ω1 ≈ ω2
2 t)
A(t ) = 2 A cos(
ω1 − ω 2
合振动的振幅在0--2A之间随 周期性变化，时强 之间随t周期性变化 合振动的振幅在 振幅 之间随 周期性变化， 时弱，合振动不是简谐振动。 时弱，合振动不是简谐振动。 合振幅时强时弱的现象称为拍 合振幅时强时弱的现象称为拍。 合振幅在单位时间内变化的次数称拍频 拍频。 合振幅在单位时间内变化的次数称拍频。 拍频
两个同方向、 频率简谐运动合成 合成后 两个同方向、同频率简谐运动合成后，仍然为 简谐运动 振动频率仍为ω 运动， 频率仍为 简谐运动，振动频率仍为ω. 太原理工大学物理系
A、ϕ0 可由旋转矢量法导出，这比用解析法方便。 、 可由旋转矢量法导出，这比用解析法方便 方便。
v A2
0
2 1
ω
v A
ϕ 20 ϕ x2
太原理工大学物理系
一
两个同方向同频率简谐运动的合成 设有两个同频率的谐振动，表达式分别为： 设有两个同频率的谐振动，表达式分别为：
x1 = A1 cos( ω t + ϕ10 ) x2 = A2 cos( ω t + ϕ 20 )
合振动位移 x = x1+ x2 由 三角函数可以证明
x = A cos( ω t + ϕ 0 )
太原理工大学物理系
π
2 2
10
v ϕ 0A
x1
1
x
x
A = A + A + 2 A1 A2 cos(ϕ20 − ϕ10 ) A1 sin ϕ10 + A2 sin ϕ 20 tan ϕ 0 = A1 cos ϕ10 + A2 cos ϕ 20
太原理工大学物理系
讨论两种特殊情况
A = A + A + 2 A1 A2 cos(ϕ20 − ϕ10 ) ± ± 1）同相位 ∆ϕ = ϕ 20 − ϕ10 = 2k π (k = 0 ， 1， 2,L) ）
∆ν = ν 1 − ν 2
太原理工大学物理系
拍现象
太原理工大学物理系
例8 两个同方向的简谐振动曲线如图所示， 两个同方向的简谐振动曲线如图所示，求合 振动方程。 振动方程。
A1
A2
x1
x2
t
太原理工大学物理系
解：由振动曲线得
ϕ10 =
π
2
ϕ 20
3π = 2
A1 > A2
合振动方程
x = ( A1 − A2 ) cos(ωt + ) 2 T π = ( A1 − A2 ) cos( t + ) 2π 2
2 1 2
x
ϕ0
x
o
T
A = A1 + A2 x = ( A1 + A2 ) cos( ω t + ϕ ) ϕ0 = ϕ20 = ϕ10 + 2k π
太原理工大学物理系
A ω
A2
A1
o
t
A = A + A + 2 A1 A2 cos(ϕ20 − ϕ10 ) ∆ ± 2）反相位 ϕ = ϕ 20 − ϕ10 = ( 2k + 1) π( k = 0 ， 1, L) x1 = A1 cos ω t x = ( A2 − A1 ) cos(ωt + π) x 2 = A 2 cos( ω t + π ) A = A1 − A2