两个简谐振动的合成
谐振动分析(三)两个同方向同频率简谐运动的合成
o
o
A1
A2
A
T
t
A A1 A2
x (A A )cos(t )
1
2
2 1 2k π
3
物理学
第五版
谐运动分析(三)
（2）相位差 (2k 1) π(k 0，1, )
2
1
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A2 A1)cos(t )
2
1
(2k
1)π
4
物理学
第五版
小结
（1）相位差
2
1
2k
π
A A1 A2
谐运动分析(三)
(k 0，1， ) 加强
（2）相位差
2
1
(2k 1) π
(k 0，1， )
A A A
1
2
减弱
（3）一般情况
A1 A2 A A1 A2
5
物理学
第五版
谐运动分析(三)
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
x 阻尼振动位移时间曲线
A
Ae t
Aet cost
O
T A
t
( 0)
21
物理学
第五版
三种阻尼的比较
谐运动分析(三)
(a)欠阻尼
2 0
2
(b)过阻尼
2 0
2
(c)临界阻尼
2 0
2
x
b
oc
t
a
22
物理学
第五版
谐运动分析(三)
例 有一单摆在空气（室温为 20C）中来 回摆动. 摆线长l 1.0 m，摆锤是半径r 5.0103 m 的铅球.求（1）摆动周期；（2）振幅减小 10％所需的时间；（3）能量减小10％所需 的时间；（4）从以上所得结果说明空气的 粘性对单摆周期、振幅和能量的影响.
大学物理实验6 简谐振动的合成
云南大学软件学院 实验报告课程： 大学物理实验 学期： 任课教师： 班级： = 学号： == 序号： = 姓名： = 成绩：实验6 简谐振动的合成内容一 同方向同频率简谐振动的合成两个简谐振动的方程为使用matlab 编写程序，求x1,x2,合振动的波形，讨论相位差对合成振动的影响。
相位差至少讨论4中情况（1.为0°;2.为180°；3.小于180°；4.大于180°），要求所有波形画在同一个figure 中。
()()⎩⎨⎧+=+=222111cos cos ϕωϕωt A x t A x内容二 相互垂直方向同频率简谐振动的合成两个简谐振动的方程为使用matlab 编写程序，求x,y,合振动的波形，讨论相位差对合成振动的影响。
相位差至少讨论4中情况（1.为0°;2.为180°；3.小于180°；4.大于180°），要求所有波形画在同一个figure 中。
()()⎩⎨⎧+=+=y y x x t A y t A x ϕωϕωcos cos内容三相互垂直方向不同频率简谐振动的合成(李萨如图形) 使用matlab编写程序，画李萨如图形，要求：1.至少4种频率比2.至少8种相位差3.所有图形画在同一个figure中，添加标注。
如：cleart = 0:0.01:4;Ax = 1;Ay = 3;w1 = 1; w2 = 1./2;w3 = 2./3;w4 = 3./4;w5 = 2./5;m0 = 0;m1 = 0;m2 = pi./4;m3 = pi./2;m4 = 3.*pi./4;m5 = pi;m6 = 5.*pi./4; m7 =3.*pi./2;m8 = 7.*pi./4; x0 = Ax.*cos(2.*pi*t+m0);y11 = Ay.*cos(2.*w1.*pi*t+m1);y12 = Ay.*cos(2.*w1.*pi*t+m2);y13 = Ay.*cos(2.*w1.*pi*t+m3);y14 = Ay.*cos(2.*w1.*pi*t+m4);y15 = Ay.*cos(2.*w1.*pi*t+m5);y16 = Ay.*cos(2.*w1.*pi*t+m6);y17 = Ay.*cos(2.*w1.*pi*t+m7);y18 = Ay.*cos(2.*w1.*pi*t+m8);y21 = Ay.*cos(2.*w2.*pi*t+m1);y22 = Ay.*cos(2.*w2.*pi*t+m2);y23 = Ay.*cos(2.*w2.*pi*t+m3);y24 = Ay.*cos(2.*w2.*pi*t+m4);y25 = Ay.*cos(2.*w2.*pi*t+m5);y26 = Ay.*cos(2.*w2.*pi*t+m6);y27 = Ay.*cos(2.*w2.*pi*t+m7);y28 = Ay.*cos(2.*w2.*pi*t+m8);y31 = Ay.*cos(2.*w3.*pi*t+m1);y32 = Ay.*cos(2.*w3.*pi*t+m2);y33 = Ay.*cos(2.*w3.*pi*t+m3);y34 = Ay.*cos(2.*w3.*pi*t+m4);y35 = Ay.*cos(2.*w3.*pi*t+m5);y36 = Ay.*cos(2.*w3.*pi*t+m6);y37 = Ay.*cos(2.*w3.*pi*t+m7);y38 = Ay.*cos(2.*w3.*pi*t+m8);y41 = Ay.*cos(2.*w4.*pi*t+m1);y42 = Ay.*cos(2.*w4.*pi*t+m2);y43 = Ay.*cos(2.*w4.*pi*t+m3);y44 = Ay.*cos(2.*w4.*pi*t+m4);y45 = Ay.*cos(2.*w4.*pi*t+m5);y46 = Ay.*cos(2.*w4.*pi*t+m6);y47 = Ay.*cos(2.*w4.*pi*t+m7);y48 = Ay.*cos(2.*w4.*pi*t+m8);y51 = Ay.*cos(2.*w5.*pi*t+m1);y52 = Ay.*cos(2.*w5.*pi*t+m2);y53 = Ay.*cos(2.*w5.*pi*t+m3);y54 = Ay.*cos(2.*w5.*pi*t+m4);y55 = Ay.*cos(2.*w5.*pi*t+m5);y56 = Ay.*cos(2.*w5.*pi*t+m6);y57 = Ay.*cos(2.*w5.*pi*t+m7);y58 = Ay.*cos(2.*w5.*pi*t+m8);subplot(5,8,1);plot(x0,y11);Axis([-4 4 -4 4]);text(-16,0,'ω =1');text(-2,7,'0');text(-16,7,'相位差');subplot(5,8,2);plot(x0,y12);Axis([-4 4 -4 4]);text(-2,7,'π/4'); subplot(5,8,3);plot(x0,y13);Axis([-4 4 -4 4]);text(-2,7,'π/2'); subplot(5,8,4);plot(x0,y14);Axis([-4 4 -4 4]);text(-2,7,'3π/4'); subplot(5,8,5);plot(x0,y15);Axis([-4 4 -4 4]);text(-2,7,'π');subplot(5,8,6);plot(x0,y16);Axis([-4 4 -4 4]);text(-2,7,'5π/4'); subplot(5,8,7);plot(x0,y17);Axis([-4 4 -4 4]);text(-2,7,'3π/2'); subplot(5,8,8);plot(x0,y18);Axis([-4 4 -4 4]);text(-2,7,'7π/4'); subplot(5,8,9);plot(x0,y21);Axis([-4 4 -4 4]);text(-16,0,'ω = 1/2'); subplot(5,8,10);plot(x0,y22);Axis([-4 4 -4 4]);subplot(5,8,11);plot(x0,y23);Axis([-4 4 -4 4]);subplot(5,8,12);plot(x0,y24);Axis([-4 4 -4 4]);subplot(5,8,13);plot(x0,y25);Axis([-4 4 -4 4]);subplot(5,8,14);plot(x0,y26);Axis([-4 4 -4 4]);subplot(5,8,15);plot(x0,y27);Axis([-4 4 -4 4]);subplot(5,8,16);plot(x0,y28);Axis([-4 4 -4 4]);subplot(5,8,17);plot(x0,y31);Axis([-4 4 -4 4]);text(-16,0,'ω = 2/3'); subplot(5,8,18);plot(x0,y32);Axis([-4 4 -4 4]);subplot(5,8,19);plot(x0,y33);Axis([-4 4 -4 4]);subplot(5,8,20);plot(x0,y34);Axis([-4 4 -4 4]);subplot(5,8,21);plot(x0,y35);Axis([-4 4 -4 4]);subplot(5,8,22);plot(x0,y36);Axis([-4 4 -4 4]);subplot(5,8,23);plot(x0,y37);Axis([-4 4 -4 4]);subplot(5,8,24);plot(x0,y38);Axis([-4 4 -4 4]);subplot(5,8,25);plot(x0,y41);Axis([-4 4 -4 4]);text(-16,0,'ω = 3/4'); subplot(5,8,26);plot(x0,y42);Axis([-4 4 -4 4]);subplot(5,8,27);plot(x0,y43);Axis([-4 4 -4 4]);subplot(5,8,28);plot(x0,y44);Axis([-4 4 -4 4]);subplot(5,8,29);plot(x0,y45);Axis([-4 4 -4 4]);subplot(5,8,30);plot(x0,y46);Axis([-4 4 -4 4]);subplot(5,8,31);plot(x0,y47);Axis([-4 4 -4 4]);subplot(5,8,32);plot(x0,y48);Axis([-4 4 -4 4]);subplot(5,8,33);plot(x0,y51);Axis([-4 4 -4 4]);text(-16,0,'ω = 2/5'); subplot(5,8,34);plot(x0,y52);Axis([-4 4 -4 4]);subplot(5,8,35);plot(x0,y53);Axis([-4 4 -4 4]);subplot(5,8,36);plot(x0,y54);Axis([-4 4 -4 4]);subplot(5,8,37);plot(x0,y55);Axis([-4 4 -4 4]);subplot(5,8,38);plot(x0,y56);Axis([-4 4 -4 4]);subplot(5,8,39);plot(x0,y57);Axis([-4 4 -4 4]);subplot(5,8,40);plot(x0,y58);Axis([-4 4 -4 4]);。
10.2 两个简谐振动的合成
2
2
频率都较大且频率差很小的两个同方向简谐
振动，在合成时会产生合振幅时强、时弱的现 象，这称为拍。
拍频 ：单位时间内振动加强或减弱的次数
振幅 2Acos (2 1)t 的频率
2 由于是绝对值，所以
2
2
1
2
2
1
拍频等于两个分振动的频率之差
10.2.3 互相垂直的同频率简谐振动的合成
质点按分振动的周 期作左旋正椭圆运动
A1=A2：左旋圆运动
（5）当 2 1 取其他值时，合振动的轨迹一
般为斜椭圆。 与上述合成过程相反，一个圆运动或椭圆运
动可以分解成两个互相垂直的同频率简谐振动 这在分析光的偏振时要经常用到
*10.2.4 互相垂直的不同频率简谐振动的合成
合振动的轨迹一般是不稳定的。但当两个分 振动的频率比恰好等于简单的整数比时，合振 动的轨迹是稳定的封闭曲线，称为李萨如图。
李萨如图
判定两种频率是否成整数比，据此可由已知 频率确定未知频率。
x1 A1 cos( t 1)
x2 A2 cos( t 2 )
合振动仍是一个角 频率为ω的简谐振动：
x x1 x2 Acos( t )
A A12 A22 2A1 A2 cos(2 1) tan A1 sin 1 A2 sin 2
A1 cos1 A2 cos2
（3）2
1
2
，y 比 x 超前
2
：
x2 y2 1 A12 A22
质点的运动轨迹是以
坐标轴为主轴的正椭圆 （或圆） 不是简谐振动!
谐振动分析(三)两个同方向同频率简谐运动的合成
A
f (02 p2 )2 4 2p2
t
dA 0 d p
x A0 e
cos(t ) A cos( p t )
28
物理学
第五版
谐运动分析(三)
共振频率
r | 2 |
2 0 2
A
共振频率 小阻尼 阻尼 0
3
物理学
第五版
谐运动分析(三)
（2）相位差 2 1 (2k 1) π (k 0 ， 1, )
x
A1
x
2
o
o
T
t
x ( A2 A1 ) cos( t ) A A1 A2 2 1 (2k 1)π
4
A
A2
物理学
第五版
物理学
第五版
谐运动分析(三)
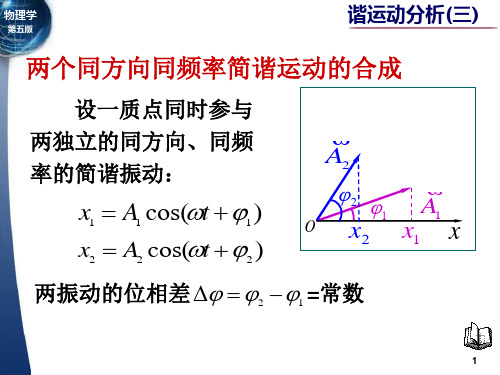
两个同方向同频率简谐运动的合成
设一质点同时参与 两独立的同方向、同频 率的简谐振动：
A2
2
O
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
x2
1
x1
A1
x
两振动的位相差 2 1 =常数
1
物理学
第五版
5
解 （2） 有阻尼时 A' Ae t ln( 1 ) 0 . 9 t t 174 s 3 min 0.9 A Ae 1
1
E 0.9E, t ? （ 3）
E ' A ' （ 3） ( ) 2 e 2t E A 1 ) ln( 2t 0.9 87 s 1.5 min 0.9 e t2 2
机械振动 习题解答
©物理系_2015_09《大学物理AII 》作业 No.01 机械振动班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、 判断题：（用“T ”表示正确和“F ”表示错误）1/3/5 2 4[ F ] 1．只有受弹性力作用的物体才能做简谐振动。
解：如单摆在作小角度摆动的时候也是简谐振动，其回复力为重力的分力。
[ F ] 2．简谐振动系统的角频率由振动系统的初始条件决定。
解：P5. 根据简谐振子角频率公式mk=ω，可知角频率是一个完全由振动系统本身性质决定的常量，与初始条件无关。
我们也将角频率称为固有角频率。
[ F ] 3．单摆的运动就是简谐振动。
解：P14-15 单摆小角度的摆动才可看做是简谐振动。
[ T ] 4．孤立简谐振动系统的动能与势能反相变化。
解：P9 孤立的谐振系统 机械能守恒，动能势能反相变化。
[ F ] 5．两个简谐振动的合成振动一定是简谐振动。
解: 同向不同频率的简谐振动的合成结果就不一定是简谐振动。
总结：1、3、5小题均为简谐振动的定义性判断.简谐运动是最基本也是最简单的一种机械振动。
当某物体进行简谐运动时，物体所受的力跟位移成正比，并且力总是指向平衡位置。
二、选择题：1. 把单摆从平衡位置拉开，使摆线与竖直方向成一微小角度θ，然后由静止放手任其振动，从放手时开始计时。
若用余弦函数表示其运动方程，则该单摆振动的初相位为[ C ] (A) θ; (B) π23; (C) 0; (D) π21。
解：对于小角度摆动的单摆，可以视为简谐振动，其运动方程为：()()0cos ϕωθθ+=t t m ，根据题意，t = 0时，摆角处于正最大处，θθ=m，即：01cos cos 0000=⇒=⇒==ϕϕθϕθθ。
类似公式： ()()0cos ϕω+=t A t x2．一个简谐振动系统，如果振子质量和振幅都加倍，振动周期将是原来的 [D] (A) 4倍(B) 8倍(C) 2倍(D)2倍解： P5 公式(12.1.8) m T k m T m k T ∝⇒=⇒⎪⎭⎪⎬⎫==/2/2πωωπ,所以选D 。
简谐振动的合成
x1 (t ) = a cosωt x2 (t ) = a cos(ωt + δ ) x3 (t ) = a cos(ωt + 2δ )
C
Nδ
R
A
aN
⋮ x N ( t ) = a cos[ ω t + ( N − 1)δ ]
O
δ
a3
a1 P
在∆COM中：A = 2 R sin( N δ / 2 ) 中 上两式相除得： 上两式相除得： 在∆OCP中： a = 2R sin(δ / 2) 中
2
A2 y= x 为直线方程 A1
利用旋转矢量合成
∆ϕ = 0
2 1
y
8 7 6
4 4
y
1 2
3
3 7 6
4Байду номын сангаас
8
x
5
5 3
2 1
播 放 动 画
16
5 6 7
x
8
2. |ϕ 2
− ϕ1 | π =
2 2
反相位
y
x y 2xy =0 + + A1 A2 A1 A2
3
利用旋转矢量法求合振动也可得到相同的结果。 •利用旋转矢量法求合振动也可得到相同的结果。 取质点振动的平衡位置O为 取质点振动的平衡位置 为 坐标原点，振动方向沿OX轴。A 坐标原点，振动方向沿 轴 2 点作两个长度分别为A 从O点作两个长度分别为 1、 点作两个长度分别为 ϕ2 ϕ A2的矢量 A1 , A2 ，它们在 它们在t=0时 时 与X轴的夹角分别为ϕ1、ϕ2。 轴的夹角分别为ϕ 轴的夹角分别为
x1 = 4 cos 3t ,
= A cos(3t + ϕ )
二、同方向不同频率两个简谐振动的合成剖析
2 A cos 2 1
2
t
cos 1 2 t 2
位
移x
合振动 分振动1
振幅周期性变化
分振动2
2 21
oLeabharlann TT23T
2T
2
t
为一复杂振动
着重研究1
,
相近情况
2
——拍现象（Beat)
即 1- 2 << 1 or 2
x 2Acos 2 1 t cos 1 2 t
声音强弱的变化快 6秒中变化了6次，有6 拍
声音强弱的变化慢6秒中变化了3次，有3 拍
x 2Acos 2 1 t cos 1 2 t
2 2
x x x1 x2 x1 x2 o
| 振幅2变化缓慢1 |
2
一个强弱变化所需的时间
A A12 A22 2A1 A2 A1 A2
(2)两个振动反相
x
20 10 (2k 1) , k o,1,2,...
由A A12 A22 2A1 A2 cos(20 10 )
o
A A12 A22 2A1 A2 A1 A2
2010
x20
0
x10
AM
A1
x0
t o .P x
同方向同频率两个简谐振动的合成仍为简谐振动。
讨论两个特例
x
(1)两个振动同相
20 10 2k , k 0,1,2,...
由 A A12 A22 2A1 A2 cos(20 10 ) o
2 2
振幅随时间的变化非常缓慢
x
第二节 两个简谐振动的合成
A12 A22 2A1A2 cos(02 01)
A A12 A22 2A1A2 cos
[注：cos( ) cos cos sin sin ]
A值的讨论，有三种情况：
(1) 2k
cos 1
A A1 A2
A值最大
(2) (2k 1) cos 1
A A1 A2 (3) 为其它值
波器显示屏上出现合成结果的图形，见右图。求x ?
解：
x y
m n
Y方向切点数 X方向切点数
x 3 x y 2 1000
x 1500 Hz
本节小结
同方向
1
2
简谐振动 A A12 A22 2A1A2 cos
同方向 1 2 拍 2 1
垂直方向
x m y n
李萨如图
x y
两个简谐振动的步调比较
同相：若两个简谐振动的频率相同、初相位相同，则两个简谐 振动的位移同时达到最大和最小。
x
1
2
t3
t1
t2
t4
t
0 ,同相
反相：若两个简谐振动的频率相同、初相位相差π，则一个振
动到达最大位移处时，另一个振动到达反向最大位移处。
1
x
t1
t2
t3
t4
t
2
,反相
超前与落后：若两个简谐振动的频率相同，初相位之差为
Y2 B2
1
X 0 t1 0 Y B
t2
2
X A Y 0
X 0 t3 Y B
t4
3 2
X A Y 0
t4 t3
t2
t1 Y超前π/2
右旋振动
t1 t2
t3
t4 Y落后π/2
重庆理工大学振动、波动部分答案(新)
大学物理学——振动和波振 动班级 学号 姓名 成绩内容提要1、简谐振动的三个判据（1）；（2）；（3）2、描述简谐振动的特征量： A 、T 、γ；T1=γ，πγπω22==T3、简谐振动的描述：（1）公式法 ；（2）图像法；（3）旋转矢量法4、简谐振动的速度和加速度：)2cos()sin(v00πϕωϕωω++=+-==t v t A dt dx m ； a=）（）（πϕωϕωω±+=+=0m 0222t a t cos -dtxd A 5、振动的相位随时间变化的关系：6、简谐振动实例弹簧振子：，单摆小角度振动：，复摆：0mgh dt d 22=+θθJ ,T=2mghJπ 7、简谐振动的能量：222m 21k 21A A Eω==系统的动能为：）（ϕωω+==t sin m 21mv 212222A E K ；系统的势能为：）ϕω+==t (cos k 21kx 21222A E P8、两个简谐振动的合成（1）两个同方向同频率的简谐振动的合成合振动方程为：）（ϕω+=t cos x A 其中，其中；。
＊(2) 两个同方向不同频率简谐振动的合成拍：当频率较大而频率之差很小的两个同方向简谐运动合成时，其合振动的振幅表现为时而加强时而减弱的现象，拍频：12-γγγ=＊（3）两个相互垂直简谐振动的合成合振动方程：）（1221221222212-sin )(cos xy 2y x ϕϕϕϕ=--+A A A A ，为椭圆方程。
练习一一、 填空题1．一劲度系数为k 的轻弹簧，下端挂一质量为m 的物体，系统的振动周期为T 1。
若将此弹簧截去一半的长度，下端挂一质量为m/2的物体，则系统的周期T 2等于 。
2．一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为：A ＝ ；=ω ;=ϕ 。
3．如图，一长为l 的均匀细棒悬于通过其一端的光滑水平固定轴上，做成一复摆。
已知细棒绕过其一端的轴的转动惯量J ＝3/2ml ，此摆作微小振动的周期为 。
两个同方向同频率的简谐运动的合成
2）相位差 2 1 (2k 1)π
(k 0 ， 1, )
A A1 A2
合成的振幅最小
合成的振动的初相和振幅大的分振动的初相相同
4 –2 两个同方向同频 1)π (k 0 ， 1, )
x1 A1 cost x2 A2 cos(t π ) x ( A2 A1 ) cos(t π)
2 A2 cos 2 A12 cos 2 1 A2 cos 2 2 2 A1 A2 cos 1 cos 2 2 A2 sin 2 A12 sin 2 1 A2 sin 2 2 2 A1 A2 sin 1 sin 2
2 A2 A12 A2 2 A1 A2 cos 1 cos 2 sin 1 sin 2
A2
2
0
A
x2
x A cos(t )
x x1 x2
x2
1
x1
A1
x
x
A1 sin 1 A2 sin 2 tan A1 cos 1 A2 cos 2 2 2 A A1 A2 2 A1 A2 cos( 2 1 )
4 –2 两个同方向同频率振动的合成 根据余弦定理
3）一般情况
A A1 A2
相互削弱
A1 A2 A A1 A2
4 –2 两个同方向同频率振动的合成
本节练习 1 （D） 2. 两个分振动的圆频率相同，所以，合振动 旋转矢量的大小为常量，合振动的圆频率 也和分振动的圆频率相同。
4 –2 两个同方向同频率振动的合成
作业
习题 4-4
x
x
2
o 2
A 2
力学第二版习题答案第九章
第九章基本知识小结⒈物体在线性回复力F = - kx ，或线性回复力矩τ= - c φ作用下的运动就是简谐振动，其动力学方程为 ,02022=+x dt x d ω（x 表示线位移或角位移）；弹簧振子：ω02=k/m ，单摆：ω02=g/l ，扭摆：ω02=C/I.⒉简谐振动的运动学方程为 x = Acos(ω0t+α)；圆频率、频率、周期是由振动系统本身决定的，ω0=2π/T=2πv ；振幅A 和初相α由初始条件决定。
⒊在简谐振动中，动能和势能互相转换，总机械能保持不变；对于弹簧振子，22021221A m kA E E p k ω==+。
⒋两个简谐振动的合成⒌阻尼振动的动力学方程为 022022=++x dt dx dtx d ωβ。
其运动学方程分三种情况：⑴在弱阻尼状态（β＜ω0），振动的方向变化有周期性，220'),'cos(βωωαωβ-=+=-t Ae x t ，对数减缩 = βT ’.⑵在过阻尼状态（β＞ω0），无周期性，振子单调、缓慢地回到平衡位置。
⑶临界阻尼状态（β=ω0），无周期性，振子单调、迅速地回到平衡位置⒍受迫振动动力学方程 t f x dt dx dt x d ωωβcos202022=++； 其稳定解为 )cos(0ϕω+=t A x ，ω是驱动力的频率，A 0和φ也不是由初始条件决定,222220004)(/ωβωω+-=f A 2202ωωβωϕ--=tg 当2202βωω-=时，发生位移共振。
9.2.1 一刚体可绕水平轴摆动。
已知刚体质量为m ，其重心C 和轴O 间的距离为h ，刚体对转动轴线的转动惯量为I 。
问刚体围绕平衡位置的微小摆动是否是简谐振动？如果是，求固有频率，不计一切阻力。
解：规定转轴正方向垂直纸面向外，忽略一切阻力，则刚体所受力矩τ= - mghsin φ因为是微小摆动，sin φ≈φ,∴τ= - mgh φ，即刚体是在一线性回复力矩作用下在平衡位置附近运动，因而是简谐振动。
简谐振动的合成
(A1 sin1 A2 sin2 )sint
合振幅
令： A1 cos1 A2 cos2 Acos 代入上式：
A1 sin1 A2 sin2 Asin
2
x ( A1 cos1 A2 cos2)cost (A1 sin1 A2 sin2 )sint
Acos cost Asin sint Acos(t ) x Acos(t )
x1(t) a cost
M aN
x2 (t) a cos(t ) x3(t) a cos(t 2 )
C
R N
A
a3
xN (t) a cos[t (N 1) ]O a1 P
在COM中：A 2R sin(N / 2)
上两式相除得：
在OCP中： a 2Rsin( / 2)
7
A a sin(N / 2) sin / 2
若 A1 A2, A 2A1
2.当 2 1 （2k 1） (k 0,1,2, ) 时,
A
A12
A
2 2
2 A1
A2
cos(
2
1
)
| A1 A2 | 合振动振幅最小。
若 A1 A2, A 0
A2
3.一般情况 | A1 A2 | A | A1 A2 |
5
A A2 A1
A2 A A1 A A1
第二节
简谐振动的合成
1
一、同方向同频率简谐振动的合成
在同一直线上同频率的两个简谐振
动分别为：
x1 A1 cos(t 1),
x2 A2 cos( t 2 )
• 代数方法： 振动合成
x x1 x2 A1 cos(t 1) A2 cos(t 2 )
(A1 cos1 A2 cos2) cost
5-3 、 5-4 简谐振动的合成
ϕ
A2
x
O C A1
N −1 ∆ϕ ϕ = 合振动表达式 2 x ( t ) = A cos( ω t + ϕ ) sin(N∆ϕ / 2) N −1 = A0 cos(ω t + ∆ϕ ) sin(∆ϕ / 2) 2
讨论1： 讨论 ： 当 δ
= ±2kπ k = 0,1,2,L sin(N∆ϕ / 2) A = lim A0 = NA0 sin(∆ϕ / 2)
四、两个相互垂直的同频率简谐振动的合成
某质点同时参与两个同频率的互相垂直方向的简谐运动
x = A1 cos(ω t + ϕ 1 ) y = A2 cos(ω t + ϕ 2 )
合振动的轨迹方程为
x y 2 xy 2 cos(ϕ 2 − ϕ 1 ) = sin (ϕ 2 − ϕ 1 ) + 2− 2 A1 A2 A1 A2
'
各分振动矢量依次相接， 各分振动矢量依次相接，构 成闭合的正多边形， 成闭合的正多边形，合振动 的振幅为零。 的振幅为零。
三、同方向不同频率的简谐振动的合成
某质点同时参与两个不同频率且在同一条直线上的简谐振动
x1 = A1 cos(ω 1 t + ϕ 1 )
x 2 = A2 cos(ω 2 t + ϕ 2 )
A2 y=− x A1
y
x2 y2 2 xy + 2+ =0 2 A1 A2 A1 A2
x
合振动的轨迹是一条通过原点的直线
讨论3 讨论
∆ϕ = ϕ 2 − ϕ 1 = π / 2 x2 y2 合振动的轨迹是的椭圆 合振动的轨迹是的椭圆 + 2 =1 2 A1 A2 方程， 方程，且顺时针旋转
物理-同一直线上简谐振动的合成 频谱分析
三、同一直线上两个异频谐振动的合成
合振动 x 2Acos(2 1 t ) cos(2 1 t)
2
2
若 2 1 1 2
2
2
随时间缓变
随时间快变
合振动可视作
频率 振幅
1 2 2
2A cos 2 1 t
2
的准周期运动！
两个频率相差不大的同方向简谐运动叠加后， 出现合振动振幅时而加强时而减弱的现象称为“拍”。
一、同一直线上同频谐振动的合成
设一个质点同时参与两个沿同一直线的简谐振动，
这两个简谐振动的频率均为ω ，振幅分别为
初相位分别为
它们的振动表达式分别为：
分振动
x1 A1 cos( t 1 ) x2 A2 cos( t 2 )
合振动 x x1 x2
A1 cos(t 1) A2 cos(t 2 )
t
2
)
(m)
x2 2cos(10 t ) (m)
求：（1）合振动的表达式；
（2）若另有 x3 3cos(10 t ) (m)
则 分别为何值时，三个简谐振动叠加后，合振动
的振幅分别为最大与最小？
三、同一直线上两个异频谐振动的合成
合振动的“振幅”： 2A cos 2 1 t
2 单位时间内合振动振幅加强或减弱的次数——拍频
cos 2 1 t
2
的周期为π ，故振幅变化周期τ 满足：
2 1
2
2 2 1
拍频
三、同一直线上两个异频谐振动的合成
同一直线上两个频率接近的简谐振动的合成
OCP 2CPO (CPO CPP)
二、同一直线上N个同频谐振动的合成
(2) 确定合振动初相位
COP COM
第三十二讲：简谐振动的合成
第三十二讲 §8.2 简谐振动的合成一、两个同方向同频率简谐振动的合成1、合振动仍然为简谐振动简谐振动1：()111cos ϕω+=t A x 简谐振动2：()222cos ϕω+=t A x合振动：()()()ϕωϕωϕω+=+++=+=t A t A t A x x x cos cos cos 2211212、合振动的振幅：()()22211222112sin sin cos cos A ϕϕϕϕA A A A +++=()1212212221sin sin cos cos 2ϕϕϕϕ+++=A A A A ()12212221cos 2ϕϕ-++=A A A A 3、合振动的初相位：22112211cos cos sin sin tan ϕϕϕϕϕA A A A ++==邻边对边 4、合振动的最大值，相长的条件：两分振动相位相同，相位差：() 3,2,1,0212=±=-=∆k k πϕϕϕ⇒()1cos 12=-ϕϕ ⇒ 212122212A A A A A A A +=++=5、合振动的最小值，相消的条件：两分振动相位相反，相位差：() 3,2,1,01212=+±=-=∆k k πϕϕϕ）（ ⇒()1cos 12-=-ϕϕ ⇒ 212122212A A A A A A A -=-+= 其他值：2121A A A A A +-练习题1. 一物体同时参与两个同方向的简谐振动：)212c o s (04.01π+π=t x (SI), )2cos(03.02π+π=t x (SI) 求此物体的振动方程．解：设合成运动（简谐振动）的振动方程为 )cos(φω+=t A x则 )c o s(2122122212φφ-++=A A A A A ①以 A 1 = 4 cm ，A 2 = 3 cm ，π=π-π=-212112φφ代入①式，得5cm 3422=+=A cm 2分又 22112211c o s c o s s i n s i n a r c t gφφφφφA A A A ++= ② ≈127°≈2.22 rad 2分 ∴)22.22cos(05.0+π=t x (SI) 1分练习题2. 两个同方向简谐振动的振动方程分别为 )4310cos(10521π+⨯=-t x (SI), )4110cos(10622π+⨯=-t x (SI) 求合振动方程．解：依合振动的振幅及初相公式可得φ∆++=c o s 2212221A A A A A 22210)4143cos(65265-⨯π-π⨯⨯⨯++= m 21081.7-⨯= m 2分)4/c o s (6)4/3c o s (5)4/s i n (6)4/3s i n (5a r c t gπ+ππ+π=φ = 84.8°=1.48 rad 2分则所求的合成振动方程为 )48.110cos(1081.72+⨯=-t x (SI)1分练习题3. 两个同方向的简谐振动的振动方程分别为x 1 = 4×10-2cos2π)81(+t (SI), x 2 = 3×10-2cos2π)41(+t (SI) 求合振动方程．解：由题意 x 1 = 4×10-2cos)42(π+πt (SI)x 2 =3×10-2cos)22(π+πt (SI) 按合成振动公式代入已知量，可得合振幅及初相为22210)4/2/cos(2434-⨯π-π++=A m= 6.48×10-2 m 2分)2/cos(3)4/cos(4)2/sin(3)4/sin(4arctgπ+ππ+π=φ=1.12 rad 2分 合振动方程为 x = 6.48×10-2 cos(2πt +1.12) (SI) 1分练习题4. 一质点同时参与两个同方向的简谐振动，其振动方程分别为 x 1 =5×10-2cos(4t + π/3) (SI) , x 2 =3×10-2sin(4t - π/6） (SI) 画出两振动的旋转矢量图，并求合振动的振动方程．解： x 2 = 3×10-2 sin(4t - π/6)= 3×10-2cos(4t - π/6- π/2)= 3×10-2cos(4t - 2π/3)．作两振动的旋转矢量图，如图所示． 图2分由图得：合振动的振幅和初相分别为A = (5-3)cm = 2 cm ，φ = π/3． 2分合振动方程为 x = 2×10-2cos(4t + π/3) (SI)1分小结：简谐振动的合成，与旋转矢量的解法作业：P33 8—16；8—17；预习：§8—2二、两个同方向不同频率简谐振动的合成 拍频三、相互垂直的简谐振动的合成1、同频率的相互垂直的简谐振动的合成2、不同频率的相互垂直的简谐振动的合成第三十二讲 §8.2 简谐振动的合成 8-16 解：设两质点的振动表达式分别为：)cos()cos(2211ϕωϕω+=+=t A x t A x 由图题可知，一质点在21A x =处时对应的相位为： 32/arccos 1πϕω==+A A t 同理：另一质点在相遇处时，对应的相位为：352/arccos2πϕω==+A A t 故相位差)()(12ϕωϕωϕ∆+-+=t t πππϕϕ3433512=-=-= 若21υυ与的方向与上述情况相反，故用同样的方法，可得：πππϕϕϕ∆32)3(312=--=-= 8-17 解：由图题8-17(图在课本上P 200)所示曲线可以看出，两个简谐振动的振幅相同，即m 05.021==A A ,周期均匀s 1.0=T ，因而圆频率为：ππω202==T 由x -t 曲线可知，简谐振动1在t=0时，,010=x 且010>υ，故可求得振动1的初位相πϕ2310=. 同样，简谐振动2在t=0时，πϕυ==-=202020,0,05.0可知m x 故简谐振动1、2的振动表达式分别为： mt x t x )20cos(05.0)2320cos(05.021ππππ+=+=因此，合振动的振幅和初相位分别为：m A A A A A 210202122211025)cos(2-⨯=-++=ϕϕ 2021012021010cos cos sin sin arctan ϕϕϕϕϕA A A A ++= ππ4541a r c t a n 或== 但由x-t 曲线知，t=0时，πϕ45,05.021应取因此-=+=x x x . 故合振动的振动表达式：m t x )4520cos(10252ππ+⨯=-习题8-16图。
8.5 简谐运动的合成
ν 2 ν 1
2
t ) cos( 2 π
ν 2 +ν 1
2
t +)
振幅部分 振动频率 振幅
合振动频率
ν = (ν 1 + ν 2 ) 2
A = 2 A1 cos 2π
ν 2 ν 1
2
t
Amax = 2A1
Amin = 0
振幅是随时间变化的， 振幅是随时间变化的，由于振幅的改变也是周期 性的，因此就出现振动忽强忽弱的现象。 性的，因此就出现振动忽强忽弱的现象。
y A2
A2 y= x A1
o
A1
x
x 2 y 2 2 xy + 2 cos( 2 1 ) = sin 2 ( 2 1 ) 2 A1 A2 A1 A2
2） 2 1 = π
3） 2 1 = ± π 2
2 2
A2 y= x A1
o
y
A2
x y + 2 =1 2 A1 A2
π y = A2 cos(ωt + ) 2
合成振动为： 合成振动为： x = x1 + x2 = A1 cos(ω1t + ) + A2 cos(ω 2 t + ) 利用三角函数公式可得
x = 2 A cos(
ω2 ω1
2
t ) cos(
ω2 + ω1
2
t +)
= 2 A cos( 2 π
ν 2 ν 1
2
t ) cos( 2 π
ν 2 +ν 1
两个同方向不同频率简谐运动的合成
频率相近的两个同方向简谐振动的合振动是振幅随 频率相近的两个同方向简谐振动的合振动是振幅随 相近的两个同方向简谐振动的合振动是 时间周期性变化的特殊简谐振动 称为拍振动 的特殊简谐振动， 拍振动。 时间周期性变化的特殊简谐振动，称为拍振动。 单位时间内振动加强或减弱的周期数叫拍频。 单位时间内振动加强或减弱的周期数叫拍频。 拍频 由
物理-相互垂直的简谐运动的合成
y A2 x A1
质点离开 平衡位置 的位移
r(t) A12 A22 cos(t 1 )
y
A2
o A1 x
合振动是与分振动同频率的简谐振动
一、两个相互垂直的谐振动的合成
x A1
2
y A2
2
2xy cos(2 A1 A2
1 )
s in2 ( 2
1 )
(3)
若
2
1
2
x2 A12
y2 A22
合运动的 轨道方程
( x )2 ( y )2 2xycos sin2
A1
A2
A1 A2
其中： (2 1 )t (2 1 ) ——随时间变化
一般情况下，合运动的轨迹是不稳定的。
一、两个相互垂直的谐振动的合成
分振动： x A1 cos(ω1t φ1 ) y A2 cos(ω2t φ2 )
二、振动频谱分析
数学上已经证明：
任意周期函数（周期为T）：x(ωt) 其中 ω 2π /T
均可展开为三角级数
基频
x(ωt ) a0 (ak cos kωt bk sin kωt )
k 1
k次谐频
1 T/2
a0 T
f (ωt )dt
T / 2
2
ak T
T /2
f (ωt)cos kωtdt (k 0)
x A1
2
y A2
2
2xy cos(2
A1 A2
1 )
s in2 ( 2
1 )
合运动一般是在 x A1, y A2 范围内的一个椭圆。
一、两个相互垂直的谐振动的合成
2
2
x A1
y A2
三角函数法对同方向同频率简谐振动合成的求解
三角函数法对同方向同频率简谐振动合成的求解
同方向同频率简谐振动是指两个物体以相同的角频率且方向一致地做简谐振动。
这种振动常常出现在机械振动、波动和电磁振动等领域中。
因此，对同方向同频率简谐振动的合成求解是很重要的。
三角函数法是求解简谐振动合成问题的常用方法，它利用三角函数的性质，将振动方程表示为三角函数的形式，从而方便进行进一步的计算。
下面我们将介绍三角函数法对同方向同频率简谐振动合成的求解步骤。
（1）假设两个物体分别做简谐振动，振幅为A1和A2，初始相位分别为φ1和φ2，角频率均为ω。
（2）写出两个物体的振动方程：
x1 = A1sin(ωt + φ1)
（4）根据三角函数的和差公式，将上式化简为：
x = [A1cos(φ1) + A2cos(φ2)]sin(ωt) + [A1sin(φ1) + A2sin(φ2)]cos(ωt)（6）求出两个简谐振动的振幅和相位，即可求出合成振动的振幅和相位。
振幅：
相位：
（7）利用上式求出合成振动的振幅和相位后，可以得到合成振动的振动方程：
其中，A为合成振动的振幅，φ为合成振动的相位，ω为角频率，t为时间。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x2 A12
y2 A22
2xy A1 A2
cos(2
1)
sin 2 (2
1)
椭圆方程。质点的运动轨迹是椭圆。
（1）2 1 0 ，两分振动同相：
x A1 y A2 质点在Ⅰ、Ⅲ象限沿 过原点的直线运动。t时 刻质点离开原点的位移
s x2 y2
A12 A22 cos( t )
A1=A2：右旋圆运动
（4）2
1
2
，y 比 x 落后 2 ：
x2 y2 1 A12 A22
质点按分振动的周 期作左旋正椭圆运动
A1=A2：左旋圆运动
（5）当 2 1 取其他值时，合振动的轨迹一
般为斜椭圆。 与上述合成过程相反，一个圆运动或椭圆运
动可以分解成两个互相垂直的同频率简谐振动 这在分析光的偏振时要经常用到
*10.2.4 互相垂直的不同频率简谐振动的合成
合振动的轨迹一般是不稳定的。但当两个分 振动的频率比恰好等于简单的整数比时，合振 动的轨迹是稳定的封闭曲线，称为李萨如图。
李萨如图
判定两种频率是否成整数比，据此可由已知 频率确定未知频率。
以上有不当之处，请大家给与批评指正， 谢谢大家！
15
A A12 A22 2A1A2 A1 A2 振动相消，合振幅极小。
A A12 A22 2A1A2 A1 A2 当A1=A2时，A=0，即两个等幅反相的振动互 相抵消。
（3）当 2 1 取其他值时： |A1 A2|< A < A1+ A2
10.2.2 同方向、不同频率简谐振动的合成
拍频 ：单位时间内振动加强或减弱的次数
振幅 2Acos (2 1)t 的频率
2 由于是绝对值，所以
2
1
2
2
2
1
拍频等于两个分振动的频率之差
10.2.3 互相垂直的同频率简谐振动的合成
质点同时参与沿x、y轴方向的两个同频率的 简谐振动
x A1 cos( t 1), y A2 cos( t 2 )
合振动是频率与分振动相同的简谐振动
（2）2 1 ，两分振动反相：
x A1 y A2
质点在Ⅱ、Ⅳ象限 沿过原点的直线作简谐 振动，频率与分振动相 同。
（3）2
1
2
，y 比 x 超前
2
：
x2 A12
y2 A22
1
质点的运动轨迹是以
坐标轴为主轴的正椭圆 （或圆） 不是简谐振动!
按顺时针方向作右旋正 椭圆运动，运动周期仍等 于分振动的周期。
10.2 两个简谐振动的合成
同方向、同频率简谐振动的合成
10.2.1 同方向、同频率简谐振动的合成 质点同时参与两个同方向、 同频率的简谐振动
x1 A1 cos( t 1)
x2 A2 cos( t 2 )
合振动仍是一个角 频率为ω的简谐振动：
x x1 x2 Acos( t )
A A12 A22 2A1 A2 cos(2 1) tan A1 sin 1 A2 sin 2
A1 cos1 A2 cos2
A A12 A22 2A1 A2 cos(2 1) （1）两分振动同相：2 1 2k , k 0,1,2,
cos(2 1) 1
A A12 A22 2A1 A2 A1 A2 振动相长，合振幅极大。
（2）两分振动反相：2 1 (2k 1) , k 0,1,2, cos(2 1) 1
x1 Acos1t, x2 Acos2t, 设 2 1
x
x1
x2
2 A c os
(2
1)t
2
cos
(1
2
2
)t
合振动不是简谐振动。一种重要的特殊情况：
2、1 较大，2 1 ຫໍສະໝຸດ 1 2振幅：2Acos (2 1)t ，角频率：1 2
2
2
频率都较大且频率差很小的两个同方向简谐
振动，在合成时会产生合振幅时强、时弱的现 象，这称为拍。