同方向的简谐振动的合成
合集下载
谐振动分析(三)两个同方向同频率简谐运动的合成
o
o
A1
A2
A
T
t
A A1 A2
x (A A )cos(t )
1
2
2 1 2k π
3
物理学
第五版
谐运动分析(三)
（2）相位差 (2k 1) π(k 0，1, )
2
1
x
x
A1
2 o
o
Tt
A
A2
A A1 A2
x (A2 A1)cos(t )
2
1
(2k
1)π
4
物理学
第五版
小结
（1）相位差
2
1
2k
π
A A1 A2
谐运动分析(三)
(k 0，1， ) 加强
（2）相位差
2
1
(2k 1) π
(k 0，1， )
A A A
1
2
减弱
（3）一般情况
A1 A2 A A1 A2
5
物理学
第五版
谐运动分析(三)
二 两个相互垂直的同频率的简谐
运动的合成 x A1 cos(t 1)
x 阻尼振动位移时间曲线
A
Ae t
Aet cost
O
T A
t
( 0)
21
物理学
第五版
三种阻尼的比较
谐运动分析(三)
(a)欠阻尼
2 0
2
(b)过阻尼
2 0
2
(c)临界阻尼
2 0
2
x
b
oc
t
a
22
物理学
第五版
谐运动分析(三)
例 有一单摆在空气（室温为 20C）中来 回摆动. 摆线长l 1.0 m，摆锤是半径r 5.0103 m 的铅球.求（1）摆动周期；（2）振幅减小 10％所需的时间；（3）能量减小10％所需 的时间；（4）从以上所得结果说明空气的 粘性对单摆周期、振幅和能量的影响.
简谐运动的合成
所以，拍频是振动 cos(
2
1 2 (
拍频（振幅变化的频率）
2 1
2 t)
的频率的两倍。
2 1
2
) 2 1
8.2
四
简谐运动的合成
第八章 机械振动
两个相互垂直的同频率简谐运动的合成 x A1 cos( t 1 )
y A 2 cos( t 2 )
( k 0 ， 1 ， 2, )
1）相位差 2 1 2 k π
x
o A
A2
x
o
T
1
t
x ( A1 A 2 ) cos( t )
A
A A1 A 2
2 1 2k π
8.2
简谐运动的合成
A
2 1 2 2
x n A n cos( t n )
A
1 A1
x x1 x 2 x n
x A cos( t )
2
A2
A3 3
o
x
多个同方
简谐运动的合成
第八章 机械振动
x 1 A 0 cos t x 2 A 0 cos( t )
2
T π
T
1
2 1
2 1
拍频（振幅变化的频率）
8.2
简谐运动的合成
第八章 机械振动
由于振幅是周期性变化的，所以合振动不再是 简谐振动。
当 与 都很大，且相差甚微时，可将 1 2 2 视为振幅部分，合成振动是以 为角频率的 ( 2 1 ) / 2 近似谐振动。 2 1 1 2
2
1 2 (
拍频（振幅变化的频率）
2 1
2 t)
的频率的两倍。
2 1
2
) 2 1
8.2
四
简谐运动的合成
第八章 机械振动
两个相互垂直的同频率简谐运动的合成 x A1 cos( t 1 )
y A 2 cos( t 2 )
( k 0 ， 1 ， 2, )
1）相位差 2 1 2 k π
x
o A
A2
x
o
T
1
t
x ( A1 A 2 ) cos( t )
A
A A1 A 2
2 1 2k π
8.2
简谐运动的合成
A
2 1 2 2
x n A n cos( t n )
A
1 A1
x x1 x 2 x n
x A cos( t )
2
A2
A3 3
o
x
多个同方
简谐运动的合成
第八章 机械振动
x 1 A 0 cos t x 2 A 0 cos( t )
2
T π
T
1
2 1
2 1
拍频（振幅变化的频率）
8.2
简谐运动的合成
第八章 机械振动
由于振幅是周期性变化的，所以合振动不再是 简谐振动。
当 与 都很大，且相差甚微时，可将 1 2 2 视为振幅部分，合成振动是以 为角频率的 ( 2 1 ) / 2 近似谐振动。 2 1 1 2
简谐运动的合成
x = ( 2 A1 cos 2 π
ν 2 −ν 1
2
t ) cos 2 π
ν 2 +ν1
2
t
振幅部分 振动频率 ν = (ν 1 + ν 2 ) 2 振幅 A = 2 A1 cos 2 π
合振动频率
ν 2 −ν 1
2
振 动
Amax = 2A1
t
Amin = 0
15
第九章
物理学
第五版
9-5
简谐运动的合成
y
ϕ （1） 2 −ϕ1 = 0或 2 π ） A2 y= x A1
A2
A1
o
x
ϕ （2） 2 − ϕ1 = π ） A2 y=− x A1
第九章 振 动
y
A2
A1
o
x
7
物理学
第五版
9-5
简谐运动的合成
x 2 y 2 2 xy 讨 + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 论 A12 A2 A1 A2
A
ϕ1
ϕ
A 1
O
x2
x1
xx
两个同方向同频率简谐运动合成后仍 两个同方向同频率简谐运动合成后仍 合成 频率的简谐 简谐运动 为同频率的简谐运动
第九章 振 动
2
物理学
第五版
9-5
简谐运动的合成
（1）相位差 ∆ϕ = ϕ 2 − ϕ1 = 2k π (k = 0，1，2,⋯ ） ± ± )
x
ϕ
A2
x
o
y = A2 cos(ωt + ϕ 2 )
椭圆方程） 质点运动轨迹 （椭圆方程）
x 2 y 2 2 xy + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 2 A1 A2 A1 A2
ν 2 −ν 1
2
t ) cos 2 π
ν 2 +ν1
2
t
振幅部分 振动频率 ν = (ν 1 + ν 2 ) 2 振幅 A = 2 A1 cos 2 π
合振动频率
ν 2 −ν 1
2
振 动
Amax = 2A1
t
Amin = 0
15
第九章
物理学
第五版
9-5
简谐运动的合成
y
ϕ （1） 2 −ϕ1 = 0或 2 π ） A2 y= x A1
A2
A1
o
x
ϕ （2） 2 − ϕ1 = π ） A2 y=− x A1
第九章 振 动
y
A2
A1
o
x
7
物理学
第五版
9-5
简谐运动的合成
x 2 y 2 2 xy 讨 + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 论 A12 A2 A1 A2
A
ϕ1
ϕ
A 1
O
x2
x1
xx
两个同方向同频率简谐运动合成后仍 两个同方向同频率简谐运动合成后仍 合成 频率的简谐 简谐运动 为同频率的简谐运动
第九章 振 动
2
物理学
第五版
9-5
简谐运动的合成
（1）相位差 ∆ϕ = ϕ 2 − ϕ1 = 2k π (k = 0，1，2,⋯ ） ± ± )
x
ϕ
A2
x
o
y = A2 cos(ωt + ϕ 2 )
椭圆方程） 质点运动轨迹 （椭圆方程）
x 2 y 2 2 xy + 2− cos(ϕ 2 − ϕ1 ) = sin 2 (ϕ 2 − ϕ1 ) 2 A1 A2 A1 A2
振动之同方向的简谐振动的合成
合振幅等于原来两个简谐振动的 振幅之差的绝对值，振动减弱。
如果A1 = A2，则合振动的 结果使质点处于静止状态。
一般情况下，合振幅介于A1 + A2和|A1 - A2|之间。
如果第一个振 动的振幅和初 相分别为 0.03m和0，
第二个振动 的振幅和初 相分别为 0.04m和0，
两个振动同相， 合振动加强，振 幅达到0.07m 。
{范例5.9} 同一直线上的简谐振动的合成
2 [讨论] x = cos(ωt + φ), A A12 A2 2 A1 A2 cos( 2 1 ) M ω ①当两个分振动同相时 ω Δφ = φ2 - φ1 = 2kπ,(k = 0，±1，±2，...) A ω A 2 因为cos(φ2 - φ1) = 1，所以 φ A 2 2 φ 2 φ1 1 P A A1 A2 2 A1 A2 A1 A2 可见：合振幅等于原来两个简谐 Ox x x 2 1 振动的振幅之和，振动加强。 x ②当两个分振动反相时 Δφ = φ2 - φ1 = (2k + 1)π ,(k = 0，±1，±2，...) 2 2 A A A 因为cos(φ2 - φ1) = -1，所以 1 2 2A 1 A2 | A 1 A2 |
如果有7个分振动，相差依次为20度，各个分振动的振幅相同，位相差恒定。 将各个 分振动 叠加之 后，振 幅越来 越大， 初位相 也越来 越大。
矢量首尾相接形成多边形的 一部分，最后首尾相接的矢 量就是合振动，合振幅为A = 5.4ΔA ，初相为60度。
取10 个分 振动， 相差 依次 为30 度。
如果两个振动 的振幅不变， 角度分别是0 和90，x2超前 x1的相位π/2，
合振幅为 0.05m，初 相的度数 达到53。
5.4 同方向同频率简谐振动的合成
第5章 机械振动
x2 3cos(2 t ) cm 2
解 合振动的振幅为
2 A A12 A2 2 A1 A2 cos 2 1 5 cm
第5章 机械振动
5.4 同方向同频率简谐振动的合成
合振动的初相位为 A1 sin 1 A2 sin 2 3 tg A1 cos 1 A2 cos 2 4 初相位在第二象限，解得 或由旋转矢量图易得
x
o 2
A 2
A1
A A1 A2 2
o
T
t
第5章 机械振动
A
5.4 同方向同频率简谐振动的合成
A
A A 2 A1 A2 cos( 2 1 )
2 1 2 2
相位差
2 1
(k 0 ， 1 ， 2 )
相互加强
1）相位差
2k π
5.4 同方向同频率简谐振动的合成
两个同方向同频率简谐振动的合成
x1 A1 cos(t 1 ) x2 A2 cos(t 2 )
A2
2
0
A
x
x
x x1 x2
x A cos(t )
2 1 2 2
x2
1
x1
A1
A A A 2 A1 A2 cos( 2 1 )
3＝ 2k ，k 0,1, 2,
当 3 1＝ (2k 1)，k 0,1, 2, 时，即 x1 与 x3 相 位相反时，合振动的振幅最小，由于 1 ，故 3＝ (2k 1) ，k 0,1, 2,
即
3＝ 2k，k 0,1, 2,
4 5
同方向同频率简谐振动合成问题求解方法的研究
电子技术与软件工程Electronic Technology & Software Engineering电子技术Electronic Technology 同方向同频率简谐振动合成问题求解方法的研究贾冬梅（中北大学信息商务学院山西省晋中市030600 ）摘要：本文分别运用解析法和旋转矢量法来求解两个同方向同频率简谐振动的合成问题并分析总结了它们冬自的特点.通过对比发 现：运用旋转矢量法比解析法更为直观有效，它可以生免去对物理公式的记忆和复杂的数学计算.但是在一般情形下，运用解析法求解更为有效.对于合振动初相位的确定，运用旋转矢量法比解析法更加直观、有效和便捷.关键词：振动合成；解析法；旋转矢量法；振幅；初相简谐振动是机械振动中最简单、最基本的振动形式，任何复杂 的振动都可以看作是简谐振动的合成旳。
而同方向同频率的简谐振 动的合成又是简谐振动的合成中最简单最重要的形式，它为波干涉 和衍射现象的分析奠定了理论基础，因此研究同方向同频率简谐振 动的合成有着十分重要的意义。
寻求一种高效便捷的求解简谐振动 合振动的振动的方法成为了解决同方向同频率简谐振动的合成的关 键3」。
对于同方向同频率简谐振动的合成问题，大学物理教材中 常使用旋转矢量法和解析法来进行讨论分析‘网。
下面分别运用解 析法和旋转矢量法来求解同方向同频率简谐振动合成问题，分析总 结它们各自的特点，为这类问题的分析和求解提供一些参考和借鉴。
1两个同方向同频率简谐振动的合成设两个简谐振动都沿着x 轴方向振动，平衡位置都为坐标原点， 它们振动的角频率3,振幅分别为A]和A2，初相分别为®和％， 它们的振动方程分别为：x,=A| cos （（ot+（p]） x 2=A 2 cos （（ot+（p 2）求这两个解析振动的合振动。
1. 1解析法由于两个简谐振动都沿着X 轴方向振动，所以这两个简谐振动在任一时刻合振动的位移也应在X 轴方向上，且合振动的位移X 等 于这两个分振动位移的代数和，即：X=X]+x 2将分振动的方程X1和X2代入上式展开整理：x = x }+x 2= A } COS （＜zX + % ） + 厦2 COS （m + 02 ）=4 cos （p 、cos - /1] sin （p } cos cotA 2 cos （p 2 cos cot- A 2s\n （p 2 sin cut=（A, cos （p 、+ A 2 cos %） cos cot sin （p 、4- A 2 sin （p 2） sin cot 令 A cos （p=A] cos （p]+A 2 cos （p 2 A sin （p=A 1 sin （P]+A 2 sin （p 2 得至lj x=A cos （p coscot-A sin （p sin （ot=A cos （（ot+（p ）这一结果表明：两个同方向同频率简谐振动的合振动依旧是一 个简谐振动，且合振动的频率与分振动的频率相同都等于3,合振 动的振幅和初相可以表示为：A = J （/sin 0）2 +（/cos （p ）2=J A ： + / j + 2A t A 2 cos （02 - ％）川 sin 0 _ A x sin ® + A 2 sin （p 2t a n （p =------—-------------------A cos （p A x cos （p 、+ A 2 cos （p 21.2旋转矢量法如图1所示，4和力2分别为两个分振动的旋转矢量，它们以相 同的角速度绕o 点做逆时针转动，t=Os 时它们与x 轴正向的夹角分 别为卩和①。
谐振动分析(三)两个同方向同频率简谐运动的合成
x A cos( p t )
A
f (02 p2 )2 4 2p2
t
dA 0 d p
x A0 e
cos(t ) A cos( p t )
28
物理学
第五版
谐运动分析(三)
共振频率
r | 2 |
2 0 2
A
共振频率 小阻尼 阻尼 0
3
物理学
第五版
谐运动分析(三)
（2）相位差 2 1 (2k 1) π (k 0 ， 1, )
x
A1
x
2
o
o
T
t
x ( A2 A1 ) cos( t ) A A1 A2 2 1 (2k 1)π
4
A
A2
物理学
第五版
物理学
第五版
谐运动分析(三)
两个同方向同频率简谐运动的合成
设一质点同时参与 两独立的同方向、同频 率的简谐振动：
A2
2
O
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
x2
1
x1
A1
x
两振动的位相差 2 1 =常数
1
物理学
第五版
5
解 （2） 有阻尼时 A' Ae t ln( 1 ) 0 . 9 t t 174 s 3 min 0.9 A Ae 1
1
E 0.9E, t ? （ 3）
E ' A ' （ 3） ( ) 2 e 2t E A 1 ) ln( 2t 0.9 87 s 1.5 min 0.9 e t2 2
A
f (02 p2 )2 4 2p2
t
dA 0 d p
x A0 e
cos(t ) A cos( p t )
28
物理学
第五版
谐运动分析(三)
共振频率
r | 2 |
2 0 2
A
共振频率 小阻尼 阻尼 0
3
物理学
第五版
谐运动分析(三)
（2）相位差 2 1 (2k 1) π (k 0 ， 1, )
x
A1
x
2
o
o
T
t
x ( A2 A1 ) cos( t ) A A1 A2 2 1 (2k 1)π
4
A
A2
物理学
第五版
物理学
第五版
谐运动分析(三)
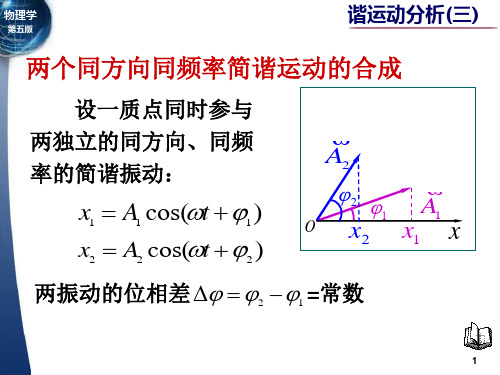
两个同方向同频率简谐运动的合成
设一质点同时参与 两独立的同方向、同频 率的简谐振动：
A2
2
O
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
x2
1
x1
A1
x
两振动的位相差 2 1 =常数
1
物理学
第五版
5
解 （2） 有阻尼时 A' Ae t ln( 1 ) 0 . 9 t t 174 s 3 min 0.9 A Ae 1
1
E 0.9E, t ? （ 3）
E ' A ' （ 3） ( ) 2 e 2t E A 1 ) ln( 2t 0.9 87 s 1.5 min 0.9 e t2 2
简谐振动的合成
x1 (t ) = a cosωt x2 (t ) = a cos(ωt + δ ) x3 (t ) = a cos(ωt + 2δ )
C
Nδ
R
A
aN
⋮ x N ( t ) = a cos[ ω t + ( N − 1)δ ]
O
δ
a3
a1 P
在∆COM中：A = 2 R sin( N δ / 2 ) 中 上两式相除得： 上两式相除得： 在∆OCP中： a = 2R sin(δ / 2) 中
2
A2 y= x 为直线方程 A1
利用旋转矢量合成
∆ϕ = 0
2 1
y
8 7 6
4 4
y
1 2
3
3 7 6
4Байду номын сангаас
8
x
5
5 3
2 1
播 放 动 画
16
5 6 7
x
8
2. |ϕ 2
− ϕ1 | π =
2 2
反相位
y
x y 2xy =0 + + A1 A2 A1 A2
3
利用旋转矢量法求合振动也可得到相同的结果。 •利用旋转矢量法求合振动也可得到相同的结果。 取质点振动的平衡位置O为 取质点振动的平衡位置 为 坐标原点，振动方向沿OX轴。A 坐标原点，振动方向沿 轴 2 点作两个长度分别为A 从O点作两个长度分别为 1、 点作两个长度分别为 ϕ2 ϕ A2的矢量 A1 , A2 ，它们在 它们在t=0时 时 与X轴的夹角分别为ϕ1、ϕ2。 轴的夹角分别为ϕ 轴的夹角分别为
x1 = 4 cos 3t ,
= A cos(3t + ϕ )
振动合成与分解
从数学上讲 任何形式的周期函数都可通过付里叶级数分解 成一系列不同频率、不同振幅的谐振动之和； 成一系列不同频率、不同振幅的谐振动之和；而非 周期振动可通过傅里叶积分把它展成无数个频率连 续分布的谐振动。 续分布的谐振动。 将任一周期性振动 x(t +T) = x(t) 按付立叶级数展开 a0 ∞ x (t ) = + ∑ (an cos nω t + bn sin nω t ) 2 n=1 2 π 若周期振动的频率为： 若周期振动的频率为：ν ω =2 = πν T 则各分振动的频率为:ν、2ν、3ν、… 则各分振动的频率为: （基频 , 二次谐频 , 三次谐频 , …） ） 由于所包含的频率取分立值，这类频谱称为离散谱。 由于所包含的频率取分立值，这类频谱称为离散谱。
二. 同方向不同频率简谐振动的合成 分振动 合振动
x2 = Acos(ω2t +ϕ2)
x = x + x2 1
1 1 x = 2 A cos [(ω 2 − ω1 )t + (ϕ 2 − ϕ1 )] ⋅ cos [(ω 2 + ω1 )t + (ϕ 2 + ϕ1 )] 2 2
x = Acos(ω t +ϕ1) 1 1
图(a) 中实线所代表的周期性振动可分解为基频 倍频的两个简谐振动的叠加。 和3倍频的两个简谐振动的叠加。 倍频的两个简谐振动的叠加 而图(b)则是一种“方波”振动信号， 而图 则是一种“方波”振动信号，它所包含 则是一种 的简谐振动成分就多了。 的简谐振动成分就多了。 这里用竖直线段在横坐标上的位置代表所包含 简谐振动的频率，竖直线高度代表所对应振幅， 简谐振动的频率，竖直线高度代表所对应振幅，该 称为振动频谱 图(c)称为振动频谱。 称为振动频谱。
同方向、不同频率的简谐振动的合成
合振幅 Acos cost Asin sin t
的仍 简然 谐是 振同 动频 。率
Acos(t )
3
式中：
A A12 A22 2A1A2 cos(2 1)
arctg A1 sin1 A2 sin2 A1 cos1 A2 cos2
可见：
2 1 2k
k 0,1,2,
A A1 A2
2Acos (2 1）t cos[ (2 1)t ]
2
2
当1与2 都很大，且相差甚微时，可将
| 2Acos(2 1)t / 2 | 视为振幅变化部分，
合成振动是以 (2 1) / 2 为角频率的谐振动。
其振幅变化的周期是由振幅绝对值变化来决定， 即振动忽强忽弱，所以它是近似的谐振动.
这种合振动忽强忽弱的现象称为拍。 10
arctg A1 sin 1 A2 sin 2
讨论一：
A1 cos1 A2 cos2
2 1 2k k 0,1,2,
A A1 A2 合振幅最大。
当 A1 A2 称为干涉相长。
A A2
A 2A1
A1
6
讨论二：
2 1 (2k 1)
k 0,1,2,
A2
A | A1 A2 |
A
1动、的2相位1 差0在视缓为慢同地频变率化的，合所成以，质不点过运两动个的振轨
道将不断地从下图所示图形依次的循环变化。
当 0 2 1 时是顺时针转；
sin(
20
10 )
x2 A12
y2 A22
2 xy A1 A2
cos
sin2
上式是个椭圆方程，具体形状由
(20 10) 相位差决定。
质点的运动方向与 有关。当 0 时，
的仍 简然 谐是 振同 动频 。率
Acos(t )
3
式中：
A A12 A22 2A1A2 cos(2 1)
arctg A1 sin1 A2 sin2 A1 cos1 A2 cos2
可见：
2 1 2k
k 0,1,2,
A A1 A2
2Acos (2 1）t cos[ (2 1)t ]
2
2
当1与2 都很大，且相差甚微时，可将
| 2Acos(2 1)t / 2 | 视为振幅变化部分，
合成振动是以 (2 1) / 2 为角频率的谐振动。
其振幅变化的周期是由振幅绝对值变化来决定， 即振动忽强忽弱，所以它是近似的谐振动.
这种合振动忽强忽弱的现象称为拍。 10
arctg A1 sin 1 A2 sin 2
讨论一：
A1 cos1 A2 cos2
2 1 2k k 0,1,2,
A A1 A2 合振幅最大。
当 A1 A2 称为干涉相长。
A A2
A 2A1
A1
6
讨论二：
2 1 (2k 1)
k 0,1,2,
A2
A | A1 A2 |
A
1动、的2相位1 差0在视缓为慢同地频变率化的，合所成以，质不点过运两动个的振轨
道将不断地从下图所示图形依次的循环变化。
当 0 2 1 时是顺时针转；
sin(
20
10 )
x2 A12
y2 A22
2 xy A1 A2
cos
sin2
上式是个椭圆方程，具体形状由
(20 10) 相位差决定。
质点的运动方向与 有关。当 0 时，
简谐振动的合成
(A1 sin1 A2 sin2 )sint
合振幅
令： A1 cos1 A2 cos2 Acos 代入上式：
A1 sin1 A2 sin2 Asin
2
x ( A1 cos1 A2 cos2)cost (A1 sin1 A2 sin2 )sint
Acos cost Asin sint Acos(t ) x Acos(t )
x1(t) a cost
M aN
x2 (t) a cos(t ) x3(t) a cos(t 2 )
C
R N
A
a3
xN (t) a cos[t (N 1) ]O a1 P
在COM中：A 2R sin(N / 2)
上两式相除得：
在OCP中： a 2Rsin( / 2)
7
A a sin(N / 2) sin / 2
若 A1 A2, A 2A1
2.当 2 1 （2k 1） (k 0,1,2, ) 时,
A
A12
A
2 2
2 A1
A2
cos(
2
1
)
| A1 A2 | 合振动振幅最小。
若 A1 A2, A 0
A2
3.一般情况 | A1 A2 | A | A1 A2 |
5
A A2 A1
A2 A A1 A A1
第二节
简谐振动的合成
1
一、同方向同频率简谐振动的合成
在同一直线上同频率的两个简谐振
动分别为：
x1 A1 cos(t 1),
x2 A2 cos( t 2 )
• 代数方法： 振动合成
x x1 x2 A1 cos(t 1) A2 cos(t 2 )
(A1 cos1 A2 cos2) cost
《大学物理》同方向的简谐振动的合成
同方向的简谐振动的合成
§10-5 同方向的简谐振动的合成
1.同方向同频率的两个简谐振动的合成
设一质点同时参与沿同一方向的两个独立的 同频率的简谐振动，两个简谐振动的频率为 ω，
振动方向为 X 轴方向，以 x1和 x2 分别代表同一
个质点的两个运动位移：
x1 A1 cos(t 10) x2 A2 cos(t 20)
解：已知 A = 20 cm
A1 = 17.3 cm A2 =[A2 +A12 -2AA1cos( - １)]1/2
= 10 cm
o
A
A2
１ A1 x
∵A2 = A12 + A22 + 2A1A2 cos ( 1 - 2 ) ∴ cos (1 - 2 ) = [A2 - A12 - A22] / 2A1A2
同相迭加，合振幅最大。
(2)当D 2010(2k+1) (k=0及 正负整数), cos(20-10)=0, 有
O
A1
A A1 A2 A A1 A2
A2
O
X
反相迭加，合振幅最小。 当A1=A2 时，A=0。
(3)通常情况下，合振幅介于 和
之间。
A1 A2 A1 A2
补例1两个同方向同频率的简谐振动，其合 振动的振幅为 20 cm，与第一个简谐振动的 相位差为 - １= π/6，若第一个简谐动的振 幅为 17.3 cm，试求： 1、第二个简谐振动的振幅 A2 2、第一、二两个简谐振动的相位差 1 - 2
旋转矢量图示法
矢量沿X 轴之投影表征了合运动的规律。
A1
10
X
O
x2
x x1
A
同方向同频率的两个简谐振动的合成
§10-5 同方向的简谐振动的合成
1.同方向同频率的两个简谐振动的合成
设一质点同时参与沿同一方向的两个独立的 同频率的简谐振动，两个简谐振动的频率为 ω，
振动方向为 X 轴方向，以 x1和 x2 分别代表同一
个质点的两个运动位移：
x1 A1 cos(t 10) x2 A2 cos(t 20)
解：已知 A = 20 cm
A1 = 17.3 cm A2 =[A2 +A12 -2AA1cos( - １)]1/2
= 10 cm
o
A
A2
１ A1 x
∵A2 = A12 + A22 + 2A1A2 cos ( 1 - 2 ) ∴ cos (1 - 2 ) = [A2 - A12 - A22] / 2A1A2
同相迭加，合振幅最大。
(2)当D 2010(2k+1) (k=0及 正负整数), cos(20-10)=0, 有
O
A1
A A1 A2 A A1 A2
A2
O
X
反相迭加，合振幅最小。 当A1=A2 时，A=0。
(3)通常情况下，合振幅介于 和
之间。
A1 A2 A1 A2
补例1两个同方向同频率的简谐振动，其合 振动的振幅为 20 cm，与第一个简谐振动的 相位差为 - １= π/6，若第一个简谐动的振 幅为 17.3 cm，试求： 1、第二个简谐振动的振幅 A2 2、第一、二两个简谐振动的相位差 1 - 2
旋转矢量图示法
矢量沿X 轴之投影表征了合运动的规律。
A1
10
X
O
x2
x x1
A
同方向同频率的两个简谐振动的合成
5-3 、 5-4 简谐振动的合成
ϕ
A2
x
O C A1
N −1 ∆ϕ ϕ = 合振动表达式 2 x ( t ) = A cos( ω t + ϕ ) sin(N∆ϕ / 2) N −1 = A0 cos(ω t + ∆ϕ ) sin(∆ϕ / 2) 2
讨论1： 讨论 ： 当 δ
= ±2kπ k = 0,1,2,L sin(N∆ϕ / 2) A = lim A0 = NA0 sin(∆ϕ / 2)
四、两个相互垂直的同频率简谐振动的合成
某质点同时参与两个同频率的互相垂直方向的简谐运动
x = A1 cos(ω t + ϕ 1 ) y = A2 cos(ω t + ϕ 2 )
合振动的轨迹方程为
x y 2 xy 2 cos(ϕ 2 − ϕ 1 ) = sin (ϕ 2 − ϕ 1 ) + 2− 2 A1 A2 A1 A2
'
各分振动矢量依次相接， 各分振动矢量依次相接，构 成闭合的正多边形， 成闭合的正多边形，合振动 的振幅为零。 的振幅为零。
三、同方向不同频率的简谐振动的合成
某质点同时参与两个不同频率且在同一条直线上的简谐振动
x1 = A1 cos(ω 1 t + ϕ 1 )
x 2 = A2 cos(ω 2 t + ϕ 2 )
A2 y=− x A1
y
x2 y2 2 xy + 2+ =0 2 A1 A2 A1 A2
x
合振动的轨迹是一条通过原点的直线
讨论3 讨论
∆ϕ = ϕ 2 − ϕ 1 = π / 2 x2 y2 合振动的轨迹是的椭圆 合振动的轨迹是的椭圆 + 2 =1 2 A1 A2 方程， 方程，且顺时针旋转
8.5 简谐运动的合成
ν 2 ν 1
2
t ) cos( 2 π
ν 2 +ν 1
2
t +)
振幅部分 振动频率 振幅
合振动频率
ν = (ν 1 + ν 2 ) 2
A = 2 A1 cos 2π
ν 2 ν 1
2
t
Amax = 2A1
Amin = 0
振幅是随时间变化的， 振幅是随时间变化的，由于振幅的改变也是周期 性的，因此就出现振动忽强忽弱的现象。 性的，因此就出现振动忽强忽弱的现象。
y A2
A2 y= x A1
o
A1
x
x 2 y 2 2 xy + 2 cos( 2 1 ) = sin 2 ( 2 1 ) 2 A1 A2 A1 A2
2） 2 1 = π
3） 2 1 = ± π 2
2 2
A2 y= x A1
o
y
A2
x y + 2 =1 2 A1 A2
π y = A2 cos(ωt + ) 2
合成振动为： 合成振动为： x = x1 + x2 = A1 cos(ω1t + ) + A2 cos(ω 2 t + ) 利用三角函数公式可得
x = 2 A cos(
ω2 ω1
2
t ) cos(
ω2 + ω1
2
t +)
= 2 A cos( 2 π
ν 2 ν 1
2
t ) cos( 2 π
ν 2 +ν 1
两个同方向不同频率简谐运动的合成
频率相近的两个同方向简谐振动的合振动是振幅随 频率相近的两个同方向简谐振动的合振动是振幅随 相近的两个同方向简谐振动的合振动是 时间周期性变化的特殊简谐振动 称为拍振动 的特殊简谐振动， 拍振动。 时间周期性变化的特殊简谐振动，称为拍振动。 单位时间内振动加强或减弱的周期数叫拍频。 单位时间内振动加强或减弱的周期数叫拍频。 拍频 由
简谐运动的合成与分解
m
(
2 0
2
)2
4
2
2
共振
A
（1）位移共振（图1）
在一定条件下，振幅出现极大值，振动 剧烈的现象。
共振
2 0
2
2
（2）速度共振（图2）
0
一定条件下，速度幅A极大的现象。
vm
共振 0
即速度共振时，速度与策动力同相，一周期内策动力
总作正功，此时向系统输入的能量最大。
0
总结：
两个同方向频率相同的简谐振动的合成仍为简谐振动。 合振幅与两振动的相位差有关，可用旋转矢量图求得。
如果两振动的频率相差较大但有简单的整数比五谐振分析和频谱在自然界和工程技术中我们所遇到的振动大多不是简谐振动而是复杂的振动处理这类问题往往把复杂振动看成由一系列不同频率的间谐振动组合而成也就是把复杂振动分解为一系列不同频率的间谐振动这样分解在数学上的依据是傅立叶
本讲主要内容： 一、同方向同频率两个简谐振动的合成 二、同方向不同频率两个简谐振动的合成 三、两个互相垂直同频率简谐振动的合成 四、两个互相垂直不同频率简谐振动的合成 五、谐振分析和频谱
A1 sin10 A2 sin20 A1 cos10 A2 cos20
2010
x20
0
x10
AM
A1
x0
t o .P x
同方向同频率两个简谐振动的合成仍为简谐振动。
讨论两个特例 x
(1)两个振动同相
20 10 2k , k 0,1,2,...
合成振动
由 A A12 A22 2A1 A2 cos(20 10 ) o
解：
A A1 A2
A2
A1 A2 A
O
2
三角函数法对同方向同频率简谐振动合成的求解
三角函数法对同方向同频率简谐振动合成的求解简谐振动是物理学中常见的一种运动形式，它具有周期性、振幅相等、频率相同的特点。
在一些物理问题中，我们需要对多个同方向、同频率的简谐振动进行合成，以求得其合成振动后的运动规律。
而三角函数法是一种常用的数学方法，可以用来对这种问题进行求解。
本文将介绍三角函数法对同方向同频率简谐振动合成的求解过程，并给出具体的计算方法。
我们来看看什么是同方向同频率的简谐振动。
同方向是指振动的方向相同，即物体在振动过程中只沿着一个方向上做来回运动；同频率是指振动的频率相同，即两个或多个振动的周期都相同。
假设有两个同向同频率的简谐振动分别为x_1(t)=A_1\cos(\omegat+\varphi_1)和x_2(t)=A_2\cos(\omega t+\varphi_2)，其中A_1和A_2分别为振幅，\omega为角频率，\varphi_1和\varphi_2为初始相位。
要求解这两个简谐振动的合成振动，可以使用三角函数法。
三角函数法的基本思想是将两个简谐振动用三角函数表达式表示，然后将它们相加，再利用三角函数的和差化积公式将其合并为一个三角函数，最后根据初相位和振幅的关系求得合成振动的表达式。
下面我们以具体的例子来说明三角函数法对同方向同频率简谐振动合成的求解过程。
假设有两个同向、同频率的简谐振动x_1(t)=3\cos(2t+\frac{\pi}{4})和x_2(t)=4\cos(2t+\frac{\pi}{3})，现在要求解它们的合成振动。
接下来，利用三角函数的和差化积公式将上式合并为一个三角函数。
根据公式\cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}，我们有：x(t)=2\cos(2t+\frac{5\pi}{12})\cos(\frac{\pi}{12})+2\sin(2t+\frac{\pi}{12})\si n(\frac{\pi}{12})根据初相位和振幅的关系，我们可以得到合成振动的最终表达式为x(t)=2\sqrt{7}\cos(2t+\frac{5\pi}{12}+\theta)，其中\theta=\arctan(\frac{1}{\sqrt{7}})。
简谐振动的合成
8.2 简谐振动的合成
一、同方向、同频率谐振动的合成 质点同时参与两个同方向同频率的谐振动:
x1(t) A1 cos(t 1)
A
x2 (t) A2 cos(t 2 )
A2
x x1 x2 Acos(t )
A A12 A22 2A1A2 cos(2 1) 2
tg A1 sin1 A2 sin2
1 2
r A
X
合振动初相位
1 2
两分振动相互加强
A1 X A2
o
x=x1+x2
t
A A12 A22 2A1 A2 cos(2 1 )
若两分振动反相位：
2 1 (2k 1) k 0,1, 2, r
合振幅最小
r A1
A A1 A2 合振动初相位
r 2 A
A2 o
1
X
若A1>A2 1 若A1<A2 2
A1 cos1 A2rcos2
O
1
x2
A1
x1
x
x
结论 ①合矢量 A即为合振动所对应的旋转矢量。
②合振动仍为简谐振动，振动角频率仍为ω。
分析 A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相位：
2 1 2k k 0,1, 2,
合振幅最大
A A1 A2
o
r
A2
r
A1
4
求合振动的振动方程。
解：
2
T
20
x(cm) 5
x1 x2
A1 A2 5cm
0.1
o 0.05
且 t 时0
-5
r
A2
x10 0, v10 f 0; x20 5cm
一、同方向、同频率谐振动的合成 质点同时参与两个同方向同频率的谐振动:
x1(t) A1 cos(t 1)
A
x2 (t) A2 cos(t 2 )
A2
x x1 x2 Acos(t )
A A12 A22 2A1A2 cos(2 1) 2
tg A1 sin1 A2 sin2
1 2
r A
X
合振动初相位
1 2
两分振动相互加强
A1 X A2
o
x=x1+x2
t
A A12 A22 2A1 A2 cos(2 1 )
若两分振动反相位：
2 1 (2k 1) k 0,1, 2, r
合振幅最小
r A1
A A1 A2 合振动初相位
r 2 A
A2 o
1
X
若A1>A2 1 若A1<A2 2
A1 cos1 A2rcos2
O
1
x2
A1
x1
x
x
结论 ①合矢量 A即为合振动所对应的旋转矢量。
②合振动仍为简谐振动，振动角频率仍为ω。
分析 A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相位：
2 1 2k k 0,1, 2,
合振幅最大
A A1 A2
o
r
A2
r
A1
4
求合振动的振动方程。
解：
2
T
20
x(cm) 5
x1 x2
A1 A2 5cm
0.1
o 0.05
且 t 时0
-5
r
A2
x10 0, v10 f 0; x20 5cm
16-2简谐运动的合成
ϕ
v a2
a4 v a3 α
Q
α
2
α
x
Nα sin 2 ∴A= a α sin 2
16 – 2
简谐运动的合成
v M
1 1 Q∠ M = (π − Nα)， CO = (π −α) CO ∠ P 2 2
v a5
α
N −1 ∴ = ∠ P −∠ M = ϕ α CO CO 2
C
α
N α v α
所以合振动为
2π 2π ω= = = π s -1 T 2 -π ϕ= 2 )m
由旋转矢量图可知合振动的振幅及初相分别为
A = A2 − A1 = 0.08 − 0.04 = 0.04 m） （
所以合振动为
x = 0 . 04 cos( πt −
π 2
16 – 2 简谐运动的合成 二、N 二、N 个同方向同频率简谐运动的合成
简谐运动的合成
3．分振动方程分别为 x1 = 3 cos(50πt + 0.25π ) ． ) 制 和 x 2 = 4 cos(50πt + 0.75π （SI制） 则它们的合振动表达式为： 则它们的合振动表达式为： （ ） （A）x = 2 cos(50πt + 0.25π ) ） （B） x = 5 cos(50πt ) ） （C） = 5 cos(50πt + ） x （D） x ）
v A 2
ϕ2
0
ω
v A
xx
x = x1 + x2 x = A cos( ω t + ϕ )
2 1 2 2
ϕ1 x2 x1
ϕ
v A 1
A = A + A + 2 A1 A2 cos(ϕ 2 − ϕ1 ) A1 sin ϕ 1 + A2 sin ϕ 2 tan ϕ = A1 cos ϕ 1 + A2 cos ϕ 2
同方向的简谐振动的合成
旋转矢量图示法
A A 2A 1
2A
02
A 1
O
1
01
2
x
x
x
X
A 矢量沿X 轴之投影表征了合运动的规律。
同方向同频率的两个简谐振动的合成
讨论： (1) 当 D 20102kp (k=0 及 正 负整数)，cos(20-10)=1, 有
2A
A A 2A 1
O
1A
X
同相迭加，合振幅最大。 (2) 当 D 2010(2k+1)p (k=0 及 正负整数), cos(20-10)=0, 有
2
1A
A 1A A
O
2A
X
反相迭加，合振幅最小。 当A1=A2 时，A=0。
(3)通常情况下，合振幅介于 2A 1A 和 2A 1A 之间。
两个简谐振动合成得：
x = x 1+ x 2
x 2 A cos(
2 1
2
t ) cos(
2 1
2
t 0 )
同方向不同频率的两个简谐振动的合成
拍
因1
~ 2 , 2 1 1 或 2 , 有
2 1
1 2
2 在两个简谐振动的位移合成表达式中，第一项随时 间作缓慢变化, 第二项是角频率近于 1或 的简谐函 2 2 数。合振动可视为是角频率为 (1 2 )、振幅为 2 A cos ( 2 1 )t 2 的简谐振动。
同方向同频率的两个简谐振动的合成
例15-4 N个同方向、同频率的简谐振动，它们的振幅相等， 初相分别为0, a, 2a, ..., 依次差一个恒量a，振动表达式可 写成 t soc a x
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
合振动的振幅随时间作缓慢的周期性的变化， 合振动的振幅随时间作缓慢的周期性的变化，振 动出现时强时弱的拍现象 拍现象。 动出现时强时弱的拍现象。 拍频:单位时间内强弱变化的次数。 拍频:单位时间内强弱变化的次数。 ω2 − ω1 γ= = γ 2 − γ1 2π
同方向不同频率的两个简谐振动的合成 拍
同方向同频率的两个简谐振动的合成
C
r A
O
r a1
r r a3 α a2
α
r a4 α
rα a5
M
X
因各个振动的振幅相同且相差依次恒为 α ，上图 为圆心的圆周上， 中各个矢量的起点和终点都在以 C为圆心的圆周上， 为圆心的圆周上 根据简单的几何关系， 根据简单的几何关系，可得
∠OCM = Nα
同方向同频率的两个简谐振动的合成
x1
t
x2
t
x
t
同方向不同频率的两个简谐振动的合成 拍
反相迭加，合振幅最小。 反相迭加，合振幅最小 当A1=A2 时，A=0。 。 (3)通常情况下，合振幅介于 通常情况下， 通常情况下 和 之间。 之间。
同方向同频率的两个简谐振动的合成
个同方向、同频率的简谐振动，它们的振幅相等， 例15-4 N个同方向、同频率的简谐振动，它们的振幅相等， 15初相分别为0, , 2a, 依次差一个恒量a， 初相分别为0, a, 2 , ..., 依次差一个恒量 ，振动表达式可 写成
求它们的合振动的振幅和初相。 求它们的合振动的振幅和初相。
采用旋转矢量法可使问题得到简化， 解:采用旋转矢量法可使问题得到简化，从而避开 烦琐的三角函数运算。 烦琐的三角函数运算。 根据矢量合成法则， 个简谐振动对应的旋转矢 根据矢量合成法则，N个简谐振动对应的旋转矢 量的合成如下图所示： 量的合成如下图所示：
在三角形∆ 在三角形 OCM中,OM 的长度就是和振动位移矢 量的位移, 就是和振动的初相， 量的位移,角度 ∠MOX 就是和振动的初相，据此得
Nα A = 2OCsin 2
考虑到 a = 2OCsin
α
Nα α A = asin sin 2 2 φ = ∠MOX = ∠COX − ∠COM 1 1 N −1 = (π −α) − (π − Nα) = α 2 2 2 同相合成) 当 α = 0 时(同相合成)，有 A = Na, φ = 0 。
合位移： x = x1 + x2 = Acos(ωt + φ0 ) 合位移：
2 A = A2 + A2 + 2A A2 cos(φ20 − φ10 ) 1 1
合振动仍然是简谐振动，其方向和频率与原来相同。 合振动仍然是简谐振动，其方向和频率与原来相同。
同方向同频率的两个简谐振动的合成
ቤተ መጻሕፍቲ ባይዱ
同方向同频率的两个简谐振动的合成
两个简谐振动合成得： 两个简谐振动合成得：
x = x 1+ x 2
x = 2Acos(
ω2 − ω1
2
t)⋅ cos(
ω2 + ω1
2
t + φ0 )
同方向不同频率的两个简谐振动的合成 拍
因ω1
~ ω2 , ω2 − ω1 << ω1 或 ω2 , 有
ω2 + ω1
≈ ω1 ≈ ω2
2 在两个简谐振动的位移合成表达式中， 在两个简谐振动的位移合成表达式中，第一项随时 间作缓慢变化, 间作缓慢变化, 第二项是角频率近于 ω1或ω2 的简谐函 数。合振动可视为是角频率为 (ω1 + ω2 ) 2 、振幅为 2Acos (ω2 − ω1)t 2 的简谐振动。 的简谐振动。
§15-5 同方向的简谐振动的合成
1.同方向同频率的两个简谐振动的合成
设一质点同时参与沿同一方向(x轴 的两个独 设一质点同时参与沿同一方向 轴)的两个独 立的同频率的简谐振动，两个振动位移为： 立的同频率的简谐振动，两个振动位移为：
x1 = A cos(ωt + φ10 ) 1
x2 = A2 cos(ωt + φ20 )
旋转矢量图示法
矢量沿X 轴之投影表征了合运动的规律。 矢量沿 轴之投影表征了合运动的规律。
同方向同频率的两个简谐振动的合成
讨论： 讨论： (1) 当 ∆φ=φ 20−φ10=2kπ (k=0 及 正 负整数)，cos(φ20-φ10)=1, 有 负整数 同相迭加，合振幅最大。 同相迭加，合振幅最大。 (2)当 ∆φ=φ 20−φ10=(2k+1)π (k=0及 当 及 正负整数), 正负整数 cos(φ20-φ10)=0, 有
2
2.同方向不同频率的两个简谐振动的合成 拍
当两个同方向简谐振动的频率不同时， 当两个同方向简谐振动的频率不同时，在旋转矢 量图示法中两个旋转矢量的转动角速度不相同，二者 量图示法中两个旋转矢量的转动角速度不相同， 的相位差与时间有关， 的相位差与时间有关，合矢量的长度和角速度都将随 时间变化。 时间变化。 很接近， 两个简谐振动的频率ω1和 ω 2很接近，且 ω 2 > ω1
同方向不同频率的两个简谐振动的合成 拍
同方向同频率的两个简谐振动的合成
C
r A
O
r a1
r r a3 α a2
α
r a4 α
rα a5
M
X
因各个振动的振幅相同且相差依次恒为 α ，上图 为圆心的圆周上， 中各个矢量的起点和终点都在以 C为圆心的圆周上， 为圆心的圆周上 根据简单的几何关系， 根据简单的几何关系，可得
∠OCM = Nα
同方向同频率的两个简谐振动的合成
x1
t
x2
t
x
t
同方向不同频率的两个简谐振动的合成 拍
反相迭加，合振幅最小。 反相迭加，合振幅最小 当A1=A2 时，A=0。 。 (3)通常情况下，合振幅介于 通常情况下， 通常情况下 和 之间。 之间。
同方向同频率的两个简谐振动的合成
个同方向、同频率的简谐振动，它们的振幅相等， 例15-4 N个同方向、同频率的简谐振动，它们的振幅相等， 15初相分别为0, , 2a, 依次差一个恒量a， 初相分别为0, a, 2 , ..., 依次差一个恒量 ，振动表达式可 写成
求它们的合振动的振幅和初相。 求它们的合振动的振幅和初相。
采用旋转矢量法可使问题得到简化， 解:采用旋转矢量法可使问题得到简化，从而避开 烦琐的三角函数运算。 烦琐的三角函数运算。 根据矢量合成法则， 个简谐振动对应的旋转矢 根据矢量合成法则，N个简谐振动对应的旋转矢 量的合成如下图所示： 量的合成如下图所示：
在三角形∆ 在三角形 OCM中,OM 的长度就是和振动位移矢 量的位移, 就是和振动的初相， 量的位移,角度 ∠MOX 就是和振动的初相，据此得
Nα A = 2OCsin 2
考虑到 a = 2OCsin
α
Nα α A = asin sin 2 2 φ = ∠MOX = ∠COX − ∠COM 1 1 N −1 = (π −α) − (π − Nα) = α 2 2 2 同相合成) 当 α = 0 时(同相合成)，有 A = Na, φ = 0 。
合位移： x = x1 + x2 = Acos(ωt + φ0 ) 合位移：
2 A = A2 + A2 + 2A A2 cos(φ20 − φ10 ) 1 1
合振动仍然是简谐振动，其方向和频率与原来相同。 合振动仍然是简谐振动，其方向和频率与原来相同。
同方向同频率的两个简谐振动的合成
ቤተ መጻሕፍቲ ባይዱ
同方向同频率的两个简谐振动的合成
两个简谐振动合成得： 两个简谐振动合成得：
x = x 1+ x 2
x = 2Acos(
ω2 − ω1
2
t)⋅ cos(
ω2 + ω1
2
t + φ0 )
同方向不同频率的两个简谐振动的合成 拍
因ω1
~ ω2 , ω2 − ω1 << ω1 或 ω2 , 有
ω2 + ω1
≈ ω1 ≈ ω2
2 在两个简谐振动的位移合成表达式中， 在两个简谐振动的位移合成表达式中，第一项随时 间作缓慢变化, 间作缓慢变化, 第二项是角频率近于 ω1或ω2 的简谐函 数。合振动可视为是角频率为 (ω1 + ω2 ) 2 、振幅为 2Acos (ω2 − ω1)t 2 的简谐振动。 的简谐振动。
§15-5 同方向的简谐振动的合成
1.同方向同频率的两个简谐振动的合成
设一质点同时参与沿同一方向(x轴 的两个独 设一质点同时参与沿同一方向 轴)的两个独 立的同频率的简谐振动，两个振动位移为： 立的同频率的简谐振动，两个振动位移为：
x1 = A cos(ωt + φ10 ) 1
x2 = A2 cos(ωt + φ20 )
旋转矢量图示法
矢量沿X 轴之投影表征了合运动的规律。 矢量沿 轴之投影表征了合运动的规律。
同方向同频率的两个简谐振动的合成
讨论： 讨论： (1) 当 ∆φ=φ 20−φ10=2kπ (k=0 及 正 负整数)，cos(φ20-φ10)=1, 有 负整数 同相迭加，合振幅最大。 同相迭加，合振幅最大。 (2)当 ∆φ=φ 20−φ10=(2k+1)π (k=0及 当 及 正负整数), 正负整数 cos(φ20-φ10)=0, 有
2
2.同方向不同频率的两个简谐振动的合成 拍
当两个同方向简谐振动的频率不同时， 当两个同方向简谐振动的频率不同时，在旋转矢 量图示法中两个旋转矢量的转动角速度不相同，二者 量图示法中两个旋转矢量的转动角速度不相同， 的相位差与时间有关， 的相位差与时间有关，合矢量的长度和角速度都将随 时间变化。 时间变化。 很接近， 两个简谐振动的频率ω1和 ω 2很接近，且 ω 2 > ω1