第9章简谐振动的合成
合集下载
简谐振动的合成
x
A1
2
o
A A1 A2
o
相互削弱
A
A2
3）一般情况 A1 A2 A A1 A2
21
2.n个同方向同频率简谐运动的合成
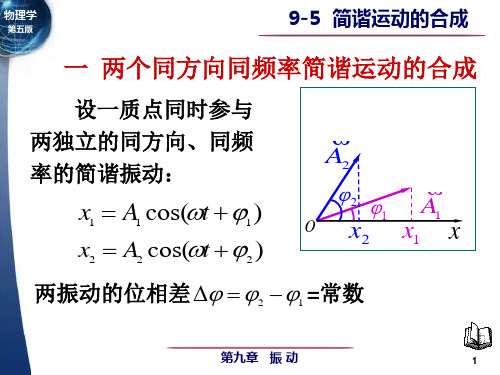
x1 A1 cos(t 1) x2 A2 cos(t 2 )
xn
An
cos(t
n
)
x x1 x2 xn
19
讨论 A A12 A22 2A1A2 cos(2 1) 1）相位差 2 1 2kπ (k 0，1， 2,)
x
o
A1
A2
A
A A1 A2
相互加强
20
A A12 A22 2A1A2 cos(2 1) 2）相位差 2 1 (2k 1)π (k 0，1, )
dt 2
J ml 2
d 2
g
2 g
l 2
dt 2 l
cos(t ) m
g
l
T 2π l g
转
A
动
l
正 向
FT m
O
P
10
复摆
M l F
转动正向
O
M mgl sin J J d2
dt 2
l
*C
24
频率较大而频率之差很小的两个同方 向简谐运动的合成，其合振动的振幅时而 加强时而减弱的现象叫拍.
x1 A1 cos1t A1 cos2π1t x2 A2 cos2t A2 cos2π2t
mgl J d2
dt 2
P
令 2 mgl
大学物理第九章振动学基础
处2向AX轴负方向运动,而 2
试用旋转矢量法求这两个谐振动的初相差。 以及两个质点第一次通过平衡位置的时刻。
解：设两质点的谐振动方程分别为
x1
A cos (2
T
t
10)
20 A
x2
A cos (2
T
t
20)
10
4
20
0
3
4
A
2
1 10
O
X
质点1第一次经过平衡位置的时刻
t (2 / T )t 4
第九章 振动学基础
第九章 振动学基础
9-0 教学基本要求 9-1 简谐振动的规律 9-2 简谐振动的描述 9-3 简谐振动的合成
教学基本要求
一、理解简谐振动的基本特征, 了解研究谐振子模型的意义. *二、能建立一维简谐振动的微分方程, 能根据给定的初始条 件写出一维简谐振动的运动方程, 并理解其物理意义.
O后，仅因回复力(弹性力) 和惯性而自由往返运动.
F kx ma
F弹
x ox
a
d2x dt 2
F
m
k x m
d2x dt 2
k m
x
0
令 2 k
m
有
d2x dt 2
2
x
0
弹簧振子的振动微分方程(动力学方程)
解微分方程得
(1) 位移时间关系(振动方程)
x A cos(t )
(2)速度时间关系
2. 简谐振动的能量有什么特点?
3. 简谐振动的周期由什么因素决定？如何计算一简谐 振动的周期？
4. 研究谐振子模型的意义何在？
一、简谐振动的定义
1.弹簧振子 一个劲度系数为k的轻质弹簧的一端固定，另一端
大学物理 第9章 简谐振动
9.1 简谐振动的定义
9.2 简谐振动的规律 9.3 简谐振动的合成
9.1 简谐振动的定义
9.1.1 弹簧振子的振动
9.1.2 简谐振动的定义
9.1.3 单摆的运动规律
9.1.4 LC振荡回路中电容器 上电量的变化规律
振动是与人类生活和科学技术密切相关的一种 基本运动形式。
广义的振动 一物理量在某一定值附近周期性变化的现象称振动。
下面我们重点对合振动的振幅进行讨论
A A1 A2 2 A1 A2 cos( 2 1 )
2 2
t 2 t 1 2 1
讨论：两种特殊情况
(1) 21=2k (k=0,1,2,…) 两分振动同相
A A1 A 2
o
考虑方向 F mg 简谐振动！
mg
0
F ma mg
t 0
l
又 a
l d
2
dv dt
l
d
2
dt
2
T
F
O
dt
2
g
即
d 2 g 0 2 l dt
d （v l ） dt
mg
g l
2 T 2
2
x
A x A y cos t
2 2
（2）相位差 y x ，轨迹方程为
x Ax y Ay 0
x
2 2
y
2 2
2
xy Ax Ay
cos(
Ax
Ay
y
x ) sin (
2
y
9.2 简谐振动的规律 9.3 简谐振动的合成
9.1 简谐振动的定义
9.1.1 弹簧振子的振动
9.1.2 简谐振动的定义
9.1.3 单摆的运动规律
9.1.4 LC振荡回路中电容器 上电量的变化规律
振动是与人类生活和科学技术密切相关的一种 基本运动形式。
广义的振动 一物理量在某一定值附近周期性变化的现象称振动。
下面我们重点对合振动的振幅进行讨论
A A1 A2 2 A1 A2 cos( 2 1 )
2 2
t 2 t 1 2 1
讨论：两种特殊情况
(1) 21=2k (k=0,1,2,…) 两分振动同相
A A1 A 2
o
考虑方向 F mg 简谐振动！
mg
0
F ma mg
t 0
l
又 a
l d
2
dv dt
l
d
2
dt
2
T
F
O
dt
2
g
即
d 2 g 0 2 l dt
d （v l ） dt
mg
g l
2 T 2
2
x
A x A y cos t
2 2
（2）相位差 y x ，轨迹方程为
x Ax y Ay 0
x
2 2
y
2 2
2
xy Ax Ay
cos(
Ax
Ay
y
x ) sin (
2
y
简谐振动的合成
x1 (t ) = a cosωt x2 (t ) = a cos(ωt + δ ) x3 (t ) = a cos(ωt + 2δ )
C
Nδ
R
A
aN
⋮ x N ( t ) = a cos[ ω t + ( N − 1)δ ]
O
δ
a3
a1 P
在∆COM中：A = 2 R sin( N δ / 2 ) 中 上两式相除得： 上两式相除得： 在∆OCP中： a = 2R sin(δ / 2) 中
2
A2 y= x 为直线方程 A1
利用旋转矢量合成
∆ϕ = 0
2 1
y
8 7 6
4 4
y
1 2
3
3 7 6
4Байду номын сангаас
8
x
5
5 3
2 1
播 放 动 画
16
5 6 7
x
8
2. |ϕ 2
− ϕ1 | π =
2 2
反相位
y
x y 2xy =0 + + A1 A2 A1 A2
3
利用旋转矢量法求合振动也可得到相同的结果。 •利用旋转矢量法求合振动也可得到相同的结果。 取质点振动的平衡位置O为 取质点振动的平衡位置 为 坐标原点，振动方向沿OX轴。A 坐标原点，振动方向沿 轴 2 点作两个长度分别为A 从O点作两个长度分别为 1、 点作两个长度分别为 ϕ2 ϕ A2的矢量 A1 , A2 ，它们在 它们在t=0时 时 与X轴的夹角分别为ϕ1、ϕ2。 轴的夹角分别为ϕ 轴的夹角分别为
x1 = 4 cos 3t ,
= A cos(3t + ϕ )
9-5(新)简谐运动的合成
物理学
第五版
9-5 简谐运动的合成 相互垂直不同频率的简谐振动的合成：李萨如图
链接
第九章
振 动
31
物理学
第五版
本章目录
选择进入下一节：
9-2 旋转矢量 9-3 单摆和复摆 9-4 简谐运动的能量 9-5 简谐运动的合成 9-6 阻尼振动 受迫振动 共振 9-7 电磁振荡
第九章 振 动
32
第九章 振 动
y
A2
A1
o
x
15
物理学
第五版
9-5
简谐运动的合成
2 2 x y 2 xy 讨 2 cos( ) sin ( 2 1 ) 2 1 2 2 论 A1 A2 A1 A2
（3）2 1 π 2
y
A2
x y 2 1 2 A1 A2
2
2
o
A1
2
2
第九章
振 动
14
物理学
第五版
9-5
简谐运动的合成
2 2 x y 2 xy 讨 2 cos( ) sin ( 2 1 ) 2 1 2 2 论 A1 A2 A1 A2
y
2 1 0或 2 π （ 1） A2 y x A1
A2
o
A1
x
2 1 π （ 2） A2 y x A1
x (2 A1 cos 2 π
2 1
2
t ) cos 2 π
2 1
2
t
2 1 2π T π 2
1 T 2 1
拍频（振幅变化的频率）
2 1
第九章
振 动
25
物理学
第五版
简谐振动的合成
π
3 π
0.104sin 5 π 6
0.104cos 5 π
2 3
π
3
6
所以，合振动的运动方程为：
x 0.12 cos π t 2 π 2 3
1.3 两个同方向、不同频率 简谐振动的合成
两个同方向、不同频率简谐振动的合成结果比较复杂，为了
便于理解，设两分振动的振幅和初相相同，则两分振动的运动方
上式表明，当两个分振动反相，即其相位差为π的奇数倍时， 合振动的振幅为两个分振动振幅之差的绝对值，合成结果为两 个振动相互减弱，此时合振幅最小。若两分振动的振幅相等， 则此时合振动振幅为零。
一般情况下，相位差Δφ并不是π的整数倍，此时，合振幅就 介于|A1－A2|和A1＋A2之间。
【例10-5】一质点同时参与两个同方向、同频率的简谐振动 周期都为4s，振幅分别为A1＝0.06m，A2＝0.104m，初相分别为
x＝x1＋x2＝A1cos（ωt＋φ1）＋A2cos（ωt＋φ2） 应用旋转矢量法可以更直观、更简洁的得出合振动的规律。
如下图所示，取坐标轴Ox，画出两个分振动的旋转矢量A1和 A2，它们在Ox轴上的投影x1和x2分别表示两个分振动的位移。根 据平行四边形法则，可作出合矢量A＝A1＋A2，它在Ox轴上的投 影x表示合振动的位移，可以看出，x＝x1＋x2。t＝0时，合矢量A 与Ox轴的夹角为φ。
的频率相近，且有|ω1－ω2|＜＜（ω1＋ω2）时，上式中，
cos 1 2 t 项随时间快速变化，而 cos1 2 t 项随时间缓慢
2
2
变化。因此，可以将此合振动看作是角频率为
1
2
2
1
2，振
幅为 2Acos 1 2 t 的简谐振动。这种振幅时大时小作缓慢周期性
简谐振动的合成
8
合成振动表达式：
x(t ) A cos(1t ) A cos( 2 t )
( 2 1 t ） ( 2 1 )t 2 A cos cos[ ] 2 2
当 1与 2 都很大，且相差甚微时，可将 | 2 A cos( 2 1 )t / 2 |视为振幅变化部分， 合成振动是以 ( 2 1 ) / 2 为角频率的谐振动。
17
2 1 0
2 1
4
2 1
2
3 2 1 4
5 4
3 2
7 4
18
2、如果两个互相垂直的振动频率成整数比，
合成运动的轨道是封闭曲线，运动也具有 周期。这种运动轨迹的图形 称为李萨如图形。 用李萨如图形 在无线电技术 中可以测量频 率：
4
上面得到：
A A12 A22 2 A1 A2 cos( 2 1 )
讨论一：
A1 sin 1 A2 sin 2 arctg A1 cos1 A2 cos 2
k 0,1,2,
合振幅最大。
2 1 2k
A A1 A2
当 A1 A2 称为干涉相长。
2
2 2 0 x 0 令k m 0 x 2 T 0 x(t ) A cos( 0 t 0 )
g 0 g mgl sin 0 2 l l I 为m绕O点转动的转动惯量 O mgh sin I mgh 2 C 0 mgh 0 I I 简谐振动的能量 * 任一简谐振动总能量 mg
x2 y2 2 xy 2 2 cos sin 2 A1 A2 A1 A2
上式是个椭圆方程，具体形状由 ( 20 10 )相位差决定。 质点的运动方向与 有关。当 0 时， 质点沿顺时针方向运动；当 2 时， 质点沿逆时针方向运动。 当 A1 A2 时，正椭圆退化为圆。
合成振动表达式：
x(t ) A cos(1t ) A cos( 2 t )
( 2 1 t ） ( 2 1 )t 2 A cos cos[ ] 2 2
当 1与 2 都很大，且相差甚微时，可将 | 2 A cos( 2 1 )t / 2 |视为振幅变化部分， 合成振动是以 ( 2 1 ) / 2 为角频率的谐振动。
17
2 1 0
2 1
4
2 1
2
3 2 1 4
5 4
3 2
7 4
18
2、如果两个互相垂直的振动频率成整数比，
合成运动的轨道是封闭曲线，运动也具有 周期。这种运动轨迹的图形 称为李萨如图形。 用李萨如图形 在无线电技术 中可以测量频 率：
4
上面得到：
A A12 A22 2 A1 A2 cos( 2 1 )
讨论一：
A1 sin 1 A2 sin 2 arctg A1 cos1 A2 cos 2
k 0,1,2,
合振幅最大。
2 1 2k
A A1 A2
当 A1 A2 称为干涉相长。
2
2 2 0 x 0 令k m 0 x 2 T 0 x(t ) A cos( 0 t 0 )
g 0 g mgl sin 0 2 l l I 为m绕O点转动的转动惯量 O mgh sin I mgh 2 C 0 mgh 0 I I 简谐振动的能量 * 任一简谐振动总能量 mg
x2 y2 2 xy 2 2 cos sin 2 A1 A2 A1 A2
上式是个椭圆方程，具体形状由 ( 20 10 )相位差决定。 质点的运动方向与 有关。当 0 时， 质点沿顺时针方向运动；当 2 时， 质点沿逆时针方向运动。 当 A1 A2 时，正椭圆退化为圆。
高二物理竞赛简谐振动的合成课件
根据x0= A 1 cos1+ A 2 cos2的正负确定反正切函数是否加上
合振动是简谐振动, 其频率仍为
分析
A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相：
2 1 2k k 0,1, 2,
A A1 A2 两分振动相互加强
若两分振动反相:
2 1 (2k 1) k 0,1, 2,
拍频 : 单位时间内强弱变化的次数
=| 2- 1|
(1)在波动的传播过程中，任意时刻的动能和势能不仅大小相等而且相位相同，同时达到最大，同时等于零。
由于振动的相位随距离的增加而落后的关系，与平面波类似，球面简谐波的波函数：
拍频 : 单位时间内强弱变化的次数 在一个周期T内通过S1和S2面的能量应该相等
合振动可看作振幅缓变的简谐振动
=|2-1|
拍 2 1
或：T 2 2 1
t t t
波的能量
波不仅是振动状态的传播，而且也是伴随着振
动能量的传播。
dV
1. 波的能量
o
u x
有一平面简谐波
yAcos[(tx)]
u
在x处取一体积元dV 质量为 dmdV
质点的振动速度 vyA sin[(tx)]
t
u
T 0
T0
u
T
w 1 A22
2
0sin2d 2
2. 波的能流和能流密度
在单位时间内通过一定截面的波动能量为能流
P w u dtS wuS
dt
在一个周期中的平均能流为
1T
PT0Pdt wuS
udt
us
能流密度 通过垂直于波线截面单位面积上的能流。
大小： I dP wu dS
合振动是简谐振动, 其频率仍为
分析
A A12 A22 2A1 A2 cos(2 1 )
若两分振动同相：
2 1 2k k 0,1, 2,
A A1 A2 两分振动相互加强
若两分振动反相:
2 1 (2k 1) k 0,1, 2,
拍频 : 单位时间内强弱变化的次数
=| 2- 1|
(1)在波动的传播过程中，任意时刻的动能和势能不仅大小相等而且相位相同，同时达到最大，同时等于零。
由于振动的相位随距离的增加而落后的关系，与平面波类似，球面简谐波的波函数：
拍频 : 单位时间内强弱变化的次数 在一个周期T内通过S1和S2面的能量应该相等
合振动可看作振幅缓变的简谐振动
=|2-1|
拍 2 1
或：T 2 2 1
t t t
波的能量
波不仅是振动状态的传播，而且也是伴随着振
动能量的传播。
dV
1. 波的能量
o
u x
有一平面简谐波
yAcos[(tx)]
u
在x处取一体积元dV 质量为 dmdV
质点的振动速度 vyA sin[(tx)]
t
u
T 0
T0
u
T
w 1 A22
2
0sin2d 2
2. 波的能流和能流密度
在单位时间内通过一定截面的波动能量为能流
P w u dtS wuS
dt
在一个周期中的平均能流为
1T
PT0Pdt wuS
udt
us
能流密度 通过垂直于波线截面单位面积上的能流。
大小： I dP wu dS
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
临界阻尼：物体不作往复运动的极限。 决定的积分常数。 从周期运动变为非周期振动 。 阻尼装置用于减振或仪器指针调节。 ③ 0 时，阻尼较大（过阻尼），此方程的解：
x (t ) C1e
2 ( 2 0 )t
C2 e
(
2 2 0 )t
无振动发生、非周期运动 x
k 令 m
2 0
2m
d2 x dx 2 2 0 x 0 2 dt dt
固有角频率 0 阻尼因子
k m 由系统本身的性质决定。
2m 由阻力系数决定。
3、 阻尼振动的动力学方程的解： ① 0 时，阻尼较小（欠阻尼）， 此方程的解：
x(t ) Ae t cos(t )
A
A1
x1 A1 cos(t 1 )
x2 A2 cos(t 2 )
合振动的运动方程：
2
o x2 x x1 x2 A cos(t )
2 1 2
1
x1
x
x
A
A A2 2 A1 A2 cos( 2 1 )
A1 sin 1 A2 sin 2 arctg A1 cos 1 A2 cos 2
5.A、B两弹簧的倔强系数分别为kA, kB,其质量均可忽略不计， 今将二弹簧连接起来并竖直悬挂，当系统静止时，而弹簧的弹 性势能EpA与EpB之比
①
E pA
E pA E pB
E pA k B kA E pA k B 2 kA ② 2 ③ ④ E pB k B kB E pB k A E pB k A 2
上式是个椭圆方程，具体形状由 ( 20 10 ) 相位差决定。 质点的运动方向与 有关。当 0 时， 质点沿顺时针方向运动；当 2 时， 质点沿逆时针方向运动。 当 A1 A2 时，正椭圆退化为圆。
2 2
4)
2 1 3 / 2
C1 , C 2 是由初始条件
欠阻尼 临界阻尼 过阻尼
决定的积分常数。
o
t
二、受迫振动： 1、 受迫振动的定义： 系统在周期性外力持续作用下所发生的振动。 策动力： F F0 cost 阻尼力: 弹性力:
v
kx
kx
m
F
x
2、 受迫振动的运动微分方程：
f
d2 x m 2 kx v F0 cos t dt d2 x dx m 2 kx F0 cos t dt dt
( 2 1 )
2k (k 0、 1、 2....)
（ 2k 1 ） (k 0、 1 、 2....)
A t
M
反相:
5、旋转矢量法：
t
o
t0 A p x
§9 - 3 简谐振动的合成 A2 一、同方向同频率谐振动的合成：
A2
2 1
A1 A2 2 A1 A cos( 1 ) 10cm
2
A A2 A
2
2
(10 3) 10 400
2 2
A2
30
20
10 3
A
A2 A1 , 1 2 / 2
A1
二、两个同方向不同频率谐振动的合成：
x1 (t ) A1 cos(1t 1 ) x2 (t ) A2 cos(2t 2 )
§9- 3 阻尼振动、受迫振动和共振
一、阻尼振动： 振幅随时间而减小的振动叫做阻尼振动。 1、阻尼的分类 a、摩擦阻尼：机械能转化为热能。 b、辐射阻尼：能量辐射出去，形成波（音叉、乐器等）。 2、阻尼振动的动力学方程： 实验表明当速度不太大时：
k
x
m o
F
fr
m
p
x
dx 为阻力系数。 粘滞阻力： f r v dt 2 d dx 动力学方程： m x kx 2 dt dt
x2 y2 轨迹： 2 2 1 A1 A2
y 比x 位相滞后/2，椭圆轨道运动的方向时逆时针， 即左旋的。
x A1 cos(t 1 ) y A2 cos(t 1 3 / 2)
3 2
两 相 互 垂 直 同 频 率 不 同 相 位 差
简 谐 运 动 的 合 成 图
合成结果仍为简谐运动 合振动与分振动在同一方向，且有相同频率。
几何方法
Y
A
A2
2
A2 sin 2
A1
1
A2 cos 2
A1 sin 1
X
A1 cos1
A
2 A12 A2 2 A1 A2 cos( 2 1 )
A1 sin 1 A2 sin 2 arctg A1 cos1 A2 cos 2
x y cos 20 cos10 sint sin( 20 10 ) A1 A2
x y sin 20 sin 10 cost sin( 20 10 ) A1 A2
x y 2 xy 2 cos sin 2 2 A1 A2 A1 A2
(2t 2 ) (1t 1 ) (2 1 )t ( 2 1 )
设两振动的振幅相同，初相相同。
x1 (t ) A cos(1t ) x2 (t ) A cos( 2t )
合振动的运动方程为：
x(t ) A cos(1t ) A cos(2t )
E pA
2
2 1 1 mg ( mg ) 2 2 k A (x A ) k A ( ) 2 2 kA 2k A
kA kB
A B
m
E pB
2 1 1 mg ( mg ) k B (x B )2 k B ( )2 2 2 kB 2k B
E pA E pB
kB kA
6.在t=0时，周期为T振幅为A的单摆分别处于图a、b、c三种状 态，若选单摆的平衡位置为x轴的原点，x轴指向右方，则单摆 作小角度摆动的振动表达式（用余弦表示）分别为
复习
1、简谐振动的定义式：
d2 x 2 x0 2 dt
或：
x A cos(t )
2、简谐振动的动力学特征： 物体受力与位移成正比而方向相反。
3、简谐振动的运动学特征：
f kx
k x m
物体的加速度与位移成正比而方向相反。 a
4、描述简谐振动的物理量: ① 振幅A： ② 角频率 ：
• 两振动的频率成整数比时，轨迹称为李萨如图形。
李 萨 如 图
1 0
π π 3π π 2 0, , , , 8 4 8 2
1 m 2 n
测量振动频率 和相位的方法
1.一弹簧振子作谐振动，总能量为E，如果谐振动振幅增加 为原来的两倍，重物的质量增为原来的4倍，则它的总能量 E变为 A: E/4; B: E/2; C: 2E; D: 4E
k F 2 令 0 ; ；h 0 m 2m m
d2 x dx 2 2 0 x h cost 2 dt dt
合振幅出现时大时小的现象 — 拍现象
三、方向垂直、同频率简谐振动的合成 设一个质点同时参与了两个振动方向相互 垂直的同频率简谐振动，即
Perpendicular Direction
x A1 cos(t 10 ); y A2 cos(t 20 ) x cost cos10 sin t sin 10 A1 y cost cos 20 sin t sin 20 A2 解出 sin t cost 并平方后相加可得质点的轨迹方程 x y cos 20 cos10 sin t sin( 20 10 ) A1 A2
反相， 合振幅最小
A | A1 A2 |
A
A2 A1
当A1 = A2 时，质点静止。 3） 一般情况（相位差任意）
2 1 k
A2
A
A1 A2
A A1 A2
A1
相位差在同频率简谐振动合成中起决定性作用
例题：两个同方向同频率的简谐振动，其合振动的振幅其合 振幅为20cm,与第一简谐振动的相位差为φ---φ1=π/6,若第一个简 谐振动的振幅为 10 3cm 17.3cm 则第二个谐振动的振幅为 cm, 。 第一、二两个谐振动的相位差φ2---φ1= 解：由矢量合成法则：
Hale Waihona Puke a : t 0, x0 0, v v0 0, x0 A cos 0,
t a : x A cos(2 ) T 2 t b : x A cos(2 ) T 2 t c : x A cos(2 ) T
v0
v0
v0 0
/ 2,3 / 2, v A sin 0, 3 / 2即 - /2 b : t 0, x0 0, v v0 0, x0 A cos 0, / 2,3 / 2, v A sin 0, / 2
四、两个相互垂直的不同频率简谐振动的合成
x A1 cos(1t 1 ) y A2 cos(2t 2 )
一般情况下，合振动轨道不是封闭曲线，但当频率有简 单的整数比关系时，形成稳定的封闭曲线，称为李萨如图 形（P246）。
x A1 cos(1t 1 ) y A2 cos( 2t 2 )
式中：
2 0 2
x
A0e t cos(t )
A0e t
o
t
欠阻尼特点：
振幅随时间 t 作指数衰减。 近似为简谐振动。 阻尼振动周期比系统的固有周期长。