第八章 扭转问题
工程力学第四版电子课件gclx8最新

1 A B
2 C
3 n D
T2 = −m2 − m3 = −(4.78 + 4.78) = −9.56kN⋅ m
10
③绘制扭矩图 Draw the torque diagram
T max = 9.56 kN ⋅ m
BC段为危险截面。 段为危险截面。 段为危险截面 Section BC is dangerous section .
目 的
①确定扭矩变化规律 To determine the rule of change of the torque |T| max 截面 的确定
purposes
To determine the location of dangerous section
8
[例1]已知:一传动轴, n =300r/min,主动轮输入 P1=500kW,从动轮输出 P2=150kW, 例 已知 一传动轴, 已知: , , , P3=150kW,P4=200kW,试绘制扭矩图。 , ,试绘制扭矩图。 Example 1 The transmission shaft is shown as Fig.the input power of driver wheel C is 500KW The export powers of driven wheel A,Band D are 150KW,150KW,200KW.To draw the torque diagram of the transmission shaft .
3
8–1 扭转的概念及外力偶矩的计算
Concepts of torsion and how to calculate the external couple moment 轴:工程中以扭转为主要变形的构件。如:机器中的传动轴、钻杆等。 工程中以扭转为主要变形的构件。 机器中的传动轴、钻杆等。 Shaft :the members create torsion deformation due to subjected to the external moments.such as the transmission shafts and drill pipes of the machines . 扭转的外力特点:外力的合力为一力偶, 扭转的外力特点:外力的合力为一力偶,且力偶的作用面与直杆的轴线 垂直。 垂直。 external forces:Two couples that have the same magnitude moment, the opposite direction and the plane of couples perpendicular to the axial line 变形特点: 变形特点:各横截面绕轴线发生相对转动 The deformation is that the external loads tend to twist one segment of the body with respect to the other
工程力学第八章圆轴的扭转详解

轴AB间的相对扭转角为:AB=TL/GIP
单位长度的扭转角为:q =AB/L=T/GIP
扭转刚度条件则为: qmax[q ] ---许用扭转角 机械设计手册建议:[q ]=0.25~0.5/m; 精度高的轴;
[q ]=0.5~1.0/m; 一般传动轴。
整理课件
32
3.扭转圆轴的设计
强度条件: t max T /WT [t ]
Mo
Mo
假想切面
取左边部分
Mo
外力偶
T 内力偶
由平衡方程: T M o 整理课件
平衡
4
返回主目录
Mo
Mo
T
取左边部分
Mo 假想切面
外力偶
扭矩
由平衡方程:
平衡
Mo
TMo T
取右边部分 T
T 和T 是同一截面上的内力, 应当有相同的大小和正负。
整理课件
扭矩
外力偶
平衡
5
扭矩的符号规定:
Mo
T
正
Mo
T
1)已知二轴长度及所受外力矩完全相同。若二轴截 面尺寸不同,其扭矩图相同否? 相同 若二轴材料不同、截面尺寸相同, 各段应力是否相同?相同 变形是否相同? 不同
2)下列圆轴扭转的切应力分布图是否正确?
T
o
o
o
o
T
T
T
整理课件
24
8.3.3 扭转圆轴任一点的应力状态
研究两横截面相距dx的任一A处单位厚度微元,左 右两边为横截面,上下两边为过轴线的径向面。
3) 计算扭转角AC
AC
TAB l AB GIPAB
+ T BC lBC GIPBC
整理课件
第八章扭转

# 根据几何 关系,有
g CC rdj
AC dx
g CC rdj
AC dx
g
GG EG
dj
dx
(8-2)
根据应力应变关 系,即剪切虎克 定律
Gg
G
dj
dx
(8-3)
再根据静力学关系
A dA T
A dA
G 2 dj dA T
A
dx
钢,[]=40MPa,G=80×103MPa, = 1º/m。
(1)计算扭矩
马达的功率通过传动轴传递给两个车轮,故每个 车轮所消耗的功率为
N k轮
Nk 2
3.7 2
1.85kW
轴CD各截面上的扭矩等于车轮所受的外力偶 矩T轮,则
T
T轮
9550
Nk轮 n
9550 1.85 32.6
543N
Mn2
mc
AB段 BC段
Mn1设为正的 Mn2设为正的
M n1 mA 76.4 Nm
M n2 114.6 Nm
4、扭矩图 将扭转轴的扭矩沿截面的分布用图形表示
例8-2 已知A轮输入功率为65kW,B、C、D轮输出功率分别为 15、30、20kW,轴的转速为300r/min,画出该轴扭矩图。
TB
•m
(2) 计算轴的直径
由强度条件得
T
WT [ ]
0.2d 3 T
[ ]
T
543
d 3 0.2[ ] 3 0.2 40106 0.0407m 4.07cm
选取轴的直径 d=4.5cm。
(3)校核轴的刚度
T GI p
180
80 109
《工程力学》第 8 章 扭 转解析

受扭后,圆周线与纵向直线之间原来的直角改变 了一数量。物体受力变形时,直角的这种改变量 (以弧度计)称之为切应变。
11:02
工程力学电子教案
扭
转
18
T
g (rad)
T
φ
l
根据圆筒横截面本身以及施加的力偶的极对称 性容易判明,圆筒表面同一圆周线上各处的切应变 均相同。因此,在材料为均匀连续这个假设条件下, 圆筒横截面上与此切应变相应的切应力其大小在外 圆周上各点处必相等;至于此切应力的方向,从相 应的切应变发生在圆筒的切向平面可知,系
11:02
工程力学电子教案
扭
转
25
理论分析和实验都表明,对于各向同性材料, 剪切弹性模量与其它两弹性参数E和n 之间存在下列 关系:
E G 2(1 n )
泊松比
以上即为薄壁圆筒受扭时的变形与应力理论。 它是实心圆杆扭转时变形与应力理论的基础。
11:02
工程力学电子教案
扭
转
26
§8-2 圆杆扭转时的应力与变形
11:02
工程力学电子教案
扭
转
4
T a
A m O o
m
b b T o′ b′ O B
m
l
T
m
MT x
由图示任意横截面m- m左边一段杆的平衡条 件可知,受扭杆件横截面上的内力是一个作用于 横截面平面内的力偶。这一力偶之矩称为扭矩, 常用符号MT表示。
11:02
工程力学电子教案
扭
转
5
T
a A O o
工程力学电子教案
扭
转
1
第8章 扭
转
§8-0 扭矩和扭矩图 §8-1 薄壁圆筒扭转时的应力与应变 §8-2 圆杆扭转时的应力与变形 §8-3 强度条件及刚度条件 §8-4 等直圆杆在扭转时的应变能
《材料力学》第八章组合变形

(2)内力分析,确定危险截面—整个轴;
M=600(kN·cm) FN=15(kN)
(3)应力计算,确定危险点—a、b点;
P产生拉伸正应力: t
FN AFNd 2源自4FNd 24
M拉产弯生组弯合曲:的正应力:wmax
M Wy
M
d3
32
32M
d3
P M= a Pe
补例8.1 已知: P=2kN,L求=:1mσm,Iazx=628×104mm4,Iy=64×1040mm2740 2844
解:1.分解P力。 Py Pcos φ Pz Psin φ 2.画弯矩图,确定危险截面--固定端截面。 3.画应力分布图,确定危险点—A、 B点
σ” σ’
A
x
y
Pyl
M
z
践中,在计算中,往往忽略轴力的影响。
4.大家考虑扭转、斜弯曲与拉(压)的组合怎么处理?
例8.5 图8.14a是某滚齿机传动轴AB的示意图。轴的直径为35 mm,材料为45钢, [σ]=85 MPa。轴是由P=2.2kW的电动机通过
带轮C带动的,转速为n=966r/min。带轮的直径为D=132 mm,
Mz Py l - x Pcosφ l - x Mcosφ My Pz l - x Psinφ l - x Msinφ
式中的总弯矩为:M Pl- x
3.计算两个平面弯曲的正应力。在x截面上任取一点A(z 、y),
与弯矩Mz、My对应的正应力分别为σ’和σ”,故
- Mz y , - M yz
第八章 组合变形
基本要求: 掌握弯曲与拉伸(或压缩)的组合、扭转与弯曲的组合 的强度计算。
重点: 弯曲与拉伸(或压缩)的组合,扭转与弯曲的组合。
《工程力学》第八章 扭转
• 规定为负。因此,同一截面左右两侧的扭 矩,不但数值相等,而且符号相同。
• 3)扭矩图
• 为了显示整个轴上各截面扭矩的变化规律, 可用横坐标表示截面位置,纵坐标表示各 截面扭矩的大小,按适当比例尺绘出扭矩 图,以便确定最大扭矩数值及危险截面。
• §8-3 薄壁圆筒的扭转纯剪切
• 一、薄壁圆筒扭转时横截面上的应力
• 式中θmax和[θ]的单位为度/米(°/m)。
图8-21 *§8-6 圆轴扭转时的变形能
• 当轴扭转时,轴内将积蓄变形能。扭转实 验表明,在弹性范围内受扭圆轴端面的扭 转角φ与外力偶矩m成正比。如图8-22所 示,当等截面圆轴承受的外力偶矩从零逐 渐增到m时,其扭转角也从零增加到φ。
• 所以,外力偶矩所做的功 • 将 代入上式 • 于是得到扭转时的变形能为
即
上式表明:在互相垂直的两个平面上,剪应力必然 成对存在,且数值相等;二者都
• 垂直于两平面的交线,其方向则共同指向
• 或共同背离两平面的交线,这种关系称为 剪应力互等定理。在图8-9所示微体的四 个侧面上,只存在剪应力而无正应力,这种 受力状态称为纯剪切。
• 三、剪切虎克定律
• 薄壁圆筒的扭转实验表明(图8-10),当剪 应力不超过材料的比例极限τp时,剪应力τ 与剪应变γ成正比,即
为了保证圆轴扭转时不发生破坏,要求它在工作 时危险截面上的最大工作剪应力τmax不 超 过 材料的许用扭转剪应力[τ],所以扭转强度条件 为
• 三、圆轴扭转的刚度条件 • 在生产中要限制轴产生过大的扭转变形。
扭转变形过大,将会引起较大的扭转振动, 影响机器的正常运转和工件的加工质量。 为了保证轴的刚度,通常规定轴的最大单 位长度扭转角θmax不超过许用扭转角[θ], 即刚度条件为
工程力学第八章:扭转
d
I p A 2 dA 2 d
2 D 2 d 2
d
O
D
32 D 4 (1 4 ) 32
(D4 d 4 )
( d ) D
4. 应力分布
(实心截面)
(空心截面)
工程上广泛采用空心截面圆轴:提高强度,节约材料,结构轻 便,应用广泛。
第一节 传动轴的外力偶矩 扭矩及扭矩图
一、圆轴扭转的概念 轴:工程中以扭转为主要变形的构件。如:机器中的传动轴、
石油钻机中的钻杆等。 扭转:受力特点是外力的合力为一力偶,且力偶的作用面与直
杆的轴线垂直。变形特点是横截面形状大小未变,只是绕轴线
发生相对转动。
剪应变 扭转角
A
B
O
A Me
O
B Me
T1 M eA 274 N.m
M eA
T2 M eA M eB 75 N.m
M eB M eC
T
x
75 N.m
274 N.m
第二节 圆轴扭转横截面上的切应力与强度计算
一、等直圆轴扭转变形实验及实验结果
实验结果:
※各圆周线绕轴线相对旋转了一个角度,但大小、形状和相邻两
M eA
1
M eB
2
M eC
对AB段
1 2
M 0
M eA
1
T1
扭矩按右手螺旋法 则设定为正
T1 M eA 274 N.m
对BC段
M eA
1
M 0
M eB
2
T2ቤተ መጻሕፍቲ ባይዱ
扭矩按右手螺旋 法则设定为正
T2 M eA M eB 75 N.m
《土木工程-力学》第八章 扭转
其中 2 d A A
称为横截面的极惯性矩Ip,
它是横截面的几何性质。
以Ip
2 d A 代入上式得:
A
dj T
d x GI p
从而得等直圆杆在线弹性范围内扭转时,横截面上任一点
处切应力计算公式
t
ρ
G
T GIp
T
Ip
30
T
t max
d T
t max
D
t max
t
T
Ip
横截面周边上各点处 r)的
由 t d A r T 根据应力分布可知 Me A
tr0
d A T,于是有
A
t dA
t
r0
T d
A
A
T
r0 (2πr0 )
T
2πr02
引进 A0 πr02 ,上式亦可写作
t T 2 A0
m r0
x m
20
§8-4 切应力互等定理和剪切胡克定律 1. 单元体·切应力互等定理
以横截面、径向截面以及与表面平行的面(切向 截面)从受扭的薄壁圆筒或等直圆杆内任一点处截取 一微小的正六面体——单元体。
{M
e }Nm
2π
{n} r m in 60
103
因此,在已知传动轴的转速n(亦即传动轴上
每个轮的转速)和主动轮或从动轮所传递的功率P
之后,即可由下式计算作用于每一轮上的外力偶
矩: 6
{Me }Nm
9.55 103
{P}kw {n}r
Nm
min
{Me }Nm
9.55 {P}kw {n}r
kN m
kN
m
M2
M3
(9.55 150) 300
第八章园轴的扭转_工程力学
第八章 圆轴的扭转工程构件一般可分为三类。
第四章已指出:杆是某一方向尺寸远大于其它二方向尺寸的构件,若杆件的轴线为直线,则称为直杆。
此外,若构件在某一方向的尺寸远小于其它二方向的尺寸,称之为板。
若构件在x 、y 、z 三个方向的尺寸具有相同的数量级,则称为块体。
本课程主要讨论直杆,这是一种最简单的构件。
如同4.4节所述,在空间任意力系的作用下,杆件截面内力的最一般情况是六个分量都不为零,其变形是很复杂的。
为了简化讨论,我们将杆的基本变形分成为三类,即拉压、扭转、弯曲,如图4.3所示。
前面已经讨论了在轴向载荷作用下杆的拉伸和压缩;现在再来研究杆的另一类基本变形,即扭转问题。
§8.1扭转的概念和实例工程中承受扭转的构件是很常见的。
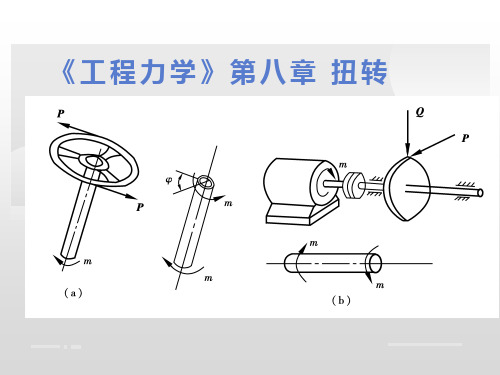
如图8.1所示的汽车转向轴,驾驶员操纵方向盘将力偶作用于转向轴AB 的上端,转向轴的下端B 则受到来自转向器的阻抗力偶的作用,使转向轴AB 发生扭转。
又如图8.2中的传动轴,轮C 上作用着主动力偶矩,使轴转动;轮D 输出功率,受到阻力偶矩的作用,轴CD 也将发生扭转。
以上二例都是承受扭转的构件实例。
由于工程中承受扭转的构件大多为圆截面直杆,故称之为轴。
本章亦仅限于讨论直圆轴的扭转问题。
图8.2 传动轴图8.3所示为等截面直圆轴扭转问题的示意图。
扭转问题的受力特点是:在各垂直于轴线的平面内承受力偶作用。
如在图8.3中,圆轴AB 段两端垂直于轴线的平面内,各作用有一个外力偶M 0,此二力偶的力偶矩相等而转向相反,故是满足平衡方程的。
圆轴扭转问题的变形特点是:在上述外力偶系的作用下,圆轴各横截面将绕其轴线发生相对转动;任意两横截面间相对转过的角度,称为相对扭转角,以φ表示。
图8.3中,φAB 表示截面B 相对于截面A 的扭转角。
必须指出,工程中的传动轴,除受扭转作用外,往往还伴随有弯曲、拉伸(压缩)等其它形式的变形。
这类问题属于组合变形,将在以后研究。
§8.2 扭矩与扭矩图已知轴所传递的功率、转速,可利用6.3节提供的“功率、转速与传递的扭矩之关系”来计算作用于传动轴上的外力偶矩M 0。
工程力学(扭转)课件
扭转力的作用
01
02
03
传递扭矩
在机械系统中,扭转力用 于传递扭矩,实现动力的 传递和转换。
平衡系统
在建筑结构中,扭转力用 于平衡不同方向的力和扭 矩,保持结构的稳定。
调整结构
在桥梁、高层建筑等大型 结构中,扭转力用于调整 结构的形状和稳定性。
扭转力的分类
按作用方式
可分为静态扭转力和动态扭转力。 静态扭转力作用缓慢,变形量较 小;动态扭转力作用迅速,变形
抗扭强度的计算
抗扭强度的计算公式通常基于剪切应 力的极限值或剪切模量,具体公式取 决于材料的性质和受力条件。
除了理论计算,还可以通过实验测试 来测定材料的抗扭强度。实验方法包 括扭转试验、弯曲试验和压缩试验等。
对于金属材料,可以根据弹性力学理 论计算抗扭强度。对于复合材料和复 合结构,需要考虑各组分材料的性能 以及它们之间的相互作用。
未来发展
随着科技的不断进步,工程力学 (扭转)的研究将更加深入和广
泛。
未来研究将更加注重实验和数值 模拟的结合,探索扭转变形的微
观机制和宏观表现。
随着新材料和新工艺的出现,扭 转变形的研究将更加关注材料性
能和结构优化设计。
THANKS
力矩的计算公式
M=FL,其中M为力矩,F 为力,L为力臂。
力臂
从转动轴到力的垂直距离。
力矩的平衡
平衡状态
物体保持静止或匀速直线运动的 状态。
力矩平衡条件
合力矩为零,即所有外力矩的代 数和为零。
平衡方程
∑M=0,其中∑表示求和符号, M表示外力矩。
力矩的传递
传递方式
通过轴承、齿轮等机械零件将力矩传递给其他部件。
扭矩与弹性模量的关系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直杆的扭转
扭转问题中应力和位移 椭圆截面的扭转 扭转问题的薄膜比拟
矩形截面杆的扭转
薄壁杆的扭转
扭转问题的位移解法
扭转问题中应力和位移
问题: (1)等截面直杆,截面形状可以任意; (2)两端受有大小相等转向相反的扭矩 M ; (3)两端无约束,为自由扭转,不计体力 ; 求:杆件内的应力与位移?
l xz s m yz s 0
将 、 l、m 代入上述边界条件,有
dy dx ( )( ) 0 y ds x ds
dy dx 0 y ds x ds
dy dx 0 y ds x ds
d 0 ds
2 f1 0, 2 z 2 f2 0, 2 x
2 f2 0 2 z 2 f1 0, 2 y
f1 u0 y z z y K1 yz
f 2 v0 z x x z K 2 zx f f 又由: 2 1 0 得: x y z K 2 z z K1 z 0
zx 0 z zy 0 z xz yz 0 x y
基本方程的求解
2 yz 0
(a)
2 zx 0
(b)
—— 扭转问题的相容方程
—— 平衡方程
由式(a)的前二式,得
zx zx ( x, y) zy zy ( x, y ) —— 二元函数
分部积分,得:
yX xY dxdy y x dxdy y y x x dxdy
zx zy
y C D
同理,得:
B y dy dx A y
D x dx dy C x dxdy
代入后三式,有
再几何方程方程代入,有
u 0, v 0, w 0, y x z w v 1 , (f) y z G x u w 1 , v u 0 z x G y x y
积分前三式,有
f 3 f 2 1 ( x, y) , y z G x f1 f 3 1 ( x, y) , z x G x f 2 f1 0 x y
zx 0
2
—— 扭转问题的相容方程 (b) (c)
边界条件: (1)侧面:
(2)端面:
l zx s m zy s 0 (∵n = 0, X Y Z 0) Xdxdy zxdxdy 0
(d)
Y dxdy zy dxdy 0 (e) (f) yX xY dxdy y zx x zy dxdy M
其中: i内 , Ai内 —— 分别为第i个内边界上φ的值和第i 个内边界所围的面积。 结论:等直杆的扭转问题归结为解下列方程:—— 应力函数法
i 1
n
泛定方程:
定解条件:
2 C
s 0
2 dxdy M
zx xz , y zy yz x
zx xz , y zy yz x
(x,y)——扭转应力函数
—— (Prandtl)应力函数
3. 扭转问题杆件位移与变形
u Kyz v Kzx
w 1 Ky, x G y w 1 Kx, y G x
表明:在杆件的侧面上(横截 面的边界上),应力函数 应 取常数。 又,应力函数 差一常数不影响应力分量的大小, 于是对单连体(实心杆)可取:
s 常数
s 0
—— 扭转问题的定解条件之一。 对于多连体(空心杆)问题, 在每一边 界上均为常数,但各个常数一般不相等,因此, 只能将其中的一个边界上取 s=0,而其余边界 上则取不同的常数,如:
zx 0 z zy 0 z xz yz 0 x y
相容方程:
2 C
—— 相容方程
(a)
s 0
—— 侧面边界条件
2 dxdy M
2
zx 0
2
(b)
2. 扭转问题应力的求解 ——应力函数法
X dxdy 0,
(c)
(d) Y dxdy 0, yX xY dxdy M , (e) 对式(c),应有
zx xz , y zy yz x
X dxdy zxdxdy y dxdy B ( )dx 0 dy dx B A A y
由此可见: 对每个横截面(z =常数) 它在 x y 面上的投影形状不变,而只 是转动一个角度 =Kz 。
其中: u0、v0 、x、y、z 和 以前相同,代表刚体位移。
v v0 z x x z Kzx
若不计刚体位移,只保留与 变形有关的位移,则有
d K dz
K —— 单位长度杆件的扭转角 。
2GK
2
将其对照下式:
2 C
可见:
2 w 1 2 K, 2 xy G y 2w 1 2 K, 2 yx G x
C 2GK
实际问题中,K 可通过实验测得。
小 结:
1. 扭转问题按应力求解的基本方程 平衡微分方程: 应力函数的确定
1. 扭转应力函数
求解方法: 按应力求解; 半逆解法 —— 由材料力学中某些结果 出发,求解。 材料力学结果: (1) 0 (∵自由扭转)
x y z
(2)侧表面: 扭转问题的未知量:
zx , zy
xy 0
——为三向应力状态,且不是轴对称问题。
扭转问题的基本方程 平衡方程:
从中求得:
u Kyz v Kzx
将其用极坐标表示:
由
ur u cos v sin u u sin v cos ur 0, u Krz
将式(10-6)代入,有:
K 2 K1 K
代入 f1、f2 和 u、v 得:
u u0 y z z y Kyz
s 0
0
s Ci Ci
i
——由位移单值条 件确定。
zx xz , y zy yz x
(2)上端面:(l 0
l x s m yx s n zx s X l xz s m yz s n z s Z
u Kyz v Kzx 1 将其代入: w v , y z G x u w 1 , z x G y
有:
将两式相减,得:
1 1 0 2K 2 2 G y G x 1 2 0 2K G
2 2
w 1 Ky, x G y w 1 Kx, y G x
同理,对式(d),应有
yX xY dxdy y
对式(e):
Y dxdy 0
zx
x zy dxdy
y y x x dxdy
y dxdy x dxdy y x B D y dy dx x dx dy A y C x
x yx zx X 0 x y z xy y zy Y 0 x y z xz yz z Z 0 x y z
得:
zx 0 z zy 0 z xz yz 0 x y
(a)
—— 扭转问题的平衡方程
相容方程:
2Θ (1 ) 2 x 2 0 x 2Θ (1 ) 2 y 2 0 y 2Θ (1 ) 2 z 2 0 z 2 yz 0
2Θ (1 ) 2 yz 0 yz 2Θ (1 ) 2 zx 0 zx 2Θ (1 ) 2 xy 0 xy
—— 扭转杆件的位移
C K 2G
D M K
2 或:K 2G
也称普朗特尔(Prandtl)应力函数
zx xz , y zy yz x
将应力代入相容方程(b),有
2 yz 0
2 zx 0
(b)
—— 扭转问题的相容方程
y 0, 2 0 x
l , m 0, n 0
0 0 0 0
l x s m yx s n zx s X l xy s m y s n zy s Y 0
0 0 0
l xz s m yz s n z s Z
dy l cos( N , x) cos ds dx m cos( N , y) sin ds
由式(a)的第三式,得
zx , zy y x
于是有:
xz yz x y
由微分方程理论,可知:一定存 在一函数(x,y),使得:
zx xz , y zy yz x
(x,y)——扭转应力函数
2
2 0, y 2 0, x
由此可解得:
2 C
结论: 等直杆的扭转问题归结为: 按相容方程确定应力函数(x, y),然后确定应力分量,并使 其满足边界条件。
—— 用应力函数表示的相容方程 式中:C 为常数。
定解条件——边界条件 (1)侧表面: 0 0
将其代入式(e):
yB B y A A dy dx dxdy
y A dy dx
B
yX xY dxdy M
得到:
