专题测试卷——解直角三角形(一)(基础版)

合集下载

(完整版)初三解直角三角形练习题基础

初三解直角三角形练习题一、真空题： 1、在Rt △ABC 中，∠B ＝900，AB ＝3，BC ＝4，则sinA= 2、在Rt △ABC 中，∠C ＝900，AB ＝,35cm BC cm=则SinA= cosA= 3、Rt △ABC 中，∠C ＝900，SinA=54,AB=10,则BC ＝4、α是锐角，若sin α=cos150,则α＝若sin53018\=0.8018，则cos36042\=5、 ∠B 为锐角，且2cosB －1＝0则∠B ＝6、在△ABC 中，∠C ＝900，∠A ，∠B ，∠C 所对的边分别为a ，b ，c ，a ＝9，b ＝12，则sinA= sinB=7、 Rt △ABC 中，∠C ＝900，tanA=0.5,则cotA= 8、在Rt △ABC 中，∠C ＝900，若b a 32=则tanA= 9．等腰三角形中，腰长为5cm ，底边长8cm ，则它的底角的正切值是10、若∠A 为锐角，且tan 2A+2tanA －3＝0则∠A ＝ 11、Rt △ABC 中，∠A ＝600，c=8，则a ＝，b ＝ 12、在△ABC 中，若32=c ,b ＝3，则tanB= ,面积S ＝ 13、在△ABC 中，AC ：BC ＝1：3，AB ＝6，∠B ＝，AC ＝ BC ＝ 14、在△ABC 中，∠B ＝900，AC 边上的中线BD ＝5，AB ＝8，则tanACB= 二、选择题1、在Rt △ABC 中，各边的长度都扩大2倍，那么锐角A 的正弦、余弦值（） A 、都扩大2倍 B 、都扩大4倍 C 、没有变化 D 、都缩小一半2、若∠A 为锐角，且cotA ＜3，则∠A （）A 、小于300B 、大于300C 、大于450且小于600D 、大于600 3、在Rt △ABC 中，已知a 边及∠A ，则斜边应为（） A 、asinA B 、A a sin C 、acosA D 、Aa cos 4、等腰三角形底边与底边上的高的比是2：3，则顶角为（） A 、600 B 、900 C 、1200 D 、15005、在△ABC 中，A ，B 为锐角，且有sinA ＝cosB ，则这个三角形是（）A 、等腰三角形 B 、直角三角形 C 、钝角三角形 D 、锐角三角形6、有一个角是300的直角三角形，斜边为1cm ，则斜边上的高为（）A 、41cmB 、21cmC 、43cmD 、23cm三、求下列各式的值1、sin 2600+cos 26002、sin600－2sin300cos3003. sin300－cos 24504. 2cos450+|32 |5. 0045cos 360sin 2+ 6. 130sin 560cos 300-7. 2sin 2300·tan300+cos600·cot300 8. sin 2450-tan 2300四、解答下列各题1、在Rt △ABC 中，∠C ＝900，，AB ＝13，BC ＝5，求sinA, cosA, tanA, cotA2. 在Rt △ABC 中，∠C ＝900，若1312sin =A 求cosA, sinB, cosB3. 在Rt △ABC 中，∠C ＝900，b=17, ∠B=450,求a, c 与∠A四、根据下列条件解直角三角形。

解直角三角形基础训练题

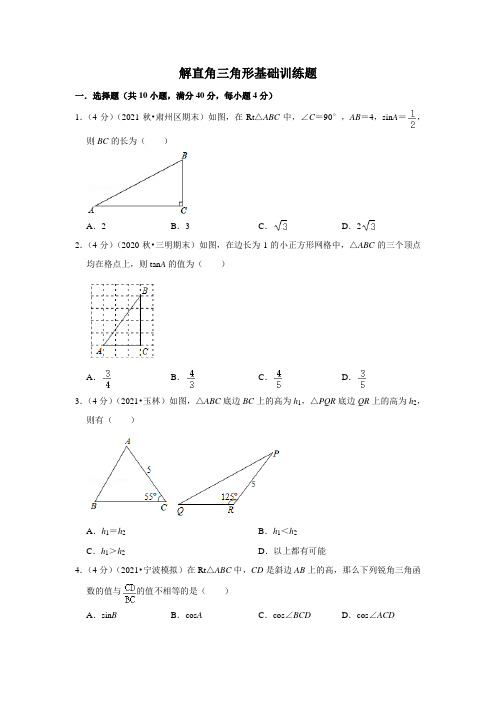
解直角三角形基础训练题一．选择题（共10小题，满分40分，每小题4分）1．（4分）（2021秋•肃州区期末）如图，在Rt△ABC中，∠C＝90°，AB＝4，sin A＝，则BC的长为（）A．2B．3C．D．22．（4分）（2020秋•三明期末）如图，在边长为1的小正方形网格中，△ABC的三个顶点均在格点上，则tan A的值为（）A．B．C．D．3．（4分）（2021•玉林）如图，△ABC底边BC上的高为h1，△PQR底边QR上的高为h2，则有（）A．h1＝h2B．h1＜h2C．h1＞h2D．以上都有可能4．（4分）（2021•宁波模拟）在Rt△ABC中，CD是斜边AB上的高，那么下列锐角三角函数的值与的值不相等的是（）A．sin B B．cos A C．cos∠BCD D．cos∠ACD5．（4分）（2021秋•钢城区期末）在Rt△ABC中，∠C＝90°，cos A＝，AB＝10，则AC 的长为（）A．3B．4C．6D．86．（4分）（2021秋•岱岳区期末）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，D为垂足．若AC＝8，BC＝6，则sin∠ACD的值为（）A．B．C．D．7．（4分）（2021秋•万州区期末）在△ABC中，∠A、∠B为锐角，cos A＝，tan B＝，则△ABC的形状为（）A．等腰三角形B．等边三角形C．直角三角形D．锐角三角形8．（4分）（2022•锦江区校级开学）在Rt△ABC中，∠ACB＝90°，BC＝12，tan B＝，则AB的长为（）A．8B．12C．13D．189．（4分）（2021秋•启东市期末）如图，在平面直角坐标系xOy中，AB＝2，连结AB 并延长至C，连结OC，若满足OC2＝BC•AC，tanα＝3，则点C的坐标为（）A．（﹣2，6）B．（﹣3，9）C．（﹣，）D．（﹣，）10．（4分）（2022•绿园区校级一模）如图，电线杆AB的中点C处有一标志物，在地面D 点处测得标志物的仰角为32°，若点D到电线杆底部点B的距离为a米，则电线杆AB的长可表示为（）A．米B．米C．2a•cos32°米D．2a•tan32°米二．填空题（共6小题，满分30分，每小题5分）11．（5分）（2021秋•长春期末）如图，在△ABC中，CD⊥AB，垂足为D．若AB＝12，CD ＝6，tan A＝，则sin B的值为．12．（5分）（2021秋•船营区校级期末）如图，在Rt△ABC中，∠C＝90°，点D在AC上，∠DBC＝∠A，若AC＝4，cos A＝，则BD的长度为．13．（5分）（2021秋•温江区校级月考）在Rt△ABC中，∠ACB＝90°，∠A＝30°，则AC：BC＝．14．（5分）（2021秋•巴中期末）定义：等腰三角形中底边与腰的比叫做顶角正对（sad），即在△ABC中，AB＝AC，顶角A的正对记作sadA，这时sadA＝．如图，若在△ABC中，AB＝AC，sin B＝，则sadA的值是．15．（5分）（2021秋•城关区期末）如图，在Rt△ABD中，AB＝6，tan∠ADB＝，点C 为斜边BD的中点，P为AD上任一点，过点P作PE⊥AC于点E，PF⊥BD于点F，则PE+PF＝．16．（5分）（2020秋•德江县期末）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F，若AC＝6，tan B＝，则CE＝．三．解答题（共5小题，满分50分，每小题10分）17．（10分）（2021秋•五华区校级期末）在Rt△ABC中，∠C＝90°，∠B＝25°，b＝10，解这个直角三角形（结果保留小数点后一位）．（参考数据：sin25°≈0.42，cos25°≈0.91，tan25°≈0.47）18．（10分）（2021秋•长丰县期末）如图，在△ABC中，AB＝5，AC＝8，∠A＝60°．（1）求BC的长．（2）求sin B．19．（10分）（2021春•徐汇区校级月考）如图，在△ABC中，∠ACB＝90°，∠CAB＞∠B，CD是斜边AB上的中线，过点A作∠CAE＝∠B，交BC于点E，交CD于点H，且AH ＝2CH．（1）求sin B的值；（2）当CD＝时，求BE的长．20．（10分）（2020秋•宁德期末）如图，在四边形ABCD中，∠ABC＝90°，AD＝BD，BC ＝CD．（1）若BD＝13，AB＝10，求cos∠CBD的值；（2）设△ABD的面积为S1，△BCD的面积为S2，求证：＝4cos2∠CBD．21．（10分）（2021•苏州二模）如图，∠ABC＝45°，其中P、Q分别是射线BA、BC上的点，BP＝3．（1）给出条件①PQ＝4；②∠BPQ＝105°；③PQ＝6．能使BQ的长唯一确定的条件是；（2）在题（1）中选一个使BQ的长唯一确定的条件，求出此时BQ的长度．。

解直角三角形测试题及答案

《解直角三角形》整章测试【1】一、选择题（每小题3分，共24分）1.在Rt △ABC 中， ∠C=90︒，AB=4，AC=1，则cos A 的值是（）（A ）154(B)14(C)15 (D)４2.计算：2)130(tan -︒＝（）(Ａ)331-(B)13- (Ｃ)133-（D ）１－3 3.在ABC ∆中，,A B ∠∠都是锐角，且sinA ＝21， cosB ＝23，则ABC ∆的形状（）（A ）直角三角形（B ）钝角三角形（C ）锐角三角形（D ）不能确定4.如图，在Rt ABC △中，3tan 2B =，23BC =，则AC 等于（）（A ）3（B ）4（C ）43（D ）65.如图，小颖利用有一个锐角是30°的三角板测量一棵树的高度，已知她与树之间的水平距离BE 为5m ，AB 为1.5m （即小颖的眼睛距地面的距离），那么这棵树高是（） (A)（53332+）m (B)（3532+）m (C)533m (D)4m 6．因为1sin 302=，1sin 2102=-，所以sin 210sin(18030)sin 30=+=-；因为2sin 452=，2sin 2252=-，所以sin 225sin(18045)sin 45=+=-，由此猜想，推理知：一般地当α为锐角时有sin(180)sin αα+=-，由此可知：sin 240=（）（A ）12-(B)22-(C)32- (D)3-7．如图，客轮在海上以30km/h 的速度由B 向C 航行，在B 处测得灯塔A 的方位角为北偏东80，测得C 处的方位角为南偏东25，航行1小时后到达C 处，在C 处测得A 的方位角为北偏东20，则C 到A 的距离是（）(A)156km(B)152km (C)15(62)+km(D)5(632)+km北东ABC8.如图，在Rt ABC △中，906cm A AC ∠==，，8cm AB =，把AB 边翻折，使AB 边落在BC 边上，点A 落在点E 处，折痕为BD ，则sin DBE ∠的值为（）(A)13(B)310(C)37373(D)1010二、填空题（每小题3分，共24分） 9．计算sin 60tan 45cos30-的值是．10. 用“>”或“<”号填空：1sin 50cos 402-0．（可用计算器计算） 11.在Rt ABC △中，90C ∠=，:3:4BC AC =，则cos A =． 12．如图，一架梯子斜靠在墙上，若梯子到墙的距离AC =3米，3cos 4BAC ∠=，则梯子AB 的长度为米．13.如图，一轮船由南向北航行到O 处时，发现与轮船相距40海里的A 岛在北偏东33方向．已知A 岛周围20海里水域有暗礁，如果不改变航向，轮船（填“有”或“没有”）触暗礁的危险．（可使用科学计算器）14. 如图，在菱形ABCD 中，DE ⊥AB ，垂足为E ，DE=6cm ，3sin 5A =，则菱形ABCD 的面积是__________2cm ． 15.根据指令[s,A]（s ≥0,0°≤A ＜360°）机器人在平面上能完成如下动作：先在原地逆时针旋转角度A ，再朝其面对的方向沿直线行走距离s ．现在机器人在平面直角坐标系的原点，且面对y 轴的负方向，为使其移动到点（－3，3），应下的指令是．16. 有古诗“葭生池中”今有方池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问：水深、葭长各几何？（1丈=10尺）回答：水深，葭长. 17.（本题8分）计算：242(2cos 45sin 60)4︒-︒+． 18.（本题10分）某校数学兴趣小组在测量一座池塘边上A B ，两点间的距离时用了以下三种测量方法，如下图所示．图中a b c ，，表示长度，β表示角度．请你分别求出AB 的长度（用含有a b c β，，，字母的式子表示）．（1）______AB = （2）______AB = （3）______AB =19.（本题10分）小强家有一块三角形菜地，量得两边长分别为40m ，50m ，第三边上的高为30m ，请你帮小强计算这块菜地的面积（结果保留根号）． 20.（本题12分）海中有一个小岛P ，它的周围18海里内有暗礁，渔船跟踪鱼群由西向东航行，在点A 测得小岛P 在北偏东60°方向上，航行12海里到达B 点，这时测得小岛P 在北偏东45°方向上．如果渔船不改变航线继续向东航行，有没有触礁危险？请说明理由．（1A C B a b（2AC B a β （3AC B aD Ec b A BCD EA BC21.（本题12分）如图，AC是某市环城路的一段，AE，BF，CD都是南北方向的街道，其与环城路AC的交叉路口分别是A，B，C．经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东30°方向上，AB＝2km，∠DAC＝15°．（1）求B，D之间的距离；（2）求C，D之间的距离．四、附加题（本题20分）22.现代家居设计的“推拉式”钢窗，运用了轨道滑行技术，纱窗装卸时利用了平行四边形的不稳定性，操作步骤如下：（1）将矩形纱窗转化成平行四边形纱窗后，纱窗上边框嵌入窗框的上轨道槽（如图1）．（2）将平行四边形纱窗的下边框对准窗框的下轨道槽（如图2）．（3）将平行四边形纱窗还原成矩形纱窗，同时下边框嵌入窗框的下轨道槽（如图3）．在装卸纱窗的过程中，如图所示α∠的值不得小于81，否则纱窗受损．现将高96cm的矩形纱窗恰好安装在上、下槽深分别为0.9cm，高96cm（上、下槽底间的距离）的窗框上．试求合理安装纱窗时α∠的sin810.987=0.990=sin830.993=0.995=cos90.987=0.990=0.993=0.995=章《解直角三角形》整章测试答案：～8 BABA ACDD三、17.解：2=原式2=-2=18.解：（1）AB=（2）tanAB aβ=（3）acABb=．19．解：分两种情况：（1）当ACB∠为钝角时，BD是高，90ADB∴∠=．在Rt BCD△中，40BC=，30BD=∴CD==．在Rt ABD△中，50AB=，ABC中山路文化路D和平路45°15°30°环城路EF 图1 2 图3∴40AD ==．40AC AD CD ∴=-=-，新课标第一网∴211(4030(600)22ABC S AC BD ==-⨯=-△．（2）当ACB ∠为锐角时， BD 是高，90ADB BDC ∴∠=∠=，在Rt ABD △中，5030AB BD ==，，40AD ∴==．同理CD ==∴(40AC AD CD =+=+，∴211(4030(600)22ABC S AC BD ==+⨯=+△．综上所述：2(600)ABC S =±△.20．解：有触礁危险．理由：过点P 作PD ⊥AC 于D ．设PD 为x ，在Rt △PBD 中，∠PBD=90°－45°＝45°． ∴BD ＝PD ＝x ．在Rt △PAD 中，∵∠PAD ＝90°－60°＝30°，∴x ．xAD 330tan =︒=∵BD ，AB AD +=∴x ．x +=123 ∴)13(61312+=-=x ．∵，＜18)13(6+∴渔船不改变航线继续向东航行，有触礁危险．21. 解：（1）由题意得，∠EA D =45°，∠FBD=30°． ∴∠EAC=∠EA D +∠DA C =45°+15°=60°． ∵ AE∥BF∥CD，∴ ∠FBC=∠EAC =60°． ∴ ∠DBC=30°．又∵ ∠DBC=∠DAB+∠ADB， ∴ ∠ADB=15°．∴∠DAB=∠ADB．∴ BD=AB=2．即B ，D 之间的距离为2km ．（2）过B 作BO⊥DC，交其延长线于点O ，在Rt△DBO 中，BD=2，∠DBO=60°． ∴ DO=2×sin60°=2×323=,BO=2×cos60°=1．在Rt△CBO 中，∠CBO=30°，CO=BOtan30°=33， ∴ CD=DO－CO=332333=-（km ）．即C ，D 之间的距离为332km ． 22. 解：能够合理装上平行四边形纱窗时的最大高度：960.995.1-=（cm ）能够合理装上平行四边形纱窗时的高：96sin α∠或96cos(90)α-∠·°当81α∠=°时，纱窗高：96sin81960.98794.75295.1=⨯=<° ∴此时纱窗能装进去，当82α∠=°时，纱窗高：96sin82960.99095.0495.1=⨯=<° ∴此时纱窗能装进去．当83α∠=°时，纱窗高：96sin83960.99395.32895.1=⨯=>° ∴此时纱窗装不进去．因此能合理装上纱窗时α∠的最大值是82°.。

解直角三角形测试题[1][1].doc

解直角三角形复习4.当45° v A <90°时,下列不等式中正确的是（u 46. 若等腰三角形腰长为4,而积是4,则这个等腰三角形顶角的度数为（ A. 30° B. 30° 或 150° C. 60°D. 60° 或 120° 7. 如图，梯子（长度不变）跟地血所成的锐角为A ,关于ZA 的三介函数值与梯子的倾斜程度之间，叙述正确的是（）。

A. sin A 的值越大，梯子越陡C. tan A 的值越小，梯子越陡 8. 如图,在等腰梯形ABCD 中，AB 〃CD,某水库人坝的横断面是梯形，坝内斜坡的坡度z = l ：V3，坝外斜坡的坡度/• = 1:1,则两个坡角的和为（A. 90°B. 60°C. 75°D. 105°二、填空题（每小题5分，共20分）11. 若ZA 为锐角，cosA=—,则 sinA= 。

13 12. 在坡度为1:2的山坡上种树，要求株距（相邻两树间的水平距离）是6米，斜坡上相邻两树间的坡而距离是3. 如果ZA 是锐角，且sin A = cos A ,那么ZA=(A. 30°B.45°C. 60° 4 如果 Q 是锐角，口 since = g,贝 0 cos(90° - a) = 143 3 A. -B. -C.- 5 4 5 在AABC 中，A, B 为锐角，且有sin A = cosfi , A.等腰三角形 B.直角三和形D. 90°0.1 5 则这个三角形是 C.钝角三角形（） D.锐角三如形A. tan A > cos A > sin AC- sin A > tan A > cos A5-在 RtAABC 中，ZC=90° ,B. cos A > tan A > sin A D. tan A > sin A > cos A 4 cosA=—,那么tanB 的值为( 5B. cos A 的值越大，梯子越陡 D.陡缓程度与ZA 的函数对角线AC 平分ZBAD, ZB=60° , CD=2cm,则梯形ABCD 的面积为（cm 2. A. 3^3 B. 6 C. 673 D. 129.如图，沿AE 折克矩形纸片ABCD,使点D 落在BC 边的点F 处。

第1章解直角三角形单元测试(A卷基础篇)(浙教版)(解析版)

第1章解直角三角形单元测试(A卷基础篇）【浙教版】参考答案与试题解析一．选择题（共10小题，每小题3分，共30分）1．（3分）（2020•滨湖区二模）锐角三角函数tan30°的值是（）A．1 B．C．D．【思路点拨】直接利用特殊角的三角函数值得出答案．【答案】解：tan30°＝．故选：B．【点睛】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．2．（3分）（2020•龙泉驿区模拟）如图，在Rt△ABC中，∠C＝90°，AB＝13，BC＝12，AC＝5，则下列三角函数表示正确的是（）A．sin A＝B．cos A＝C．tan A＝D．tan B＝【思路点拨】根据锐角三角函数定义分别表示即可．【答案】解：A、sin A＝＝，故原题说法正确；B、cos A＝＝，故原题说法错误；C、tan A＝＝，故原题说法错误；D、tan B＝＝，故原题说法错误；故选：A．【点睛】此题主要考查了锐角三角函数定义，关键是掌握正弦：我们把锐角A的对边a与斜边c的比叫做∠A的正弦，记作sin A．余弦：锐角A的邻边b与斜边c的比叫做∠A的余弦，记作cos A．正切：锐角A的对边a与邻边b的比叫做∠A的正切，记作tan A．3．（3分）（2020•雅安）如图，在Rt△ACB中，∠C＝90°，sin B＝0.5，若AC＝6，则BC的长为（）A．8 B．12 C．6D．12【思路点拨】根据锐角三角函数的边角间关系，先求出AB，再利用勾股定理求出BC．【答案】解：法一、在Rt△ACB中，∵sin B＝＝＝0.5，∴AB＝12．∴BC＝＝＝6．故选：C．法二、在Rt△ACB中，∵sin B＝0.5，∴∠B＝30°．∵tan B＝＝＝，∴BC＝6．故选：C．【点睛】本题考查了解直角三角形．掌握直角三角形的边角间关系是解决本题的关键．4．（3分）（2020•拱墅区校级模拟）在锐角△ABC中，，则∠A＝（）A．30°B．45°C．60°D．75°【思路点拨】直接利用偶次方的性质以及绝对值的性质结合特殊角的三角函数值得出∠C＝60°，∠B＝45°，进而得出答案．【答案】解：∵，∴tan C＝，sin B＝，∴∠C＝60°，∠B＝45°，∴∠A＝75°．故选：D．【点睛】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．5．（3分）（2020•如皋市一模）如图，一辆小车沿倾斜角为α的斜坡向上行驶13m，若sinα＝，则小车上升的高度是（）A．5m B．6m C．6.5m D．12m【思路点拨】根据正弦的定义列式计算，得到答案．【答案】解：设小车上升的高度是xm，∵sinα＝，∴＝，解得，x＝5，故选：A．【点睛】本题考查的是解直角三角形的应用﹣坡度坡角问题，掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键．6．（3分）（2020•丰泽区校级模拟）如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝3，BC＝2，tan A＝，则CD的值为（）A．B．C．D．2【思路点拨】延长AD、BC，两线交于O，解直角三角形求出OB，求出OC，根据勾股定理求出OA，求出△ODC∽△OBA，根据相似三角形的性质得出比例式，代入求出即可．【答案】解：延长AD、BC，两线交于O，∵在Rt△ABO中，∠B＝90°，tan A＝＝，AB＝3，∴OB＝4，∵BC＝2，∴OC＝OB﹣BC＝4﹣2＝2，在Rt△ABO中，∠B＝90°，AB＝3，OB＝4，由勾股定理得：AO＝5，∵∠ADC＝90°，∴∠ODC＝90°＝∠B，∵∠O＝∠O，∴△ODC∽△OBA，∴＝，∴＝，解得：DC＝，故选：C．【点睛】本题考查了勾股定理，解直角三角形和相似三角形的性质和判定等知识点，能正确作出辅助线（构造出直角三角形）是解此题的关键．7．（3分）（2020•宿迁模拟）如图，△ABC的三个顶点均在格点上，则tan A的值为（）A．B．C．2 D．【思路点拨】直接利用网格结合锐角三角函数关系得出tan A＝，进而得出答案．【答案】解：如图所示：连接BD，BD＝＝，AD＝＝2，AB＝＝，∵BD2+AD2＝2+8＝10＝AB2，∴△ADB为直角三角形，∴∠ADB＝90°，则tan A＝＝＝．故选：A．【点睛】此题主要考查了解直角三角形，正确构造直角三角形是解题关键．8．（3分）（2020•松北区二模）如图，在A处测得点P在北偏东60°方向上，在B处测得点P在北偏东30°方向上，若AP＝6千米，则A，B两点的距离为（）千米．A．4 B．4C．2 D．6【思路点拨】证明AB＝PB，在Rt△P AC中，求出PC＝3千米，在Rt△PBC中，解直角三角形可求出PB的长，则可得出答案．【答案】解：由题意知，∠P AB＝30°，∠PBC＝60°，∴∠APB＝∠PBC﹣∠P AB＝60°﹣30°＝30°，∴∠P AB＝∠APB，∴AB＝PB，在Rt△P AC中，∵AP＝6千米，∴PC＝P A＝3千米，在Rt△PBC中，∵sin∠PBC＝，∴PB＝＝＝6千米．故选：D．【点睛】本题考查的是解直角三角形的应用，掌握锐角三角函数的定义及方向角是解题的关键．9．（3分）（2019秋•金乡县期末）如图，△ABC中，cos B＝，sin C＝，BC＝7，则△ABC的面积是（）A．B．12 C．14 D．21【思路点拨】作AD⊥BC于D，直接利用特殊角的三角函数值得出∠B的度数，再利用锐角三角函数关系表示出AD，BD，DC的长，进而得出答案．【答案】解：作AD⊥BC于D，如图所示：∵cos B＝，∴∠B＝45°，∵sin C＝，∴设AD＝3x，则AC＝5x，DC＝4x，BD＝3x，∵BC＝7，∴BD+DC＝3x+4x＝7x＝7，解得：x＝1，故AD＝3，则△ABC的面积是：×3×7＝．故选：A．【点睛】此题主要考查了特殊角的三角函数值以及三角形面积求法，正确表示出AD，BD，DC的长是解题关键．10．（3分）（2020春•罗湖区校级月考）如图，一块矩形木板ABCD斜靠在墙边（OC⊥OB，点A，B，C，D，O在同一平面内），已知AB＝a，AD＝b，∠BCO＝x，则点D到OB的距离等于（）A．a sin x+b sin x B．a cos x+b cos xC．a sin x+b cos x D．a cos x+b sin x【思路点拨】如图，过点D作DE⊥OC于点E，则点D到OB的距离等于OE的长．根据矩形性质及解直角三角形可得OC＝BC•cos x＝b cos x，CE＝CD•sin x＝a sin x，进而可得点D到OB的距离．【答案】解：如图，过点D作DE⊥OC于点E，则点D到OB的距离等于OE的长．∵四边形ABCD是矩形，∴∠BCD＝90°，CD＝AB＝a，AD＝BC＝b，∴∠CDE＝∠BCO＝x，∴OC＝BC•cos x＝b cos x，CE＝CD•sin x＝a sin x，∴OE＝OC+CE＝b cos x+a sin x．则点D到OB的距离等于b cos x+a sin x．故选：C．【点睛】本题考查了解直角三角形的应用，解决本题的关键是掌握解直角三角形．二．填空题（共6小题，每小题4分，共24分）11．（4分）（2020•宁波模拟）已知sinα＝（α为锐角），则tanα＝．【思路点拨】根据sin2α+cos2α＝1，tanα＝计算．【答案】解：∵sin2α+cos2α＝1，∴cosα＝＝，∴tanα＝＝＝，故答案为：．【点睛】本题考查的是同角的三角函数的关系，掌握sin2α+cos2α＝1，tanα＝是解题的关键．12．（4分）（2020•天河区模拟）在Rt△ABC中，∠C＝90°，sin B＝，若斜边上的高CD＝2，则AC＝．【思路点拨】首先证明∠ACD＝∠B，推出＝，设AD＝3k，AC＝5k，则CD＝4k＝2，求出k即可解决问题．【答案】解：如图，∵CD⊥AB，∴∠CDB＝90°，∵∠ACB＝90°，∴∠ACD+∠DCB＝90°，∠B+∠DCB＝90°，∴∠ACD＝∠B，∴sin∠ACB＝sin B＝，∴＝，设AD＝3k，AC＝5k，则CD＝4k＝2，∴k＝，∴AC＝，故答案为．【点睛】本题考查解直角三角形，解题的关键是熟练掌握基本知识，学会利用参数解决问题，属于中考常考题型．13．（4分）（2020•奉贤区一模）小明从山脚A出发，沿坡度为1：2.4的斜坡前进了130米到达B点，那么他所在的位置比原来的位置升高了50米．【思路点拨】小明所在的位置比原来的位置升高了x米，根据坡度的概念用x表示出小明前进的水平宽度，根据勾股定理计算，得到答案．【答案】解：设小明所在的位置比原来的位置升高了x米，∵坡度为1：2.4，∴小明前进的水平宽度为2.4米，由勾股定理得，x2+（2.4x）2＝1302，解得，x＝50，即小明所在的位置比原来的位置升高了50米，故答案为：50．【点睛】本题考查的是解直角三角形的应用﹣坡度坡角问题，掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键．14．（4分）（2020•德阳）如图，海中有一小岛A，它周围10.5海里内有暗礁，渔船跟踪鱼群由西向东航行．在B点测得小岛A在北偏东60°方向上，航行12海里到达D点，这时测得小岛A在北偏东30°方向上．如果渔船不改变航线继续向东航行，那么渔船还需航行 4.5海里就开始有触礁的危险．【思路点拨】过A作AC⊥BD于点C，求出∠CAD、∠CAB的度数，求出∠BAD和∠ABD，根据等角对等边得出AD＝BD＝12，根据含30度角的直角三角形性质求出CD，根据勾股定理求出AC即可．【答案】解：只要求出A到BD的最短距离是否在以A为圆心，以10.5海里的圆内或圆上即可，如图，过A作AC⊥BD于点C，则AC的长是A到BD的最短距离，∵∠CAD＝30°，∠CAB＝60°，∴∠BAD＝60°﹣30°＝30°，∠ABD＝90°﹣60°＝30°，∴∠ABD＝∠BAD，∴BD＝AD＝12海里，∵∠CAD＝30°，∠ACD＝90°，∴CD＝AD＝6海里，由勾股定理得：AC＝＝6（海里），如图，设渔船还需航行x海里就开始有触礁的危险，即到达点D′时有触礁的危险，在直角△AD′C中，由勾股定理得：（6﹣x）2+（6）2＝10.52．解得x＝4.5．渔船还需航行4.5海里就开始有触礁的危险．故答案是：4.5．【点睛】考查了勾股定理的应用和解直角三角形，此题是一道方向角问题，结合航海中的实际问题，将解直角三角形的相关知识有机结合，体现了数学应用于实际生活的思想．15．（4分）（2019秋•靖江市校级月考）等腰三角形的面积为，一条边长为5，则底角的正切值等于3或或．【思路点拨】由题意知腰和底边不确定，应分两种情况进行讨论①腰长为5；②底边为5；进行求解即可．【答案】解：在△ABC中，∵AB＝AC，∴∠B＝∠C，①当△ABC是锐角三角形，AB＝5时，过C作CD⊥AB于D，如图1所示：∵S△ABC＝AB•CD＝，∴×5•CD＝，∴CD＝3．在Rt△ACD中，由勾股定理，得AD＝＝4，∴BD＝5﹣4＝1，∴tan B＝＝＝3；当△ABC是钝角三角形，AB＝5时，过C作CD⊥AB于D，如图2所示：同理得：CD＝3，AD＝4，则BD＝AB+AD＝9，∴tan B＝＝＝；②当BC＝5时，过A作AD⊥BC于D，如图3所示：∵AB＝AC，∴BD＝CD＝，∵S△ABC＝BC•AD＝，∴×5•AD＝，∴AD＝3．∴tan B＝＝＝；综上所述，底角的正切值等于3或或；故答案为：3或或．【点睛】本题考查了等腰三角形的性质，正切函数的定义以及勾股定理．由于不确定腰长和底边，应分情况进行讨论．此题利用了分类讨论的思想．16．（4分）（2020•槐荫区二模）在如图所示的正方形网格中，每个小正方形的边长都是1，线段AB与CD 交于点E，则cos∠CEA＝．【思路点拨】将线段CD平移到线段AF，使C与A重合，那么CD∥AF，根据平行线的性质得出∠CEA ＝∠BAF．利用勾股定理得出AF＝，BF＝2，AB＝5，由勾股定理的逆定理可得∠AFB＝90°，在Rt△ABF中求出cos∠BAF＝＝，那么cos∠CEA＝cos∠BAF＝．【答案】解：如图，将线段CD平移到线段AF，使C与A重合，∴CD∥AF，∴∠CEA＝∠BAF．由勾股定理得，AF＝＝，BF＝＝2，AB＝＝5，∴AF2+FB2＝AB2，∴∠AFB＝90°，在Rt△ABF中，cos∠BAF＝＝，∴cos∠CEA＝cos∠BAF＝，故答案为：．【点睛】本题考查了解直角三角形，平移的性质，平行线的性质，勾股定理及其逆定理，锐角三角函数，准确作出辅助线构造直角三角形是解题的关键．三．解答题（共7小题，共66分）17．（6分）在Rt△ABC中，∠C＝90°．根据下列条件求∠A的正弦、余弦、正切的值．（1）AC＝，BC＝2．（2）AB＝7，BC＝5．（3）AC＝BC．（4）sin B＝【思路点拨】（1）利用勾股定理求出AB即可解决问题．（2）利用勾股定理求出AC即可解决问题．（3）设AC＝k，BC＝k，利用勾股定理求出AB即可解决问题．（4）设AC＝5k，QAB＝13k，则BC＝12k，由此即可解决问题．【答案】解：（1）∵∠C＝90°，AC＝，BC＝2，∴AB＝＝＝，∴sin A＝＝＝，cos A＝＝＝，tan A＝＝＝．（2））∵∠C＝90°，AB＝7，BC＝5，∴AC＝＝＝2，∴sin A＝＝，cos A＝＝，tan A＝＝＝．（3）∵AC＝BC，∴可以假设AC＝k，BC＝k，∵∠C＝90°，∴AB＝＝2k，∴sin A＝＝＝，cos A＝＝＝，tan A＝＝＝．（4）∵sin B＝＝，∴可以假设AC＝5k，QAB＝13k，则BC＝12k，∴sin A＝＝＝，cos A＝＝＝，tan A＝＝＝．【点睛】本题考查解直角三角形，勾股定理等知识，解题的关键是熟练掌握基本知识，学会利用参数解决问题，属于中考常考题型．18．（8分）计算：（1）sin45°﹣cos60°+tan60°；（2）cos230°+sin230°﹣tan45°；（3）sin30°﹣tan30°+cos45°．【思路点拨】根据特殊角的三角函数值，代入计算即可．【答案】解：（1）原式＝﹣+＝+；（2）原式＝（）2+（）2﹣1＝+﹣1＝0；（3）原式＝﹣+＝﹣．【点睛】本题考查了特殊角的三角函数值及实数的运算．掌握特殊角的三角函数值是解决本题的关键．19．（8分）（2019秋•丽水期末）如图，在△ABC中，∠B＝45°，AC＝5，cos C＝，AD是BC边上的高线．（1）求AD的长；（2）求△ABC的面积．【思路点拨】（1）由高的定义可得出∠ADC＝∠ADB＝90°，在Rt△ACD中，由AC的长及cos C的值可求出CD的长，再利用勾股定理即可求出AD的长；（2）由∠B，∠ADB的度数可求出∠BAD的度数，进而可得出∠B＝∠BAD，利用等角对等边可得出BD 的长，再利用三角形的面积公式即可求出△ABC的面积．【答案】解：（1）∵AD⊥BC，∴∠ADC＝∠ADB＝90°．在Rt△ACD中，AC＝5，cos C＝，∴CD＝AC•cos C＝3，∴AD＝＝4．（2）∵∠B＝45°，∠ADB＝90°，∴∠BAD＝90°﹣∠B＝45°，∴∠B＝∠BAD，∴BD＝AD＝4，∴S△ABC＝AD•BC＝×4×（4+3）＝14．【点睛】本题考查了解直角三角形、勾股定理、等腰三角形的性质以及三角形的面积，解题的关键是：（1）通过解直角三角形及勾股定理，求出CD，AD的长；（2）利用等腰三角形的性质，找出BD的长．20．（10分）（2020•宿迁）如图，在一笔直的海岸线上有A，B两个观测站，A在B的正西方向，AB＝2km，从观测站A测得船C在北偏东45°的方向，从观测站B测得船C在北偏西30°的方向．求船C离观测站A的距离．【思路点拨】如图，过点C作CD⊥AB于点D，从而把斜三角形转化为两个直角三角形，然后在两个直角三角形中利用直角三角形的边角关系列出方程求解即可．【答案】解：如图，过点C作CD⊥AB于点D，则∠CAD＝∠ACD＝45°，∴AD＝CD，设AD＝x，则AC＝x，∴BD＝AB﹣AD＝2﹣x，∵∠CBD＝60°，在Rt△BCD中，∵tan∠CBD＝，∴＝，解得x＝3﹣．经检验，x＝3﹣是原方程的根．∴AC＝x＝（3﹣）＝（3﹣）km．答：船C离观测站A的距离为（3﹣）km．【点睛】本题考查了解直角三角形的应用﹣方向角问题，解决本题的关键是掌握方向角定义．21．（10分）（2020•拱墅区校级模拟）已知：如图，在△ABC中，AD⊥BC于点D，E是AD的中点，连接CE并延长交边AB于点F，AC＝13，BC＝8，cos∠ACB＝．（1）求tan∠DCE的值；（2）求的值．【思路点拨】（1）由三角函数定义求出CD＝5，由勾股定理得出AD＝12，求出ED＝AD＝6，由三角函数定义即可得出答案；（2）过D作DG∥CF交AB于点G，求出BD＝BC﹣CD＝3，由平行线分线段成比例定理得出＝＝，＝＝1，得出AF＝FG，设BG＝3x，则AF＝FG＝5x，BF＝FG+BG＝8x，即可得出答案．【答案】解：（1）∵AD⊥BC，∴∠ADC＝90°，在Rt△ADC中，AC＝13，cos∠ACB＝＝，∴CD＝5，由勾股定理得：AD＝＝12，∵E是AD的中点，∴ED＝AD＝6，∴tan∠DCE＝＝；（2）过D作DG∥CF交AB于点G，如图所示：∵BC＝8，CD＝5，∴BD＝BC﹣CD＝3，∵DG∥CF，∴＝＝，＝＝1，∴AF＝FG，设BG＝3x，则AF＝FG＝5x，BF＝FG+BG＝8x∴＝．【点睛】本题考查了解直角三角形、勾股定理、平行线分线段成比例定理等知识；熟练掌握解直角三角形和平行线分线段成比例定理是解题的关键．22．（12分）（2020•吉州区一模）“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图1所示的“三等分角仪”能三等分任一角．其抽象示意图如图2所示，由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC＝CD＝DE＝5cm，点D，E可在槽中滑动．（1）求证：∠BDE＝3∠BOE．（2）若OD＝8cm．①求∠BDE的度数；②求点D到OA的距离．（参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75，sin66°≈0.92，cos66°≈0.40，tan66°≈2.24）【思路点拨】（1）根据等腰三角形的性质得到∠O＝∠CDO，∠DCE＝∠CED，根据三角形外角的性质即可得到结论；（2）①过C作CF⊥CD于F，根据等腰三角形的性质得到OF＝DF＝OD＝4，根据三角函数的定义即可得到结论；②过D作DH⊥OA于H，根据三角函数的定义即可得到结论．【答案】（1）证明：∵OC＝CD＝DE，∴∠O＝∠CDO，∠DCE＝∠CED，∵∠DCE＝∠O+∠CDO＝2∠O，∴∠CED＝2∠O，∴∠BDE＝∠O+∠DEC＝∠O+2∠O＝3∠BOE；（2）解：①过C作CF⊥CD于F，∵CO＝CD，∴OF＝DF＝OD＝4，∵OC＝5，∴cos∠BOE＝＝＝0.8，∴∠BOE＝36°，∴∠BDE＝2∠BOE＝108°；②过D作DH⊥OA于H，∵∠BOE＝36°，OD＝8，∴DH＝OD•sin36°＝8×0.6＝4.8，即点D到OA的距离4.8cm．【点睛】本题考查了解直角三角形的应用，等腰三角形的性质，三角形外角的性质，正确的作出辅助线构造直角三角形是解题的关键．23．（12分）（2020•海陵区一模）水坝的横截面是梯形ABCD，现测得坝顶DC＝4m，坡面AD的坡度i为1：1，坡面BC的坡角β为60°，坝高3m，（≈1.73）求：（1）坝底AB的长（精确到0.1）；（2）水利部门为了加固水坝，在保持坝顶CD不变的情况下降低AD的坡度（如图），使新坡面DE的坡度i为1：，原水坝底部正前方2.5m处有一千年古树，此加固工程对古树是否有影响？请说明理由．【思路点拨】（1）分别过C、D作CF⊥AB，DH⊥AB，垂足分别为F、H，易得四边形CDHF是矩形，从而CD＝HF＝4m，DH＝CF＝3m，在Rt△ADH中，由坡度i＝1：1，易得AH＝DH＝3m，在Rt△BCF 中，坡面BC的坡角β为60°，坝高3m，易得BF，则AB＝AH+HF+FB＝8.7m；（2）由题意得，Rt△EDH中，由坡面DE的坡度i为1：，易得AE＝EH﹣AH的值进而与2.5m比较即可．【答案】解：（1）如图，分别过C、D作CF⊥AB，DH⊥AB，垂足分别为F、H，得四边形CDHF是矩形，∴CD＝HF＝4m，DH＝CF＝3m，在Rt△ADH中，由坡度i＝1：1，得AH＝DH＝3m，在Rt△BCF中，∠B＝60°，CF＝3m，得BF＝m，则AB＝AH+HF+FB＝7+1.7≈8.7m；则坝底AB的长约为8.7m；（2）由题意得，Rt△EDH中，DH：EH＝1：，∴EH＝3m，则AE＝EH﹣AH＝3﹣3≈2.2m，2.2m＜2.5m，所以没有影响．【点睛】本题考查了解直角三角形的应用﹣坡度坡角问题，解决本题的关键是掌握坡度坡角定义．。

解直角三角形测试题与答案

解直角三角形测试题与答案一、选择题（每小题 5 分，共 25 分）1、在直角三角形中，若一个锐角为 30°，斜边与较小直角边的和为 12，则斜边的长为（）A 4B 6C 8D 10答案：C解析：设较小直角边为 x，则斜边为 2x，由题意得 2x ＋ x ＝ 12，解得 x ＝ 4，所以斜边为 8。

2、在 Rt△ABC 中，∠C ＝ 90°，sinA ＝，则 tanB 的值为（）A B C D答案：D解析：因为 sinA ＝，设 BC ＝ 4x，AB ＝ 5x，则 AC ＝ 3x，所以tanB ＝。

3、如图，在△ABC 中，∠C ＝ 90°，AC ＝ 8，∠A 的平分线 AD ＝，则 BC 的长为（）A 12B 10C 8D 6答案：B解析：因为 AD 是∠A 的平分线，所以∠CAD ＝∠BAC。

在Rt△ACD 中，cos∠CAD ＝，即，解得 CD ＝ 6。

在 Rt△ABC 中，BC ＝。

4、已知在 Rt△ABC 中，∠C ＝ 90°，tanA ＝，则 sinA 的值为（）A B C D答案：B解析：设 BC ＝ 3x，AC ＝ 4x，则 AB ＝ 5x，所以 sinA ＝。

5、如图，在菱形 ABCD 中，DE⊥AB，cosA ＝，BE ＝ 2，则tan∠DBE 的值是（）A B 2C D答案：C解析：因为 cosA ＝，设 AD ＝ 5x，AE ＝ 3x，则 DE ＝ 4x。

因为BE ＝ 2，所以 5x 3x ＝ 2，解得 x ＝ 1，所以 DE ＝ 4。

在 Rt△BDE 中，tan∠DBE ＝。

二、填空题（每小题 5 分，共 25 分）1、在 Rt△ABC 中，∠C ＝ 90°，若 sinA ＝，AB ＝ 10，则 BC＝＿_______。

答案：6解析：因为 sinA ＝，所以，设 BC ＝ 3x，AB ＝ 5x，因为 AB ＝10，所以 5x ＝ 10，解得 x ＝ 2，所以 BC ＝ 6。

《解直角三角形》全章复习与巩固(基础篇)九年级数学下册基础知识专项讲练

专题1.17《解直角三角形》全章复习与巩固（基础篇）（专项练习）一、单选题1．2sin60°的值等于（）A ．12B ．3C ．2D 2．如图，在Rt ABC △中，90B ∠=︒，下列结论中正确的是（）A ．sin BC A AB=B ．cos BC A AC=C ．tan AB C BC=D ．cos AC C BC=3．如图，在坡角为α的山坡上栽树，要求相邻两树之间的水平距离为6米，那么相邻两树在坡面上的距离AB 为（）A ．6cos αB ．6cos αC ．6sin αD ．6sin α4．如图，为了测量河岸A 、B 两地间的距离，在与AB 垂直的方向上取点C ，测得AC ＝a ，ABC α∠=，那么A 、B 两地的距离等于（）A ．tan a αB ．tan a α⋅C ．sin a α⋅D ．cos a α⋅5．点()sin 60,cos30︒︒关于y 轴对称的点的坐标是（）．A ．12⎛- ⎝⎭B ．1,2⎛ ⎝⎭C ．22⎛⎫- ⎪ ⎪⎝⎭D ．⎝⎭6．如图，在平面直角坐标系中，点A 的坐标为(﹣1，2)，以点O 为圆心，将线段OA 逆时针旋转，使点A 落在x 轴的负半轴上点B 处，则点B 的横坐标为（）AB C D7．已知，斜坡的坡度i =1：2，小明沿斜坡的坡面走了100米，则小明上升的距离是（）A ．B ．20米C ．D ．1003米8．为扩大网络信号的辐射范围，某通信公司在一座小山上新建了一座大型的网络信号发射塔．如图，在高为12米的建筑物DE 的顶部测得信号发射塔AB 顶端的仰角∠FEA ＝56°，建筑物DE 的底部D 到山脚底部C 的距离DC ＝16米，小山坡面BC 的坡度（或坡比）i ＝1：0.75，坡长BC ＝40米（建筑物DE 、小山坡BC 和网络信号发射塔AB 的剖面图在同一平面内，信号发射塔AB 与水平线DC 垂直），则信号发射塔AB 的高约为（）（参考数据：sin56°≈0.83，cos56°≈0.56，tan56°≈1.48）A ．71.4米B ．59.2米C ．48.2米D ．39.2米9．如图，在ABC ∆中，90ACB ∠=︒．边BC 在x 轴上，顶点,A B 的坐标分别为()2,6-和()7,0．将正方形OCDE 沿x 轴向右平移当点E 落在AB 边上时，点D 的坐标为（）A ．3,22⎛⎫ ⎪⎝⎭B ．()2,2C ．11,24⎛⎫ ⎪⎝⎭D ．()4,210．某车库出口安装的栏杆如图所示，点A 是栏杆转动的支点，点E 是栏杆两段的联结点．当车辆经过时，栏杆AEF 最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB ⊥BC ，EF ∥BC ，∠AEF ＝143°，AB ＝1.18米，AE ＝1.2米，那么适合该地下车库的车辆限高标志牌为（）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）A ．B ．C ．D ．二、填空题11．在Rt △ABC 中，∠C ＝90°，AB ＝2，BC sin2A＝_____．12．若关于x 的方程x 2+sin α=0有两个相等的实数根，则锐角α的度数为___．13．如图，P （12，a ）在反比例函数60y x=图象上，PH ⊥x 轴于H ，则tan ∠POH 的值为_____．14．如图，在矩形ABCD 中，DE AC ⊥，垂足为点E ．若4sin 5ADE ∠=，4=AD ，则AB 的长为______．15．如图所示的网格是正方形网格，图形的各个顶点均为格点，则∠1+∠2=_____．16．如图，在ABC ∆中，1sin 3B =，tan C =3AB =，则AC 的长为_____．17．如图，ABC 的顶点B C 、的坐标分别是(1,0)、，且90,30ABC A ∠=︒∠=︒，则顶点A 的坐标是_____．18．如图，在菱形ABCD 中，∠A =60°，AB =6．折叠该菱形，使点A 落在边BC 上的点M 处，折痕分别与边AB ，AD 交于点E ，F ．当点M 与点B 重合时，EF 的长为________；当点M 的位置变化时，DF 长的最大值为________．三、解答题19．计算：（1sin 602︒；（2）26tan 30cos30tan 602sin 45cos 60︒-︒︒-︒+︒ ．20．如图，在Rt △ABC 中，∠C =90°，D 是BC 边上一点，AC =2，CD =1，设∠CAD =α．(1)求sin α、cos α、tan α的值；(2)若∠B =∠CAD ，求BD 的长．21．如图，为了测得旗杆AB 的高度，小明在D 处用高为1m 的测角仪CD ，测得旗杆顶点A 的仰角为45°，再向旗杆方向前进10m ，又测得旗杆顶点A 的仰角为60°，求旗杆AB 的高度．22．如图，在平面直角坐标系中，已知△ABC 三个顶点的坐标分别是A （2，2），B （4，0），C （4，﹣4）．（1）请在图中，画出△ABC向左平移6个单位长度后得到的△A1B1C1；（2）以点O为位似中心，将△ABC缩小为原来的12，得到△A2B2C2，请在图中y轴右侧，画出△A2B2C2，并求出∠A2C2B2的正弦值．23．如图，大楼底右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D 处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上）．已知AB＝80m，DE＝10m，求障碍物B，C两点间的距离．（结果保留根号）24．如图，某校教学楼AB后方有一斜坡，已知斜坡CD的长为12米，坡角α为60°．根据有关部门的规定，∠α≤39°时，才能避免滑坡危险．学校为了消除安全隐患，决定对斜坡CD进行改造，在保持坡脚C不动的情况下，学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全？（结果取整数）（参考数据：sin 39°≈0.63，cos 39°≈0.78，tan 39°≈0.81，≈1.41）参考答案1．D【分析】根据特殊锐角三角函数值代入计算即可．解：2sin60°＝故选：D ．【点拨】本题考查特殊角三角函数值，熟知sin60°的值是正确计算的关键．2．C【分析】根据锐角三角函数的定义解答．解：在Rt △ABC 中，∠B =90°，则sin ,cos ,tan ,cos BC AB AB BCA A C C AC AC BC AC====．故选：C ．【点拨】本题考查锐角三角函数，熟练掌握锐角三角函数的定义是解题关键．3．B【分析】根据余弦的定义计算，判断即可．解：在Rt △ABC 中，6BC =米，ABC α∠=，∵cos BCABC AB∠=，∴6cos BC AB ABC coa α==∠，故选：B ．【点拨】本题考查的是解直角三角形的应用坡度坡角问题，掌握坡度坡角的概念、熟记锐角三角函数的定义是解题的关键．4．A【分析】根据正切的定义计算选择即可．解：∵tanα=ACAB，∴AB =tan tan AC aαα=，故选A ．【点拨】本题考查了正切的定义即对边比邻边，熟练掌握正切的定义是解题的关键．5．C【分析】先利用特殊角的三角函数值得出点的坐标，再写出其关于y 轴对称的坐标即可．解：∵sin60°cos30°，）关于y 轴对称的点的坐标是（．故选：C ．【点拨】本题考查了特殊角的三角函数值和关于坐标轴对称的点的特征，掌握特殊角的三角函数值是解决本题的关键．6．C【分析】利用勾股定理求出OA ，可得结论．解：∵A （﹣1，2），∴OA由旋转的性质可知，OB ＝OA∴B 0）．故选：C ．【点拨】本题考查坐标与图形变化-旋转，解直角三角形等知识，解题的关键是利用勾股定理求出OA 即可．7．A【分析】根据坡度意思可知1tan 2A ∠=，设BC h =米，则2AC h =米，由勾股定理可得：222AB AC BC =+，即2221004h h =+，求出h 即可．解：如图：由题意可知：1tan 2A ∠=，100AB =米，设BC h =米，则2AC h =米，由勾股定理可得：222AB AC BC =+，即2221004h h =+，解得：h =米，h =-．故选：A【点拨】本题考查勾股定理，坡度坡比问题，解题的关键是理解坡度的意思，找出BC ，AC之间的关系．8．D【分析】延长EF交AB于点H，DC⊥AB于点G，可得四边形EDGH是矩形，根据小山坡面BC的坡度i＝1：0.75，即43BGCG=，求得BG＝32，CG＝24，再根据三角函数即可求出信号发射塔AB的高．解：如图，延长EF交AB于点H，DC⊥AB于点G，∵ED⊥DG，∴四边形EDGH是矩形，∴GH＝ED＝12，∵小山坡面BC的坡度i＝1：0.75，即43 BGCG=，设BG＝4x，CG＝3x，则BC x，∵BC＝40，∴5x＝40，解得x＝8，∴BG＝32，CG＝24，∴EH＝DG＝DC+CG＝16+24＝40，BH＝BG﹣GH＝32﹣12＝20，在Rt△AEH中，∠AEH＝56°，∴AH＝EH•tan56°≈40×1.48≈59.2，∴AB＝AH﹣BH＝59.2﹣20＝39.2（米）．答：信号发射塔AB的高约为39.2米．故选：D．【点拨】本题主要考查解直角三角形，熟练掌握三角函数是解题的关键．9．B【分析】先画出E 落在AB 上的示意图，如图，根据锐角三角函数求解O B '的长度，结合正方形的性质，从而可得答案．解：由题意知：()2,0,C - 四边形COED 为正方形，,CO CD OE ∴==90,DCO ∠=︒()()2,2,0,2,D E ∴-如图，当E 落在AB 上时，()()2,6,7,0,A B - 6,9,AC BC ∴==由tan ,AC EO ABC BC O B'∠=='62,9O B∴='3,O B '∴=734,2,OO OC ''∴=-==()2,2.D ∴故选.B 【点拨】本题考查的是平移的性质的应用，同时考查了正方形的性质，图形与坐标，锐角三角函数，掌握以上知识是解题的关键．10．A【分析】延长BA 、FE ，交于点D ，根据AB ⊥BC ，EF ∥BC 知∠ADE =90°，由∠AEF =143°知∠AED =37°，根据sin ∠AED AD AE=，AE =1.2米求出AD 的长，继而可得BD 的值，从而得出答案．解：如图，延长BA 、FE ，交于点D ．∵AB ⊥BC ，EF ∥BC ，∴BD ⊥DF ，即∠ADE =90°．∵∠AEF =143°，∴∠AED =37°．在Rt △ADE 中，∵sin ∠AED AD AE=，AE =1.2米，∴AD =AE •sin ∠AED =1.2×sin37°≈0.72(米)，则BD =AB +AD =1.18+0.72=1.9(米)．故选：A ．【点拨】本题考查了解直角三角形的应用，解题的关键是结合题意构建直角三角形，并熟练掌握正弦函数的概念．11．12【分析】根据∠A 的正弦求出∠A ＝60°，再根据30°的正弦值求解即可．解：∵sin BC A AB ==∴∠A ＝60°，∴1sin sin 3022A ︒==．故答案为12．【点拨】本题考查了特殊角的三角函数值，熟记30°、45°、60°角的三角函数值是解题的关键．12．30°##30度解：∵关于x 的方程2sin 0x α+=有两个相等的实数根，∴(241sin 0 ，α=-⨯⨯=解得：1sin 2α=∴锐角α的度数为30°．故答案为∶30°13．512解：∵P （12，a ）在反比例函数60y x =图象上，∴a=6012=5，∵PH ⊥x 轴于H ，∴PH=5，OH=12，∴tan ∠POH=512，故答案为512．14．3【分析】在Rt ADE △中，由正弦定义解得165AE =，再由勾股定理解得DE 的长，根据同角的余角相等，得到sin sin ADE ECD ∠=∠，最后根据正弦定义解得CD 的长即可解题．解：在Rt ADE △中，4sin 5AE ADE AD ∠==4AD = 165AE ∴=125DE ∴===DE AC⊥ 90ADE EDC EDC ECD ∴∠+∠=∠+∠=︒ADE ECD∴∠=∠4sin sin 5DE ADE ECD CD ∴∠=∠==534CD DE ∴=⋅=在矩形ABCD 中，3AB CD ==故答案为：3．【点拨】本题考查矩形的性质、正弦、勾股定理等知识，是重要考点，难度较易，掌握相关知识是解题关键．15．45°【分析】根据等角的正切值相等得出∠1=∠3，再根据特殊角的三角函数值即可得出答案．解：如图所示：由题意可得：11tan 3,tan 122BC CF AB EF ∠==∠==∴∠1=∠3，tan 1FM FAM AM∠== 122345FAM ∴∠+∠=∠+∠=∠=︒故答案为：45°．【点拨】本题考查了特殊角的三角函数以及等角三角函数关系，由图得出∠1=∠3是解题的关键．16【分析】过A 作AD 垂直于BC ，在直角三角形ABD 中，利用锐角三角函数定义求出AD 的长，在直角三角形ACD 中，利用锐角三角函数定义求出CD 的长，再利用勾股定理求出AC 的长即可．解：过A 作AD BC ⊥，在Rt ABD ∆中，1sin 3B =，3AB =，∴sin 1AD AB B =⋅=，在Rt ACD ∆中，tan 2C =，∴AD CD =CD ，根据勾股定理得：AC =．【点拨】此题考查了解直角三角形，涉及的知识有：锐角三角函数定义，以及勾股定理，熟练掌握各自的性质是解本题的关键．17．【分析】根据B C 、的坐标求得BC 的长度,60CBO ∠=︒，利用30度角所对的直角边等于斜边的一半，求得AC 的长度，即点A 的横坐标，易得//AC x 轴，则C 的纵坐标即A 的纵坐标．解：B C 、的坐标分别是(1,0)、2BC ∴=tan OC CBOOB∴∠==60CBO ∴∠=︒90,30ABC A ∠=︒∠=︒60,24ACB AC BC ∴∠=︒==//AC x ∴轴A ∴．故答案为：．【点拨】本题考查了含30°角的直角三角形，用到的知识点有特殊角的三角函数，在直角三角形中，30度角所对的直角边等于斜边的一半，熟记特殊角的三角函数是解题的关键．18．6-【分析】当点M 与点B 重合时，EF 垂直平分AB ，利用三角函数即可求得EF 的长；根据折叠的性质可知，AF =FM ,若DF 取最大值，则FM 取最小值，即为边AD 与BC 的距离DG ，即可求解.解：当点M 与点B 重合时，由折叠的性质知EF 垂直平分AB ，∴AE =EB =12AB =3，在Rt △AEF 中，∠A =60°，AE =3，tan60°=EF AB，∴EF当AF 长取得最小值时，DF 长取得最大值，由折叠的性质知EF 垂直平分AM ，则AF =FM ，∴FM ⊥BC 时，FM 长取得最小值，此时DF 长取得最大值，过点D 作DG ⊥BC 于点C ，则四边形DGMF 为矩形，∴FM =DG ，在Rt △DGC 中，∠C =∠A =60°，DC =AB =6，∴DG =DC∴DF 长的最大值为AD -AF =AD -FM =AD -DG故答案为：【点拨】本题考查了菱形的性质，折叠的性质，解直角三角形，解题的关键是灵活运用所学知识解决问题．19．（1（2）1【分析】（1）根据二次根式与特殊角的三角函数值即可求解；（2）根据特殊角的三角函数值即可求解．解：（1）原式＝11232-＝16（2）原式21316221222=⨯-⨯=--=-【定睛】此题主要考查实数的运算。

解直角三角形单元测试题(基础题) 含答案

解直角三角形单元测试题一、选择题：1、在△ABC中，若三边BC、CA、AB满足 BC:CA:AB=5:12:13，则sinA的值是( )A. B. C. D.2、已知∠A为锐角，且sinA≤，则（）A.0°≤A≤60°B.60°≤A ＜90°C.0°＜A ≤30°D.30°≤A≤90°3、在Rt△ABC中，∠C=90°，∠B=60°，那么sinA+cosB的值为（）A.1B.C.D.4、已知在Rt△ABC中，∠C=90°，sinA=，则tanB的值为（）A． B． C． D．5、如图，点A、B、O是正方形网格上的三个格点，⊙O的半径为OA，点P是优弧上的一点，则cos∠APB的值是（）A．45° B．1 C． D．无法确定6、如图，A、B、C三点在正方形网格线的交点处，若将△ABC绕着点A逆时针旋转得到△AC′B′，则tanB′的值为（）A． B． C． D．7、如图，已知在△ABC中，cosA=，BE、CF分别是AC、AB边上的高，联结EF，那么△AEF和△ABC的周长比为（）A．1：2 B．1：3 C．1：4 D．1：98、如图，小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4 m，测得仰角为60°.已知小敏同学身高(AB)为1.6 m,则这棵树的高度约为(结果精确到0.1 m,≈1.73)( )A．3.5 m B．3.6 m C．4.3 m D．5.1 m9、如图，有一轮船在A处测得南偏东30°方向上有一小岛P，轮船沿正南方向航行至B处，测得小岛P在南偏东45°方向上，按原方向再航行10海里至C处，测得小岛P在正东方向上，则A，B之间的距离是( )A．10海里 B．(10－10)海里 C．10海里 D．(10－10)海里10、如图，在△ABC中，∠BAC=90°，AB=AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为( )A. B.－1 C．2－ D.11、如图是拦水坝的横断面，斜坡AB的水平宽度为12米，斜面坡度为1：2，则斜坡AB的长为( )A.4米B.6米C.12米 D． 24米12、如图，在高度是90米的小山A处测得建筑物CD顶部C处的仰角为30°，底部D处的俯角为45°，则这个建筑物的高度CD是（）（结果可以保留根号）A．30（3+）米 B．45（2+）米C．30（1+3）米 D．45（1+）米二、填空题:13、求值：sin60°•tan30°= ．14、如图，∠1的正切值等于．15、如图，在菱形ABCD中，DE⊥AB，，BE=2，则________.16、如图，一人乘雪橇沿坡比1:的斜坡笔直滑下72米，那么他下降的高度为米.17、如图，小岛在港口的南偏东45°方向、距离港口81海里处.甲船从出发，沿方向以9海里/h的速度驶向港口;乙船从港口出发，沿南偏西60°方向，以18海里/h的速度驶离港口.现两船同时出发，当甲船在乙船的正东方向时，行驶的时间为h.(结果保留根号)18、如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点P，则tan∠APD的值是．三、计算题:19、.20、计算：四、解答题:21、已知顶点为A(2，一1)的抛物线与y轴交于点B，与x轴交于C、D两点，点C坐标(1，O)；(1)求这条抛物线的表达式；(2)连接AB、BD、DA，求cos∠ABD的大小；(3)点P在x轴正半轴上位于点D的右侧，如果∠APB=45°，求点P的坐标．22、如图，在△ABC中，∠ACB=90°，AB=5，tanA=，将△ABC沿直线l翻折，恰好使点A与点B重合，直线l分别交边AB、AC于点D、E；（1）求△ABC的面积；（2）求sin∠CBE的值．23、如图，AD是△ABC的中线，tanB=，cosC=，AC=.求：(1)BC的长；(2)sin∠ADC的值．24、先化简，再求代数式的值÷（﹣），其中a=2cos30°﹣tan45°，b=2sin30°．25、如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m,DE=10m,求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据：≈1.414，≈1.732）26、南沙群岛是我国的固有领土，现在我南海渔民要在南沙群岛某海岛附近进行捕鱼作业，当渔船航行至B处时，测得该岛位于正北方向20（1＋）海里的C处，为防止某国的巡警干扰，就请求我A处的鱼监船前往C处护航，已知C位于A处的北偏东45°方向上，A位于B的北偏西30°的方向上，求A、C之间的距离．27、如图1，某超市从底楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，求二楼的层高BC（精确到0.1米）．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）参考答案1、C2、C3、A4、A5、C6、B7、B8、D9、D10、A11、B12、A13、答案为：．14、答案为：．15、答案为：216、答案为：3617、答案为：18、答案为：2，19、.20、=1+2-（+1）-+2=221、解：（1）∵顶点为A（2，﹣1）的抛物线经过点C（1，0），∴可以假设抛物线的解析式为y=a（x﹣2）2﹣1，把（1，0）代入可得a=1，∴抛物线的解析式为y=x2﹣4x+3．（2）令y=0，x2﹣4x+3=0，解得x=1或3，∴C（1，0），D（3，0），令x=0，y=3, ∴B（0,3）∵OB=OD=3，∴∠BDO=45°，∵A（2，﹣1），D（3，0），∴∠ADO=45°，∴∠BD A=90°，∴（3）∵∠BDO=∠DPB+∠DBP=45°，∠APB=∠DPB+∠DPA=45°，∴∠DBP=∠APD，∵∠PDB=∠ADP=135°，∴△PDB∽△ADP，∴PD2=BD•AD=3=6，∴PD=，∴OP=3+，∴点P（3+，0）．22、解：（1）∵∠ACB=90°，tanA=，∴=，∴AC=2BC，在Rt△ABC中，BC2+AC2=AB2，即BC2+4BC2=25，解得BC=，所以，AC=2，△ABC的面积=AC•BC=××2=5；（2）设CE=x，则AE=AC﹣CE=2﹣x，∵△ABC沿直线l翻折点A与点B重合，∴BE=AE=2﹣x，在Rt△BCE中，BC2+CE2=BE2，即2+x2=（2﹣x）2，解得x=，所以，CE=，BE=2﹣x=2﹣=，所以，sin∠CBE===．23、(1)过点A作AE⊥BC于点E，∵cosC＝，∴∠C＝45°.∴在Rt△ACE中，CE＝AC·cosC＝1.∴AE＝CE＝1.在Rt△ABE中，tanB＝，即＝，∴BE＝3AE＝3.∴BC＝BE＋CE＝4.(2)∵AD是△ABC的中线，∴CD＝BC＝2.∴DE＝CD－CE＝1.∵AE⊥BC，DE＝AE，∴∠ADC＝45°.∴sin∠ADC＝.24、解：原式=÷=×=，当a=2cos30°﹣tan45°=2×﹣1=﹣1，b=2sin30°=2×=1时，原式===．25、解：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．则DE=BF=CH=10m，在直角△ADF中，∵AF=80m﹣10m=70m，∠ADF=45°，∴DF=AF=70m．在直角△CDE中，∵DE=10m，∠DCE=30°，∴CE===10（m），∴BC=BE﹣CE=70﹣10≈70﹣17.32≈52.7（m）．答：障碍物B，C两点间的距离约为52.7m．26、解：作AD⊥BC于D，设AD＝x，依题意可知∠ABC＝30°，∠ACB＝45°，在Rt△ADC中，CD＝AD＝x，在Rt△ADB中∵＝tan30°，∴BD＝AD＝x，∵BC＝CD＋BD＝x＋x＝20（1＋），即x＋x＝20（1＋），解之得x＝20，∴AC＝AD＝20．∴A、C之间的距离为20海里．27、解：延长CB交PQ于点D．∵MN∥PQ，BC⊥MN，∴BC⊥PQ．∵自动扶梯AB的坡度为1：2.4，∴．设BD=5k米，AD=12k米，则AB=13k米．∵AB=13米，∴k=1，∴BD=5米，AD=12米．在Rt△CDA中，∠CDA=90゜，∠CAD=42°，∴CD=AD•tan∠CAD≈12×0.90≈10.8米，∴BC≈5.8米．答：二楼的层高BC约为5.8米．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

中考数学专题测试卷（九）（基础版）
解直角三角形
(时间：90分钟满分：120分)
班级姓名学号成绩
一、选择题：（每小题3分，共36分）
1. 由直角三角形中的已知元素，求出所有未知元素的过程，叫做解直角三角形，已知一个直角三角形中：①两条边的长度，②两个锐角的度数，③一个锐角的度数和一条边的长度．利用上述条件中的一个，能解这个直角三角形的是（）
A ．①②
B ．①③
C ．②③
D ．①②③
2. 在Rt ABC ∆中，︒=∠90C ，5=AB ，2=AC ，则A cos 的值是（）
A.
521 B.52 C.2
21 D.25 3. 如图，Rt △ABC ,∠C =900,AB =6,cosB =23 ,则BC 的长为（）（A ）4 (B )2 5 (C ) 18 1313 (D ) 121313 4. 把△ABC 三边的长度都扩大为原来的3倍，则锐角A 的正弦函数值【】 A ．不变 B ．缩小为原来的13
C ．扩大为原来的3倍
D ．不能确定
5. 在△ABC 中，若22cos =A ，3tan =B ，则这个三角形一定是（）
（A ）锐角三角形（B ）直角三角形（C ）钝角三角形（D ）等腰三角形
6. 如图是某水库大坝横断面示意图．其中AB 、CD 分别表示水库上下底面的水平线，∠ABC =120°，BC 的长是50m ，则水库大坝的高度h 是（）
A ．25m
B ．25m
C ．25m
D ．m
7. 如图，某游乐场一山顶滑梯的高为h ，滑梯的坡角为α，那么滑梯长l 为( )
A ．h sin a
B ．h tan a
C ．h cos a
D ．h ·sin α 8. 点M （-sin60°，cos60°）关于x 轴对称的点的坐标是（）
A 、（23，2
1） B 、（-23，-21） C 、（-23，21） D 、（-21，-23）第3
A B C h (第7题图) l a 第3题 A
B C 第9题
9. 如图，小正方形边长为1，连接小正方形的三个顶点，可得△ABC ，则AC 边上
的高是（）．
A ．3510
B ．322
C ．355
D ．455
10. 如图，一艘海轮位于灯塔P 的南偏东70°方向的M 处，它以每小时40海里的
速度向正北方向航行，2小时后到达位于灯塔P 的北偏东40°的N 处，则N 处与灯塔P 的距离为 ( )
A ．40海里
B ．60海里
C ．70海里
D ．80海里
11. 如图，两条宽度都为1的纸条，交叉重叠放在一起，且它们的交角为α，则它们
重叠部分（图中阻影部分）的面积为（）
A . αsin 1
B . α
cos 1 C . αsin D . 1
12. 如图，从热气球C 处测得地面A 、B 两点的俯角分别为30°、45°，如果此时热
气球C 处的高度CD 为100米，点A 、D 、B 在同一直线上，则AB 两点煌距离是
【】
A ．200米
B ．2003米
C ．2203米
D ．100(3＋1)米
二、填空题：（每小题3分，共18分）
13. 在△ABC 中∠C =90°，AB =5，BC =4，则tanA = .
14. 计算：．
15. 某斜坡的坡度为i=1：3，则该斜坡的坡角为_________度．
16. 如图，角α的顶点为O ，它的一边在x 轴的正半轴上，另一边OA 上有一点P （3，
4），则 sin α= ．
17. 如图，将45°的∠AOB 按下面的方式放置在一把刻度尺上：顶点O 与尺下沿的端点重合，OA 与尺下沿重合.OB 与尺上沿的交点B 在尺上的读书恰为2厘米，若按相同的方式将37°的∠AOC 放置在该刻度尺上，则OC 与尺上沿的交点C 在尺上的读数为厘米.（结果精确到0.1厘米，参考数据
sin 370≈0.60,cos 370≈0.80,tan 370≈0.75）
18. 在一自助夏令营活动中，小明同学从营地A 出发，要到A 地的北偏东
60°方向的
C 处，他先沿正东方向走了200m 到达
B 地，再沿北偏东30°方向走，恰能到达
目的地C （如图），那么，由此可知，B 、C 两地相距
m ．
第10
第11题第12题第16题第17C
B A O
4321第18
三、计算题：（每小题6分，共12分）
19. 如图，在△ABC 中，∠A =30°，∠B =45°，AC =32，求AB 的长。

20. 如图，在一次测量活动中，小华站在离旗杆底部(B 处)6米的D 处，仰望旗杆顶
端A ，测得仰角为60°，眼睛离地面的距离ED 为1.5米．试帮助小华求出旗杆AB 的高度．(结果精确到0.1米，3 1.732 )
四、解答题：（每小题8分，共16分）
21. 如图，一段河坝的横截面为梯形ABCD ，试根据图中数据，求出坝底宽AD ．（i =CE ：
ED ，单位：m ）
22. 国家海洋局将中国钓鱼岛最高峰命名为“高
华峰”，并对钓鱼岛进行常态化立体巡航．，
在一次巡航过程中，巡航飞机飞行高度为
2001米，在点A 测得高华峰顶F 点的俯角为
30°，保持方向不变前进1200米到达B 点后
测得F 点俯角为45°，如图．请据此计算钓鱼岛的最高海拔高度多少米．（结果保留根号）
五、解答题：（每小题9分，共18分）
23. 如图，在△ABC 中，AD 是BC 边上的高，AE 是BC 边上的中线，∠C =45°，sinB =，
AD =1．（1）求BC 的长；（2）求tan ∠DAE 的值．
第19题
第23
第
20第21题
第
22
24. 如图，一居民楼底部B 与山脚P 位于同一水平线上，小李在P 处测得居民楼顶
A 的仰角为60°，然后他从P 处沿坡角为45°的山坡上走到C 处，这时，PC =30m ，点C 与点A 在同一水平线上，A 、
B 、P 、
C 在同一平面内．
（1）求居民楼AB 的高度；
（2）求C 、A 之间的距离．（结果保留根号）
六、解答题：（25题9分，26题11分，共20分）
25. 如图，小山顶上有一信号塔AB ，山坡BC 的倾角为30°，现为了测量塔高AB ，
测量人员选择山脚C 处为一测量点，测得塔顶仰角为45°，然后顺山坡向上行走100米到达E 处，再测得塔顶仰角为60°，求塔高AB （结果保留整数，≈1.73
，≈1.41）
26. 如图在Rt △ABC 中，∠ACB=90°，D 是边AB 的中点，BE ⊥CD ，垂足为点E ．已
知AC=15，cosA=
35
．（1）求线段CD 的长；（2）求sin ∠DBE 的值．
C P A B 4560（第24题图）。