三角形的外心及性质
三角形的外心和性质

三角形的外心和性质三角形是平面几何中的基本图形,它具有独特的性质和特征。
其中一项重要的性质就是它们具有外心。
本文将探讨三角形的外心及其相关性质。
一、三角形的外心外心是指一个三角形外接圆的圆心,也是三条外接线的交点。
在任意给定的三角形ABC中,存在一个唯一的外接圆,而外接圆的圆心即为三角形的外心。
二、三角形外心的性质1. 外心到三角形三个顶点的距离相等在一个三角形的外接圆中,外心到三个顶点的距离是相等的。
换句话说,在三角形ABC中,OA = OB = OC,其中O表示外心,A、B、C为三个顶点。
2. 外心位于三角形三条外角的角平分线的交点三角形的三条外角的角平分线交于一点,这个交点就是三角形的外心。
即∠BOC = ∠A,∠COA = ∠B,∠AOB = ∠C。
3. 外心是三角形内心和垂心的共轭点对于任意一个三角形ABC,外心O是其内心I和垂心H的共轭点。
这意味着OI与OH关于三角形的边相互垂直。
4. 外心到各顶点的连线是三角形的高的中垂线在一个三角形ABC中,外心O到三个顶点的连线分别为OA、OB、OC,这些连线同时也是三角形ABC的高线和中垂线。
即OA ⊥ BC,OB ⊥ AC,OC ⊥ AB。
5. 外心是三角形周长最小的圆的圆心在所有可以包围一个给定三角形的圆中,外接圆具有最小的周长。
这也意味着外心到三个顶点的距离是最小的。
三、三角形外心的计算方法已知一个三角形的三个顶点的坐标,以下是计算外心坐标的方法:1. 计算三角形ABC的边长a、b、c;2. 计算三角形ABC的三个顶点所在直线的中垂线斜率的倒数k1、k2、k3;3. 根据垂直直线的斜率关系,计算垂直于各边的中垂线方程常数项c1、c2、c3;4. 解联立方程组,得到外心的坐标(x, y)。
四、总结三角形的外心是指三角形外接圆的圆心,具有多项重要性质和特点。
在解决一些与三角形相关的问题时,外心的概念和性质往往会被广泛应用。
同时,通过给定三角形的顶点坐标,我们可以计算出外心的具体位置。
三角形四心及性质

三角形四心三角形四心要点诠释:(1)三角形的内心、重心都在三角形的内部.(2)钝角三角形的垂心、外心都在三角形的外部.(3)直角三角形的垂心为直角顶点,外心为直角三角形斜边的中点.(4)锐角三角形的垂心、外心都在三角形的内部.1、三角形外心:三角形的外心是三角形三条垂直平分线的交点(或三角形外接圆的圆心) 。
三角形的三条垂直平分线必交于一点已知:△ABC中,AB,AC的垂直平分线DO,EO相交于点O求证:O点在BC的垂直平分线上证明:连结AO,BO,CO,∵DO垂直平分AB,∴AO=BO∵EO垂直平分AC,∴AO=CO∴BO=CO即O点在BC的垂直平分线上三角形的外心的性质:1.三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.2三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合。
3. 锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合4.OA=OB=OC=R5.∠BOC=2∠BAC,∠AOB=2∠ACB,∠COA=2∠CBA(圆心角=2同弧圆周角)6.S△ABC=abc/4R2、三角形的内心:三角形的内心是三角形三条内角平分线的交点(或内切圆的圆心)。
三角形三条角平分线必交于一点证明己知:在△ABC中,∠A与∠B的角平分线交于点O,连接OC求证:OC平分∠ACB证明:过O点作OD,OE,OF分别垂直于AC,BC,AB,垂足分别为D,E,F∵AO平分∠BAC,∴OD=OF;∵BO平分∠ABC,∴OE=OF ;∴OD=OF∴O在∠ACB角平分线上∴CO平分∠ACB三角形内心的性质:1.三角形的三条角平分线交于一点,该点即为三角形的内心2.三角形的内心到三边的距离相等,都等于内切圆半径r3.r=2S/(a+b+c)4.在Rt△ABC中,∠C=90°,r=(a+b-c)/2.5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/26.S△ABC=[(a+b+c)r]/2 (r是内切圆半径)3、三角形的垂心:三角形的垂心是三角形三边上的高的交点(通常用H表示)。
三角形的外心与内心的性质

三角形的外心与内心的性质三角形是几何学中最基本的图形之一,而三角形的外心与内心则是三角形内外接圆的特殊点。
本文将重点讨论外心与内心的性质及其与三角形的关系。
一、外心的性质外心是三角形外接圆的圆心,也被称为三角形的Circumcenter。
对于任意的三角形ABC,我们可以通过以下性质来确定外心的位置:1. 外心是三角形三个垂直平分线的交点。
垂直平分线是指从三角形的各个顶点到对边中点的垂直平分线。
2. 外心到三角形的每条边的距离都相等,即OC=OA=OB。
其中,O 表示外心,A、B、C表示三角形ABC的顶点。
3. 三角形的外接圆的直径等于三角形的最长边,即2R=BC,其中R 表示外接圆的半径,BC表示三角形的最长边。
二、内心的性质内心是三角形内切圆的圆心,也被称为三角形的Incenter。
内切圆是唯一与三角形的三个边相切的圆,因此内心也是三角形三个角的角平分线的交点。
对于任意的三角形ABC,我们可以通过以下性质来确定内心的位置:1. 内心是三角形三条角平分线的交点。
角平分线是指从三角形的各个顶点出发,将相邻两边的夹角平分的线。
2. 三条角平分线的交点到三个顶点的距离相等,即ID=IE=IF。
其中,I表示内心,D、E、F表示三角形ABC的顶点。
3. 内接圆的半径可以通过公式r = S / p来计算,其中r表示内接圆的半径,S表示三角形的面积,p表示三角形的半周长。
三、外心与内心之间的关系1. 外心、内心和重心共线。
重心是三角形三条中线的交点。
这条共线性质被称为欧拉线。
2. 外心到三个顶点的距离大于内心到三个顶点的距离,并且外心到顶点的距离之间存在大小关系。
3. 外心和内心的连线与三角形的三个角相对应。
四、实际应用外心和内心的性质在实际应用中有广泛的应用。
例如,在三角测量中,可以通过求解外心和内心的位置来计算三角形的形状和尺寸。
此外,在工程设计中,外心和内心的性质也被用于定位和计算结构的稳定性。
总结:三角形的外心与内心是三角形内外接圆的特殊点,它们具有一系列的性质。
三角形“四心”定义与性质
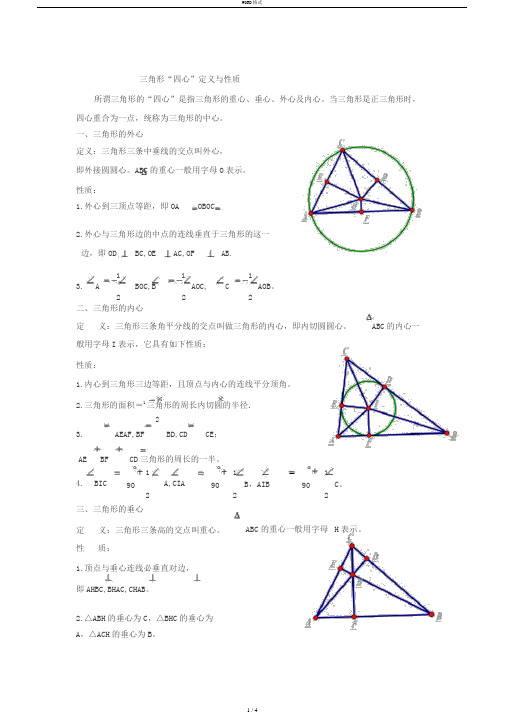
三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC的重心一般用字母O表示。
性质:1.外心到三顶点等距,即OA OB OC。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即OD BC,OE AC,OF AB.3. A 1BOC,B1AOC,C1AOB。
2 2 2二、三角形的内心定义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC的内心一般用字母I表示,它具有如下性质:性质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=1三角形的周长内切圆的半径.23. AEAF,BF BD,CD CE;AE BF CD三角形的周长的一半。
4. BIC1A,CIA1B,AIB1C。
90 90 902 2 2三、三角形的垂心定义:三角形三条高的交点叫重心。
ABC的重心一般用字母H表示。
性质:1.顶点与垂心连线必垂直对边,即AHBC,BHAC,CH AB。
2.△ABH的垂心为C,△BHC的垂心为A,△ACH的垂心为B。
四、三角形的“重心”:定义:三角形三条中线的交点叫重心。
ABC 的重心一般用字母G 表示。
性质:1. 顶点与重心G 的连线必平分对边。
2. 重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GA2GD,GB2GE,GC2GF3.重心的坐标是三顶点坐标的平均值.即x G x A x B xC,y Gy A y B yC .334.向量性质:(1)GAGB GC0 ;(2)PG 1(PAPB PC),31S5.S BGC SCGASAGBABC 。
3五、三角形“四心”的向量形式:结论1:若点O 为 ABC 所在的平面内一点,满足OAOB OBOC OCOA ,则点O 为 ABC 的垂心。
空间几何中的三角形外心定理

空间几何中的三角形外心定理在空间几何中,三角形是非常重要的图形之一。
三角形的外心定理是研究三角形外接圆及其性质的一条基本定理。
本文将介绍三角形外心定理的定义、性质以及证明过程,并探讨它在解题中的应用。
一、三角形外心定理的定义三角形外心定理是指:三角形的三条垂直平分线的交点即为该三角形外接圆的圆心。
这个交点就是三角形的外心。
二、三角形外心定理性质三角形外心定理具有以下性质:1. 外心到三角形各顶点的连线长度相等三角形外接圆的圆心到三个顶点的距离相等。
即若O为三角形ABC的外心,则AO = BO = CO。
证明:连接AO、BO、CO并延长至外圆弧上。
由三角形的外心定理可知,AO等于外心到三角形的第一条垂直平分线的交点A'的距离,而A'在外圆上。
同理,BO和CO等于外心到第二条和第三条垂直平分线的交点的距离,且这两点也在外圆上。
因此,AO = BO = CO。
2. 三角形的外接圆过三个顶点三角形的外接圆经过三个顶点A、B、C。
证明:由三角形外心定理可知,三个垂直平分线相交于外心O,而O在外接圆上。
因此,外接圆过三个顶点A、B、C。
3. 外接圆的直径等于边长中最长的那条边对于任意三角形ABC,若AB > BC > AC,则AB为外接圆的直径。
证明:连接AO。
由三角形外心定理可知,AO = BO。
又由于AO和BO是外接圆的半径,所以AB为外接圆的直径。
三、三角形外心定理的应用三角形外心定理在解题中具有重要的应用。
例如,可以利用外心的性质求解三角形的周长、面积以及各边长之间的关系。
1. 求解三角形的周长已知三角形的三个顶点坐标,可以通过计算外心到各个顶点的距离,进而求解三角形的周长。
2. 求解三角形的面积已知三角形的三个顶点坐标,可以通过计算外心到各个顶点的距离,进而求解三角形的面积。
根据海伦公式,三角形的面积与三边长度之间存在一定的关系。
3. 探究三角形的特殊性质通过研究三角形外心与顶点之间的关系,可以发现三角形的一些特殊性质。
三角形的外心与内心

三角形的外心与内心三角形是初等几何学中最基本的图形之一,而三角形的外心和内心也是其中的重要概念。
本文将详细介绍三角形的外心与内心的定义、性质和求解方法。
一、三角形的外心三角形的外心是一个特殊的点,可以用来确定三角形的一些性质。
我们先来看一下外心的定义。
1. 定义三角形ABC的外心是一个点O,它与三角形的三个顶点A、B、C 都在同一条直线上,并且AO=BO=CO。
2. 性质外心有以下重要性质:a) 外心是三角形三条边所在的直线的垂直平分线的交点。
b) 外心到三角形的三个顶点的距离相等,即OA=OB=OC。
c) 外心到三角形的三条边的距离相等,即OD=OE=OF。
其中,D、E、F分别是AB、BC、CA的垂直平分线与外心O的交点。
3. 求解方法我们可以使用以下方法求解三角形的外心:确定外心。
b) 利用外心性质b)可以通过计算三个顶点到外心的距离来确定外心。
c) 利用外心性质c)可以通过计算外心到三个边的距离来确定外心。
二、三角形的内心与外心类似,三角形的内心也是一个重要的点,可以用来确定三角形的一些性质。
接下来我们来了解一下内心的定义、性质和求解方法。
1. 定义三角形ABC的内心是一个点I,它到三角形的三条边的距离之和最小。
2. 性质内心有以下重要性质:a) 内心是三角形三条边的角平分线的交点。
b) 内心到三角形的三个顶点的距离相等,即IA=IB=IC。
c) 内心到三角形的三条边的距离之和等于三角形的周长。
3. 求解方法我们可以使用以下方法求解三角形的内心:确定内心。
b) 利用内心性质b)可以通过计算三个顶点到内心的距离来确定内心。
c) 利用内心性质c)可以通过计算内心到三个边的距离之和来确定内心。
三、三角形外心与内心的关系三角形的外心和内心之间有一定的关系。
具体来说,外心、内心和三个顶点构成的四点共线。
这条线被称为欧拉线,它具有重要的几何意义和应用价值。
欧拉线上的点还有其他一些特殊名称,比如与外心相对的点叫做垂心,与内心相对的点叫做内垂心。
三角形的内心外心和重心的特性

三角形的内心外心和重心的特性在几何学中,三角形是最基本的几何形状之一,而三角形的内心、外心和重心则是三角形的特殊点。
它们具有独特的性质和重要的几何意义,本文将对三角形的内心、外心和重心进行详细讨论。
一、内心内心是指三角形内部的一个点,它与三角形的三边相切。
若三角形的三条边分别为a、b、c,对应的内角分别为A、B、C,则内心可以表示为I。
内心的特性包括以下几点:1. 内心到三角形三边的距离相等:内心到三角形的任意一条边的距离都相等,这个距离也被称为内心的半径。
内心与三角形三边的切点被称为内接圆圆心,该圆即为内接圆。
2. 以内心为圆心的圆与三角形的三边都相切:内心到三角形三边的垂线都经过切点,因此内心到三角形的任意一条边的垂线长度都相等。
3. 内心是重心与垂心所确定的直线的交点:内心、重心和垂心是三个特殊点,它们位于同一条直线上,这条直线被称为欧拉线。
二、外心外心是指三角形外部的一个点,它与三角形的三个顶点都相切。
若三角形的三个顶点分别为A、B、C,则外心可以表示为O。
外心的特性包括以下几点:1. 外心到三角形的三个顶点距离相等:外心到三角形的任意一个顶点的距离都相等,这个距离也被称为外心的半径。
外心是三角形外接圆圆心,该圆即为外接圆。
2. 外心是垂直三角形的三条中垂线的交点:中垂线是连接每条边中点和对边顶点的线段,三角形的三条中垂线交于一点,该点即为外心。
3. 外心是重心与斜心所确定的直线的交点:外心、重心和斜心是三个特殊点,它们位于同一条直线上,这条直线被称为欧拉线。
三、重心重心是指由三角形的三个顶点向三条中线的交点构成的一个点。
若三角形的三个顶点分别为A、B、C,则重心可以表示为G。
重心的特性包括以下几点:1. 重心将三角形的每一条中线二等分:中线是由每个顶点与对边中点构成的线段,重心到每条中线的距离都是中线长度的二分之一。
2. 重心是三角形重心与外心所确定的直线的中点:重心与外心和重心连线的中点位于一条直线上。
三角形的外心及性质

三角形外心及性质定义三角形外接圆的圆心叫做三角形的外心.三角形外接圆的圆心也就是三角形三边中垂线的交点,三角形的三个顶点就在这个外接圆上三条中垂线共点证明∵l、m为中垂线∴AF=BF=FC所以BC中垂线必过F三角形外心的性质设⊿ABC的外接圆为☉G(R),角A、B、C的对边分别为a、b、c,p=(a+b+c)/2.性质1:(1)锐角三角形的外心在三角形内;(2)直角三角形的外心在斜边上,与斜边中点重合;(3)钝角三角形的外心在三角形外.性质2:∠BGC=2∠A,(或∠BGC=2(180°-∠A).性质3:∠GAC+∠B=90°证明:如图所示延长AG与圆交与P∵A、C、B、P四点共圆∴∠P=∠B∵∠P+∠GAC=90°∴∠GAC+∠B=90°性质4:点G是平面ABC上一点,点P是平面ABC上任意一点,那么点G 是⊿ABC外心的充要条件是:(1)向量PG=(tanB+tanC)向量PA+(tanC+tanA)向量PB+(tanA+tanB)向量PC)/2(tanA+tanB+tanC).或(2)向量PG=(cosA/2sinBsinC)向量PA+(cosB/2sinCsinA)向量PB+(cosC/2sinAsinB)向量PC.性质5:三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.外心到三顶点的距离相等。
性质6:点G是平面ABC上一点,那么点G是⊿ABC外心的充要条件(向量GA+向量GB)·向量AB= (向量GB+向量GC)·向量BC=(向量GC+向量GA)·向量CA=0.三角形外心的做法分别作三角形两边的中垂线交点计作O以O为圆心OA为半径画圆圆O即为所求外心的求法设三角形三边及其对角分别为a、b、c,∠A、∠B、∠C正弦定理有r=a/(2sinA)=b/(2sinB)=c/(2sinC)r=abc/(4S△ABC)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形外心及性质
定义
三角形外接圆的圆心叫做三角形的外心.
三角形外接圆的圆心也就是三角形三边中垂线的交点,三角形的三个顶点就在这个外接圆上
三条中垂线共点证明
∵l、m为中垂线
∴AF=BF=FC
所以BC中垂线必过F
三角形外心的性质
设⊿ABC的外接圆为☉G(R),角A、B、C的对边分别为a、b、c,
p=(a+b+c)/2.
性质1:(1)锐角三角形的外心在三角形内;
(2)直角三角形的外心在斜边上,与斜边中点重合;
(3)钝角三角形的外心在三角形外.
性质2:∠BGC=2∠A,(或∠BGC=2(180°-∠A).
性质3:∠GAC+∠B=90°
证明:如图所示延长AG与圆交与P
∵A、C、B、P四点共圆
∴∠P=∠B
∵∠P+∠GAC=90°
∴∠GAC+∠B=90°
性质4:点G是平面ABC上一点,点P是平面ABC上任意一点,那么点G是⊿ABC外心的充要条件是:
(1)向量PG=(tanB+tanC)向量PA+(tanC+tanA)向量PB+(tanA+tanB)向量PC)/2(tanA+tanB+tanC).
或(2)向量PG=(cosA/2sinBsinC)向量PA+(cosB/2sinCsinA)向量PB+(cosC/2sinAsinB)向量PC.
性质5:三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.外心到三顶点的距离相等。
性质6:点G是平面ABC上一点,那么点G是⊿ABC外心的充要条件(向量GA+向量GB)·向量AB= (向量GB+向量GC)·向量BC=(向量GC+向量GA)·向量CA=0.
三角形外心的做法
分别作三角形两边的中垂线交点计作O
以O为圆心OA为半径画圆
圆O即为所求
外心的求法
设三角形三边及其对角分别为a、b、c,∠A、∠B、∠C 正弦定理有r=a/(2sinA)=b/(2sinB)=c/(2sinC)
r=abc/(4S△ABC)。
