复杂平均数问题
复杂平均数应用题

五年级奥数复杂平均数姓名____________ 成绩____________知识点:1.平均数的概念:是指在一组数据中所有数据之和再除以数据的个数。
2.较复杂的平均数问题的特点是:题中直接或间接地给出几个不相等的同类量,与相对应的份数,求这些同类数的平均数。
解答这些平均数问题一定要牢记以下数量关系:平均数=总数量÷总分数; 总数量=平均数×总份数; 总份数=总数量÷平均数回家作业:1.已知9个数的平均数是72,去掉一个数后,余下的数平均数为78,去掉的数是多少?2.某班有40名学生,期中数学考试,有两名同学因故缺考,这时班级平均分为89分,缺考的同学补考各得99分,这个班级中考平均分是多少分?3.有5个数,其平均数为138,按从小到大排列,从小端开始前3个数的平均数为127,从大端开始顺次取出3个数,其平均数为148,则第三个数是多少?4.某5个数的平均值为60,若把其中一个数改为80,平均值为70,这个数是多少?5.如果三个人的平均年龄为22岁.年龄最小的没有小于18岁.那么最大年龄可能是多少岁?6.数学考试的满分是100分,六位同学的平均分是91分,这6个同学的分数各不相同,其中一个同学得65分,那么居第三名的同学至少得多少分?7.在一次登山比赛中,小刚上山时每分钟走40米,18分钟达到山顶,然后按原路下山,每分钟走60米,小刚往返的平均速度是每分钟走多少米?8.某校有100名学生参加数学竞赛,平均分是63分,其中男生平均分是60分,女生平均分是70分,男同学比女同学多多多少人?9.一些同学分一些书,若平均每人分若干本,还余14本,若每人分9本,则最后一人分得6本,那么共有学生多少人?10.有几位同学参加语文考试,赵峰的得分如果再提高13分,他们的平均分就达到90分,如果赵峰的得分降低5分,他们的平均分就只得87分,那么这些同学共有多少人?11.有四个数每次取三个数,算出它们的平均数再加上另一个数,用这种方法计算了四次,分别得到以下四个数:86,92,100,106那么原4个数的平均数是多少?参考答案:一、填空题1.已知9个数的平均数是72,去掉一个数后,余下的数平均数为78,去掉的数是24.考点:平均数的含义及求平均数的方法.1923992分析:根据“9个数的平均数是72”,可以求出这9个数的和是多少;再根据“去掉一个数后,余下的数平均数为78”,又可求出余下的8个数的和是多少;进一步求出去掉的数是多少.解答:解:9个数的和:72×9=648,余下的8个数的和:78×8=624,去掉的数是:648﹣624=24.答;去掉的数是24.故答案为;24.点评:解决此题关键是根据平均数先求出9个数与8个数的和,再进一步求出去掉的数.2.某班有40名学生,期中数学考试,有两名同学因故缺考,这时班级平均分为89分,缺考的同学补考各得99分,这个班级中考平均分是89.5分.考点:平均数的含义及求平均数的方法.1923992分析:先根据“平均分×人数=总成绩”分别计算出两名补考的学生总成绩和(40﹣2)名同学的总成绩,然后相加求出全班同学的总成绩,用“总成绩÷全班总人数=平均成绩”即可;解答:解:[89×(40﹣2)+99×2]÷40,=3580÷40,=89.5(分);答:这个班级中考平均分是89.5分;故答案为:89.5.点评:解答此题的关键是先求出全班同学的总成绩,用“总成绩÷全班总人数=平均成绩”即可;3.有5个数,其平均数为138,按从小到大排列,从小端开始前3个数的平均数为127,从大端开始始顺次取出3个数,其平均数为148,则第三个数是135.考点:平均数的含义及求平均数的方法.1923992分析:先根据平均数的含义列式127×3求出从小端开始前3个数的和,列式148×3求出从大端开始的3个数的和,相加可知为5个数的和+第三个数,再减去5个数的和即可求解.解答:解:127×3+148×3﹣138×5=381+444﹣690=135.故答案为:135.点评:考查了平均数的含义,本题共5个数,从小端开始前3个数的和+从大端开始的3个数的和=5个数的和+第三个数.4.某5个数的平均值为60,若把其中一个数改为80,平均值为70,这个数是30.考点:平均数的含义及求平均数的方法.1923992分析:由平均数是60,可以得出这5个数的总和是60×5=300,若平均数是70,那么总和就是70×5=350,从这里可以看出这个数比原来多了50,80﹣50=30.所以这个数原来是30.解答:解:80﹣(70×5﹣60×5),=80﹣(350﹣300),=80﹣50,=30;答:这个数是30.故答案为:30.点评:此题考查了平均数的灵活应用.5.如果三个人的平均年龄为22岁.年龄最小的没有小于18岁.那么最大年龄可能是28岁.考点:平均数的含义及求平均数的方法.1923992分析:先求三个人的年龄和,再假设有两个年龄小的,则可以求出最大年龄的可能值.解答:解:三人年龄和:22×3=66(岁),设有两个人的年龄最小,和为19×2=38,所以,最大年龄可能是:66﹣38=28(岁).答:最大年龄可能是28岁.故答案为:28.点评:此题主要考查平均数的含义.6.数学考试的满分是100分,六位同学的平均分是91分,这6个同学的分数各不相同,其中一个同学得65分,那么居第三名的同学至少得95分.考点:平均数的含义及求平均数的方法.1923992分析:先得到第一、二名最多可得100+99=199(分),根据求平均数的方法可得第三、四、五名的平均分为:(91×6﹣100﹣99﹣65)÷3=94(分),由于这6个同学的分数各不相同,可得第三名最少95(分).解答:解:100+99=199(分),(91×6﹣100﹣99﹣65)÷3=282÷3=94(分).故第三名最少95(分).故答案为:95.点评:考查了平均数的含义及求平均数的方法,本题得到除了前面两名同学和得65分外的三名同学的平均分是解题的难点,是竞赛题型,有一定的难度.7.在一次登山比赛中,小刚上山时每分钟走40米,18分钟达到山顶,然后按原路下山,每分钟走60米,小刚往返的平均速度是每分48米.考点:平均数的含义及求平均数的方法.1923992分析:要求小刚往返的平均速度是每分多少米,先根据“速度×时间=路程”,计算出从山下到山顶的路程;然后根据“时间=路程÷速度”求出下山的时间;因为根据上、下山的路程相等,继而用“往返总路程÷往返总时间=平均速度”,代入数值解答即可.解答:解:(40×18×2)÷[18+40×18÷60],=1440÷30,=48(米);答:小刚往返的平均速度是每分48米.故答案为:48.点评:此题解答的关键是抓住往返路程不变这一条件,根据路程、时间和速度三者之间的关系以及平均数的求法进行解答即可.8.某校有100名学生参加数学竞赛,平均分是63分,其中男生平均分是60分,女生平均分是70分,男同学比女同学多40人.考点:平均数的含义及求平均数的方法.1923992分析:要求男同学比女同学多多少人,先要分别求出男生和女生的人数;用男生人数减去女生人数即可;根据“平均分×人数=总成绩”,先求出全班总成绩为63×100=6300分;假设100人都是男同学,则总分为60×100=6000分;这样就比总成绩少了6300﹣6000=300分,因为一名男生比一名女生少考了70﹣60=10分,则女生人数为300÷10=30人;进而得出男生人数为100﹣30=70人,继而根据题意求出结论.解答:解:女生:(63×100﹣60×100)÷(70﹣60),=300÷10,=30(人),男生:100﹣30=70(人),70﹣30=40(人);答:男同学比女同学多40人.故答案为:40.点评:解答此题的关键是认真分析,根据平均数、人数和总成绩之间的关系,进行分析解答即可.9.一些同学分一些书,若平均每人分若干本,还余14本,若每人分9本,则最后一人分得6本,那么共有学生17 人.考点:逻辑推理;盈亏问题.1923992分析:因为每人分9本,则最后一人分得6本,所以最后一人少9﹣6=3(本);因为原来最后还剩14本的,可是现在少了3本,所以又分出去了14+3=17(本);因为只有1×17=17;所以有17个学生,每人又多分了1本.解答:解:(14+3)×1=17(人);答:那么共有学生17人;故答案为:17.点评:此题属于较复杂的逻辑推理题,解答此题时应结合题意,分析要全面,进而通过推理,得出结论.10.有几位同学参加语文考试,赵峰的得分如果再提高13分,他们的平均分就达到90分,如果赵峰的得分降低5分,他们的平均分就只得87分,那么这些同学共有 6 人.考点:盈亏问题.1923992分析:找出对应量,利用盈亏分数的和除以平均分之差,即为参加考试的人数.解答:解:(13+5)÷(90﹣87)=6(人).故答案为:6.点评:此题属典型的盈亏问题,关键是明白盈亏分数的和除以平均分之差,即为参加考试的人数.11.有四个数每次取三个数,算出它们的平均数再加上另一个数,用这种方法计算了四次,分别得到以下四个数:86,92,100,106那么原4个数的平均数是48 .考点:平均数的含义及求平均数的方法.1923992分析:设这四个数为A,B,C,D,根据“平均数×个数=总数”,则:(A+B+C)÷3+D=86,(A+C+D)÷3+B=92,(A+B+D)÷3+C=100,(B+C+D)÷3+A=106,将这四个式子的左边和右边分别相加得:2A+2B+2C+2D=384;则A+B+C+D=192,(A+B+C+D)÷4=48;解答:解:根据分析得:(86+92+100+106)÷2÷4,=384÷2÷4,=48;故答案为:48.点评:解答此题的关键是根据平均数的计算方法列出式子,然后通过分析,得出:后来得到的四个数的和是原来四个数和的2倍,进而进行解答即可.。
求较复杂的平均数应用题

求较复杂的平均数应用题上海小学陈英教学目标:1、掌握较复杂的平均数应用题的数量关系和解题方法。
2、逐步建立求平均数的简单统计思想。
3、会正确解答较复杂的平均数应用题。
4、用求平均数的方法,结合学生生活实际,解决问题。
教学重点:求较复杂的平均数应用题的数量关系和解题方法。
教学难点:根据要求的平均数确定按什么平均分,并能整理出;要求的平均数所对应的总数和总份数。
教学过程:一、引入。
1、同学们听,(媒体铃声)(配音)让我们跟着欢欢和乐乐去奇奇乐园看看。
出示(门票图)这是他们两家的门票费用表,根据这些数据,你能提出两步计算的数学问题吗?生:平均每家的门票费是多少?师:谁来列式?生:(260+420)÷2师:这个式子的数量关系是什么?生:两家总的门票费÷人家数=平均每家门票费(媒体出示)2、我们知道欢欢家有3人,乐乐家有5人。
现在你还能提出怎样的平均数问题?生:这两家,平均每人的门票费是多少元?师:好。
谁愿意解答这个问题?生:(260+420)÷(3+5)师:你是怎么思考的?生:两家总的门票费用÷两家总人数=平均每人的门票费(媒体出示)师:这两个式子不同在哪里?为什么不同?师:这是我们四年级学过的平均数问题,解题时的基本数量关系式是什么?师:出示:总数÷总份数=平均数(板书)二、新授1、师:欢欢和乐乐进入游乐园,玩了很多游乐项目。
平均每个游乐项目要花去多少钱呢?请大家仔细读题。
(媒体出示)欢欢和乐乐两家上午玩了4个游乐项目,平均每个项目用去20元,下午玩了6个游乐项目,共用去180元。
问:平均每个项目用去多少元?(学生默读题目)2、学生试做(省略答句。
)3、交流。
说说思考过程根据学生的回答,教师板书:(20×4+180)÷(4+6)4、这道题和我们四年级时学的简单平均数应用题相比,有什么不同?列式的时候又要注意什么?小组讨论交流。
5、小结:这就是我们今天所要学习的“较复杂的平均数应用题”。
求较复杂平均数

(160×5+156×4 +169×2 +145×2 +165×2 +151×3 +172 +148+163+158 ) ÷22 =3476 ÷22 =158(cm)
7 6 10
8 6 7
8 7 9
(4×8+5×11)÷ (4+11)
某小学四年级一班同学春节收到的压岁钱情况如下
组别 人数 平均钱数(元) 一组 12 285 二组 10 360 三组 10 410 四组 12 320
你能算出全班平均每个同学收到压岁钱多少元吗?
(285×12+360×10+410×10+320×12)÷(12+10+10+12) =14960÷44 =340(元)
平均每个队员投篮多少个?
学校评选最佳篮球运动员。 评选规则:采取去掉一个最高分,去掉一个最低分, 再求其他分数平均数的方法计算成绩。委3 评委4 评委5 评委6 评委7 得分
2号 10
4号 5号
6 9
9 8 10
7 7 8
8 8 9
8 8 9
随着生活水平的提高,同学们每年的压岁钱也 随着提高,每个同学的压岁钱多少不一,有的 同学的压岁钱买了学习用品,有的同学的钱买 了玩具,有的同学的钱买了生活用品,还有的 同学的钱买了零食,更有的同学的钱进了网吧, 也有的同学的钱存了起来…… 1、同学们,你的压岁钱是多少,你认为怎样 使用比较合理? 2、调查一下我们班每个(也可以是一部分) 同学的压岁钱,并计算一下每个人的平均 压岁钱是多少?
较复杂的平均数教学设计

第七单元统计第一课时信息窗1较复杂的平均数教学设计教学目标:1、结合实例,进一步理解平均数的意义,会计算较复杂的平均数。
2、能根据具体情况运用平均数解决与分析实际问题,体会平均数在统计中的用处。
教学重难点及突破:重点:掌握求较复杂平均数的方法,进一步掌握对数据整理的方法,能对数据结果进行简单分析。
难点:能对统计结果进行简单分析。
突破:首先创设情境,根据情境提出问题,让学生独立尝试解决问题,从而引出求平均数的方法和整理数据的方法,体会统计的必要性。
统计后,重视对统计结果的分析,感知统计的作用。
教学设计:一、情境激趣,谈话导入。
同学们,老师遇到个难题,想请你们帮忙解决一下,有兴趣吗?生:有。
师:好,请看大屏幕。
1、课件展示情境图。
小红的成绩:语文84、数学100、英语98.小明的成绩:语文95、数学97、英语93.教师提问:怎样知道谁的成绩更好些呢?学生可能想到:(1)看看谁的高分比较多?(2)计算每人的总分进行比较。
(3)比较每人的平均分。
2、比较三种方法,感悟求平均数的必要性,进一步理解平均数的意义。
第一种方法:误差较大。
第二种方法:虽然能比较出成绩的多少,但看不出每人的整体水平。
第三种方法:既能比较出成绩的多少,也能看出每人的整体水平。
所以求出每人的平均成绩比较可行。
3、小结:在比较几组数据的整体水平时可用求它们的平均数的办法进行比较。
引出平均数(板书:求平均数)(设计意图):让学生替老师解决困难,提高学生的学习热情,调动他们的积极性,激发他们的求知欲,好奇心。
让学生感到数学就发生在自己身边,激发解决问题的欲望,引出求平均数的问题,从而体会统计的必要性以及统计与生活的密切联系。
二、层层诱导,探索新知。
(一)计算简单的平均数。
师:怎样求平均成绩呢?生:先求每人的总分数,再除以科目数3,就得平均分。
师:好,请大家计算一下。
课桌左面的同学计算小红平均分,右面的同学计算小明的平均分。
小红平均分:(84+100+98)÷3=94小明平均分:(95+97+93)÷3=9594<95小明成绩更好些。
复杂计算问题
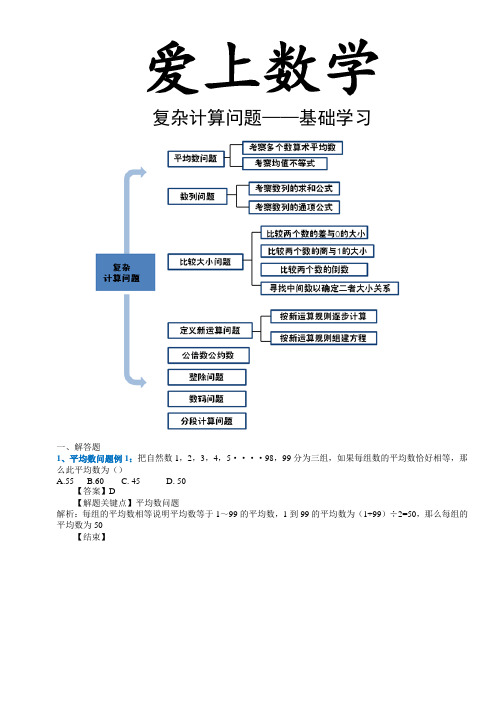
爱上数学复杂计算问题——基础学习一、解答题1、平均数问题例1:把自然数1,2,3,4,5····98,99分为三组,如果每组数的平均数恰好相等,那么此平均数为()A.55B.60C. 45D. 50【答案】D【解题关键点】平均数问题解析:每组的平均数相等说明平均数等于1~99的平均数,1到99的平均数为(1+99)÷2=50,那么每组的平均数为50【结束】3、均值不等式例1:已知a ,b ,c 为不全相等的正数,则a(b 2+c 2)+b(c 2+a 2)+c(a 2+b 2)>( ) . A.6abc B.7abc C.8abc D.9abc【答案】A【解题关键点】 222a b ab +≥(当且仅当a=b 时取“=”号)。
解析:观察要证不等式的两端都是关于a ,b ,c 的3次多项式,左侧6项,右侧6项,左和右积,具备均值不等式的特征。
∵ b 2+c 2≥2bc, a>0, ∴ a(b 2+c 2)≥2abc 同理,b(c 2+a 2)≥2bac, c(a 2+b 2)≥2cab, 又 ∵a ,b ,c 不全相等, ∴ 上述三个不等式中等号不能同时成立,因此 a(b 2+c 2)+b(c 2+a 2)+c(a 2+b 2)>6abc 。
【结束】5、数列的求和例1: A,B,C,D ,E 五个人在一次满分为100分的考试中,得分都大于91的整数。
如果A,B,C 的平均分为95分,B,C,D 的平均分为94分,A 是第一名,E 是第三名得96分,则D 的得分是() A.96分 B. 98分 C. 97分 D. 99分【答案】C【解题关键点】平均数问题解析;A,B,C 的平均分为95分,那么A,B,C 的和为285,B,C,D 的平均分为94分,那么B,C,D 的和为282,所以A 和D 的差为3,显然B 项和D 项一定被排除,否则A 的得分将大于100分,如果D 等于96分,则意味D 和E 并列得三名,则B 和C 中必然有一个为第二名,也即成绩要大于96分,则B 和C 中的另一个的成绩一定要小于91分,显然不符题意,所以D 的得分只能为97分,所以选C.【结束】6、数列的通项公式例1:有一串数,第一个数是6,第二个数是3,从第二个数起,每一个数都比它前面的那个数与后面那个数的和小5,那么这串数,从第一个起到第400个数为止的400个数之和是() A.1991 B. 1992 C. 1993 D. 1995【答案】D【解题关键点】考察数列的通项公式 解析:法一:因为115n n n a a a -+=++,所以115n n n a a a +-=-+,从第三个数起343254365,54,57a a a a a a a =-+=-+==-+=前400个数的和为122132399398239955?···52385S a a a a a a a a a a =++-++-+++-+=++⨯。
503第三章 数量关系应用题(9)——较复杂的平均数问题

第三章 数量关系应用题(9)——较复杂的平均数问题[知识提要]部队里两个士兵在比赛打靶,小林打了5次,小刘只打了4次,他们的成绩分别如下表所示:如果把每一个人的每次打靶的分数加起来,除以这人打靶的总次数,那么就可以计算出这个人的平均成绩,这样就可以知道哪一个的平均成绩比较高(也就是哪一个人获胜)了。
小林的平均成绩为:(8+7+9+7+9)÷5=8环小刘的平均成绩为:(6+7+10+5)÷4=7环所以小林的平均成绩高,小林获胜。
在这里,小林的打靶成绩是5个数,小刘的打靶成绩是4个数。
像在小林和小刘的成绩这种“几个数”的比较的时候,最常用也是最简便的办法就是求它们的平均数。
求几个数的平均数,通常有两种办法,我们来看下面这道题:向阳小学篮球队一共有10名球员,他们的身高分别为(单位:厘米)157 148 161 138 155 162 153 146 158 142 那么他们的平均身高是多少?第一个方法是把所有的身高加起来,除以球员数量157+148+161+138+155+162+153+156+158+142=15201520÷10=152(厘米)第二个办法是先取一个最小的数,例如138,把它看成“基数”,然后算出其他各数与这个“基数”的差,求出这些差的平均数,最后再加上这个“基数”(19+10+23+0+17+24+15+8+20+4)÷10=140138+140÷10=152(厘米)因此,对若干个数求平均数,有如下两个办法:在这一章中我们就将通过一些简单的例子,让同学们来好好理解什么叫“平均”。
解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数。
[经典例题][例1]乐乐3次数学测验都得了83分,后来他加倍努力,在第4次测验中得了95分。
那么乐乐4次测验的平均成绩是多少?[分析]这道题就是计算平均数,按照“知识提要”中求平均数的办法,有如下两种解法:[解答1]可以先计算4次测验的总分,然后除以4:(83×3+95)÷4=86[解答2]可以把83分看成“基数”,然后求出95分与83分的差为95-83=12分。
4年级-18- 平均数问题 -难版

第18讲平均数问题知识梳理把几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的相等的数就是平均数。
如何灵活运用平均数的数量关系解答一些稍复杂的问题呢?下面的数量关系必须牢记:平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数典型例题【例1】★有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?【解析】(1)1箱苹果+1箱梨+1箱橘子=42×3=136(个);(2)1箱桃+1箱梨+1箱橘子=36×3=108(个)(3)1箱苹果+1箱桃=37×2=72(个)由(1)(2)两个等式可知:1箱苹果比1箱桃多126-108=18(个),再根据等式(3)就可以算出:1箱桃有(74-18)÷2=28(个),1箱苹果有28+18=46(个)。
1箱苹果和1箱桃共有多少个:37×2=74(个)1箱苹果比1箱桃多多少个:42×3-36=18(个)1箱苹果有多少个:28+18=46(个)【小试牛刀】一次考试,甲、乙、丙三人平均分91分,乙、丙、丁三人平均分89分,甲、丁二人平均分95分。
问:甲、丁各得多少分?【解析】甲113 丁77【例2】★一次数学测验,全班平均分是91.2分,已知女生有21人,平均每人92分;男生平均每人90.5分。
求这个班男生有多少人?【解析】女生每人比全班平均分高92-91.2=0.8(分),而男生每人比全班平均分低91.2-90.5=0.7(分)。
全体女生高出全班平均分0.8×21=16.8(分),应补给每个男生0.7分,16.8里包含有24个0.7,即全班有24个男生。
【小试牛刀】两组学生进行跳绳比赛,平均每人跳152下。
甲组有6人,平均每人跳140下,乙组平均每人跳160下。
乙组有多少人?【解析】9人【例3】★五一班同学数学考试平均成绩91.5分,事后复查发现计算成绩时将一位同学的98分误作89分计算了。
小学数学六年级数学难题

较复杂的平均数问题班级姓名求平均数,要知道两个条件:总数量和总份数。
关键是确定总数量和总数量相对应的总份数。
解题规律:(1)总数量÷总份数=平均数(2)平均数×总份数=总数量(3)总数量÷平均数=总份数例1:小红上学期共参加五次测试,前两次的平均分是93分,后三次的平均分是88分,小红这五次测试的平均分是多少?例2:甲、乙、丙三个数的平均数是6,甲、乙两个数的平均数是4,乙、丙两个数的平均数是5.3,乙数是多少?甲、丙两个数的平均数是多少?例3:有四箱水果,苹果、梨、桔子平均每箱42个,梨、桔子、桃平均每箱36个,苹果和桃平均每箱37个,一箱苹果和一箱桃各有多少个?例4:有五个数从大到小排列,其平均数是38,前三个数的平均数是27,后三个数的平均数是48,中间的一个数是多少?例5:五名裁判给一名运动员评分,去掉一个最高分和一个最低分,平均得分9.58分,如果只去掉一个最高分,平均分是9.46分,如果只去掉一个最低分,平均分是9.66分,求这名运动员的最高得分和最低得分。
【尝试实践1】1、甲、乙两数的平均数是18,甲、丙两数的平均数是17,乙、丙两数的平均数是19,求甲、乙、丙三个数各是多少?2、小英前四次英语测验的平均成绩是92.5分,第五次测验得了100分,她这五次的平均成绩是多少?3、甲、乙、丙、丁四人称体重,乙、丙、丁三个共重120千克,甲、丙、丁三人共重126千克,甲、丁二人的平均体重是40千克,求四人的平均体重。
4、一次登山比赛,小华上山时每分钟走60米,18分到达山顶,按原路下山时,每分钟走90米,求小华上、下山往返一次的平均速度。
例6:小明在上学期的前五次数学测验中的平均成绩是88分,为了使平均成绩达到92.5分,小明要连续考多少次满分(每次满分是100分)?例7:小芳与四名同学一起参加数学竞赛,那四个同学的成绩分别是78分、91分、82分、79分,小芳的成绩比五人的平均成绩还高6分,小芳的成绩在五人中排在第几?例8:有一个人从甲地到乙地,前一半时间骑自行车,每小时行14.5千米,后一半时间步行,步行速度为每小时4.8千米,这个人从甲地到乙地的平均速度是多少?【尝试实践2】1、小华读一本书,第一天读了83页,第二天读了74页,第三天读了71页,第四天读了64页,第五天读的比这五天的平均页数多3.2页,小华第五天读了多少页?2、小强前几次数学测试的平均分是84分,这一次要考100分,这样才能把这几次的平均分提高到86分,这一次是第几次考试?3、五(2)班的女同学人数是男同学人数的一半,男同学的平均体重是41千克,女同学的平均体重是35千克,那么,全班同学的平均体重是多少千克?4、一辆汽车以每小时100千米的速度从甲地开往乙地,到达乙地后又以每小时60千米的速度从乙地返回甲地,求这辆汽车往返甲、乙两地的平均速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复杂平均数问题
1、有五个数它们的平均数是60。
如果把这五个数按从大到小的顺序排列,那么
前三个数的平均数是70,后三个数的平均数是50。
求中间这个数是多少?
2、小明参加了四次语文测验,平均成绩是68分,他想在下次语文测验后,把五
次的平均成绩提高到70以上(含70分)。
那么,在下次测验中,他至少要得多少分?
3、有5个数的平均数是54,小英在计算这5个数的平均数时把其中一个数错看
成了84,求出的平均数是64,求原来那个数是多少?
4、五(1)班数学考试平均成绩是91.5分,事后发现,计算平均成绩时将其中
一位同学的98分误作89分计算了,经重新计算后,全班的平均成绩是91.7分,问五(1)班有多少名学生?
5、数学成绩公布前,英子四门功课的平均分是89分。
数学成绩公布后,她五门
功课的成绩提高了2分。
求英子的数学考了多少分?
6、有五个小朋友,五人的平均体重是24千克。
每次选出四个小朋友算出他们体
重的平均数分别是20千克,25、26千克和22千克。
问这五个小朋友的平均体重是多少千克?
7、七位老人的平均年龄是72岁。
较大的四位老人的平均年龄是80岁,较小的
四位老人的平均年龄是65岁。
求这7位老人中年龄居中的是多少岁?
8、两组学生进行跳绳比赛,平均每人每分钟跳152次,甲组有学生9人,平均
每人每分钟跳160次,如果乙组学生平均每人跳140次,那么乙组有学生多少人?
9、张勇前九次打靶的平均成绩是7.8环,第十次打靶至少要得多少环才能把平
均成绩提高到8环以上?
10、把1.2、3.7、6.5、2.9、4.6分别填在下图5个○中,再在每个□中填
上和它相连的三个○中的平均数,再把三个□中的数的平均数填在△中,找出一种填法,使△的数尽可能小,那么△中填的数是多少?。
