高三数学专题外接球汇编
高考数学 外接球30题-含答案
Hale Waihona Puke 一、单选题 1．在三棱锥 A BCD 中， BAC 120, BDC 60 ，二面角 A BC D 为直二面角，
当三棱锥 A BCD 的体积的最大值为 1 时，其外接球的表面积为（ ） 3
A．
10π 3
B．10π
C． 20π 3
D． 20π
试卷第 1页，共 30页
2．已知三棱锥 P ABC 满足 PA PB PC BC 2 3， BAC 60 ．则其外接球 O 的
S
ABC
的外接球体积分别为V1
， V2
，V，则
V1
V2 V
的取值范围是（
）
A．
2 2
,1
B． 1, 2
C． 2, 2
D． 3, 2
试卷第 10页，共 30页
11．如图， ABCD 为直角梯形， AB ∥CD, AD DC, AD 3,CD 3, AB 2 3 .连 AC ， 将△ADC 沿 AC 翻折成三棱锥 D ABC ，当三棱锥 D ABC 外接球表面积的最小值时， 二面角 D AC B 的余弦值为（ ）
A． 80 3 π 3
B．
70 3
π
C． 20π
D． 80 π 3
试卷第 3页，共 30页
4．在四面体
ABCD
中，
AB
BC
，
AB
AD
，向量
BC
与
AD
的夹角为
2π 3
，若
AB
6
，
BC AD 3 ，则该四面体外接球的表面积为（ ）
A．18π
B． 36π
C． 54π
D． 72π
试卷第 4页，共 30页
高中数学空间几何体的外接球专题(附经典例题与解析)
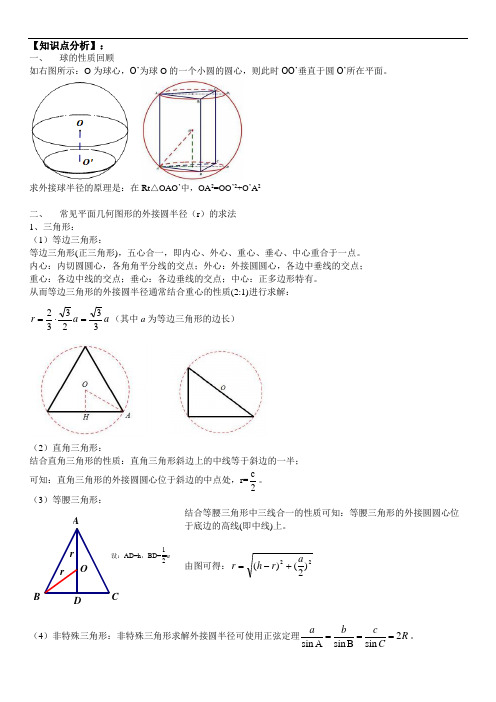
【知识点分析】： 一、 球的性质回顾如右图所示：O 为球心，O’为球O 的一个小圆的圆心，则此时OO’垂直于圆O’所在平面。
求外接球半径的原理是：在Rt △OAO ’中，OA 2=OO ’2+O ’A 2二、 常见平面几何图形的外接圆半径（r ）的求法1、三角形：（1）等边三角形：等边三角形(正三角形)，五心合一，即内心、外心、重心、垂心、中心重合于一点。
内心：内切圆圆心，各角角平分线的交点；外心：外接圆圆心，各边中垂线的交点；重心：各边中线的交点；垂心：各边垂线的交点；中心：正多边形特有。
从而等边三角形的外接圆半径通常结合重心的性质(2:1)进行求解：a a r 332332=⋅=（其中a 为等边三角形的边长）（2）直角三角形：结合直角三角形的性质：直角三角形斜边上的中线等于斜边的一半；可知：直角三角形的外接圆圆心位于斜边的中点处，r=2c 。
（3）等腰三角形： 结合等腰三角形中三线合一的性质可知：等腰三角形的外接圆圆心位于底边的高线(即中线)上。
由图可得：22)2()(a r h r +-=（4）非特殊三角形：非特殊三角形求解外接圆半径可使用正弦定理2sin sin sin a b c R C===A B 。
rrAD=h ，BD=12a B CO2、四边形常见具有外接圆的四边形有：正方形、矩形、等腰梯形，其中正方形与长方形半径求解方法转化为直角三角形，等腰梯形的外接圆圆心不在中学考察范围内。
外接圆圆心是在圆心到各个顶点距离相同的点；外接球球心则是球心到几何体各个顶点距离相同的点。
结论：几何体的外接球球心与底面外心的连线垂直于底面，(也即球心落在过底面外心的垂线上，)简单称之为：球心落在底面外心的正上方。
【相似题练习】2．半径为2的球的内接三棱锥P﹣ABC，PA＝PB＝PC＝2，AB＝AC＝BC，则三棱锥的高为（）A．3B．C．2D．3【知识点分析】：类型一：直（正）棱柱:上下两底面三角形的外心连线与侧棱平行与底面垂直，从而球心O 必位于上下两底面外心连线的中点处，即121'AA OO =，从而R 可求.【相似题练习】1．三棱柱ABC ﹣A 1B 1C 1中，底面ABC 是边长为2的正三角形，侧棱AA 1垂直于底面ABC ，且AA 1＝4，则此三棱柱外接球的表面积为（ ）A ．B ．C ．D ．【知识点分析】：类型二：侧棱垂直底面的三棱锥，法一：补形法：该几何体可由正三棱柱沿平面PBC 切割得来，故可转化为原三棱柱的外接球；法二：先确定底面三角形ABC 的外心O’，从而球心位于O’的正上方，即OO’ ⊥平面ABC ，同时：OP=OA ，故，过O 作OM ⊥PA 于M ，此时M 必为PA 中点，从而四边形OMAO’为矩形，所以PA AM OO 21'==，在直角三角形OO’A 中有：222'OO r R +=.【相似题练习】2．已知在三棱锥P ﹣ABC 中，△ABC 是边长为2的正三角形，若PA ⊥底面ABC 且PA ＝2，则该三棱锥的外接球的表面积为（ ）A ．32πB ．28πC ．24πD ．20π3．在三棱锥P ﹣ABC 中，PA ⊥平面ABC ，PA ＝2，AB ＝4，AC ＝3，∠BAC ＝，则三棱锥P ﹣ABC 的外接球的半径R ＝（ ）A ．B ．C ．D ．【知识点分析】：类型三：正三棱锥：由底面正三角形边长可得r ，在直角三角形OO’A 中，222'OO r R +=，故只需确定OO’的长度即可，结合图形，OO’=PO’-OP=H-R ，代入222)(R H r R -+=即可求解.【相似题练习】3．正三棱锥P ﹣ABC 侧棱长为，侧棱与底面ABC 所成的角为60°，则该正三棱锥外接球半径为 .2．某几何体的三视图如图所示，其中网格纸上小正方形的边长为1，则该几何体的外接球的表面积为（ ）【知识点分析】：类型四：侧面垂直于底面的三棱锥：设△ABC和△PAB的外心分别为O’,O’’，则PM⊥AB，球心设为O，则OO’ ⊥平面ABC，OO’’⊥平面PAB，从而四边形OO’MO’’是矩形，可得：OO’=O’’M，在Rt△OO’C中用勾股定理求解.【讲透例题】1．在四面体A﹣BCD中，AB＝5，BC＝CD＝3，DB＝2，AC＝4，∠ACD＝60°，则该四面体的外接球的表面积为．解析：如图：取AB的中点O，在△ACD中，由余弦定理得：AD2＝AC2+CD2﹣2×AC×CD cos60°＝13，在△ABD中，∵AB2＝BD2+AD2，∴∠ADB＝90°，∴OA＝OB＝OD，在△ABC中，∵AB2＝BC2+AC2，∴∠ACB＝90°，∴OA＝OB＝OC，∴OA＝OB＝OC＝OD，∴O为四面体ABCD的外接球的球心，其半径R＝AB＝，∴S球＝4πR2＝4π（）2＝25π．故答案为：25π．【相似题练习】4.在三棱锥P-ABC中，面PAB⊥面ABC，三角形ABC和三角形PAB均为等边三角形，且AB=3，求该几何体外接球半径.2．在边长为2的菱形ABCD中，，将菱形ABCD沿对角线AC折起，使得平面ABC⊥平面ACD，则所得三棱锥A﹣BCD的外接球表面积为（）A．B．C．D．1．已知点A是以BC为直径的圆O上异于B，C的动点，P为平面ABC外一点，且平面PBC⊥平面ABC，BC＝3，PB＝2，PC＝，则三棱锥P﹣ABC外接球的表面积为．5、如图，在四棱锥P﹣ABCD中，底面ABCD为长方形，PA⊥底面ABCD，AD＝AP＝2，AB＝2，E为棱PD中点．（1）求证：PD⊥平面ABE；（2）求四棱锥P﹣ABCD外接球的体积．1．如图，在正四棱锥P﹣AMDE，底面AMDE的边长为2，侧棱PA＝，B，C分别为AM，MD的中点．F为棱PE的中点，平面ABF与棱PD，PC，PM分别交于点G，H，K．（1）求证：AB∥FG；（2）求正四棱锥P﹣AMDE的外接球的表面积．1．如图，四凌锥P﹣ABCD而底面ABCD是矩形，侧面PAD是等腰直角三角形∠APD＝90°，且平面PAD⊥平面ABCD．（Ⅰ）求证：平面PAD⊥平面PCD；（Ⅱ）在AD＝2，AB＝4，求三棱锥P﹣ABD的体积；（Ⅲ）在条件（Ⅱ）下，求四棱锥P﹣ABCD外接球的表面积．7、如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，已知其俯视图是正三角形，则该四棱锥的外接球的表面积是（）A．B．C．19πD．22π课后作业：1．如图，一个正三棱柱的主视图是长为，宽为2的矩形，俯视图是边长为的正三角形，则它的外接球的表面积等于（）A．16πB．12πC．8πD．4π2．某四面体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此四面体的外接球的表面积为（）A．πB．3πC．πD．π3．某四棱锥的三视图如图所示，则该棱锥的外接球的表面积为（）A．3πB．C．6πD．12π4．四棱锥P﹣ABCD中，ABCD为矩形，AD＝2，AB＝2，PA＝PD，∠APD＝，且平面PAD⊥平面ABCD．（1）证明：PA⊥PC；（2）求四棱锥P﹣ABCD的外接球的体积．参考答案与解析12．（5分）已知A，B，C为球O的球面上的三个点，⊙O1为△ABC的外接圆．若⊙O1的面积为4π，AB＝BC＝AC＝OO1，则球O的表面积为（）A．64πB．48πC．36πD．32π【解答】解：由题意可知图形如图：⊙O1的面积为4π，可得O1A＝2，则AO1＝AB sin60°，，∴AB＝BC＝AC＝OO1＝2，外接球的半径为：R＝＝4，球O的表面积：4×π×42＝64π．故选：A．1．1．一个几何的三视图如图所示，它们都是腰长为1的等腰直角三角形，则该几何体的外接球的体积等于（）A．B．C．πD．2π解析：由三视图可知：该几何体是一个如图所示的三棱锥，其中底面是一个两直角边都为1的直角三角形，PC⊥底面ABC，且PC＝1．将此三棱锥恢复为棱长为1的正方体，可知该正方体的外接球的直径即为正方体的对角线，∴V外接球＝＝．故选：B．1．半径为2的球的内接三棱锥P﹣ABC，PA＝PB＝PC＝2，AB＝AC＝BC，则三棱锥的高为（）A．3B．C．2D．3【解答】解：三棱锥P﹣ABC中，PA＝PB＝PC＝2，AB＝AC＝BC，如图，过点p作PM⊥平面ABC的垂足为M，则球O的内接三棱锥P﹣ABC的球心O在PM所在直线上，∵球O的半径为2，∴OB＝OP＝2，∴由余弦定理得cos∠BPM＝＝∴∠BPM＝30°，∴在Rt△PMB中，∠PBM＝60°，∴PM＝PB sin∠PBM＝3．故选：D．1．三棱柱ABC﹣A1B1C1中，底面ABC是边长为2的正三角形，侧棱AA1垂直于底面ABC，且AA1＝4，则此三棱柱外接球的表面积为（）A．B．C．D．【解答】解：∵正三棱柱ABC﹣A1B1C1的中，底面边长为2，高为4，由题意可得：三棱柱上下底面中心连线的中点，到三棱柱顶点的距离相等，说明中心就是外接球的球心，∴正三棱柱ABC﹣A1B1C1的外接球的球心为O，外接球的半径为r，表面积为：4πr2．球心到底面的距离为2，底面中心到底面三角形的顶点的距离为：＝，所以球的半径为r＝＝．外接球的表面积为：4πr2＝π故选：D．2．已知在三棱锥P﹣ABC中，△ABC是边长为2的正三角形，若PA⊥底面ABC且PA＝2，则该三棱锥的外接球的表面积为（）A．32πB．28πC．24πD．20π【解答】解：由正弦定理可知，正△ABC的外接圆的直径为，∵PA⊥平面ABC，所以，该三棱锥的外接球的直径为，则．因此，该三棱锥的外接球的表面积为4πR2＝20π．故选：D．3．在三棱锥P﹣ABC中，PA⊥平面ABC，PA＝2，AB＝4，AC＝3，∠BAC＝，则三棱锥P﹣ABC的外接球的半径R＝（）A．B．C．D．【解答】解：∵AC＝3，AB＝4，∠BAC＝，∴由余弦定理可得BC＝，∴△ABC外接圆的半径r＝，设球心到平面ABC的距离为d，则d＝PA＝1．由勾股定理可得R ＝，故选：D ．3．正三棱锥P ﹣ABC 侧棱长为，侧棱与底面ABC 所成的角为60°，则该正三棱锥外接球半径为 1 ． 【解答】解：过点P 作PH ⊥平面ABC 于H ，则∵AH 是PA 在平面ABC 内的射影 ∴∠PAH 是直线PA 与底面ABC 所成的角，得∠PAH ＝60°， ∴Rt △PAH 中，AH ＝PA cos60°＝，PH ＝PA sin60°＝设三棱锥外接球的球心为O ，∵PA ＝PB ＝PC ，∴P 在平面ABC 内的射影H 是△ABC 的外心由此可得，外接球心O 必定在PH 上，连接OA 、OB 、OC ∵△POA 中，OP ＝OA ， ∴∠OAP ＝∠OPA ＝30°，可得PA ＝OA ＝，∴三棱锥外接球的半径R ＝OA ＝1故答案为：1．2．某几何体的三视图如图所示，其中网格纸上小正方形的边长为1，则该几何体的外接球的表面积为（ ）A ．16πB ．12πC ．9πD ．8π【解答】解：根据几何体的三视图转换为直观图为：该几何体为底面为等腰直角三角形，高为2的三棱锥体． 如图所示：所以该三棱锥体的外接球的球心为O ，外接球的半径为OA ＝r ，则：，解得．故S ＝．故选：C ．4.在三棱锥P-ABC 中，面PAB ⊥面ABC ，三角形ABC 和三角形PAB 均为等边三角形，且AB=3，求该几何体外接球半径.由题可得：333,2331'''=====AB r PM M O OO ,所以215'22=+=OO r R2．在边长为2的菱形ABCD中，，将菱形ABCD沿对角线AC折起，使得平面ABC⊥平面ACD，则所得三棱锥A﹣BCD的外接球表面积为（）A．B．C．D．【解答】解：∵在边长为2的菱形ABCD中，；如图，由已知可得，△ABC与△ACD均为等边三角形，取AC中点G，连接BG，DG，则BG⊥AC，∴DG＝⇒cos∠GDA＝⇒∠GDA＝⇒∠ADC＝；∵二面角B﹣AC﹣D为直二面角，则BG⊥平面ACD，分别取△BCD与△ABD的外心E，F，过E，F分别作两面的垂线，相交于O，则O为三棱锥A﹣BCD的外接球的球心，由△BCA与△ACD均为等边三角形且边长为2，可得OE＝OF＝DG＝．∴DE＝DG﹣GE＝．∴OD＝＝＝．∴三棱锥A﹣BCD的外接球的表面积为4π×R2＝4π×（）2＝．故选：C．1．已知点A是以BC为直径的圆O上异于B，C的动点，P为平面ABC外一点，且平面PBC⊥平面ABC，BC＝3，PB＝2，PC＝，则三棱锥P﹣ABC外接球的表面积为10π．【解答】解：因为O为△ABC外接圆的圆心，且平面PBC⊥平面ABC，过O作面ABC的垂线l，则垂线l一定在面PBC内，根据球的性质，球心一定在垂线l，∵球心O1一定在面PBC内，即球心O1也是△PBC外接圆的圆心，在△PBC中，由余弦定理得cos B＝，⇒sin B＝，由正弦定理得：，解得R＝，∴三棱锥P﹣ABC外接球的表面积为s＝4πR2＝10π，故答案为：10π．1．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，PA⊥底面ABCD，AD＝AP＝2，AB＝2，E为棱PD 中点．（1）求证：PD⊥平面ABE；（2）求四棱锥P﹣ABCD外接球的体积．【解答】证明：（1）∵PA⊥底面ABCD，AB⊂底面ABCD，∴PA⊥AB，又∵底面ABCD为矩形，∴AB⊥AD，PA∩AD，又PA⊂平面PAD，AD⊂平面PAD，∴AB⊥平面PAD，又PD⊂平面PAD，∴AB⊥PD，AD＝AP，E为PD中点，∴AE⊥PD，AE∩AB＝A，AE⊂平面ABE，AB⊂平面ABE，∴PD⊥平面ABE．解：（II）四棱锥P﹣ABCD外接球球心是线段BD和线段PA的垂直平分线交点O，由已知BD＝＝＝4，设C为BD中点，∴AM＝2，OM＝AP＝1，∴OA＝＝＝3，∴四棱锥P﹣ABCD外接球的体积是＝36π．1．如图，在正四棱锥P﹣AMDE，底面AMDE的边长为2，侧棱PA＝，B，C分别为AM，MD的中点．F为棱PE的中点，平面ABF与棱PD，PC，PM分别交于点G，H，K．（1）求证：AB∥FG；（2）求正四棱锥P﹣AMDE的外接球的表面积．【解答】（1）证明：在正方形AMDE中，因为B是AM的中点，所以AB∥DE．又因为AB⊄平面PDE，DE⊂平面PDE,所以AB∥平面PDE．因为AB⊂平面ABF，且平面ABF∩平面PDE＝FG，所以AB∥FG．（2）解：连接AD，EM，相交于O′，易得AO′＝，PO′＝．由正四棱锥P﹣AMDE的对称性，得正四棱锥P﹣AMDE得外接球球心在线段PO′上，不妨设为O点．设OA＝OP＝R，则OO′＝﹣R，∵AO2＝AO′2+OO′2，∴R2＝2+（﹣R）2，∴R＝∴S＝4πR2＝，∴正四棱锥P﹣AMDE的外接球的表面积为．1．如图，四凌锥P﹣ABCD而底面ABCD是矩形，侧面PAD是等腰直角三角形∠APD＝90°，且平面PAD⊥平面ABCD．（Ⅰ）求证：平面PAD⊥平面PCD；（Ⅱ）在AD＝2，AB＝4，求三棱锥P﹣ABD的体积；（Ⅲ）在条件（Ⅱ）下，求四棱锥P﹣ABCD外接球的表面积．【解答】解：（I）∵四边形ABCD是矩形，∴AD⊥CD，又∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，CD⊂平面ABCD，∴CD⊥平面PAD，∵CD⊂平面PCD，∴平面PAD⊥平面PCD．（II）过P作PE⊥AD，垂足为E，∵△PAD是等腰直角三角形，∠APD＝90°，∴PE＝＝1．∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，PE⊂平面PAD，PE⊥AD，∴PE⊥平面ABCD，∴V棱锥P﹣ABD＝S△ABD•PE＝••2•4•1＝．（III）取BD中点M，过M作MN⊥平面ABCD，则球心O在直线MN上，连接AM，则AM＝＝．∵PE⊥平面ABCD，∴MN∥PE．∵四棱锥P﹣ABCD内接于球，，∴OA＝＝．∴S⊙O＝4πOA2＝20π．∴E为外心，∴OM＝1．如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，已知其俯视图是正三角形，则该四棱锥的外接球的表面积是（）A．B．C．19πD．22π【解答】解：几何体的直观图如图：是长方体的一部分，上底面PCD的外接圆的半径：O1D＝＝，几何体的外接球的半径为：OD＝＝，该四棱锥的外接球的表面积是：4＝π．故选：A．课后作业答案：1．如图，一个正三棱柱的主视图是长为，宽为2的矩形，俯视图是边长为的正三角形，则它的外接球的表面积等于（）A．16πB．12πC．8πD．4π【解答】解：设正三棱柱的外接球的半径为R，则∵俯视图是边长为的正三角形∴底面三角形外接圆的半径为＝1，∵正三棱柱的高为2∴正三棱柱的外接球的半径为＝∴正三棱柱的外接球的表面积等于4π×＝8π故选：C．2．某四面体的三视图如图所示，正视图、侧视图、俯视图都是边长为1的正方形，则此四面体的外接球的表面积为（）A．πB．3πC．πD．π【解答】解：由三视图可知：该四面体是正方体的一个内接正四面体．∴此四面体的外接球的直径为正方体的对角线长＝．∴此四面体的外接球的表面积为表面积＝＝3π．故选：B．3．某四棱锥的三视图如图所示，则该棱锥的外接球的表面积为（）A．3πB．C．6πD．12π【解答】解：由题意可知，几何体的直观图如图：是四棱锥D1﹣ABCD，是棱长为1的正方体的一部分，外接球奇数正方体的外接球，取得直径是体对角线，r＝，外接球的表面积为：4＝3π．故选：A．4．四棱锥P﹣ABCD中，ABCD为矩形，AD＝2，AB＝2，PA＝PD，∠APD＝，且平面PAD⊥平面ABCD．（1）证明：PA⊥PC；（2）求四棱锥P﹣ABCD的外接球的体积．【解答】证明：（1）设AD的中点为E，则∵PA＝PD，∴PE⊥AD，∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，∴PE⊥平面ABCD，∵PA在平面ABCD内的射影为AE，AE⊥CD，∴PA⊥CD，∵PA⊥PD，CD∩PD＝D，∴PA⊥平面PCD∴PA⊥PC；解：（2）连接AC交BD于F，球心O在底面的射影必为点F，取截面PEF，PE＝，EF＝1．假设OF＝x，则由OA2＝x2+4＝1+得x＝0，∴球的半径为2，∴四棱锥P﹣ABCD的外接球的体积为＝．。
高中数学 外接球专题训练
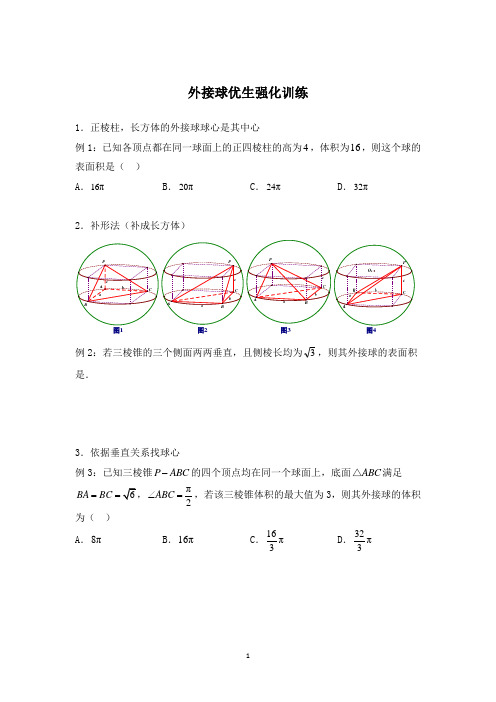
外接球优生强化训练1．正棱柱，长方体的外接球球心是其中心例1：已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ ） A ．16π B ．20πC ．24πD ．32π2．补形法（补成长方体）图2图3例2：若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是．3．依据垂直关系找球心例3：已知三棱锥P ABC -的四个顶点均在同一个球面上，底面ABC △满足BA BC ==π2ABC ∠=，若该三棱锥体积的最大值为3，则其外接球的体积为（ ） A ．8πB ．16πC ．16π3D ．32π3强化训练一、单选题1．棱长分别为2、3、5的长方体的外接球的表面积为（ ） A ．4π B ．12πC ．24πD ．48π2．设三棱柱的侧棱垂直于底面，所有棱的长都为23，顶点都在一个球面上，则该球的表面积为（ ） A ．12π B ．28πC ．44πD ．60π3．把边长为3的正方形ABCD 沿对角线AC 对折，使得平面ABC ⊥平面ADC ，则三棱锥D ABC -的外接球的表面积为（ ） A ．32π B ．27πC ．18πD ．9π4．某几何体是由两个同底面的三棱锥组成，其三视图如下图所示，则该几何体外接球的面积为（ ）A ．2πaB ．22πaC ．23πaD ．24πa5．三棱锥A BCD -的所有顶点都在球O 的表面上，AB ⊥平面BCD ，2BC BD ==，243AB CD ==O 的表面积为（ ）A ．16πB ．32πC ．60πD ．64π6．如图1111ABCD A B C D -是边长为1的正方体，S ABCD -是高为1的正四棱锥，若点S ，1A ，1B ，1C ，1D 在同一个球面上，则该球的表面积为（ ）A ．9π16B ．25π16C ．49π16D ．81π167．已知球O 的半径为R ，A ，B ，C 三点在球O 的球面上，球心O 到平面ABC 的距离为12R ，2AB AC ==，120BAC ∠=︒，则球O 的表面积为（ ） A ．16π9B ．16π3C ．64π9D ．64π38．已知正四棱锥P ABCD -(底面四边形ABCD 是正方形，顶点在底面的射影是底面的中心)的各顶点都在同一球面上，底面正方形的边长为10，若该正四棱锥的体积为503，则此球的体积为（ ） A ．18π B ．86 C ．36π D ．323π9．如图，在ABC △中，6AB BC ==，90ABC ∠=︒，点D 为AC 的中点，将ABD △沿BD 折起到PBD △的位置，使PC PD =，连接PC ，得到三棱锥P BCD -．若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）A ．7πB ．5πC ．3πD ．π10．四面体A BCD -中，60ABC ABD CBD ∠=∠=∠=︒，3AB =，2CB DB ==，则此四面体外接球的表面积为（ ） A ．19π2B ．1938π24C ．17πD ．1717π611．将边长为2的正ABC △沿着高AD 折起，使120BDC ∠=︒，若折起后A B C D 、、、四点都在球O 的表面上，则球O 的表面积为（ ） A ．7π2B ．7πC ．13π2D ．13π312．在三棱锥A BCD -中，6AB CD ==，5AC BD AD BC ====，则该三棱锥的外接球的表面积为（ ） A 4343πB 4343πC ．43π2D ．43π二、填空题13．棱长均为6的直三棱柱的外接球的表面积是_________．14．已知棱长都相等正四棱锥的侧面积为163，则该正四棱锥内切球的表面积为________．15．已知三棱柱111ABC A B C -的侧棱垂直于底面，各顶点都在同一球面上，若该32AB =，1AC =，60BAC ∠=︒，则此球的表面积等于______．16．在三棱锥A BCD -中，AB AC =，DB DC =，4AB DB +=，AB BD ⊥，则三棱锥A BCD -外接球的体积的最小值为_____．外接球优生强化训练答案1．正棱柱，长方体的外接球球心是其中心例1：已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（） A ．16π B ．20πC ．24πD ．32π【答案】C【解析】162==h a V ，2=a ，24164442222=++=++=h a a R ，24πS =，故选C ．2．补形法（补成长方体）图2图3例2：若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是． 【答案】9π【解析】933342=++=R ，24π9πS R ==．3．依据垂直关系找球心例3：已知三棱锥P ABC -的四个顶点均在同一个球面上，底面ABC △满足6BA BC ==，π2ABC ∠=，若该三棱锥体积的最大值为3，则其外接球的体积为（） A ．8π B ．16π C ．16π3D ．32π3【答案】D【解析】因为ABC △是等腰直角三角形，所以外接球的半径是11232r =⨯=，设外接球的半径是R ，球心O 到该底面的距离d ，如图，则1632ABC S =⨯=△，3BD =，由题设116336ABC V S h h ==⨯=△，最大体积对应的高为3SD h ==，故223R d =+，即()2233R R =-+，解之得2R =，所以外接球的体积是3432ππ33R =，故答案为D ．强化训练一、单选题1．棱长分别为235的长方体的外接球的表面积为（） A ．4π B ．12π C ．24π D ．48π【答案】B【解析】设长方体的外接球半径为R ，由题意可知：()()(22222235R =++，则：23R =，该长方体的外接球的表面积为24π4π312πS R ==⨯=．本题选择B 选项．2．设三棱柱的侧棱垂直于底面，所有棱的长都为23，顶点都在一个球面上，则该球的表面积为（） A ．12π B ．28π C ．44π D ．60π【答案】B【解析】设底面三角形的外接圆半径为r ，由正弦定理可得：232sin60r =︒，则2r =， 设外接球半径为R ，结合三棱柱的特征可知外接球半径()222327R =+=， 外接球的表面积24π28πS R ==．本题选择B 选项．3．把边长为3的正方形ABCD 沿对角线AC 对折，使得平面ABC ⊥平面ADC ，则三棱锥D ABC -的外接球的表面积为（） A ．32π B ．27π C ．18π D ．9π【答案】C【解析】把边长为3的正方形ABCD 沿对角线AC 对折，使得平面ABC ⊥平面ADC ，则三棱锥D ABC -的外接球直径为32AC =，外接球的表面积为24π18πR =，故选C ．4．某几何体是由两个同底面的三棱锥组成，其三视图如下图所示，则该几何体外接球的面积为（）A ．2πaB ．22πaC ．23πaD ．24πa【答案】C【解析】由题可知，该几何体是由同底面不同棱的两个三棱锥构成，其中底面是2a 的正三角形，一个是三条侧棱两两垂直，且侧棱长为a 的正三棱锥，另一个是棱长为2a 的正四面体，如图所示：该几何体的外接球与棱长为的正方体的外接球相同，因此外接球的直径即为正方体的体对角线，所以222323R a a a a R =++⇒=，所以该几何体外接球面积22234π4π3πS R a ⎫==⨯=⎪⎪⎝⎭，故选C ． 5．三棱锥A BCD -的所有顶点都在球O 的表面上，AB ⊥平面BCD ，2BC BD ==，243AB CD ==O 的表面积为（）A ．16πB ．32πC ．60πD ．64π【答案】D【解析】因为2BC BD ==，23CD =()22222231cos 2222CBD +-∠==-⨯⨯，2π3CBD ∴∠=， 因此三角形BCD 外接圆半径为122sin CDCBD=∠，设外接球半径为R ，则222=2+412162AB R ⎛⎫=+= ⎪⎝⎭，2=4π64πS R ∴=，故选D ．6．如图1111ABCD A B C D -是边长为1的正方体，S ABCD -是高为1的正四棱锥，若点S ，1A ，1B ，1C ，1D 在同一个球面上，则该球的表面积为（）A ．9π16B ．25π16C ．49π16D ．81π16【答案】D【解析】如图所示，连结11A C ，11B D ，交点为M ，连结SM ，易知球心O 在直线SM 上，设球的半径R OS x ==，在1Rt OMB △中，由勾股定理有：22211OM B M B O +=，即：()22222x x -+=⎝⎭，解得：98x =，则该球的表面积229814π4ππ816S R ⎛⎫==⨯= ⎪⎝⎭．本题选择D 选项．7．已知球O 的半径为R ，A ，B ，C 三点在球O 的球面上，球心O 到平面ABC 的距离为12R ，2AB AC ==，120BAC ∠=︒，则球O 的表面积为（） A ．16π9B ．16π3C ．64π9D ．64π3【答案】D【解析】由余弦定理得：44222cos12023BC +-⨯⨯︒ 设三角ABC 外接圆半径为r 232r =，则2r =，又22144R R =+，解得：2163R =，则球的表面积2644ππ3S R ==．本题选择D 选项． 8．已知正四棱锥P ABCD -(底面四边形ABCD 是正方形，顶点在底面的射影是底面的中心)的各顶点都在同一球面上，底面正方形的边长为10，若该正四棱锥的体积为503，则此球的体积为（） A ．18π B ．86 C ．36π D ．323π【答案】C 【解析】如图，设正方形ABCD 的中点为E ，正四棱锥P ABCD -的外接球心为O ， 105EA ∴正四棱锥的体积为503，21501033P ABCD V PE -∴=⨯⨯=， 则5PE =，5OE R ∴=-，在AOE △中由勾股定理可得：()2255R R -+=，解得3R =，34π36π3V R ∴==球，故选C ．9．如图，在ABC △中，6AB BC ==90ABC ∠=︒，点D 为AC 的中点，将ABD △沿BD 折起到PBD △的位置，使PC PD =，连接PC ，得到三棱锥P BCD -．若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（）A ．7πB ．5πC ．3πD ．π【答案】A【解析】由题意得该三棱锥的面PCD 是边长为3的正三角形，且BD ⊥平面PCD ， 设三棱锥P BDC -外接球的球心为O ，PCD △外接圆的圆心为1O ，则1OO ⊥面PCD ，∴四边形1OO DB 为直角梯形，由3BD =，11O D =，及OB OD =，得72OB =，∴外接球半径为72R =，∴该球的表面积274π4π7π4S R ==⨯=．故选A ．10．四面体A BCD -中，60ABC ABD CBD ∠=∠=∠=︒，3AB =，2CB DB ==，则此四面体外接球的表面积为（） A ．19π2B ．1938π24C ．17πD ．1717π6【答案】A 【解析】由题意，BCD △中，2CB DB ==，60CBD ∠=︒，可知BCD △是等边三角形，3BF = ∴BCD △的外接圆半径23r BE ==，3FE ， ∵60ABC ABD ∠=∠=︒，可得7AD AC ==6AF =AF FB ⊥，∴AF BCD ⊥，∴四面体A BCD -高为6AF ．设外接球R ，O 为球心，OE m =，可得：222r m R +=……①，()2226πEF R -+=……②由①②解得：198R =．四面体外接球的表面积：2194ππ2S R ==．故选A ． 11．将边长为2的正ABC △沿着高AD 折起，使120BDC ∠=︒，若折起后A B C D 、、、四点都在球O 的表面上，则球O 的表面积为（） A ．7π2B ．7πC ．13π2D ．13π3【答案】B【解析】BCD △中，1BD =，1CD =，120BDC ∠=︒，底面三角形的底面外接圆圆心为M ，半径为r ，由余弦定理得到3BC =，再由正弦定理得到321sin120r r =⇒=︒， 见图示：AD 是球的弦，3DA =将底面的圆心M 平行于AD 竖直向上提起，提起到AD 的高度的一半，即为球心的位置O ，∴3OM =OMD 中，应用勾股定理得到OD ，OD 即为球的半径． ∴球的半径3714OD +=24π7πOD ⨯=；故选B ． 12．在三棱锥A BCD -中，6AB CD ==，5AC BD AD BC ====，则该三棱锥的外接球的表面积为（） A 4343πB 4343πC ．43π2D ．43π【答案】D【解析】分别取AB ，CD 的中点E ，F ，连接相应的线段CE ，ED ，EF ，由条件，4AB CD ==，5BC AC AD BD ====，可知，ABC △与ADB △，都是等腰三角形，AB ⊥平面ECD ，∴AB EF ⊥，同理CD EF ⊥，∴EF 是AB 与CD 的公垂线，球心G 在EF 上，推导出AGB CGD △≌△，可以证明G 为EF 中点，2594DE =-=，3DF =，1697EF =-=，∴72GF =，球半径743942DG =+=，∴外接球的表面积为24π43πS DG =⨯=． 故选D ．二、填空题13．棱长均为6的直三棱柱的外接球的表面积是_________． 【答案】84π【解析】由正弦定理可知底面三角形的外接圆半径为161232sin6023r =⨯==︒，则外接球的半径()2232391221R =++， 则外接球的表面积为24π4π2184πS R ==⨯=．14．已知棱长都相等正四棱锥的侧面积为163，则该正四棱锥内切球的表面积为________． 【答案】(32163π-【解析】设正四棱锥的棱长为a ，则234163⎫=⎪⎪⎝⎭4a =． 于是该正四棱锥内切球的大圆是如图PMN △的内切圆，其中4MN =，23PM PN ==22PE = 设内切圆的半径为r ，由PFO PEN ≅△△，得FO POEN PN =，即22223r r -=， 解得226231r ==+∴内切球的表面积为()224π4π6232163πS r ===-．15．已知三棱柱111ABC A B C -的侧棱垂直于底面，各顶点都在同一球面上，若该32AB =，1AC =，60BAC ∠=︒，则此球的表面积等于______． 【答案】8π【解析】∵三棱柱111ABC A B C -32AB =，1AC =，60BAC ∠=︒，1121sin 6032AA ∴⨯⨯⨯︒⨯=12AA ∴=，2222cos60412BC AB AC AB AC =+-⋅︒=+-，3BC ∴=，设ABC △外接圆的半径为R ，则2sin 60BCR ︒＝，1R ∴=， 112+=24π28π⨯=．故答案为8π． 16．在三棱锥A BCD -中，AB AC =，DB DC =，4AB DB +=，AB BD ⊥，则三棱锥A BCD -外接球的体积的最小值为_____． 【答案】82π3【解析】如图所示，三棱锥A BCD -的外接圆即为长方体的外接圆，外接圆的直径为长方体的体对角线AD ，设AB AC x ==，那么4DB DC x ==-，AB BD ⊥，所以22AD AB DB =+．由题意，体积的最小值即为AD 最小，()224AD x x =+-所以当2x =时，AD 的最小值为22， 82π。
高三数学专题外接球
高三数学专题外接球1．正棱柱，长方体的外接球球心是其中心例1：已知各顶点都在同一球面上的正四棱柱的高为，体积为，则这个球的表面积是（ ） A ．B ．C ．D ．2．补形法（补成长方体）例2：若三棱锥的三个侧面两两垂直，且侧棱长均为，则其外接球的表面积是 ． 3．依据垂直关系找球心例3：已知三棱锥的四个顶点均在同一个球面上，底面满足，若该三棱锥体积的最大值为3，则其外接球的体积为（ ） A ．B ．C ．D ．一、单选题1．棱长分别为2、、的长方体的外接球的表面积为（ ） A ．B ．C ．D ．2．设三棱柱的侧棱垂直于底面，所有棱的长都为，顶点都在一个球面上，则该球的表面积为（ ） A ．12πB ．28πC ．44πD ．60π20π24π32π图2图3P ABC -ABC △BA BC ==π2ABC ∠=16π16π332π324π48π3．把边长为3的正方形沿对角线对折，使得平面平面，则三棱锥的外接 球的表面积为（ ） A ．B ．C ．D ．4．某几何体是由两个同底面的三棱锥组成，其三视图如下图所示，则该几何体外接球的面积为（ ）A ．B ．C ．D ．5．三棱锥的所有顶点都在球的表面上，平面，，，则球的表面积为（ ）A ．B ．C ．D ．6．如图是边长为1的正方体，是高为1的正四棱锥，若点，，，，在同一个球面上，则该球的表面积为（ ）A ．B ．C ．D ．7．已知球的半径为，，，三点在球的球面上，球心到平面的距离为，，ABCD ABC ⊥ADC D ABC -32π27π22πa 23πa 24πa A BCD -AB ⊥BCD 2BC BD ==2AB CD ==32π60π64π1111ABCD A B C D -S ABCD-9π1625π1649π1681π16ABC 12R 2AB AC ==，则球的表面积为（ ） A ．B ．C ．D ．8．已知正四棱锥(底面四边形是正方形，顶点在底面的射影是底面的中心)，若该正四棱锥的体积为，则此球的体积为（ ）A ．B ． C． D ．9．如图，在中，，点为的中点，将沿折起到的位置，使，连接，得到三棱锥．若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）A ．B ．C ．D ．10．四面体中，，，，则此四面体外接球的表面积为（ ）A ．BC ． D11．将边长为2的正沿着高折起，使，若折起后四点都在球的表面上，则球的表面积为（ ）A ．B ．C ．D ．12．在三棱锥中，，，则该三棱锥的外接球的表面积为（ ）120BAC ∠=︒16π916π364π964π3P ABCD -ABCD 50336πABC △AB BC ==90ABC ∠=︒ABD △PBD △PC PD =P BCD -A BCD -60ABC ABD CBD ∠=∠=∠=︒3AB =2CB DB ==19π2ABC △120BDC ∠=︒A B C D 、、、7π213π213π3A BCD -6AB CD ==5AC BD AD BC ====ABC ．D ．二、填空题13．棱长均为6的直三棱柱的外接球的表面积是_________．14．已知棱长都相等正四棱锥的侧面积为，则该正四棱锥内切球的表面积为________．15．已知三棱柱的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，，，，则此球的表面积等于______．16．在三棱锥中，，，，，则三棱锥外接球的体积的最小值为_____． 1．正棱柱，长方体的外接球球心是其中心例1：已知各顶点都在同一球面上的正四棱柱的高为，体积为，则这个球的表面积是（ ） A ． B ．20πC ．24πD ．32π【答案】C【解析】162==h a V ，2=a ，24164442222=++=++=h a a R ，24πS =，故选C ． 2．补形法（补成长方体）例2：若三棱锥的三个侧面两两垂直，且侧棱长均为，则其外接球的表面积是 ． 【答案】43π243π111ABC A B C -2AB =1AC =60BAC ∠=︒A BCD -AB AC =DB DC =4AB DB +=AB BD ⊥A BCD-图2图3【解析】933342=++=R ，24π9πS R ==． 3．依据垂直关系找球心例3：已知三棱锥P ABC -的四个顶点均在同一个球面上，底面ABC △满足BA BC ==π2ABC ∠=，若该三棱锥体积的最大值为3，则其外接球的体积为（ ） A ． B ．16πC ．16π3D ．32π3【答案】D【解析】因为ABC △是等腰直角三角形，所以外接球的半径是12r =的半径是，球心到该底面的距离，如图，则1632ABC S =⨯=△，BD 116336ABC V S h h ==⨯=△，最大体积对应的高为3SD h ==，故223R d =+，即()2233R R =-+，解之得2R =，所以外接球的体积是3432ππ33R =，故答案为D ．一、单选题1．棱长分别为2、、的长方体的外接球的表面积为（ ） A ．B ．C ．24πD ．48π【答案】B【解析】设长方体的外接球半径为，由题意可知：()222222R =++，则：23R =，该长方体的外接球的表面积为24π4π312πS R ==⨯=．本题选择B 选项．2．设三棱柱的侧棱垂直于底面，所有棱的长都为面积为（ ） A ．12π B ．28π C ．44π D ．60π【答案】B【解析】设底面三角形的外接圆半径为，由正弦定理可得：2r 2r =， 设外接球半径为，结合三棱柱的特征可知外接球半径22227R =+=，外接球的表面积24π28πS R ==．本题选择B 选项．3．把边长为3的正方形ABCD 沿对角线对折，使得平面ABC ⊥平面ADC ，则三棱锥D ABC -的外接球的表面积为（ ） A ．32π B ．27πC ．D ．【答案】C【解析】把边长为3的正方形ABCD 沿对角线对折，使得平面ABC ⊥平面ADC ， 则三棱锥D ABC -的外接球直径为AC =24π18πR =，故选C ． 4．某几何体是由两个同底面的三棱锥组成，其三视图如下图所示，则该几何体外接球的面积为（ ）A ．B ．22πaC ．23πaD ．24πa【答案】C【解析】由题可知，该几何体是由同底面不同棱的两个三棱锥构成，的正四面体，如图所示：该几何体的外接球与棱长为 的正方体的外接球相同，因此外接球的直径即为正方体的体对角线，所以2R R =⇒，所以该几何体外接球面积2224π4π3πS R a ⎫==⨯=⎪⎪⎝⎭，故选C ．5．三棱锥A BCD -的所有顶点都在球的表面上，AB ⊥平面BCD ，2BC BD ==，2AB CD == ）A ．B ．32πC ．60πD ．64π【答案】D【解析】因为2BC BD ==，CD =(222221cos 2222CBD +-∠==-⨯⨯，2π3CBD ∴∠=， 因此三角形BCD 外接圆半径为122sin CDCBD=∠，设外接球半径为，则222=2+412162AB R ⎛⎫=+= ⎪⎝⎭，2=4π64πS R ∴=，故选D ．6．如图1111ABCD A B C D -是边长为1的正方体，S ABCD -是高为1的正四棱锥，若点，，，，在同一个球面上，则该球的表面积为（ ）A ．9π16B ．25π16C ．49π16D ．81π16【答案】D【解析】如图所示，连结11A C ，11B D ，交点为，连结SM ，易知球心在直线SM 上，设球的半径R OS x ==，在1Rt OMB △中，由勾股定理有：22211OM B M B O +=，即：()2222x x -+=⎝⎭，解得：98x =，则该球的表面积229814π4ππ816S R ⎛⎫==⨯= ⎪⎝⎭．本题选择D 选项．7．已知球的半径为，，，三点在球的球面上，球心到平面ABC 的距离为12R ，2AB AC ==，120BAC ∠=︒，则球的表面积为（ ）A ．16π9B ．16π3C ．64π9D ．64π3【答案】D【解析】由余弦定理得：BC ==设三角ABC 2r =，则2r =，又22144R R =+，解得：2163R =，则球的表面积2644ππ3S R ==．本题选择D 选项． 8．已知正四棱锥P ABCD -(底面四边形ABCD 是正方形，顶点 在底面的射影是底面的中心)503，则此球的体积为（ ）A ．B ．C ．36πD ．【答案】C 【解析】如图，设正方形ABCD 的中点为，正四棱锥P ABCD -的外接球心为， EA ∴正四棱锥的体积为503，215033P ABCD V PE -∴=⨯⨯=， 则5PE =，5OE R ∴=-，在AOE △中由勾股定理可得：()2255R R -+=，解得3R =，34π36π3V R ∴==球，故选C ．9．如图，在ABC △中，AB BC ==90ABC ∠=︒，点为的中点，将ABD △沿折起到PBD △的位置，使PC PD =，连接，得到三棱锥P BCD -．若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）A ．B ．C ．D ．【答案】A【解析】由题意得该三棱锥的面PCD 是边长为的正三角形，且BD ⊥平面PCD ， 设三棱锥P BDC -外接球的球心为，PCD △外接圆的圆心为，则1OO ⊥面PCD ，∴四边形1OO DB 为直角梯形，由BD11O D =，及OB OD =，得OB =R =∴该球的表面积274π4π7π4S R ==⨯=．故选A ． 10．四面体A BCD -中，60ABC ABD CBD ∠=∠=∠=︒，3AB =，2CB DB ==，则此四面体外接球的表面积为（ ）A ．19π2BC ．D 【答案】A【解析】由题意，BCD △中，2CB DB ==，60CBD ∠=︒，可知BCD △是等边三角形，BF =∴BCD △的外接圆半径r BE ==，FE ， ∵60ABC ABD ∠=∠=︒，可得AD AC =可得AF =∴AF FB ⊥，∴AF BCD ⊥，∴四面体A BCD -高为AF =设外接球，为球心，OE m =，可得：222r m R +=……①， )222πEF R +=……②由①②解得：R =2194ππ2S R ==．故选A ． 11．将边长为2的正ABC △沿着高折起，使120BDC ∠=︒，若折起后A B C D 、、、四点都在球的表面上，则球的表面积为（ ）A ．7π2B ．C ．13π2D ．13π3【答案】B【解析】BCD △中，1BD =，1CD =，120BDC ∠=︒， 底面三角形的底面外接圆圆心为，半径为，由余弦定理得到BC =21r r =⇒=， 见图示：是球的弦，DA =的位置，∴OM =OMD 中，应用勾股定理得到，即为球的半径．∴球的半径OD =．该球的表面积为24π7πOD ⨯=；故选B ． 12．在三棱锥A BCD -中，6AB CD ==，5AC BD AD BC ====，则该三棱锥的外接球的表面积为（ ）A B C ．43π2 D ．43π【答案】D【解析】分别取，的中点，，连接相应的线段，，， 由条件，4AB CD ==，5BC AC AD BD ====，可知，ABC △与ADB △，都是等腰三角形，AB ⊥平面ECD ，∴AB EF ⊥，同理CD EF ⊥，∴是与的公垂线， 球心在上，推导出AGB CGD △≌△，可以证明为中点，4DE ==，3DF =，EF =∴GF =DG =24π43πS DG =⨯=． 故选D ．二、填空题13．棱长均为6的直三棱柱的外接球的表面积是_________．【答案】84π【解析】由正弦定理可知底面三角形的外接圆半径为1612sin602r =⨯==︒ 则外接球的半径R ， 则外接球的表面积为24π4π2184πS R ==⨯=．14．已知棱长都相等正四棱锥的侧面积为，则该正四棱锥内切球的表面积为________．【答案】(32π-【解析】设正四棱锥的棱长为，则24⎫=⎪⎪⎝⎭4a =．于是该正四棱锥内切球的大圆是如图PMN △的内切圆，其中4MN =，PM PN ==PE =．设内切圆的半径为，由PFO PEN ≅△△，得FO PO EN PN =，即2r =，解得r ==∴内切球的表面积为(224π4π32πS r ===-． 15．已知三棱柱111ABC A B C -的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，2AB =，1AC =，60BAC ∠=︒，则此球的表面积等于______．【答案】【解析】∵三棱柱111ABC A B C -的侧棱垂直于底面，棱柱的体积为，2AB =，1AC =，60BAC ∠=︒，1121sin 602AA ∴⨯⨯⨯︒⨯12AA ∴=， 2222cos60412BC AB AC AB AC =+-⋅︒=+-，BC ∴=，设ABC △外接圆的半径为，则2sin 60BC R ︒＝，1R ∴=， =24π8π⨯=．故答案为．16．在三棱锥A BCD -中，AB AC =，DB DC =，4AB DB +=，AB BD ⊥，则三棱锥A BCD -外接球的体积的最小值为_____．【解析】如图所示，三棱锥A BCD -的外接圆即为长方体的外接圆，外接圆的直径为长方体的体对角线，设AB AC x ==，那么4DB DC x ==-，AB BD ⊥，所以AD =．由题意，体积的最小值即为最小，AD 2x =时，的最小值为。
2023高考数学考点专题复习——立体几何之外接球(原卷版)
2023考点专题复习——立体几何之外接球类型一、墙角模型（长方体，正方体）——公式：2222R a b c =++例1、长方体的长，宽，高分别为321，其顶点都在球O 的球面上，则球O 的体积为（ ） A ．43π B ．12πC ．48π D ．323π例2、已知三棱锥P BCD -中，BC CD ⊥，PB ⊥底面BCD ，1BC =，2PB CD ==，则该三棱锥的外接球的体积为（ ）A ．74πB ．92πC ．278πD ．259π 例3、已知正方体外接球的体积是323π，那么正方体的体对角线等于（ ） A 23B ．4 C 42D 43 例4、据《九章算术》记载，“鳖臑”为四个面都是直角三角形的三棱锥．如图所示，现有一个“鳖臑”，PA ⊥底面ABC ，AB BC ⊥，且2PA AB BC ===，三棱锥外接球表面积为（ ）A ．10πB ．12πC ．14πD ．16π例5、在正三棱锥P ABC -中，PA PB ⊥，P 到平面ABC 的距离为2，则该三棱锥外接球的表面积为（ ）A ．36πB ．16πC ．163πD ．4π例6、如图在正三棱锥S ABC -中，,M N 分别是棱,SC BC 的中点，Q 为棱AC 上的一点，且12AQ QC =，MN MQ ⊥，若22AB =S ABC -的外接球的体积为（ ）A ．12πB 43C ．3πD ．43π练习1、《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为“阳马”．现有一“阳马”P ABCD -，PA ⊥平面ABCD ，4AB =，PAD △的面积为4，则该“阳马”外接球的表面积的最小值为（ ） A ．24π B ．28π C ．32π D ．36π练习2、在三棱锥A BCD -中，已知AC ⊥平面BCD ，BC BD ⊥，且3AC =2BC =，5BD =棱锥外接球的表面积为（ ）A ．12πB ．7πC ．9πD ．8π练习3、已知三棱锥P ABC -的四个顶点在球O 的球面上，PA PB PC ==，ABC ∆是边长为2正三角形，E ，F 分别是PA ，AB 的中点，90CEF ∠=︒，则球O 的体积为 ．练习4、《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑，若三棱锥P ABC -为鳖臑，PA ⊥平面ABC ，4PA BC ，3AB =，AB BC ⊥，若三棱锥P ABC -的所有顶点都在球O 上，则球O 的半径为（ ） A 41 B ．34 C ．38 D ．32练习5、在《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑（biē nào ）．已知在鳖臑M ABC -中，MA ⊥平面ABC ，4MA AB BC ===，则该鳖臑的外接球的表面积为（ ）A ．12πB ．24πC ．48πD ．96π练习6、三棱锥P ABC -中，ABC ∆是边长为2的正三角形，PA PB PC ==，E ，F 分别是PA ，AB 的中点，且CE EF ⊥，则三棱锥P ABC -接球的表面积为( )A ．6πB ．12πC ．24πD ．36π练习7、若棱长为2( )A ．12πB ．24πC ．36πD ．144π练习8、在四面体ABCD 中，BCD ∆是边长为2的等边三角形，ABD ∆是以BD 为斜边的等腰直角三角形，平面ABD ⊥平面ABC ，则四面体ABCD 的外接球的表面积为 ．练习9、《九章算术》是我国古代的数学名著，书中对几何学的研究比西方早一千多年.在该书中，将底面为直角三角形，且侧棱垂直于底面的三棱柱称为堑堵；将底面为矩形，一侧棱垂直于底面的四棱锥称为阳马；将四个面均为直角三角形的四面体称为鳖臑.如图，在堑堵111ABC A B C -中，AC BC ⊥，3AC =，鳖臑11A BCC -的体积为2，则阳马111A BCC B -外接球表面积的最小值为__________．练习10、在长方体1111ABCD A B C D -中，四边形ABCD 是边长为2的正方形，1D B 与DC 所成的角是60︒，则长方体的外接球表面积是（ ）A ．16πB ．8πC ．4πD ．2π练习11、已知矩形ABCD ，1AB =，2AD =E 为AD 的中点，现分别沿,BE CE 将ABE ∆，DCE ∆翻折，使点,A D 重合，记为点P ，则几何体P BCE -的外接球表面积为（ ）A ．10πB ．5πC ．52πD 55π练习12、在三棱锥P ABC -中，三条棱PA PB PC 、、两两垂直，且122PA PB PC ===、、.若点Q 为三棱锥P ABC -的外接球球面上任意一点，则Q 到面ABC 距离的最大值为______.练习13、已知三棱锥S ABC -中，1SA SB SC ===，且SA 、SB 、SC 两两垂直，P 是三棱锥S ABC -外接球面上一动点，则P 到平面ABC 的距离的最大值是A 3B 3C 23D 43类型二、对棱相等模型（补形为长方体）公式：2228x y z R ++=例1、在四面体ABCD 中，若3AB CD ==，2AC BD ==，5AD BC ==ABCD 的外接球的表面积为( )A ．2πB ．4πC ．6πD ．8π例2、已知四面体ABCD 中，5AB CD =10BC AD ==，13AC BD =在同一球面上，则此球的表面积为( )A ．42πB ．43πC ．14πD ．16π例3、如图，在三棱锥P ABC -中，3PA BC =，2PB AC ==，5PC AB ==，则三棱锥P ABC -外接球的体积为( )A 2πB 3πC 6πD ．6π练习1、在三棱锥P ABC -中，4PA BC ==，5PB AC ==，11PC AB ==，则三棱锥P ABC -的外接球的表面积为( )A ．26πB ．12πC ．8πD ．24π练习2、已知在四面体ABCD 中，22,5AB CD AD AC BC BD ======，则四面体ABCD 的外接球表面积为 ．练习3、在四面体ABCD 中，2AC BD ==，5AD BC =7AB CD =则其外接球的表面积为 ． 练习4、在ABC 中，2,2,10,8,,,AB m AC n BC AB AC E F G ===+=分别为,,AB BC AC 三边中点，将,,BEF AEG GCF 分别沿EF EG GF 、、向上折起，使A B C 、、重合，记为S ，则三棱锥S EFG -的外接球表面积的最小值为（ ）A ．292πB ．233πC ．14πD ．9π类型三、汉堡模型（圆柱、直棱柱）（一条棱垂直于底面）——公式：2222h r R ⎛⎫+= ⎪⎝⎭例1、已知直三棱柱111ABC A B C -的各顶点都在同一球面上，若1AB AC ==，12AA =，120BAC ∠=︒，则此球的表面积等于 ．例2、在直三棱柱111ABC A B C -中，若1,6,8,6⊥===AB BC AB BC AA ，则该直三棱柱外接球的表面积为（ ）A ．72πB ．114πC ．136πD ．144π例3、设直三棱柱111ABC A B C -的所有顶点都在一个球面上，1AB AC AA ==，120BAC ∠=︒，且底面ABC 的面积为23 ）A ．16πB 4010πC ．40πD ．64π例4、已知正六棱柱111111—ABCDEF A B C D E F 的每个顶点都在球O 的球面上，且3AB =，14AA =，则球O 的表面积为（ ）A ．42πB ．48πC ．50πD ．52π练习1、表面积为81π的球，其内接正四棱柱（底面是正方形的直棱柱）的高是7，则这个正四棱柱的底面边长为______．练习2、已知正三棱柱111ABC A B C -的外接球表面积为40π，则正三棱柱111ABC A B C -的所有棱长之和的最大值为______．练习3、在直三棱柱111ABC A B C -中，90BAC ∠=︒且14BB =，已知该三棱柱的体积为2，则此三棱柱外接球表面积的最小值为______．练习4、已知四棱锥P -ABCD 中，PA ⊥平面ABCD ，底面ABCD 是矩形，33AD AB PA ==，若四棱锥P -ABCD 外接球的表面积为11π，则四棱锥P -ABCD 的体积为（ ）A ．3B ．2C 2D ．1练习5、《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥M ABC -为鳖臑，MA ⊥平面ABC ，AB BC ⊥，2AB BC ==，4MA =，三棱锥M ABC -的四个顶点都在球O 的球面上，则球O 的表面积为（ ）A ．9πB ．16πC ．20πD ．24π 练习6、已知三棱锥S ABC -中， SA ⊥平面ABC ，3AB BC CA ===S ABC -外接球O 的表面积为100π，则球O 的体积为_______，异面直线SA ，OB 所成角的余弦值为________． 练习7、已知三棱锥S ABC -中，SA ⊥平面ABC ，4SA =，3BC =60BAC ∠=，则三棱锥S ABC -外接球的表面积为______．练习8、已知在三棱锥P ABC -中，4PA =，26BC =3PB PC ==，PA ⊥平面PBC ，则三棱锥P ABC -的外接球的表面积是（ ）A ．43πB ．42πC ．48πD ．46π练习9、已知三棱锥P BCD -中，BC CD ⊥，PB ⊥底面BCD ，1BC =，2PB CD ==，则该三棱锥的外接球的体积为（ ）A ．74πB ．92πC ．278πD ．259π 练习10、已知在三棱锥A BCD -中，AB ⊥平面BCD ，3,4,2AB AC AD CD ====，则三棱锥A BCD -外接球的表面积为（ ）A ．40π3B ．15πC ．52π3D ．20π练习11、三棱锥A BCD -的所有顶点都在球O 的表面上，AB ⊥平面BCD ，2BC BD ==，243AB CD ==，则球O 的表面积为（ ）A ．16πB ．32πC ．60πD ．64π练习12、如图，在ABC △中，6AB BC ==90ABC ∠=︒，点D 为AC 的中点，将ABD △沿BD 折起到PBD △的位置，使PC PD =，连接PC ，得到三棱锥P BCD -．若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）A ．7πB ．5πC ．3πD ．π练习13、已知三棱锥A BCD -的所有顶点都在球O 的球面上，且AB ⊥平面BCD ，23AB =4AC AD ==，22CD =，则球O 的表面积为( )A ．20πB ．18πC ．36πD ．24π练习14、正三角形ABC 的边长为2,将它沿高AD 翻折,使点B 与点C 2,此时四面体ABCD 外接球表面积为（ ）A 55B 77C ．5πD ．7π练习15、已知三棱锥P ABC -的四个顶点在球O 的球面上，PA ⊥平面ABC ，2PA AB BC ===，PB 与平面PAC 所成的角为30︒，则球O 的表面积为( )A ．6πB ．12πC ．16πD ．48π练习16、在三棱锥—P ABC 中，PA ⊥平面ABC ，2,30APC S ABC ∆=∠=︒，则三棱锥—P ABC 的外接球体积的最小值为（ ）A ．4πB ．43πC ．64πD ．323π练习17、直三棱柱ABC −A 1B 1C 1外接球表面积为16π，AB =2，若ΔABC ，矩形ABB 1A 1外接圆的半径分别为r 1,r 2，则r 1+r 2的最大值为（ ）A ．2√2B ．3C ．√10D ．2√3练习18、已知正三棱柱111ABC A B C -，侧面11BCC B 的面积为43则该正三棱柱外接球表面积的最小值为（ ）A ．4πB ．8πC ．3πD ．16π练习19、已知直三棱柱111ABC A B C -外接球的表面积为8π，90BAC ∠=︒．若,E F 分别为棱11,BC B C 上的动点，且1BE C F =，则直线EF 被该三棱柱外接球球面截得的线段长为（ ）A ．22B ．2C ．4D ．不是定值练习20、已知三棱锥D ABC -中，2AB AC AD ===，2DAB DAC π∠=∠=，23BAC π∠=，则点A 到平面BCD 的距离为 ，该三棱锥的外接球的体积为 ． 类型四、心有所依模型（圆锥、正棱锥）公式：()222222h r h R r R R h +-+=⇒= 例1、如图，已知一底面半径为1，体积为π的圆锥内接于球O （其中球心O 在圆锥内），则球O 的表面积为( )A ．1009πB ．209πC ．203πD ．503π 例2、三棱锥P ABC -3且,1,3PA PB PC AB AC BC =====则三棱锥外接球的表面积为____________．例3、在正三棱锥P ABC -中，23AB =P ABC -的体积是43P ABC -外接球的表面积是（ ）A ．5πB ．15πC ．25πD ．35π例4、已知正四棱锥P ABCD -的底面边长为2P A 与底面ABCD 所成的角为45°，顶点P ，A ，B ，C ，D 在球O 的球面上，则球O 的体积是（ ）A ．16πB ．323πC ．8πD 82 练习1、已知三棱锥P ABC -的四个顶点均在同一个球面上，底面ABC △满足6BA BC ==π2ABC ∠=，若该三棱锥体积的最大值为3，则其外接球的体积为（ ） A ．8π B ．16π C ．16π3 D ．32π3练习2、一块边长为10cm 的正方形铁片如图所示，将它的阴影部分截下，然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器，则这个正四棱锥的外接球的表面积( )A ．2894π B ．28916π C ．28948π D ．28964π练习3、已知球O 是圆锥1PO 的外接球，圆锥1PO 的母线长是底面半径的3倍，且球O 的表面积为818π，则圆锥1PO 的侧面积为 ． 练习4、如图1111ABCD A B C D -是边长为1的正方体，S ABCD -是高为1的正四棱锥，若点S ，1A ，1B ，1C ，1D 在同一个球面上，则该球的表面积为（ ）A ．9π16B ．25π16C ．49π16D ．81π16练习5、已知正四棱锥P ABCD -(底面四边形ABCD 是正方形，顶点P 在底面的射影是底面的中心)的各顶点10503，则此球的体积为（ ） A ．18πB ．86C ．36πD ．323π练习6、已知一个圆锥内接于球O （圆锥的底面圆周及顶点均在同一球面上），圆锥的高是底面半径的3倍，圆锥的侧面积为910π，则球O 的表面积为 ．练习7、已知正四棱锥P ABCD -的所有顶点都在球O 的球面上，且正四棱锥P ABCD -的底面面积为6，侧面积为67O 的体积为（ ）A ．323π B 287 C ．1254π D 1253练习8、圆锥SD （其中S 为顶点，D 为底面圆心）的侧面积与底面积的比是2:1，则圆锥SD 与它外接球（即顶点在球面上且底面圆周也在球面上）的体积比为A ．9:32B ．8:27C ．9:22D ．9:28练习9、已知正三棱锥S ABC -，底面是边长为3的正三角形ABC ，3SA =，点E 是线段AB 的中点，过点E 作三棱锥S ABC -外接球O 的截面，则截面面积的最小值是( )A ．3πB ．94πC ．2πD ．74π 练习10、已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上．若该球的体积为36π，且333l ≤≤正四棱锥体积的取值范围是（ ）A ．8118,4⎡⎤⎢⎥⎣⎦B ．2781,44⎡⎤⎢⎥⎣⎦C ．2764,43⎡⎤⎢⎥⎣⎦D ．[18,27]类型五、垂面模型——公式：222212()2lr r R +-=例1、在边长为4的正方形ABCD 中，E ，F ，G 分别为AD ，BC ，AB 的中点，现将矩形CDEF 沿EF 折起，使平面CDEF 与平面ABFE 所成的二面角为直二面角，则四面体CEGF 的外接球的表面积为___________．例2、在三棱锥P ABC -中，4PA PB BC ===，8AC =，AB BC ⊥．平面PAB ⊥平面ABC ，若球O 是三棱锥P ABC -的外接球，则球O 的表面积为( )A ．25πB ．60πC ．72πD ．80π例3、已知三棱锥P ABC -的四个顶点在球O 的球面上，2PA PC BC ===，4AB =，120APC ∠=︒，平面PAC ⊥平面ABC ，则球O 的体积为( )A ．45πB 165C 205D ．85π例4、矩形ABCD 中，4AB =，3BC =，沿AC 将矩形ABCD 折成一个直二面角B AC D --，则四面体ABCD 的外接球的体积为 ．练习1、如图，正方形ABCD 与正方形ACEF 所在的平面互相垂直，1AB =，点A ，B ，C ，D ，E ，F 在同一个球面上，则该球的体积是( )A 3πB ．43πC 82πD ．323π 练习2、已知ABC ∆是以BC 为斜边的直角三角形，P 为平面ABC 外一点，且平面PBC ⊥平面ABC ，3BC =，22PB =5PC =，则三棱锥P ABC -外接球的体积为（ ）A ．10πB 10πC ．53πD 510π练习3、已知点A 是以BC 为直径的圆O 上异于B ，C 的动点，P 为平面ABC 外一点，且平面PBC ⊥平面ABC ，3BC =，22PB =5PC =，则三棱锥P ABC -外接球的表面积为 ．练习4、在三棱锥P ABC -中，4AB AC ==，120BAC ∠=︒，43PB PC ==，平面PBC ⊥平面ABC ，则三棱锥P ABC -外接球的表面积为 ．练习5、在菱形ABCD 中，60DAB ∠=︒，将这个菱形沿对角线BD 折起，使得平面DAB ⊥平面BDC ，若此时三棱锥A BCD -的外接球的表面积为5π，则AB 的长为 ．练习6、在三棱锥P ABC -中，平面PAB ⊥平面ABC ，25,6,3AP AB ACB π==∠=，且直线PA 与平面ABC 所成角的正切值为2，则该三棱锥的外接球的表面积为( )A ．13πB ．52πC ．523πD 5213π练习7、如图，已知四棱锥P ABCD -的底面为矩形，平面PAD ⊥平面ABCD ，22AD =2PA PD AB ===，则四棱锥P ABCD -的外接球的表面积为( )A ．2πB ．4πC ．8πD ．12π练习8、如图，在直角梯形ABCD 中，//AB CD ，AB AD ⊥.已知222CD AB AD a ===.将ABD △沿直线BD 翻折成1A BD ，连接1A C .当三棱锥1A BCD -的体积取得最大值时，异面直线1A C 与BD 所成角的余弦值为___________；若此时三棱锥1A BCD -外接球的体积为43π，则a 的值为___________.类型六、折叠模型例1、已知边长为23的菱形ABCD 中，60BAD ∠=︒，沿对角边BD 折成二面角A BD C --为120︒的四面体ABCD ，则四面体的外接球的表面积为 ．例2、如图：边长为3ABCD ，60DAB ∠=，将ABD ∆沿BD 折起到图中PBD ∆的位置，使得二面角P BD C --的大小为60，则三棱锥P BCD -的外接球表面积等于_______．例3、已知空间四边形ABCD ，CD BD ⊥，3CD =3AB BD AD ===，二面角A -BD -C 是120︒，若A ､B ､C ､D 四点在同一球面上，则该球的表面积是（ ）A ．15πB ．18πC ．21πD ．24π 练习1、如图，把两个完全相同的直三角尺SBC ，SAC 斜边重合，沿其斜边SC 折叠形成一个120°的二面角，其中2SA SB ==，且3AB =SABC 外接球的表面积为（ ） A ．4π B ．163π C ．3π D ．203π 练习2、已知边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕进行折叠，使图 2ACBDO折后的2BDC π∠=，则过A ，B ，C ，D 四点的球的表面积为（ ）A ．3πB ．4πC ．5πD ．6π练习3、已知菱形ABCD 中，2AB AC ==，将其沿对角线BD 折成四面体ABCD ，使得二面角A BD C --的大小为3π，若该四面体的所有顶点在同一个球面上，则该球的表面积为（ ） A ．523π B 5239C ．269πD 2639练习4、四边形ABDC 是菱形，60BAC ∠=，3AB =沿对角线BC 翻折后，二面角A -BD -C 的余弦值为13-，则三棱锥D -ABC 的外接球的体积为_____．类型七、两个Rt ∆共斜边拼接模型例1、在矩形ABCD 中，==4,3AB BC ，沿AC 将矩形ABCD 折成一个直二面角--B AC D ，则四面体ABCD 的外接球的体积为（ ）A ．π12512B ．π1259C ．π1256D ．π1253例2、三棱锥-P ABC 中，平面⊥PAC 平面ABC ， =2AC ，⊥PA PC ，⊥AB BC ，则三棱锥-P ABC的外接球的半径为例3、把边长为3的正方形ABCD 沿对角线AC 对折，使得平面ABC ⊥平面ADC ，则三棱锥D ABC -的外接球的表面积为（ ） A ．32πB ．27πC ．18πD ．9π练习1、在平行四边形ABCD 中，满足2AB AD AB =，2224AB BD =-，若将其沿BD 折成直二面角A BD C --，则三棱锥A BCD -的外接球的表面积为( ) A ．16π B ．8π C ．4π D ．2π练习2、已知三棱锥A -BCD 中，22CD =2BC AC BD AD ====，则此几何体外接球的表面积为（ ） A 2πB ．2πC 82πD ．8π练习3、如图，在四棱锥P -ABCD 中，底面是菱形，PB ⊥ 底面ABCD ，O 是对角线AC 与BD 的交点，若1PB =，3APB π∠=，则三棱锥P BOC -的外接球的体积为（ ）A ．23π B ．43π C ．53π D ．2π练习4、如图，在三棱柱111ABC A B C -中，11114A B AC ==，S 为棱11B C 上一点，且90ASC ∠=︒，AB ⊥平面ACS ，则三棱锥S ABC -的外接球的表面积为 ．类型八、非特殊模型（万能模型）例1、如图，在三棱锥A BCD -中，AB AC BC BD CD ====，二面角A BC D--的余弦值为13-，若三棱锥A BCD -的体积为13，则三棱锥A BCD -外接球的表面积为______．例2、如图，在三棱锥A BCD -中，2AB BC AC CD ====，120BCD ∠=︒，二面角A BC D --的大小为120︒，则三棱锥A BCD -的外接球的表面积为（ ） A ．823πB ．803πC ．27πD ．2449π练习1、已知矩形ABCD ，1AB =，2AD =，点E 为BC 边的中点将ABE ∆沿AE 翻折，得到四棱锥B AECD -，且平面BAE ⊥平面AECD ，则四面体B ECD -的外接球的表面积为( ) A ．72πB ．4πC ．92πD ．5π练习2、在棱长为2的正方体1111ABCD A B C D -中，M ，N ，Q 分别为棱11A B ，11B C ，1BB 的中点，点P 为棱1CC 上的动点，则P MNQ V -的最大值为 12，若点P 为棱1CC 的中点，三棱锥M PQN -的顶点在同一个球面上，则该球的表面积为 ． 、练习3、已知三棱锥B ACD -中，2AB BC AC ===，2CD BD ==BC 的中点为E ，DE 的中点恰好为点A 在平面BCD 上的射影，则该三棱锥外接球半径的平方为（ ）14 15B2511C．2511D．1511A．。
高考数学立体几何专题：外接球
b2
1 a2 3
PO1
b2
1 a2 3
OO1
PO1
PO
b2 1 a2 R ； 3
在 RtOO1A 中：根据勾股定理得到：
OO12 AO12 AO2 (
b2 1 a2 R)2 ( 3 a)2 R2 b2 1 a2 2
第二部分：柱体的外接球半径 【计算步骤】 第一步：计算底面的外接圆的半径。 第二步：计算直柱体的外接球的半径。 直柱体的外接球的球心：上下底面的外接圆圆心连线的中点为球心。如下图所示：
第3页共8页
其中： O1 为下底面的外接圆的圆心， O2 为上底面的外接圆的圆心， O 为 O1O2 的中点（直柱体外接球的球心）； r 为上下底面的外接圆的半径， R 为直柱体的外接球的半径。
2
训练：求下列图形的外接圆半径。
（Ⅰ）在 ABC 中： AB AC ， AB 3 ， AC 4 ； （Ⅱ）在 ABC 中： AB AC 3 ， BC 2 5 ； （Ⅲ）在正 ABC 中： AB 3 ；
3 （Ⅳ）在 ABC 中， AB 2 ， BC 3， AC 2 ； （Ⅴ）在矩形 ABCD 中： AB 6 ， BC 3 ； （Ⅵ）在正方形 ABCD 中： AB 2 。
根据勾股定理得到： R2 r 2 ( h )2 r 2 h2 R r 2 h2 。
2
4
4
【训练一】：已知：在直三棱柱 ABC A1B1C1 中： AB AC ， AB AC 2 ， AA1 2 。 求解：直三棱锥 ABC A1B1C1 的外接球的半径。
【训练二】：已知：在正三棱柱 ABC A1B1C1 中： AB 3 ， BB1 2 3 。 求解：直三棱锥 ABC A1B1C1 的外接球的半径。
高中数学立体几何外接球专题练习(含解析)
高中数学立体几何外接球专题练习(含解析)1.已知菱形ABCD满足|AB|=2，∠ABC=120°，将菱形ABCD沿对角线AC折成一个直二面角B-AC-D，则三棱锥B-ACD外接球的表面积为（）。
A。
πB。
8πC。
7πD。
4π2.如图，四面体ABCD中，面ABD和面BCD都是等腰直角三角形，AB=BD=BC=1，∠CBD=60°，且二面角A-BD-C的大小为120°，∠BAD=45°，若四面体ABCD的顶点都在球O上，则球O的表面积为（）。
A。
12πB。
20πC。
24πD。
36π3.如图，网格纸上小正方形的边长为2，粗实线及粗虚线画出的是某四棱锥的三视图，则该四棱锥的外接球的表面积为（）。
A。
28πB。
32πC。
41πD。
31π4.已知一个几何体是由半径为2的球挖去一个三棱锥得到（三棱锥的顶点均在球面上）．若该几何体的三视图如图所示（侧视图中的四边形为菱形），则该三棱锥的体积为（）。
A。
4/3B。
2/3C。
8/3D。
16/35.已知一个几何体的三视图如图所示，则该几何体的表面积是（）。
A。
2+2+2B。
4+4+2C。
2+4+4D。
4+4+46.某三棱锥的三视图如图所示，则它的外接球表面积为（）。
A。
25πB。
20πC。
16πD。
40π7.如图是某几何体的三视图，则该几何体的表面积是（）。
A。
18+2B。
15+2C。
12+2D。
18+48.在四面体ABCD中，AD⊥底面ABC，DE⊥AC，E为棱BC的中点，DG⊥BE，点G在AE上且满足AG=2GE，若四面体ABCD的外接球的表面积为S，则tan∠AGD=S/12.A。
1/2B。
1C。
2D。
49.在三棱锥S-ABC中，∠ASB=90°，SA=SB=SC=2，且三棱锥S-ABC的体积为8/3，则该三棱锥的外接球的表面积为（）。
A。
4πB。
16πC。
36πD。
72π10.如图所示，正方形ABCD的边长为2，切去阴影部分围成一个正四棱锥，则当正四棱锥体积最大时，该正四棱锥外接球的表面积为（）。
(完整版)高考外接球内切球专题练习
高考外接球与内接球专题练习（1）正方体，长方体外接球1. 如图所示，已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为2，长为2的线段MN 的一个端点M 在棱DD 1上运动，另一端点N 在正方形ABCD 内运动，则MN 的中点的轨迹的面积为（ ）A. 4πB. 2πC. πD. 2π 2. 正方体的内切球与其外接球的体积之比为（ ） A. 1:3 B. 1:3 C. 1:33 D. 1:93. 长方体ABCD ﹣A 1B 1C 1D 1的8个顶点在同一个球面上，且AB=2，AD=3，AA 1=1， 则该球的表面积为（ ）A. 4πB. 8πC. 16πD. 32π4. 底面边长为1，侧棱长为2的正四棱柱的各顶点均在同一球面上，则该球的体积为A. 323π B. 4π C. 2π D. 43π 5. 已知正三棱锥P ﹣ABC ，点P ，A ，B ，C 都在半径为3的球面上，若P A ，PB ，PC 两两垂直，则球心到截面ABC 的距离为 _________ ．6. 在三棱椎A ﹣BCD 中，侧棱AB ，AC ，AD 两两垂直，△ABC ，△ACD ，△ADB 的 面积分别为22，32，62，则该三棱椎外接球的表面积为（ ） A. 2π B. 6π C. 46π D. 24π7. 设A 、B 、C 、D 是半径为2的球面上的四点，且满足AB ⊥AC 、AD ⊥AC 、AB ⊥AD ， 则S △ABC +S △ABD +S △ACD 的最大值为（ ）A. 4B. 8C. 12D. 168. 四面体ABCD 中，已知AB=CD=29，AC=BD=34，AD=BC=37，则四面体的 外接球的表面积为（ ）A. 25πB. 45πC. 50πD. 100π9. 如图，在三棱锥S ﹣ABC 中，M 、N 分别是棱SC 、BC 的中点，且MN ⊥AM ，若AB=22，则此正三棱锥外接球的体积是A. 12πB. 43πC. 433π D. 123π 10. 已知三棱锥P ABC -的顶点都在同一个球面上（球O ），且2,6PA PB PC ===， 当三棱锥P ABC -的三个侧面的面积之和最大时，该三棱锥的体积与球O 的体积的比值为（ ）A. 316πB. 38πC. 116πD. 18π （2）直棱柱外接球11. 已知三棱柱ABC ﹣A 1B 1C 1的6个顶点都在球O 的球面上，若AB=3，AC=4，AB ⊥AC ， AA 1=12，则球O 的半径为A. 3172B. 210C. 132D. 310 12. 设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，则该球的表面 积为（ ）A. 2a πB. 273a πC. 2113a π D. 25a π 13. 直三棱柱ABC ﹣A 1B 1C 1的各顶点都在同一球面上，若AB=AC=AA 1=2，∠BAC=120°， 则此球的表面积等于_________ ．14. 三棱锥S ﹣ABC 的所有顶点都在球O 的表面上，SA ⊥平面ABC ，AB ⊥BC ，又SA=AB=BC=1，则球O 的表面积为（ ）A. 32πB. 32π C. 3π D. 12π 15. 已知球O 的面上四点A 、B 、C 、D ，DA ⊥平面ABC ，AB ⊥BC ，DA=AB=BC=3， 则球O 的体积等于 _________ ．（3）正棱锥外接球16. 棱长均相等的四面体ABCD 的外接球半径为1，则该四面体的棱长为___________17. 如图，在等腰梯形ABCD 中，AB=2DC=2，∠DAB=60°，E 为AB的中点，将△ADE 与△BEC 分别沿ED 、EC 向上折起，使A 、B重合于点P ，则P ﹣DCE 三棱锥的外接球的体积为（ ）A. 4327πB. 62π C. 68π D. 624π 18. 已知三棱锥P ABC -的所有顶点都在表面积为28916π的球面上，底面ABC 是边长为 3的等边三角形，则三棱锥P ABC -体积的最大值为__________19. 正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积 为（ ）A. 814π B. 16π C. 9π D. 274π 20. 已知正三棱锥P ﹣ABC 的顶点均在球O 上，且P A=PB=PC=25，AB=BC=CA=23， 则球O 的表面积为（ ）A. 25πB. 1256πC. 52π D. 20π21. 在球O 的表面上有A 、B 、C 三个点，且3AOB BOC COA π∠=∠=∠=，△ABC 的外接圆半径为2，那么这个球的表面积为（ ） A. 48π B. 36π C. 24π D. 12π 22. 半径为2的半球内有一内接正六棱锥P ﹣ABCDEF ，则此正六棱锥的侧面积是 ____．23. 表面积为23的正八面体的各个顶点都在同一个球面上，则此球的体积为（ ）A. 23πB. 3π C. 23π D. 223π 24. 正四棱锥P ﹣ABCD 底面的四个顶点A 、B 、C 、D 在球O 的同一个大圆上，点P 在球面 上，如果163P ABCD V -=，则求O 的表面积为（ ） A. 4π B. 8π C. 12π D. 16π（4）棱锥外接球25. 已知A ，B ，C ，D 在同一个球面上，AB ⊥平面BCD ，BC ⊥CD ，若AB=6，213AC =， AD=8，则此球的体积是 _________ ．26. 在矩形ABCD 中，AB=4，BC=3，沿AC 将矩形ABCD 折成一个直二面角B ﹣AC ﹣D ， 则四面体ABCD 的外接球的体积为（ ）A. 12512πB. 1259πC. 1256πD. 1253π 27. 点A ，B ，C ，D 在同一个球的球面上，AB=BC=2，AC=22，若四面体ABCD 体积 的最大值为43，则该球的表面积为（ ） A. 163π B. 8π C. 9π D. 12π 28. 四棱锥S ﹣ABCD 的底面ABCD 是正方形，侧面SAB 是以AB 为斜边的等腰直角三角 形，且侧面SAB ⊥底面ABCD ，若AB=23，则此四棱锥的外接球的表面积为（ ）A. 14πB. 18πC. 20πD. 24π29. 三棱锥S ﹣ABC 的四个顶点都在球面上，SA 是球的直径，AC ⊥AB ，BC=SB=SC=2， 则该球的表面积为（ ）A. 4πB. 6πC. 9πD. 12π30. 已知四棱锥V ﹣ABCD 的顶点都在同一球面上，底面ABCD 为矩形，AC∩BD=G ，VG ⊥平面ABCD ，AB=3，AD=3，VG=3，则该球的体积为（ ）A. 36πB. 9πC. 123πD. 43π（5）内接球31. 一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（ ）A. 1B. 2C. 3D. 432. 在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，若AB BC ⊥，6,8AB BC ==，13AA =，则V 的最大值为A. 4πB. 92πC. 6πD. 323π 33. 已知球O 与棱长为4的正四面体的各棱相切，则球O 的体积为（ ） A. 823π B. 833π C. 863π D. 1623π 34. 把一个皮球放入一个由8根长均为20的铁丝接成的四棱锥形骨架内，使皮球的表面 与8根铁丝都有接触点（皮球不变形），则皮球的半径为（ ）A. 103B. 10C. 102D. 3035. 棱长为23的正四面体内切一球，然后在正四面体和该球形成的空隙处各放入一个小 球，则这些球的最大半径为（ ）A. 2B. 22C. 24D. 2636. 如图，在四面体ABCD 中，截面AEF 经过四面体的内切球球心O ，且与BC ，DC 分别截于E 、F ，如果截面将四面体分成体积相等的两部分，设四棱锥A ﹣BEFD 与三棱锥A ﹣EFC的表面积分别是S 1，S 2，则必有（ ）A. S 1＜S 2B. S 1＞S 2C. S 1=S 2D. S 1，S 2的大小关系不能确定（6）球的截面问题37. 平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为，则此球的体 积为（ ）A. 6πB. 43πC. 46πD. 63π38. 已知三棱锥S ﹣ABC 的所有顶点都在球O 的球面上，△ABC 是边长为1的正三角形， SC 为球O 的直径，且SC=2，则此棱锥的体积为（ ）A. 26B. 36C. 23D. 2239. 高为2的四棱锥S ﹣ABCD 的底面是边长为1的正方形，点S ，A ，B ，C ，D 均在半 径为1的同一球面上，则底面ABCD 的中心与顶点S 之间的距离为（ ）A. 102B. 232+C. 32D. 240. 已知三棱锥S ﹣ABC 的各顶点都在一个半径为r 的球面上，球心O 在AB 上，SO ⊥底面ABC ，AC =，则球的体积与三棱锥体积之比是（ ）A. πB. 2πC. 3πD. 4π41. 在半径为13的球面上有A ，B ，C 三点，AB=6，BC=8，CA=10，则（1）球心到平面ABC 的距离为 _________ ；（2）过A ，B 两点的大圆面与平面ABC 所成二面角为（锐角）的正切值为 ____．42. 设A 、B 、C 、D 是球面上的四个点，且在同一平面内，AB=BC=CD=DA=3，球心到 该平面的距离是球半径的一半，则球的体积是（ ）A. B. C. D.43. 已知过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半，且AB=BC=CA=2， 则球面面积是（ ） A. 169π B. 83π C. 4π D. 649π 44. 已知OA 为球O 的半径，过OA 的中点M 且垂直于OA 的平面截球面得到圆M ． 若圆M 的面积为3π，则球O 的表面积等于 _________ ．45. 三棱锥P ﹣ABC 的各顶点都在一半径为R 的球面上，球心O 在AB 上，且有P A=PB=PC ， 底面△ABC 中∠ABC=60°，则球与三棱锥的体积之比是 _________ ．46. 已知H 是球O 的直径AB 上一点，:1:2AH HB =，AB ⊥平面α，H 为垂足，α截 球O 所得截面的面积为π，则球O 的表面积为__________（7）旋转体的外接内切47. 半径为4的球O 中有一内接圆柱．当圆柱的侧面积最大时，球的表面积与该圆柱的侧面 积之差是 _________ ．48. 将4个半径都是R 的球体完全装入底面半径是2R 的圆柱形桶中，则桶的最小高度 是 _________ ．1. D ；2. C ；3. B ；4. D ；5. 3； 6. B ； 7. B ； 8. C ； 9. B ；10. A ； 11. C ； 12. B ； 13. 20π； 14. C ； 15. 92π； 16. ；17. C ； 19. A ； 20. A ； 21. A ； 22. ； 23. A ； 24. D ； 25. 2563π； 26. C ； 27. C ； 28. D ； 29. B ； 30. D ； 31. B ； 32. B ； 33. A ； 34. B ； 35. C ； 36. C ； 37. B ； 38. A ； 39. A ； 40. D ；41. 12；3；42. A；43. D；44. 16π；45.3；46.92π47. 30π；48.(2R+；。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高三数学专题外接球1．正棱柱，长方体的外接球球心是其中心例1：已知各顶点都在同一球面上的正四棱柱的高为，体积为，则这个球的表面积是（ ） A ．B ．C ．D ．2．补形法（补成长方体）例2：若三棱锥的三个侧面两两垂直，且侧棱长均为，则其外接球的表面积是 ． 3．依据垂直关系找球心例3：已知三棱锥的四个顶点均在同一个球面上，底面满足，若该三棱锥体积的最大值为3，则其外接球的体积为（ ） A ．B ．C ．D ．一、单选题1．棱长分别为2、、的长方体的外接球的表面积为（ ） A ．B ．C ．D ．2．设三棱柱的侧棱垂直于底面，所有棱的长都为，顶点都在一个球面上，则该球的表面积为（ ）20π24π32π图2图3P ABC -ABC △BA BC ==π2ABC ∠=16π16π332π324π48πA ．12πB ．28πC ．44πD ．60π3．把边长为3的正方形沿对角线对折，使得平面平面，则三棱锥的外接 球的表面积为（ ） A ．B ．C ．D ．4．某几何体是由两个同底面的三棱锥组成，其三视图如下图所示，则该几何体外接球的面积为（ ）A ．B ．C ．D ．5．三棱锥的所有顶点都在球的表面上，平面，，，则球的表面积为（ ）A ．B ．C ．D ．6．如图是边长为1的正方体，是高为1的正四棱锥，若点，，，，在同一个球面上，则该球的表面积为（ ）A ．B ．C ．D ．ABCD ABC ⊥ADC D ABC -32π27π22πa 23πa 24πa A BCD -AB ⊥BCD 2BC BD ==2AB CD ==32π60π64π1111ABCD A B C D -S ABCD-9π1625π1649π1681π167．已知球的半径为，，，三点在球的球面上，球心到平面的距离为，，，则球的表面积为（ ） A ．B ．C ．D ．8．已知正四棱锥(底面四边形是正方形，顶点在底面的射影是底面的中心)，若该正四棱锥的体积为，则此球的体积为（）A ．B ．C ．D ．9．如图，在中，，点为的中点，将沿折起到的位置，使，连接，得到三棱锥．若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）A ．B ．C ．D ．10．四面体中，，，，则此四面体外接球的表面积为（ ）A ．BC ． D11．将边长为2的正沿着高折起，使，若折起后四点都在球的表面上，则球的表面积为（ ）A ．B ．C ．D ．12．在三棱锥中，，，则该三棱锥的外接球ABC 12R 2AB AC ==120BAC ∠=︒16π916π364π964π3P ABCD -ABCD 50336πABC △AB BC ==90ABC ∠=︒ABD △PBD △PC PD =P BCD -A BCD -60ABC ABD CBD ∠=∠=∠=︒3AB =2CB DB ==19π2ABC △120BDC ∠=︒A B C D 、、、7π213π213π3A BCD -6AB CD ==5AC BD AD BC ====的表面积为（ ）ABC ．D ．二、填空题13．棱长均为6的直三棱柱的外接球的表面积是_________．14．已知棱长都相等正四棱锥的侧面积为，则该正四棱锥内切球的表面积为________．15．已知三棱柱的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，，，，则此球的表面积等于______．16．在三棱锥中，，，，，则三棱锥外接球的体积的最小值为_____． 1．正棱柱，长方体的外接球球心是其中心例1：已知各顶点都在同一球面上的正四棱柱的高为，体积为，则这个球的表面积是（ ） A ． B ．20πC ．24πD ．32π【答案】C【解析】162==h a V ，2=a ，24164442222=++=++=h a a R ，24πS =，故选C ． 2．补形法（补成长方体）例2：若三棱锥的三个侧面两两垂直，且侧棱长均为，则其外接球的表面积是 ．43π243π111ABC A B C -2AB =1AC =60BAC ∠=︒A BCD -AB AC =DB DC =4AB DB +=AB BD ⊥A BCD-图2图3图4【答案】【解析】933342=++=R ，24π9πS R ==． 3．依据垂直关系找球心例3：已知三棱锥P ABC -的四个顶点均在同一个球面上，底面ABC △满足BA BC ==π2ABC ∠=，若该三棱锥体积的最大值为3，则其外接球的体积为（ ） A ． B ．16πC ．16π3D ．32π3【答案】D【解析】因为ABC △是等腰直角三角形，所以外接球的半径是12r =的半径是，球心到该底面的距离，如图，则1632ABC S =⨯=△，BD 116336ABC V S h h ==⨯=△，最大体积对应的高为3SD h ==，故223R d =+，即()2233R R =-+，解之得2R =，所以外接球的体积是3432ππ33R =，故答案为D ．一、单选题1．棱长分别为2、、的长方体的外接球的表面积为（ ）A ．B ．C ．24πD ．48π【答案】B【解析】设长方体的外接球半径为，由题意可知：()222222R =++，则：23R =，该长方体的外接球的表面积为24π4π312πS R ==⨯=．本题选择B 选项．2．设三棱柱的侧棱垂直于底面，所有棱的长都为面积为（ ） A ．12π B ．28π C ．44π D ．60π【答案】B【解析】设底面三角形的外接圆半径为，由正弦定理可得：2r 2r =， 设外接球半径为，结合三棱柱的特征可知外接球半径22227R =+=，外接球的表面积24π28πS R ==．本题选择B 选项．3．把边长为3的正方形ABCD 沿对角线对折，使得平面ABC ⊥平面ADC ，则三棱锥D ABC -的外接球的表面积为（ ） A ．32π B ．27πC ．D ．【答案】C【解析】把边长为3的正方形ABCD 沿对角线对折，使得平面ABC ⊥平面ADC ， 则三棱锥D ABC -的外接球直径为AC =24π18πR =，故选C ． 4．某几何体是由两个同底面的三棱锥组成，其三视图如下图所示，则该几何体外接球的面积为（ ）A ．B ．22πaC ．23πaD ．24πa【答案】C【解析】由题可知，该几何体是由同底面不同棱的两个三棱锥构成，的正四面体，如图所示：该几何体的外接球与棱长为 的正方体的外接球相同，因此外接球的直径即为正方体的体对角线，所以2R R =⇒，所以该几何体外接球面积2224π4π3πS R a ⎫==⨯=⎪⎪⎝⎭，故选C ．5．三棱锥A BCD -的所有顶点都在球的表面上，AB ⊥平面BCD ，2BC BD ==，2AB CD == ）A ．B ．32πC ．60πD ．64π【答案】D【解析】因为2BC BD ==，CD =(222221cos 2222CBD +-∠==-⨯⨯，2π3CBD ∴∠=， 因此三角形BCD 外接圆半径为122sin CDCBD=∠，设外接球半径为，则222=2+412162AB R ⎛⎫=+= ⎪⎝⎭，2=4π64πS R ∴=，故选D ．6．如图1111ABCD A B C D -是边长为1的正方体，S ABCD -是高为1的正四棱锥，若点，，，，在同一个球面上，则该球的表面积为（ ）A ．9π16B ．25π16C ．49π16D ．81π16【答案】D【解析】如图所示，连结11A C ，11B D ，交点为，连结SM ，易知球心在直线SM 上，设球的半径R OS x ==，在1Rt OMB △中，由勾股定理有：22211OM B M B O +=，即：()2222x x -+=⎝⎭，解得：98x =，则该球的表面积229814π4ππ816S R ⎛⎫==⨯= ⎪⎝⎭．本题选择D 选项．7．已知球的半径为，，，三点在球的球面上，球心到平面ABC 的距离为12R ，2AB AC ==，120BAC ∠=︒，则球的表面积为（ ）A ．16π9B ．16π3C ．64π9D ．64π3【答案】D【解析】由余弦定理得：BC ==设三角ABC 2r =，则2r =，又22144R R =+，解得：2163R =，则球的表面积2644ππ3S R ==．本题选择D 选项． 8．已知正四棱锥P ABCD -(底面四边形ABCD 是正方形，顶点 在底面的射影是底面的中心)503，则此球的体积为（ ）A ．B ．C ．36πD ．【答案】C 【解析】如图，设正方形ABCD 的中点为，正四棱锥P ABCD -的外接球心为， EA ∴正四棱锥的体积为503，215033P ABCD V PE -∴=⨯⨯=， 则5PE =，5OE R ∴=-，在AOE △中由勾股定理可得：()2255R R -+=，解得3R =，34π36π3V R ∴==球，故选C ．9．如图，在ABC △中，AB BC ==90ABC ∠=︒，点为的中点，将ABD △沿折起到PBD △的位置，使PC PD =，连接，得到三棱锥P BCD -．若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）A ．B ．C ．D ．【答案】A【解析】由题意得该三棱锥的面PCD 是边长为的正三角形，且BD ⊥平面PCD ， 设三棱锥P BDC -外接球的球心为，PCD △外接圆的圆心为，则1OO ⊥面PCD ，∴四边形1OO DB 为直角梯形，由BD11O D =，及OB OD =，得OB =R =∴该球的表面积274π4π7π4S R ==⨯=．故选A ． 10．四面体A BCD -中，60ABC ABD CBD ∠=∠=∠=︒，3AB =，2CB DB ==，则此四面体外接球的表面积为（ ）A ．19π2BC ．D 【答案】A【解析】由题意，BCD △中，2CB DB ==，60CBD ∠=︒，可知BCD △是等边三角形，BF =∴BCD △的外接圆半径r BE ==，FE ， ∵60ABC ABD ∠=∠=︒，可得AD AC =可得AF =∴AF FB ⊥，∴AF BCD ⊥，∴四面体A BCD -高为AF =设外接球，为球心，OE m =，可得：222r m R +=……①， )222πEF R +=……②由①②解得：R =2194ππ2S R ==．故选A ． 11．将边长为2的正ABC △沿着高折起，使120BDC ∠=︒，若折起后A B C D 、、、四点都在球的表面上，则球的表面积为（ ）A ．7π2B ．C ．13π2D ．13π3【答案】B【解析】BCD △中，1BD =，1CD =，120BDC ∠=︒， 底面三角形的底面外接圆圆心为，半径为，由余弦定理得到BC =21r r =⇒=， 见图示：是球的弦，DA =的位置，∴OM =OMD 中，应用勾股定理得到，即为球的半径．∴球的半径OD =．该球的表面积为24π7πOD ⨯=；故选B ． 12．在三棱锥A BCD -中，6AB CD ==，5AC BD AD BC ====，则该三棱锥的外接球的表面积为（ ）A B C ．43π2 D ．43π【答案】D【解析】分别取，的中点，，连接相应的线段，，， 由条件，4AB CD ==，5BC AC AD BD ====，可知，ABC △与ADB △，都是等腰三角形，AB ⊥平面ECD ，∴AB EF ⊥，同理CD EF ⊥，∴是与的公垂线， 球心在上，推导出AGB CGD △≌△，可以证明为中点，4DE ==，3DF =，EF =∴GF =DG =24π43πS DG =⨯=． 故选D ．二、填空题13．棱长均为6的直三棱柱的外接球的表面积是_________．【答案】84π【解析】由正弦定理可知底面三角形的外接圆半径为1612sin602r =⨯==︒ 则外接球的半径R ， 则外接球的表面积为24π4π2184πS R ==⨯=．14．已知棱长都相等正四棱锥的侧面积为，则该正四棱锥内切球的表面积为________．【答案】(32π-【解析】设正四棱锥的棱长为，则24⎫=⎪⎪⎝⎭4a =．于是该正四棱锥内切球的大圆是如图PMN △的内切圆，其中4MN =，PM PN ==PE =．设内切圆的半径为，由PFO PEN ≅△△，得FO POEN PN =，即2r =，解得r ==∴内切球的表面积为(224π4π32πS r ===-．15．已知三棱柱111ABC A B C -的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，2AB =，1AC =，60BAC ∠=︒，则此球的表面积等于______．【答案】【解析】∵三棱柱111ABC A B C -的侧棱垂直于底面，棱柱的体积为，2AB =，1AC =，60BAC ∠=︒，1121sin 602AA ∴⨯⨯⨯︒⨯12AA ∴=，2222cos60412BC AB AC AB AC =+-⋅︒=+-，BC ∴=，设ABC △外接圆的半径为，则2sin 60BC R ︒＝，1R ∴=， =24π8π⨯=．故答案为．16．在三棱锥A BCD -中，AB AC =，DB DC =，4AB DB +=，AB BD ⊥，则三棱锥A BCD -外接球的体积的最小值为_____．【解析】如图所示，三棱锥A BCD -的外接圆即为长方体的外接圆，外接圆的直径为长方体的体对角线，设AB AC x ==，那么4DB DC x ==-，AB BD ⊥，所以AD =．由题意，体积的最小值即为最小，AD 2x =时，的最小值为。