吉林大学机械原理课后题答案xiti知识讲解
机械原理_吉林大学中国大学mooc课后章节答案期末考试题库2023年

机械原理_吉林大学中国大学mooc课后章节答案期末考试题库2023年1.锥齿轮的不根切最少齿数比斜齿轮不根切最少齿数大。
()参考答案:错误2.直齿圆锥齿轮的传动比与分度圆锥角有关。
()参考答案:正确3.机械原理的研究对象是机器和()。
参考答案:机构4.盖房子用的吊车是机器。
参考答案:正确5.抓举工件的机械手是机构。
参考答案:错误6.构件的定义是()。
参考答案:运动的最小单元7.原动件的自由度F=()。
参考答案:18.计算机构自由度时,PL代表()。
参考答案:低副总数9.复合铰链回转副的数目m为()。
参考答案:构件数减110.渐开线直齿圆柱齿轮传动的重合度等于实际啮合线段与()的比值。
参考答案:基圆周节11.渐开线直齿圆柱齿轮与齿条啮合时,其啮合角恒等于齿轮()的压力角。
参考答案:分度圆12.一对标准渐开线直齿圆柱齿轮要正确啮合,其()必须相等。
参考答案:模数13.渐开线上基圆的压力角为()。
参考答案:0°14.机构处于死点位置时,压力角与传动角分别为()。
参考答案:a=90°,g=0°;15.铰链四杆机构中,取最短杆对边为机架时得到双摇杆机构。
( )参考答案:正确16.铰链四杆机构中,取最短杆为机架时得到双曲柄机构。
( )参考答案:错误17.在连杆机构中,希望传动角越小越好,压力角越大越好。
( )参考答案:错误18.单销外槽轮机构槽轮的运动时间总是大于静止时间。
()参考答案:错误19.渐开线斜齿圆柱齿轮的当量齿数zv总是大于其实际齿数z。
()参考答案:正确20.判定机构是否能动的条件是()。
参考答案:F>021.机构是由原动件和从动件系统组成的。
参考答案:错误22.用飞轮调节周期性速度波动,可使机械系统达到匀速运转。
()参考答案:错误23.等效动力学模型中的等效质量是根据机械中瞬时动能相等的原则求出的。
()参考答案:正确24.只有两构件重合点的加速度分析才有哥氏加速度。
吉林大学机械原理课后题答案xiti8

习 题8.1 在图8.1所示单销四槽轮机构中,已知拨盘1转一周,槽轮停歇时间为15秒,求主动拨盘1的转速n 1及槽轮在一周期内的运动时间t d 。
解:槽轮机构的运动系数25.04224z 22z t t t j d d =⨯-=-=+=τ s 15t j =s 575.01525.025.01t 25.0t jd =⨯=-=∴ 拨盘运动一周的时间:s 20155t t t j d =+=+=min /r 32060n 1==∴8.2 试分析单万向联轴节中瞬时传动比不恒等于1的原因。
使双万向联轴节传动比恒等于1的条件是什么?解:单万向联轴节的传动比为:1221331cos sin 1cos i ϕααωω-== 当α为一常数时,i 31是随ϕ1的变化而变化的,1i 31≠∴可用双万向联轴节,使得131=i ,条件为:①中间轴叉平面应在同一平面内,②2312αα=。
8.3 对图8-9所示的棘轮机构,为保证棘爪能顺利进入棘轮齿底,应满足什么条件?解:为了保证工作时棘爪自动嵌入棘轮齿槽内,应使棘轮齿面倾斜角α大于摩擦角ϕ。
8.4 为什么不完全齿轮机构主动轮首、末两轮齿的齿高一般要削减?加上瞬心线附加杆后,是否仍须削减?为什么?解:为了保证不完全齿轮在主动轮正、反转和进入啮合的瞬时不与从动轮发生干涉,因此,主动轮的首、末两齿顶高要削减一点。
若加上瞬心线附加杆后,可不用削减。
因瞬心线附加杆可帮助从动轮的转速由零逐渐增加到正常的转速,可避免干涉。
8.5差动螺旋机构结构特点是什么?解:差动螺旋机构的结构特点是两螺旋相同。
8.6机构的组合和组合机构有何区别?解:机构的组合是各子机构保持原有结构及各自相对的独立。
组合机构是一种封闭式的传动机构,即利用一机构去约束或封闭另一个多自由度机构。
机械原理课后习题答案

机械原理课后习题答案1. 两个质量分别为m1和m2的物体,它们分别靠在光滑水平面上的两个弹簧上,两个弹簧的弹性系数分别为k1和k2。
求当两个物体分别受到的外力分别为F1和F2时,两个物体的加速度分别是多少?答,根据牛顿第二定律,物体受到的合外力等于物体的质量乘以加速度,即F=ma。
根据这个公式,可以得出两个物体的加速度分别为a1=F1/m1,a2=F2/m2。
2. 一个质量为m的物体,靠在光滑水平面上的弹簧上,弹簧的弹性系数为k。
求当物体受到外力F时,物体的加速度是多少?答,同样根据牛顿第二定律,物体受到的合外力等于物体的质量乘以加速度,即F=ma。
根据这个公式,可以得出物体的加速度为a=F/m。
3. 一个质量为m的物体,靠在光滑水平面上的弹簧上,弹簧的弹性系数为k。
求当物体受到外力F时,弹簧的位移是多少?答,根据胡克定律,弹簧的位移与受到的外力成正比,即F=kx,其中x为弹簧的位移。
解出x=F/k,即弹簧的位移与外力成反比。
4. 一个质量为m的物体,靠在光滑水平面上的弹簧上,弹簧的弹性系数为k。
求当物体受到外力F时,弹簧的振动周期是多少?答,根据弹簧的振动周期公式T=2π√(m/k),可以得出弹簧的振动周期与物体的质量和弹簧的弹性系数有关,与受到的外力无关。
5. 一个质量为m的物体,靠在光滑水平面上的弹簧上,弹簧的弹性系数为k。
求当物体受到外力F时,弹簧的振幅是多少?答,根据弹簧振动的公式x=Acos(ωt+φ),可以得出弹簧的振幅与受到的外力无关,只与弹簧的弹性系数和物体的质量有关。
求当物体受到外力F时,弹簧的振动频率是多少?答,根据弹簧振动的公式f=1/2π√(k/m),可以得出弹簧的振动频率与受到的外力无关,只与弹簧的弹性系数和物体的质量有关。
7. 一个半径为r的圆盘,靠在光滑水平面上的弹簧上,弹簧的弹性系数为k。
求当圆盘受到外力F时,圆盘的加速度是多少?答,根据牛顿第二定律,物体受到的合外力等于物体的质量乘以加速度,即F=ma。
机械原理课后习题答案

第四章课后习题4—12图示为一曲柄滑块机构的三个位置,F为作用在活塞上的力转动副A及B上所画的小圆为摩擦圆,试决定在此三个位置时作用在连杆AB上的作用力的真实方向(构件重量及惯性力略去不计)。
解:上图中构件2受压力。
因在转动副A处2、1之间的夹角∠OAB在逐渐减小,故相对角速度ω21沿顺时针方向,又因2受压力,故FR12应切于摩擦圆的下方;在转动副B处,2、3之间的夹角∠OBA在逐渐增大,相对角速度ω23也沿顺时针方向,故FR32应切于摩擦圆的上方。
R32解:上图构件2依然受压力。
因在转动副A处2、1之间的夹角∠OAB逐渐减小,故相对角速度ω21沿顺时针方向,又因2受压力,故F R12应切于摩擦圆的下方;在转动副B处,2、3之间的夹角∠OBA逐渐减小,故相对角速度ω23沿逆时针方向,F R32应切于摩擦圆的下方。
解:上图构件2受拉力。
因在转动副A处2、1之间的夹角∠OAB在逐渐增大,故相对角速度ω21沿顺时针方向,又因2受拉力,故FR12应切于摩擦圆的上方;在转动副B处,2、3之间的夹角∠OBA逐渐减小,故相对角速度ω23沿顺时针方向,FR32应切于摩擦圆的下方。
4-13 图示为一摆动推杆盘形凸轮机构,凸轮1沿逆时针方向回转,F为作用在推杆2上的外载荷,试确定凸轮1及机架3作用给推杆2的总反力FR12及FR32方位(不考虑构件的重量及惯性力,解:经受力分析,FR12的方向如上图所示。
在FR12的作用下,2相对于3顺时针转动,故FR32应切于摩擦圆的左侧。
补充题1 如图所示,楔块机构中,已知γ=β=60°,Q =1000N 格接触面摩擦系数f =0.15,如Q 为有效阻力,试求所需的驱动力F 。
解:对机构进行受力分析,并作出力三角形如图。
对楔块1,R 21R310F F F ++=由正弦定理有21sin(602sin(90R F F ϕϕ+-=))o o ① 对楔块2,同理有R12R320Q F F ++=sin(90sin(602ϕϕ+-=))o o ②sin(602sin(602F Q ϕϕ+=⋅-))o o且有2112R R F F = ,8.53arctgf ϕ==o ③联立以上三式,求解得F =1430.65N2 如图示斜面机构,已知:f (滑块1、2与导槽3相互之间摩擦系数)、λ(滑块1的倾斜角)、Q (工作阻力,沿水平方向),设不计两滑块质量,试确定该机构等速运动时所需的铅重方向的驱动力F 。
吉林大学机械原理课后题答案xiti10

习 题10.1 如图所示的盘形转子,存在有4个不平衡质量。
它们的大小及其向径分别为m 1=10kg ,r 1=100mm ;m 2=8kg ,r 2=150mm ;m 3=7kg ,r 3=200试对该转子进行平衡设计。
解:根据转子静平衡公式,设平衡质量和向径分别为m b0r m r m r m r m r m b b 44332211=++++∴根据上述公式画质径积向量图,取 mm kgm w /05.0=μ⎪⎪⎭⎪⎪⎬⎫⋅=⨯==⋅=⨯==⋅=⨯==⋅=⨯==mm kg 5001005r m W mm kg 14002007r m W mm kg 12001508r m W mm kg 100010010r m W 444333222111mmkg 700r m r m mr W mm kg 400r m r m mr W 4422y y 1133x x ⋅=-==⋅-=+-==m kg 81.0mm kg 23.806700400mr mr r m 222y2xb b ⋅=⋅=+=+=∴︒==∴===255.6075.1arctan 75.1400700mr mr tan xy θθ b W ∴与x 轴正向夹角为:︒=︒-︒=74.299255.60360α设mm r b 100=,kg 1.810023.806r r m m bb b b ===∴ ,b b r m的方向为︒=74.299α题10.1图α2110.2 如图所示为一均质圆盘转子,工艺要求在圆盘上钻4个圆孔,圆孔直径及孔心到转轴O 的距离分别为:d 1=40mm ,r 1=120mm ;d 2=60mm ,r 2=d 4=70mm,r 4=90mm ;方位如图。
转子厚度为10mm 解:圆柱体的体积为:h r ⋅2πkg292.0g 334.2926.712714.3h 2d m kg149.0g 15.1496.712514.3h 2d m kg215.0g 776.2146.712614.3h 2d m kg 095.0g 46.956.712414.3h 2d m 2244223322222211==⨯⨯⎪⎭⎫⎝⎛⨯=⋅⋅⎪⎭⎫ ⎝⎛⋅===⨯⨯⎪⎭⎫⎝⎛⨯=⋅⋅⎪⎭⎫ ⎝⎛⋅===⨯⨯⎪⎭⎫⎝⎛⨯=⋅⋅⎪⎭⎫ ⎝⎛⋅===⨯⨯⎪⎭⎫⎝⎛⨯=⋅⋅⎪⎭⎫ ⎝⎛⋅=∴ρπρπρπρπ若该构件平衡,则0r m r m r m r m r m b b 44332211=++++cmkg 628.29292.0r m cm kg 639.111149.0r m cm kg 15.210215.0r m cm kg 14.112095.0r m 44332211⋅=⨯=⋅=⨯=⋅=⨯=⋅=⨯=根据质径积的向量分布:cmkg 367.130sin r m 30sin r m 60sin r m mr cm kg 48.130cos r m 30cos r m 60cos r m r m mr 443322y 44332211x ⋅=︒-︒+︒=⋅-=︒-︒-︒+=则不平衡质径积为cm kg 015.2367.148.1mr mr r m 222y 2x b b⋅=+=+=''∴题10.2图m x︒==∴===738.24924.0arctan 924.048.1367.1mr mr tan xy θθ 不平衡质径积与x 轴正向夹角为:︒=︒-︒=26.137738.24180α所以若使该转子平衡,应在︒=26.137α方向上除去cm kg r m b b ⋅=''015.2的质径积;或在b b r m ''相反方向上加上b b r m ,即⎪⎩⎪⎨⎧︒=︒+='⋅=26.317180x r m cm kg 015.2r m b b b b αα轴夹角为与10.3 在图示的刚性转子中,已知各不平衡质量和向径的大小分别为m 1=10kg ,r 1=400mm ;m 2=15kg ,r 2=300mm ;m 3=20kg ,r 3=200mm ;m 4=20kg ,r 4=300mm ;方位如衡向径r '"b 及r 'b 和r解:在平面T '中,kg 33.132032m l 3l 2m 33=⨯==' 其中mm 200l l l l 342312====kg 51531m l 3l 1m 22=⨯==' T '面平衡:0r m r m r m r m b b 223344=''+'+'+cm kg 6.34130sin r m 30sin r m r m cmkg 096.47030cos r m r m r m 2233y 2244x ⋅-=︒'-︒'-='⋅=︒'+='3m 2 题10.3图bb rcm kg 1.5816.341096.470r m r m r m 222y 2x b b⋅=+='+'='' ︒=-︒=-︒=144096.4706.341arctan180mr mr arctan180xy α所以cm kg 1.581r m b b⋅='',方向:︒=144α 题设mm 500r b =',kg 62.115005811r r m m b b bb=='''='∴ 在平面T ''中,kg 667.62031m l 3l 1m 33=⨯=='',kg 101532m l 3l 2m 22=⨯==''T ''面平衡:0r m r m r m r m b b 332211=''''+''+''+cmkg 6.11630sin r m r m r m r m cmkg 81.25930cos r m r m 223311y 22x ⋅=︒''-''-=''⋅-=︒''-=''cm kg 8.2846.11681.259r m r m r m 222y 2x b b⋅=+=''+''='''' ︒=-︒=''''-︒=83.33581.2596.116arctan360r m r m arctan360xy α所以ob b83.335cm kg 8.284r m =⋅=''''α,题设mm 500r b ='',kg 7.55002848m b==''∴10.4 图示为一用于航空燃气轮机的转子,其质量为100kg ,其质心至两平衡平面Ⅰ及Ⅱ的距离分别为l 1=200mm ,l 2=800mm ,平衡等级及在平衡平面Ⅰ、Ⅱ内的许用不平衡量。
机械原理包含课后答案

第一章绪论一、教学要求(1)明确本课程研究的对象和内容,及其在培养机械类高级工程技术人才全局中的地位、任务和作用。
(2)对机械原理学科的发展现状有所了解。
二、主要内容1.机械原理课程的研究对象机械原理(Theory of Machines and Mechanisms)是以机器和机构为研究对象,是一门研究机构和机器的运动设计和动力设计,以及机械运动方案设计的技术基础课。
机器的种类繁多,如内燃机、汽车、机床、缝纫机、机器人、包装机等,它们的组成、功用、性能和运动特点各不相同。
机械原理是研究机器的共性理论,必须对机器进行概括和抽象内燃机与机械手的构造、用途和性能虽不相同,但是从它们的组成、运动确定性及功能关系看,都具有一些共同特征:1)人为的实物(机件)的组合体。
2)组成它们的各部分之间都具有确定的相对运动。
3)能完成有用机械功或转换机械能。
机构是传递运动和动力的实物组合体。
最常见的机构有连杆机构、凸轮机构、齿轮机构、间歇运动机构、螺旋机构、开式链机构等。
它们的共同特征是:(1)人为的实物(机件)的组合体。
(2)组成它们的各部分之间都具有确定的相对运动。
2.机械原理课程的研究内容1、机构的分析1)机构的结构分析(机构的组成、机构简图、机构确定运动条件等);2)机构的运动分析(机构的各构件的位移、速度和加速度分析等);3)机构的动力学分析(机构的受力、效率、及在外力作用下机构的真实运动规律等);2、机构的综合(设计):创新的过程1)常用机构的设计与分析(连杆机构、凸轮机构、齿轮机构、常用间歇机构等);2)传动系统设计(选用、组装、协调机构)通过对机械原理课程的学习,应掌握对已有的机械进行结构、运动和动力分析的方法,以及根据运动和动力性能方面的设计要求设计新机械的途径和方法。
3 机械原理课程的地位和作用机械原理是以高等数学、物理学及理论力学等基础课程为基础的,研究各种机械所具有的共性问题;它又为以后学习机械设计和有关机械工程专业课程以及掌握新的科学技术成就打好工程技术的理论基础。
吉林大学机械原理课后题答案xiti4
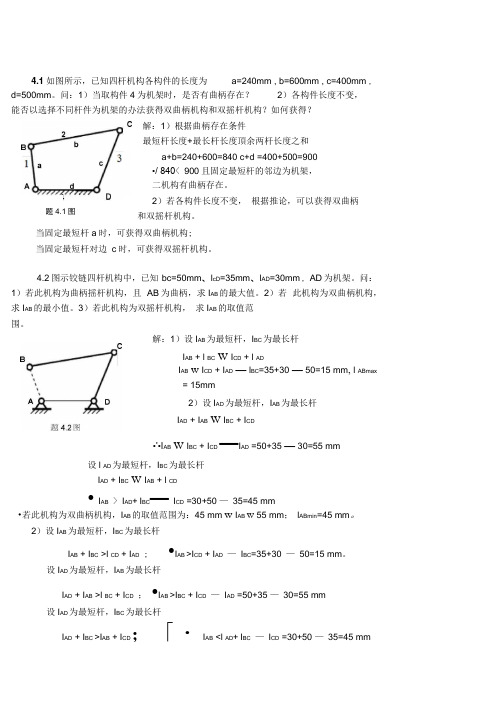
4.1如图所示,已知四杆机构各构件的长度为a=240mm , b=600mm , c=400mm , d=500mm。
问:1)当取构件4为机架时,是否有曲柄存在?2)各构件长度不变,能否以选择不同杆件为机架的办法获得双曲柄机构和双摇杆机构?如何获得?解:1)根据曲柄存在条件最短杆长度+最长杆长度頂余两杆长度之和a+b=240+600=840 c+d =400+500=900•/ 840< 900且固定最短杆的邻边为机架,二机构有曲柄存在。
2)若各构件长度不变,根据推论,可以获得双曲柄题4.1图和双摇杆机构。
当固定最短杆a时,可获得双曲柄机构;当固定最短杆对边c时,可获得双摇杆机构。
4.2 图示铰链四杆机构中,已知bc=50mm、l cD=35mm、l AD=30mm , AD 为机架。
问:1)若此机构为曲柄摇杆机构,且AB为曲柄,求I AB的最大值。
2)若此机构为双曲柄机构,求I AB的最小值。
3)若此机构为双摇杆机构,求I AB的取值范围。
解:1)设I AB为最短杆,I BC为最长杆I AB + l BC W I CD + l ADI AB w I CD + I AD—l BC=35+30—50=15 mm, l ABmax= 15mm2)设I AD为最短杆,I AB为最长杆I AD + I AB W I BC + I CD•'•I AB W I BC + I CD —I AD =50+35 —30=55 mm设l AD为最短杆,I BC为最长杆I AD + I BC W I AB + l CD•I AB > I AD+I BC—I CD =30+50 —35=45 mm•若此机构为双曲柄机构,I AB的取值范围为:45 mm w I AB W 55 mm;l ABmin=45 mm。
2)设I AB为最短杆,I BC为最长杆I AB + I BC >l CD + I AD ; •I AB >I CD + I AD—I BC=35+30—50=15 mm。
吉林大学机械原理课后题答案xiti9

习 题9.1如图所示为一机床工作台的传动系统。
设已知各齿轮的齿数分别为Z 1、Z 2、Z 2'、Z 3,齿轮3的分度圆半径为r 3,各齿轮的转动惯量分别为J 1、J 2、J 2'、J 3,工作台和被加工零件的重量之和为G 。
当取齿轮1为等效构件时,试求该机械系统的等效转动惯量J 。
解:()()2231'2233221'2212231'2232231'23221'221212133212'2212211e Z Z Z Z g Gr J ZZ J J J Z Z Z Z g Gr Z Z Z Z J ZZ J J J vg G J J J J J ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛++=⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=ωωωωωωω 9.2在图示六杆机构中,设已知滑块5的质量m=20kg ,l AB =l ED =l EF =200mm ,ϕ1=ϕ2=ϕ3=90︒,作用在滑块5上的力P=500N 。
当取曲柄1为等效构件时,求机构图示位置的等效转动惯量J 和力P 的等效力矩。
解:2151v m J ⎪⎪⎭⎫ ⎝⎛=ω由题意知:AB B C E l v v v v 2121215==== 22211AB 1kgm 2.02200202l 1m J =⎪⎭⎫ ⎝⎛⨯=⎪⎪⎭⎫ ⎝⎛=∴ωωm .N 5022.05002l P v P M 11AB 15=⎪⎭⎫⎝⎛⨯=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛=ωωω 9.3在图示轮系中,设已知各轮的齿数Z 1=Z 2’=20,Z 2=Z 3=40,各轮的转动惯量J 1=J 2’=0.01kg ⋅m 2,J 2=J 3=0.04 kg ⋅m 2。
作用在轴O 3上的阻力矩M 3=40N ⋅m 。
当取齿轮1为等效构件时,试求机构的等效转动惯量和阻抗力矩M 3的等效力矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
吉林大学机械原理课后题答案x i t i5.1在直动从动件盘形凸轮机构中,已知升程h=50mm,其所对应的凸轮推程运动角为o=。
试计算:1)当凸轮转速为n=30rpm时,等2速、等加等减速、余弦加速和正弦加速度四种运动规律的V max, a max值2 )当转速增加到n=300rpm时,V max和a max值分别增加几倍?当n 30时,v max 200,a max 800。
当n 300 时,V max 2000 , a max 80000余弦加速度运动规律:1.57 h 1.57 2 50 157 V maxV max增加10倍,a max增加100倍a max 4.93 h 2 4.93 4 50 2 986解:n30当n 30时, ;当n300 时,10等速运动规律: 502倍。
当n 30寸, 100 ;300 时,v 1000 ;V max 增加10等加速等减速运动规律: V max 2h 2 50/ 22004h a max 20 4 502 /42 8002222 0V max 增加10倍,a max 增加100倍6.28 h 2 6.28 4 50 22 2当n 30时, v max 200,a max1256 。
当 n 300 时,V max 2000,a max 125600V max 增加10倍,a max 增加100倍。
5.2如图示为滚子从动件盘形凸轮机构,凸轮为一偏心圆盘。
试用图解法作出:1)凸轮的理论廓线;2)凸轮的基圆;3)图示位置的压力 角;4)从动件在图示位置的位移s 及凸轮的转角 ;5)从动件的升程h 及凸轮的推程运动角正弦加速度运动规律:V max2h2 50 / 2a max1256(a)(b)解:(a)作图过程如下图所示: (b)作图过程如下图所示:sMr or o O5.3如图示为滚子摆动从动件盘形凸轮机构,凸轮为一偏心圆盘,试用图解法作出:1)凸轮的基圆;2)图示位置的压力角;3)从动件轮的推程运动角001max 01vF解:作图过程如下图所示:题5.3图5.4试用作图法设计一偏置直动滚子从动件盘形凸轮机构的凸轮廓线已知凸轮r o=3Omm,滚子半径r r=10mm。
从动件运动规律为:凸轮转角〜150 0时,从动件等速上升16mm ; 150°〜180°时从动件远休;180°〜300°时从动件等加速等减速下降16mm, 300°〜360°时从动件近休。
解:取长度比例尺i = 0.001m/mm,将从动件运动规律画出来,禾U用反转法图解凸轮设计如下:zt J h=141 2 * 15(3 430°5 6188飞—-60^s)5.5试用作图法设计一个直动平底从动件盘形凸轮机构凸轮的轮廓曲线。
设已知凸轮基圆半径r o=3Omm,从动件平底与导路的中心线垂直,凸轮顺时针方向等速转动。
当凸轮转过12O0时从动件以余弦加速度运动上升20mm,再转过150°时,从动件又以余弦加速度运动回到原位,凸轮转过其余90°时,从动件静止不动。
解:取i 0.001m/mm,根据从动件运动规律画出运动曲线。
禾U用反转法图解凸轮设计如下:)4'J Lo/mmO 211r o =25mm , l oQ 2=60mm , r r =8mm 。
凸轮顺时针方向等速转动,要求当凸轮转过180°时,从动件以余弦加速度运动向上摆动 25°,转过一周中的其 余角度时,从动件以正弦加速度运动摆回到原位置。
用图解法设计凸轮5'6' 下:利用反转法图解凸轮设计如i = 0.001m/mm ,将从动件3 4 5 602(602179O 25O 28O 213 O 24O 22O 212O 21)5.7试用解析法求对心直动滚子从动件盘形凸轮机构的理论廓线与实际廓线的坐标值,计算间隔取为15。
,并核算各位置处凸轮机构的压力 角。
已知其基圆半径r o =1Omm,凸轮顺时针方向等速转动,当转过 时,从动件以正弦加速度运动上升 30mm,再转过90°时,从动件弦加速度运动规律回到原位,凸轮转过一周的其余角度时, 不动。
解:根据题意将凸轮机构放在直角坐标系下如图所示。
从动件运动规律为:s h1 215 3sin 015 2 3 sin 3 cos 345 ,ds cos 31 d回程段h s 1 cos 0s15 1 2ds2 230 sind3近休止段: s0,ds0,210dcos 23120 210x4升程段30 120求得理论和实际轮廓线。
5.8试求一对心平底从动件盘形凸轮机构凸轮廓线的坐标值。
已知从 动件的平底与导路垂直,凸轮的基圆半径r 0=45m m ,凸轮沿逆时针方向等速转动。
当凸轮转过120°时,从动件以等加等减速运动上升 15mm, 再转过90°理论轮廓线坐标:实际轮廓线坐标:r 0 s sin 50 s sin r 0 s cos 50 s cos x r r cos x 10 cos tany r r siny 10sindx dx / ddydy / d70 s cos ds sin d 70 s sindscos将上述公式编入程序,为自变量,当0 360变化时,即可dydx d dy d时,从动件以正弦加速度运动规律回到原位置,凸轮转过一d实际轮廓线坐标:ds45dsx 「0 s s incos s sincos ddds . 45ds yr °s c ossin s cossindd5.9用解析法计算题5.6中凸轮理论廓线和实际廓线的坐标值,计算间隔取为10ds2h~2 0 15 1o2 135——360 120s h 1ss1 .2 sin0 s2151 ?2 1 . sin 4 2 1203 23ds 30 cos 48 1d3近休止段: s 0,ds 0, 210 360210回程:d解:从动件运动规律为:理论轮廓线坐标:实际轮廓线坐标:x x r r cos x 8 cos y y r r sin y 8 sindx dx / d tandy dy / ddx d d 60 cos50 d 1 cos dyd60 sin501 sinddmax1 cos升程段2d5sind72回程段0ss1 . max1sin25 11sin 2362d 5cos 2 21d3651 cos7220 s2xa sin l sin0 y a cos l cos60si n 50 sin 60 cos 50cos2arccos2alarccos2 2 26050 252 60 5024.2a 2l 2r °升程前半段:s 2h 260 22200ds4h120d2290s h ds 2h2230 1 290 1805.10已知一偏置直动尖顶从动件凸轮机构,升程h=30mm, 0=180°,r o=4Omm 凸轮顺时针转动,导路偏在凸轮轴心左侧,偏距e=5mm,从动件运动规律为等加等减运动。
计算=0 ° 90°180°时,凸轮机构的压力角ds ds厂ds厂e55佝召:tan ----d d d用牛. t an , ---------\』'r0 e2 s .40252 s39.69 s升程后半段:从动件运动规律:5.11已知一尖顶移动从动件盘形凸轮机构的凸轮以等角速度1沿顺时针方向转动,从动件的升程 h=50mm ,升程段的运动规律为余弦加速 度,推程运动角为:0=90。
,从动件的导路与凸轮转轴之间的偏距 e=10mm,凸轮机构的许用压力角 =30°。
求:1)当从动件的升程为工 作行程时,从动件正确的偏置方位;2)按许用压力角计算出凸轮的最小 基圆半径r o (计算间隔取15°)0sds 0, 0; d0 5 arctan7.1839.69 0当90 时,s ds 15,d6019.11; 丄19.11 5 …“arctan14.4739.6919.11当180时,s "ds 门30,0;d0 5 arctan4.10439.69 30当0时,导路应偏在转轴左侧,如图示(2)根据 求r o 的公式为:ds/d 2 e i2ds2r o . —— se1.733 ——10s 100tandhs1 co )s25 1 cos 2升程段:20 90ds50 sin 2d将上述公式编入程序 为自变量,变化范围为0 90,即可求出一系列r o 值。
解:根据题意凸轮机构如下图示:(1)根据公式:tandse d2 2 r°e s若使在升程阶段 小,则公式中e 前应取-“'值。
