逐点比较法直线插补圆弧插补实例
实验一 逐点比较法圆弧和直线插补实验

Y B(xe,ye)
M(xm,ym)
Rm R
A(x0,y0)
O 图3 圆弧插补原理图 X
圆弧插补原理参见上图,对于第一象限逆圆,设圆弧的起点为 A(x0,y0),终点为 B(xe,ye), 圆弧半径为 R。加工点为 M(xm,ym),它与圆心的距离为 Rm,则
(1)偏差计算
Fm
=
Rm2
− R2
=
xm2
p102=p102-p104 p101=p101+1 x-0.1 else p102=p102+p103 p101=p101+1 y0.1
;计算新的偏差值(Fi+1=Fi-ya) ;步数计数器加一 ;X方向进分别是(-0.1 -0.5 -1.0) ;偏差判别(若P102小于0表示刀具在直线下方) ;计算新的偏差值(Fi+1=Fi+xa) ;步数计数器加一 ;Y方向进给分别是(0.1 0.5 1.0)
endif
endwhile
close
(3)根据直线插补编成格式,编写所给圆弧插补程序。 各组的圆弧的插补任务是: u 第一组:圆弧半径 50,第二象限顺圆;
第二组:圆弧半径 50,第二象限逆圆; 第三组:圆弧半径 60,第三象限顺圆; 第四组:圆弧半径 60,第三象限逆圆; 第五组:圆弧半径 70,第四象限顺圆; 第六组:圆弧半径 70,第四象限逆圆; open prog7 clear linear inc p101=0 p102=0 p103=0 p104=50 while(p101!>100) if(p102!<0) y0.5 p101=p101+1 p102=p102-2*p104+1 p104=p104-1 else -x0.5 p101=p101+1 p102=p102-2*p103+1 p103=103-1 endif endwhile close
圆弧插补(逐点比较法)20页文档

Fi<0
O Fi≥0
X Fi<0 Fi≥0
2、圆弧插补的象限处理
前面的圆弧插补(顺圆、逆圆)只限于第一象限,其他 情况如图所示: Y
O
X
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
代入偏差函数,得Pi+1点的偏差为: Fi+1 = Fi-2Yi + 1
当Fi<0时,向+X方向进给一步,动点由Pi(Xi,Yi) 移动到 Pi+1(Xi +1,Yi),则新动点的坐标为 Xi+1=Xi +1
代入偏差函数,得Pi+1点的偏差为:
Fi+1 = Fi + 2Xi + 1
所以,第一象限顺时针圆弧插补加工时偏差加工的递推 公式为:
10 F9=1 -X F10=F9-2X9+1 = 0, X10=0,Y10=5 ∑=0
加工过程为: Y 5
4 3
2 1
O
1 23 45
X
(三)象限处理 1、直线插补的象限处理 前面的公式只适用于第一象限,对于其他象限直线,偏
差函数用│X│和 │Y│代替X,Y。则进给方向为:
Y Fi<0 Fi≥0 Fi≥0
X
同理,对于第一象限顺圆加工时,即B→A,当Fi≥0时, 应向-Y方向进给一步,当Fi<0时,应向+X方向进给 一步。
Y
B(Xe,Ye)
Pi(Xi,Yi)
数控机床插补原理

对圆弧,提供起点、终点、顺圆或逆圆、以及圆心相对于起点的位置。为满
足零件几何尺寸精度要求,必须在刀具(或工件)运动过程中实时计算出满足 线形和进给速度要求的若干中间点(在起点和终点之间),这就是数控技术中
插补(Interpolation)的概念。据此可知,插补就是根据给定进给速度和给定
轮廓线形的要求,在轮廓已知点之间,确定一些中间点的方法,这种方法称 为插补方法或插补原理。
Xm+1=Xm+1, Ym+1=Ym
新的偏差为
Fm+1=Ym+1Xe-Xm+1Ye=Fm-Ye
若Fm<0时,为了逼近给定轨迹,应向+Y方向进给一步,走一步后新的坐标值为
Xm+1=Xm, Ym+1=Ym +1
新的偏差为
Fm+1=Fm+Xe
4. 终点判别法
逐点比较法的终点判断有多种方法,下面主要介绍两种:
直到∑为零时,就到了终点。
2.2
不同象限的直线插补计算
上面讨论的为第一象限的直线插补计算方法,其它三个象
限的直线插补计算法,可以用相同的原理获得,表5-1列出了
四个象限的直线插补时的偏差计算公式和进给脉冲方向,计 算时,公式中Xe,Ye均用绝对值。
表1-1 四个象限的直线插补计算
逐点比较法插补实验报告

实验报告实验内容:逐点比较法直线和圆弧插补2011年9月25日院系:物科院班级:085 学号:07080518 姓名:陈实实验目的:利用逐点比较法的插补原理,编写直角坐标系下的直线、圆弧插补程序,观察屏幕上仿真的运动轨迹,掌握逐点比较法的插补原理。
实验原理:逐点比较发是基于动点与理想曲线院函数的比较来实现插补的。
逐点比较法的插补过程,每走一步要进行一下四个步骤:偏差判别:根据偏差值确定刀具相对加工曲线的位置坐标进给:根据偏差判别的结果,决定控制线沿哪个坐标进给一步以接近曲线偏差计算:计算新加工店相对曲线的偏差,作为下一步偏差判别的依据终点判别:判别是否到达终点,未到达终点则返回第一步继续插补,到终点则停止1、逐点比较法直线插补原理:逐点比较法在第一象限的直线插补原理如下图所示,其他象限情况可依次类推。
现加工OE直线,如果刀具动点在OE直线上方或在线上,则令刀具沿X正方向进给一步;若刀具动点在OE直线下方,则令刀具沿Y轴正方向进给一步,如此循环直到加工到E点。
判别刀具动点的位置根据偏差函数判别公式:根据这个公式可以推到出两种不同情况下的地推公式:对于插补终点的判别,可以采用单向的计数长度法,即:取计数长度M等于Xe、Ye中的大者,并设该坐标方向为计数方向。
插补时,仅在该方向上产生进给时,计数长度减一。
图1的逐点比较法中,工作循环的结束条件就是M减为0.2、逐点比较法圆弧插补原理:逐点比较法在第一象限的圆弧插补原理如图所示,其他象限可一次类推:对于第一象限的逆圆弧,如果动点在圆弧的外侧则令刀具动点沿X轴负方向进给一步。
如果动点在圆弧的内侧则令刀具沿Y轴正方向进给一步。
圆弧的偏差计算公式为:根据这个公式同样可推导出圆弧插补的两种不同情况下的递推公式:对于插补终点的判别,同样可以采用单向的计数长度法,不过对于圆弧,计数的方向并不取决于终点坐标中的大者,而是取决于圆弧终点处。
逐点比较法插补中需要编写插入部分流程图:插入程序:intM,Fi=0,Fi0,Fi1,xi,yi,i=0 ,num=-1;bool Gx; M=Xe+Ye;moveto(x0,y0);setcolor(10);line(x0,y0,x0+Xe*delta,y0-Ye*delta);xi=x0;yi=y0;setcolor(12);while(M>0){getch();if(Fi>=0){linerel(delta,0); xi=xi+delta;Fi0=Fi-Ye;Fi=Fi0; num++;dis_msg(num,Fi,1,0,Fi0,M);}else{linerel(0,-delta);Fi1=Fi+Xe;yi=yi-delta;Fi=Fi1;num++;dis_msg(num,Fi,0,1,Fi1,M);}M--;}圆弧插补实验程序:int M,Fi=0,Fi0,Fi1,xi=R,yi=0,i=0,num=0; M=R;setcolor(10);moveto(x0,y0);arc(x0,y0,0,90,R*delta);setcolor(12);moveto(x0+xi*delta,y0);while(M>0){getch();if(Fi>=0){linerel(-delta,0);Fi0=Fi-2*xi+1;Fi=Fi0;xi=xi--;M--;dis_msg(num,Fi,1,0,Fi0,M);}else{linerel(0,-delta);Fi1=Fi+2*yi+1;Fi=Fi1;yi=yi++;dis_msg(num,Fi,0,1,Fi1,M);}num=num++;}实验中所遇问题分析:1、圆弧插补:Fi0与Fi1的计算,xi,yi计算先写入为:Fi0=Fi-2*xi*delta+1;Fi1=Fi+2*yi*delta+1;xi=xi-delta;yi=yi+delta;但是,实行以后出现的结果不正确,如图,分析:2、关于计数长度M:在直线插补中使用的是双向计数长度 M=xe+ye,插补路线会比较准确。
逐点比较法圆弧插补

逐点比较法圆弧插补逐点比较法圆弧插补过程与直线插补过程类似,每进给一步也都要完成四个工作节拍:偏差判别、坐标进给、偏差计算、终点判别。
但是,逐点比较法圆弧插补以加工点距圆心的距离大于还是小于圆弧半径来作为偏差判别的依据。
如图5-7所示的圆弧AB,其圆心位于原点O(0,0),半径为R,令加工点的坐标为P(xi,yj),则逐点比较法圆弧插补的偏差判别函数为当F=0时,加工点在圆弧上;当F>0时,加工点在圆弧外;当F<0时,加工点在圆弧内。
同插补直线时一样,将Fi,j=0同Fi,j>0归于一类。
下面以第一象限圆弧为例,分别介绍顺时针圆弧和逆时针圆弧插补时的偏差计算和坐标进给情况。
1.插补第一象限逆圆弧1)当Fi,j≥0时,加工点P(xi,yj)在圆弧上或圆弧外,-X方向进给一个脉冲当量,即向趋近圆弧的圆内方向进给,到达新的加工点Pi-1,j,此时xi -1=xi-1,则新加工点Pi-1,j的偏差判别函数Fi-1,j为(2)当Fi,j<0时,加工点P(xi,yj)在圆弧内,+Y方向进给一个脉冲当量,即向趋近圆弧的圆外方向进给,到达新的加工点Pi,j+1,此时yj+1=yj+1,则新加工点Pi,j+1的偏差判别函数Fi,j+12.插补第一象限顺圆弧1)当Fi,j≥0时,加工点P(xi,yj)在圆弧上或圆弧外,-Y方向进给一个脉冲当量,即向趋近圆弧的圆内方向进给,到达新的加工点Pi,,j-1,此时yj-1=yj-1,则新加工点Pi,j-1的偏差判别函数Fi,j-1为2)当Fi,j<0时,加工点P(xi,yj)在圆弧内,+X方向进给一个脉冲当量,即向趋近圆弧的圆外方向进给,到达新的加工点Pi+1,j,此时xi+1=xi +1,则新加工点Pi+1,j的偏差判别函数为Fi+1,j由以上分析可知,新加工点的偏差是由前一个加工点的偏差Fi,j及前一点的坐标值xi、yj递推出来的,如果按式(5-6)、(5-7)、(5-8)、(5-9)计算偏差,则计算大为简化。
逐点比较法

即
Fi1 Fi X e
6
在插补计算、进给的同时还要进行终点判别。常用终点判 别方法是:
设置一个长度计数器,从直线的起点走到终点,刀具沿
X 轴应走的步数为X e,沿Y 轴走的步数为Ye,计数器中存入 X和Y两坐标进给步数总和∑=∣Xe∣+∣Ye∣,当X 或Y
坐标进给时,计数长度减一,当计数长度减到零时,即∑= 0时,停止插补,到达终点。
终点判别:判断是否到达终点,若到 达x ,结束插补;否则,继续以上四个
步骤(如图3-3所示)。
图3-3 逐点比较法工作循环图
3
2. 直线插补
图3-4所示第一象限直线OE为给定轨迹,其方程为
XeY-XYe=0
(3-1)
P(X,Y)为动点坐标,与直线的关系有三种情况:
(1)若P1点在直线上方,则有XeY-XYe>0 E (2) 若P点在直线上,则有 XeY-XYe=0
2.由偏差方程确定加工动点引起的偏 差符号(若要计算偏差量,则偏差方程系数不能简 化)。
3.下一步插补方向确定原则:向使加 工偏差减小、并趋向轨迹终点的方向插补
.(将偏差等于零的情况并入偏差大于零的情况)。
4.关于插补量:每次插补一个脉冲当 量的位移
12
3. 圆弧插补
在圆弧加工过程中,可用动点到圆心的距离来描述刀具位置与 被加工圆弧之间关系。
b) 逆圆弧
图3-9 第一象限顺、逆圆弧
14
偏差递推简化:对第一象限顺圆,Fi≥0,动点Pi(Xi,Yi)应 向-Y向进给,新的动点坐标为(Xi+1,Yi+1),且Xi+1=Xi,Yi +1=Yi-1,则新点的偏差值为:
15
若Fi<0时,沿+X向前进一步,到达(Xi+1,Yi)点,新点
例题:逐点比较法

-、逐点比较法1、直线L1:起点坐标O (0, 0),终点坐标A (4, 6)(1)分析1)直线L1为第一象限内直线2)插补总步数:M=x e+y e=4+6=103)若偏差任0,则刀具向+A x方向进给一步,偏差f i+1j = f.. - y e4)若偏差f<0,则刀具向+A y方向进给一步,偏差f. .+1= f.. + x e(2)列表计算(3)2、直线L2:起点坐标O (0, 0),终点坐标A (-6, 3)(1)分析1)直线L2为第二象限内直线2)插补总步数:M=l x e l+y e=6+3=93)若偏差任0,则刀具向-A x方向进给一步,偏差f i+1j = f.. - y e4)若偏差f<0,则刀具向+A y方向进给一步,偏差f, .+1= f.. +lx e\ (2)(3)3、直线L3:起点坐标O (0, 0),终点坐标A (-5, -8)(1)分析1)直线L3为第三象限内直线2)插补总步数:M=l x e l+l y e l=5+8=133)若偏差任0,则刀具向-A x方向进给一步,偏差f,+1. = f.. -\y\4)若偏差f<0,则刀具向-A y方向进给一步,偏差f,,+1 = f.. +\x\(2)列表计算(3)绘制进给脉冲图(略)4、直线L4:起点坐标O (0, 0),终点坐标A (7, -4)(1)分析1)直线L4为第四象限内直线2)插补总步数:M=x+\y\=7+4=113)若偏差任0,则刀具向+A x方向进给一步,偏差f i+1j = f.. -\y\4)若偏差f<0,则刀具向-A y方向进给一步,偏差f. .+1= f.. + x e(2)(3)5、圆弧NR1:起点坐标A (4, 0),终点坐标E (0, 4)(1)分析1)圆弧NR1为第一象限逆圆2)插补总步数:M=\(x0-x e)\+\(y0-y e)\=4+4=83)若偏差任0,则刀具向-A x方向进给一步,偏差f,+1 . = f.. ~2x. + 14)若偏差f<0,则刀具向+A y方向进给一步,偏差f, .+1 = f.. + 2y.+ 1 (2)列表计算(3)绘制进给脉冲图(略)6、圆弧NR2:起点坐标A (0, 5),终点坐标E (-5, 0)(1)分析1)圆弧NR2为第二象限逆圆2)插补总步数:M=l(x0-x e)l+l(j0-j e)l=5+5=103)若偏差任0,则刀具向-颂方向进给一步,偏差f.,+1 = f.. - 2y.+ 14)若偏差f<0,则刀具向-A x方向进给一步,偏差f,+1 . = f.. ~2x. + 1 (2)列表计算(3)绘制进给脉冲图(略)7、圆弧NR3:起点坐标A (-6, 0),终点坐标E (0, -6)(1)分析1)圆弧NR3为第三象限逆圆2)插补总步数:M=l(x0-x g)l+l(y0-y g)l=6+6=123)若偏差任0,则刀具向+A x方向进给一步,偏差f i+1j = f.. + 2x. + 14)若偏差f<0,则刀具向-A y方向进给一步,偏差f. .+1 = f.. - 2y. + 1 (2)列表计算(3)8、圆弧NR4:起点坐标A (0, -7),终点坐标E (7, 0)1)圆弧NR4为第四象限逆圆2)插补总步数:M=\(x Q-x e)\+\(y Q-y e)\=7+7=143)若偏差任0,则刀具向+A y方向进给一步,偏差f.,+1 =f.. + 2y.+ 14)若偏差f<0,则刀具向+A x方向进给一步,偏差f i+1j =加+ 2x. + 1(2)(3)9、圆弧SR1:起点坐标A (0, 4),终点坐标E (4, 0)(1)分析1)圆弧SR1为第一象限顺圆2)插补总步数:M=\(x0-x e)\+\(y0-y e)\=4+4=83)若偏差f N0,则刀具向-A y方向进给一步,偏差f, .+1 = f.. ~2y.+ 14)若偏差f<0,则刀具向+A x方向进给一步,偏差f.+1. = f.. + 2x. + 1(2)(3)绘制进给脉冲图(略)10、圆弧SR2:起点坐标A (-5,0),终点坐标E (0,5)(1)分析1)圆弧SR2为第二象限顺圆2)插补总步数:M=\(x0-x e)\+\(y0-y e)\=5+5=103)若偏差f N0,则刀具向+A x方向进给一步,偏差f,+1. = f.. + 2x. + 14)若偏差f<0,则刀具向+A y方向进给一步,偏差f, .+1 = f.. + 2y.+ 1 (2)列表计算(3)绘制进给脉冲图(略)11、圆弧SR3:起点坐标A (0, -6),终点坐标E (-6, 0)(1)分析1)圆弧SR3为第三象限顺圆2)插补总步数:M=l(x0-x e)l+l(y0-y e)l=6+6=123)若偏差任0,则刀具向+颂方向进给一步,偏差f i+1j = f,. + 2y.+ 14)+1= "j - 2x.+ 1 (2)列表计算(3)12、圆弧SR4:起点坐标A (7, 0),终点坐标E (0, -7)(1)分析1)圆弧SR4为第四象限顺圆2)插补总步数:M=l(x0-x e)l+l(y0-y e)l=7+7=143)若偏差任0,则刀具向-A x方向进给一步,偏差f. .+1 = f.j - 2x. + 14)+1.(3二、数值积分法(DDA)1、直线L1:起点坐标O (0, 0),终点坐标A (4, 6)(1)分析1)直线L1为第一象限内直线2)x e=4=100B;y e=6=110B3)取积分累加器容量N=3位4)x被积函数寄存器J vx= x e;y被积函数寄存器J vy= y e5)初始时:x累加器J Rx= 0;y累加器J Ry= 06)当J Rx累加超过3位溢出时,则在x方向分配一进给脉冲+A x7)当J Ry累加超过3位溢出时,则在y方向分配一进给脉冲+颂(2)列表计算:(3)绘制进给脉冲图(略)2、直线L2:起点坐标O(0,0),终点坐标A(-6,3)(1)分析1)直线L2为第二象限内直线2)x e=l-6l=110B;y e=3=011B3)取积分累加器容量N=3位4)x被积函数寄存器J vx= x e;y被积函数寄存器J vy= y e5)初始时:x累加器J Rx= 0;y累加器J Ry= 06)当J Rx累加超过3位溢出时,则在x方向分配一进给脉冲-A x 7)当J Ry累加超过3位溢出时,则在y方向分配一进给脉冲+A y (2)列表计算二进制累加:累加N3):累加(3)绘制进给脉冲图(略)3、直线L3:起点坐标O(0,0),终点坐标A(-5,-8)(1)分析1)直线L3为第三象限内直线2)x e=|-5|=101B;y e=|-8|=1000B3)取积分累加器容量N=4位4)x被积函数寄存器J vx= x e;y被积函数寄存器J vy= y e5)初始时:x累加器J Rx= 0;y累加器J Ry= 06)当J Rx累加超过4位溢出时,则在x方向分配一进给脉冲-A x 7)当J Ry累加超过4位溢出时,则在y方向分配一进给脉冲-A y (2)列表计算二进制累加:(3)绘制进给脉冲图(略)4、直线L4:起点坐标O (0, 0),终点坐标A (7, -4)(1)分析1)直线L4为第四象限内直线2)x e=7=111B;y e=l-4l=100B3)取积分累加器容量N=3位4)x被积函数寄存器J vx= x e;j被积函数寄存器J vy= y e5)初始时:x累加器J Rx= 0;j累加器J Ry= 06)当J Rx累加超过3位溢出时,则在x方向分配一进给脉冲+A x 7)当J Ry累加超过3位溢出时,则在j方向分配一进给脉冲-颂(2)列表计算二进制累加:N3):(3)绘制进给脉冲图(略)5、圆弧NR1:起点坐标A (4, 0),终点坐标E (0, 4)(1)分析1)圆弧NR1为第一象限逆圆2)x0=4=100B;y0=0=000B3)取积分累加器容量N=3位4)初始时:x被积函数寄存器J vx= y0;y被积函数寄存器J vy= x05)初始时:x累加器J Rx= 0;y累加器J Ry= 06)当J Rx累加超过3位溢出时,则在x方向分配一进给脉冲-A x,相应在J vy中对x 坐标的修正为减一7)当J Ry累加超过3位溢出时,则在y方向分配一进给脉冲+A y,相应在J vx中对y 坐标的修正为加一(2)列表计算(3)绘制进给脉冲图(略)7、圆弧NR3:起点坐标A (-6, 0),终点坐标E (0, -6)(1)分析1) 圆弧NR3为第三象限逆圆 2) 扁=I-6I=110B ; y 0=0=000B 3) 取积分累加器容量N=3位4) 初始时:x 被积函数寄存器J vx = y 0; y 被积函数寄存器J vy = x 0 5) 初始时:x 累加器J Rx = 0; y 累加器J Ry = 06) 当J Rx 累加超过3位溢出时,则在x 方向分配一进给脉冲+A x ,相应在J vy 中对x 坐标的修正为减一7) 当J Ry 累加超过3位溢出时,则在y 方向分配一进给脉冲-颂,相应在J vx 中对y坐标的修正为加一(2)列表计算_8_ 9 10 11 12 1314(-44) (-4,4) (-5,3) (-5,3)(-3+4=7 7+4=11 (3)停止累加2+4=6 6+4=10(2) 2+5=7 7+5=12(4) 4+6=10(2) 2+6=8(0)停止累加0 1 0 1 1 1 0(3) 绘制进给脉冲图(略)8、圆弧NR4:起点坐标A (0, -7),终点坐标E (7, 0)(1)分析1) 圆弧NR4为第四象限逆圆 8) x 0=0=000B ; j 0=|-7l=111B 9) 取积分累加器容量N=3位10) 初始时:x 被积函数寄存器J vx = y 0; y 被积函数寄存器J vy = x 0 11) 初始时:x 累加器J Rx = 0; y 累加器J Ry = 012) 当J Rx 累加超过3位溢出时,则在x 方向分配一进给脉冲+A x ,相应在J vy 中对 x 坐标的修正为加一2) 当J Ry 累加超过3位溢出时,则在y 方向分配一进给脉冲+A y ,相应在J vx 中对y 坐标的修正为减一(2)列表计算10 11 12 13 14 15(-4,-6) (-3,-6) (-2,-6) (-1,-7+6=13(5) 5+6=11(3) 3+6=9 (1) 1+6=7 7+6=13 (5)停止累加1 1 1 0 1 0停止累加(3)绘制进给脉冲图(略)9、圆弧SR1:起点坐标A (0, 4),终点坐标E (4, 0)(1)分析1) 圆弧SR1为第一象限顺圆 2) x 0=0=000B ; j 0=4=100B 3) 取积分累加器容量N=3位4) 初始时:x 被积函数寄存器J vx = y 0; y 被积函数寄存器J vy = x 0 5) 初始时:x 累加器J Rx = 0; y 累加器J Ry = 06) 当J Rx 累加超过3位溢出时,则在x 方向分配一进给脉冲+A x ,相应在J vy 中对x坐标的修正为加一7) 当J Ry 累加超过3位溢出时,则在y 方向分配一进给脉冲-颂,相应在J vx 中对y坐标的修正为减一(2)列表计算11 12 13 1415(7, -4) (7, - 3) (7, - 2)-6+5=11⑶3+7=10(2) 2+7=9(1) 1+7=8(0) 0+7=7 7+7=14(6)停止累加1 1 0 1 0(3)绘制进给脉冲图(略)10、圆弧SR2:起点坐标A (-5, 0),终点坐标E (0, 5)(1)分析1)圆弧SR2为第二象限顺圆 2) x 0=l-5l=101B ; j 0=0=000B 3) 取积分累加器容量N=3位4) 初始时:x 被积函数寄存器J vx = y 0; y 被积函数寄存器J vy = x 0 5) 初始时:x 累加器J Rx = 0; y 累加器J Ry = 06) 当J Rx 累加超过3位溢出时,则在x 方向分配一进给脉冲+A x ,相应在J vy 中对x 坐标的修正为减一7) 当J Ry 累加超过3位溢出时,则在y 方向分配一进给脉冲+A y ,相应在J vx 中对y 坐标的修正为加一(2)列表计算12 13 1415(4,2)g (41) (4,1) (4,0)3+4=7 7+4=11(3) 3+4=7 7+4=11(3)停止累加1 0 1 0(3)绘制进给脉冲图(略)11、圆弧SR3:起点坐标A (0, -6),终点坐标E (-6, 0)(1)分析1)圆弧SR3为第三象限顺圆 2) x 0=0=000B ; y 0=l-6l=110B 3) 取积分累加器容量N=3位4) 初始时:x 被积函数寄存器J vx = y 0; y 被积函数寄存器J vy = x 0 5) 初始时:x 累加器J Rx = 0; y 累加器J Ry = 06) 当J Rx 累加超过3位溢出时,则在x 方向分配一进给脉冲-A x ,相应在J vy 中对x 坐标的修正为加一7) 当J Ry 累加超过3位溢出时,则在y 方向分配一进给脉冲+A y ,相应在J vx 中对y 坐标的修正为减一(2)列表计算141514(-6,-1)15(-6,0)停止累加0(3)绘制进给脉冲图(略)12、圆弧SR4:起点坐标A (7, 0),终点坐标E (0, -7)(1)分析1)圆弧SR4为第四象限顺圆2)x0=7=111B;j0=0=000B3)取积分累加器容量N=3位4)初始时:x被积函数寄存器J vx= y0;y被积函数寄存器J vy= x05)初始时:x累加器J Rx= 0;y累加器J Ry= 06)当J Rx累加超过3位溢出时,则在x方向分配一进给脉冲-A x,相应在J vy中对x 坐标的修正为减一7)当J Ry累加超过3位溢出时,则在y方向分配一进给脉冲-A y,相应在J vx中对y 坐标的修正为加一(2)列表计算(3)绘制进给脉冲图(略)。
数控机床逐点比较法圆弧插补
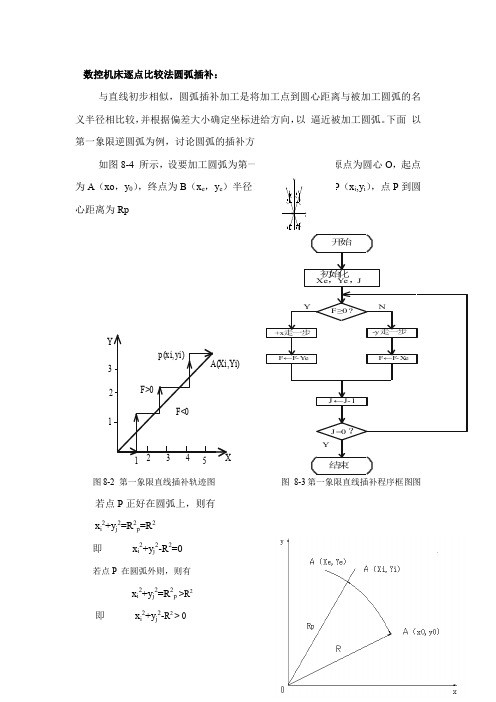
第一象限逆圆弧为例,讨论圆弧的插补方法。
如图8-4 所示,设要加工圆弧为第一象限逆圆弧AB ,原点为圆心O ,起点为A (xo ,y 0),终点为B (x e ,y e )半径R ,瞬时加工点为P (x i ,y i ),点P 到圆心距离为Rp<0+△y>0-△x <0+△x <0+△y>0-△x<0-△y <0-△y>0+△x yx图8-2 第一象限直线插补轨迹图 图 8-3第一象限直线插补程序框图图12345X123YF>0p(xi,yi)A(Xi,Yi)F<0开始初始化Xe ,Y e ,JF≥0?+x 走一步F←F -Y e F←F -X e-y 走一步YNJ ←J-1J =0?Y结束若点P 在圆弧内则,则有x i2+y j2=R2p<R2即x i2+y j2-R2 < 0显然,若令F i,j= x i2+y j2-R2(8-4)图8-4 逆圆弧插补则有:(1)F i,j= F i,j=0, 则点P在圆弧上(2)F i,j >0则点P在圆弧外则(3)F i,j<0则点P在圆弧不则常将8-4称为圆弧插补偏差判别式。
当F i,j≥时,为逼近圆弧,应向-x方向进给一步;当F i,j<0时,应向+y 方向走一步。
这样就可以获得逼近圆弧的折线图。
与直线插补偏差计算相似,圆弧插补的偏差的计算也采用递推的方法以简化计算。
若加工点P(x i,y i)在圆弧外或者圆弧上,则有:F i,j=x i2+y j2-R2≥0 为逼近该圆沿-x方向进给一步,移动到新加工点P(x i=1,y i),此时新加工点的坐标值为x i+1=x i-1,y i=y i新加工点的偏差为:F i+1,j=(x i-1)2+y i2-R2=x i2-2x i+1+ y i2-R2= x i2+ y i2-R2+1即F i+1,j= F i,j-2x i+1 (8-5)若加工P(x i,y i)在圆弧内,则有F i,j=x i2+y j2-R2<0若逼近该圆需沿+y方向进给一步,移到新加工点P(x i,y i),此时新加工点的坐标值图8-5 第一象限圆弧插补程序框图为新加工点的偏为:F i,j+1=x i2+(y i+1)2-R2=x i2+ y i2+1 -R2= x i2+ y i2-R2+1+2y iF i,j+1= F i,j-2y i+1 (8-6)从(8-5)和式(8-6)两式可知,递推偏差计算仅为加法(或者减法)运算,大大降低了计算的复杂程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
逐点比较法直线插补
(1)偏差函数构造
对于第一象限直线OA上任一点(X,Y):X/Y = Xe/Ye
若刀具加工点为Pi(Xi,Yi),则该点的偏差函数Fi可表示为:
若Fi= 0,表示加工点位于直线上;
若Fi> 0,表示加工点位于直线上方;
若Fi< 0,表示加工点位于直线下方。
(2)偏差函数字的递推计算
采用偏差函数的递推式(迭代式):既由前一点计算后一点
Fi =Yi Xe -XiYe
若Fi>=0,规定向+X 方向走一步
Xi+1 = Xi +1
Fi+1 = XeYi –Ye(Xi +1)=Fi –Ye
若Fi<0,规定+Y 方向走一步,则有
Yi+1 = Yi +1
Fi+1 = Xe(Yi +1)-YeXi =Fi +Xe
(3)终点判别
直线插补的终点判别可采用三种方法。
1)判断插补或进给的总步数:2)分别判断各坐标轴的进给步数;3)仅判断进给步数较多的坐标轴的进给步数。
(4)例
对于第一象限直线OA,终点坐标Xe=6 ,Ye=4,插补从直线起点O开始,故F0=0 。
终点判别是判断进给总步数N=6+4=10,将其存入终点判别计数器中,每进给一步减1,若N=0,则停止插补。
逐点比较法圆弧插补(1)偏差函数构造
任意加工点Pi(Xi,Yi),偏差函数Fi可表示为
若Fi=0,表示加工点位于圆上;
若Fi >0,表示加工点位于圆外;
若Fi <0,表示加工点位于圆内
(2)偏差函数的递推计算
1) 逆圆插补
若F ≥0,规定向-X 方向走一步
若Fi<0,规定向+Y 方向走一步
2) 顺圆插补
若Fi ≥0,规定向-Y 方向走一步
若Fi<0,规定向+y 方向走一步
(3)终点判别
1)判断插补或进给的总步数: 2)分别判断各坐标轴的进给步数: (4)例
对于第一象限圆弧AB ,起点A (4,0),终点B (0,4)
⎩⎨⎧+-=-+-=-=++12)1(122211i i i i i i i X F R Y X F X X ⎩⎨⎧++=-++=+=++12)1(122211i i i i i i i Y F R Y X F Y Y ⎩⎨⎧+-=--+=-=++12)1(122211i i i i i i i Y F R Y X F Y Y ⎩⎨⎧++=-++=+=++12)1(122211i i i i i i i X F R Y X F X X b
a b a Y Y X X N -+-=b
a x X X N -=
b a y Y Y N -=
如有侵权请联系告知删除,感谢你们的配合!。
