材料力学第4章_new
04_FLAC3D5.0_结构单元和接触面

工程师 李振 2014.3.27-3.28 ITASCA(武汉)咨询有限公司
FLAC3D 5.0培训日程安排
2014.3.27~ 2014.3.28
1. FLAC3D V5.0界面操作 2. FLAC3D基本操作方法vs应用流程; 3. FLAC3D内置Fish语言的应用; 4. FLAC3D结构单元vs接触单元;
4.1、简支梁(beam单元)承受两个相等集中载荷
A simply supported beam is loaded by two equal concentrated loads, symmetrically placed as shown in Figure 1.9. The shear and moment diagrams for this configuration are also shown in the figure.The shear force magnitude,V, is equal to the applied concentrated load,P. The maximum moment,Mmax, occurs between the two loads and is equal to Pa. The maximum deflection of the beam,max, occurs at the center and is given by AISC (1980, p. 2-116) as
3、结构单元的参数取值
梁单元 锚索单元
•
• • • • • •
emod——弹性模量,E
nu——泊松比,ν xcarea——横截面积,A
•
• •
emod——弹性模量, E
材料力学课件全套

§2 2 轴向拉伸或压缩时横截面上的内力和应力
m
F m
F
FN
FN
Fx 0
FN F0 FN F
1 截面法求内力
F 1假想沿mm横截面将
杆切开
2留下左半段或右半段
F 3将弃去部分对留下部分
的作用用内力代替
4对留下部分写平衡方程 求出内力即轴力的值
目录
§2 2 轴向拉伸或压缩时横截面上的内力和应力
1kPa=103N/m2 1MPa=106N/m2 1GPa=109N/m2
目录
§1 5 变形与应变
1 位移 MM'
M'
刚性位移; 变形位移
2 变形
M
物体内任意两点的相对位置发生变化
取一微正六面体
y
g
两种基本变形:
线变形
L
—— 线段长度的变化
角变形
——线段间夹角的变化 o
M
x
L'
x+s
M'
N'
N
x
圣 维 南 原 理
目录
§2 2 轴向拉伸或压缩时横截面上的内力和应力
目录
§2 2 轴向拉伸或压缩时横截面上的内力和应力
例题2 2
A 1
图示结构;试求杆件AB CB的应
力 已知 F=20kN;斜杆AB为直径
20mm的圆截面杆,水平杆CB为 15×15的方截面杆。
45° B
C
2
FN1
F
y
F N 2 45° B x
建于隋代605年的河北赵州桥桥长64 4米;跨径37.02米,用石2800吨
目录
§1 1 材料力学的任务
材料力学课件第1-4章

1.1 材料力学的任务
一.工程要求
设 机械 计 结构
零件
构件 (可变形固体)
?
要求:构件具有足够的承载能力
5
1.1 材料力学的任务
构件的承载能力
1.强度 2.刚度
?
3.稳定性 1.什么叫构件的强度、刚度、稳定性?
2.什么时候构件具有足够的强度、刚度、稳定性? 强度 ----构件抵抗破坏的能力
刚度 ----构件抵抗变形的能力
3. 截面形状和尺寸与承载关系
方法 1. 实验手段 2. 理论分析
几何方面 物理方面
静力方面
9
工程实例
强度
刚度
稳定性
稳定性
10
1.2 可变形固体的性质及其基本假设
构件
可变形固体
材料
1.连续性 2.均匀性 3.各向同性
11
1.2 可变形固体的性质及其基本假设
4. 小变形条件 原始尺寸原理
物体的变形是客观存在的,当结构的支反力没 有求出时,变形是无法求解的,为了应用静力平 衡方程,求出支反力,引入小变形原理(原始尺寸 原理)
例2. 一悬臂吊车,载荷 F=15kN,A C 1 . 9 m B C 0 . 8 m 当F 移到A点时 求AB 杆横截面上的应力。
B
d 20mm
解: 1.求外力
F y 0 F AB sin F 0
得
FAB
F sin
C y
ox
F FAB
FAC
A
F
sin
0.8 0.388 0.82 1.92
公式推导
1.实验观察: 直线平移 2.推理: 面平移
3.假设:平面假设
= C1, = C2
《材料力学教学课件》材料力学-第4章modify共48页文档

为了揭示承载物体内的内力,通常 采用截面法(section method)。
这种方法是,用一假想截面将处于 平衡状态下的承载物体截为A、B两部分。
为了使其中任意一部分保持平衡,必 须在所截的截面上作用某个力系,这 就是A、B两部分相互作用的内力。
根据牛顿第三定律,作用在A部分截 面上的内力与作用在B部分同一截面上 的内力在对应的点上,大小相等、方 向相反。
关于材料的基本假定
均匀连续性假定 各向同性假定
关于材料的基本假定
均匀连续性假定
关于材料的基本假定
连续问题
微观不连续 ,宏观连续 。
关于材料的基本假定
球墨铸铁的 显微组织
关于材料的基本假定
普通钢材的 显微组织
关于材料的基本假定
均匀连续性假定
均 匀 连 续 性 假 定 (homogenization and continuity assumption)—假定材料均匀、无空隙地 分布于物体所占的整个空间。
Mx M
杆件受力与变形的基本形式
剪切
剪切(shearing) 在平行于杆横截面 的两个相距很近的 平面内,方向相对 地作用着两个横向 力,当这两个力相 互错动并保持二者 之间的距离不变时, 杆件将产生剪切变 形。
剪力这个名字已经很形象了,类似被剪刀 剪断一样
例如剪刀去剪一物体时,物体所受 到两剪刀口的作用力就是剪力。
武警战士用手劈砖(见视频)
弹性杆件的外力与内力
截面法
截面法步骤
确定杆件横截面上的内力分量的基本方法—截面法,一 般包含下列步骤:
首先应用工程静力学方法,确定作用在杆件上的所有未知 的外力。
在所要考察的横截面处,用假想截面将杆件截开,分为两 部分。
工程力学材料力学第四完整版本习题答案解析
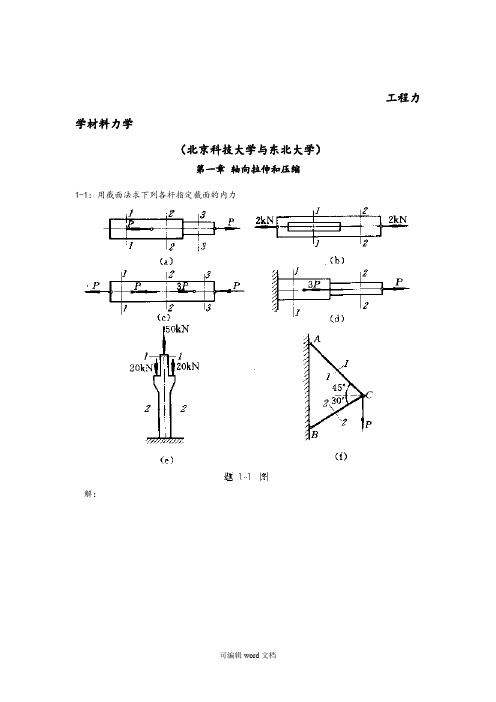
工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104,CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
工程力学-材料力学第4版习题答案
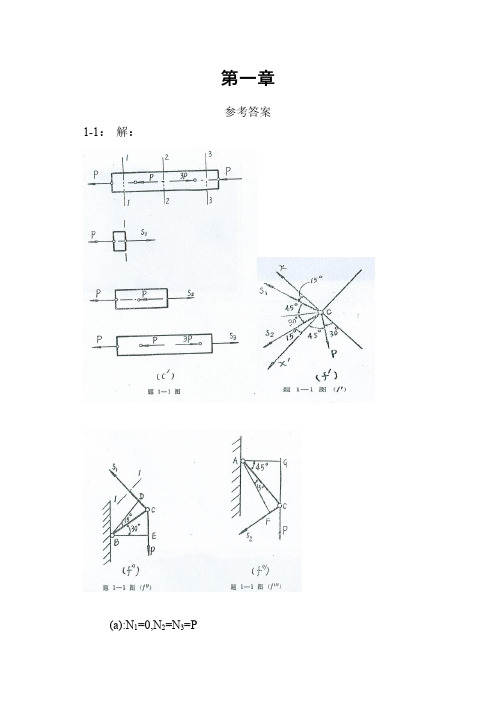
第一章参考答案1-1:解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3=-P(d):N1=-2P,N2=P(e):N1=-50N,N2=-90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2PS =8.72MPa上端双螺孔截面:σ3=3PS =9.15Mpa∴σmax =15.4Mpa1-4:解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5MPa1-5:解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS =38.1MPa1-6:解:(1)σAC =-20MPa,σCD =0,σDB =-20MPa;△l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2)∴AB l ∆=-0.02mm1-7:解:31.8127AC AC CB CB P MPa S P MPa S σσ====AC AC AC L NL EA EA σε===1.59*104,CB CB CB L NL EA EA σε===6.36*1041-8:解: Nll EAl l ε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:解:208,0.317E GPa ν==1-10:解:[][]max59.5MPa σσ=<1-11:解:(1)当45o α=,[]11.2σσ=>强度不够(2)当60o α=,[]9.17σσ=<强度够1-12:解:[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13:解:[]max 200213MPa MPaσ=<1-14:解: 1.78, 1.26d cm d cm==拉杆链环1-15解:BC F ==70.7kN70.70.505140F S FS σσ=∴=== 查表得:45*45*31-16解:(1)[]2401601.5s s n σσ===MPa [][]24P S P dσσπ≤∴≤24.4D mm∴=(2)2119.51602P P MPa MPaS d σπ===≤⎛⎫ ⎪⎝⎭1-17解:(1)2*250*6154402D F P A N π⎛⎫=== ⎪⎝⎭78.4AC F MPa S σ==300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F SF S Nσσ===='61544014.521542390F n F ===≈1-18解:P=119kN1-19解:::3:4:535()44AB BC AB BC S P S S P S P =∴==拉,[][][]112841123484AB AB S A kN S P kNP kN σ=====同理所以最大载荷84kN1-20解:P=33.3kN1-21解:71,,12123A B C P F F P F P ===1-22解:10MAX MPaσ=-1-23解:A B X R R R=∴==∑t r l l ∆=∆t AB l l tα∆=21211111223533131.3cd R AC DB CD AC CD CD AF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA t R l S MPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1一螺栓连接如图所示,已知P=200kN ,=2cm ,螺栓材料的许用切应力[τ]=80Mpa,试求螺栓的直径。
材料力学第四章PPT课件

180
8 0 1 390 2 42D 0 1 4(1 84 0 )1.89
③右端面转角为:
L
T
dx
220x dx
10x2
0 GPI
0 GPI
GPI
2 0
0.033(弧度)
40Nm T
2021/6/7
dx x
x
29
例7 某传动轴设计要求转速n = 500 r / min,输入功率N1 = 500马 力, 输出功率分别 N2 = 200马力及 N3 = 300马力,已知:
202123l的一段杆两截面间相对扭转角单位是弧度为gitl最后叠加值计算可分段求解的受扭构件由多个等截面圆轴组成的正负相对应的正负和扭矩注意202124如图所示阶梯轴
第四章 扭 转
主讲教师:郭慧珍
2021年6月29日星期二
2021/6/7
1
第四章
概述 常见的扭转现象
扭转
传动轴转动
汽车中的转向轴
计算扭转角
f 2
T li i
AC
GI 2021/6/i71
pi
B max
TB RB I PB
100 103 11
(22 4 18 4 )
86.7MPa 32
.. .0.06ra 9d
所以, max86.7MPa 25
§ 4.4 圆轴扭转时的强度和刚度计算
1、圆轴扭转的强度条件:
max
Tmax WP
33
§ 4.5 等直圆杆的扭转超静定问题
解决扭转超静定问题的方法步骤: 列平衡方程; 找几何方程——变形协调方程;(解题关键) 解由平衡方程和补充方程组成的方程组。
2021/6/7
34
材料力学-课件4-5

2020/5/10
2020/5/10
2020/5/10
2020/5/10
12
F
h2
z
aa
x
1
2 dx
y a y a
12 y
h2
y A
y1
dA y
b
M MdM
F
N
1
FN *2FN *1ybdx0
FN*1 A*1dA
A*
My1 Iz
dA
M Iz
A* y1dA
FN*2
A* 2dA A*
MdMy1dA Iz
aa 12
(2)若该梁是由两个矩形截面的厚板条沿图示截面上的ab线(实际是一水平面)
胶合而成,为了保证该梁的胶合连接强度,水平接合面上的许用切应力值
是多少?
F1
F2
q
80
B
B
A
B
C
3m 34 3m
6m
22 4
300
D
z
14
50
a b 148.5
200
12 36
最大拉应力发生在B截面上
14最3大 6 压1 应3 10 3 力6.1发3 59 M 5生M5 在P8 P1 1 Fa0 sa= 0 4 0 4 .05 的0 8 截1面 3 0 上
max
F sh2 8IZ
F sh 2 8 bh 3
12
3F s 2A
A
y
2020/5/10
2020/5/10
2020/5/10
例题 4.33
如图所示倒T型外伸梁,已知q=3kN/m,F1=12kN,F2=18kN,形心主
惯性矩IZ=39800cm4。(1)试求梁的最大拉应力和最大压应力及其所在的位置;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F 横截面:
FB d FB
FS,F
MF F
B
d FB
ΣFy=0, FB+FS,F=0 , FS,F=- FB
=- (F1a+ F2b ) / l
ΣMF=0, - MF+FB×d=0 , MF= FA×d
=d× (F1a+ F2b ) /
l
§4-4 剪力方程和弯矩方程 剪力图和弯矩图
q
例题4-2
FS max=ql
M max=ql 2 / 2
目录
§4-4 剪力方程和弯矩方程 剪力图和弯矩图
F
a
b
A
C
x1 x2
FAY
l
FS Fb / l
Fa / l
Fab/ l
M
例题4-3
图示简支梁C点受集中力作用。
B
试写出剪力和弯矩方程,并画 出剪力图和弯矩图。
解:1.确定约束力
FBY
MA=0, MB=0
M FN
FAy
FS
M FN
FS
Fx 0
Fy 0 Mc 0
FN 0 FS FAy F1 M FAy x F1(x a)
FS剪力,平行于
横截面的内力合力
M 弯矩,垂直于
横截面的内力系的 合力偶矩 FBy
目录
§4-3 剪力和弯矩
M FN
M FN
FAy
FS
FS
截面上的剪力对所选梁
+
例: 已知简支梁 F 1,> F 2, a,b,c,d,l, 如图。求 E , F横截面的内力。
b
a F1
F2
A
c EC
D
F d
B
l
解: 1)求梁的约束反力,并画上正确方向反力。
b
a F1
F2
A FA
c EC
D
F d
l
B FB
解的:
FA= (F1(l -a)+ F2(l -b) ) / l FB= (F1a+ F2b) / l
例题4-4
a
A x1
FAY
M /l
b
图示简支梁C点受集中力偶作用。
M
试写出剪力和弯矩方程,并画
C
B x2
出剪力图和弯矩图。
解:1.确定约束力
l
FBY
MA=0, MB=0
FAy=M / l FBy= -M / l
2.写出剪力和弯矩方程
Ma/ l
Mb/ l
AC FS x1 =M / l 0 x1 a
Fa
ME
3Fa 2
目录
例4.1: 已知 轧制力F =104kN, q= F/0.8= 1.25 ×104 kN/m 如图。求E ,C横截面的内力。
400 400
A
CE
D
B
830
830
解:
1)求梁的约束反力,并画上正确方向反力。 FA= FB=q×0.8/2=F/2=5×103kN 。
400 400
2)截面法求内力 - E 横截面:
A
E
c
FA
设FS,E ,ME 为正剪力正弯矩。
y
FS,E
A
E c
ME
x
FA
ΣFy=0, FA-FS,E=0 , FS,E= FA
=(F1(l -a)+ F2(l -b) ) / l
ΣME=0, ME-FA×c=0 , ME= FA×c c = (F1(l -a)+ F2(l -b) ) / l
A
FA
CE 830
D
830
B
FB
A
FA
FS,C
C MC
830
A
FA
400
FS,E
C
E ME
830
设FS, ,M 为正剪力正弯矩。
A
FA
FS,C
C MC
830
ΣFy=0, FA-FS,C=0 , FS,C= FA=5×103kN
ΣMC=0, MC - FA×0.43 =0 , MC= 2.15×103kN∙m
悬臂梁受均布载荷作用。
x
试写出剪力和弯矩方程,并
q
l
x
FS
M x
FS x
画出剪力图和弯矩图。
解:任选一截面x ,写出
剪力和弯矩方程
ql
FS x=qx
0 x l
M x=qx2 / 2 0 x l
x
ql2 / 2
依方程画出剪力图和弯矩图
由剪力图、弯矩图可见。最
M
ql2 / 8
大剪力和弯矩分别为
x
第四章 弯曲内力
目录
第四章 弯曲内力
❖ §4-1 ❖ §4-2 ❖ §4-3 ❖ §4-4
❖ §4-5 ❖ §4-6
弯曲的概念和实例 受弯杆件的简化 剪力和弯矩 剪力方程和弯矩方程 剪力图和弯矩图 载荷集度、剪力和弯矩间的关系 平面曲杆的弯曲内力
目录
§4-1 弯曲的概念和实例
起重机大梁
目录
§4-1 弯曲的概念和实例
车削工件
目录
§4-1 弯曲的概念和实例
火车轮轴
目录
§4-1 弯曲的概念和实例
弯曲特点 以弯曲变形为主的杆件通常称为梁
目录
§4-1 弯曲的概念和实例
平面弯曲
对称弯曲 平面弯曲: 弯曲变形后的轴线为平面曲线, 且该
平面曲线仍与外力共面。
目录
§4-1 弯曲的概念和实例
常见弯曲构件截面
目录
§4-2 受弯杆件的简化
FAy
5F 3
Fy 0
2F
FSE
5F 3
FSE
F 3
MO 0
ME
3Fa 2
2F
a 2
ME
5F 3
3a 2
目录
§4-3 剪力和弯矩
FSE
O
ME
FAy
ME
O
FSE FBy析右段得到:
FBy
Fy 0 FSE FBy 0
FSE
FBy
F 3
Mo 0
ME
FBy
3a 2
梁的载荷与支座
•集中载荷 •分布载荷 •集中力偶
固定铰支座
活动铰支座
固定端
目录
§4-2 受弯杆件的简化
目录
§4-2 受弯杆件的简化
吊车大梁简化
均匀分布载荷 简称均布载荷
目录
§4-2 受弯杆件的简化
静定梁的基本形式
FAx
FAy FAx
FAx MA
FAy FAy
简支梁
FBy
外伸梁
FBy
悬臂梁
目录
§4-3 剪力和弯矩
段上任意一点的矩为顺时针
转向时,剪力为正;反之为
负。
截面上的弯矩
使得梁呈凹形为正;
+
反之为负。
目录
FBy
_
_
§4-3
FAy 2. 用截面法研究内力
FSE
O
ME
FAy
剪力和弯矩
例题4-1
解:1. 确定支反力
Fy 0
FAy FBy 2F
MA 0
FBy FBy 3a Fa 2F a
FBy
F 3
设FS, ,M 为正剪力正弯矩。 400 FS,E
A
FA
C
E ME
830
ΣFy=0, FA-FS,E-q×0.4=0 , FS,E= FA - q×0.4 =5×103 - 1.25
×104×0.4 = 0
ΣME=0, ME + q×0.4×0.4/2- FA×0.83=0, ME= FA×0.83-q×0.4×0.4/2=3150kN∙m
FAy=Fb/l FBy=Fa/l
2.写出剪力和弯矩方程
x AC FS x1=Fb / l 0 x1 a
M x1=Fbx1 / l 0 x1 a
CB FS x2 = Fa / l a x2 l
M x2 =Fal x2 / l a x2 l
x 3. 依方程画出剪力图和弯矩图。
目录
§4-4 剪力方程和弯矩方程 剪力图和弯矩图
