对流_扩散方程源项识别反问题的MCMC方法_曹小群
对流扩散方程clank

对流扩散方程clank标题:对流扩散方程的概述引言概述:对流扩散方程是数学中常见的描述物质传输过程的方程。
它在众多领域中都有广泛的应用,如流体力学、热传导、质量传输等。
本文将从五个大点出发,详细阐述对流扩散方程的相关内容。
正文内容:1. 对流扩散方程的基本概念1.1 对流扩散方程的定义1.2 对流扩散方程的一般形式1.3 对流扩散方程的物理意义2. 对流项与扩散项的影响2.1 对流项的作用2.2 扩散项的作用2.3 对流项与扩散项的相互作用3. 对流扩散方程的解析解与数值解3.1 解析解的求解方法3.2 数值解的求解方法3.3 解析解与数值解的比较4. 对流扩散方程的边界条件和初值条件4.1 边界条件的选择与影响4.2 初值条件的确定与影响4.3 边界条件和初值条件的耦合效应5. 对流扩散方程的应用领域5.1 流体力学中的应用5.2 热传导中的应用5.3 质量传输中的应用总结:对流扩散方程是描述物质传输过程的重要方程,其基本概念包括方程的定义、形式和物理意义。
对流项和扩散项是方程中的两个关键因素,它们分别对物质传输起到对流和扩散的作用,并且相互作用影响着传输过程。
对流扩散方程的求解可以采用解析解和数值解两种方法,它们各有优劣,需要根据具体情况选择。
边界条件和初值条件是方程求解中必要的条件,它们的选择与确定对结果有重要影响。
对流扩散方程在流体力学、热传导和质量传输等领域都有广泛应用,它为我们理解和解决实际问题提供了重要的数学工具。
总之,对流扩散方程是一个复杂而重要的数学方程,它在物质传输过程中起着关键作用。
深入理解和研究对流扩散方程,对于解决实际问题具有重要意义。
二维非稳态对流扩散方程反问题的混沌粒子群算法

二维非稳态对流扩散方程反问题的混沌粒子群算法陈亚文;邹学文【摘要】为了求解二维非稳态对流扩散方程的参数反问题,利用有限元方法给出其正问题的求解,将结果作为附加条件,结合混沌局部搜索算法的优点,提出了一种改进的混沌粒子群优化算法.数值模拟结果表明此方法所得到参数反演的数值解与真解误差很小,目标值达到10-4,精度较高.%In order to solve two-dimensional non-steady-state convection-diffusion equation of the parameters inverse problem, using the finite element method to give its positive question solution as additional conditions, and combining with the advantages of chaotic local search algorithm,an improved chaotic particle swarm optimization algorithm is proposed. The simulation result shows that the error between the numerical solution of parameter inversion and the true solution is very small, the target value is up to 10-4. The method has higher accuracy.【期刊名称】《西安工业大学学报》【年(卷),期】2011(031)005【总页数】4页(P470-473)【关键词】群体智能;对流扩散方程;混沌局部搜索;粒子群优化;反问题【作者】陈亚文;邹学文【作者单位】(西安理工大学理学院,西安710054;西安理工大学理学院,西安710054【正文语种】中文【中图分类】TP301.6对流扩散方程描述了物质传输及热传递的综合过程,在水利工程、环境工程及化工、冶金、航空等研究领域里受到了充分重视,因此对流扩散方程的数值求解一直是人们关注的问题之一[1-2].对于其反问题,一般都可归结为一类优化问题,此优化问题一般为多峰值高度非线性优化问题,如何进行有效求解引起了人们广泛重视. 群智能(Swarm Intelligence,SI)作为一种新兴的演化计算技术已成为越来越多研究者的关注焦点,它与人工生命,特别是进化策略以及遗传算法有着极为特殊的联系.群智能在没有集中控制且不提供全局模型的前提下,为寻找复杂的分布式问题求解方案提供了基础.目前,群智能理论研究领域有两种主要的算法,蚁群优化算法(Ant Colony Optimization Algorithm,ACOA)和粒子群算法(Particle Swarm Optimization,PSO).基于对鸟群、鱼群的模拟,Eberhart和Kennedy 于1995年提出粒子群优化算法.这些研究可以称为群体智能[3].PSO最初是处理连续优化问题的,目前其应用已扩展到组合优化问题.由于其简单、有效的特点,PSO已经得到了众多学者的重视和研究.Shi等提出了惯性因子w线性递减的改进算法,大大提高了基本PSO算法的性能.Vanden Bergh通过使粒子群中最佳粒子始终处于运动状态,得到保证收敛到局部最优的改进算法,但其性能不佳.Mendes等研究粒子群的拓扑结构,分析粒子间的信息流,提出了一系列的拓扑结构.Angeline将选择算子引入到PSO中,选择每次迭代后较好的例子并复制到下一代,以保证每次迭代的粒子群都具有较好的性能.文中采用PSO算法与有限元算法相结合的方法,给出了参数反演的数值结果,精度较高,表明算法的可行性和有效性.1 问题的提出考虑二维非稳态对流扩散方程当方程式(1)中的系数k(x,y,t),b1(x,y,t),b2(x,y,t),c(x,y,t),源项 f(x,y,t),初始条件φ(x,y),边界条件φ*(x,y,t)及常数σ为已知时,式(1)就构成了非稳态对流扩散方程的正演问题.假设 b1(x,y,t),b2(x,y,t),c(x,y,t),f(x,y,t),φ(x,y),φ*(x,y,t),σ及β(x,y,t)均为已知函数,再给出附加条件其中h(x,y,t)为已知函数,这样式(1)和式(2)便构成了反演系数k(x,y,t)的数学模型.2 求解方法考虑到h(x,y,t)只能在一些测量点得到,例如它们以T为采样周期,在t=iT (0,1,2,…,I)可以测量得到.并假设φi(x,y)是区域Ω上的基函数,并且令对于适当的n,以一组有限的基函数之和(x,y,t)来逼近k(x,y,t),则该类反问题为从已知的函数及附加条件来确定(x,y,t),由于基函数已定,确定(x,y,t)实际上是确定一个n维向量(a1,a2,…,an).令对应于(x,y,t)定解问题方程式(1)的解记为则反问题[4-5]便可转化为如下的最优化问题[6]ΓIt ={(x,y,t)∈ Γ1,t∈ [0,IT]},把式(3)作为粒子群算法[7]的适应值函数,适时调整参数a1,a2,…,an,使式(3)达到最小,那么就可得到k(x,y,t)的最优逼近解3 混沌粒子群算法混沌粒子群算法是混沌优化和粒子群优化两者的结合.对于给定的优化函数,通过将搜索过程对应为混沌轨道的遍历过程,可使搜索过程具有避免陷入局部极小的能力.将智能算法与经典算法相结合来构造一些高效的新的混合算法是目前解决优化问题的一个重要方向[8].文中的基本思想是采取混沌粒子群算法与有限元方法相结合求解二维非稳态对流扩散方程反问题,循环使用PSO算法与有限元方法,直到满足预定的优化目标为止. 混沌粒子群算法中涉及到混沌局部搜索算法(Chaotic Local Search,CLS),CLS的算法步骤为① 令k=0,将决策变量,j=1,2,…,n,按下式映射为0到1之间的混沌变量其中xmax,j和xmin,j分别为第j维变量的搜索上下界;② 计算下步迭代的混沌变量③ 将混沌变量转换为决策变量④ 根据决策变量对新解进行评价,若新解优于初始解X(0)=[,,…,]或者混沌搜索已达到最大迭代步数,将新解作为CLS的搜索结果,否则置k=k+1,转②.混沌搜索算法通常需要大量的迭代步数才可获得较好的解,且对初始解十分敏感,为了克服混沌搜索的缺点,将PSO算法与混沌搜索相结合,得到混沌粒子群算法.PSO算法只用于全局搜索,而CLS则根据PSO的结果进行局部搜索.混沌粒子群算法的步骤为① 设置当前参数,N为粒子数目;c1为学习因子1;c2为学习因子2;w为惯性权重;M为最大迭代次数;D为问题的维数;bound为位置的范围;v(i,j)为粒子的位置;xmax为自变量搜索域的最大值;xmin为自变量搜索域的最小值;maxC为混沌搜索的最大步骤.②随机初始化种群中各微粒的位置和速度.用下式初始化种群中各微粒的位置:③ 评价每个微粒的适应度,将当前各微粒的位置和适应值存储在各微粒的pbest 中,将所有pbest中适应值最优个体的位置和适应值存储于gbset中;④ 用下式更新每个微粒的速度和位置;⑤ 计算每个微粒的目标函数值,然后保留群体中性能最好的20%的微粒;⑥对群体中的最佳微粒执行混沌局部搜索,并更新其gbest及群体的gbest;⑦ 满足停止条件(通常为预设的运算精度或迭代次数),搜索停止,输出结果,否则转⑧;⑧ 按下面的式子收缩搜索区域其中xg,j为当前pbest的第j维变量的值;⑨ 在收缩后的空间内随机产生群体中剩余的80%的微粒,转③.在上面的混沌搜索的算法过程中,为了保持种群的多样性,加强搜索的发散性,在保留一定数量优秀微粒的同时,算法根据群体的最佳位置动态收缩搜索区域,并在收缩区域内随机产生微粒来替代性能较差的微粒.4 数值模拟数值模拟时,预先给出参数k(x,y,t)的真值,并求解正问题,计算出相应的附加条件,然后反求其参数.文中采用有限元法求解正问题.在单位矩形Ω=[0,1]×[0,1]上,考虑方程为时间采样分别取为t=0.2,t=0.5,即I=2,0<t<1,空间变量y的离散步长取为0.05.给定k(x,y,t),可通过有限元法求出u|x=1 =h(1,y,t),并把它作为附加条件.文中给定k(x,y,t)=5+3x+3y+5t.此时混沌粒子群算法的适应值函数可取为用a1+a2x+a3y+a4t逼近k(x,y,t),-6<ai <6,a1,a2,a3,a4 为反演参数,数值模拟中参数设置为N =60,c1=2,c2=2,w=0.8,M =200,D=4,xmax = 10*ones(1,4),xmin =-10*ones(1,4),maxC=100,模拟结果见表1.表1 参数反演结果Tab.1 Results of parameter inversion由表1的结果可以看出,利用混沌粒子群算法所得到参数反演的数值解与真解误差很小,说明文中算法在求解此类问题中是可行、有效的.5 结论文中在基本的粒子群算法的基础上,成功的将其与有限元方法相结合,在求解二维非稳态对流扩散方程反问题上显示了该算法的优越性,并且在数值模拟中也进一步说明了:文中提出的算法对偏微分方程反问题均适用,该算法可以更快、更稳定地收敛到问题的全局最优解.文中考虑的是对流扩散方程系数反问题,鉴于所提算法的良好的优化性能,下一步考虑将它应用到初始条件和边界条件反问题的求解中.【相关文献】[1]章争荣,张湘伟.对流扩散方程的数值流形格式及其稳定性分析[J].西安交通大学学报,2010,44(1):117.ZHANG Zheng-rong,ZHANG Xiang-wei.Numerical Manifold Scheme for Convection Diffusion Equation and Its Stability Analysis[J].Journal of Xi’an Jiaotong University,2010,44(1):117.(in Chinese)[2]陈翠霞,张小峰.求解一维对流扩散方程的一种新方法[J].武汉大学学报:工学版,2010,43(1):10.CHEN Cui-xia,ZHANG Xiao-feng.A New Solution to One-dimensional Convection-diffusion Equation[J].Journal of Wuhan University:Engineering Science Edition,2010,43(1):10.(in Chinese)[3]NATSUKI H.Particle Swarm Optimization with Gaussian Mutation[C]//In Proceedings of the IEEE Swarm Intelligence Symposium.Indianapolis,Indiana,USA,2003:72.[4]Dinh Nho Hào,Reinhardt H J.On a Sideways Parabolic Equation[J].Inverse Problems,1997,13(4):297.[5]Charles L,Karr I,Yakushin,K N.Solving Inverse Initial-value,Boundary-value Problems Via Genetic Algorithm[J].Engineering Applications of Artificial Intelligence,2000,13(6):625.[6]吴志健,康立山,邹秀芬.一种解函数优化问题的精英子空间演化算法[J].计算机应用,2003,23(2):13.WU Zhi-jian,KANG Li-shan,ZOU Xiu-fen.An Elitesubspace Evolutionary Algorithm for Solving Function Optimization Problems[J].Computer Applications,2003,23(2):13.(in Chinese)[7]魏静萱,王宇平.求解约束优化问题的改进粒子群算法[J].系统工程与电子技术,2008,30(4):739.WEI Jing-xuan,WANG Yu-ping.Smooth Scheme and Line Search Based Particle Optimization for Constrained Optimization Problems[J].Systems Engineering and Electronics,2008,30(4):739.(in Chinese)[8]袁益让,杜宁,王文洽,等.非线性多层渗流系统的数值方法及其应用[J].应用数学和力学学报,2006,27(11):1319.YUAN Yi-rang,DU Ning,WANG Wen-qia,etal.Numerical Method and Application for the Three-dimensional Nonlinear System of Dynamics of Fluids in Porous Media[J].Applied Mathematics and Mechanics,2006,27(11):1319.(in Chinese)。
二维非稳态对流扩散方程反问题的混沌粒子群算法

41 7
( ,)边界条件 ( , £ 及常数 为已知时 , z3 , , z , ) 式() 1 就构 成 了非稳 态对 流 扩散 方 程 的正演 问题 .
假 设 b( Y ,2z, ,( ,)f( Y,) lz, ,)b( ,)cx, £ , x, £ , ( ) ( Y,)a p x, ,)均 为 已知 函数 , z, , z, £ , ̄ ( Y 再给 出附 加条件 “I = h x, = ( Y,) = () 2
第 3 卷第 5 1 期 21 年 1 01 月 西安工
业
大
学
学
报
Vo. 1No 5 13 .
Oc. 0 1 t2 1
J u n l f ’n Te h oo ia iest o r a a c n lgc l o Xi Unv ri y
文章编 号 : 1 7 — 9 5 2 1 ) 54 00 6 39 6 (0 1 0 —7— 4
二维 非稳 态 对 流扩 散 方程 反 问题 的混 沌 粒子 群 算 法
陈亚 文,邹学文
( 西安 理工 大学 理学 院, 西安 70 5 ) 10 4
摘
要: 为了求解二维非稳 态对流扩散方程的参数反 问题 , 利用有限元方法给出其正问题的
求解 , 结 果作 为附加 条件 , 将 结合 混沌局部搜 索算 法的优 点 , 出 了一种 改进 的混 沌 粒子 群 优 提
,
群、 鱼群 的模 拟 , ehr Ebrat和 Ken d n ey于 19 95年
提 出粒子群 优化算法. 这些研究可 以称 为群体智
能[. S 3 P O最初是处理连续优化问题的, ] 目前其应 用 已扩展到组合优化 问题. 由于其简单 、 有效 的特
对流扩散方程的一种基于界面罚条件的非重叠区域分解法

对流扩散方程的一种基于界面罚条件的非重叠区域分解法曹丹;肖勇【摘要】应用基于界面罚条件的非重叠区域分解法求解稳态对流占优的对流扩散方程,分析了该方法的相容性,并对其有限元解进行了误差估计,证明当将罚参数ε选取得足够小时,用k阶有限元空间来逼近弱解空间,能得到最优阶的误差估计。
%We applied a non-overlapping domain decomposition method via a penalization on the interface to convection-dominated convection-diffusion equations and analyzed its consistency. And the finding is that the error estimates are optimal when used finite elements of degree k and set the parameter ε small enough.【期刊名称】《铜仁学院学报》【年(卷),期】2014(000)004【总页数】5页(P152-156)【关键词】非重叠区域分解法;对流扩散方程;罚条件;有限元;误差估计【作者】曹丹;肖勇【作者单位】湖南农业大学东方科技学院,湖南长沙 410001;湖南农业大学东方科技学院,湖南长沙 410001【正文语种】中文【中图分类】O2411.引言区域分解法是一类数值求解偏微分方程的有效方法,它基于分而治之的思想,将求解区域分解成若干个形状相对规则的子域,然后在各子域中分别求解问题[1]。
本文以稳态对流扩散方程为基本模型,讨论一种基于界面罚条件的非重叠区域分解法。
问题描述如下[2]:其中υ为扩散系数。
本文仅讨论区域Ω为二维的情形,并将边界取为齐次边界条件,对于非齐次边界条件,我们可以得到类似的结论。
为保证方程的解存在且唯一,假设其中的系数满足以下条件:2.基于罚条件的非重叠区域分解法的有限元格式构造2.1.预备知识有限元解实际上是微分方程弱形式的解在有限维空间的投影。
一类对流-扩散方程源项反问题的数值解法

同伦摄 动方 法[ 有别 于传统 的摄 动方 法 , 1 它不依 赖小参 数 , 而是应 用 同伦技 术 , 造 一个 含嵌 入参 数 p 构
∈[ ,] 0 1 的方 程 , 然后把 嵌人参 数作 为小参 数. 这种方 法 既克服 了传统 摄 动理论 的不 足 , 充分应 用 了各 种摄 又 动方法 . 文献 EJ 用 同伦摄 动方法 求解 了 B r es 程 和 Kotwe —eVr s方 程 的解 ;文献 E J利用 同 3利 ugr 方 re gd i e 4 伦摄动方 法分 别求解 了一类 非齐 次抛 物型偏 微分 方程 和一类 非线 性偏 微 分方 程 的解 ;文献 E 3利用 同伦 摄 s
f x,) 问题 称 为源项 识别 问题. ( 的
反演 f x,) 往要增 加其 他 附加 条件 , ( £往 比如通过 终值 条件 “( , )或 边界上 的观 测值 “( ,) 柏来 z T ,z £ l
反演 f x,) 一般来 说 , 定 f x,)的反问题 是非 线性 的 , 文采用 的附加 条件 为 终值 条件 ( , ) 对实 ( . 决 ( 本 zT.
Vo . 9 NO 6 13 .
NO V. 2 0 01
一
类对 流 一扩 散 方程 源项 反 问题 的数 值 解 法
阮周 生 ,王 泽 文 ,何 杰
( 华理 工 大 学 数 学与 信 息科 学 学 院 , 西 抚 州 34 0 ) 东 江 4 0 0
摘
要 : 用 函数 逼 近 与 同伦 摄 动 方 法 , 一 类 对 流 一 扩 散 方 程 源 项 识 别 问 题 转 化 为 分 布 参 数 系 统 的 最 优 利 将
MCMC方法介绍

MCMC方法介绍MCMC(Markov Chain Monte Carlo)方法是一种统计模拟方法,可用于高维参数空间中的复杂问题。
它结合了Markov链和Monte Carlo方法,通过生成一个与所需分布相关的马尔科夫链来近似分布的抽样。
MCMC方法的核心思想是利用马尔科夫链的收敛性质来模拟概率分布。
该方法通过选择一个合适的初试状态并定义一个状态跳转规则,使马尔科夫链足够接近所需分布,从而得到分布的近似抽样。
具体而言,MCMC方法通过以下几个步骤实现:1.选择一个初始状态:从分布中随机选择一个初始状态作为马尔科夫链的初始状态。
2. 定义状态跳转规则:定义一种状态跳转规则,使得从当前状态到下一个状态的转移满足其中一种概率分布。
常见的状态跳转规则有Metropolis-Hastings算法和Gibbs采样算法。
3.进行状态跳转:根据状态跳转规则,从当前状态跳转到下一个状态。
这个过程是基于马尔科夫链的收敛性质,在连续的状态跳转过程中逐渐逼近所需分布。
4.迭代状态跳转:迭代进行状态跳转,直到马尔科夫链收敛到稳定的状态。
稳定状态将近似表示所需分布。
1.贝叶斯推断:MCMC方法可用于贝叶斯推断中的参数估计和模型选择。
通过构建参数的后验概率分布,利用MCMC方法对参数空间进行抽样,可以获得参数的近似后验分布和模型的边缘似然分布。
2.隐马尔科夫模型:MCMC方法可以用于隐马尔科夫模型的参数估计和状态推断。
通过定义状态跳转规则和观测概率分布,MCMC方法可以从观测数据中推断出隐含的状态和模型参数。
3.概率图模型:MCMC方法在概率图模型中的应用比较广泛,如贝叶斯网络、马尔科夫随机场等。
通过定义状态转移规则和随机潜在变量的条件概率分布,MCMC方法可以从给定数据中对潜在变量进行抽样,从而进行模型推断和学习。
4.高维积分:MCMC方法可用于高维积分的近似计算,如计算多维积分、求解期望值等。
通过构建状态转移规则和定义目标概率分布,MCMC 方法可以将积分问题转化为马尔科夫链上的状态转移问题,从而使用蒙特卡洛方法进行近似计算。
第五章对流扩散问题(假扩散)
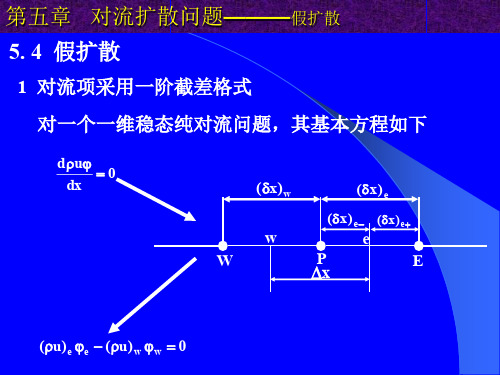
该问题的数值解如下:
1 n i
u t n u t n (1 ) i i 1 x x
MUD : du d ux d (( ) ) dx dx 2 dx
第五章 对流扩散问题———假扩散
由图可以看出,在区间 P 2 ,中心差分格式预报的 P 值优于迎风格式的预报值。对比这两种格式,其扩散项 的处理是完全相同的,所不同的仅仅是对流项的处理上 ,在中心差分格式中对流项的差分格式具有二阶精度, 而在迎风格式中对流项的差分格式只具有一阶精度。在 区间 P 2 ,两种格式预报 P值所表现出的差异性恰恰是 这两种格式精度不同的体现。观察上图,迎风格式所预 报的 P值具有该高不高和该低不低的特点,这一特点正 是由一阶精度迎风格式所引起的扩散系数为 ux / 2 的 假扩散项造成的。也反映了假扩散项的影响。
n n ux ut 2 n ( ) i u( ) i (1 )( 2 ) i O( x 2 , t 2 ) t x 2 x x
由此可以看出,我们前边得到的差分方程所逼近的是 一个非稳态对流扩散问题,而非原型问题所要求的非 稳态对流问题。
第五章 对流扩散问题———假扩散
1 n (1 P
ut n ut n ) P W x x
用编号法表示
1 n i
1 n , n 在点 (i, n) i i 1
u t n u t n (1 ) i i 1 x x
做Taylor展开
n n u 2 n 1 2 n ( ) i u( ) i ( 2 ) i x ( 2 ) i t O( x 2 , t 2 ) t x 2 x 2! t
第五章 对流扩散问题———假扩散
将 i 1 和 i 1 台劳 级数展开代入
氮素转化模型_mcmc算法_概述说明以及解释

氮素转化模型mcmc算法概述说明以及解释1. 引言1.1 概述在当今科学研究中,模型的应用已经成为一种普遍的方法,氮素转化模型是其中具有重要意义的一个领域。
氮素转化模型可以帮助我们更好地理解和预测氮素的转化过程,对于农业生产、环境保护和生态系统管理等方面具有重要的实际应用价值。
MCMC算法则是在统计建模和贝叶斯分析中常用的方法之一。
通过利用随机采样方式和马尔可夫链蒙特卡洛(MCMC)采样技术,MCMC算法可以对复杂的概率模型进行推断和参数估计。
在氮素转化模型中应用MCMC算法可以提供关键性的参数估计结果,并为进一步研究和改进提供基础。
本文旨在对氮素转化模型和MCMC算法进行综述,并详细解释了它们之间的关系以及如何应用于氮素转化模型中。
1.2 文章结构本文主要分为五个部分:引言、氮素转化模型、MCMC算法概述、氮素转化模型的MCMC算法解释以及结论部分。
在引言部分,我们将简要介绍本文的研究内容,包括对氮素转化模型和MCMC 算法的概述。
同时还将阐明文章的结构,以便读者更好地理解全文组织和内容安排。
在氮素转化模型部分,我们将详细定义和背景知识,介绍氮素转化模型的原理和应用领域。
通过深入了解氮素转化过程和相关模型,有助于读者对后续章节的理解和技术方法的应用。
在MCMC算法概述部分,我们将介绍MCMC的基本概念、算法步骤以及其在实际案例中的应用。
这一部分作为后续章节中MCMC算法与氮素转化模型结合的基础,将为读者提供必要的背景知识。
在氮素转化模型的MCMC算法解释部分,我们将详细探讨MCMC算法在氮素转化模型中的具体应用,并解释参数估计方法及实现过程。
此外,我们还将讨论该算法存在的优势和局限性。
最后,在结论部分,我们会对全文进行总结回顾,并展望未来研究中可能存在的发展方向和挑战。
1.3 目的本文的主要目的是概述氮素转化模型和MCMC算法,并解释它们之间的关系以及如何应用于氮素转化模型中。
通过本文的阐述,读者能够对氮素转化模型和MCMC算法有一个全面且深入的了解,并理解其在科学研究和实际应用中的重要性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DOI:10.3969/j.issn.1000-4874.2010.02.001水动力学研究与进展A辑2009年第2期 1281 引言对流-扩散方程是描述粘性流体运动的非线性Burgers方程的线性化模型,它可以刻画许多自然现象,如:水体和大气中污染物的输移、扩散和降解,海水盐度和温度的扩散,流体流动与传热和电化学反应等。
研究对流-扩散模型具有重要的理论价值和实际意义,它已经广泛应用于环境科学、能源开发、流体力学和电子科学等领域。
总的来说,目前关于对流-扩散方程的研究大致可以分为两个方面。
一方面是在给定初边值条件下,通过不同的数值计算方法求解对流-扩散方程,以模拟研究对象(例如:温度、盐度和污染物等)在时间和空间上的发展演化,这类问题可以统称为正问题。
迄今为止已经有很多成熟方法求解对流-扩散方程,如有限差分方法(FDM)[1,2,3]、有限体积方法(FVM)[4,5,6]和有限元方法(FEM)[7,8,9]等。
另外一方面是关于对流-扩散方程反问题的研究,即通过所研究对象的观测资料来估计和识别方程中的参数、源项、边界和初始条件等。
从某种意义上讲,反问题的求解是对流-扩散模型研究中一个更重要的问题,因为它的正确与否直接影响模型的可靠性。
由于偏微分方程反问题固有的非线性和不适定性[10], 对流-扩散方程反问题的求解会存在巨大困难,通常的方法常常导致求解失败。
近年来, 国内外学者关于对流-扩散反问题开展了广泛研究。
Andreas Kirsch对一维扩散方程逆过程反问题进行了稳定性分析,并给出了误差估计公式[11]。
Yildiz[12]、刘继军等[13-16]对相关问题采用Tikhonov 正则化方法进行了深入研究。
闵涛等[17]以函数逼近和Tikhonov正则化为基础,利用算子识别摄动法和线性化技术,建立了河流水质纵向弥散系数反问题的迭代算法,并进行了数值试验。
闵涛等[18]利用有限元法求解了二维稳态对流-扩散方程,并利用迭代法对二维稳态对流-扩散方程参数反演进行了研究。
闵涛等[19]利用遗传算法就对流-扩散方程的源项识别反问题进行了研究。
潘军峰等[20]对一维对流-扩散方程的反问题利用Tikhonov正则化方法进行了研究。
吴自库等[21]结合利用伴随同化方法和处理数学物理反问题的技巧就对流-扩散方程逆过程的反问题进行了数值研究。
综上所述,由于对流-扩散方程反问题的不适定性,所以它的求解一般要采用特殊方法,如Tikhonov正则化方法、变分伴随方法和遗传算法等等。
本文在贝叶斯理论的基础上,提出采用马尔科夫链蒙特卡罗(Markov Chain Monte Carlo,简称MCMC)方法[22,23]来识别对流-扩散方程中多个点源中的未知参数。
结合利用贝叶斯方法和MCMC算法求解反问题,具有以下优点:1) 能方便地将各种先验信息和误差信息高效地融合到问题求解过程中,减小问题的不确定性;2) 和确定性算法不同,反问题的不适定性不再是MCMC算法要考虑的问题,且计算获得的是全局最可能解,而通常的最优化算法可能陷入目标函数局部极小值;3) 能对定义在高维空间且无明确数学表达式的概率分布密度函数进行数值计算,而确定性方法无法解决此类问题;4) MCMC算法通过构造Markov链来进行随机模拟,是一种动态Monte Carlo方法,计算速度高于一般的Monte Carlo 方法和模拟退火算法,而且计算复杂度不依赖于计算空间的维数。
2 反问题模型不失一般性,用对流-扩散方程来模拟污染物在河道中的扩散,考虑对流-扩散方程的初边值问题[19,21],公式如下:221(),(,)(0,)(0,) (0,)0,(,)0,(0,)(,0)0,(0,)qi iiC C Cu E kC s x xt x xx t L TC t C L t t TC x x Lδ=⎧∂∂∂+=−+−⎪∂∂∂⎪⎪∈×⎨⎪==∈⎪=∈⎪⎩∑(1)其中C为污染物的浓度,u为流速,E为扩散系数,k为污染物的降解率,L表示河道长度。
δ是狄拉克函数,ix和is,(1,2,)i q= 分别表示多个点污染源的位置和排放强度。
假定(,)C x t在t T=时的分布已知,那么源项识别反问题就是根据这些已知distribution, the Adaptive Metropolis algorithm was used to construct the Markov Chains of unknown parameters. And the converged samples were used to estimate the unknown parameters of source term. The results of numerical experiments show that the method has many virtues, such as high accuracy, quick convergent speed and easy to program and implement with computer.Key words: convection-diffusion equation; source term; inverse problem; Markov Chain Monte Carlo method曹小群,等:对流-扩散方程源项识别反问题的MCMC 方法129的浓度分布观测来确定源项1()qiii s x x =δ−∑,即确定多个点污染源的位置和排放强度。
反问题在求解过程中通常需要将未知参数向量的估计值映射成观测空间的值,这就需要获得正问题的解算子。
本文采用的是Fourier 方法来求解对流-扩散方程,闵涛等[18]和吴自库等[21]分别采用相同的方法对系统(1)进行了求解。
首先引入下面的函数变换2(/2/4)(,)(,)e ux E u t E C x t V x t −= (2)将其代入(1)中,则(1)可转化为等价的定解问题:22(/4/2)21e()(0,)0(,)0(,0)0qu t E ux E i i i V V E kV s x x t x V t V L t V x −=⎧∂∂=−+δ−⎪∂∂⎪⎪=⎨⎪=⎪=⎪⎩∑ (3)由于方程组(3)的特征值和特征函数分别为2(π/)n n L λ= 和()sin(π/)n x n x L ϕ=,(1,2,)n =因此可利用特征函数展开法求解方程(3)。
令1(,)()()n n n V x t T t x ϕ∞==∑ (4)将(3)中第一式的右端源项也利用特征函数进行展开:2(/(4)/(2))11e ()()q u t E ux E i i n n i n s x xf x ϕ∞−==δ−=∑∑ (5)其中2(/(4)/(2))012e ()()d qL u t E ux E n i i n i f s x x x x L ϕ−==δ−=∑∫2(/(2))412e (e ())i u q t ux E E i n i i s x L ϕ−=∑将(4)和(5)式代入(3)式中,则可求得()n T t 的解为2[]/(4)2()[e e ]/(4)n t k u t E n n B T t u E kλλ−+=−++ (6) 其中/(2)12e ()i qux E i n i i B s x L ϕ−==∑将(6)式代入(4)式中,可以求出方程组(3)的解,然后将其代入(2)式中,最后求得方程组(1)的解为2()2()124212e ()(,)e/(4)i uxqE ux u t i n i i E En n s x L C x t u E kϕλ−∞−===++∑∑i2()[]4[ee ]()n u t t k En x λϕ−+− (7)为了下面表示方便,(7)式可以简化成函数映射关系1212(,)(,,,,,,,,,)q q C x t x t x x x s s s == M(,,)x t M m (8)其中M 表示对流-扩散方程(1)的解算子,m 表示由多个点污染源的位置i x 和排放强度i s ,(1,2,)i q = 构成的需要识别的未知向量。
在实际数值计算中通常要对解算子M 进行截断,截断阶数用N 表示。
3 MCMC 方法在贝叶斯统计理论中,将观测数据采集前所有关于未知参数向量m 的先验信息概率表述为先验分布()p m 。
获取观测后,根据对观测概率分布规律的了解,使用贝叶斯公式可将未知参数的先验分布改进为后验分布()p m |d ,即()()()()p p p p =m d d m m d (9)水 动 力 学 研 究 与 进 展 A 辑2009年第2期130其中(|)p d m 表示观测的条件概率密度。
d 是长度为M 的观测向量,本文中可表示为12(,,,)T Mobs obs obs C C C = d它包含了污染物在T 时刻不同位置的浓度观测。
因为观测数据已经给出,所以()p d 是一个与m 无关的常数,于是(9)式可写成()()()p p p ∝m d d m m (10)(10)式是进行贝叶斯推理的基础,通过它理论上可以获得参数的任何统计矩,如:每个参数的均值、方差和其它高阶统计量。
但实际应用中会遇到巨大困难:一方面除了非常简单的情况,后验概率密度都不存在明确的数学表达式;另一方面,采用通常的数值积分方法(如:Monte Carlo 方法)时,计算量将随未知向量维数的增加而呈指数增长。
因此贝叶斯方法几乎不能直接解决实际问题。
但是近期发展的马尔可夫链蒙特卡洛(MCMC)方法使得这种情况得到改善。
MCMC 算法可以对定义在高维随机向量空间上无明确数学表达式的概率分布p 进行抽样,其基本思想是产生大量服从分布p 的随机向量序列12I {,,,}L m m m ,其中I 为抽样数[22]。
如果向量序列满足马尔可夫性质:向量1i +m 的产生仅依赖于前一个向量i m ,而与1,2,,1i i −− 步骤的状态向量121,,,i i −− m m m 都无关,则该向量序列称为马尔可夫链。
马尔可夫性质的另一种描述是:若抽样算法当前访问的是j m 点,则下一步访问另一点i m 的概率只依赖于 j m ,而与先前访问的点无关。
马尔科夫性质意味着抽样算法完全可由转移概率矩阵P 描述,矩阵元素 ij p 表示算法在当前访问 j m 的条件下接着将要访问 i m 的条件概率。
按照构造Markov 链所用转移概率矩阵的不同,MCMC 方法的主要抽样算法有:Gibbs 抽样算法[24]、Metropolis-Hastings 算法[25]和自适应 Metropolis 算法[26]。
