中国基尼系数的估算研究重点
基尼系数分析报告
基尼系数分析报告一、引言基尼系数是衡量收入或财富分配不均的指标，它是一种统计量，可以从0到1之间进行取值，其中0代表完全的财富均等，1代表完全的财富不均。
基尼系数的计算公式如下：基尼系数=1-∑(分配比例i)^2本报告将通过对国家的数据进行基尼系数分析，以评估该国家的收入或财富分配情况。
二、数据收集与处理在本次分析中，我们选择了国家的收入数据进行分析，数据来自于该国家的统计部门，并且覆盖了多个层次和地区。
通过对这些数据进行整理和处理，我们得到了该国各个层次和地区的收入数据。
三、分析结果根据我们的数据分析，我们得出了该国家的基尼系数为0.45、根据基尼系数的取值范围，我们可以得出结论：该国家的收入分配存在一定程度的不均衡，但尚未达到严重不均的程度。
四、原因分析收入分配不均的原因有多种，以下是一些通常的原因分析：1.教育水平不同：教育水平的差异可能导致技能和知识的不均衡，限制个人的职业选择和收入水平。
2.劳动力市场状况：就业机会的不平等和薪酬水平的差异可能导致收入不均衡。
一些行业可能拥有更多的高薪就业机会，而其他行业可能只能提供低薪工作。
3.财富积累：一些个人或家庭可能通过投资和资产积累来获得更多的财富，而其他人可能没有这样的机会。
这种财富的差距会导致财富分配的不均衡。
4.政府政策：政府的税收和福利政策可能对收入分配产生影响。
一些政策可能会增加收入不平等，而其他政策可能会减少收入差距。
五、政策建议为了解决收入分配不均的问题，以下是一些建议：1.教育政策：投资于教育，提供公平的教育机会，让更多人有机会获得高质量的教育。
通过提高教育水平和培养更多的技能，可以提高个人的就业机会和收入水平。
2.劳动力市场政策：改善就业机会的平等性，通过减少就业歧视、提高最低工资水平和改善劳动法律来促进收入均等。
此外，还可以提供培训和职业指导，帮助人们提高就业能力。
3.税收和福利政策：通过调整税收系统和福利政策，减少收入不平等。
关于中国基尼系数的研究
西南财经大学第八届文献综述大赛按城乡分解我国居民收入基尼系数的研究摘要：本文介绍了按不同分组分解基尼系数的各种方法，探讨了它们之间的内在联系。
在此基础上根据按城乡分解基尼系数的方法计算了自1996年至2006年的中国基尼系数。
计算结果表明城乡之间的收入不平等是全国收入不平等的决定性因素，据此本文提出了相关的政策建议。
关键词：中国基尼系数基尼系数的分解城乡之间收入不平等城镇化The Studies on the Decomposed Chinese Gini Coefficient by Urban/Rural ResidentsAbstract: this paper introduces different approaches on decomposition of the Gini ratios based on different groups, the paper also probes the internal relationships among these methods, on the basis of the approach of decomposition the Gini ratios by rural/urban divide, the author calculates the Chinese Gini ratios from 1996 to 2006. The results indicate that the current dominant factor in the Chinese Gini coefficient is the Gini coefficient between rural and urban areas. In the light of above analyses, the author presents some suggestions for policy-makers.Keywords: The Chinese Gini Coefficient Decomposition of the Gini Coefficient Urban-rural Income Disparity UrbanizationJEL Classification: D63; I30按城乡分解我国居民收入基尼系数的研究一、引言衡量收入不平等的标准有很多，如泰尔-L指数（Theil-L）、变异系数、平均离方差（又称库茨涅茨指数）和基尼系数等。
基尼系数分析
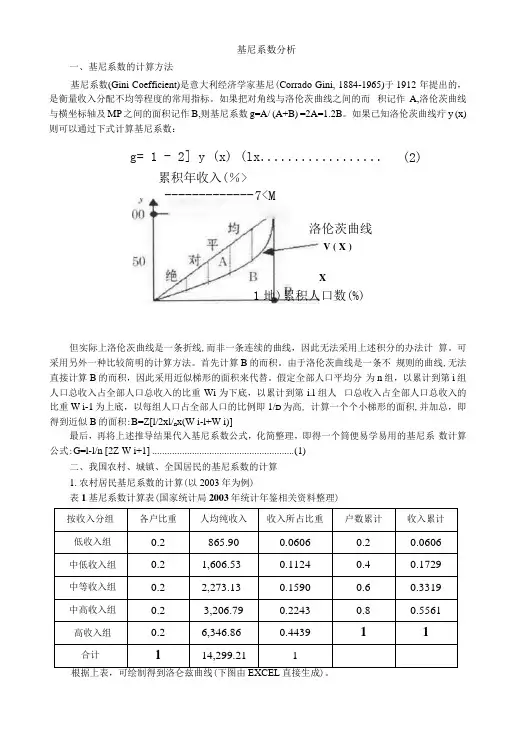
基尼系数分析一、基尼系数的计算方法基尼系数(Gini Coefficient)是意大利经济学家基尼(Corrado Gini, 1884-1965)于1912 年提出的，是衡量收入分配不均等程度的常用指标。
如果把对角线与洛伦茨曲线之间的而积记作A,洛伦茨曲线与横坐标轴及MP之间的面积记作B,则基尼系数g=A/ (A+B) =2A=1.2B。
如果已知洛伦茨曲线疔y (x)则可以通过下式计算基尼系数：g= 1 - 2] y (x) (lx (2)累积年收入(％>------------- 7<M洛伦茨曲线V ( X )X1地)累积人口数(%)但实际上洛伦茨曲线是一条折线,而非一条连续的曲线，因此无法采用上述积分的办法计算。
可采用另外一种比较简明的计算方法。
首先计算B的而积。
由于洛伦茨曲线是一条不规则的曲线,无法直接计算B的而积，因此采用近似梯形的面积来代替。
假定全部人口平均分为n组，以累计到第i组人口总收入占全部人口总收入的比重Wi为下底，以累计到第i.l组人口总收入占全部人口总收入的比重W i-1为上底，以每组人口占全部人口的比例即1/D为高, 计算一个个小梯形的面积,并加总，即得到近似B的面积:B=Z[l/2xl/n x(W i-l+W i)]最后，再将上述推导结果代入基尼系数公式，化简整理，即得一个筒便易学易用的基尼系数计算公式:G=l-l/n [2Z W i+1] (1)二、我国农村、城镇、全国居民的基尼系数的计算1.农村居民基尼系数的计算(以2003年为例)表1基尼系数计算表(国家统计局2003年统计年鉴相关资料整理)按收入分组各户比重人均纯收入收入所占比重户数累计收入累计低收入组0.2 865.90 0.0606 0.2 0.0606中低收入组0.2 1,606.53 0.1124 0.4 0.1729中等收入组0.2 2,273.13 0.1590 0.6 0.3319中高收入组0.2 3,206.79 0.2243 0.8 0.5561高收入组0.2 6,346.86 0.4439 11合计114,299.21 1根据上表，可绘制得到洛仑兹曲线(下图由直接生成)。
中国基尼系数的未来走势
中国基尼系数的未来走势1. 前言2. 基尼系数的概念和计算方法3. 中国基尼系数的历史走势和现状4. 影响中国基尼系数的因素及趋势分析5. 对中国基尼系数未来走势的预测和对策建议6. 案例分析7. 结论2.1 基尼系数的概念和计算方法基尼系数是一种用来度量一个国家或地区收入不平等程度的指标，其取值范围为0到1之间。
如果基尼系数等于0，则表示该国或地区的收入分配是完全公平的，反之则表示收入的分配越不平等。
基尼系数的计算方法非常简单，首先将一个地区的居民按照收入的大小进行排序，并将人口比例和收入比例相乘，然后将所有的乘积加总得到一个总和，最后将这个总和除以总人口，就得到了该地区的基尼系数。
3.1 中国基尼系数的历史走势和现状在改革开放之前，中国的基尼系数一直维持在一个极低的水平，一直到1980年代才开始逐渐增加。
随着中国在经济发展方面取得的巨大进步，基尼系数在1990年代和2000年代开始迅速上升，一直到2010年左右才趋于稳定。
目前，中国的基尼系数为0.467，略高于世界平均水平（0.39左右）。
4.1 影响中国基尼系数的因素及趋势分析中国基尼系数的上升主要是由于以下几个因素造成的：1）城乡收入差距。
中国的城乡人口比例是3：7，而城市居民的收入普遍较高，导致城乡收入差距较大。
2）行业和职业收入差距。
经济发展带来的巨大机遇和挑战，使得各行各业的收入出现了明显的差异，高技能人才和高质量蓝领工人的收入普遍较高，而一些传统行业和劳动密集型产业的工资低于平均水平。
3）地域收入差距。
由于中国地大物博，地理差异产生了巨大的收入差距，一些西部地区和贫困地区的经济发展水平明显低于东部沿海地区。
5.1 对中国基尼系数未来走势的预测和对策建议对于中国基尼系数未来的走势，我们认为可能出现以下趋势：1）随着城市化进程的加速和农村经济的发展，城乡收入差距将逐渐缩小。
2）政府将加大扶贫力度和产业扶贫，减少地域收入差距。
3）加强职业教育和技能培训，逐步缩小行业和职业收入差距。
基尼系数的计算方法与中国的基尼系数估计
文/更远大侠 基尼系数是 20 世纪初意大利经济学家基尼，根据劳伦茨曲线所定义的判断 收入分配公平程度的指标。是比例数值，在 0 和 1 之间，是国际上用来综合考察 居民内部tm） 基尼系数是反映一组数据离散程度的指标，其功能类似于标准差。基尼系数 （或标准差）越大，那么平均指标（以平均数为代表，还包括中位数与众数）对 于一组数据的代表性越差；基尼系数（或标准差）越小，则平均指标对于一组数 据的代表性越好。（参见任何一本统计学教材） 基尼系数的计算依赖于洛伦茨曲线。下面先介绍洛伦茨曲线，再介绍基尼系 数的计算。
三、基尼系数的定义
基尼系数定义为洛伦茨曲线与绝对平均线之间的面积与三角形 OKE 面积的 比例。如图 3 所示：
洛伦茨曲线
100 90 80 70
绝对平均线 洛伦茨曲线
E J H G F A
20
财富比例
60 50 40 30 20 10
X C
D Y K
80 100
B
40 60
O0
0
人口比例
基尼系数＝X/(X+Y)＝OABCDEJHGFO 的面积/三角形 OKE 的面积 显然，基尼系数应该在[0,1]这个区间之中。当洛伦茨曲线是绝对平均线时， 洛伦茨曲线与绝对平均线围成的面积就是 0，从而此时基尼系数等于 0，这就是 财富绝对平均分配时的基尼系数。当财富分配绝对不平等，即所有财富只集中在 一个人手里时，洛伦茨曲线就是折线 OKE，这时候的基尼系数就等于 1，因为这 时候洛伦茨曲线与绝对平均线之间的面积就等于三角形 OKE 的面积了。
700
X
A B
300
O
0在上图中，已知“0.4%的中国人占有 70%的财富”，则洛伦茨曲线为 OAE 折 线。其中 A 点坐标为（996，300），E 点坐标为（1000,1000）。为计算基尼系 数，先计算三角形 OCA、三角形 ABE 与矩形 ACKB 的面积。 三角形 OCA 的面积＝996×300/2=149400 三角形 ABE 的面积＝700×4/2=1400 矩形 ACKB 的面积=300×4=1200 从而洛伦茨曲线下方的面积＝149400＋1400＋1200＝152000 而三角形 OKE 的面积＝1000×1000/2＝500000 从而洛伦茨曲线与绝对平均线之间围成的面积＝500000－152000＝348000 从而基尼系数 g=348000/500000=0.696 因此，可以知道，中国在 2009 年的实际基尼系数应该大于 0.696。上面已 经说过，只通过一个数据所估算的基尼系数要小于实际的基尼系数。 二〇一〇年十月二十六日 10 时 29 分 21 秒
基尼系数的计算方法与中国的基尼系数估计
700
X
A B
300
O
0
C
996
K
1000
在上图中，已知“0.4%的中国人占有 70%的财富”，则洛伦茨曲线为 OAE 折 线。其中 A 点坐标为（996，300），E 点坐标为（1000,1000）。为计算基尼系 数，先计算三角形 OCA、三角形 ABE 与矩形 ACKB 的面积。 三角形 OCA 的面积＝996×300/2=149400 三角形 ABE 的面积＝700×4/2=1400 矩形 ACKB 的面积=300×4=1200 从而洛伦茨曲线下方的面积＝149400＋1400＋1200＝152000 而三角形 OKE 的面积＝1000×1000/2＝500000 从而洛伦茨曲线与绝对平均线之间围成的面积＝500000－152000＝348000 从而基尼系数 g=348000/500000=0.696 因此，可以知道，中国在 2009 年的实际基尼系数应该大于 0.696。上面已 经说过，只通过一个数据所估算的基尼系数要小于实际的基尼系数。 二〇一〇年十月二十六日 10 时 29 分 21 秒
从而所知数据越少所画的洛伦茨曲线的近似折线与绝对平均线即45度线之间的面积越小人口百比分02020404060608080100每组人口百分比0202020202甲国每组财富所占百分比101564甲国向上累计财富百分比112136100乙国每组财富所占百分比12152048乙国向上累计财富百分比173252100从而所知数据越少估算的基尼系数与真实的基尼系数相比将会变得更小
Y W Wn P1W1 W W2 P2 1 Pn n 1 2 2 2
；其向上累计的比重分别为
W1（＝w1）、W2、…、Wi、…、Wn＝1。则洛伦茨曲线下方与折线 OKE 围成的面积
基尼系数分析范文
基尼系数分析范文基尼系数（Gini coefficient），又称基尼指数，是一种衡量收入或财富分配不平等程度的统计指标。
它是一个介于0和1之间的数值，数值越接近1，表示财富分配越不平等，而数值越接近0，则表示财富分配越平等。
本文将对基尼系数进行分析，并以中国为例进行实证研究。
基尼系数的计算公式为：G=(A/B)*100其中，A为所有个体之间的平均差异总和，B为理论上的最大平均差异总和。
中国是一个拥有庞大人口和巨大经济差距的国家，处于快速发展的转型阶段。
基尼系数是评估中国收入分配不平等程度的一个重要指标。
过去数十年来，中国的基尼系数一直处于较高水平，这对中国的社会稳定和可持续发展构成了威胁。
首先，基尼系数的高水平意味着财富分配不平等，富人的收入远远高于穷人。
富人群体通常拥有更多的资源和机会，而穷人则缺乏这些机会，无法改变自己的经济状况。
这种不平等加剧了贫富差距，使社会分裂和不满情绪加剧。
其次，基尼系数的高值也反映了农村和城市之间的收入差距。
在中国的快速城市化过程中，许多农民工涌入城市寻找更好的经济机会，但他们通常只能在低薪工作中工作，收入稳定性和社会保障不足。
与此同时，城市居民通常享受更高的薪资和更好的福利，这进一步拉大了农村和城市之间的收入差距。
然而，中国政府非常重视贫富差距的问题，并采取了一系列措施来减少基尼系数。
例如，中国政府在过去几十年中实施了一系列减少贫困、促进经济发展的政策。
政府还推出了农村和城市化政策，以改善农村居民的生活条件。
这些措施在一定程度上有助于减少基尼系数，改善社会稳定。
此外，中国还推动了更加公平的教育和医疗体系，提供更多的机会给低收入家庭。
这些措施有助于改善贫困人口的基本生活条件和发展机会，从而缩小贫富差距。
然而，尽管中国政府采取了一系列的措施，但基尼系数的下降仍然存在困难。
一方面，中国经济增长的不平衡性加剧了收入差距，有些地区和行业的富人比其他地区和行业的富人更加富裕。
基尼系数指标在中国经济社会学的应用
基尼系数指标在中国经济社会学的应用基尼系数是衡量经济不平等程度的重要指标之一，在中国经济社会学中有着广泛的应用。
本文将从历史背景、计算方法、应用领域以及存在的问题等方面对基尼系数在中国的应用进行探讨。
首先，我们需要了解基尼系数的含义和历史背景。
基尼系数是由意大利经济学家基尼于1912年提出的，用于衡量经济分配的不平等程度。
该系数的取值范围为0至1，数值越接近1表示经济不平等程度越高。
在中国，基尼系数的应用始于20世纪90年代，这也与中国市场经济改革的推进和城乡居民收入差距不断扩大有关。
其次，我们来了解一下基尼系数的计算方法。
基尼系数的计算方法比较简单，它通过对个体收入或财富进行排序，计算出不同收入或财富阶段的累积收入或财富占总数的比例，然后通过对这些比例进行加权平均，即可得到基尼系数。
在实际操作中，基尼系数通常使用洛伦兹曲线来表示，曲线下的面积即为基尼系数的数值。
基尼系数在中国的应用领域非常广泛。
首先，基尼系数可以用来分析不同地区之间的经济不平等程度。
通过比较不同省份或城市的基尼系数，我们可以了解各地区经济发展的差异以及不同政策对经济不平等的影响。
其次，基尼系数还可以用来研究不同人群之间的收入或财富差距。
例如，可以通过对城乡居民、男性和女性、不同教育水平和职业的人群进行基尼系数的比较，来分析不同人群之间的社会经济差距，为相关政策的制定提供参考。
此外，基尼系数还可以用来研究收入分配政策的效果，通过比较不同政策时期的基尼系数变化，从而评估政策的效果和影响。
然而，基尼系数在应用过程中也存在一些问题。
首先，基尼系数只是一个衡量经济分配不平等程度的指标，不能完全反映社会公平正义的程度。
其次，基尼系数对数据敏感，可能受到数据不准确性和数据缺失的影响。
此外，基尼系数只是表面指标，无法深入分析不平等的原因和机制。
因此，在使用基尼系数的同时，还应结合其他指标和方法，综合分析经济不平等的问题。
综上所述，基尼系数作为一种衡量经济不平等程度的指标在中国经济社会学中有着广泛的应用。
基尼系数调研报告
基尼系数调研报告
基尼系数调研报告
基尼系数是衡量收入或财富分配不平等程度的常用指标，通常介于0和1之间。
在这份调研报告中，我们将对基尼系数进行详细研究，以评估当前社会收入不平等的状况。
首先，我们通过收集大量数据和相关研究文献，发现收入不平等程度在过去几十年里有所增加。
据统计，在大多数国家中，收入分配不均已成为社会问题的显著特征。
而在一些发展中国家中，这种不平等的程度甚至更为严重。
其次，我们对各个国家和地区的基尼系数进行了比较。
基尼系数的数值愈接近1，意味着收入不平等程度愈大。
研究表明，拉丁美洲和非洲的许多国家，尤其是在贫困程度较高的地区，基尼系数高于其他地区，这表明了该地区存在较为严重的收入不平等问题。
此外，我们还对不同社会群体之间的收入差距进行了分析。
研究显示，少数民族和女性在大多数国家中普遍面临着更高的收入不平等。
这反映出社会和性别歧视在收入分配中的影响。
最后，我们调查了一些国家和地区采取的政策措施以减轻收入不平等的情况。
我们发现，一些国家通过实施租税制度改革、提高教育和技能培训水平、推动就业机会平等等政策措施，取得了一定的成效。
然而，仍然有许多挑战需要克服，以实现更公平的收入分配。
总而言之，基尼系数是一种有助于评估收入不平等问题的重要工具。
我们的调研发现，收入不平等程度在全球范围内普遍存在，并不同程度地影响人们的生活。
政府和社会各界应加强努力，采取措施来减轻收入不平等的问题，以促进社会公平和可持续发展。
基尼系数实验报告
一、实验目的1. 理解基尼系数的概念和计算方法。
2. 通过实证分析，了解我国居民收入分配的公平程度。
3. 掌握基尼系数在经济学和社会学领域的应用。
二、实验背景基尼系数是衡量一个国家或地区居民收入分配公平程度的重要指标。
基尼系数的值介于0到1之间，值越接近0表示收入分配越公平，值越接近1表示收入分配越不公平。
近年来，我国居民收入分配差距逐渐扩大，基尼系数也呈现上升趋势，引起了广泛关注。
三、实验方法1. 数据来源：选取我国2000年至2019年的居民收入数据，数据来源于国家统计局。
2. 数据处理：对居民收入进行对数化处理，消除异方差性。
3. 计算方法：采用洛伦兹曲线法计算基尼系数。
四、实验结果与分析1. 基尼系数计算结果根据洛伦兹曲线法，我国2000年至2019年的基尼系数如下表所示：年份基尼系数2000 0.4472001 0.4612002 0.467...2019 0.477从表中可以看出，我国2000年至2019年的基尼系数呈上升趋势，说明收入分配差距逐渐扩大。
2. 收入分配公平程度分析根据基尼系数的计算结果，我国居民收入分配公平程度如下：- 2000年：基尼系数为0.447，表示收入分配较为公平。
- 2019年：基尼系数为0.477，表示收入分配不公平程度较高。
由此可见，我国居民收入分配公平程度有所下降，收入分配差距逐渐扩大。
3. 基尼系数应用分析基尼系数在经济学和社会学领域具有广泛的应用。
例如，在经济学领域，基尼系数可以用于衡量一个国家或地区的收入分配政策效果；在社会学领域，基尼系数可以用于研究收入分配与社会不平等之间的关系。
五、结论1. 我国2000年至2019年的基尼系数呈上升趋势，收入分配差距逐渐扩大。
2. 基尼系数可以有效地衡量一个国家或地区的收入分配公平程度，为政策制定提供依据。
3. 针对我国收入分配差距扩大的问题，政府应采取有效措施，促进收入分配公平。
六、实验总结通过本次实验，我们了解了基尼系数的概念、计算方法及其在经济学和社会学领域的应用。
中国基尼指数
中国基尼指数基尼系数是一种常用的经济学工具，用以衡量一个国家或地区收入分配的不平等程度。
中国作为一个发展中的国家，其基尼指数一直备受关注，因为收入分配不平等一直是中国社会面临的一个重要问题。
本文将从几个方面探讨中国基尼指数的现状、影响因素以及可能的解决办法。
中国基尼指数的现状中国的基尼系数自上世纪80年代以来一直呈现出上升的趋势。
尤其是在经济快速增长的同时，城乡收入差距、地区发展不平衡等问题变得更加突出。
据统计，中国的基尼系数在过去几十年中一直高于0.4，甚至有的地区更是超过0.5，表明收入不平等问题十分严重。
影响中国基尼指数的因素中国基尼指数居高不下的原因有很多，主要包括以下几个方面：1.城乡分割：城乡收入差距巨大是中国基尼系数居高不下的主要原因之一。
城市居民的收入远高于农村居民，导致整体收入分配不平等。
2.行业差异：不同行业之间的收入差距也是一个重要因素。
高科技、金融等行业的收入往往远高于传统制造业、服务业等行业，导致收入分配不公平。
3.教育资源不均：教育资源的不均衡也是造成收入不平等的重要原因。
优质教育资源主要集中在一线城市和发达地区，农村地区和欠发达地区的教育资源相对匮乏，导致贫困地区居民的收入水平较低。
4.封建思想：一些封建思想对收入分配不平等也有一定的影响。
传统的等级观念、家族社会观念等因素都会影响到个人的经济地位，进而影响整体收入不平等的现状。
解决中国基尼指数问题的建议要解决中国基尼指数持续居高不下的问题，需要综合施策，从多个方面入手：1.加大收入再分配力度：通过税收政策、社会保障制度等手段，加大对高收入群体的税收压力，增加对低收入群体的帮助，实现收入再分配的目的。
2.优化教育资源配置：加大对农村地区和欠发达地区教育资源的投入，提高教育普及率和质量，缩小教育资源不均衡现象，为贫困群体提供更多的机会。
3.鼓励创业创新：通过一系列政策措施，鼓励创业创新，促进新兴产业的发展，创造更多就业机会，拉动经济增长，实现经济社会的持续发展。
如何正确测算我国居民收入基尼系数
在收入分配研 究中, 最具 吸引 力和挑 战性的 当数 收入差距研究, 而研究 收入差 距学 者们用 的最多 的指 标是基尼系 数 ( G in i Coefficient) 。但世 界上 可能 没有 任何一个国家像中 国一样, 学 者们 测算出 的基尼 系数 值如此之多, 对收入差距程度判断的分歧如此之大, 以 至于迄今也没有一个比较权威的答案。回顾近年来的 收入分配研究, 国内比较突出的要数赵人伟、李实等为 代表的课题组和以 陈宗胜为 代表 的部分 学者, 其 中最 引人注目的 是李实 和陈宗 胜在 《经济 研究》2000 年第 7 期以及 2002 年 第 5期 两度 针 锋相 对地 对一 些 问题 进行了论战。应该说两人的争论对研究我国居民收入 分配很有启示, 争论澄 清的一 些问 题以及 倡导的 研究 方法对今后 正 确研 究我 国居 民 收入 有非 常重 要 的意 义。本文主要就李实和陈宗胜争论的一个焦点问题 - 基尼系数的测算, 结 合中国 居民 收入的 实际状 况谈 谈个人的一些看法。
6 v2k KkGk = 0. 063。假如 G = 0. 4, 则相对误差达到 15. k
8% , 应该说如此大的误差是不能被轻易忽视的。此外, 如果利用国家统计局对外公布的组距式分组数列测算
农村收入基尼系数, 虽然分组较多, 但由于我们一般只 能取每组的组中值作 为该组均 值的 估计值, 这时 不仅
人力来改进国家统计 局的数 据的全 面性 和细分 程度, 研究出改进 这套 数 据的 规范 方 法 0。要 说明 的是, 统 计局搜集的主要是一些对国民经济发展比较重要且易 于被搜集的显性数据, 诸如灰色收入、黑色收入等一些 隐性数据是不可能被 客观准 确地搜 集到 的, 这正 是很 多人对统计部门公布 的数据 产生不 信任 的主要 原因。 笔者以为, 如何根据统 计部门 搜集到 的显 性数据 科学 推算出一些隐性数据, 正是需 要我们 去深 入研究 的课 题 (比如地下经济的测算等 ) 。当然必 要时, 为了 一定 的研究目的, 单独通过抽样调查搜集一些数据, 以弥补 统计部门数据的不 足, 也是 无可 厚非的。 具体到 居民 收入而言, 笔者认为应 该以统 计部门 的数 据为基 础来 测算收入的基尼系数, 同时逐步解决好两个问题: 一是 提高统计部门数据的 质量, 二 是科学 测算 灰色收 入和 黑色收入的大小及 分布状 况。当前 最重要 的是, 统计 部门应该发挥其独特的资源优势, 加大投入, 充分发挥
中国基尼系数最优值实证分析的开题报告
中国基尼系数最优值实证分析的开题报告题目：中国基尼系数最优值实证分析研究背景和意义：基尼系数是描述收入差距的重要指标之一，也是国际上常用的评估社会经济公平性的指标之一。
基尼系数越小表示收入分配越均衡，反之表示收入分配不均。
在中国这个正在崛起的经济大国，收入分配问题一直是困扰社会发展的重大问题。
近年来，中国政府对收入分配问题的重视程度不断提高，并发布了一系列政策措施来改善收入分配不均的问题。
同时，学者们也在研究如何通过社会政策和经济政策来降低基尼系数。
因此，本研究将以中国为研究对象，探究中国基尼系数的最优值，并分析其影响因素，对中国的社会经济发展具有重要的理论和实践意义。
研究问题和目标：本研究的研究问题为：中国基尼系数最优值是多少？该最优值的影响因素有哪些？研究目标为：1.探究中国基尼系数的演变历程和变化特征，分析近几年来收入分配的变化趋势；2.建立中国基尼系数的优化模型，确定中国基尼系数的最优值；3.分析影响中国基尼系数的主要因素，探究降低基尼系数的策略和措施。
研究方法和步骤：1.文献研究法：通过阅读和梳理大量的国内外文献，了解基尼系数的理论基础和计算方法，了解中国基尼系数的演变历程和变化特征，提高研究的科学性和可靠性。
2.时间序列分析法：通过时间序列建模，对中国基尼系数的发展趋势进行预测并分析其变化规律，确定中国基尼系数的最优值。
3.因子分析法：通过因子分析，确定影响中国基尼系数的主要因素，包括经济因素、政策因素和社会因素等，为制定降低基尼系数的政策和措施提供科学依据。
研究预期结果：1.探究中国基尼系数的演变历程和变化特征，分析近几年来收入分配的变化趋势，为研究中国基尼系数最优值提供数据支持和理论基础；2.建立中国基尼系数的优化模型，得出中国基尼系数的最优值，为制定收入分配政策和措施提供科学依据；3.分析影响中国基尼系数的主要因素，为研究降低基尼系数的策略和措施提供重要参考。
研究依据和数据：本研究的数据来源主要为国家统计局发布的《中国统计年鉴》、《中国财富报告》等官方数据和经济学、社会学等领域的相关文献。
对估算我国基尼系数的一些看法
Ａ ｂ ｔ ａ ｔ Ｔｈ ｈｒ ｅｂａ ｉ ｏ ｄ ｔｏ ｓｏ ｓｉ ａｉ ｎ ｎ ｘ ａｅ ａ ｈｅ ｉ ｅ ｉ ｎ ｓ ｉ ｃ ｍｅ， ｃ ｒｅ ｔｄ ｔ ｎ ｌｎｇ， ｓ ｒ ｃ ： ｅ ｔ ｅ ｓｃ ｃ ｎ ｉｉ ｎ ｆｅ ｔｍ ｔｎｇ Ｇｉ ｉＩ ｄｅ ｒ ｕｔ ｎｔｃ ｒ ｓｄｅ ｔ ’ ｎ ｏ ｏｒ ｃ ａａ ｈａ ｄ ｉ
一
差异 ， 是家 庭 总收 入 ， 是 可 支 配 收入 或纯 收 入 ， 还 以 及 在 货 币收入 中是 否 要 扣 除 所 得税 等 ， 都会 影 响 到
基 尼 系数 的估 算 。进入 世 纪 以来 ， 内一些 学者 １ 国 如陈 宗胜 （ ０ １ ， 人 伟 、 实 （ ０ ２ 等 质 疑 国 家 ２０ ） 赵 李 ２０ ） 统计 局公 布 的居 民收 入数 据 的可 靠 性 。其 实 ， 想 要
ａ ｄ ａ ｐｒｐｒａｅ ｅ ｔｍａ ｉｇ ｍｅｈｏ Ｔｈｅｄｅａ ｌ ｎ ｄ ｔ ｏ ｌｃｉ ｇ ｗｈｉｈ ｓ ｏ ｌ ｅ ｐａｄ ａｔ ｎｉ ｎ ａ ｅｆｒ ｔ ｓ ｕｓ ｅ ｎ ｔ ｉ ｎ ｐ ｏ ｉｔ ｓｉ ｔｎ ｔ ｄ． ｔｉｓｉ ａ ａ ｃ ｌｅ ｔｎ ｃ ｈ ｕ ｄ ｂ ｉ ｔｅ ｔｏ ｒ ｓｌ ｄｉｃ ｓ ｄ ｉ ｈ ｓ ｉ ｙ
法 以及 得 到 的 启 示 。 关键 词 ： 尼 系数 ； 计 资 料 ； 算 方 法 基 统 估
中 图 分 类 号 ：２ ２ Ｆ２ 文献标识码 ： Ａ 文 章 编 号 ： ０ ２— ５ ５ ２ １ ） ９— ０ ７— ４ １０ ４ ６ （０ ２ ０ ０ ５ ０
Ｓ ｍ ｅ Ｖｉ ｗｓ ｔ ｗａ ｄ ｈｅ Ｇ ｉ ｎｄ ｘ ｏ ｏ ｅ ｏ ｒ ｓ ｔ ｎｉＩ ｅ ｆ Ｃｈｉ ａ ｎ
我国基尼系数与经济增长研究分析
我国基尼系数与经济增长研究分析【摘要】基尼系数是国际上用来综合考察某国居民内部收入分配差异状况的重要分析指标，基尼系数过大，将威胁一个国家的政治稳定和社会经济持续发展。
本文通过对中国基尼系数和GDP增长率的回归模型分析，得出中国基尼系数和GDP增长率呈现负相关关系，即收入差距的扩大对经济增长率的提高产生了负面影响，并将基尼系数引入IS-LM模型，试图解释这一分析结果。
【关键词】基尼系数GDP增长率经济增长一、导言自1978年改革开放以来，随着我国GDP的高速增长，社会经济的发展带来了人民生活水平的显著提高，人均收入三十年来大幅增加。
GDP总量的快速提升促使社会经济进入了转型期，收入渠道的多元化促使了中国居民收入格局的多样化，却也带来了经济利益在不同群体间的重新调整和社会收入分配的矛盾与冲突的加剧问题，这突出体现在反应收入分配方面收入分配不平等程度的基尼系数的日益扩大，如何正确认识和处理好GDP增长和收入分配差距过大的矛盾，关系到我国的改革、发展和稳定的大局，也关系到社会主义本质所要求的“共同富裕”目标的实现。
二、理论基础基尼系数是由洛伦兹曲线派生出的衡量收入分配不平等程度的指标。
洛伦兹曲线是反应社会收入分配不平等程度的几何直观表示，它的横轴表示收入从低到高的累计人数占总人数的百分比，纵轴表示累计收入占总收入的百分比。
它是用不同收入集团的收入额占总收入的份额来测定收入分配的不平等程度。
基尼系数是由洛伦兹曲线派生的衡量收入不平等程度的指标，它被定义为图1中阴影部分面积S与三角形OAB面积S的比值：G=S阴影S OAB=S阴影0.5=2S阴影通常把基尼系数G=0.4作为收入分配贫富差距的“警戒线”。
若G0.6以上表示收入高度不平均。
三、实证分析（一）近年来中国经济增长和基尼系数的现状分析为了分析中国经济增长和基尼系数的关系，我们按照统一计算标准，选取样本区间为15年的数据，以GDP增长率作为反应经济增长的变量和以全国的基尼数作为反应基尼系数的变量，数据如下表：利用上述数据和SPASS软件，做GDP增长率和全国基尼系数的线性回归分析。
我国全体居民收入基尼系数的一个估算方法
我国全体居民收入基尼系数的一个估算方法
我国全体居民收入基尼系数的一个估算方法*
● 洪兴建
【摘要】摘要:如何估计我国全体居民收入基尼系数，是一项非常重要而又异常复杂的工作。
本文首先推导了一个基尼系数的回归计算方法及其对应的标准误差，然后通过将城乡分组数据合并的方式，实证分析了我国全体居民收入基尼系数以及置信区间。
【期刊名称】兰州商学院学报
【年(卷),期】2012(028)005
【总页数】4
【关键词】关键词:基尼系数;回归估算;标准误差
一、引言
伴随着我国社会经济的不断发展，收入差距持续扩大成为各界人士广泛讨论的话题，这其中基尼系数是经常提及的一个统计指标，很多人是根据基尼系数的数值及其变动趋势来评价我国收入分配问题。
在探讨我国居民收入差距时，我们所依据的通常只是一个调查样本的微观数据，很多情况下甚至仅为该调查样本的分组数据，因而如何根据样本的微观数据或分组数据，对总体基尼系数作出一定置信度的估计，无疑具有重大的现实意义。
本文重点探讨基尼系数的标准误差估算方法，目的是对我国全体居民收入基尼系数进行估计。
在传统的统计学教材中，关于算术平均数的标准误差估计是一个重点内容，但基尼系数的标准误差估计一般教材几乎没有涉及到。
目前估算基尼系数标准误差的方法主要有两类:一类是非参数统计分析中的刀切法(Jackknife)和自助法(Bootstrap)(Yitzhaki，1991;Xu，2000)，另外一类是基于回归的估计方法。
中国基尼系数预测及分析
作者： 张焕波[1,2] 王铮[1,2,3]
作者机构： [1]中国科学院科技政策与管理科学研究所,北京100080 [2]中国科学院研究生院,北京100080 [3]华东师范大学地理信息系统教育部重点实验室,上海200062
出版物刊名： 管理评论
页码： 37-42页
主题词： 基尼系数 城镇化 Kuznets曲线
摘要：社会发展中的均等问题是增长理论的重要课题。
基尼系数作为度量均等的主要经济指标之一．一直为理论界和宏观政策部门所关注。
论文通过对中国基尼系数的理论分析和实证研究，发现我国的城镇化过程主导着我国基尼系数的波动历程。
在未来十几年里仍然会起重要作用。
并且发现与前我国基尼系数的发展已经到了接近或达到倒u型曲线顶点的水平。
实施不同的宏观政策，达到倒U型曲线顶点的时间不同。
在论文分析的几种情景中，最早2005年，最晚到2010年，基尼系数将开始下降。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
经济评论2009年第3期ECONOMIC REVIEW No.32009中国基尼系数的估算研究王祖祥张奎孟勇*摘要:中国的收入不平等受到了国内外的广泛关注。
公开出版物上的收入分配数据都是分组形式的,这给收入不平等的测算带来困难。
本文采用城乡收入分配统计分布的构造方法,利用中国统计年鉴(1995-2005)的收入分配数据估算了我国的基尼系数。
结果表明,我国目前城镇与农村两部门内部的基尼系数都不大,都没有超过0.34,但从2003年开始,我国的加总基尼系数已经超过了0.44,远远越过了警戒水平0.4。
实际上,基尼系数的分解公式说明,影响我国收入不平等程度的关键因素是目前巨大的城乡收入差距,是这一因素决定了我国的基尼系数必然很大。
关键词:收入分配洛伦兹曲线基尼系数密度函数中国的收入不平等程度受到了国内外的广泛关注,出现了各种各样的基尼系数估计值。
我国每年在中国统计年鉴中都发布收入分配数据,但一般认为利用该数据难以估算基尼系数(王学力,2000),一是因为这种数据是分组形式的,城镇收入分配数据中只列出了从低到高若干个收入组的平均收入与人口份额,农村收入分配中只给出了各个收入区间及各个区间内的家庭百分数,二是城乡数据分列。
实际上,寻求收入分配的统计分布是现代收入分配分析活跃的研究领域,洛伦兹曲线正是从收入分配的密度函数出发而定义的,又按定义,基尼系数是洛伦兹曲线与平等收入线之间面积的2倍,可见基尼系数的估算应建立在收入分配统计分布或洛伦兹曲线的准确测算的基础上。
实际工作中,在只有分组数据可用的条件下,可以先估计收入分配的密度函数,从而得到相应的洛伦兹曲线,或直接估算洛伦兹曲线,最后再估计基尼系数。
国外经济理论文献中基尼系数的估算一般遵循两种途径,一是利用分户数据直接估计收入分配的密度函数从而估算基尼系数,二是利用分组数据估计洛伦兹曲线,然后再估算基尼系数。
我国统计部门的城乡收入分配调查的分户数据不对外公开,因此本文考虑使用统计年鉴中的分组数据。
实际上,使用统计年鉴中的数据时,城镇基尼系数的估算可以使用第二种方法,而对于农村收入分配数据,由于缺少各个收入区间内的平均收入信息使得不能利用第二种方法。
王祖祥(2006)提出了根据我国收入分配分组数据构造收入分配密度函数的方法,估算了我国中部六省的基尼系数。
使用这种方法,只要相关部门提供信息量不高的分组数据,就可以计算我国任何部门、任何地域的基尼系数与其他大多数收入不平等指数,还可以利用现代收入分配分析方法对我国的收入分配进行进一步的分析。
本文利用王祖祥(2006)提出的方法(同时改进了其中城镇密度函数的构造方法),估算了我国最近10年的基尼系数,实际计算表明,我国目前城镇与农村两部门内部的基尼系数都不大,都没有超过0.34,但从2003年开始,我国的加总基尼系数已经超过了0.44,远远越过了警戒水平0.4。
实际上,基尼系数的分解公*王祖祥,武汉大学经济与管理学院,邮政编码:430072,电子信箱:zxwang@;张奎,武汉大学经济与管理学院,邮政编码:430072;孟勇,山西财经大学统计学院,邮政编码:034000,电子信箱:m7025y@。
本文研究得到了国家社科基金重点项目(批准号04AJL002)与湖北省社会科学基金重点项目湖北省农村贫困动态评估研究的资助。
国内很多学者考虑了我国基尼系数的估算问题,例如李实等(1998)、李强等(1995)、胡祖光(2004)、董静和李子奈(2004)等。
使用我国统计年鉴中的分组数据,Chotikapanich等(2007)也考虑了我国的基尼系数,该文利用一种经验分布来逼近我国农村分组数据,计算得到的农村基尼系数与本文结果相差不大。
式说明,影响我国目前收入不平等的决定因素是农村与城镇之间的收入差距。
从最后得到的全国洛伦兹曲线可见,2004年中占人口份额50%的低收入群体所拥有的收入份额只有20%左右,人口份额为10%的高收入端拥有近32%的总收入,这部分人口拥有的总收入是最低收入端10%群体的近20倍。
因此,我国的收入不平等问题的动向值得关注。
一、城乡加总基尼系数的计算公式我国城乡两部门收入分配数据分列,如何加总两部门的收入分配进而形成全国的加总收入分配一直是困扰我国经济理论界的一个问题。
实际上,一旦收入分配密度函数的估算问题得到解决,这一问题将迎刃而解。
这里先讨论基尼系数的一种分解公式,再说明收入分配统计分布的加总方法。
收入分配的洛伦兹曲线L(p)在收入分配分析中具有重要地位,L(p)表示人口份额等于p的低收入端拥有的总收入份额,因此L(p)是定义于[0,1]区间上的函数。
按经济意义,它应满足如下条件:(1)L(p)是p的增函数,即有L (p) 0。
因为所考虑的低收入端人口份额p越大,该群体拥有的总收入份额应越大。
(2)L(p)是凸函数,即满足L (p) 0。
因为p增加到p+ p时,人口份额 p所代表的是收入更高的群体,因此p增加时,L(p)应以更大比例增加。
(3)L(p) 0,因为收入份额不能是负数。
(4)L(0)=0,L(1)=1。
如果对于任何p [0,1]都有L(p)=p,则此洛伦兹曲线是所谓平等收入线。
对于任何洛伦兹曲线L(p),基尼系数定义为L(p)与平等收入线之间面积的2倍。
记农村与城镇两部门人口的总数为n,记农村人口数为n1,城镇人口数为n2,记第i 个部门内的收入分配为Yi=(yi1,yi2, ,yini),即第i个部门内第k个成员的收入为yik,本文恒假定任何成员的收入都大于或等于零。
两部门的收入分配合在一起构成全国的收入分配Y。
记第i个部门内成员的平均收入为 i,记第i个ni部门内的成员占总成员的份额为pi=可见总平均收入为 =(n1 1+n2 2)=p1 1+p2 2,下面记第i个nnni i部门的所有成员拥有总收入的份额为si=。
n按定义,第j个部门内的基尼系数可以表示为:Gj=2nj j又记:G12=[ n1n2( 1+ 2)i=1n1njnji=1r=1yji-yjrn2(1)r=1y1i-y2r](2)同样定义G21,可见有G21=G12。
记全国基尼系数为G(Y),Dagum(1997)给出了基尼系数的如下分解公式:G(Y)=p1s1G1+p2s2G2+p1s2G12+p2s1G21=p1s1G1+p2s2G2+(p1s2+p2s1)G12(3)由此即可计算我国城乡合一的基尼系数。
Dagum称G12为两部门的扩展基尼系数,它反映了两部门的组间不平等程度。
(3)式是离散条件下精确的基尼系数公式,由于只能得到分组形式的收入分配数据,因此不能用它进行实际计算。
如果已知农村与城镇收入分配的洛伦兹曲线,分别记为L1(p)与L2(p),或已知两个收入分配的密度函数,例如记为f1(x)与f2(x),则由连续条件下的基尼系数定义,农村与城镇的基尼系数G1与G2有如下公式:Gi=1-20Li(p)dp=1- i在连续分配条件下,对应于(2)式的公式为:G12=1+ 21yf(y)dyf(x)dxx0ii(4)x-yf(x)f(y)dxdy1(5)与绝大部分国外学者一样,笔者用连续分布来逼近离散的收入分配,这样,估计我国基尼系数的关键是构造收入分配的近似密度函数,只要这一问题解决了,将(4)式与(5)式代入(3)式即得到我国的基尼系数,同时还得到了反映两部门之间不平等的指标G12。
由(5)式容易看出,当 2> 1时,如果收入分配Y1与Y2的收入范围不重叠,则有G12= 2- 1。
又直观上可见Y1与Y2的重叠程度越小,则G12越大,因此G12还反映了两个收入分配的收入范围的重叠程度。
这样,(3)式中最右边第三项将对我国的基尼系数有重要影响,因为我国城乡收入差距很大,即两部门收入分配的重叠程度不大,从而可以预料G12会很大。
又我国农村人口比例p1较大,而城镇人口拥有的总收入份额s2也较大,因此(3)式中G12的系数p1s2+p2s1将不小。
这两方面因素决定我国的基尼系数不会小。
注意到有:1- 2=(x-y)g(x)g(y)dxdy 0012 x-yg(x)g(y)dxdy0012因此得到G12的下界估计:G12 1- 21+ 2例如2003年我国农村人均纯收入为 .24,城镇平均可支配收入为 .20,考虑这两个1=26222=8472分配构成全国收入分配Y时就有:G12 0.5272875注意到将上述G12的下界代入(3)式可以得到基尼系数的一个下界。
归纳起来得到: 定理1:中国收入分配的基尼系数可以表示为(3)式,基尼系数的下界为:p1s1G1+p2s2G2+(p1s2+p2s1) 1- 21+ 2其中pi、si、 i与Gi分别是部门i内的人口份额、收入份额、平均收入与基尼系数,G12是两部门的扩展基尼系数。
显然,如果估计得到了城镇与农村收入分配的密度函数,分别记为f1(x)与f2(x),记相应分布函数分别为F1(x)与F2(x),F1(x)表示城镇人口中收入不高于x的人口占城镇总人口的份额,F2(x)表示农村人口中收入不高于x的人口占农村总人口的份额,于是全国人口中收入不高于x的人口占全国总人口的份额应为:于是全国收入分配的密度函数应为:F(x)=p1F1(x)+p2F2(x),F(x)即全国收入分配的统计描述。
f(x)=p1f1(x)+p2f2(x)。
按洛伦兹曲线与基尼系数的定义,如果估计得到了两部门的密度函数f1(x)与f2(x),就可以得到整个国家的洛伦兹曲线L(p)的另一公式:L(p)=其中,p=F(x),而全国基尼系数公式为:G(y)=1- 0 0yf(y)dy xxf(x) yf(y)dydx 0其中, 是全国平均收入。
因此,如果得到了两部门的密度函数,一是可以利用(5)式估计两部门之间的收入不平等,二是可以通过定理1得到基尼系数的下界估计,三是可以通过(4)式与(3)式或上述积分计算两部门或全国的基尼系数。
同时,利用这些密度函数还可以进行收入分配的其他分析。
可见,获得收入分配密度函数的方法本身具有重要意义。
二、城镇密度函数的构造方法一般各国统计部门都是通过抽样调查对收入分配进行估计,又由于保密等原因,一般将抽样数据化成分组形式予以发布,理论界只能在这种数据的基础上对收入分配进行分析。
根据可能得到的数据形式,可以直接估算收入分配的密度函数,第三部分构造农村收入分配的密度函数时将采用这一方法。
也可以从估计洛伦兹曲线入手获得密度函数,这里采将用这一方法获得城镇收入分配的密度函数,将按经济意义与数学性质王祖祥(2006)使用了这种加总公式,Chotikapanich等(2007)也是使用这种加总分布计算我国基尼系数的。
选择适当的函数作为洛伦兹曲线的经验公式,再利用分组数据估计其中的参数,从而得到近似洛伦兹曲线,最后利用洛伦兹曲线与密度函数的关系而得到后者。