浙江省温州市新力量联盟2018-2019学年高二上学期期中联考技术试题答案
2019-2020学年浙江省温州新力量联盟高二上学期期中联考试题 物理

2019学年第一学期温州市新力量联盟期中联考高二年级物理学科参考答案命题人:夏雪克 温州市第21中学 审题人:郑振 沙城高中一、选择题(45分)二、非选择题(55分)17.(8分)(1)刻度尺 (2)重锤离计时器太远 (3)0.98~1.00 (4)sm 25.018.(6分)(1)C (2) Ω1200 mA 0.29 19.(6分) (1)由牛顿第二定律11ma F F f =−得: 11a F F m f−=………………2分代入数据得:kg m 1=……………………………………………1分(2)由牛顿第二定律22ma F F f =−得: mF F a f−=22……………2分代入数据得: 228s ma =………………………………………1分20.(7分) (1)导体棒做匀速直线运动时处于平衡状态,由平衡条件得:mgsinθ=μmgcosθ+B 2L 2vR+r………………………2分 代入数据解得:v =5m s ⁄………………………1分(2)导体棒产生的感应电动势E =BLv………………………1分电路电流I =E R+r ………………………1分灯泡消耗的功率P =I 2R ………………………1分 代入数据解得:P=1W ………………………1分21.(14分) (1)小球在A 点受力分析得:R v m mg F AA 2=−…………1分在B 点受力分析得:R v m mg F BB 2=−……………1分小球由A 点到B 点,根据动能定理可得:−μmgx =12mv B 2−12mv A2…………………1分 由以上式子,可以求得: RmgxF F F B A μ2=−=∆………………………………1分 结合图象求得:μ=0.2 ………………………………………………1分(2)小球n 次经过B 点,如果满足下列式子,就无法通过圆O 2:E K0−nμmgx −mg2R <12mv D 2…………………………………………2分v D =√gR …………………………………………1分求得n >2.1,即第3次经过B 点后就无法通过圆O 2继续运动了。
浙江省温州市新力量联盟2018-2019学年高二上学期期末考试通用技术学科 答案
2018学年第一学期温州新力量联盟期末联考
高二年级通用技术学科参考答案
一、选择题(本部分共13小题,每小题2分,共26分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)
1-5:BCADA 6-10:ADCBC 11-13:DDC
非选择题部分
二、非选择题(本部分共4题,第14题6分,第15小题6分,第16题3分,第17题9分,共24分)
14.(1)②①④(顺序不可颠倒)(2)②⑤(顺序可以颠倒)(3)③
15、(1)B (2) C (3) A (4) A (5) A (6) D
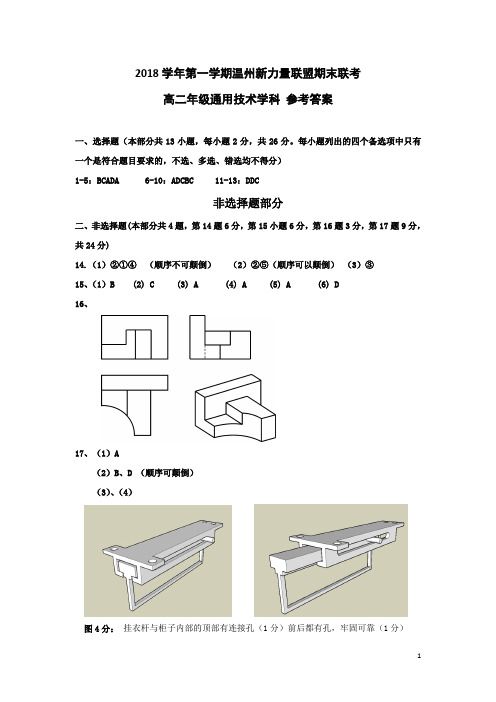
16、
17、(1)A
(2)B、D (顺序可颠倒)
(3)、(4)
图4分:挂衣杆与柜子内部的顶部有连接孔(1分)前后都有孔,牢固可靠(1分)
挂衣杆位置可连续可调(1分)
整体结构立体、美观(1分)
尺寸2分:整体尺寸700mm~1200mm 或伸缩结构范围500mm (1分)挂衣杆与柜子内部的顶部连接孔直径5以上(1分)。
2018-2019学年浙江省温州市新力量联盟高二(上)期末数学试卷(解析版)

一、选择题(每题 4 分,共 40 分)在每小题给出的四个选项中,只有一项是符合题目要求 的 1. (4 分)已知平面 α 的法向量为(2,﹣4,﹣2) ,平面 β 的法向量为(﹣1,2,k) ,若 α ∥β,则 k=( A.﹣2 ) B.﹣1 C.1 D.2
,0) ,O 为坐标原点.
(1)求椭圆的标准方程; (2)A,B 是椭圆 C 上的两动点,求△AOB 的面积的最大值; (3)当△AOB 的面积取最大值时,求线段 AB 的中点 M 的轨迹方程.
第 5 页(共 16 页)
2018-2019 学年浙江省温州市新力量联盟高二(上)期末 数学试卷
参考答案与试题解析
A.30° 8. (4 分)如图,椭圆
B.45° +
C.60°
D.90°
=1(a>b>0)的左焦点为 F,右顶点为 A,点 B 在椭圆上,
且 BF⊥x 轴,直线 AB 交 y 轴于点 P,若
=3
,则椭圆的离心率是(
)
A.
B.
C.
D.
9. (4 分)如图,在直三棱柱 ABC﹣A1B1C1 中,D,E 分别是 A1B1,BB1 的中点,点 P 在该 直三棱柱表面上运动,且满足 EP⊥BD,∠BAC=90°,AB=AA1=AC=2,则点 P 的轨 迹形成的曲线的长等于( )
2
20. (13 分)如图,在平行四边形 PBCD 中,PB=4,PD=2
,∠DPB=45°,AD⊥AB,
将△PAD 沿 AD 翻折,使得平面 PAD⊥平面 ABCD,E 是 PD 的中点,
(1)求证:PD⊥平面 ABE;
第 4 页(共 16 页)
2023-2024学年浙江省温州市新力量联盟高二(上)期中数学试卷【答案版】

2023-2024学年浙江省温州市新力量联盟高二(上)期中数学试卷一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求)1.直线l :x +2y +2=0在y 轴上的截距是( ) A .﹣1B .1C .﹣2D .22.圆C 1:(x −4)2+y 2=4与圆C 2:x 2+(y −3)2=16的位置关系是( ) A .相离B .相交C .内切D .外切3.若{a →,b →,c →}构成空间的一个基底,则下列向量不共面的是( )A .c →+b →,b →,b →−c →B .a →,a →+b →,a →−b →C .a →+b →,a →−b →,c →D .a →+b →,a →+b →+c →,c →4.正方体ABCD ﹣A 1B 1C 1D 1中,E ,F 分别为D 1C 1,BB 1的中点,则异面直线AE 与FC 所成角的余弦值为( )A .√515B .4√515 C .−2√515D .2√5155.直线l :y =﹣2x +1在椭圆y 22+x 2=1上截得的弦长是( )A .√103B .2√53C .8√59D .5√236.点P 是圆C :(x +1)2+(y ﹣2)2=1上的动点,直线l :(m ﹣1)x +my +2=0是动直线,则点P 到直线l 的距离的最大值是( ) A .4B .5C .6D .77.已知F 1,F 2是椭圆C 的两个焦点,P 是C 上的一点,若PF 1⊥PF 2,且∠PF 2F 1=60°,则C 的离心率为( ) A .1−√32B .2−√3C .√3−12D .√3−18.已知E ,F 是圆C :x 2+y 2﹣2x ﹣4y +1=0的一条弦,且CE ⊥CF ,P 是EF 的中点,当弦EF 在圆C 上运动时,直线l :x ﹣y ﹣3=0上存在两点A ,B ,使得∠APB ≥π2恒成立,则线段AB 长度的最小值是( ) A .2√2B .4√2C .6√2D .8√2二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,全部选对的得5分,有选错的得0分,部分选对的得2分)9.已知直线l 的方向向量是a →,两个平面α,β的法向量分别是m →,n →,则下列说法中正确的是( ) A .若a →∥m →,则l ⊥α B .若a →⋅m →=0,则l ⊥α C .若m →∥n →,则α⊥βD .若m →⋅n →=0,则α⊥β10.已知点M 椭圆C :4x 2+9y 2=36上一点,椭圆C 的焦点是F 1,F 2,则下列说法中正确的是( ) A .椭圆C 的长轴长是9B .椭圆C 焦距是2√5C .存在M 使得∠F 1MF 2=90°D .三角形MF 1F 2的面积的最大值是2√511.已知两点A (﹣5,﹣1),B (0,4)点P 是直线l :y =2x ﹣1上的动点,则下列结论中正确的是( ) A .存在P (1,1)使|P A |+|PB |最小B .存在P(12,0)使|P A |2+|PB |2最小C .存在P (5,9)使|P A |﹣|PB |最小D .存在P (0,﹣1)使||P A |﹣|PB ||最小12.已知曲线C :(|x |﹣1)2+(|y |﹣1)2=8,则( ) A .曲线C 上两点间距离的最大值为4√2B .若点P (a ,a )在曲线C 内部(不含边界),则﹣3<a <3 C .若曲线C 与直线y =x +m 有公共点,则﹣6≤m ≤6D .若曲线C 与圆x 2+y 2=r 2(r >0)有公共点,则3≤r ≤3√2 三、填空题(本大题共4小题,每小题5分,共20分) 13.直线√3x +y −2=0的倾斜角为 .14.圆C 1和圆C 2的圆心分别为C 1(1,2),C 2(3,4),半径都为√2,写出一条与圆C 1和圆C 2都相切的直线的方程是 .15.正四面体ABCD 的所有棱长都是2,E ,F 分别是BC ,DC 的中点,则AE →⋅BF →= . 16.如图,三角形ABC 中,AB =BC =4,∠B =90°,D 为AC 中点,E 为BC 上的动点,将△CDE 沿DE 翻折到C ′DE 位置,使点C ′在平面ABC 上的射影H 落在线段AB 上,则当E 变化时,二面角C ′﹣DE ﹣A 的余弦值的最小值是 .四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(10分)已知直线2x ﹣3y ﹣1=0和直线x +y ﹣3=0的交点为P .(1)求过点P且与直线2x﹣y﹣1=0平行的直线l1的方程;(2)求线段OP(O为原点)的垂直平分线l2的方程.18.(12分)已知圆C的圆心C在直线y=2x上,且经过A(﹣1,0),B(3,0)两点.(1)求圆C的方程;(2)直线l:mx+y﹣3m﹣1=0与圆C交于E,F两点,且|EF|=2√3,求实数m的值.19.(12分)如图,已知四棱锥P﹣ABCD中,P A⊥平面ABCD,AB⊥AD,AD∥BC,P A=AB=AD=2BC =2,E为PD中点.(1)求证:CE∥平面P AB;(2)求直线CE与平面P AC所成角的正弦值.20.(12分)为了保证我国东海油气田海域的海上平台的生产安全,海事部门在某平台O的正东方向设立了观测站A,在平台O的正北方向设立了观测站B,它们到平台O的距离分别为6海里和m(m>0)海里,记海平面上到观测站A和平台O的距离之比为2的点P的轨迹为曲线C,规定曲线C及其内部区域为安全预警区(如图).(1)以O为坐标原点,1海里为单位长度,OA所在直线为x轴,OB所在直线为y轴,建立平面直角坐标系,求曲线C的方程;(2)海平面上有渔船从A出发,沿AB方向直线行驶,为使渔船不进入预警区,求m的取值范围.21.(12分)如图,三棱柱ABC﹣A1B1C1的底面是边长为2的等边三角形,CC1=2,∠ACC1=60°,点D,E分别是线段AC,CC1的中点,二面角C1﹣AC﹣B为直二面角.(1)求证:A1C⊥平面BDE;(2)若点P为线段B1C1上的动点(不包括端点),求锐二面角P﹣DE﹣B的余弦值的取值范围.22.(12分)如图,已知椭圆C 的焦点为F 1(﹣1,0),F 2(1,0),离心率为√22,椭圆C 的上、下顶点分别为A ,B ,右顶点为D ,直线l 过点D 且垂直于x 轴,点Q 在椭圆C 上(且在第一象限),直线AQ 与l 交于点N ,直线BQ 与x 轴交于点M . (1)求椭圆C 的标准方程;(2)判定△AOM (O 为坐标原点)与△ADN 的面积之和是否为定值?若是,请求出该定值;若不是,请说明理由.2023-2024学年浙江省温州市新力量联盟高二(上)期中数学试卷参考答案与试题解析一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求)1.直线l :x +2y +2=0在y 轴上的截距是( ) A .﹣1B .1C .﹣2D .2解:将x =0代入直线方程x +2y +2=0,可得2y +2=0,解得y =﹣1. 故选:A .2.圆C 1:(x −4)2+y 2=4与圆C 2:x 2+(y −3)2=16的位置关系是( ) A .相离B .相交C .内切D .外切解:圆C 1:(x ﹣4)2+y 2=4的圆心(4,0),半径为:2; 圆C 2:x 2+(y ﹣3)2=16的圆心(0,3),半径为:4; 两个圆心的距离为:√32+42=5,两个圆的半径和为:2+4=6,半径差为:4﹣2=2, 2<5<6; 所以两个圆相交. 故选:B .3.若{a →,b →,c →}构成空间的一个基底,则下列向量不共面的是( )A .c →+b →,b →,b →−c →B .a →,a →+b →,a →−b →C .a →+b →,a →−b →,c →D .a →+b →,a →+b →+c →,c →解:对于A ,b →=12(c →+b →)+12(b →−c →),所以c →+b →,b →,b →−c →三个向量共面,故A 错误,对于C ,假设a →+b →,a →−b →,c →三个向量共面,则存在非零实数x ,y ,满足a →+b →=x(a →−b →)+yc →,整理可得(x −1)a →+(−x −1)b →+yc →=0,因为a →,b →,c →不共面,所以x ﹣1=﹣x ﹣1=y =0,无解,所以假设不成立,则a →+b →,a →−b →,c →三个向量不共面,故C 正确,对于B ,a →=12(a →+b →)+12(a →−b →),所以a →,a →+b →,a →−b →三个向量共面,故B 错误,对于D ,c →=(a →+b →+c →)−(a →+b →),所以a →+b →,a →+b →+c →,c →三个向量共面,故D 错误. 故选:C .4.正方体ABCD ﹣A 1B 1C 1D 1中,E ,F 分别为D 1C 1,BB 1的中点,则异面直线AE 与FC 所成角的余弦值为( )A .√515B .4√515C .−2√515D .2√515解:以D 为坐标原点,建立空间直角坐标系,设正方体ABCD ﹣A 1B 1C 1D 1中棱长为2,则A (2,0,0),E (0,1,2),F (2,2,1),C (0,2,0), AE →=(﹣2,1,2),FC →=(﹣2,0,﹣1), 设异面直线AE 与FC 所成角为θ,则cos θ=|AE →⋅FC →||AE →|⋅|FC →|=23⋅√5=2√515, ∴异面直线AE 与FC 所成角的余弦值为2√515. 故选:D .5.直线l :y =﹣2x +1在椭圆y 22+x 2=1上截得的弦长是( )A .√103B .2√53C .8√59D .5√23解:联立{y =−2x +1y 22+x 2=1,消去y 并整理得6x 2﹣4x ﹣1=0,此时Δ>0,所以直线l 与椭圆有两个交点,不妨设A (x 1,y 1),B (x 2,y 2), 由韦达定理得x 1+x 2=23,x 1x 2=−16,则直线l 在椭圆上截得的弦长|AB |=√1+k 2⋅|x 1−x 2|=√1+22⋅√(x 1+x 2)2−4x 1x 2=√5•√(23)2−4×(−16)=5√23. 故选:D .6.点P 是圆C :(x +1)2+(y ﹣2)2=1上的动点,直线l :(m ﹣1)x +my +2=0是动直线,则点P 到直线l 的距离的最大值是( ) A .4B .5C .6D .7解:圆C :(x +1)2+(y ﹣2)2=1,可知圆心C (﹣1,2),半径r =1, 上的直线l :(m ﹣1)x +my +2=0整理可得m (x +y )﹣x +2=0, 可得直线l 恒过定点Q (2,﹣2),当CQ ⊥l 时,P 到直线的距离最大,且为r +|CQ |, 即1+√(−1−2)2+[2−(−2)]2=1+5=6. 故选:C .7.已知F 1,F 2是椭圆C 的两个焦点,P 是C 上的一点,若PF 1⊥PF 2,且∠PF 2F 1=60°,则C 的离心率为( ) A .1−√32B .2−√3C .√3−12D .√3−1解:F 1,F 2是椭圆C 的两个焦点,P 是C 上的一点,若PF 1⊥PF 2,且∠PF 2F 1=60°,可得椭圆的焦点坐标F 2(c ,0),所以P (12c ,√32c ).可得:c 24a 2+3c 24b 2=1,可得14e 2+34(1e2−1)=1,可得e 4﹣8e 2+4=0,e ∈(0,1),解得e =√3−1.法二,由题意可得|PF 1|=√3c ,|PF 2|=c , ∴2a =|PF 1|+|PF 2|=√3c +c ,∴ca =√3+1=√3−1.故选:D .8.已知E ,F 是圆C :x 2+y 2﹣2x ﹣4y +1=0的一条弦,且CE ⊥CF ,P 是EF 的中点,当弦EF 在圆C 上运动时,直线l :x ﹣y ﹣3=0上存在两点A ,B ,使得∠APB ≥π2恒成立,则线段AB 长度的最小值是( ) A .2√2B .4√2C .6√2D .8√2解:由圆C 的方程化为标准方程:(x ﹣1)2+(y ﹣2)2=4,可知圆心C(1,2),半径r=√2,又CE⊥CF,P是EF的中点,所以∠CEF=∠CFE=45°,|CP|=|EF|2=2√22=√2,所以点P的轨迹方程为:(x﹣1)2+(y﹣2)2=2,圆心为点C(1,2),半径R=√2.若直线l:x﹣y﹣3=0上存在两点A,B,使得∠APB≥π2恒成立,则以AB为直径的圆与圆(x﹣1)2+(y﹣2)2=√2的位置关系为内切或内含.而点C(1,2)到直线l的距离d=|1−2−3|√1+(−1)2=2√2,设AB的中点为M,则|CM|=d≤|AB| 2,所以|AB|≥2d=4√2,即|AB|的最小值为4√2.故选:B.二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,全部选对的得5分,有选错的得0分,部分选对的得2分)9.已知直线l的方向向量是a→,两个平面α,β的法向量分别是m→,n→,则下列说法中正确的是()A.若a→∥m→,则l⊥αB.若a→⋅m→=0,则l⊥αC.若m→∥n→,则α⊥βD.若m→⋅n→=0,则α⊥β解:对于A,若a→∥m→,则l⊥α,故A正确;对于B,若a→⋅m→=0,则l∥α或l⊂α,故B错误;对于C,若m→∥n→,则α∥β,故C错误;对于D,若m→⋅n→=0,则α⊥β,故D正确.故选:AD.10.已知点M椭圆C:4x2+9y2=36上一点,椭圆C的焦点是F1,F2,则下列说法中正确的是()A.椭圆C的长轴长是9B.椭圆C焦距是2√5C.存在M使得∠F1MF2=90°D.三角形MF1F2的面积的最大值是2√5解:椭圆C:4x2+9y2=36即x29+y24=1,可得a =3,b =2,故c =√9−4=√5, 所以椭圆C 的长轴长是2a =6,A 错; 焦距是2c =2√5,B 对;当M 与A 重合时,三角形MF 1F 2的高最大,此时三角形MF 1F 2的面积也最大,面积的最大值是:12×2c×b =12×2√5×2=2√5,故D 对;当M 与A 重合时,∠F 1MF 2=2∠F 1AO 最大, 而tan ∠F 1AO =√52>1=tan45°, 故此时的∠F 1MF 2=2∠F 1AO >90°, 故C 正确. 故选:BCD .11.已知两点A (﹣5,﹣1),B (0,4)点P 是直线l :y =2x ﹣1上的动点,则下列结论中正确的是( ) A .存在P (1,1)使|P A |+|PB |最小B .存在P(12,0)使|P A |2+|PB |2最小C .存在P (5,9)使|P A |﹣|PB |最小D .存在P (0,﹣1)使||P A |﹣|PB ||最小解:对于A :设点B 关于直线l 的对称点为C (m ,n ),所以{n+42=2×m+02−1n−4m−0×2=−1,所以{m =4n =2,所以C (4,2),所以|P A |+|PB |≥|AC |,当且仅当P 为AC 与l 交点时满足题意, 又因为AC :y −2=−1−2−5−4(x −4),即AC :y =13x +23, 所以{y =13x +23y =2x −1,所以{x =1y =1,所以P (1,1),故A 正确;对于B :设P (x ,2x ﹣1),所以(|P A |)2+(|PB |)2=(x +5)2+(2x ﹣1+1)2+x 2+(2x ﹣1﹣4)2, 所以(|PA|)2+(|PB|)2=10[(x −12)2+194], 当且仅当x =12时,(|P A |)2+(|PB |)2有最小值,此时2x ﹣1=0,所以P(12,0),故B 正确;对于C :如下图,根据A ,B 与l 的位置关系可判断出|P A |﹣|PB |有最大值,无最小值,故C 错误;对于D :因为|P A ﹣|PB |≥0,取等号时|P A |=|PB |,即P 为AB 垂直平分线与l 的交点, 因为AB 垂直平分线方程为y −−1+42=−14−(−1)0−(−5)(x −−5+02),即y =﹣x ﹣1, 所以 {y =−x −1y =2x −1,所以{x =0y =−1,所以P (0,﹣1),故D 正确. 故选:ABD .12.已知曲线C :(|x |﹣1)2+(|y |﹣1)2=8,则( ) A .曲线C 上两点间距离的最大值为4√2B .若点P (a ,a )在曲线C 内部(不含边界),则﹣3<a <3 C .若曲线C 与直线y =x +m 有公共点,则﹣6≤m ≤6D .若曲线C 与圆x 2+y 2=r 2(r >0)有公共点,则3≤r ≤3√2解:分x ,y 的符号讨论曲线的形状,画出曲线C :(|x |﹣1)2+(|y |﹣1)2=8的图象如图所示:对于A ,曲线C 上两点的最大距离为d =√(1+1)2+(1+1)2+4√2=6√2,故A 错误; 对于B ,在曲线(x ﹣1)2+(y ﹣1)2=8(x >0,y >0)中,取y =x ,可得x =3, 由P (a ,a )在曲线的内部(不含边界),则﹣3<a <3,故B 正确;对于C :由图象可得,直线y =x +m 与半圆(x +1)2+(y ﹣1)2=8(x <0,y >0)相切时,截距m 最大, 由√2=2√2,可得m =6或m =﹣2(舍去),直线y =x +m 与半圆(x ﹣1)2+(y ﹣1)2=8(x >0,y <0)相切时,截距m 最小, 由√2=2√2,可得m =﹣6或m =2(舍去),∴若曲线C 与直线y =x +m 有公共点,则﹣6≤m ≤6,故C 正确;对于D :由线(|x |﹣1)2+(|y |﹣1)2=8与坐标轴的交点为(0,±(1+√7)),(±(1+√7),0), 当圆x 2+y 2=r 2(r >0)过点(0,±(1+√7)),(±(1+√7),0)时,r 最小,最小值为1+√7,故D 错误. 故选:BC .三、填空题(本大题共4小题,每小题5分,共20分) 13.直线√3x +y −2=0的倾斜角为 120° . 解:直线√3x +y −2=0的斜率为−√3, ∴tan α=−√3, ∴α=120°, 故答案为:120°.14.圆C 1和圆C 2的圆心分别为C 1(1,2),C 2(3,4),半径都为√2,写出一条与圆C 1和圆C 2都相切的直线的方程是 y =﹣x +5(或y =x ﹣1或y =x +3) .解:圆C 1和圆C 2的圆心分别为C 1(1,2),C 2(3,4),半径都为√2, |C 1C 2|=√(3−1)2+(4−2)2=2√2,两个圆的位置关系是外切,k C 1C 2=4−23−1=1,中点坐标(2,3), 所以一条公切线方程为:y ﹣2=﹣(x ﹣3),即y =﹣x +5. 设与圆C 1和圆C 2都相切的直线方程为y =x +b ,可得√2=|1−2+b|√2,解得b =﹣1或b =3, 所以公切线方程为:y =﹣x +5或y =x ﹣1或y =x +3. 故答案为:y =﹣x +5(或y =x ﹣1或y =x +3).15.正四面体ABCD 的所有棱长都是2,E ,F 分别是BC ,DC 的中点,则AE →⋅BF →= 12.解:正四面体ABCD 的所有棱长都是2,E ,F 分别是BC ,DC 的中点, 如图所示:取FC 的中点G ,连接EG ,AG ,在△AEG 中,由于AE =√3,BF =√3,EG =√32,AG =√(12)2+(√3)2=√132,故∠AEG 为异面直线AE 和BF 所成的角; 故cos <AE →,AF →>=cos∠AEG =(√3)2+(√32)2−(√132)22⋅3⋅√32=16; 故AE →⋅AF →=|AE →||AF →|cos <AE →,AF →>=√3×√3×16=12. 故答案为:12.16.如图,三角形ABC 中,AB =BC =4,∠B =90°,D 为AC 中点,E 为BC 上的动点,将△CDE 沿DE 翻折到C ′DE 位置,使点C ′在平面ABC 上的射影H 落在线段AB 上,则当E 变化时,二面角C ′﹣DE ﹣A 的余弦值的最小值是 4√2−5 .解:过点H 作HG ⊥DE 交DE 于G 点,连接C ′G ,CG ,如下图所示:因为C 在平面ABC 内的射影为H 点,所以C ′H ⊥平面ABC ,所以C ′H ⊥DE , 又因为HG ⊥DE ,CH ∩HG =H ,所以DE ⊥平面CHG ,所以DE ⊥CG , 所以二面角C ′﹣DE ﹣A 的平面角为∠C ′GH ,且cos ∠C ′GH =HGC′G, 又因为DE ⊥C 'G ,所以DE ⊥CG ,易知C ,G ,H 三点共线,且CG =CG , 则cos ∠C ′GH =HGCG ,在平面ABC 中建立平面直角坐标系如下图所示:设E (0,m ),因为C 在平面ABC 内的射影为H 点,所以可知m ∈(0,2),又D (﹣2,2),C (0,4),所以DE :y =m−22x +m ,CH :y =−2m−2x +4, 所以{y =m−22x +m y =−2m−2x +4,所以{x =2(m−2)(4−m)m 2−4m+8y =4m 2−12m+16m 2−4m+8,所以G(2(m−2)(4−m)m 2−4m+8,4m 2−12m+16m 2−4m+8), 所以cos ∠C ′GH =HG C′G =y G −y H y C −y G=4m 2−12m+16m 2−4m+8−04−4m 2−12m+16m 2−4m+8=4m 2−12m+1616−4m =m 2−3m+44−m,设4﹣m =t ∈(2,4),所以cos ∠C ′GH =(4−t)2−3(4−t)+4t =t 2−5t+8t ≥t +8t −5≥2√t ×8t−5=4√2−5,当且仅当t =8t,即t =2√2,即m =4−2√2时取等号,所以(cos ∠C ′GH )min =4√2−5, 故答案为:4√2−5.四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(10分)已知直线2x ﹣3y ﹣1=0和直线x +y ﹣3=0的交点为P . (1)求过点P 且与直线2x ﹣y ﹣1=0平行的直线l 1的方程; (2)求线段OP (O 为原点)的垂直平分线l 2的方程. 解:(1)联立方程组{2x −3y −1=0x +y −3=0,得{x =2y =1,∴P (2,1),设l 1:2x ﹣y +m =0,代入P (2,1),得4﹣a +m =0, 解得m =﹣3,∴直线l 1的方程为2x ﹣y ﹣3=0;(2)∵k OP =1−02−0=12,OP 中点坐标为(1,12),∴OP 的垂直平分线方程为y −12=−2(x ﹣1), 整理得4x +2y ﹣5=0,∴线段OP(O为原点)的垂直平分线l2的方程为4x+2y﹣5=0.18.(12分)已知圆C的圆心C在直线y=2x上,且经过A(﹣1,0),B(3,0)两点.(1)求圆C的方程;(2)直线l:mx+y﹣3m﹣1=0与圆C交于E,F两点,且|EF|=2√3,求实数m的值.解:(1)由题意设圆心C(a,2a),半径r=|AC|=|BC|,即√(a+1)2+(2a)2=√(a−3)2+(2a)2,解得a=1,即圆心C(1,2),半径r=|AC|=√(1+1)2+(2×1)2=2√2,所以圆C的方程为:(x﹣1)2+(y﹣2)2=8;(2)由(1)可得圆心C到直线l的距离d=|m+2−3m−1|√1+m2=|1−2m|√1+m2,由题意可得|EF|=2√r2−d2=2√3,可得d2=r2﹣3=8﹣3=5,所以√1+m2=√5,整理可得:m2+4m+4=0,解得m=﹣2.即实数m的值为﹣2.19.(12分)如图,已知四棱锥P﹣ABCD中,P A⊥平面ABCD,AB⊥AD,AD∥BC,P A=AB=AD=2BC =2,E为PD中点.(1)求证:CE∥平面P AB;(2)求直线CE与平面P AC所成角的正弦值.解:(1)证明:取P A的中点M,连接BM,ME,∵E为PD的中点,∴ME∥AD且ME=12 AD,∵BC∥AD且BC=12 AD,∴ME∥BC且ME=BC,∴四边形MEBC为平行四边形,∴BM∥CE,又∵CE⊄面P AB,BM⊂面P AB,∴CE∥平面P AB.(2)证明:∵P A ⊥平面ABCD ,DC ⊂平面ABCD ,∴P A ⊥DC , 过C 作CC ′⊥AD ,交AD 于C ′,则CC ′=1,C ′D =1, ∴CD =√2,又AC =√2,∴AC 2+CD 2=2+2=AD 2,∴DC ⊥AC ,又AC ∩P A =A , ∴DC ⊥平面P AC ,又DC ⊂平面PDC , ∴平面P AC ⊥平面PDC .取PC 中点F ,连接EF ,则EF ∥DC , ∴DC ⊥平面P AC ,则EF ⊥平面P AC , ∴∠ECF 为直线EC 与平面P AC 所成的角, CF =12PC =√32,EF =12CD =√22,∴EC =√34+24=√52, ∴sin ∠ECF =EF CF =√22√52=√105, 即直线EC 与平面P AC 所成角的正弦值为√105.20.(12分)为了保证我国东海油气田海域的海上平台的生产安全,海事部门在某平台O 的正东方向设立了观测站A ,在平台O 的正北方向设立了观测站B ,它们到平台O 的距离分别为6海里和m (m >0)海里,记海平面上到观测站A 和平台O 的距离之比为2的点P 的轨迹为曲线C ,规定曲线C 及其内部区域为安全预警区(如图).(1)以O 为坐标原点,1海里为单位长度,OA 所在直线为x 轴,OB 所在直线为y 轴,建立平面直角坐标系,求曲线C 的方程;(2)海平面上有渔船从A 出发,沿AB 方向直线行驶,为使渔船不进入预警区,求m 的取值范围.解:(1)不妨设P (x ,y ),O (0,0),A (6,0), 因为海平面上到观测站A 和平台O 的距离之比为2, 所以|PA||PO|=2,即√(x −6)2+y 2=2√x 2+y 2, 整理得(x +2)2+y 2=16,所以曲线C 是以(﹣2,0)为圆心,4为半径的圆, 则曲线C 的方程为(x +2)2+y 2=16; (2)易知A (6,0),B (0,m ),若过AB 的直线不过坐标原点且不与坐标轴垂直, 此时直线AB 的方程为x6+y m=1(m >0),即mx +6y ﹣6m =0(m >0),若渔船从A 出发,沿AB 方向直线行驶且不进入预警区, 此时直线AB 与圆C 切, 而圆心C 到直线AB 的距离为4, 即d =|−2m−6m|√m 2+36=4,①又m >0,②联立①②,解得m =2√3,综上,满足条件的m 的取值范围为(2√3,+∞).21.(12分)如图,三棱柱ABC ﹣A 1B 1C 1的底面是边长为2的等边三角形,CC 1=2,∠ACC 1=60°,点D ,E 分别是线段AC ,CC 1的中点,二面角C 1﹣AC ﹣B 为直二面角. (1)求证:A 1C ⊥平面BDE ;(2)若点P 为线段B 1C 1上的动点(不包括端点),求锐二面角P ﹣DE ﹣B 的余弦值的取值范围.(1)证明:连接AC 1,如图所示:在三棱柱ABC﹣A1B1C1中,四边形AA1C1C为菱形,∴A1C⊥AC1,∵D,E分别为AC,CC1中点,∴DE∥AC1,∴A1C⊥DE,又D为线段AC中点,△ABC是等边三角形,∴BD⊥AC,又二面角C1﹣AC﹣B为直二面角,即平面AA1C1C⊥平面ABC,且平面AA1C1C∩平面ABC=AC,BD⊂平面ABC,∴BD⊥平面AA1C1C,又A1C⊂平面AA1C1C,∴BD⊥A1C,又BD∩DE=D,BD⊂平面BDE,DE⊂平面BDE,∴A1C⊥平面BDE;(2)解:∵CA=CC1=2,∠ACC1=60°,∴△ACC1为等边三角形,∴C1D⊥AC,∵平面AA1C1C⊥平面ABC,平面AA1C1C∩平面ABC=AC,C1D⊂平面ACC1A1,∴C1D⊥平面ABC,则建立以D为坐标原点,以DB,DA,DC1所在直线分别为x,y,z轴的空间直角坐标系D﹣xyz,如图所示:则D (0,0,0),B (√3,0,0),E (0,−12,√32),C 1(0,0,√3), B 1(√3,1,√3),C (0,﹣1,0),A 1(0,2,√3), ∴DB →=(√3,0,0),DE →=(0,−12,√32), C 1B 1→=(√3,1,0),CA 1→=(0,3,√3), 设P (x ,y ,z ),C 1P →=λC 1B 1→(0<λ<1), 则有(x ,y ,z −√3)=(√3λ,λ,0),∴x =√3λ,y =λ,z =√3,即P(√3λ,λ,√3), ∴DP →=(√3λ,λ,√3), 由(1)得A 1C ⊥平面BDE ,∴平面BDE 的一个法向量CA 1→=(0,3,√3), 设平面PDE 的法向量n →=(a ,b ,c),则{n →⋅DE →=−12b +√32c =0n →⋅DP →=√3λa +λb +√3c =0,取c =1,则b =√3,a =﹣1−1λ,∴平面PDE 的法向量为n →=(−1−1λ,√3,1), ∴|cos <CA 1→,n →>|=|CA 1→⋅n →||CA 1→|⋅|n →|=4√32√3×√4+(−1−1λ)2=2√2(1λ+12)2+92,∵λ∈(0,1),∴1λ∈(1,+∞),∴|cos <CA 1→,n →>|=2√2(1λ+12)2+9223,∴|cos <CA 1→,n →>|∈(0,23),故锐二面角P ﹣BD ﹣E 的余弦值的取值范围为(0,23).22.(12分)如图,已知椭圆C 的焦点为F 1(﹣1,0),F 2(1,0),离心率为√22,椭圆C 的上、下顶点分别为A ,B ,右顶点为D ,直线l 过点D 且垂直于x 轴,点Q 在椭圆C 上(且在第一象限),直线AQ 与l 交于点N ,直线BQ 与x 轴交于点M . (1)求椭圆C 的标准方程;(2)判定△AOM (O 为坐标原点)与△ADN 的面积之和是否为定值?若是,请求出该定值;若不是,请说明理由.解:(1)因为椭圆C 的焦点为F 1(﹣1,0),F 2(1,0), 所以椭圆C 的半焦距c =1, 又椭圆C 的离心率e =c a =√22, 所以椭圆C 的长半轴a =ce =√2, 可得b =√a 2−c 2=1, 则椭圆C 的方程为x 22+y 2=1;(2)由(1)知A (0,1),B (0,﹣1),D(√2,0), 不妨设Q (x 0,y 0),x 0>0,y 0>0, 因为点Q 在椭圆C 上, 所以x 022+y 02=1, 此时直线AQ 的方程为y =y 0−1x 0x +1, 当x =√2时,解得y =√2(y0−1)x 0+1, 即N (√2,√2(y 0−1)x 0+1), 直线BQ 的方程为y =y 0+1x 0x −1, 当y =0时,解得x =x0y 0+1,即M(x 0y 0+1,0), 易知点N 在x 轴上方, 所以|DN|=√2(y0−1)x 0+1,|OM|=xy 0+1,则S △AOM +S △ADN =12|OM|⋅|OA|+12|DN|⋅|OD|=12|OM|+√22|DN| =12⋅x 0y 0+1+√22(√2(y 0−1)x 0+1)=√22+x 02(y 0+1)+y 0−1x 0 =√22+x 02+2y 02−22x 0(y 0+1)=√22.故△AOM (O 为坐标原点)与△ADN 的面积之和是定值,定值为√22.。
浙江省温州新力量联盟2018-2019学年高二上学期期中生物试题

A.随 pH 升高,该酶催化反应的最适温度也逐渐升高 B.当 pH 为 8 时,影响反应速率的主要因素是底物浓度和酶浓度 C.当 pH 为任何一固定值时,实验结果都可以证明温度对反应速率的影响 D.该酶催化反应的最适温度为 35℃左右,最适 pH 约为 8
19. 在显微镜下观察洋葱根尖有丝分裂装片时,下列哪些步骤有利于细胞的分离
A.②③①④③
B.④③②②①
C.②①④①③
浙江省温州新力量联盟2018-2019学年高二上学期期中生物试题
D.④③②①①
27. 下列关于“碱基互补配对原则”和“DNA 复制特点”具体应用的叙述,不正确的是( ) A.某双链 DNA 分子中,G 占碱基总数的 38%,其中一条链中的 T 占该 DNA 分子全部碱基总数的 5%,那么另一条链中 T 占该 DNA 分子全部 碱基总数的比例为 7% B.一个有 2000 个碱基的 DNA 分子,碱基对可能的排列方式有 41000 种 C.已知一段信使 RNA 有 30 个碱基,其中 A+U 有 12 个,那么转录成信使 RNA 的一段 DNA 分子中 C+G就有 30 个 D.将精原细胞的 l 对同源染色体的 2 个 DNA 都用 15N 标记,只提供含 14N 的原料,该细胞进行 1 次有丝分裂后再减数分裂,产生的 8 个精子 中(无交叉互换现象)含15N,14N 标记的 DNA 的精子所占比例依次是50%、100%
浙江省温州新力量联盟2018-2019学年高二上学期期中生物试题
一、单选题
1. 生活在沙漠中的仙人掌的细胞中含量最多的化合物是 ( )
A.蛋白质
B.糖类
C.水
D.无机盐
2. 用高倍显微镜观察一个正常的活细胞时,发现没有叶绿体,则该细胞( ) A.一定不是植物细胞 B.一定不能进行光合作用 C.一定是异养生物 D.一定能进行有机物的分解
浙江省温州市新力量联盟2018-2019学年高二上学期期中联考语文试题 Word版含答案

2018 学年第一学期“温州新力量联盟”期中联考高二年级语文学科试题考生须知:1.本卷共8 页,满分120 分,考试时间110 分钟。
2.答题前在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字。
3.所有答案必须写在答题卷上,写在试卷上无效。
4 .考试结束后,只需上交答题卷。
一、选择题(本大题共13 小题,每小题3 分,共39 分)1.下列各项加点字读音完全正确的一项是()A.龟.裂(jūn)栏楯. (shǔn) 濒.临(bīn)莞.尔一笑(wǎn)B.吮.吸(shǔn)笨拙.(zhuó)祈.祷(qí)悄.无声息(qiǎo)C.筵.席(yàn)骄横. (hèng) 攒.射(cuán)呱.呱坠地(guā)D.卓.绝(zhuó)绯.闻(fěi)凝眸.(móu)三缄.其口(jiān)2.下列各句中没有错别字的一项是()A.我呵气,熔化一角的冰凌,透过湿润的玻璃遥望那种辽阔的白——我知道,看似无痕的雪地上其实有着细碎的纹饰。
B.他们把那些硬片放在铁臼里捣碎研细,筛成细末应用。
细末里不免掺合着铁臼上磨下来的铁屑,他们利用吸铁石除掉它。
C.她脸上的光辉会掩盖了星星的明亮,正像灯光在朝阳下黯然失色一样;在天上的她的眼睛,会在太空中大放光明,使鸟儿误认为黑夜已经过去而唱出它们的歌声。
D.这是我知道的,凡我所编辑的期刊,大概是因为往往有始无终之故罢,销行一向就甚为廖落,然而在这样的生活艰难中,毅然预定了《莽原》全年的就有她。
3.下列各句中,加点的熟语使用正确的一项是()A.在语文老师的严格要求下,我逐渐改掉了文.不.加.点.的毛病。
B.自然与人类休.戚.相.关.,任何人都不能为了眼前利益,破坏人类赖以生存的自然环境!C.我很希望在这一问题上,在这一颗“基因原子弹”爆炸之前,通过我的努力与建立国际性的合作,防.患.于.未.然.,杜绝灾难发生。
2018学年第一学期温州新力量联盟期末联考高二年级通用技

2018 学年第一学期温州新力量联盟期末联考高二年级通用技术学科 试题命题:白象中学 金扬磨题: 温溪高中 翁先祥第二部分 通用技术(50 分)一、选择题(本部分共 13 小题,每小题 2 分,共 26 分。
每小题列出的四个备选项中只有一个 是符合题目要求的,不选、多选、错选均不得分)1、随着技术的发展,市场上出现了如图所示的蓝牙音箱,应用了多项新技术,从技术的性质角 度分析,以下说法中正确的是() A.此蓝牙音箱,只需通过手机远程控制即可调节音量,体现了技术具有保护人的作用B.呆萌的造型,小巧的身材,形态新颖,体现了技术的创新性C.该蓝牙音箱定价贵,电池续航时间短,体现了技术的两面性D.可连接手机蓝牙,具备蓄电功能,随身携带,灵活方便,体现了技术的综合性 2.“汽车穿梭餐厅”是一种主要为汽车驾驶者服务的餐厅,这种餐厅在汽车普及率很高的发达 国家已经非常普遍,在中国,专门为驾驶者提供饮食服务的餐厅也渐渐出现了。
下列说法中不. 恰.当.的是( ) A 、只要把汽车开到餐厅门口,车主不用下车就能买到想要的美餐,大大节省了消费者的时间,实现了人机关系的高效目标B 、该餐厅车道下设有感应器,一旦车辆进入,店内服务人员就能及时获取车辆进入信息,并运用店内先进的通信设备进行沟通,准确快速地准备所需餐点,体现了技术在餐饮领域的重要作用C 、“汽车穿梭餐厅”专门为驾驶者提供饮食服务,考虑了人的心理需求D 、该餐厅设有“点餐车道入口”的指示牌,便于司机把车开到点餐窗口,主要考虑了人机关系 中信息的交互3、人们不断探索宇宙,对飞行器可靠性、耐久性等指标的要求也越来越高。
考虑到成本因素, 许多试验由计算机仿真技术来代替,设计与试验融为一体,这是一项及其复杂的综合技术。
该 试验的方法属于( )A.虚拟试验法B.模拟试验法C.优选试验法D.强化试验法4.如图所示是一款头戴护耳式耳机及评价图,音质好,护耳柔软舒适,两耳间距可以轻松调节, 以下对坐标图的分析中不.恰.当.的是( )图A.该产品简约时尚,形态较新颖B.该产品的音质如身临其境,透彻清晰,实用性好C.坐标图评价的依据是事先制定的设计要求与设计的一般原则相结合D.该产品非常符合经济原则5、如图所示为一款 led 植物补光灯,该产品可轻松固定在桌子一侧,采用管状式设计,简约美观,采用 led 芯片,节能环保。
浙江省温州市新力量联盟2018-2019学年高二上学期期末考试信息技术试题

2018 学年第一学期温州新力量联盟期末联考高二年级技术学科试题命题:白象中学陈栩杨彬夏磨题:温溪高中陈苗苗考生须知:1.本试题卷分两部分,第一部分信息技术满分50分,第二部分通用技术满分50分。
全卷共14 页,第一部分1-8页,第二部分1-6页。
满分100分,考试时间90 分钟。
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号。
3.所有答案必须写在答题卷上,写在试卷上无效。
4.考试结束后,只需上交答题卷。
第一部分信息技术(共50分)一、选择题(本大题共12小题,第小题2分,共24分,每小题列出的四个备选项中只有一个是符合题目要求的,不选、错选、多选均不得分)1.下列说法正确的是()A.“VR全景”使用户体验到身临其境的感觉,所以它采用的是人工智能技术。
B.信息可以脱离它所反映的事物被存储、保留和传播,所以信息可以脱离载体C.“蓝牙”音箱是一种主要用于将声音的模拟信号转换为数字信号的设备D.“抖音”的走红使得微视频成为时下热门的信息表达方式2.使用Word软件编辑某文档,部分界面如图所示:第2题图下列说法正确的是()A.文档中文字环绕方式为“嵌入环绕”。
B.接受所有修订后,第六行的内容变成“一怪味便向所有人宣告面世。
”。
C.用户“桑三博客2”对“APP”添加了批注。
D.利用“自动更正”功能可以将文中所有的“APP”改成“应用程序”。
3.小丽用 UltraEdit 软件观察“新高考‘7 选3’”这几个字,显示的十六进制内码如图所示。
则“10 选4”这几个字对应的内码用十六进制表示是()则"10选4"这几个字对应得内码用十六进制表示是()A.40 D1 A1 34B.31 30 D1 A1 32C.34 D1 A1 40D.31 30 D1 A1 344.关于在ACCESS数据表中的操作,下列说法正确的是()A.在数据表打开状态下可以对数据表进行重命名B.在数据表视图中设置为主键的字段是不能删除的C.字段数据类型若为“自动编号”,则新值一定是递增的D.日期类型的字段可以输入“2018\12\12”5 .某算法流程图如图所示:第5题图执行该流程图后,输出i,k的值分别是A.102,9B.102,8C.100,9D.100,86.用GoldWave软件编辑音频文件“音乐.wav”,界面如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018学年第一学期温州新力量联盟期中联考
高二年级技术学科参考答案
第一部分信息技术(共50分)
一、选择题(本大题共12小题,每小题2分,共24分,在每小题给出的四个选项中,只有一个符合题目要求)
二、非选择题(本大题共5小题,共26分,其中13题4分,14题4分,15题7分,16题4分,
17题7分)
13.(1)○4○3○1○2(1分)
(2)文章.jpg (1分)、文章.txt (1分)、○1(1分)14.(1)罗中学籍.accdb (1分)
(2) 2018级(1分)、 B (1分)
(3)一个字段(1分)
15.(1) =C25/B25*E25 (1分)
(2)数据保留两位小数(其他等价答案)(2分)
(3) 15-19岁(1分)
(4) A5:A25,C5:D25 (2分)、 0-4岁(1分)
16.(1) caption (1分)
(2)① a=text1.text (1分)、② mid(b,i,1) (2分)
17.(1) Command1 (1分)
(2)① len(s) (2分)、② m1*10+val(s1) (2分)③ str(t) (1分)(3) 8932 (1分)
第二部分通用技术(共50分)
一、选择题(本大题共13小题,每小题2分,共26分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)
二、非选择题(本大题共 3 小题,第 14 小题 5 分,第 15 小题 7 分,第 15 小题 12 分,共
24 分)
14.(5分,每空一分)
(1) C A D ;(有顺序)
(2) B , D
15.根据轴测图,补全三视图中缺少的七条图线(每条线1分,共7分)
16.(12分)
(1) A (1分)
(2) B C (2分)
(3)(4)共(9分,草图部分6分,尺寸部分3分)
草图略,
草图部分6分,其中连续可调2分,高度可调2分,设计合理2分。
