第七章弯曲变形第二节叠加法
合集下载
材料力学07弯曲变形_2叠加法

第六节 简单超静定梁
q
A
B
l
求解简单超静定梁的基本步骤 ——
1. 解除多余约束,以相应的多余未知力代之作用,得到原超静 定梁的相当系统;
2. 根据多余约束处的位移条件,建立变形协调方程;
3. 计算相当系统在多余约束处的相应位移,由变形协调方程得 补充方程;
4. 由补充方程求出多余未知力,即转为静定问题。
F
2EI
EI
A
B
C
Байду номын сангаас
l/2
l/2
[例3] 外伸梁如图,试用叠加法计算截面 C 的挠度 wC 和转角C ,
设梁的抗弯刚度 EI 为常量。
F
A
B
C
l
a
[例4] 如图,在简支梁的一半跨度内作用均布载荷 q ,试用叠加 法计算截面 C 的挠度 wC。设梁的抗弯刚度 EI 为常量。
q
A
C
B
l/2
l/2
第五节 弯曲刚度计算
max
400
故梁的刚度满足要求
[例2] 图示工字钢简支梁,在跨中承受集中力 F 作用。已知 F =
35 kN,跨度 l = 4 m ,许用应力 [ ] = 160 MPa ,许用挠度 [w ] =
l / 500 ,弹性模量 E = 200 GPa 。试选择工字钢型号。
解: 1)强度计算
最大弯矩
M max
w Fl3 max 48EIz
根据梁的刚度条件
w Fl3 ≤w l
max 48EIz
500
得梁截面对中性轴的惯性矩
Iz
≥ 500Fl2 48E
2.92 105
m4
叠加法求梁弯曲变形

( )F1F2 ( )F1 ( )F2
二、叠加法应用 结合查表4.2,求某特定截面的挠度和转角。
例 如图示的简支梁,抗弯刚度为EI,集中载荷F,均布 载荷q,求wC及θ A、θB。
F q
A
B C
2
2
wC
wC q
wC F
5ql 4 384EI
Fl 3 48EI
A
B
A
q
A
F
ql 3 24EI
θ
′
B
θ
″
B
w′A w″A
θ
″
B
12 2
Fl 2 16EI
例 试用叠加法求图示的简支梁跨度中点的挠度wC 和
两端截面的转角θ A、θB ,梁的抗弯刚度为EI 。
5(q 2)l 4
5ql 4
wC1 384EI
768EI
A1
B1
(q 2)l3 24EI
ql 3 48EI
wC 2 0
A2
B2
(q
2)(l 2)3 24EI
叠加法求梁的变形 ---基本原理及应用
一、叠加法 1.力的独立作用原理
线弹性结构发生小变形时,力对结构的作用不因 其它力的存在而改变。
2.叠加原理 线弹性梁发生小变形时,挠度和转角与载荷是线 性关系,所以几种载荷共同作用下的挠度和转角, 等于每个载荷单独作用下挠度和转角的叠加。
(w)F1F2 (w)F1 (w)F2
1)在qa单独作用时,
B
qa(qa) 2 16EI
qa 3 4EI
wA
B
a
qa 4 4EI
2)在均布载荷q单独作用时 逐段刚化法
左段刚化,BA段为悬臂梁
二、叠加法应用 结合查表4.2,求某特定截面的挠度和转角。
例 如图示的简支梁,抗弯刚度为EI,集中载荷F,均布 载荷q,求wC及θ A、θB。
F q
A
B C
2
2
wC
wC q
wC F
5ql 4 384EI
Fl 3 48EI
A
B
A
q
A
F
ql 3 24EI
θ
′
B
θ
″
B
w′A w″A
θ
″
B
12 2
Fl 2 16EI
例 试用叠加法求图示的简支梁跨度中点的挠度wC 和
两端截面的转角θ A、θB ,梁的抗弯刚度为EI 。
5(q 2)l 4
5ql 4
wC1 384EI
768EI
A1
B1
(q 2)l3 24EI
ql 3 48EI
wC 2 0
A2
B2
(q
2)(l 2)3 24EI
叠加法求梁的变形 ---基本原理及应用
一、叠加法 1.力的独立作用原理
线弹性结构发生小变形时,力对结构的作用不因 其它力的存在而改变。
2.叠加原理 线弹性梁发生小变形时,挠度和转角与载荷是线 性关系,所以几种载荷共同作用下的挠度和转角, 等于每个载荷单独作用下挠度和转角的叠加。
(w)F1F2 (w)F1 (w)F2
1)在qa单独作用时,
B
qa(qa) 2 16EI
qa 3 4EI
wA
B
a
qa 4 4EI
2)在均布载荷q单独作用时 逐段刚化法
左段刚化,BA段为悬臂梁
材料力学:第七章 弯曲变形

刚度设计依据
(1) 挠度w大小取决于M, E, I三个参数 应该取较小的M, 较大的E, I
(2) 弯矩M大小取决于载荷\约束分布及梁跨度大小
(3) 截面惯性矩I 大小和截面形状有关,
弹性模量E大小和材料有关
Iz =
y2dA,
A
当A大小一定时, y越大, I 越大
梁的合理刚度设计
选择I 较大的薄壁横截面形状
1 度静不定 选 FBy 为多余力, 去约 束, 写出位移边界条件
-变形协调条件 -物理方程
利用边界条件 解出未知力
列平衡方程,求其他约束力:
-补充方程
分析方法与步骤:
判断梁的静不定度
用多余力代替多余约
束的作用,得相当系统
相当系统
相当系统有多种选择:
计算相当系统在多余约
束处的位移,并根据变形 协调条件建立补充方程。
例题
解:
()
()
例题
例题
解:
()
()
()
例题
图示组合梁,EI=常数,求 wB 与qA
例题
解:
P378, 情况8
()
P377, 情况1,2
()
例题
图示刚架,求截面 C 的铅垂位移
例题
解:
位移w1包括AB弯曲 和AB扭转两部分
例题
矩形截面梁, 自由端承受集中载荷F作用, 该载荷与对 称轴y的夹角为θ, 用叠加法计算自由端求自由端截面形心C
的位移d
解:
例题
一般情况下
挠曲轴与外力作用面一般不重合
§6 简单静不定梁
静不定度与多余约束 简单静不定梁分析方法
静不定度与多余约束
静不定度 4-3= 1
(1) 挠度w大小取决于M, E, I三个参数 应该取较小的M, 较大的E, I
(2) 弯矩M大小取决于载荷\约束分布及梁跨度大小
(3) 截面惯性矩I 大小和截面形状有关,
弹性模量E大小和材料有关
Iz =
y2dA,
A
当A大小一定时, y越大, I 越大
梁的合理刚度设计
选择I 较大的薄壁横截面形状
1 度静不定 选 FBy 为多余力, 去约 束, 写出位移边界条件
-变形协调条件 -物理方程
利用边界条件 解出未知力
列平衡方程,求其他约束力:
-补充方程
分析方法与步骤:
判断梁的静不定度
用多余力代替多余约
束的作用,得相当系统
相当系统
相当系统有多种选择:
计算相当系统在多余约
束处的位移,并根据变形 协调条件建立补充方程。
例题
解:
()
()
例题
例题
解:
()
()
()
例题
图示组合梁,EI=常数,求 wB 与qA
例题
解:
P378, 情况8
()
P377, 情况1,2
()
例题
图示刚架,求截面 C 的铅垂位移
例题
解:
位移w1包括AB弯曲 和AB扭转两部分
例题
矩形截面梁, 自由端承受集中载荷F作用, 该载荷与对 称轴y的夹角为θ, 用叠加法计算自由端求自由端截面形心C
的位移d
解:
例题
一般情况下
挠曲轴与外力作用面一般不重合
§6 简单静不定梁
静不定度与多余约束 简单静不定梁分析方法
静不定度与多余约束
静不定度 4-3= 1
第七章 弯曲变形

w
B2
wC 2
(ql)l 3 48 EI
第六节 梁变形的叠加解法
ql 3 ql3 ql 3 11ql3 B B1 B 2 B3 24 EI 3EI 16 EI 48 EI
5ql 4 3ql 4 (ql)l 3 11ql 4 wC wC1 wC 2 wC 3 384 EI 48 EI 48 EI 384 EI
dy = dx
第一节 弯曲变形的基本概念
约束对位移的影响
没有约束无法确定位移
第一节 弯曲变形的基本概念
连续光滑曲线;铰支座对位移的限制
第一节 弯曲变形的基本概念
连续光滑曲线;固定端对位移的限制
第二节 挠曲线近似微分方程
力学公式
1 M ( x) ( x) EI z
数学公式
以上两式消去
a Fa 3F 拐点 (-)
a
(+)
M 图
极值,在挠度最大处,截
面的转角不一定为零,在 弯矩最大处,挠度不一定
Fa
最大。
下凸
上凸
直线
第四节 梁的刚度校核
刚度条件:
y max [ y ],
max
[ ]
[y]——许用挠度,[]——许用转角
工程中, [y]常用梁的计算跨度l 的若干分之一表示,例如: l l ~ 对于桥式起重机梁: [ y] 500 750 对于一般用途的轴:
y f (x)
y (x )
y
水平方向位移:高阶微 量,忽略不计。
第一节 弯曲变形的基本概念
角位移:横截面相对于原
来位置转过的角度,以表
示。亦可以用该截面处的
y
材料力学-第7章 弯曲变形

引言
梁弯曲问题的近似和简化
q( x)
M0
ML
Q0
QL
弯曲问题中,不考虑轴向拉伸。因此,梁内力只有弯矩和剪力 下面,我们分别考虑弯矩和剪力引起的弯曲变形效果
材料力学-第7章 弯曲变形
挠度曲线 垂直于轴线的横截面弯曲后仍为平面,仍 垂直于轴线,只是相互间转动一个角度
M
弯矩引起的弯曲变形
M
剪力引起的弯曲变形
例题
2
已知:简支梁受力如 图所示。FP、EI、l均为已 知。 求:加力点B的挠度和 支承A、C处的转角。
材料力学-第7章 弯曲变形
§7- 3 计算梁位移的积分法
解:1. 确定梁约束力 首先,应用静力学方法求得 梁在支承A、C二处的约束力分别 如图中所示。 解:2. 分段建立梁的弯矩方程 因为B处作用有集中力FP,所以需要分为AB和BC两段 建立弯矩方程。 在图示坐标系中,为确定梁在0~l/4范围内各截面上的 弯矩,只需要考虑左端A处的约束力3FP/4;而确定梁在l/4~ l范围内各截面上的弯矩,则需要考虑左端A处的约束力 3FP/4和荷载FP。
Q
垂直于轴线的横截面弯曲后不垂直于轴线
Q
材料力学中一般考虑细长梁,顾而可以忽略剪力引起的变形,只 考虑弯矩引起的变形。因为所有横截面始终与轴线垂直,所以,梁的 弯曲变形可以仅用轴线来表征。空间的梁简化成一轴线。
材料力学-第7章 弯曲变形
挠度曲线
问题1: 如何表征梁的弯曲变形
-用什么物理量来描述梁的变形
( x)
w
x
x
( x)
w( x)
材料力学-第7章 弯曲变形
挠度曲线
* 弯曲变形的表征
梁在弯曲变形后,横截面的位置将发生改变,这种位置 的改变称为位移 (displacement) 。梁的位移包括三部分:
梁弯曲问题的近似和简化
q( x)
M0
ML
Q0
QL
弯曲问题中,不考虑轴向拉伸。因此,梁内力只有弯矩和剪力 下面,我们分别考虑弯矩和剪力引起的弯曲变形效果
材料力学-第7章 弯曲变形
挠度曲线 垂直于轴线的横截面弯曲后仍为平面,仍 垂直于轴线,只是相互间转动一个角度
M
弯矩引起的弯曲变形
M
剪力引起的弯曲变形
例题
2
已知:简支梁受力如 图所示。FP、EI、l均为已 知。 求:加力点B的挠度和 支承A、C处的转角。
材料力学-第7章 弯曲变形
§7- 3 计算梁位移的积分法
解:1. 确定梁约束力 首先,应用静力学方法求得 梁在支承A、C二处的约束力分别 如图中所示。 解:2. 分段建立梁的弯矩方程 因为B处作用有集中力FP,所以需要分为AB和BC两段 建立弯矩方程。 在图示坐标系中,为确定梁在0~l/4范围内各截面上的 弯矩,只需要考虑左端A处的约束力3FP/4;而确定梁在l/4~ l范围内各截面上的弯矩,则需要考虑左端A处的约束力 3FP/4和荷载FP。
Q
垂直于轴线的横截面弯曲后不垂直于轴线
Q
材料力学中一般考虑细长梁,顾而可以忽略剪力引起的变形,只 考虑弯矩引起的变形。因为所有横截面始终与轴线垂直,所以,梁的 弯曲变形可以仅用轴线来表征。空间的梁简化成一轴线。
材料力学-第7章 弯曲变形
挠度曲线
问题1: 如何表征梁的弯曲变形
-用什么物理量来描述梁的变形
( x)
w
x
x
( x)
w( x)
材料力学-第7章 弯曲变形
挠度曲线
* 弯曲变形的表征
梁在弯曲变形后,横截面的位置将发生改变,这种位置 的改变称为位移 (displacement) 。梁的位移包括三部分:
北京航空航天大学-材料力学课件ppt-14+第七章+弯曲变形
3. 求 wC
17 Fa 3
A
Fa
C
B
wC 2
wC1
wB
wC
wC1 wC 2
48EI
4EA
D
a
H
4. 比较弯曲与拉压位移 A bh, I bh3 12
设b×h矩形截面
17 Fa 3 48EI
Fa 4EA
17
a h
2
结论: (如果题意没有要求),拉压与弯曲共同
作用时,拉压引起的位移可以忽略。
18
第七章 弯曲变形
§7-6 简单静不定梁
• 静不定度与多余约束
q(x)
M
5-3=2 度静不定
q(x)
F
6-3 = 3 度静不定
静不定度 =支反力(力偶)数-有效平衡方程数 多余约束 多于维持平衡所必须的约束
静不定度=多余约束数 多余反力 与多余约束相应的支反力或支力偶矩
19
第七章 弯曲变形
静定基与相当系统
例: 求图示外伸梁C点 的挠度和转角
q
C B
l
a
q
仅考虑BC段变形(刚化AB,可
A
视BC为悬臂梁)
qa4 wC1 8EI ()
C1
qa 3 6EI
()
B
l
qa
仅考虑AB段变形(刚化BC)
A
B
C2
B2
qa2l 6EI
()
总挠度和转角
wC 2
B2a
qa3l 6EI
()
l
qa 3 wC wC1 wC 2 24EI (3a 4l ) ()
0
0
wB 0, B 0
A
B
25
用叠加法求弯曲变形
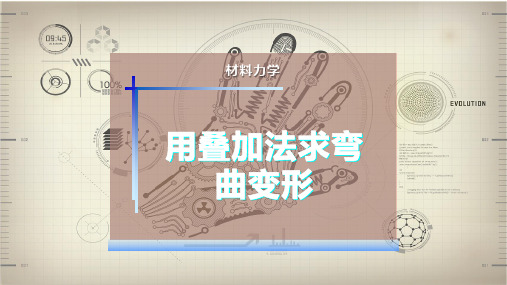
yC
3 i 1
yCi
5ql4 384EI
ql 4 48EI
ql4 16EI
11ql4 ( ) 384EI
B
3
Bi
i 1
ql3 24EI
ql3 16EI
ql3 3EI
11ql3 ( ) 48EI
目录
材料力学 材料力学
用叠加法求弯曲变形
例4 已知:悬臂梁受力如图示,q、l、
yC
EI均为已知。求C截面的挠度yC和转角C
材料力学
材料力学
用叠加法求弯曲变形
设梁上有n 个载荷同时作用,任意截面上的弯矩 为M(x),转角为 ,挠度为y,则有:
EI
d2y dx2
EIy''
M(x)
若梁上只有第i个载荷单独作用,截面上弯矩
为 M i ( x) ,转角为 i ,挠度为 yi ,则有:
EIy''i Mi ( x)
材料力学
7-4
解 1)首先,将梁上的载荷变成有表可查 的情形
为了利用梁全长承受均布载荷 的已知结果,先将均布载荷延长至梁 的全长,为了不改变原来载荷作用的 效果,在AB 段还需再加上集度相同、 方向相反的均布载荷。
目录
材料力学 材料力学
用叠加法求弯曲变形
2)再将处理后的梁分解为简单载荷作用
yC
的情形,计算各自C截面的挠度和转角。
等于在各个载荷单独作用时的挠度或转角的代数 和。这就是计算弯曲变形的叠加原理。
材料力学
目录
材料力学 材料力学
用叠加法求弯曲变形
例3 已知简支梁受力如图示,q、l、EI 均为已知。求C 截面的挠度yC ;B截面的 转角B
用叠加法求弯曲变形

a=0.1m
A
A
D
B
C
200mm F1=1kN F2=2kN
B
D
C
F2
=+ =+
A
D
B
F1=1kN
A B
C
C
A
F2=2kN
B
aC
F2
F2 M
DB
C
l=400mm
a=0.1m
解:(1)结构变换,查表求简
A
D
B
200mm F1=1kN
图1
D
C
单载荷变形.
F2=2kN
1B
F1l 2 16EI
C
w1C
wA
qa4 3EI
qa4 4EI
7qa4 12EI
二、刚度条件(Stiffness condition)
1.数学表达式(Mathematical formula)
wmax [w]
max [ ] [w]和 [ ] 是构件的许可挠度和转角.
2. 刚度条件的应用(Application of stiffness condition) (1)校核刚度( Check the stiffness of the beam) (2)设计截面尺寸(Determine the allowable load on the beam)
求梁跨中点的挠度 wC和支座处横截面的转角A , B 。
Me
q
A
B
C
l
解:将梁上荷载分为两
Me
项简单的荷载,如图所示
A
wC (wC)q (wC)Me
(a)
5ql 4 Mel 2 384EI 16EI
(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3)建立补充方程
11Fl 3 FBl 3 wB 0 96 EI 6 EI
4)求解多余未知力
解得
11F FB 13.75 kN 16
FB 13.75 kN
5) 强度计算 作弯矩图
最大弯矩
M max 2.03 kN m
根据梁的弯曲正应力
强度条件
max
M max 95.7 MPa Wz
1
F1a3 F1a3 3EI 2EI 5F1a3 6EI
a
A
B1
B
C
B F
1
a
C1
B
C
a
a
F2
2)在F2 和单独作用下
F1
A
B
C
wC F
2
F1 2a 3EI
3
aF wC F
1
2
5F1a3 8F2a3 6EI 3EI
查型钢表,得 Iz = 1660 cm4
梁的最大挠度发生在中间截 面,为
w max
由于
5ql 4 7.26 103 m = 7.26 mm 384 EI
w max
l 7.26 mm < w 7.5 mm 400
故梁的刚度满足要求
[例2] 图示工字钢简支梁,在跨中承受集中力 F 作用。已知 F = 35 kN,跨度 l = 4 m ,许用应力 [ ] = 160 MPa ,许用挠度 [w ] = l / 500 ,弹性模量 E = 200 GPa 。试选择工字钢型号。
是叠加原理.
1.载荷叠加(Superposition of loads)
多个载荷同时作用于结构而引起的变形等于每个载荷单独作用于结构而引起 的变形的代数和.
( F1 , F2 , , Fn ) 1 ( F1 ) 2 ( F2 ) n ( Fn )
w( F1 , F2 , , Fn ) w1 ( F1 ) w2 ( F2 ) wn ( Fn )
B
F
C
EI
l /2
F
l /2
2)令BC 不变形,只考虑AB变形
B
C1
C
F
A
B
M e Fl / 2
C
2)令BC 不变形,只考虑AB变形 ( a )在F作用下
A
3
2EI
B
F
EI
C
w
C2
F
5F l / 2 6 2 EI
l /2
l /2
F
A
B
( b )在Me作用下 Me l / 2 B2 Me 2 EI
A
F
wmax
B
2)刚度计算 最大挠度发生于跨中截面,为
w max Fl 3 48EI z
l /2
l /2
根据梁的刚度条件
w max
Fl 3 l ≤ w 48EI z 500
得梁截面对中性轴的惯性矩
500 Fl 2 Iz ≥ 2.92 105 m4 48E
查型钢表,No. 22a 工字钢的 Wz = 3.09 104 m3、Iz =3.40105 m4 ,
[例5] 图示简支梁由 No. 18 工字钢制成,长度 l = 3 m ,受 q = 24 kN/m 的均布载荷作用。材料的弹性模量 E = 210 GPa ,许用应 力 [ ] = 150 MPa ,梁的许可挠度 [w ] = l / 400 。试校核梁的强度 和刚度。
w
q
B
l
x
解: 1)强度校核 最大弯矩
一、梁的刚度条件
w max ≤ w
式中,[w] 为梁的许用挠度
二、提高梁的弯曲刚度的措施 1. 合理选材 选用弹性模量 E 较高的材料 结论:用高强度合金钢取代普通碳钢对于提高弯曲刚度没有意义 2. 采用合理的截面形状 选用具有较高 Iz / A 比值的截面形状 结论:工字形截面较为合理 3. 减小梁的跨度
4. 由补充方程求出多余未知力,即转为静定问题。
[例3] 图示圆形截面梁,承受集中力 F 作用。已知 F = 20 kN,跨度 l = 500mm,截面直径 d = 60 mm,材料的许用应力 [ ] = 100 MPa,
试校核该梁的强度。
解: 1)解除多余约束 2)建立变形协调方程
wB 0
同时满足梁的强度和刚度要求,故可选取No. 22a 工字钢。
q
第六节 简单超静定梁
A
B
l
求解简单超静定梁的基本步骤 —— 1. 解除多余约束,以相应的多余未知力代之作用,得到原超静 定梁的相当系统; 2. 根据多余约束处的位移条件,建立变形协调方程;
3. 计算相当系统在多余约束处的相应位移,由变形协调方程得 补充方程;
l /2
l /2
F
A
B
M e Fl / 2
C
F
A
B
C
C2 F
B2 F
F l / 2
3
3EI 3Fl 3 16 EI
7 Fl 3 48EI
A
M e Fl / 2
B2 M e
B
C
C2 M e
[例3] 外伸梁如图,试用叠加法计算截面 C 的挠度 wC 和转角C , 设梁的抗弯刚度 EI 为常量。 解:
2.结构形式叠加(逐段刚化法)
[例1] 图示悬臂梁,同时承受集中载荷 F1 和 F2 的作用。设梁的 抗弯刚度为 EI,试用叠加法计算自由端 C 的挠度 wC 。 解:1)在F1 和单独作用下
F1
A
B
B F
1
F1a 2EI
2
C
a
F1
A
1
a
F2
wB F
1
F1a3 3EI
1
wC F wB F B F a
解: 1)强度计算
最大弯矩
M max Fl 3.5 104 N m 4
F
A
B
l /2
l /2
根据梁的正应力强度条件,得梁的抗弯截面系数
Wz ≥
M max
3.5 104 N m 4 3 2.19 10 m 160 106 Pa
Wz ≥ 2.19 104 m3
A
a
F1 B
C
a
F2
[例2] 阶梯悬臂梁如图,试求自由端端 C 的挠度 wC 。已知 BC 段 梁的抗弯刚度为为 EI、AB 段梁的抗弯刚度为为 2EI。
解:该梁可看做由悬臂梁AB和固定在横截面B上的悬臂梁BC组成
1)令AB不变形,只考虑BC变形
wC1 F l / 2 3EI
3
A
2EI
F
A
l
B
C
a
[例4] 如图,在简支梁的一半跨度内作用均布载荷 q ,试用叠加 法计算截面 C 的挠度 wC 。设梁的抗弯刚度 EI 为常量。 解:
A
q
C
l /2 l /2
B
叠加法的要点 ——
1)叠加法适用前提:线弹性、小变形 2)记住常用结论 3)必须画出叠加变形图
4)掌握叠加法的常用技巧
第五节 弯曲刚度计算
M e Fl / 2
C
F
2
w
B2
Me
M e l / 2 4EI
e
A
w
C2 M e
wB M B M l / 2
e
B2 F
B
C
C2 F
Ml M ll e e 16EI 4EI 2 3M el 2 16EI
2
A
M e Fl / 2
B2 M e
B
C
C2 M e
2)令BC 不变形,只考虑AB变形
wC2 wC2
Me
2
wC2
3
A
F
2EI
B
F
EI
C
3M el 5Fl 16 EI 96 EI 3 Fl / 2 l 2 5Fl 3 16EI 96EI 7 Fl 3 48 EI wC wC1 wC2
A
M max
ql 27 103 N m 8
2
查型钢表,Wz = 186 cm3, 根据弯曲正应力强度条件
max
M max 27 103 146 MPa < 150 MPa 6 Wz 185 10
故梁的强度满足要求
w
q
wmax
2)梁的刚度校核
A
l
B
x
100MPa
结论:该梁的强度符合要求
第四节 计算弯曲变形的叠加法 (Beam deflections by superposition ) 一、叠加原理 (Superposition)
梁的变形微小, 且梁在线弹性范围内工作时, 梁在几项荷载
(可以是集中力, 集中力偶或分布力)同时作用下的挠度和转角, 就分别等于每一荷载单独作用下该截面的挠度和转角的叠加. 当 每一项荷载所引起的挠度为同一方向(如均沿w轴方向), 其转角 是在同一平面内(如均在 xy 平面内)时,则叠加就是代数和. 这就
11Fl 3 FBl 3 wB 0 96 EI 6 EI
4)求解多余未知力
解得
11F FB 13.75 kN 16
FB 13.75 kN
5) 强度计算 作弯矩图
最大弯矩
M max 2.03 kN m
根据梁的弯曲正应力
强度条件
max
M max 95.7 MPa Wz
1
F1a3 F1a3 3EI 2EI 5F1a3 6EI
a
A
B1
B
C
B F
1
a
C1
B
C
a
a
F2
2)在F2 和单独作用下
F1
A
B
C
wC F
2
F1 2a 3EI
3
aF wC F
1
2
5F1a3 8F2a3 6EI 3EI
查型钢表,得 Iz = 1660 cm4
梁的最大挠度发生在中间截 面,为
w max
由于
5ql 4 7.26 103 m = 7.26 mm 384 EI
w max
l 7.26 mm < w 7.5 mm 400
故梁的刚度满足要求
[例2] 图示工字钢简支梁,在跨中承受集中力 F 作用。已知 F = 35 kN,跨度 l = 4 m ,许用应力 [ ] = 160 MPa ,许用挠度 [w ] = l / 500 ,弹性模量 E = 200 GPa 。试选择工字钢型号。
是叠加原理.
1.载荷叠加(Superposition of loads)
多个载荷同时作用于结构而引起的变形等于每个载荷单独作用于结构而引起 的变形的代数和.
( F1 , F2 , , Fn ) 1 ( F1 ) 2 ( F2 ) n ( Fn )
w( F1 , F2 , , Fn ) w1 ( F1 ) w2 ( F2 ) wn ( Fn )
B
F
C
EI
l /2
F
l /2
2)令BC 不变形,只考虑AB变形
B
C1
C
F
A
B
M e Fl / 2
C
2)令BC 不变形,只考虑AB变形 ( a )在F作用下
A
3
2EI
B
F
EI
C
w
C2
F
5F l / 2 6 2 EI
l /2
l /2
F
A
B
( b )在Me作用下 Me l / 2 B2 Me 2 EI
A
F
wmax
B
2)刚度计算 最大挠度发生于跨中截面,为
w max Fl 3 48EI z
l /2
l /2
根据梁的刚度条件
w max
Fl 3 l ≤ w 48EI z 500
得梁截面对中性轴的惯性矩
500 Fl 2 Iz ≥ 2.92 105 m4 48E
查型钢表,No. 22a 工字钢的 Wz = 3.09 104 m3、Iz =3.40105 m4 ,
[例5] 图示简支梁由 No. 18 工字钢制成,长度 l = 3 m ,受 q = 24 kN/m 的均布载荷作用。材料的弹性模量 E = 210 GPa ,许用应 力 [ ] = 150 MPa ,梁的许可挠度 [w ] = l / 400 。试校核梁的强度 和刚度。
w
q
B
l
x
解: 1)强度校核 最大弯矩
一、梁的刚度条件
w max ≤ w
式中,[w] 为梁的许用挠度
二、提高梁的弯曲刚度的措施 1. 合理选材 选用弹性模量 E 较高的材料 结论:用高强度合金钢取代普通碳钢对于提高弯曲刚度没有意义 2. 采用合理的截面形状 选用具有较高 Iz / A 比值的截面形状 结论:工字形截面较为合理 3. 减小梁的跨度
4. 由补充方程求出多余未知力,即转为静定问题。
[例3] 图示圆形截面梁,承受集中力 F 作用。已知 F = 20 kN,跨度 l = 500mm,截面直径 d = 60 mm,材料的许用应力 [ ] = 100 MPa,
试校核该梁的强度。
解: 1)解除多余约束 2)建立变形协调方程
wB 0
同时满足梁的强度和刚度要求,故可选取No. 22a 工字钢。
q
第六节 简单超静定梁
A
B
l
求解简单超静定梁的基本步骤 —— 1. 解除多余约束,以相应的多余未知力代之作用,得到原超静 定梁的相当系统; 2. 根据多余约束处的位移条件,建立变形协调方程;
3. 计算相当系统在多余约束处的相应位移,由变形协调方程得 补充方程;
l /2
l /2
F
A
B
M e Fl / 2
C
F
A
B
C
C2 F
B2 F
F l / 2
3
3EI 3Fl 3 16 EI
7 Fl 3 48EI
A
M e Fl / 2
B2 M e
B
C
C2 M e
[例3] 外伸梁如图,试用叠加法计算截面 C 的挠度 wC 和转角C , 设梁的抗弯刚度 EI 为常量。 解:
2.结构形式叠加(逐段刚化法)
[例1] 图示悬臂梁,同时承受集中载荷 F1 和 F2 的作用。设梁的 抗弯刚度为 EI,试用叠加法计算自由端 C 的挠度 wC 。 解:1)在F1 和单独作用下
F1
A
B
B F
1
F1a 2EI
2
C
a
F1
A
1
a
F2
wB F
1
F1a3 3EI
1
wC F wB F B F a
解: 1)强度计算
最大弯矩
M max Fl 3.5 104 N m 4
F
A
B
l /2
l /2
根据梁的正应力强度条件,得梁的抗弯截面系数
Wz ≥
M max
3.5 104 N m 4 3 2.19 10 m 160 106 Pa
Wz ≥ 2.19 104 m3
A
a
F1 B
C
a
F2
[例2] 阶梯悬臂梁如图,试求自由端端 C 的挠度 wC 。已知 BC 段 梁的抗弯刚度为为 EI、AB 段梁的抗弯刚度为为 2EI。
解:该梁可看做由悬臂梁AB和固定在横截面B上的悬臂梁BC组成
1)令AB不变形,只考虑BC变形
wC1 F l / 2 3EI
3
A
2EI
F
A
l
B
C
a
[例4] 如图,在简支梁的一半跨度内作用均布载荷 q ,试用叠加 法计算截面 C 的挠度 wC 。设梁的抗弯刚度 EI 为常量。 解:
A
q
C
l /2 l /2
B
叠加法的要点 ——
1)叠加法适用前提:线弹性、小变形 2)记住常用结论 3)必须画出叠加变形图
4)掌握叠加法的常用技巧
第五节 弯曲刚度计算
M e Fl / 2
C
F
2
w
B2
Me
M e l / 2 4EI
e
A
w
C2 M e
wB M B M l / 2
e
B2 F
B
C
C2 F
Ml M ll e e 16EI 4EI 2 3M el 2 16EI
2
A
M e Fl / 2
B2 M e
B
C
C2 M e
2)令BC 不变形,只考虑AB变形
wC2 wC2
Me
2
wC2
3
A
F
2EI
B
F
EI
C
3M el 5Fl 16 EI 96 EI 3 Fl / 2 l 2 5Fl 3 16EI 96EI 7 Fl 3 48 EI wC wC1 wC2
A
M max
ql 27 103 N m 8
2
查型钢表,Wz = 186 cm3, 根据弯曲正应力强度条件
max
M max 27 103 146 MPa < 150 MPa 6 Wz 185 10
故梁的强度满足要求
w
q
wmax
2)梁的刚度校核
A
l
B
x
100MPa
结论:该梁的强度符合要求
第四节 计算弯曲变形的叠加法 (Beam deflections by superposition ) 一、叠加原理 (Superposition)
梁的变形微小, 且梁在线弹性范围内工作时, 梁在几项荷载
(可以是集中力, 集中力偶或分布力)同时作用下的挠度和转角, 就分别等于每一荷载单独作用下该截面的挠度和转角的叠加. 当 每一项荷载所引起的挠度为同一方向(如均沿w轴方向), 其转角 是在同一平面内(如均在 xy 平面内)时,则叠加就是代数和. 这就
