数学实验报告格式
数学调查实验报告(3篇)

第1篇一、实验背景随着社会经济的快速发展,数学作为一门基础学科,在各个领域都发挥着重要作用。
为了提高学生的数学素养,激发学生学习数学的兴趣,培养学生的实践能力,我们开展了一次数学调查实验。
本次实验旨在了解学生在数学学习中的困难、需求以及兴趣点,为今后的数学教学提供参考。
二、实验目的1. 了解学生在数学学习中的困难、需求以及兴趣点;2. 分析学生数学学习现状,为教师改进教学方法提供依据;3. 培养学生的实践能力,提高学生的数学素养。
三、实验方法1. 实验对象:选取我校高一年级100名学生作为实验对象;2. 实验内容:设计调查问卷,包括数学学习困难、需求、兴趣点等方面;3. 实验步骤:(1)制定调查问卷;(2)发放问卷,收集数据;(3)对数据进行分析处理;(4)撰写实验报告。
四、实验结果与分析1. 数学学习困难分析(1)学生在数学学习中的困难主要集中在以下几个方面:①基础知识掌握不牢固;②解题技巧不足;③缺乏对数学问题的思考能力;④学习兴趣不高。
(2)针对以上困难,教师可以采取以下措施:①加强基础知识教学,帮助学生打好基础;②开展解题技巧培训,提高学生解题能力;③引导学生学会思考,培养问题意识;④激发学生学习兴趣,提高学习积极性。
2. 数学学习需求分析(1)学生在数学学习中的需求主要包括:①提高数学成绩;②掌握解题技巧;③提高逻辑思维能力;④拓展知识面。
(2)针对以上需求,教师可以采取以下措施:①制定合理的教学计划,确保教学目标达成;②注重解题技巧训练,提高学生解题能力;③开展思维训练活动,培养学生的逻辑思维能力;④丰富教学内容,拓展学生的知识面。
3. 数学学习兴趣点分析(1)学生在数学学习中的兴趣点主要包括:①数学竞赛;②数学应用;③数学趣味知识;④数学史。
(2)针对以上兴趣点,教师可以采取以下措施:①举办数学竞赛,激发学生学习兴趣;②结合实际生活,开展数学应用教学;③引入数学趣味知识,提高学生学习兴趣;④介绍数学史,培养学生的数学文化素养。
数学实验报告范文

input x@@;
cards;
4.8 4.7 5.0 5.2 4.7 4.9 5.0 4.6 4.7
;
proc means clm maxdec=3;
run;
输出结果为:
Analysis Variable : X
Lower 95.0% CLM Upper 95.0% CLM
数学实验报告
日期:20年月日
班级
姓名
学号
实验名称
参数的区间估计
实验目的:
复习参数估计的基本理论,熟练掌握sas系统对总体均值、方差进行估计。掌握利用sas系统处理估计理论相关的实际问题。
实验原理与数学模型:(填写所需的基本数学公式、定理、概念等)
单个正态总体 情况:
1、均值 的置信区间
(a)当 已知时,置信水平为 的置信区间为
--------------------------------
4.695 4.994
--------------------------------
均值的置信水平为95%的置信区间为(4.695,4.994)
思考与深入:
(随便写一下自己想法)
教师评语及评分:
(b) 当 未知时,置信水平为 的置信区间为
Hale Waihona Puke (余略)实验所用软件及版本:
SAS13
实验任务:(填写实验问题)
1、若样本4.8 4.7 5.0 5.2 4.7 4.9 5.0 4.6 4.7来自于正态总体,求均值的区
间估计。(1)置信水平为95% (2)置信水平为90%
实验过程记录(含:基本步骤、主要程序清单及异常情况记录等):
数学实验报告单
(3)构造线段 CD,选中 CD 所在的直线、点 A 和点 B,单击“显示”
/“隐藏对象”。
(4)在直线上任取一点 E(除 D 点外),连接 CE。
(5)选中线段 CD、CE,点击“度量”菜单中的“长度”,量出 CD 和
CE 的长,依次选中点 C、E、D,点击“度量”/“角度”,测量∠CED
实
的大小。
数学实验报告单
实验名称 实验目的 实验要求 实验工具
垂线段最短
设计人 唐晓霞
通过用刻度尺测量和几何画板软件两种方式经理“垂线段最短”的发 现过程。 经历实践活动的过程,学会寻找思考问题的着眼点,掌握研究问题的 方法,领悟数学思想。
刻度尺、三角尺、装有几何画板软件的计算机等。
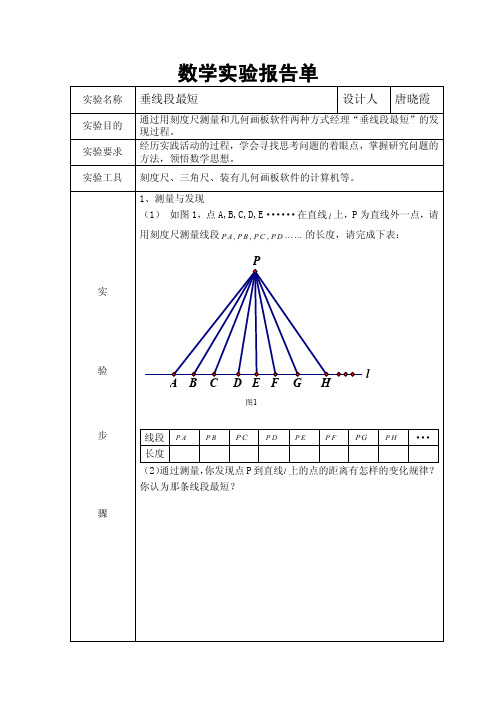
1、测量与发现 (1) 如图 1,点 A,B,C,D,E······在直线 l 上,P 为直线外一点,请 用刻度尺测量线段 P A , P B , P C , P D 的长度,请完成下表:
CE = 4.73厘米
C
CED = 65.87°
A
B DE
图2
1、独立猜想、操作; 2、学生交流、小组合作; 3、学生汇报、上台演示
实验结论
实 验 收 获
P
实
验
l
A B C DEF G H
图1
步
线段 P A
PB
PC
PD PE
PF
P G P H ···
长度
(2)通过测量,你发现点 P 到直线l 上的点的距离有怎样的变化规律? 你认为那条线段最短?
骤
2、操作与验证
(1)打开几何画板软件,画直线 AB、直线 AB 外的点 C。
(2)选中点 C 和直线 AB,点击“构造”/“垂线”,交直线 AB 于点 D。
数学实验报告 (1)

(1)参数方程:z=2^2^/2^2^sin y x y x ++(-8<=x<=8,-8<=y<=8) (2)程序:[X,Y]=meshgrid(-8::8);r=sqrt(x.^2+y.^2)+eps;Z=sin(r)./r;Mesh(x,y,z)Axis square(3)程序的输出结果:3:球面,椭球面,双叶双曲面,单叶双曲面1球面: (4):参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *R z R y R x 0π<=θ<2* 0<=ϕ<π (5)程序:u=[0:pi/60:2*pi];v=[0:pi/60:pi];[U,V]=meshgrid(u,v);R=3;X=R*sin(v).*cos(u);Y=R*sin(v).*sin(u);Z=R*cos(v);Surf(x,y,z);axis equal;(3)程序输出结果:2椭球面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕcos *sin *sin *cos *sin *c z b y a x 0<=θ<2*π 0<=ϕ<=π (2)程序:ezsurf(‘3*sin(u)*cos(v) ,’3*sin(u)*sin(v)’,’1*cos(u)’,[0,pi,0,2*pi]);(3)程序的输出结果:3单叶双曲面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕtan sin *sec *cos *sec *z a y a x 0<=θ<2*π -π/2<ϕ<π/2 (2)程序:ezsurf(‘3*sec(u)*cos(v),’3*sec(u)*sin(v)’,’5*tan(u)’,[-pi/2,pi/2,0,2*pi]);axis auto(3)输出程序结果:4双叶双曲面: (1)参数方程:⎪⎩⎪⎨⎧===ϕθϕθϕsec *sin *tan *cos *tan *c z b y a x 0<=θ<2*π -π<ϕ<3*π/2,ϕ≠π/2(2)程序:ezsurf(‘3*tan(u)*cos(v)’,’3*tan(u)*sin(v)’,’5*sec(u)’,[-pi/2,3*pi/2,0,2*pi]);axis auto(4) (3)输出程序结果:抛物螺线: (1)参数方程:⎪⎩⎪⎨⎧===2^*sin **cos **t c z t t b y t t a x 0<T<+∞ (2)程序:ezplot3(‘2*t*cos(t)’,’2*t*sin(t)’,’t.^2/3’,[0,50]);(3)输出程序结果:(5)马鞍面: (1)参数方程:z=x^2/9-y^2/4 (-25<=x<=25,-25<=y<=25)(2)程序:[X,Y]=meshgrid(-25:1:25);Z=X.^2/9-Y.^2/4;Surf(X,Y,Z)Title(‘马鞍面’)grid off(3)输出程序结果:(6)黎曼函数:(1)程序:n=100;x=[];y=[];k=1;for q=2:nfor p=1:q-1if gcd(q,p)==1 %利用函数gcd(m,n)可求m和n的最大公约数x(k)=p/q;y(k)=1/q;k=k+1;endendendplot(x,y,’.b’); axis([0,1,0,1])(2)程序输出结果:。
数学实验报告样本

数学实验报告实验序号:3 日期:2013年12 月14 日11(2k +=【调试结果】k x1 x2 x30 0.8 1.5 41 -0.81335 2.0766 1.61042 0.89679 1.9105 1.973 -1.7856 1.8956 1.89844 -1.9037 1.8955 1.89555 -1.8955 1.8955 1.8955所求的解是:x1=-1.,x2=1.,x3=1.,迭代步数:5【情况记录】1.对分法简单,然而,若在是有几个零点时,只能算出其中一个零点,它不能求重根,也不能求虚根.另一方面,即使在上有零点,也未必有。
这就限制了对分法的使用范围。
对分法只能计算方程的实根。
对分法的收敛速度较慢,它常用来试探实根的分布区间,或求根的近似值.寻找满足定理条件的等价形式是难于做到的。
事实上,如果为的零点,若能构造等价形式而,由的连续性,一定存在的邻域,其上有,这时若初值迭代也就收敛了。
由此构造收敛迭代式有两个要素,其一,等价形式应满足;其二,初值必须取自的充分小邻域,这个邻域大小决定于函数,及做出的等价形式。
松弛法的加速效果明显,甚至不收敛的迭代函数经加速后也能获得收敛.松弛法要先计算'()kx,在使用中有时不方便,而Altken 公式,它的加速效果是十分明显的,它同样可使不收敛的迭代格式获得收敛。
5.牛顿法的收敛速度明显快于对分法。
牛顿法也有局限性。
牛顿法至少是二阶收敛的,而在重根附近,牛顿法是线性收敛的,且重根收敛很慢。
另外,在牛顿法中,选取适当迭代初始值是求解的前题,当迭代的初始值在某根的附近时迭代才能收敛到这个根,有时会发生从一个根附近跳向另一个根附近的情况,尤其在导数数值很小时。
小学数学趣味实验报告(3篇)

第1篇实验名称:探究“奇数和偶数的奇妙之旅”实验目的:通过趣味实验,让学生了解奇数和偶数的概念,感受数学的乐趣,培养动手操作能力和观察能力。
实验时间:2023年4月15日实验地点:小学一年级教室实验器材:数字卡片、彩笔、白纸、剪刀、胶水、透明胶带实验参与人员:一年级全体学生实验过程:一、导入1. 教师展示数字卡片,引导学生说出奇数和偶数的概念。
2. 学生分享自己对奇数和偶数的理解。
二、实验操作1. 学生每人准备一张白纸,用彩笔在纸上画出若干个数字,要求每个数字之间留有足够的空间。
2. 学生用剪刀将画出的数字剪下来,形成数字卡片。
3. 学生将奇数卡片用红色标记,偶数卡片用蓝色标记。
4. 学生将奇数卡片和偶数卡片分别用透明胶带粘贴在黑板上。
5. 教师提问:奇数卡片和偶数卡片在黑板上排列后,有什么规律?6. 学生观察、讨论,得出结论:奇数卡片之间相差2,偶数卡片之间相差2,且奇数卡片和偶数卡片交替排列。
三、实验验证1. 教师提问:如果我们把黑板上奇数卡片和偶数卡片的顺序打乱,还会出现这样的规律吗?2. 学生分组进行实验,验证打乱顺序后,奇数卡片和偶数卡片是否依然交替排列。
3. 学生分享实验结果,得出结论:无论奇数卡片和偶数卡片的顺序如何,它们都会交替排列。
四、实验拓展1. 教师提问:在生活中,我们还能找到奇数和偶数的例子吗?2. 学生分享生活中的奇数和偶数例子,如:桌子、椅子、书本、水果等。
3. 教师引导学生思考:为什么生活中有这么多奇数和偶数?4. 学生讨论,得出结论:奇数和偶数是自然界和人类社会中普遍存在的现象。
实验总结:本次趣味实验,让学生在轻松愉快的氛围中了解了奇数和偶数的概念,感受到了数学的乐趣。
通过动手操作,学生培养了观察能力和逻辑思维能力。
同时,实验拓展环节让学生将数学知识应用于生活,激发了学生的学习兴趣。
实验反思:1. 实验过程中,教师应注重引导学生观察、思考,培养学生的动手操作能力。
数学实验报告模板

篇一:数学实验报告样本数学实验报告实验序号: 3日期:2013年 12 月 14 日1234篇二:数学实验报告模板数学实验报告题目对成绩数据的统计与分析2013年12月15日对成绩数据的统计与分析一、实验目的1. 掌握matlab基础功能的使用方法,以加强大学生数学实验与数学建模能力。
2. 通过对程序设计的学习增强学生对数学问题处理方法探究的兴趣。
二、实验问题问题背景:每门课程考试阅卷完毕,任课老师都要对班中考试成绩进行统计,于是出现下面两个问题1. 统计全班人数,平均分,不及格人数及90分以上人数2. 计算0-60,60-90,90-100的成绩分布情况,绘制饼状图,凸显不及格的人。
三、建立数学模型现将以上实际问题转化为一下数学问题:现给出一个数组[a1,a2,a3······an],通过循环语句计数求出n的值,并计算数组中数值大于等于90和小于60的元素个数,绘制不同数值段(0-60,60-90,90-100)的百分比的饼状图。
四、问题求解和程序设计流程1.关于成绩,选择将成绩做成数组的形式进行处理。
2.处理则运用for-end,if-else if-end,while-end等循环语句。
3.绘制饼状图则使用一般的数学运算及一些基本绘图代码(pie命令,explode命令)。
五、上机实验结果的分析与结论1.设计程序如下:a=input (请输入成绩组a[n]=); [h,j]=size(a); zongrenshu=j; pingjunfen=0; gaofen=0;bujige=0; yiban=0; for i=1:1:j; fenshu=a(i); if fenshu>90;gaofen=gaofen+1;pingjunfen=pingjunfen+fenshu;else if fenshu<60; bujige=bujige+1;pingjunfen=pingjunfen+fenshu;else pingjunfen=pingjunfen+fenshu;endend end pingjunfen=pingjunfen/zongrenshu; yiban=zongrenshu-bujige-gaofen; x=[bujige,yiban,gaofen]; explode=[1,0,0]; pie(x,explode); zongrenshu pingjunfen bujige gaofen运行结果截图: 2.由于图片大小问题,请看下一页通过输入了一组成绩数据,得出了该数据的总人数、平均分、不及格人数及高分段人数,并绘制出了相应饼状图。
数学生活中的小实验报告

数学生活中的小实验报告引言数学是一门抽象而有趣的学科,它不仅存在于课本中,还融入到我们日常生活中的方方面面。
本文将介绍数学生活中的一些小实验,通过这些实验可以培养我们的数学思维能力和动手能力,增加对数学的兴趣和理解。
实验一:探索无穷数列实验目的通过构建一个简单的模型,观察和探索无穷数列的性质,加深对数学无穷的理解。
实验材料- 一张纸- 一支铅笔实验步骤1. 在纸上写下一个正整数,如1。
2. 在这个数的右边写上另一个正整数,即前一个数加1,如2。
3. 重复上一步的操作,不断写下下一个更大的正整数。
4. 观察无穷数列的变化。
实验结果通过实验,我们可以发现无穷数列是一个递增的数列,每个数都比前一个数大1。
这个数列是无限长的,其中每个正整数都被包含进去。
实验结论无穷数列代表了数学中“无穷”的概念,即没有边界和限制。
通过这个实验,我们可以更好地理解数学中的无穷性,并且可以将这个概念应用到更复杂的问题中。
实验二:探索质数的分布规律实验目的通过统计一定范围内的质数数量,观察质数的分布规律。
实验材料- 笔记本- 铅笔实验步骤1. 选择一个合适的范围,如1到100。
2. 逐个判断范围内的每个数是否为质数。
3. 统计质数的数量。
4. 重复上述步骤,选择不同范围进行实验。
实验结果通过实验,我们可以发现质数的分布并不是完全随机的。
在较小的范围内,质数似乎更为密集,而在较大的范围内,质数的数量稀疏。
同时,我们也可以观察到一些规律,比如2、3、5、7等质数经常出现在末尾。
实验结论根据实验结果,我们可以初步推断质数的分布并不是完全随机的,可能存在某种规律。
通过进一步的实验和研究,我们可以探索质数的分布规律,并找到更多关于质数性质的规律。
实验三:探索几何图形的面积和周长关系实验目的通过观察不同几何图形的面积和周长,探索它们之间的关系。
实验材料- 一张纸- 一支铅笔- 一把尺子实验步骤1. 选择一个几何图形,如正方形。
2. 用尺子测量正方形的边长,并计算出它的面积和周长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数学实验》实验报告(2012 年03 月30 日)班级:09级四班学号:姓名:吴永慧一、实验问题1、某公司指派5个员工到5个城市工作(每个城市单独一人),希望使所花费的总电话费用尽可能少。
5个员工两两之间每个月通话的时间表示在下面的矩阵的上三角部分(因为通话的时间矩阵是对称的,没有必要写出下三角部分),5个城市两两之间通话费率表示在下面的矩阵的下三角部分(同样道理,因为通话的费率矩阵是对称的,没有必要写出上三角部分). 试求解该二次指派问题。
通话时间d=[0 1 1 2 31 02 1 21 2 0 1 22 1 1 0 13 2 2 1 0 ]城市间通话费率c=[0 5 2 4 15 0 3 0 22 3 0 0 04 0 0 0 51 2 0 5 0]2、某校毕业生必须至少修:两门数学课、三门运筹学课、两门计算机课。
1)某学生希望所修课程最少。
2)某学生希望课程少学分多。
3)某学生觉得学分数和课程数这两大目标大致应该三七开。
3、某储蓄所营业时间为上午9:00--下午5:00,储蓄所可以雇佣两类服务员:全职:每天100元中午12:00--下午2:00之间必须安排1小时的午餐时间半职:每人40 元必须连续工作4小时1)储蓄所每天雇佣的半职服务员不超过3人,为使花费最少该如何雇佣两类服务员。
2)如果不能雇佣半时服务员,花费多少?3)如果雇佣半时服务员没有人数限制花费多少?二、问题的分析(涉及的理论知识、数学建模与求解的方法等)1、用⎩⎨⎧=城市人不去城市人去了k 0k 1i i x ik (i =1...5) ⎩⎨⎧=城市人没去城市人去了h j h j x jh 01(i =1...5)ij d 表示i 和j 的通话时间;kh c 表示城市k 和h 之间的费率,数学模型:minjh iki j k h ij kh x x d c∑∑∑∑====51515151s.t.⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧========∑∑∑∑====515151515...115 (115) (11)5...11h jh j jh k iki ik j x k x i x k x ik x 、jh x 均为0、1变量2、用⎩⎨⎧=该学生不选该课程该学生选了该课程1i x (i =1...9)1) 数学模型:min Z=∑=91i i xs.t.⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧≤--≤-≤-≤--≤-≤--≥+++≥++++≥++++02000200223221958762157431397649865354321x x x x x x x x x x x x x x x x x x x x x x x x x x x x x 0≥i x 且为整2)数学模型:max W= 987654321322343445x x x x x x x x x ++++++++s.t.⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧=≤--≤-≤-≤--≤-≤--≥+++≥++++≥++++∑=91219587621574313976498653543216020002002232i xi x x x x x x x x x x x x x x x x x x x x x x x x x x x x x 0≥i x 且为整3)数学模型:Min Y=0.7Z+0.3Ws.t.⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧=≤--≤-≤-≤--≤-≤--≥+++≥++++≥++++∑=91219587621574313976498653543216020002002232i xi x x x x x x x x x x x x x x x x x x x x x x x x x x x x x 0≥i x 且为整3、用)5...1(=i y i,表示从上午9:00--下午1:00各整时间点所雇用的半职人员的人数;用1x表示中午12:00--下午1:00之间吃饭的全职人员的人数,用2x 表示下午1:00--下午2:00之间吃饭的全职人员的人数。
数学模型:1) Min )(40)(1005432121y y y y y x x ++++++s.t.⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧≤≥++≥+++≥++++≥++++≥++++≥++++≥+++≥++∑=515215421543215432143212321212121121388656434i i y y x x y y x x y y y x x y y y y x y y y y x y y y x x y y x x y x x )均为正整数(5...1,,21=i y x x i 2) Min )(10021x x +s.t.⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≥+≥+≥+≥≥≥+≥+≥+8865643421212112212121x x x x x x x x x x x x x x 均为正整数21,x x3) Min )(40)(1005432121y y y y y x x ++++++s.t.⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≥++≥+++≥++++≥++++≥++++≥++++≥+++≥++886564345215421543215432143212321212121121y x x y y x x y y y x x y y y y x y y y y x y y y x x y y x x y x x )均为正整数(5...1,,21=i y x x i三、计算过程、结论和结果分析:一)计算过程:1、model:sets:p/1..5/;q/1..5/;linko1(p,q):x;linko2(p,q):d;linko3(q,q):c;endsetsdata:d=0 1 1 2 31 02 1 21 2 0 1 22 1 1 0 13 2 2 1 0;c=0 5 2 4 15 0 3 0 22 3 0 0 04 0 0 0 51 2 0 5 0;enddatamin=(1/2)*@sum(linko2(i,j):@sum(linko3(k,h):d(i,j)*c(k,h)*x(i,k)*x(j,h) ));@for(p(i):@sum(q(k):x(i,k))=1);@for(q(k):@sum(p(i):x(i,k))=1);@for(linkO1(i,k):@bin(x(i,k)););end2、1)model:min=x1+x2+x3+x4+x5+x6+x7+x8+x9;x1+x2+x3+x4+x5>=2;x3+x5+x6+x8+x9>=3;x4+x6+x7+x9>=2;2*x3-x1-x2<=0;x4-x7<=0;2*x5-x1-x2<=0;x6-x7<=0;x8-x5<=0;2*x9-x1-x2<=0;@bin(x1);@bin(x2);@bin(x3);@bin(x4);@bin(x5);@bin(x6);@bin(x7);@bin(x8);@bin(x9);end2)model:max=5*x1+4*x2+4*x3+3*x4+4*x5+3*x6+2*x7+2*x8+3*x9;x1+x2+x3+x4+x5>=2;x3+x5+x6+x8+x9>=3;x4+x6+x7+x9>=2;x1+x2+x3+x4+x5+x6+x7+x8+x9=6;2*x3-x1-x2<=0;x4-x7<=0;2*x5-x1-x2<=0;x6-x7<=0;x8-x5<=0;2*x9-x1-x2<=0;@bin(x1);@bin(x2);@bin(x3);@bin(x4);@bin(x5);@bin(x6);@bin(x7);@bin(x8);@bin(x9);end3)model:min=0.3*(0-5*x1-4*x2-4*x3-3*x4-4*x5-3*x6-2*x7-2*x8-3*x9)+0.7*(x1+x2+x3+ x4+x5+x6+x7+x8+x9);x1+x2+x3+x4+x5>=2;x3+x5+x6+x8+x9>=3;x4+x6+x7+x9>=2;x1+x2+x3+x4+x5+x6+x7+x8+x9=6;2*x3-x1-x2<=0;x4-x7<=0;2*x5-x1-x2<=0;x6-x7<=0;x8-x5<=0;2*x9-x1-x2<=0;@bin(x1);@bin(x2);@bin(x3);@bin(x4);@bin(x5);@bin(x6);@bin(x7);@bin(x8) ;@bin(x9);end3、1)model:min=100*(x1+x2)+40*(y1+y2+y3+y4+y5);x1+x2+y1>=4;x1+x2+y1+y2>=3;x1+x2+y1+y2+y3>=4;x2+y1+y2+y3+y4>=6;x1+y2+y3+y4+y5>=5;x1+x2+y3+y4+y5>=6;x1+x2+y4+y5>=8;x1+x2+y5>=8;y1+y2+y3+y4+y5<=3;@gin(x1);@gin(x2);@gin(y1);@gin(y2);@gin(y3);@gin(y4);@gin(y5); end2)model:min=100*(x1+x2);x1+x2>=4;x1+x2>=3;x1+x2>=4;x2>=6;x1>=5;x1+x2>=6;x1+x2>=8;x1+x2>=8;@gin(x1);@gin(x2);end3) model:min=100*(x1+x2)+40*(y1+y2+y3+y4+y5);x1+x2+y1>=4;x1+x2+y1+y2>=3;x1+x2+y1+y2+y3>=4;x2+y1+y2+y3+y4>=6;x1+y2+y3+y4+y5>=5;x1+x2+y3+y4+y5>=6;x1+x2+y4+y5>=8;x1+x2+y5>=8;@gin(x1);@gin(x2);@gin(y1);@gin(y2);@gin(y3);@gin(y4);@gin(y5); End二)运行结果:1、 Local optimal solution found.Objective value: 25.00000Extended solver steps: 13Total solver iterations: 135Variable Value X( 1, 1) 0.X( 1, 2) 0.X( 1, 3) 0.X( 1, 4) 1.X( 1, 5) 0.X( 2, 1) 0.X( 2, 2) 0.X( 2, 3) 0.X( 2, 4) 0.X( 2, 5) 1.X( 3, 1) 1.X( 3, 2) 0.X( 3, 3) 0.X( 3, 4) 0.X( 3, 5) 0.X( 4, 1) 0.X( 4, 2) 1.X( 4, 3) 0.X( 4, 4) 0.X( 4, 5) 0.X( 5, 1) 0.X( 5, 2) 0.X( 5, 3) 1.X( 5, 4) 0.X( 5, 5) 0.D( 1, 1) 0.D( 1, 2) 1.D( 1, 3) 1.D( 1, 4) 2.D( 1, 5) 3.D( 2, 1) 1.D( 2, 2) 0.D( 2, 3) 2.D( 2, 4) 1.D( 2, 5) 2.D( 3, 1) 1.D( 3, 2) 2.D( 3, 3) 0.D( 3, 4) 1.D( 3, 5) 2.D( 4, 1) 2.D( 4, 2) 1.D( 4, 3) 1.D( 4, 4) 0.D( 4, 5) 1.D( 5, 1) 3.D( 5, 2) 2.D( 5, 3) 2.D( 5, 4) 1.D( 5, 5) 0.C( 1, 1) 0.C( 1, 2) 5.C( 1, 3) 2.C( 1, 4) 4.C( 1, 5) 1.C( 2, 1) 5.C( 2, 2) 0.C( 2, 3) 3.C( 2, 4) 0.C( 2, 5) 2.C( 3, 1) 2.C( 3, 2) 3.C( 3, 3) 0.C( 3, 4) 0.C( 3, 5) 0.C( 4, 1) 4.C( 4, 2) 0.C( 4, 3) 0.C( 4, 4) 0.C( 4, 5) 5.C( 5, 1) 1.C( 5, 2) 2.C( 5, 3) 0.C( 5, 4) 5.C( 5, 5) 0.Row Slack or Surplus1 25.000002 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.10 0.11 0.由结果知:第1个人去城市4;第2个人去城市5;第3个人去城市1;第4个人去城市2;第5个人去城市3。
