图论及其应用(25)
图论及其应用

图论及其应用简介图论是计算机科学中的一个重要分支,研究的对象是由边与顶点组成的图形结构以及与其相关的问题和算法。
图论的应用广泛,涵盖了计算机科学、网络科学、物理学、社会学、生物学等多个领域。
本文将介绍图论的基本概念、常用算法以及一些实际的应用案例。
图的基本概念图由顶点(Vertex)和边(Edge)组成,记作G=(V, E),其中V为顶点的集合,E为边的集合。
图可以分为有向图和无向图两种类型。
有向图有向图中的边具有方向性,即从一个顶点到另一个顶点的边有明确的起点和终点。
有向图可以表示一种有序的关系,比如A到B有一条边,但B到A可能没有边。
有向图的表示可以用邻接矩阵或邻接表来表示。
无向图无向图中的边没有方向性,任意两个顶点之间都有相互连接的边。
无向图可以表示一种无序的关系,比如A与B有一条边,那么B与A之间也有一条边。
无向图的表示通常使用邻接矩阵或邻接表。
常用图论算法图论中有许多经典的算法,其中一些常用的算法包括:深度优先搜索(DFS)深度优先搜索是一种用于遍历或搜索图的算法。
通过从起始顶点开始,沿着一条路径尽可能深入图中的顶点,直到无法再继续前进时,返回上一个顶点并尝试下一条路径的方式。
DFS可以用于判断图是否连通,寻找路径以及检测环等。
广度优先搜索(BFS)广度优先搜索也是一种用于遍历或搜索图的算法。
不同于深度优先搜索,广度优先搜索逐层遍历顶点,先访问离起始顶点最近的顶点,然后依次访问与起始顶点距离为2的顶点,以此类推。
BFS可以用于寻找最短路径、搜索最近的节点等。
最短路径算法最短路径算法用于计算图中两个顶点之间的最短路径。
其中最著名的算法是迪杰斯特拉算法(Dijkstra’s A lgorithm)和弗洛伊德算法(Floyd’s Algorithm)。
迪杰斯特拉算法适用于没有负权边的图,而弗洛伊德算法可以处理带有负权边的图。
最小生成树算法最小生成树算法用于找到一个连通图的最小的生成树。
其中最常用的算法是普里姆算法(Prim’s Algorithm)和克鲁斯卡尔算法(Kruskal’s Algorithm)。
电子科技大学研究生试题《图论及其应用》(参考答案)

电子科技大学研究生试题《图论及其应用》(参考答案)考试时间:120分钟一.填空题(每题3分,共18分)1.4个顶点的不同构的简单图共有__11___个;2.设无向图G 中有12条边,已知G 中3度顶点有6个,其余顶点的度数均小于3。
则G 中顶点数至少有__9___个;3.设n 阶无向图是由k(k ?2)棵树构成的森林,则图G 的边数m= _n-k____;4.下图G 是否是平面图?答__是___; 是否可1-因子分解?答__是_.5.下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。
图G二.单项选择(每题3分,共21分)1.下面给出的序列中,是某简单图的度序列的是( A )(A) (11123); (B) (233445); (C) (23445); (D) (1333).2.已知图G 如图所示,则它的同构图是( D )3. 下列图中,是欧拉图的是( D )4. 下列图中,不是哈密尔顿图的是(B )5. 下列图中,是可平面图的图的是(B )AC DA B CD6.下列图中,不是偶图的是( B )7.下列图中,存在完美匹配的图是(B )三.作图(6分)1.画出一个有欧拉闭迹和哈密尔顿圈的图;2.画出一个有欧拉闭迹但没有哈密尔顿圈的图;3.画出一个没有欧拉闭迹但有哈密尔顿圈的图;解: 四.(10分)求下图的最小生成树,并求其最小生成树的权值之和。
解:由克鲁斯克尔算法的其一最小生成树如下图:权和为:20.五.(8分)求下图G 的色多项式P k (G).解:用公式(G P k -G 的色多项式:)3)(3)()(45-++=k k k G P k 。
六.(10分) 22,n 3个顶点的度数为3,…,n k 个顶点的度数为k ,而其余顶点的度数为1,求1度顶点的个数。
解:设该树有n 1个1度顶点,树的边数为m.一方面:2m=n 1+2n 2+…+kn k另一方面:m= n 1+n 2+…+n k -1 v v 13图G由上面两式可得:n 1=n 2+2n 3+…+(k -1)n k七.证明:(8分) 设G 是具有二分类(X,Y)的偶图,证明(1)G 不含奇圈;(2)若|X |≠|Y |,则G 是非哈密尔顿图。
图论及其应用

图论及其应用班级:图论1班学院:软件学院学号:2014110993姓名:张娇图论从诞生至今已近300年,但很多问题一直没有很好地解决。
随着计算机科学的发展,图论又重新成为了人们研究讨论的热点,图形是一种描述和解决问题直观有效的手段,这里给出图论在现实生活中的一些应用。
虽然最早的图论问题追溯1736年(哥尼斯堡七桥间题),而且在19世纪关于图论的许多重要结论已得出。
但是直到20世纪20年代图论才引起广大学者的注意并得以广泛接受和传播。
图论即形象地用一些点以及点与点之间的连线构成的图或网络来表示具体问题。
利用图与网络的特点来解决系统中的问题,比用线性规划等其他模型来求解往往要简单、有效得多。
图论就是研究图和网络模型特点、性质和方法的理论。
图论在许多领域,诸如物理、化学、运筹学、计算机科学、信息论、控制论、网络理论、社会科学以及经济管理等各方面都有广泛的应用,它已经广泛地应用于实际生活、生产和科学研究中。
下面对最大流问题进行探究。
最大流问题主要探究最大流问题的Ford-Fulkerson解法。
可是说这是一种方法,而不是算法,因为它包含具有不同运行时间的几种实现。
该方法依赖于三种重要思想:残留网络,增广路径和割。
在介绍着三种概念之前,我们先简单介绍下Ford-Fulkerson方法的基本思想。
首先需要了解的是Ford-Fulkerson是一种迭代的方法。
开始时,对所有的u,v属于V,f(u,v)=0(这里f(u,v)代表u到v的边当前流量),即初始状态时流的值为0。
在每次迭代中,可以通过寻找一个“增广路径”来增加流值。
增广路径可以看做是从源点s到汇点t之间的一条路径,沿该路径可以压入更多的流,从而增加流的值。
反复进行这一过程,直到增广路径都被找出为止。
举个例子来说明下,如图所示,每条红线就代表了一条增广路径,当前s到t的流量为3。
当然这并不是该网络的最大流,根据寻找增广路径的算法我们其实还可以继续寻找增广路径,最终的最大流网络如下图所示,最大流为4。
图论及其应用综述

图论综述一、简介图论是数学的一个分支。
它以图为研究对象。
图论中的图是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用点代表事物,用连接两点的线表示相应两个事物间具有这种关系。
图G=(V,E)是一个二元组(V,E)使得E⊆[V]的平方,所以E的元素是V的2-元子集。
集合V中的元素称为图G的定点(或节点、点),而集合E的元素称为边(或线)。
通常,描绘一个图的方法是把定点画成一个小圆圈,如果相应的顶点之间有一条边,就用一条线连接这两个小圆圈,如何绘制这些小圆圈和连线时无关紧要的,重要的是要正确体现哪些顶点对之间有边,哪些顶点对之间没有边。
图论本身是应用数学的一部份,因此,历史上图论曾经被好多位数学家各自独立地建立过。
关于图论的文字记载最早出现在欧拉1736年的论著中,他所考虑的原始问题有很强的实际背景。
目前,图论已形成很多分支:如随机图论、网络图论、代数图论、拓扑图论、极值图论等。
图论的应用已经涵盖了人类学、计算机科学、化学、环境保护、非线性物理、心理学、社会学、交通管理、电信以及数学本身等。
二、基本内容2.1 图的基本概念本章首先介绍了图的一些基本性质和一些不同模型的图,包括偶图,完全图和补图,引入了定点度的来描述图的性质。
其次介绍了子图的相关概念,介绍了图的一些基本运算规则,对图的路和连通性进行了阐释。
紧接着讲解了最短路算法,定义设G为边赋权图。
u与v是G中两点,在连接u与v的所有路中,路中各边权值之和最小的路,称为u与v间的最短路。
图的代数表示,包括图的邻接矩阵和图的关联矩阵。
最后对极图理论进行了简介,主要介绍了极值图论中的一个经典结论——托兰定理。
2.2 树本章主要介绍了树的概念与性质,阐述了生成树与最小生成树的基本概念与一些常用结论与定理。
树是不含圈的无圈图,也是连通的无圈图。
树是图论中应用最为广泛的一类图。
在理论上,由于树的简单结构,常常是图论理论研究的“试验田”。
图论及其应用
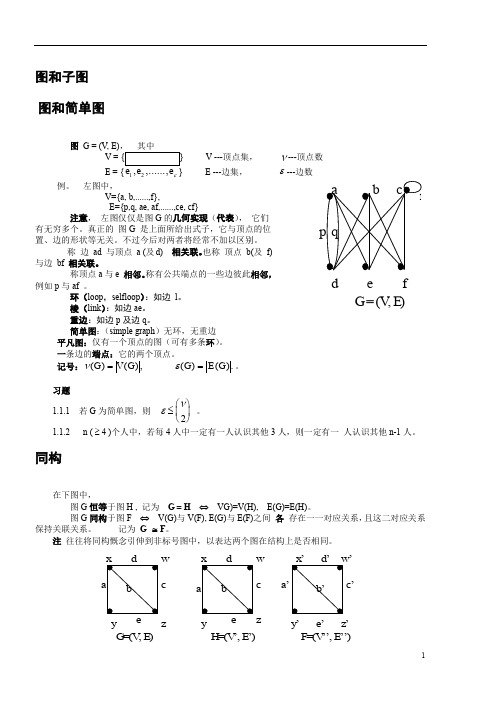
图和子图 图和简单图图 G = (V, E)V ---顶点集,ν---顶点数12ε E ---边集, ε---边数例。
左图中, V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意, 左图仅仅是图G 的几何实现(代表), 它们有无穷多个。
真正的 图G 是上面所给出式子,它与顶点的位置、边的形状等无关。
不过今后对两者将经常不加以区别。
称 边 ad 与顶点 a (及d) 相关联。
也称 顶点 b(及 f) 与边 bf 相关联。
称顶点a 与e 相邻。
称有公共端点的一些边彼此相邻,例如p 与af 。
环(loop ,selfloop ):如边 l 。
棱(link ):如边ae 。
重边:如边p 及边q 。
简单图:(simple graph )无环,无重边 平凡图:仅有一个顶点的图(可有多条环)。
一条边的端点:它的两个顶点。
记号:νε()(),()().G V G G E G ==。
习题1.1.1 若G 为简单图,则εν≤⎛⎝ ⎫⎭⎪2 。
1.1.2 n ( ≥ 4 )个人中,若每4人中一定有一人认识其他3人,则一定有一 人认识其他n-1人。
同构在下图中, 图G 恒等于图H , 记为 G = H ⇔ VG)=V(H), E(G)=E(H)。
图G 同构于图F ⇔ V(G)与V(F), E(G)与E(F)之间 各 存在一一对应关系,且这二对应关系保持关联关系。
记为 G ≅F。
注 往往将同构慨念引伸到非标号图中,以表达两个图在结构上是否相同。
de f G = (V , E )yz w cG =(V , E )w cyz H =(V ’, E ’)’a ’c ’y ’e ’z ’F =(V ’’, E ’’)注 判定两个图是否同构是NP-hard 问题。
完全图(complete graph) Kn空图(empty g.) ⇔ E = ∅ 。
V’ ( ⊆ V) 为独立集 ⇔ V’中任二顶点都互不相邻。
图论及其应用习题答案

图论及其应用习题答案图论及其应用习题答案图论是数学的一个分支,研究的是图的性质和图之间的关系。
图是由节点和边组成的,节点表示对象,边表示对象之间的关系。
图论在计算机科学、电子工程、物理学等领域有着广泛的应用。
下面是一些图论习题的解答,希望对读者有所帮助。
1. 问题:给定一个无向图G,求图中的最大连通子图的节点数。
解答:最大连通子图的节点数等于图中的连通分量个数。
连通分量是指在图中,任意两个节点之间存在路径相连。
我们可以使用深度优先搜索(DFS)或广度优先搜索(BFS)来遍历图,统计连通分量的个数。
2. 问题:给定一个有向图G,判断是否存在从节点A到节点B的路径。
解答:我们可以使用深度优先搜索(DFS)或广度优先搜索(BFS)来遍历图,查找从节点A到节点B的路径。
如果能够找到一条路径,则存在从节点A到节点B的路径;否则,不存在。
3. 问题:给定一个有向图G,判断是否存在环。
解答:我们可以使用深度优先搜索(DFS)或广度优先搜索(BFS)来遍历图,同时记录遍历过程中的访问状态。
如果在搜索过程中遇到已经访问过的节点,则存在环;否则,不存在。
4. 问题:给定一个加权无向图G,求图中的最小生成树。
解答:最小生成树是指在无向图中,选择一部分边,使得这些边连接了图中的所有节点,并且总权重最小。
我们可以使用Prim算法或Kruskal算法来求解最小生成树。
5. 问题:给定一个有向图G,求图中的拓扑排序。
解答:拓扑排序是指将有向图中的节点线性排序,使得对于任意一条有向边(u, v),节点u在排序中出现在节点v之前。
我们可以使用深度优先搜索(DFS)或广度优先搜索(BFS)来遍历图,同时记录节点的访问顺序,得到拓扑排序。
6. 问题:给定一个加权有向图G和两个节点A、B,求从节点A到节点B的最短路径。
解答:我们可以使用Dijkstra算法或Bellman-Ford算法来求解从节点A到节点B的最短路径。
这些算法会根据边的权重来计算最短路径。
数学中的图论及其应用

数学中的图论及其应用图论是一门数学基础理论,用来描述事物之间的关联。
图论主要研究节点之间的连接关系和路径问题。
它的研究对象是图,图是由节点和边组成的,边表示节点之间的连接关系,节点表示事物。
图论是一种十分实用的数学工具,它是计算机科学、物理学、化学、生物学、管理学等领域的重要工具,也是人工智能和网络科学等领域的基础。
一、图论的基本概念1.1 图图是由节点和边组成的,表示事物之间的关系。
节点是图中的基本元素,用点或圆圈表示;边是连接节点的元素,用线或箭头表示。
1.2 有向图和无向图有向图是指边有方向的图,每一条边用有向箭头表示;无向图是指边没有方向的图,每一条边用线表示。
1.3 节点的度和邻居节点节点的度是指与节点相连的边的数量,具有相同度的节点称为同阶节点;邻居节点是指与节点相连的节点。
1.4 遍历和路径遍历是指从起点出发访问图中所有节点的过程;路径是指跨越边连接的节点序列,路径长是指路径中边的数量。
二、图论的应用2.1 网络科学网络科学是研究节点和边之间的关系,以及节点和边之间的动态演化的学科。
网络科学中的图模型是节点和边的结合体,其应用包括社会网络、生物网络和物理网络等。
社会网络是指人们之间的社交网络,它描述了人与人之间的关系。
社交网络可以用图模型表示,节点表示人,边表示人与人之间的互动关系,例如朋友关系、家庭关系等。
生物网络是指由生物分子构成的网络,例如蛋白质相互作用网络、代谢网络等。
在生物网络中,节点可以表示蛋白质或基因,边可以表示蛋白质或基因之间相互作用的联系,这些联系可以进一步探究生物进化和疾病发生的机理。
物理网络是指由物理粒子构成的网络,例如网络电子、量子态等。
在物理网络中,节点可以表示量子比特或电子,边可以表示色散力或超导电性等物理现象。
2.2 计算机科学图论在计算机科学中的应用非常广泛,例如数据结构、算法设计和网络安全等方面。
图论在计算机科学中的经典应用包括最短路径算法、最小生成树算法等。
范更华-图论及其应用

旅行推销员问题
问题提出: 一个推销员从公司出发, 访问 若干指定城市, 最后返回公司,要求设计
最优旅行路线。(费用最小)
数学抽象: 城市作为点, 两点间有边相连, 如果对应的城市间有直飞航班。机票价作 为每条边的权。
旅行推销员问题
求解 : 在图中求一个圈过每点恰好一次 ,
且边的权之和最小。(最优哈密顿问题;比
在一个计算机光纤网络中,给传输信道 分配波长,两信道若有公共部分,必须得到 不同的波长。要求使用尽可能少的波长。
波长分配问题转化为图论问题
每条信道看作图的一个点。两点间有边
相连当且仅当它们对应的信道有公共部
分。波长问题等价于所构造图的点着色
问题:
给图的每个点着色,有边相连的点
须着不同的颜色。所用颜色尽可能少。
1735年, 欧拉(Euler) 证明哥尼斯堡七桥问题无 解, 由此开创了数学的一个新分支---图论. 欧拉将哥尼斯堡七桥问题转化为图论问题 : 求 图中一条迹 (walk), 过每条边一次且仅一次 . 后人将具有这种性质的迹称为欧拉迹,闭的欧拉 迹也称为欧拉回路.
欧拉定理 : 连通图存在欧拉迹当且仅当图中奇 度数的点的个数至多为 2( 若为 0, 则存在欧拉回 路,这种图称为欧拉图,也称为偶图)
图的例子
交通网
互联网
计算机处理器连接方式
集成电路板
分子结构图
分子间相互作用及信息传递
具体应用
大型高速计算机:处理器的连接方式
互联网:信息传输及控制管理
大规模集成电路:布局、布线 数据库技术:数据的存储、检索 理论计算机科学: 子图理论对计算机算法研究的应用
具体应用
DNA序列分析:图的欧拉回路问题 机器智能与模式识别:图的同构 通讯网络:连通性,可靠性 印刷电路板检测: 12万5千次降为4次(《美国科学》 Scientific American, 9 (1997), 92-94 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u
N (u ) k 1
u
N (u)
12
设п 是G的k着色方案,因为 u N (u ) k 1 ,所以, 在п 下,至少有一种颜色u及其邻域均没有用到,设该色 为m,改变u的颜色为m,其余点的着色不变,这样得到G的k 着色方案п 1.显然,п 与п 1导出的G的顶点划分不同,这 与G是唯一可着色图矛盾。 (2) 若不然,则存在G的k着色方案п 和G的两个色组C1 与C2,使得H=G[C1∪C2]不连通。设H1与H2是H的两个分支。 因为G是唯一可着色图,所以,对任意点u和其邻域 N(u), 它们在п 下,必然用完了k种颜色,否则,由(1)的 证明,得到G是非唯一可着色图。 这样,H1与H2中同时含有C1和C2中的顶点。
由于 H 也是某偶图的补,所以只需要证明 (G) cl (G)
25
证明:在 G 的正常着色方案下,每个色组对应G的一 (G ) 应该是G的最小点覆盖中包含 个顶点或者K2。这样, 的点数和边数。由补充定理:它等于G中最大独立集包含 的顶点数,即等于 G 的团数。所以有:
10
(2) 对于G2来说,G2的任意3正常着色方案导出的顶点 划分均是{{v1}, {v2,v4}{v3,v5}},所以,G2是 唯一3可着色图;例如:
v1 v2 v3 G2 v5 v2 v3 G2 v1 v5 v2 v3 v1 v5
v4
v4
v4
G2
(3) 对于G3来说,G3不是唯一3可着色图;因为:
设Hi=G[Vi∪{v}], (1≦i≦r)。则Hi是k-1可正常点着色 的,现对每个Hi进行k-1正常点着色,且v都分配同一种颜色, 那么,将着色后的Hi合在一起,得到G的k-1正常点着色方 案,这与G是k色图矛盾。所以临界图没有割点。
5
例3 求证:仅有的1临界图是k1;仅有的2临界图是K2;仅 有的3临界图奇圈。 证明:由于1色图是空图,所以1临界图只能是K1;2色 图是偶图,所以,2临界图只能是K2; 3色图必然含有奇圈, 而奇圈的色数是3,所以,3临界图只能是奇圈。 例4 求证:布鲁克斯定理等价于下述命题:若G是k临 界图(k≥4), 且不是完全图,则2m≥n(k-1)+1,其中m为G的 边数而n为顶点数。 证明:(1) 由布鲁克斯定理推例4中命题。 因G是k临界图,所以G是连通单图,又k≥4, 所以G不能 是奇圈,再由G不是完全图,所以由布鲁克斯定理有
13
如果交换C1∩V(H1)与C2∩V(H1)中顶点颜色,得到G 的k着色п 1,显然,п 与п 1的色划分是不同的。这与G的 着色唯一性矛盾。 例如,在下图G中,由黄色、红色色组导出的子图是 连通的。
v1
v2 v3 G v5
v4
14
定理3 (夏特朗)每个唯一n (n≥2)可着色图是(n-1)连通的。 证明:设G是唯一n可着色图(n≥2)。
v1 v2 v3 G3 v1
v5
v2
v3 G3
v5
v4
v4
11
下面给出唯一可着色图的几个特征。 定理2(哈拉里,1968) 设G是唯一k可着色图,k≥2, 则: (1) δ ≥k-1;
(2) 在G的任意一种k着色中,G的任意两个色组的并的 导出子图是连通的。 证明: (1) 若不然,设δ < k-1, 令d(u) =δ,则
不含三角形的三色图
不含三角形的4色图
18
数学家狄拉克1953年在其论文“k色图的构造”中提出 一个问题:对于任意大的一个正整数k, 是否存在一个图, 不包含三角形但色数是k? 上面问题分别由勃兰克.斯德卡兹(1954), 米歇尔斯基 (1955)独立作出了回答。 米歇尔斯基(1955)给出了由一个不含三角形的k色图Gk 构造一个不含三角形的k+1色图Gk+1的方法。 构造方法:设Gk的顶点是u1,u2,…,un, 添加点v1,v2,…vn和点 v。将vi与ui的所有邻点及v相连,1≦i≦n。如此得到的图就是 一个不含三角形的k+1色图。
23
对该问题的研究,早在1932年哥尼和加莱就已经涉及, 但到了1960年,完美图概念才被贝尔热正式提出。所以, 贝尔热是完美图研究的代表人物。 定义6 设G是一个图。由G中若干互不邻接的顶点作成 的子集称为G的一个点独立集;G中含顶点数最多的点独 立集称为G的最大独立集,其包含的顶点数称为独立数。 图G的点独立数记为α(G)或α。 注:关于图的覆盖与图的点独立数之间的关系,加莱得 到了一些很漂亮的结论。其中之一是:
21
1968年,罗瓦斯构造性地证明了上面定理6 注:定理6实际上是数学家凯利提出的一个猜想。
(二)、完美图简介
1、相关概念
定义4 (1)单 图G的团:若单图G的一个顶点子集S在G 中的导出子图是完全图,则称S是G的一个团;
(2) 单图G的团数:单图G的最大团包含的顶点数称为G 的团数,记为c l (G) ,即:
15
在G-S中取一个不在G1中的点u,将其染上c1色,这样得到 G的另一个n着色方案。 显然,两种着色方案导出的色划分不同,这与条件矛盾。 推论:设G是唯一n(n≥2)可着色图,п 是任意一种n着色 方案,则由п 的任意k个色组导出的子图是(k-1)连通的。 证明:显然,任意k个色组导出子图是唯一k可着色图, 由定理3得到推论结论。 注: (1) 唯一1可着色图是零图;
定义2 设简单标定图G的点色数是k, 如果在任意的k正 常点着色方案下,导出的顶点集合划分唯一,称G是唯 一k可着色图,简称唯一可着色图。
9
例5 考察下面3色图是否是唯一3可着色图。
v1 v1 v1
v2
v2 G1 v3 v3 G2
v5
v2
v3 G3
v5
v4
v4
解:(1) 对于G1来说,G1的任意3正常着色方案导出的 顶点划分均是{{v1}, {v2}{v3}},所以,G1是唯 一3可着色图;
19
例6,利用米歇尔斯基方法构造一个不含三角形的4色图。 解:注意到C5是不含三角形的3色图,于是由C5可以构造 u 出不含三角形的4色图。
1
u1 u2
v1 u5
u2
u5
v2
v
v5
u3
u4
v3
v4
不含三角形的3色图
u3
u4
不含三角形的4色图
20
注:利用米歇尔斯基方法构造一个不含三角形的k色图时, 结果图与初始图有关。 例7,设Gk是不含三角形的k色图,顶点数为f(k), 而Gk+1是 由米歇尔斯基方法构造出来的不含三角形的k+1色图,其顶点 数设为f(k+1)。求出f(k)的递推公式。 解: f (k 1) f (k ) 1 定理5 (米歇尔斯基)对于任意正整数k, 存在不含三角形的k 色图。 1961年,数学家Erdos用概率方法证明了更一般结论: 定理6 (Erdos)对于任意正整数m和n, 存在一个围长超过m 的n色图。
情形1,如果G是完全图,则G=Kn,显然G是n-1连通的。
情形2,如果G是非完全图,假若G不是(n-1)连通的,那 么其连通度k(G)≦n-2。于是G中存在点集S,|S|=n-2, 使得G-S不连通。 设п 是G的n着色方案。在该方案下,至少有两种颜色c1 与c2,S中的顶点都没有使用。
而由定理2的(2), 着c1与c2色的点导出子图必连通。所以, 着c1与c2色的顶点在G-S中的同一个分支中,设该分支为G1.
(2) 唯一2可着色图是偶图;
除此之外,没有简单的结论!
16
定理4 每个唯一4可着色可平面图都是极大可平面图。 证明:只需证明:m=3n-6即可。
一方面:G是可平面图,有:m≦3n-6;
另一方面:设G是唯一4可着色的可平面图,п 是一种4 着色方案,色组记为Vi(1≦i≦4). 因为i≠j时,G[Vi∪Vj] 是连通的,所以:
6
k≦Δ 。 再由k临界图的性质,有δ ≥k-1.所以:
2m
vV ( G )
d (v) (n 1)
k (n 1)(k 1) n(k 1) 1
(2) 由例4中命题推布鲁克斯定理。 因为连通单图G不是奇圈,也不是完全图。设G的k临 界子图是H。 情形1, H是奇圈。 在这种情况下,由于G不是奇圈,所以,H之外必然 有边和H相连,即Δ (G)≥3,另一方面,k(G)=k(H)=3,所
所以,有:
1 ( H ) (k (G ) 1) n( H )
8
即证明: (G) k (G)
2、唯一可着色图
对图的顶点进行正常着色,实际上给出图的顶点集合 的一种划分,不同的着色方案,给出的划分一般不同。 但是,也存在一类特殊图,对于任意的最优着色方案, 导出的顶点划分却是相同的。为此,我们给出如下定义。
2
定理1 临界图有如下性质 (1) k色图均有k临界子图;
(2) 每个临界图均为简单连通图;
(3) 若G是k临界图,则δ ≥k-1。
证明: (1)是显然的。
(2) 因为删掉环或平行边中的一条边并不破坏原有的顶 点正常着色,所以每个临界图是单图;又因为删掉色数 较小的分支,剩下部分的图的色数和原图色数相等,所 以,临界图必须是连通图。
本次课主要内容
与色数有关的几类图和完美图
(一)、与色数有关的几类图
(二)、完美图简介
1
(一)、与色数有关的几类图
1、临界图
定义1 若对图G的任意真子图H,都有 ( H ) (G) ,则 称G是临界图。点色数为k的临界图称为k临界图。
3临界图 4临界图
非临界图
注:临界图由狄拉克在1952年首先提出并研究。上面 的4临界图是Grotzsch在1958年提出的。
m(G[Vi Vj ]) ni n j 1
4 i 1 j i
于是:
m(G) (ni n j 1) 3n 6
