非对称平板波导色散曲线求解(附matlab程序)
色散关系的matlab

色散关系的matlab
色散是光学中一项重要的现象,指的是不同波长光在传播过程中
速度不同,导致光束发生弯曲或分散的现象。
色散关系描述了光在介
质中传播过程中波长与相速度之间的关系。
因此,了解色散关系对于
研究光学现象和设计光学器件有着重要意义。
MatLab是一种常用的计算机编程语言,可以用于实现多种科学计算和数据分析操作。
通过编写MatLab程序,可以计算和绘制色散关系
曲线。
在编写色散关系的MatLab程序中,需要考虑介质的折射率与波
长的关系,以及折射率对相速度的影响。
一般来说,介质的折射率与
波长呈现非线性关系,这也是导致色散的主要原因。
因此,在计算色
散关系时需要使用非线性函数来描述介质的折射率随波长变化的曲线。
对于不同的介质,其色散关系曲线可能具有不同的特点。
例如,
某些介质的色散关系可能在某个波长附近出现弯曲,导致光束的聚焦
效果较好;而其他的介质则可能在整个波长范围内表现出较强的色散
效应,导致光束发生相对较大的分散。
通过MatLab编写色散关系程序,可以方便地进行多组实验数据
的处理、展示和比较。
同时,由于MatLab具有高效性和可扩展性,用
户还可以对程序进行进一步的优化,加入更多的计算模型或者实验数据,以实现更精确和全面的分析和表达。
总之,MatLab编写的色散关系程序可以为研究和应用光学现象提供有力支持和帮助,对于学术研究和工程应用均有着重要的意义。
非对称对流扩散问题有限元法的MATLAB实现

注意: 这里把单元刚度矩阵写成了一个 3 & 3 ( e) 阶矩阵 , 而由 ( 7) 和 ( 8 ) 知 K pp 是 K 的第 p 行 p 列 元素 kpp 的组成部分, K 的组成部分 , K
( e)
( e) = K qp
( e) qq ( e) lq
( e) ql ( e) ll
K
( e) lp
= 1 / ( 4S ) (B 2 ) B 3 - A 2 ) A 3) dx dy +
2
# # #
为与单元 G e 对应的单元刚度矩阵 .
1 / ( 2S ) (B 3 - A 3 )L 2 dx dy
( e) 2 2 Ge Ge
x p )y ). x = xp L p + x q L q + x l L l , y = yp L p + y q L q + x l L l . 由连锁法则推出 ! 1 ! ! = ( ( yq - y l ) + ( yl - yp ) + (y p !x 2S ! Lp !L q ! yq ) ), ! Ll ! 1 ! ! = ( (x l - x q ) + ( xp - x l ) + (x q !y 2S ! Lp !L q ! xp ) ). ! Ll 2 ) 计算刚度矩阵 K 对 作三角形剖分 T h = {G e: e = 1 , 2, %, m }, 并对单元编号, 节点编号, 节点编号见图 1 . 令 K ij 则 K ij = (K ij ) n& n = ( 在单元 G e = K
用有限元法求解归结为: 先计算刚度矩阵 K 和 质量阵 M, 然后解 ( 5 ).
2
半导体光学7色散曲线
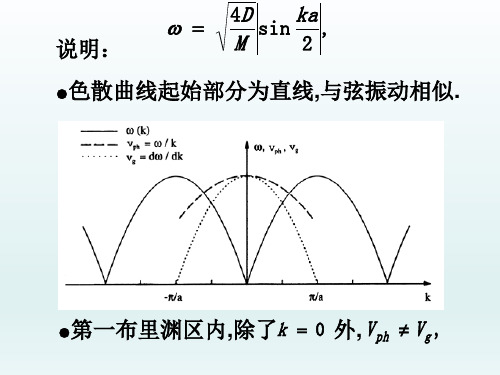
将以上所设的方程的解代入运动方程,可
得以下方程组:
2D coskaAM 2D 2m Am 0. 2D 2M AM 2D coskaAm 0,
若 AM 0,Am 0 不存在,以上方程组的
动方程.因此,驻波不会沿z方向传播.群速
度为零,这表示驻波能量稳定!!!
●平移倒格矢 G
2l
a
l
取整),色散曲
线可以从第一布里渊区移到第一布里渊
区之外.但是,
k G
4D M
sin
k
G a
2
4D M
sin
k
2 a
2
l a
4D M
sin
ka
2l
2
4D M
sin
ka
2
k .
k k G 格波频率相同.
OP:GaAs,AlAs 不重叠,驻波.
满足 niai
m ,m
2
1,2,3 ;i
A,B .
kzm
2
2m 2niai
m
niai
,
m 1,2,3 ;i A,B .
AP:GaAs,AlAs 接近,为传播模.折叠效应
是界面处AP周期性多次反射相干叠加结果.
9.9 混晶中声子 1.混晶
2
D
1
m
1
M
D
1
m
1
M
,
12
D
1
m
1
M
D
1
m
1
M
2D
1
m
1
M
,光学支
非对称平板波导色散曲线求解(附matlab程序)

光波导理论与技术第一次作业题目:非对称平板波导设计*名:**学号:************指导老师:***完成日期:2014 年03 月10 日一、题目根据以下的平板光波导折射率数据:(1)作出不同波导芯层厚度h (015h m μ<<)对应的TE 模式与TM 模式的色散图;(2)给出满足单模与双模传输的波导厚度范围; (3)确定包层所需的最小厚度a 与b 的值。
二、步骤依题意知,平板波导参数为:537.11=TE n ,510.12=TE n ,444.13=TE n ;530.11=TM n ,5095.12=TM n ,444.13=TM n 。
其中321n n n 、、分别代表芯心、上包层、下包层相对于nm 1550=λ光波的折射率。
在实际应用中,平板波导的有效折射率N 必须12n N n <<才能起到导光的作用。
经过推导,非对称平板波导的色散方程为:2212322212222210arctan arctan Nn n N N n n N m N n h k --+--+=-π (TE 模) 221232232122122222212210arctan arctan N n n N n n N n n N n n m N n h k --+--+=-π (TM 模)非对称平板波导光波模式截止时对应的芯层厚度为:(TE 模)22210222123222221arctan nn k n n n n n n m h c ---+=π2221022213222arctan nn k n n n n m h c ---+=π (TM 模)非对称平板波导上下包层的最小透射深度为:222101nn k a -=(上包层)232101nn k b -= (下包层)其中a 、b 取TE 、TM 中按上述公式计算出来的结果中的最大值。
由以上分析建立脚本m 文件PlanarWaveguide.m 与函数m 文件DispersionFun.m 及MinDepthFun.m 如下:PlanarWaveguide.m 脚本文件:close all ; clear all ; clc;NTE = linspace(1.510,1.537,1000); NTM = linspace(1.5095,1.530,1000); for m = 0:3[hTE,hTM] = DispersionFun(NTE,NTM,m); plot(hTE,NTE,'r',hTM,NTM,'b'); hold on ; end ;axis([0,15,1.5090,1.538]); xlabel('h/μm'); ylabel('N');title('非对称平板波导色散曲线'); legend('TE','TM',4); grid on;gtext('m=0');gtext('m=1');gtext('m=2');gtext('m=3'); zoom on ; clc;NTE = 1.510; NTM = 1.5095;[hTEc0,hTMc0] = DispersionFun(NTE,NTM,0) [hTEc1,hTMc1] = DispersionFun(NTE,NTM,1) [hTEc2,hTMc2] = DispersionFun(NTE,NTM,2)[aMin,bMin] = MinDepthFun()DispersionFun.m函数文件:function [hTE,hTM] = DispersionFun(NTE,NTM,m)lambda = 1.55e-6;k0 = 2*pi/lambda;n1TE = 1.537;n2TE = 1.510;n3TE = 1.444;n1TM = 1.530;n2TM = 1.5095;n3TM = 1.444;hTE = 1e6*((m*pi+atan(sqrt((NTE.^2-n2TE^2)./(n1TE^2-NTE.^2)))...+atan(sqrt((NTE.^2-n3TE^2)./(n1TE^2-NTE.^2))))./(k0*sqrt(n1TE^2-N TE.^2)));hTM = 1e6*((m*pi+atan(sqrt((n1TM^2*(NTM.^2-n2TM^2))./(n2TM^2*(n1TM^2-NT M.^2))))...+atan(sqrt((n1TM^2*(NTM.^2-n3TM^2))./(n3TM^2*(n1TM^2-NTM.^2))))). /(k0*sqrt(n1TM^2-NTM.^2)));MinDepthFun.m函数文件:function [aMin,bMin] = MinDepthFun()lambda = 1.55e-6;k0 = 2*pi/lambda;n1TE = 1.537;n2TE = 1.510;n3TE = 1.444;n1TM = 1.530;n2TM = 1.5095;n3TM = 1.444;aMinTE = 1e6/(k0*sqrt((n1TE^2-n2TE^2)));aMinTM = 1e6/(k0*sqrt((n1TM^2-n2TM^2)));if(aMinTE >= aMinTM)aMin = aMinTE;elseaMin = aMinTM;end;bMinTE = 1e6/(k0*sqrt((n1TE^2-n3TE^2)));bMinTM = 1e6/(k0*sqrt((n1TM^2-n3TM^2)));if(bMinTE >= bMinTM)bMin = bMinTE;elsebMin = bMinTM;end;三、运行结果及分析实验结果共画出0~3阶TE、TM模的非对称平板波导的色散曲线,如图1所示:510151.511.5151.521.5251.531.535h/μmN平板波导色散曲线图1 非对称平板波导色散曲线同时在命令窗口得到如下运行结果: hTEc0 = 0.8555 hTMc0 = 1.0664 hTEc1 = 3.5575 hTMc1 = 4.1711 hTEc2 = 6.2595 hTMc2 = 7.2758 aMin = 0.9883 bMin = 0.4878 运行结果表示:(1)0TE 的芯层厚度范围为: 3.55758555.0<<h m ;(2)0TM 的芯层厚度范围为: 4.17111.0664<<h m μ; (3)1TE 的芯层厚度范围为: 6.25955575.3<<h m μ; (4)1TM 的芯层厚度范围为:7.27581711.4<<h m μ; (5)上包层的最小厚度为0.9883m μ; (6)下包层的最小厚度为0.4878m μ。
利用Matlab PDETOOL提升微波技术基础教学质量——以波导模式分析为例

图1中空金属矩形波导1所示中空金属矩形波导,设其尺寸为2cm×1cm。
利用时谐形式的Maxwell方程组,容易得HelmholtzE=0,2H+k2H=0。
电场和磁场具有统据波导理论,其横向场分量可用纵向场此,求解波导模式可转变为求解纵向场方2.4675。
其结果与解析解TM1110(a)TM波最低阶的模场E z分布图(b)TE波最低阶的模场H z分布图图2模场分布图对于TE模式,其第二阶和第三阶是简并模式TE01和TE20,分别如图3(a)和(b)所示,从图中我们看出部分等值线并不是很好的平行于x轴和y轴,此两种模式关于横轴分别对称和反对称,为此,我们只仿真一半的空间,磁场关于x轴对称和反对称,结果如图3(c)和(a)TE01模场H z分布图(b)TE20模场H z分布图(c)TE模磁场H z关于x轴反对称(d)TE模磁场H z关于x轴对称图3TE模式模场H z分布图(下转第37页0.005,0.0434°。
图53结论本文采用北斗卫星载波相位技术实现雷达方位角测量,对核心技术进行研究及试验验证,方位角实测精度优于0.05。
结果表明,基于北斗载波相位差分技术的方位标定可作为雷达方位标定的一种有效手段,弥补陀螺寻北仪在方位标定中的不足。
【参考文献】[1]夏林元,鲍志雄,李成钢,等.北斗在高精度定位领域中的应用[M].中国工信出版集团,2016[2]谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009.工作参数,极大提高了学生的学习热情。
图4最低阶TE模场H z分布图结论通过以上实例,展示了如何利用Matlab PDETOOL。
含色散左手材料非对称5层平板波导的模式特性

含色散左手材料, 折射率为 n1 , 厚度为 2 d, 相对 介电常 数
1 1 1
、 相 对磁 导 率
1
和 折 射 率 n1 = iarctanh C 0- 1
均为负值, 它淀积在折射率为 n- 2 的衬底上。
tanh art anhC- 1- 2
p- 2 + p - 1 d- 1 p- 1 ( 2)
0
C01 =
- 1
0
/ ,
1
, C 12 =
1
1
/
- 1
2
, C 0- 1 =
- 2
/
- 1
, C - 1- 2 =
/
- 2
=
2
= c
=
2
= 1 覆盖层和 衬底的
r
横向衰减系数 q =
N -
r
, r = - 2 , 2, - 3,
传播常数 = k 0 N , N 为有 效折射 , m 取整数 0, 1, 2, , 对
即左
[ 2]
手材料 , 这种 材料 具有 一些 奇 异的 电磁 特性 。 2000 年 Sm it h 等 人 将 金 属 丝 板 和 开 口 谐 振 环 ( SRR) 周期性排列, 制作了世界上第一块在某频 段等效介电常数和等效磁导率同时为负值的介质 ,
*
收稿日期 : 2010- 11- 08 基金项目 : 常州大学科技基金资助 ( ZM F02020042) 作者简介 : 郑泽林 ( 1983- ) , 男 , 河南信阳人 , 硕士生 ; 通讯联系人 : 蒋美萍。
第 23 卷 第 1 期 2011 年 3 月
常州大学学报 ( 自然科学版) Journal of Changzhou U niv ersity ( Natural Science Edition)
非对称屏蔽带状线的频域有限差分解法

非对称屏蔽带状线的TM 模研究——频域有限差分法一、 非对称屏蔽带状线TM 模的理论分析本文研究的屏蔽带状线结构如图1所示[1]。
接地外导体为方形,边长为2b = 10 mm ,导带平行于上下壁,到上下壁的距离壁为1:3,即c = 7.5 mm ,到左右壁的距离为a 。
令ρ = a /b ,则导带宽度l = 2b (1-ρ),ρ的取值范围在0.3到0.7之间,导带宽度相对于外导体边长的变化率为l /2b = 1-ρ,其取值范围也在0.3到0.7之间。
图1 非对称屏蔽带状线用自由空间波阻抗η0的平方根对Maxwell 旋度方程中的电场和磁场进行归一化处理[2]:H H E E ηη⎧=⎪⎨=⎪⎩ (1.1)上式中的等号代表赋值。
设波导结构中不填充电磁介质,频域的Maxwell 旋度方程可写为:00j j k H Ek E H⎧-=∇⨯⎪⎨=∇⨯⎪⎩ (1.2)其中,k 0为自由空间波数。
在外导体和导带表面,切向电场分量为零,边界条件为,,0,00,000z y x b x b zx y b y b z y c b x l x y c b x l E E E E E E =====-≤=-≤⎧==⎪⎪==⎪⎨=⎪⎪=⎪⎩(1.3)对于TM 模,纵向磁场H z = 0,因此待求解的场分量就只剩下{E x , E y , E z , H x , H y }5个。
设波导结构在z 方向是均匀的,波沿着正z 方向传输,该结构中的场分量可表示为:{}(){}()j ,,,,,,,,,,,zxyzxyxyzxyE E E H H x y z E E EH H x y eβ-= (1.4)其中,β是相位常数。
二、频域有限差分(FDFD)原理2.1 网格划分由于各场分量关于z的函数是复指数函数,场量对z的偏导可以用–jβ代替,三维Yee网格化为压缩的二维形式,如图2所示。
E z分量位于整网格点上,E y和H x位于与y轴平行的半网格点上,E x和H y位于与x轴平行的半网格点上,H z位于Yee格的中心位置。
BPM波导matlab,用Matlab画平板波导色散图详解.doc

BPM波导matlab,⽤Matlab画平板波导⾊散图详解.doc根据以下的平板光波导在波长为1550 nm时的折射率数据,(1)作出不同波导芯厚度h(0(2)给出满⾜单模与双模传输的波导厚度范围;(3)确定包层所需的最⼩厚度a与b的值。
解答:(1)⾊散图如下:由图可得出该波导结构在1550nm波长处⼏点规律 :1、当波导芯厚度和模式相同时,TM模的等效折射率⼤于TE模的等效折射率;2、当波导芯厚度相同时,⾼阶模的等效折射率都⽐低阶的⼤很多;3、当模式⼀定时,TE模和TM模的等效折射率都随芯层厚度增⼤⽽增⼤,最后趋于稳定。
(2)某个模式(即导模)能在波导结构稳定传输,就意着它在芯层传输的 等效折射率⼤于周围介质层的折射率,否者不能在芯层稳定传输。
单模传输,那么只能允许基模传输,所以由⾊散图可知芯层厚度h应该⼤于1.0241μm,但由允许⼀阶模传输,那么芯层厚度h应该⼩于3.8554μm,所以该波导单模传输的芯层厚度范围为:1.0241μm < h < 3.8554μm。
同理可分析出双模传输的芯层厚度范围为:3.8554μm < h < 6.4458μm。
(3)由公式,,,可得, 。
单模传输时,N取临界最⼤值1.528。
则通过matlab计算可得a > 1 / p = 1.0853μm;b > 1 / q = 0.4949μm。
双模传输时,N取临界最⼤值1.5328。
则通过matlab计算可得a > 1 / p = 0.9577μm;b > 1 / q = 0.4809μm。
(4)波长放⼤⼗倍的分析由上图可知,忽略⾊散时,波长放⼤⼗倍后,为了是光波在波导中稳定传输,所需的最⼩芯层厚度变⼤了很多。
% clear all% clc;% % 画平板光波导波导层厚度h关于有效折射率N的⾊散图% syms y x% n3 = 1.4444;% lambda = 15.5;% k = 2 * pi / lambda;% figure;% for m = 0:3 %做0到3阶模的循环% %画TE模的⾊散图% n1 = 1.5350;% n2 = 1.5105;% h = ezplot(m*pi + atan(sqrt((y^2*k^2 - n2^2*k^2)/( n1^2*k^2 - y^2*k^2 ))) + atan(sqrt((y^2*k^2 - n3^2*k^2)/( n1^2*k^2 -y^2*k^2 ))) - sqrt(n1^2*k^2 - y^2*k^2 )*x,[0,45,1.44,1.54]);% set(h,'color','r','linewidth',1.2);% hold on;% %画TM模的⾊散图% n1 = 1.5365;% n2 = 1.5110;% h = ezplot(m*pi + atan((n1^2/n2^2)*sqrt((y^2*k^2 - n2^2*k^2)/( n1^2*k^2 - y^2*k^2 ))) +atan((n1^2/n3^2)*sqrt((y^2*k^2 - n3^2*k^2)/( n1^2*k^2 - y^2*k^2 ))) - sqrt(n1^2*k^2 - y^2*k^2 )*x,[0,45,1.44,1.54]);% set(h,'color','g','linewidth',1.2);% hold on;% end% %画N = 1.5105,以便判断TE模的最⼩波导厚度% y = 1.5105;% x = 0:0.1:45;% plot(x,y,'-');% hold off;%clear allclc;n3 = 1.4444;lambda = 1.55;k = 2 * pi / lambda;for m = 0:3n1 = 1.5350;n2 = 1.5105;N_TE = 1.5:0.0000001:1.5365;h_TE = (m*pi.*ones + atan(sqrt((N_TE.^2 - n2^2)./(n1^2 - N_TE.^2))) + atan(sqrt((N_TE.^2 - n3^2)./(n1^2 - N_TE.^2))))./...(sqrt(n1^2*k^2 - N_TE.^2*k^2) );n1 = 1.5365;n2 = 1.5110;N_TM = 1.5:0.0000001:1.5365;h_TM = (m*pi.*one。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光波导理论与技术第一次作业
题目:非对称平板波导设计
*名:**
学号:************
指导老师:***
完成日期:2014 年03 月10 日
一、题目
根据以下的平板光波导折射率数据:
(1)作出不同波导芯层厚度h (015h m μ<<)对应的TE 模式与TM 模式的色散图;
(2)给出满足单模与双模传输的波导厚度范围; (3)确定包层所需的最小厚度a 与b 的值。
二、步骤
依题意知,平板波导参数为:537.11=TE n ,510.12=TE n ,444.13=TE n ;
530.11=TM n ,5095.12=TM n ,444.13=TM n 。
其中321n n n 、、分别代表芯心、上
包层、下包层相对于nm 1550=λ光波的折射率。
在实际应用中,平板波导的有效折射率N 必须12n N n <<才能起到导光的作用。
经过推导,非对称平板波导的色散方程为:
2
212322212
2
22
2
1
0arctan arctan N
n n N N n n N m N n h k --+--+=-π (TE 模) 2
212
3
22
32
12212
222
2
2
1221
0arctan arctan N n n N n n N n n N n n m N n h k --+--+=-π (TM 模)
非对称平板波导光波模式截止时对应的芯层厚度为:
(TE 模)
22
21
02
22123
222
2
2
1arctan n
n k n n n n n n m h c ---+=
π22
2102
2
2
132
22arctan n
n k n n n n m h c ---+=
π (TM 模)
非对称平板波导上下包层的最小透射深度为:
22
21
01n
n k a -=
(上包层)
23
21
01n
n k b -= (下包层)
其中a 、b 取TE 、TM 中按上述公式计算出来的结果中的最大值。
由以上分析建立脚本m 文件PlanarWaveguide.m 与函数m 文件DispersionFun.m 及MinDepthFun.m 如下:
PlanarWaveguide.m 脚本文件:
close all ; clear all ; clc;
NTE = linspace(1.510,1.537,1000); NTM = linspace(1.5095,1.530,1000); for m = 0:3
[hTE,hTM] = DispersionFun(NTE,NTM,m); plot(hTE,NTE,'r',hTM,NTM,'b'); hold on ; end ;
axis([0,15,1.5090,1.538]); xlabel('h/μm'); ylabel('N');
title('非对称平板波导色散曲线'); legend('TE','TM',4); grid on;
gtext('m=0');gtext('m=1');gtext('m=2');gtext('m=3'); zoom on ; clc;
NTE = 1.510; NTM = 1.5095;
[hTEc0,hTMc0] = DispersionFun(NTE,NTM,0) [hTEc1,hTMc1] = DispersionFun(NTE,NTM,1) [hTEc2,hTMc2] = DispersionFun(NTE,NTM,2)。
