牛顿粘性定律
牛顿粘性定律

粘弹性流体的两个特性
(流体的流动形态及雷诺准数
1883年,雷诺(Reynolds)做了如下实验
Re 2000 Re 4000
Re 2000 ~ 4000
层流 湍流 过渡流
四、圆管内流体的速度分布
umax
p1 p 2 2 ur R r2 4l
第三节 流体流动现象
一、牛顿粘性定律及流体的粘度
1、牛顿粘性定律
概念: 内摩檫力; 粘性
F
a层
b层
F' du A dy
讨论
(1) 动量传递如何在牛顿粘性定律中体现? ' F du d mu d m u du
F ma m dt dt
A A dt dy
1 u u max 2
umax
ur y u max R
1 7
尼古拉则的七分之一次方定律
u 0.8umax
附:层流速度分布式的推导思路
2 p r 作用于流体柱左端面的力为: 1 作用于流体柱右端面的力为: p2r 2
流体柱外表面受的内摩擦力为:F '
四、滞流与湍流及边界层
(2) 粘度μ的单位
1Pa.S = 1000CP =10P
(3)粘度μ的物理意义
在单位接触面积上,速度梯度为1时,由流体的粘度引起的 内摩擦力的大小 。
(4) μ的影响因素
P,T
(5)混合物的粘度μ的计算
See P34~35
(6) 运动粘度ν
ν = μ/ρ
m2/s
(7) 剪应力的极值位置
二、牛顿型流体和非牛顿型流体
1、滞流
F' du A dy
关于牛顿内摩擦定律及流体粘度
利用量纲分析法可以得到:
( Re ,
d
)
式中: — 粗糙度
d
— 相对粗糙度
根据实验,得到莫狄(Moody)摩擦系数图。
0.1 0.09 0.08 0.07 0.06 0.05
e/l
0.05 0.04 0.03 0.02 0.015 0.01 0.008 0.006 0.0045
(1)流体阻力的表示方法
对应于机械能衡算的三种形式,流体阻力损失亦有三种表达形式:
R
h
f
kJ/kg m Pa
R g
p
f
R
阻力损失与压力差的区别: △pf —— 流体流经两截面间的机械能损失;
△p —— 任意两点间的压力差。
二者之间的关系:
u2 p We gz p f 2
1.4 流体流动阻力
1.4.1 流体的粘性和牛顿粘性定律
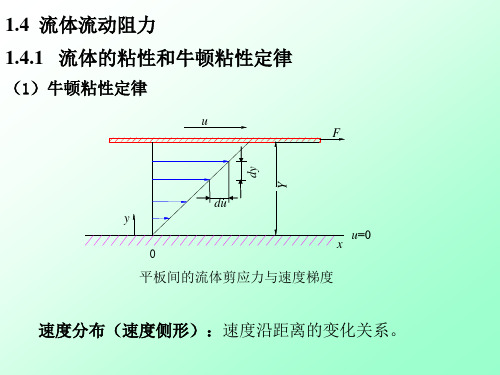
(1)牛顿粘性定律
u F dy
du
y 0 x u=0
平板间的流体剪应力与速度梯度
速度分布(速度侧形):速度沿距离的变化关系。
Y
平板间的流体剪应力与速度梯度
实测发现:
F u A Y
牛顿粘性定律:
du dy
意义:剪应力的大小与速度梯度成正比。
1.4.2 流体流动的类型---层流及湍流
(1)雷诺实验
1883年, 英国物理学家Osbone Reynolds作了如下实验。
C 墨水流线 A 玻璃管
D
B
雷诺实验
(2)雷诺实验现象
用红墨水观察管中水的流动状态 层流
(a)
过渡流
(b)
湍流
(c)
第三讲 牛顿粘性定律与雷诺实验及管路阻力计算

过渡流
(b)
湍流
(c)
两种稳定的流动状态:层流、湍流。
2016/12/1
层流:
* 流体质点做直线运动;
* 流体分层流动,层间不相混合、不碰撞; * 流动阻力来源于层间粘性摩擦力。 湍流: 主体做轴向运动,同时有径向脉动; 特征:流体质点的脉动 。 过渡流: 不是独立流型(层流+湍流), 流体处于不稳定状态(易发生流型转变)。
log m xi log i
常压下气体混合物的粘度,可用下式计算 0 .5 y M m i i 0 .5 yi M
2016/12/1
(6)流体类型
① 牛顿型流体:符合牛顿粘性定律的流体。
du dy
气体及大多数低分子量液体是牛顿型流体。 ② 非牛顿型流体
du a dy
2016/12/1
u
F
dy du
du 牛顿粘性定律: dy
y 0 x
Y
F u 实测发现: A Y
u=0
平板间的流体剪应力与速度梯度
运动着的流体内部相邻两流体层间存在相互作用力。该作 用力称为粘滞力,剪切力或者内摩擦力。 ——流体阻力产生的根源 剪应力始终与流体流动方向相反,单位面积上剪切 力称为剪应力,剪应力的大小与速度梯度成正比。
2016/12/1
(2) 流体的粘度 ① 物理意义
du dy
—— 动力粘度,简称粘度
粘度只有在运动时才显现出来,总是与速度梯度相联 系,促使流体流动产生单位速度梯度的剪应力。 (2)粘度与温度、压强的关系 (a) 液体的粘度随温度升高而减小,压强变化时, 液体的粘度基本不变。 (b)气体的粘度随温度升高而增大,随压强增加而 增加的很少。
化工原理管内流体流动现象

二、边界层的分离
B
A
S
A →C:流道截面积逐渐减小,流速逐渐增加,压 力逐渐减小(顺压梯度);
C → S:流道截面积逐渐增加,流速逐渐减小,压 力逐渐增加(逆压梯度);
S点:物体表面的流体质点在逆压梯度和粘性剪应 力的作用下,速度降为0。
SS’以下:边界层脱离固体壁面,而后倒流回来, 形成涡流,出现边界层分离。
f ( p,T )
液体 : f (T ) T ↑ → ↓ 气体 : 一般 f (T ) T ↑ → ↑
超高压 f ( p,T ) p ↑ → ↑
2. 粘度的单位 SI制:Pa·s 或 kg/(m·s) 物理制:cP(厘泊) 换算关系 1cP=10-3 Pa·s
3.运动粘度
管截面上的平均速度 :
R.
u VS A
0
u 2rdr R 2
1 2
umax
层流流动平均速度为管中心最大速度的1/2。
u ( p1 p2 ) R2
8l
u ( p1 p2 ) R2
8l
p1
p2
8lu
R2
32lu
d2
哈根-泊谡叶方程
(3)
二、湍流时的速度分布
.
剪应力 : ( e) d u
dy
e为湍流粘度,与流体的流动状况有关。
湍流速度分布 的经验式:
.
u
umax1
r R
n
1.3.4 流体流动边界层
一、边界层的形成与发展 流动边界层:存在着较大速度梯度的流体层区域,
即流速降为主体流速的99%以内的区域。
边界层厚度:边界层外缘与壁面间的垂直距离。
流体在平板上流动时的边界层:
界层区(边界层内):沿板面法向的速 度梯度很大,需考虑粘度的影响,剪应力不 可忽略。
牛顿黏性实验定律

牛顿黏性实验定律
牛顿黏性实验定律是物理学家牛顿在17th世纪提出的一条定律,它描述了物体在受到外力作用时的运动规律。
它规定,当一个物体受到外力作用时,它的运动受到两种力的影响:一种是外力,另一种是物体自身的黏性力。
物体的运动受到这两种力的共同作用,它的运动规律可以用下面的公式来表示:F=ma+bv,其中F表示外力,m表示物体的质量,a表示物体的加速度,b表示物体的黏性系数,v表示物体的速度。
牛顿黏性实验定律的发现对物理学的发展有着重要的意义,它为研究物体在受到外力作用时的运动规律提供了一个重要的理论框架。
它不仅可以用来研究物体的运动规律,而且还可以用来研究物体的变形、振动和摩擦等问题。
牛顿黏性实验定律的发现也为现代物理学的发展提供了重要的理论基础,它为研究物体的运动规律提供了一个重要的理论框架,为现代物理学的发展奠定了坚实的基础。
牛顿黏性实验定律的发现也为现代物理学的发展提供了重要的理论基础,它为研究物体的运动规律提供了一个重要的理论框架,为现代物理学的发展奠定了坚实的基础。
牛顿黏性实验定律的发现也为现代物理学的发展提供了重要的理论基础,它为研究物体的运动规律提供了一个重要的理论框架,为现代物理学的发展奠定了坚实的基础。
牛顿黏性实验定律的发现为物理学的发展做出了重要贡献,它为研究物体的运动规律提供了一个重要的理论框架,为现代物理学的发展奠定了坚实的基础。
它的发现也为现代物理学的发展提供了重要的理论基础,为研究物体的运动规律提供了一个重要的理论框架,为现代物理学的发展奠定了坚实的基础。
流体的流动现象

[例1-17]在 得无缝钢管中输送燃料油,油得运动粘度为90cSt,试求燃料油坐标滞流流动时得临界速度.
解:由于运动粘度 ,则 .滞流时,Re得临界值为2000,即
Re=du/v=2000
式中d=168-5x2=158mm=0.158m
(1—30)
图1-14中b、c、d曲线所代表的流体,其表观粘度凡都只随剪切速率而变,和剪切力作用持续的时间无关,故称为与时间无关的粘性流体,又可分为下面三种。
1)假塑性(Pseudoplastic)流体这种流体的表观粘度随剪切速率的增大而减小,τ对γ的关系为一向下弯的曲线,该曲线可用指数方程来表示:
τ=τ0+η0 (1—32)
式中τ0—屈服应力,Pa;
η0—刚性系数,Pa·s。
二、与时间有关的粘性流体.
在一定剪切速率下,表观粘度随剪切力作用时间的延长而降低或升高的流体,则为与时间有关的粘性流体。它可分为下面两种。
1)触变性(thixotropic)流体这种流体的表观粘度随剪切力作用时间的延长而降低,属于此类流体的如某些高聚物溶液、某些食品和油漆等。
[例1-16]20℃得水在内径为50mm得管内流动,流速为2m/s.试分别用法定单位制和物理单位制计算准数得数值.
解:(1)用法定单位制计算从本教材附录六查得水在20℃时
已知:管径d=0.05m,流速u=2m/s,则
Re=
(2)用物理单位制计算
u=2m/s=200cm/s, d=5cm
所以Re=99320
(1—26a)
式中 —速度梯度,即在与流动方向相垂直的y方向上流体速度的变化率;
—比例系数,其值随流体不同而异,流体的粘性愈大,其值愈大,所以称为粘滞系数或动力粘度,简称为粘度
牛顿黏性实验定律的简单解释

牛顿黏性实验定律的简单解释牛顿粘性实验定律,顾名思义,是以牛顿为代表的人所做的有关大小均匀的物体在受到外力作用时总会发生运动状态变化。
牛顿在《自然哲学的数学原理》中写道:“我想,如果某种物体,对地面的压力同它所受的重力成比例,这个物体就可能在不需要外力的推动下而发生运动。
但是,如果这种物体受到的重力和它所受的压力成比例,那么它就没有发生运动的趋势了,即当它停止下来的时候,速度为零。
”“第二实验”指的是,将两个铁球分别放置在固定在平板上的木架上,并使其保持相互平行的位置。
在离两球中点距离相等的地方画一线,此时若拉绳,让它绕过两球的中点,则只有一个球发生移动,另一个球被拖动,且动的越快,动得越远。
即两球中任何一个是相对静止的。
牛顿黏性实验定律说明,当两个不同质量的物体之间相互接触或靠近时,接触面会发生形变,从而出现一系列效应:( 1)一个物体将另一个物体紧紧包围起来,两者间有弹力;( 2)两个物体在相互挤压时有摩擦力;( 3)两个物体相互接触时产生附加力,当其它因素不变时,随着两物体间距离的增大,它们的相互作用力也随之增大,从而会导致两物体间出现剪切力,同时还会产生相互作用力,进一步增大了力的作用效果。
也就是说,物体与物体之间存在引力和斥力,所谓万有引力就是指的这种相互作用力。
“第一实验”指的是地面上有一条绳子或薄板,下面悬挂着轻质的东西(不计空气阻力,忽略摩擦力,忽略绳子弹性的影响),同时还给予向上的拉力F=-N。
当物体A放在薄板上时, F很小,由于地球引力作用,它将静止不动;若将物体B放在薄板上,那么根据万有引力的公式F=-N,所以对B施加一个很大的向下的拉力F=-M,在两力的作用下, A和B一起向下运动,并处于相对静止状态。
此时,物体A和B的距离是变小的,力的大小也会减少,因为两物体间的引力和斥力都在逐渐减弱,直至消失,那么此时两物体就会[gPARAGRAPH3],就是互相靠近、合拢,而并非是像上面一样靠拢、分开。
牛顿粘性定律与流体的粘度

⽜顿粘性定律与流体的粘度流体的流动现象--⽜顿粘性定律与流体的粘度⼯业⽣产中的许多过程都与流体的流动现象密切相关,流动现象是个极为复杂的问题,涉及⾯⼴,本节只作简要的介绍。
⼀、⽜顿粘性定律前已述及,流体具有流动性,即没有固定形状,在外⼒作⽤下其内部产⽣相对运动。
另⼀⽅⾯,在运动的状态下,流体还有⼀种抗拒内在的向前运动的特性,称为粘性,粘性是流动性的反⾯。
以⽔在管内流动时为例,管内任⼀截⾯上各点的速度并不相同,中⼼处的速度最⼤,愈靠近管壁速度愈⼩,在管壁处⽔的质点附于管壁上,其速度为零。
其他流体在管内流动时也有类似的规律。
所以,流体在圆管内流动时,实际上是被分割成⽆数极薄的圆筒层,⼀层套着⼀层,各层以不同的速度向前运动,如图1-10所⽰。
由于各层速度不同,层与层之间发⽣了相对运动,速度快的流体层对与之相邻的速度较慢的流体层发⽣了⼀个推动其向前运动⽅向前进的⼒,⽽同时速度慢的流体层对建度快的流体层也作⽤着⼀个⼤⼩相等,⽅向相反的⼒,从⽽阻碍较快的流体层向前运动。
这种运动着的流体内部相邻两流体层间的相互作⽤⼒,称为流体的内摩擦⼒,是流体粘性的表现,所以⼜称为粘滞⼒或粘性摩擦⼒。
流体在流动时的内摩擦,是流动阻⼒产⽣的依据,流体流动时必须克服内摩擦⼒⽽作功,从⽽将流体的⼀部分机械能转变为热⽽损失掉。
流体流动时的内摩擦⼒⼤⼩与哪些因素有关?可通过下⾯情况加以说明。
图1-10 流体在圆管内分层流动⽰意图图1-11 平板间液体速度变化图如图1-11所⽰,设有上下两块平⾏放置且⾯积很⼤⽽相距很近的平板,板间充满了某种液体。
若将下板固定,⽽对上板施加⼀个恒定的外⼒,上板就以恒定的速度u沿x⽅向运动。
此时,两板间的液体就会分成⽆数平⾏的薄层⽽运动,粘附在上板底⾯的⼀薄层液体也以建度。
随上板⽽运动,其下各层液体的速度依次降低,粘附在下板表⾯的液层速度为零。
实验证明,对于⼀定的液体,内摩擦⼒F与两流体层的速度差Δu成正⽐,与两层之间的垂直距离Δy 成反⽐,与两层间的接触⾯积S成正⽐,即:若把上式写成等式,就需引进⼀个⽐例系数µ,即:式中的内摩擦⼒F与作⽤⾯S平⾏。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
牛顿粘性定律
牛顿在1687年进一步假设:流体内摩擦力与两层流体间的相对速度成正比。
图B1.3.6
以平行平板流动为例<图B1.3.6),下板静止,上板速度δu,按不滑移假设,δt时间后,矩形元ABCD变形为平行四边形A'BCD'。
间距为δy的两层流体的相对速度称为速度梯度: b5E2RGbCAP
(B1.3.1>
称为角变形率或剪切变形率。
设x方向单位面积上的流体内摩擦力为τ,称为粘性切应力。
按牛顿粘性假设:
(B1.3.2>
比例系数μ称为粘度。
粘度为常数的流体称为牛顿流体。
据牛顿粘性假设和不滑移假设求解流体运动方程<B3.4),理论结果与实验吻合,验证了两个假设的合理性,因此前者<B1.3.2)式称为牛顿粘性定律,后者称为不滑移条件。
p1EanqFDPw
粘度的全称为动力粘度或绝对粘度。
牛顿流体的粘度可由<B1.3.2)式决定:
(B1.3.3>△在SI中粘度的单位是N·s/m2或Pa·s<帕秒);
在cgs制中粘度的单位是g / cm·s 或p<泊)。
1N·s/m2 =10g / cm·s 或1Pa·s =10 p
图B1.3.7
温度对流体的粘性影响较大:液体的粘度随温度升高而减小,气体则相反。
运动粘度定义为动力粘度与密度之比值:
(B1.3.4>
△ 在SI制中运动粘度的单位是m 2 / s ;
在cgs制中运动粘度的单位是cm 2 / s。
申明:
所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
