7.4载流线圈在均匀磁场中受到的磁力矩
载流线圈在均匀磁场中受到的磁力矩

M ISen B
4、载流线圈的磁矩 I
en
S 载流线圈
m
m ISen
磁矩
载流线圈在均匀磁场中的磁力矩
M ISen B
M m B
补充说明 考虑磁场的均匀性
一般情况下,小载流线圈等效于磁矩
5、磁矩在磁场中的势能
m
M m B
I
A
2 1 2 1
如将 1 / 2 的位置当成势能零点,则
Wm mB cos m B
电偶极矩 p 力矩 势能
M p E W p E
磁矩 m
M m B W m B
6、磁矩在磁场中的受力 磁矩在磁场中的势能
W m B
磁矩在磁场中的受力
F W (m B ) (m x Bx m y B y mz Bz ) m x Bx m y B y m z Bz
对 z 轴的力矩
dM rdF R sin IRd B sin R2 IB sin 2 d
对 z 轴的总力矩
2
M
dM
0
2
0
R2 IB sin 2 d R2 IB R2 IB sin
M SIen B
3、任意形状载流线圈
Topography (height)
40 μm
40 μm
B B// B
Idl1 受到的作用力
dF1 Idl1 B sin 1
dh
B
Idl2 受到的作用力
dF2 Idl2 B sin 2 dl2 in 2 dl1 sin 1 dh
dF1 dF2 IB dh
大学物理八九章部分习题解答

第8章 磁场8-10一均匀密绕直螺线管的半径为 ,单位长度上有 匝线圈,每匝线圈中的电流为 ,用毕奥—萨伐尔定律求此螺线管轴线上的磁场。
分析:由于线圈密绕,因此可以近似地把螺线管看成一系列圆电流的紧密排列,且每一匝圆电流在轴线上任一点的磁场均沿轴向。
解: 取通过螺线管的轴线并与电流形成右旋的方向(即磁场的方向)为x 轴正向,如习题8-10图解(a )所示。
在螺线管上任取一段微元dx ,则通过它的电流为dI nIdx =,把它看成一个圆线圈,它在轴线上O 点产生的磁感应强度dB 为2022322()R nIdxdB R x μ=+ 由叠加原理可得,整个螺线管在O 点产生的磁感应强度B 的大小为212022322()x Lx R nIdxB dB R x μ==+⎰⎰0212212221221[]2()()nIx x R x R x μ=-++ 由图可知12122212221212cos os ()()x x R x R x ββ==++ c ,代入上式并整理可得 021(cos cos )2nIB μββ=-式中12ββ和分别为x 轴正向与从O 点引向螺线管两端的矢径r 之间的夹角。
讨论:(1)若螺线管的长度远远大于其直径,即螺线管可视为无限长时,20β=,1βπ=,则有nI B 0μ=上式说明,无限长密绕长直螺线管内部轴线上各点磁感应强度为常矢量。
理论和实验均证明:在整个无限长螺线管内部空间里,上述结论也适用。
即无限长螺线管内部空间里的磁场为均匀磁场,其磁感应强度B 的大小为0nI μ,方向与轴线平行;(2)若点O 位于半无限长载流螺线管一端,即12πβ=,20β=或12πβ=,2βπ=时,无论哪一种情况均有nI B 021μ=------(8-19) 可见半无限长螺线管端面中心轴线上磁感应强度的大小为管内的一半;综上所述,密绕长直螺线管轴线上各处磁感应强度分布见习题8-10图解(b )所示,从图中也可看出,长直螺线管内中部的磁场可以看成是均匀的。
第7章_稳恒磁场集美大学物理答案

班级____________ 姓名______________ 学号_________________ 第7-1 毕奥—萨伐尔定律 一.选择题:1.一根载有电流I 的无限长直导线,在A 处弯成半径为R 的圆形,由于导线外有绝缘层,在A 处两导线靠得很近但不短路,则在圆心处磁感应强度B 的大小为:( C ) (A) (μ0+1)I /(2πR ) (B) μ0I /(2πR ) (C) μ0I (-1+π)/(2πR )(D) μ0I (1+π)/(4πR )2.将半径为R 的无限长导体薄壁管(厚度忽略) 沿轴向割去一宽度为h (h <<R )无限长狭缝后,再沿轴向均匀地流有电流,其面电流密度为i (即沿圆周每单位长度的电流),则管轴线上磁感应强度的大小是:( A )(A) R h i πμ2/0 (B) 0(C) R h i πμ4/0(D) h i 0μ二、计算题:3.载有电流为I 的无限长导线,弯成如图形状,其中一段是半径为R 的半圆,则圆心处的磁感应强度B 的大小为多少? 解: 选为正方向123B B B B →→→→=++1(14IB Rομπ=--2,42I B R ομπ=⋅ 34I B R ομ=∴)12(4-+=ππμοRIB4.用相同的导线组成的一导电回路,由半径为R 的圆周及距圆心为R /2的一直导线组成(如图),若直导线上一电源ε,且通过电流为I ,求圆心O处的磁感应强度。
解 设大圆弧的电流为1I ,小圆弧的电流为2I ,则12I I I +=,选为正方向根据电阻定律有1122l I Sl I S ερερ⎧=⎪⎪⎨⎪=⎪⎩可得:1122I l I l =大圆弧电流在圆心处O 产生的磁感应强度:大小为01114I l B R μπ=,方向为 小圆弧电流在圆心处O 产生的磁感应强度:大小为02224I lB Rμπ=,方向为⊗直导线电流在圆心处O 产生的磁感应强度:大小为0035cos cos 66242I I B R R μππππ⎛⎫=-= ⎪⎝⎭,方向为所以,总电流在圆心处O 产生的磁感应强度:312B B B B =++,大小为:02IB Rπ=,方向为5.如图,两线圈共轴,半径分别为1R 和2R ,电流分别为I 1 和I 2 ,电流方向相同,两圆心相距2 b ,联线的中点为O 。
大学物理复习题

图1-9 1-9(1-121、静电场的高斯定理描述了它是 场。
2、在点电荷+q 的电场中,若取图1-2中P 点处电势为零点,则M 点的电势为: 。
3、如图1-3电路中两个电容器1和2,串联以后接上电动势恒定的电源充电。
在电源保持联接的情况下,若把电介质充入电容器2中,则电容器1上的电势差 电容器1极板上的电量 ;电容器2上的电势差 电容器2极板上的电量 。
(填增大、减小、不变) 5、载有电流为I 的无限长导线,弯成如图1-5所示形状,其中有一部分为半径为R 的半圆弧,则其圆心O 点的磁感应强度的大小为 ,方向为 。
6、闭合导体回路电阻R =5 ,回路所包围面积为0.08m 2,均匀磁场垂直于线圈平面。
欲使电路中有一稳定的感应电流i = 0.08 A ,则磁感应强度的变化率为:d B /d t = T/s 。
7、产生动生电动势和感生电动势的非静电力分别为 、 。
8、磁场能量密度为: ,电场能量密度为: 。
一个电容器加了电压之后储存的电场的能量为: 。
一个自感回路,其中通有电流时,其周围空间磁场的能量为: 。
9、如图1-9,一个矩形线圈与通有相同大小电流的平行直导线在同一平面,而且处在两导线的中央,如图(1-9)所示。
(1)两电流同向且随时间均匀增大时,线圈中有无感应电流 。
(2)两电流反向且随时间均匀增大时,线圈中有无感应电流 。
10、真空中两只长直螺线管1和2,长度相等,单层密绕匝数相同,直径之比d 1/d 2 =1/2,当它们通以相同电流时,两螺线管贮存的磁能之比为W 1/W 2= 。
11、杨氏双缝干涉实验时,用红光和绿光分别做实验时,红光的干涉条纹间距比绿光图1-3图1-5 图1-2的 。
(填:宽 或 窄)。
12、获得相干光常用的方法有两种是: , 。
13、波长为 的单色光垂直照射到宽a 的单缝上,单缝后面放置一个凸透镜, 在凸透镜的焦平面上放置一个屏幕,用以观测衍射条纹,今测得屏幕上中央明条纹两侧第二级暗纹之间的距离为 d ,则透镜的焦距 f 为: 。
第6章 稳恒磁场习题

1第6章 稳恒电流的磁场一 基本要求1. 掌握磁感应强度B的概念。
2. 掌握毕奥-萨伐尔定律,并能用该定律计算一些简单问题中的磁感应强度。
3. 掌握用安培环路定律计算磁感应强度的条件及方法,并能熟练应用。
4. 理解磁场高斯定理。
5. 了解运动电荷的磁场。
6. 理解安培定律,能用安培定律计算简单几何形状的载流导体所受到的磁场力。
7. 理解磁矩的概念,能计算平面载流线圈在均匀磁场中所受到的磁力矩,了解磁力矩所作的功。
8. 理解并能运用洛伦兹力公式分析点电荷在均匀磁场(包括纯电场、纯磁场)中的受力和运动的简单情况。
9. 了解霍耳效应。
10. 了解磁化现象及其微观解释。
11. 了解磁介质的高斯定理和安培环路定理,能用安培环路定理处理较简单的介质中的磁场问题。
12. 了解各向同性介质中H 与B的联系与区别。
13. 了解铁磁质的特性。
二 内容提要1. 毕奥-萨伐尔定律 电流元Id l 在真空中某一场点产生的磁感应强度d B 的大小与电流元的大小、电流元到该点的位矢r与电流元的夹角θ的正弦的乘积成正比,与位矢大小的平方成反比,即204r l I B θπμsin d d =dB 的方向与r l I⨯d 相同,其矢量式为304r rl I B⨯=d d πμ 2. 几种载流导体的磁场 利用毕奥-萨伐尔定律可以导出几种载流导体磁场的分布,这些结果均可作公式应用。
(1)有限长直载流导线的磁感应强度的大小)cos (cos π2104θθμ-=aIB方向与电流成右手螺旋关系。
式中,a 为场点到载流直导线的距离,21θθ、分别为直导线始末两端到场点的连线与电场方向的夹角。
2(2)长载流直导线(无限长载流直导线)的磁感应强度的大小rIB πμ20=方向与电流成右手螺旋关系。
(3) 直载流导线延长线上的的磁感应强度 0=B(4) 载流圆导线(圆电流)轴线上的磁感应强度的大小2322202)(x R IR B +μ=方向沿轴线,与电流成右手螺旋关系。
载流线圈的磁矩及其在均匀磁场中所受磁力矩公式的普遍证明

载流线圈的磁矩及其在均匀磁场中所受磁力
矩公式的普遍证明
载流线圈是由导线卷成的环形结构,在通过电流后会产生磁场。
磁矩是指物体在外磁场作用下所产生的磁场强度和方向的量度。
在一个均匀磁场中,载流线圈所受的磁力矩可以通过公式进行计算。
设载流线圈的磁矩为m,磁场方向为z轴方向,磁场强度为B,载流线圈的面积为S,通过线圈的电流为I。
则载流线圈所受到的磁力矩可以表示为:
M = m×B
同时,载流线圈所受到的磁力矩也可以表示为:
M = IS×(B×n)
其中,n为载流线圈所在平面的法向量,S为载流线圈的面积。
将这两个公式相等,可以得到载流线圈磁矩的普遍公式:
m = ISn
这个公式表明了,载流线圈的磁矩与载流线圈面积和所通过的电流大小有关,与磁场强度和磁场方向无关。
这个公式在应用中可以便于我们计算载流线圈在外磁场中所受到的磁力矩,也对理解和应用磁场具有重要意义。
平面载流线圈在匀强磁场中所受的磁力矩

平面载流线圈在匀强磁场中所受的磁力矩磁力矩是磁势的物理量,它表示某一磁极的磁能合力的矢量和大小,是磁能的测量单位。
当磁场中的磁通有变化时,磁势的变化也会改变这一磁力矩的大小与方向。
因此,研究磁力矩可以更有效地研究磁通的变化特性。
为了更好地理解磁力矩,本文将结合平面载流线圈在匀强磁场中所受的磁力矩进行深入探讨。
首先,在讨论平面载流线圈在匀强磁场中受磁力矩时,需要先理解这种磁场形成的磁性物质是如何受到磁力矩影响的。
在匀强磁场中,磁性物体的磁力矩一定是沿着磁矢的方向,与磁矢方向的正负一致,这也正是由载流线圈的磁极分布所致。
因此,可以看出,在匀强磁场中,载流线圈的磁极分布是磁力矩大小与方向变化的关键因素。
其次,要深入了解平面载流线圈在匀强磁场中受磁力矩变化,就必须考虑载流线圈的磁感应特性。
一般情况下,当磁通的方向沿着磁矢的方向时,磁力矩大小会有明显的增大,而当磁通的方向与磁矢方向相反时,磁力矩的大小才会有明显的减小,这也是匀强磁场中磁力矩的变化特性。
最后,在讨论平面载流线圈在匀强磁场中所受的磁力矩时,还需要考虑载流线圈的形状和尺寸。
一般来说,在磁力矩大小相同的情况下,载流线圈的磁性特性与其形状和尺寸有关,将载流线圈的形状或尺寸改变,载流线圈所受的磁力矩也会发生变化,这是由磁场中载流线圈极化的相互叠加所致。
总而言之,我们来到研究平面载流线圈在匀强磁场中所受的磁力矩的前提下,可以看出,磁力矩的大小和方向的变化是由载流线圈的磁极分布,载流线圈的磁感应特性以及载流线圈的尺寸和形状等多种因素所共同决定的结果。
在此基础上,进一步研究磁力矩的变化特性,可以更好地了解磁场中载流线圈的特性。
综上,本文经过对平面载流线圈在匀强磁场中所受的磁力矩的探讨,可以得出结论,平面载流线圈在匀强磁场中所受的磁力矩是由载流线圈的磁极分布、载流线圈的磁感应特性以及载流线圈的尺寸和形状等多种因素决定的,研究其变化特性可以帮助我们更好地了解载流线圈本身的特性。
大物磁场答案
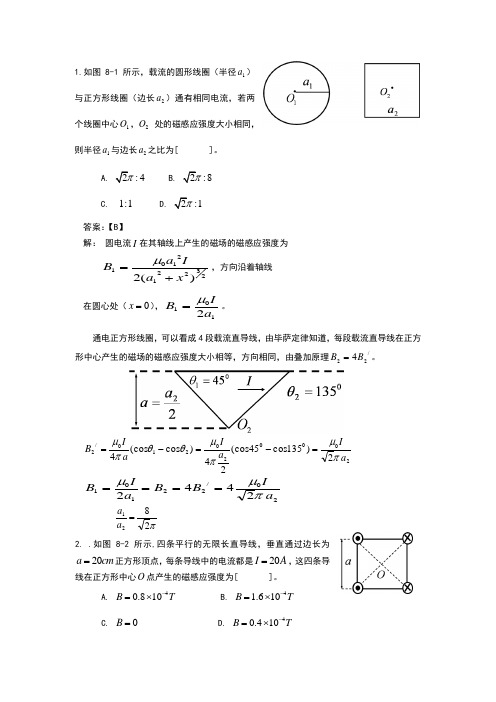
1.如图8-1所示,载流的圆形线圈(半径1a )与正方形线圈(边长2a )通有相同电流,若两个线圈中心1O ,2O 处的磁感应强度大小相同,则半径1a 与边长2a 之比为[ ]。
A. 2:4πB. 2:8πC. 1:1D. 2:1π答案:【B 】解: 圆电流I 在其轴线上产生的磁场的磁感应强度为232212101)(2x a Ia B +=μ,方向沿着轴线 在圆心处(0=x ),1012a IB μ=。
通电正方形线圈,可以看成4段载流直导线,由毕萨定律知道,每段载流直导线在正方形中心产生的磁场的磁感应强度大小相等,方向相同,由叠加原理/224B B =。
200020210/22)135cos 45(cos 24)cos (cos 4a I a I a I B πμπμθθπμ=-=-= 20/221012442a I B B a IB πμμ====π2821=a a 2. .如图8-2所示,四条平行的无限长直导线,垂直通过边长为20a cm =正方形顶点,每条导线中的电流都是20I A =,这四条导线在正方形中心O 点产生的磁感应强度为[ ]。
A. 40.810B T -=⨯B. 41.610B T -=⨯C. 0B =D. 40.410B T -=⨯答案:【A 】解:建立直角坐标系,则4根无限长载流直导线在正方形中心产生的磁感应强度为i a I B 45cos 201πμ=,j a I B 45cos 202πμ= i a IB 45cos 203πμ=,j a I B45cos 204πμ= )(45cos 2204321j i a I B B B B B+=+++=πμ T B 5108-⨯= 3.一根无限长直导线abcde 弯成图8-3所示的形状,中部bcd 是半径为R 、对圆心O 张角为0120的圆弧,当通以电流I 时,O 处磁感应强度的大小B = ,方向为 。
a 答案:)32(2600-=RI R IB πμμ+, 方向垂直纸面向里解:将整个载流导线分为三段:直线ab 、圆弧bcd 、直线de 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
闭合的载流线圈在均匀磁场中
合磁力为零
磁力矩可不为零
载流矩形线圈 载流圆形线圈 载流任意线圈
的磁力矩
1、载流矩形线圈 zB
F
en F
I
b
a
F IbB M aIbB ISB
M ISen B
定义 线圈平面的法线方向 en
力矩 势能
电偶极矩 p 磁矩 m
M pE
M mB
W p E W m B
6、磁矩在磁场中的受力
磁矩在磁场中的势能
W m B 磁矩在磁场中的受力
F W (m B)
(mx Bx my By mz Bz )
mxBx myBy mzBz
2
2
A
Md
mB sin d
mB
cos
2 1
mB(cos1
cos
2)
1
1
磁力的功,与转动的路径没有关系 势能 Wm
Wm Wm2 Wm1 mB(cos1 cos 2 ) 如将 1 / 2 的位置当成势能零点,则 Wm mBcos m B
如果磁场只有 x 方向分量Bx
F
m x Bx
m
x
(
Bx x
, B原理
deflection sensor
sample scanning tube
amplifier
computer
driving electronics
Videotape
Topography (height)
B B// B
Idl1 受到的作用力
dF1 Idl1 B sin1
dh
Idl2 受到的作用力
B
dF2 Idl2 B sin2
dl2 in2 dl1 sin1 dh
dF1 dF2 IBdh
合力为零, 但有力矩
dM x1dF1 x2dF2 IBdh(x1 x2 ) IB sin dS M IBsin S M ISen B
垂直于线圈平面与电流的方向符合右手螺旋关系
F
俯视图
I
en
a
BI
I
F
z
b
a
每条长边受到的力 IbB
力矩大小
M a cos IbB IS cos B IS sin B
M ISen B
2、载流圆线圈
磁场的平行分量对合力矩的贡献为零
电流元 Idl
en
dF IdlB sin
40 μm
40 μm
4、载流线圈的磁矩
I
en m m ISen
S
载流线圈
磁矩
载流线圈在均匀磁场中的磁力矩 M ISen B M m B
补充说明 考虑磁场的均匀性 一般情况下,小载流线圈等效于磁矩
5、磁矩在磁场中的势m能
I
B
M mB
M mBsin
当 从1 增大到 2 磁力做的负功为
对 z 轴的力矩
dM rdF
R sin IRd B sin R2 IB sin2 d
对 z 轴的总力矩
2
2
M dM R2 IB sin2 d R2 IB R2 IB sin
0
0
M SIen B
3、任意形状载流线圈
