关于2016年长郡第二届“澄池杯”竞赛
参加全国初中化学竞赛有哪些益处

参加全国初中化学竞赛有哪些益处一、学习初中化学竞赛可以得到哪些好处?在全国范围内,有“天原杯”、“学用杯”、“橙池杯(决赛)”等等众多的化学竞赛。
那么参加初中化学竞赛有哪些好处呢?1、名校的敲门砖。
初中化学竞赛在许多地区的名校自主招生环节有很大作用,天原杯在上海地区的重要性就是一个例子。
还有更多地区的高中有自主招生的笔试环节,其中化学部分的命题风格和难度,都会把各种竞赛题目作为参考。
各种竞赛的考试时间与形式大同小异,题目风格规律也有众多共同之处。
例如天原杯在每年的4月中上旬举行初赛,中下旬举行复赛。
初赛难度较易,题目由各个地区自主命题,题目的形式有所区别。
例如上海地区全部是选择题,而其他地区则是题型较为丰富。
但是总体的考查内容大同小异,难度也基本上都会略高于一般的中考难度。
决赛题目为全国统一命题,难度较大,涉及大量性质实验、探究实验、陌生方程式的书写以及复杂计算。
根据考生们在决赛中的名次,中国教育学会化学教学专业委员会授予全国一二等奖,同时也设置省市一级的奖励。
“天原杯”在上海的自主招生环节、“橙池杯(决赛)”在长沙四大名校的直升环节,都有很高的含金量。
获得初中化学竞赛的奖项,可以为进入理想的高中增添一块分量十足的筹码,提前握有加分,也可以让孩子心态更放松,在中考中获得理想成绩,升入名校。
2、培养严谨的理科思维,有利于高中化学的学习。
有人说,初中化学是理科中的文科。
何出此言呢?因为初中化学记忆性的内容比较多,需要逻辑思维的地方比起数学物理少了一些。
但是内行人一定知道,升入高中之后,化学改头换面,不在是一门读读背背的科目,同样需要严密的理科思维。
用初中习惯的学习方法来学习高中化学,很可能要遭遇当头棒喝。
这也是很多初中时的学霸,升入高中感到化学入门难的原因。
其实所谓的入门难也很好理解,因为高中化学的大门和初中就是区别很大,俨然如同两个学科。
那么如何在初中就培养真正的化学思维呢?课内的知识可能并不够,而初中化学竞赛中题目的难度,和解题所必备的方法,正是高中化学中所需要的。
北师大版九年级数学上册 第六章反比例函数及其应用练习题含答案

北师大版九年级数学上第六章反比例函数及其应用练习题基础达标训练1. (2018台州)已知电流I (安培)、电压U (伏特)、电阻R (欧姆)之间的关系为I =UR,当电压为定值时,I 关于R 的函数图象是( )2. 反比例函数y =k x(k >0),当x <0时,图象在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限第3题图3. (2018广东省卷)如图所示,在同一平面直角坐标系中,直线y =k 1x (k 1≠0)与双曲线y =k 2x(k 2≠0)相交于点A ,B 两点,已知点A 的坐标为(1,2),则点B 的坐标是( ) A. (-1,-2) B. (-2,-1) C. (-1,-1) D. (-2,-2)4. 在同一平面直角坐标系中,函数y =mx +m (m ≠0)与y =m x(x ≠0)的图象可能是( )5. (2018兰州)如图,反比例函数y =k x(x <0)与一次函数y =x +4的图象交于A ,B 两点,A ,B 两点的横坐标分别为-3,-1,则关于x 的不等式kx<x +4(x <0)的解集为( )A. x <-3B. -3<x <-1C. -1<x <0D. x <-3或-1<x <0第5题图6. (2018天津)若点A (-1,y 1),B (1,y 2),C (3,y 3)在反比例函数y =-3x的图象上,则y 1,y 2,y 3的大小关系是( )A. y 1<y 2<y 3B. y 2<y 3<y 1C. y 3<y 2<y 1D. y 2<y 1<y 37. (2018济宁)请写出一个过点(1,1),且与x 轴无交点的函数解析式:____________.8. (2018哈尔滨)已知反比例函数y =3k -1x的图象经过点(1,2),则k 的值为________. 9. (2018南宁)对于函数y =2x,当函数值y <-1时,自变量x 的取值范围________.10. (2018陕西)已知A ,B 两点分别在反比例函数y =3m x (m ≠0)和y =2m -5x (m ≠52)的图象上,若点A 与点B 关于x 轴对称,则m 的值为________.11. (2018连云港)设函数y =3x 与y =-2x -6的图象的交点坐标为(a ,b ),则1a +2b的值是________.12. (2018南京)函数y 1=x 与y 2=4x的图象如图所示,下列关于函数y =y 1+y 2的结论:①函数的图象关于原点中心对称;②当x <2时,y 随x 的增大而减小;③当x >0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是________.第12题图 第13题图13. (2018绍兴)如图,Rt △ABC 的两个锐角顶点A ,B 在函数y =k x(x >0)的图象上,AC ∥x 轴,AC=2.若点A 的坐标为(2,2),则点B 的坐标为________.14. (8分)(2018湘潭)已知反比例函数y =k x的图象过点A (3,1).(1)求反比例函数的解析式;(2)若一次函数y =ax +6(a ≠0)的图象与反比例函数的图象只有一个交点,求一次函数的解析式.15. (8分)如图,已知反比例函数y =kx的图象经过点A (4,m ),AB ⊥x 轴,且△AOB 的面积为2.(1)求k 和m 的值;(2)若点C (x ,y)也在反比例函数 y =k x的图象上,当-3≤x ≤-1时,求函数值y 的取值范围.第15题图16. (8分)如图,一次函数y =k 1x +b 与反比例函数y =k 2x的图象交于A (2,m ),B (n ,-2)两点.过点B 作BC ⊥x 轴,垂足为C ,且S △ABC =5. (1)求一次函数与反比例函数的解析式;(2)根据所给条件,请直接写出不等式k 1x +b >k 2x的解集;(3)若P (p ,y 1),Q (-2,y 2)是函数y =k 2x图象上的两点,且y 1≥y 2,求实数p 的取值范围.第16题图17. (8分)(2018河南)如图,一次函数y =-x +b 与反比例函数y =k x(x >0)的图象交于点A (m ,3)和B (3,1).(1)填空:一次函数的解析式为______________,反比例函数的解析式为______________;(2)点P 是线段AB 上一点,过点P 作PD ⊥x 轴于点D ,连接OP ,若△POD 的面积为S ,求S 的取值范围.第17题图能力提升训练1. 如图,A ,B 两点在反比例函数y =k 1x 的图象上,C ,D 两点在反比例函数y =k 2x的图象上,AC ⊥y轴于点E ,BD ⊥y 轴于点F ,AC =2,BD =1,EF =3,则k 1-k 2的值是( ) A. 6 B. 4 C. 3 D. 22. (2018云南)已知点A (a ,b )在双曲线y =5x上,若a 、b 都是正整数,则图象经过B (a ,0)、C (0,b)两点的一次函数的解析式(也称关系式)为__________.第3题图3. (2018烟台)如图,直线y =x +2与反比例函数y =kx的图象在第一象限交于点P ,若OP =10,则k 的值为________.4. (2018宁波)已知△ABC 的三个顶点为A (-1,-1),B (-1,3),C (-3,-3),将△ABC 向右平移m(m >0)个单位后,△ABC 某一边的中点恰好落在反比例函数y =3x的图象上,则m 的值为________.5. (2018成都)在平面直角坐标系x O y 中,对于不在坐标轴上的任意一点P (x ,y ),我们把点P ′(1x,1y)称为点P 的“倒影点”.直线y =-x +1上有两点A ,B ,它们的倒影点A ′,B′均在反比例函数y =k x的图象上,若AB =22,则k =__________.6. (8分)(2018德阳)如图,函数y =⎩⎪⎨⎪⎧2x ,(0≤x≤3)-x +9,(x >3)的图象与双曲线y =kx (k≠0,x >0)相交于点A (3,m)和点B .(1)求双曲线的解析式及点B 的坐标;(2)若点P 在y 轴上,连接PA ,PB ,求当PA +PB 的值最小时点P 的坐标.第6题图拓展培优训练1. (2019长郡第二届澄池杯)如图,直线y =x +4与双曲线y =k x(k ≠0)相交于A (-1,a )、B 两点,在y 轴上找一点P ,当PA +PB 的值最小时,点P 的坐标为________.第1题图 第2题图2. 如图,已知点(1,3)在函数y =k x(x >0)的图象上.正方形ABCD 的边BC 在x 轴上,点E 是对角线BD 的中点,函数y =k x(x >0)的图象又经过A 、E 两点,则点E 的横坐标为________.答案1. C 【解析】 当电压为定值时,I =UR为反比例函数,且R >0,I >0,∴只有第一象限有图象.2. C 【解析】∵在反比例函数y =k x中,k >0,∴反比例函数图象在第一、三象限内,∴当x <0时,函数图象在第三象限.3. A 【解析】如题图,A 、B 两点是关于原点对称的,又∵A 的坐标是(1,2),∴B 的坐标是(-1, -2).4. D 【解析】当m <0时,函数y =mx +m 的图象经过第二、三、四象限,函数y =mx的图象位于第二、四象限;当m >0时,函数y =mx +m 的图象经过第一、二、三象限,函数y =m x的图象位于第一、三象限,故选D.5. B 【解析】k x<x +4(x <0)表示x <0时,反比例函数图象在一次函数图象下方时x 的取值范围,∵反比例函数图象与一次函数图象交于A 、B 两点,点A 和点B 的横坐标分别为-3,-1,∴由函数图象可知,k x<x +4(x <0)的解集为:-3<x <-1.6. B 【解析】∵点A 、B 、C 在反比例函数图象上,将点A (-1,y 1),B (1,y 2),C (3,y 3)分别代入y =-3x 得,y 1=-3-1=3,y 2=-31=-3,y 3=-33=-1,∴y 2<y 3<y 1. 7. y =1x8. 19. -2<x <0 【解析】∵y <-1,即2x <-1,∴2x+1<0,整理得x (x +2)<0,解得-2<x <0.10. 1 【解析】设A (x ,y ),则B (x ,-y ),∵A 在y =3m x 上,B 在y =2m -5x上,∴⎩⎪⎨⎪⎧y =3mx-y =2m -5x,∴3m x +2m -5x=0,∴m =1. 11. -2 【解析】∵点(a ,b )是函数y =3x 与y =-2x -6的图象的交点,∴b =3a,b =-2a -6,即ab =3,2a +b =-6,则1a +2b =b +2a ab =-63=-2.12. ①③ 【解析】由函数图象可知①正确;由反比例函数在y 轴两边增减性不一样,故②错误;∵x >0,∴y =x +4x=(x)2+(2x )2-4+4=(x -2x )2+4,当x =2x时,函数有最小值,此时x =2,y =4,故函数图象最低点的坐标为(2,4),正确结论的序号是①③.13. (4,1) 【解析】∵点A (2,2)在函数y =kx (x >0)的图象上,∴2=k 2,得k =4,∵在Rt △ABC 中,AC ∥x 轴,AC =2,∴点B 的横坐标是4,∴y =44=1,∴点B 的坐标为(4,1).14. 解:(1)将点A (3,1)代入反比例函数解析式中,得1=k 3,∴k =3,∴反比例函数的解析式为y =3x;(2)已知一次函数y =ax +6(a ≠0), 联立两个解析式得⎩⎪⎨⎪⎧y =3x y =ax +6,整理得ax 2+6x -3=0①,∵一次函数与反比例函数图象只有一个交点, 则①式中Δ=62-4a ×(-3)=0, 解得a =-3≠0,∴一次函数解析式为y =-3x +6. 15. 解:(1)k =xy =2S △OAB =2×2=4,将点A (4,m)代入y =4x,得m =1;(2)当x =-3时,y =-43;当x =-1时,y =-4, ∴-4≤y ≤-43.16. 解:(1)将A (2,m ),B(n ,-2)代入y =k 2x得k 2=2m =-2n ,即m =-n ,则A (2,-n ),如解图,过A 作AE ⊥x 轴于E ,过B 作BF ⊥y 轴于F ,延长AE 、BF 交于D ,第16题解图∵A (2,-n),B (n ,-2), ∴BD =2-n ,AD =-n +2,BC =2, ∵S △ABC =12·BC ·BD ,∴12×2×(2-n)=5,解得n =-3, 即A (2,3),B (-3,-2),将A(2,3)代入y =k 2x得k 2=6,即反比例函数的解析式是y =6x,把A (2,3),B(-3,-2)代入y =k 1x +b 得⎩⎪⎨⎪⎧3=2k 1+b-2=-3k 1+b,解得k 1=1,b =1,∴一次函数的解析式是y =x +1;(2)不等式k 1x +b >k 2x的解集是-3<x <0或x >2;(3)分为两种情况:当点P 在第三象限时,要使y 1≥y 2,实数P 的取值范围是P ≤-2;当点P 在第一象限时,要使y 1≥y 2,实数P 的取值范围是P >0,综上所述,P 的取值范围是P ≤-2或P >0.17. 解:(1)y =-x +4,y =3x;(2)由(1)得3=3m,解得m =1,∴A 点坐标为(1,3),设P 点坐标为(a ,-a +4)(1≤a ≤3),则S =12OD ·PD =12a (-a +4)=-12(a -2)2+2,∵-12<0,∴当a =2时,S 有最大值,此时S =-12×(2-2)2+2=2,由二次函数的性质得,当a =1或3时,S 有最小值, 最小值为-12×(1-2)2+2=32,∴S 的取值范围是32≤S ≤2.能力提升训练1. D 【解析】设点A (m ,k 1m )、点B (n ,k 1n ),则点C(k 2m k 1,k 1m )、点D (k 2n k 1,k 1n),∵AC =2,BD =1,EF =3,∴⎩⎪⎨⎪⎧m -k 2mk 1=2k 2nk 1-n =1k 1m -k 1n =3,解得k 1-k 2=2.2. y =-5x +5或y =-15x +1 【解析】∵点A (a ,b ) 在双曲线y =5x 上,∴b =5a ,∵a ,b 都是正整数,∴a =1,b =5或a =5,b =1.①当a =1,b =5时,B (1,0),C (0,5),设一次函数的解析式为y =k 1x +b 1(k 1≠0),把B (1,0),C (0,5)代入,得⎩⎪⎨⎪⎧k 1+b 1=0b 1=5,解得⎩⎪⎨⎪⎧k 1=-5b 1=5,∴一次函数的解析式为y =-5x +5;②当a =5,b =1时,设一次函数解析式为y =k 2x +b 2(k 2≠0),把B (5,0),C (0,1)代入,得⎩⎪⎨⎪⎧5k 2+b 2=0b 2=1,解得⎩⎪⎨⎪⎧k 2=-15b 2=1,∴一次函数的解析式为y =-15x +1,综上所述,一次函数的解析式为y =-5x +5或y =-15x +1.3. 3 【解析】设点P (m ,m +2),由OP =10,可得m 2+(m +2)2=(10)2,∵m >0,解得m =1,又∵点P (1 ,3)在y =k x的图象上,∴k =3.4. 0.5或4 【解析】分两种情况讨论:①若为AC 中点(-2,-2)向右平移m 个单位后落在图象上,则有点(m -2,-2)在y =3x 上,代入得-2=3m -2,∴m =0.5;②若为AB 中点(-1,1)向右平移m 个单位后落在图象上,则有点(m -1,1)在y =3x 上,代入得1=3m -1,∴m =4,∴m 为0.5或4.5. -43【解析】设A 、B 的坐标分别为:A (a ,-a +1),B(b ,-b +1),∵AB =22,∴(a -b)2+(-a +1+b -1)2=(22)2,∴a -b =±2,由倒影点的定义得A ′(1a ,11-a ),B ′(1b ,11-b),又∵A ′、B ′都在函数y =kx 上,∴k =1a (1-a )=1b (1-b ),则a (1-a )=b (1-b ),整理得(a-b)(1-a -b)=0,∵a -b =±2,∴1-a -b =0,即a +b =1,解方程组⎩⎪⎨⎪⎧a +b =1a -b =2与⎩⎪⎨⎪⎧a +b =1a -b =-2,得⎩⎪⎨⎪⎧a =32b =-12或⎩⎪⎨⎪⎧a =-12b =32,∴k =1a (1-a )=-43.6. 解:(1)∵A (3,m )在直线y =2x 上, ∴m =2×3=6, ∴A (3,6),∵A (3,6)在双曲线y =kx上,∴k =3×6=18,∴双曲线的解析式为y =18x,当x >3时,联立解析式得 ⎩⎪⎨⎪⎧y =-x +9y =18x , 得⎩⎪⎨⎪⎧x =6y =3或⎩⎪⎨⎪⎧x =3y =6(舍去), ∴点B 的坐标为(6,3);(2)如解图,作A 关于y 轴的对称点A ′(-3,6),第6题解图 连接PA′, ∵PA ′=PA ,∴PA +PB =PA ′+PB ≥A′B , 当A ′,P ,B 三点共线,即P 在A′B 与y 轴的交点P ′处时,PA +PB 取到最小值, ∵A ′(-3,6),B (6,3),∴AB =(6+3)2+(3-6)2=310, ∴PA +PB 的最小值是310,设直线A′B 的函数关系式为y =kx +b ,已知直线过点A ′(-3,6),B (6,3),代入得⎩⎪⎨⎪⎧6=-3k +b 3=6k +b ,解得⎩⎪⎨⎪⎧k =-13b =5,∴y =-13x +5,令x =0,得y =5, ∴P ′(0,5),∴当PA +PB 取到最小值310时,点P 的坐标为(0,5). 拓展培优训练1. (0,52) 【解析】把点A 坐标代入y =x +4,得-1+4=a ,∴a =3,即A (-1,3),把点A坐标代入双曲线的解析式得3=-k ,解得k =-3,联立函数解析式得⎩⎪⎨⎪⎧y =x +4y =-3x ,解得⎩⎪⎨⎪⎧x 1=-1y 1=3(舍),⎩⎪⎨⎪⎧x 2=-3y 2=1,即点B 坐标为(-3,1),如解图,作点A 关于y 轴的对称点C ,则点C 坐标为(1,3),连接BC ,与y 轴的交点即为点P ,使得PA +PB 的值最小,设直线BC 的解析式为y =ax+b ,把B ,C 坐标代入得⎩⎪⎨⎪⎧-3a +b =1a +b =3,解得⎩⎪⎨⎪⎧a =12b =52,∴直线BC 解析式为:y =12x +52,令x =0,y =52,即点P 的坐标为(0,52).第1题解图2. 6 【解析】∵点(1,3)在函数y =k x 图象上,代入得:k =3,即y =3x,设A (a ,b),由题意知E (a +b 2,b 2),又∵函数图象在第一象限,经过点A 、E ,分别代入得⎩⎪⎨⎪⎧ab =3b 2(a +b2)=3,解得⎩⎪⎨⎪⎧a =62b =6或⎩⎪⎨⎪⎧a =-62b =-6(舍),∴点E 的横坐标为a +b 2= 6.。
长郡澄池杯初中物理竞赛选拔试题

2016年8月长郡双语物理竞赛选拔试题满分100分时量60分钟班级______ 姓名_________一、单向选择题(每题6分,共36分)1、如图所示,两平面镜A和B之间的夹角为9°自平面镜B上的某点P射出一条与B镜面成β角的光线,在β角由0°至180°范围内(不包括0°)连续变化的过程中,发现当β取某角度时,光线经镜面一次或多次反射后,恰好能返回到P点,则符合该要求的β的个数有()A.1个B.4个C.9个D.6个2、如图所示,凸透镜的焦距为5厘米,在透镜左侧l0厘米处,有一个与主光轴垂直的物体AB,在透镜右侧15厘米处放一个平面镜,镜面与凸透镜的主光轴垂直,则该光具组中,物体AB的成像情况是( )A.一个倒立实像,一个倒立虚像,一个正立实像B.一个正立实像,一个正立虚像,一个倒立虚像C.一个正立虚像,一个倒立实像,一个倒立虚像D.一个正立实像,一个倒立实像,一个正立虚像3、质量相同的实心铝球、硫酸和冰块,已知ρ铝=2.7×103kg/m3、ρ硫酸=1.8×103kg/m3、ρ冰=0.9×103kg/m3,则它们的体积之比为()A.1:2:3 B.3:2:1 C.2:3:6 D.6:3:24、如图所示,物体A靠在竖直墙面上,在竖直向上的力F作用下,A、B保持静止.物体B的受力个数为()A.2B.3C.4D.55、如图所示,一个劈形物体M放存固定的粗糙斜面上,其上面呈水平.在其水平面上放一光滑小球m.当劈形物体从静止开始释放后,观察到m和M有相对运动,则小球m在碰到斜面前的运动轨迹是()A.沿水平向右的直线B.沿斜面向下的直线C.竖直向下的直线D.无规则的曲线6、甲、乙两完全一样的容器分别装有质量相等的不同种液体,如图,它们对容器底的压强分别为P甲、P乙.则( )A.P甲= P乙B.P甲>P乙C.P甲<P乙D.条件不足,无法比较二、填空题(每空3分,共21分)7、一冰块内含有某种不溶于水的物体,放入盛有0℃水的量筒内,正好悬浮在水中,如图所示,此时量筒液面升高了4.6厘米;当冰完全熔解后,水面又下降了0.44厘米.设量筒的内横截面积为50厘米2,则该物体的密度为_________ 克/厘米3(冰的密度为0.9克/厘米3)8、有两支最小分度相同的刻度尺A和B,在室温下测同一长度时结果相同;在40℃的室内测同一长度时分别为LA和LB,但LA>LB.若将这两支尺拿到-20℃的室外测同一长度,结果分别为L′A和L′B,则L′A______L′B.(填“>”、“<”或“=”)9、有一人在平直马路上慢步(速度不变),他发现每隔t1分钟有一辆公共汽车迎面开过,每隔t2分钟有一辆公共汽车从身后开过.于是他计算出汽车站是每隔______分钟发一辆车.10、一架飞机水平匀速地从背后经某同学头顶飞过,当他听到飞机的发动机声从头顶正上方传来时,发现飞机在前上方约与地面成30°角的方向上,据此估算出飞机的速度约为声速的______倍。
长郡澄池杯数学试题及解析

1 初三·数学 2018长郡集团“澄池”杯初赛数学试题满分:100分时量:90分钟一、选择题(每小题6分,共36分)1.如果a b -=,那么代数式222a b ab a a b ⎛⎫+-⋅⎪-⎝⎭的值为( ) AB. C. D.2.如图是一个沿3×3正方形格纸的对角线AB 剪下的图形,一质点P 由A 点出发,沿格点线每次向右或向上运动1个单位长度,则点P 由A 点运动到B 点的不同路径共有( )A .4条B .5条C .6条D .7条3.如图,点E 在DBC ∆的边DB 上,点A 在DBC ∆内部,90DAE BAC ∠=∠=︒,AD AE =,AB AC =.给出下列结论:①BD CE =;②45ABD ECB ∠+∠=︒;③BD CE ⊥;④()22222BE AD AB CD =+-.其中正确的是( )A .②④B .①②③C .①③④D .①②③④4.若关于x 的分式方程2213m x x x+-=-无解,则m 的值为( ) A . 1.5-B .1C .0.5-或 1.5-D . 1.5-或25.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y (米)与甲出发的时间t (分)之间的关系如图所示,下列结论: ①甲步行的速度为60米/分;2 初三·数学②乙走完全程用了32分钟; ③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米. 其中正确的结论有( )A .1个B .2个C .3个D .4个6.如图,菱形ABCD 的边长是4厘米,60B ∠=︒,动点P 以1厘米/秒的速度自A 点出发沿AB 方向运动至B 点停止,动点Q 以2厘米/秒的速度自B 点出发沿折线BCD 运动至D 点停止.若点P 、Q 同时出发运动了t 秒,记BPQ ∆的面积为S 厘米2,下面图象中能表示S 与t 之间的函数关系的是( )A .B .C .D .二、填空题(每小题6分,共24分)7.按一定顺序排列的一列数叫做数列,如数列:1111261220⋅⋅⋅,,,,则这个数列的前2018个数的和为________.8.如图,正方形ABCD 的边长为1,点A 与原点重合,点B 在y 轴的正半轴上,点D 在x 轴的负半轴上,将正方形ABCD 绕点A 逆时针旋转至正方形'''AB C D 的位置,''B C 与CD 相交于点M ,则点M 的坐标为________.3 初三·数学9.如图,抛物线2y ax bx c =++(a ,b ,c 是常数,0a ≠)与x 轴交于A ,B 两点,顶点(),P m n .给出下列结论:①20a c +<;②若13,2y ⎛⎫- ⎪⎝⎭,21,2y ⎛⎫- ⎪⎝⎭,31,2y ⎛⎫⎪⎝⎭在抛物线上,则123y y y >>;③关于x 的方程20ax bx k ++=有实数解,则k c n ->; ④当1n a=-时,ABP ∆为等腰直角三角形.其中正确结论是________(填写序号).10.如图,在平面直角坐标系中,点1A ,2A ,3A ,…和1B ,2B ,3B ,…分别在直线15y x b =+和x 轴上.11OA B ∆,122B A B ∆,233B A B ∆,…都是等腰直角三角形.如果点()11,1A ,那么点2018A 的纵坐标是________.三、解答题(共40分)11.(共12分)某销售商准备在长沙采购一批丝绸,经调查,用10000元采购A型丝绸的件数与用8000元采购B型丝绸的件数相等,一件A型丝绸进价比一件B型丝绸进价多100元.⑴求一件A型、B型丝绸的进价分别为多少元?⑵若销售商购进A型、B型丝绸共50件,其中A型的件数不大于B型的件数,且不少于16件,设购进A型丝绸m件.①求m的取值范围.②已知A型的售价是800元/件,销售成本为2n元/件;B型的售价为600元/件,销售成本为n 元/件.如果50150n≤≤,求销售这批丝绸的最大利润w(元)与n(元)的函数关系式(每件销售利润=售价﹣进价﹣销售成本).12.(共12分)如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB AE=,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.⑴若3AH=,1HE=,求ABE∆的面积;⑵若45ACB∠=︒,求证:DF=.4 初三·数学5 初三·数学13.(共16分)如图,抛物线26y ax x c =++交x 轴于A ,B 两点,交y 轴于点C .直线5y x =-经过点B ,C . ⑴求抛物线的解析式;⑵过点A 的直线交直线BC 于点M .①当AM BC ⊥时,过抛物线上一动点P (不与点B ,C 重合),作直线AM 的平行线交直线BC 于点Q ,若以点A ,M ,P ,Q 为顶点的四边形是平行四边形,求点P 的横坐标; ②连接AC ,当直线AM 与直线BC 的夹角等于ACB ∠的2倍时,请直接写出点M 的坐标.1 初三·数学2018长郡集团“澄池”杯初赛数学试题解析一、选择题 1-6 ABDCAD二、填空题 7.20182019. 8.3(1,)3-. 9.②和④. 10.20173()2.三、解答题 11.(1)设B 型丝绸的进价为x 元,则B 型丝绸的进价为(100)x +元 则100008000100x x=+,解得400x = 经检验得:400x =是原方程的解 100500x ∴+=一件A 型丝绸进价为500元,一件B 型丝绸进价为400元 (2)①由题意得5016m mm ≤-⎧⎨≥⎩解得:1625m ≤≤②(8005002)(600400)(50)w n m n m =--+---化简得:(100)1000050w n m n =-+-已知50150n ≤≤i. 当50100n ≤<时,1000n ->,即y 随m 的增大而增大当25m =时,销售这批丝绸的利润最大最大利润25(100+10000-507512500w n n n =-=-+) ii. 当100n =时,1000n -=10000501005000y =-⨯=,即最大利润为5000w =。
2018年长郡集团澄池杯复赛数学试卷高清解析(含试题来源)
D.4 个
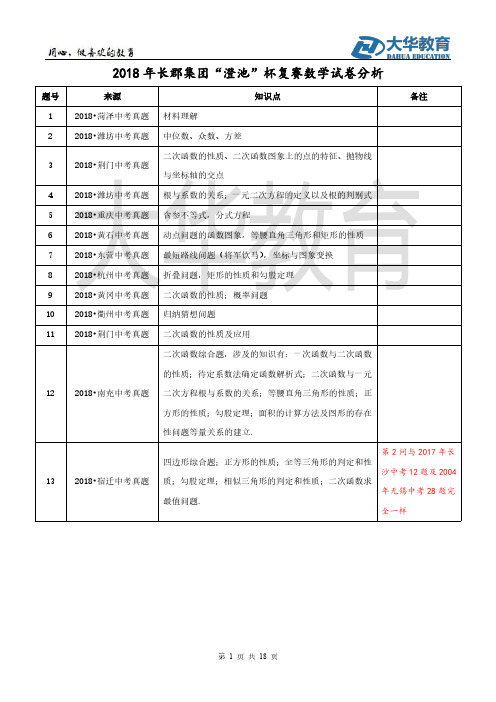
4. ( 2018• 潍坊)已知关于 x 的一元二次方程 mx2 ﹣( m+2 ) x+
m =0 有两个不相等的实数根 x1 , x2 .若 4
1 1 4m ,则 m 的值是( x1 x2
A.2 B.﹣1Leabharlann ) C.2 或﹣1 D.不存在
1 1 x 1 x 1 5. (2018•重庆)若数 a 使关于 x 的不等式组 3 ,有且仅有三个整数解,且使关于 y 的分 2 2 x a 31 x
m2 1 1 1 ,x1 x2 ,结合 4m ,即可求出 m 的值. m 4 x1 x2 m =0 有两个不相等的实数根 x1、x2, 4
【解答】解:∵关于 x 的一元二次方程 mx2﹣(m+2)x+
∴
m 0 m 2 m 2 4m 0 4
第 6 页 共 18 页
2018 年长郡集团“澄池”杯复赛数学试卷 试题解析
一.选择题(共 6 小题) 1. 【分析】根据垂直的向量满足的条件判断即可; 【解答】解:A.∵3×(﹣2)+2×3=0,∴ B.∵( 2 ﹣1) ( 2 +1)+1×1=2≠0,∴ C.∵3×(﹣ 与 与 垂直,故本选项符合题意; 不垂直,故本选项不符合题意;
第 2 页 共 18 页
式方程
3y a 12 1 有整数解,则满足条件的所有 a 的值之和是( y2 2 y
B.﹣12 C.﹣16
) D.﹣18
A.﹣10
6. (2018•黄石)如图,在 Rt△PMN 中,∠P=90°,PM=PN,MN=6cm,矩形 ABCD 中 AB=2cm,BC=10cm, 点 C 和点 M 重合,点 B、C(M) 、N 在同一直线上,令 Rt△PMN 不动,矩形 ABCD 沿 MN 所在直线以每秒 1cm 的速度向右移动,至点 C 与点 N 重合为止,设移动 x 秒后,矩形 ABCD 与△PMN 重叠部分的面积为 y, 则 y 与 x 的大致图象是( )
2016年长沙市第三届贝斯特杯中学数学教师解题比赛光荣榜 初中组
陈赛男
湖南师大附中高新实验中学
贰等
翟智
周南实验中学
贰等
阳文义
宁乡金海中学
贰等
李正荣
岳麓区学士中学
贰等
牟黎黎
湖南师大附中梅溪湖中学
贰等
戴畅蓬
麓山国际实验学校
贰等
张有芳
长沙市湖南省地质中学
贰等
刘理坤
长郡双语
贰等
欧超军
井湾子中学
贰等
郭为奥
长沙市实验中学
贰等
罗百良
明德雨花实验中学
贰等
阳小强
湖南师大附中高新实验中学
贰等
刘婷婷
长沙市开福区长雅中学
贰等
唐超
长郡双语
贰等
唐美旦
长沙市开福区长雅中学
贰等
彭琴
长沙市一中岳麓中学
贰等
陈荣
长沙市北雅中学
贰等
龚丽芳
长沙县松雅湖中学
贰等
郑玲兵
明德洞井中学
贰等
肖举文
湘一芙蓉中学
贰等
李敏
望城区白箬中学
贰等
谭勇
浏阳市文家市中学
贰等
李万胜
长沙市十五中
贰等
广益中学
贰等
马琳芝
长沙市南雅中学
贰等
曾文龙
湘一芙蓉二中
贰等
杨超慧
湖南师大附中梅溪湖中学
贰等
谢倩
湖南师大附中梅溪湖中学
贰等
胡文茜
湖南师大附中梅溪湖中学
贰等
林利
长沙外国语学校
贰等
张金印
长沙外国语学校
贰等
康志坚
明德洞井中学
贰等
2017长郡集团澄池杯初赛物理试卷

2017 长郡集团“澄池”杯初赛物理试卷一.选择题(共15 小题,满分45 分,每小题 3 分)1.西宁市中考体育测试项目中,小李同学抛出后的实心球在空中运动的轨迹如图所示,忽略空气阻力,抛出后的实心球由于()A.不受力,运动状态发生改变B.不受力,运动状态不发生改变C.受到推力的作用,运动状态发生改变D.受到重力的作用.运动状态发生改变2.用一个量筒、水、一根细针做实验来测小木块的某些物理量(ρ木<ρ水,小木块能放入量筒中),下列说法中正确的是()A.只能测木块的体积B.只能测木块所受的浮力C.只能测木块的体积、质量和密度D.木块的体积、所受的浮力、质量和密度都能测量3.物理课本放在水平桌面上,文具盒放在物理课本上,则()A.物理课本受到的重力和桌面对物理课本的支持力是一对平衡力B.物理课本对桌面的压力和桌面对物理课本的支持力是一对相互作用力C.物理课本对文具盒的支持力和文具盒对物理课本的压力是一对平衡力D.桌面对物理课本的支持力和文具盒对物理课本的压力是一对相互作用力4.太阳表面的温度约为6000℃,所辐射的电磁波中辐射强度最大的在可见光波段,人体温度约为37℃,所辐射的电磁波中辐射强度最大的在红外波段,宇宙空间内的电磁辐射相当于零下270℃的物体发出的,这种辐射称为“3K背景辐射”,“3K 背景辐射”的波段为()A.γ射线B.X 射线C.紫外线D.无线电波5.小明在用可变焦的光学照相机(一种镜头焦距大小可根据需要发生改变的光学照相机)给小兰拍了一张半身照之后,保持相机和小兰的位置不变,又给小兰拍了一张全身照.关于这个过程对相机的调节,下列说法中正确的是()A.焦距变大,像距也变大B.焦距变小,像距也变小C.焦距变大,像距变小D.焦距变小,像距变大6.水被加热烧开后,水面上方有“白色气体”;在炎热的夏天,冰块的上方也有“白色气体”()A.前者主要是由杯中水转变成的“水的气态物质”B.前者主要是由杯中水转变成的“水的液态物质”C.后者主要是由冰转变成的“水的气态物质”D.后者主要是由冰转变成的“水的液态物质”7.一物块轻轻放入盛满煤油的大烧杯中,静止后有160g 煤油溢出;将其轻轻放入盛满水的大烧杯中,静止后有180g 水溢出,已知煤油的密度是0.8×103kg/m3,则物块在水中静止时的状态及物块的密度分别是()A.下沉,1.1×103kg/m3 B.漂浮,0.85×103kg/m3C.悬浮,1.0×103kg/m3 D.漂浮,0.90×103kg/m38.如图所示,一轻弹簧上端固定在天花板上,下端连接一小球.开始时小球静止在O 点,将小球向下拉到B 点,释放小球,已知AO=OB,研究小球在竖直方向上的受力和运动情况,则()A.小球运动到0 点时将停止运动并保持静止B.小球运动到A 点时将停止运动并保持静止C.小球从B 运动到0 的过程中弹力大于重力、速度不断增大D.小球从0 运动到A 的过程中弹力大于重力、速度不断减小9.如图甲所示,放在水平地面上的物体,受到方向不变的水平拉力F的作用,其F ﹣t 和v﹣t 图象分别如图乙、丙所示,下列说法正确的是()A.当t=2s 时,物体处于静止状态,摩擦力是0B.当t=3s 时,物体受到摩擦力是7NC.4﹣6s 内,拉力F 做的功是20JD.2﹣4s 内,物体的机械能保持不变10.一均匀木板AB,B 端固定在墙壁的转轴上,木板可在竖直面内转动,木板下垫3 块C,恰好使木板水平放置,如图所示,现在水平力F 将C 由A 向B 匀速推动过程中,推力F 将()A.大小不变B.逐渐增大C.先增大后减小D.先减小后增大11.如图所示.甲和乙是叠放在水平桌面上的两个物块,它们在丙的作用下一起向右做匀速直线运动()A.乙所受摩擦力的方向向右B.甲可能不受摩擦力C.甲和丙所受的重力都不做功D.将乙拿掉后,甲的运动状态一定会发生改变12.建筑工人用如图所示的滑轮组,在4s 内将重为1500N 的物体沿水平方向匀速移动2m 的过程中,所用的拉力大小为375N,物体受到水平地面的摩擦力为物重的0.4 倍.在此过程中下列说法正确的是()A.绳子自由端沿水平方向移动了6 mB.物体受到的拉力为750NC.拉力F 的功率为750WD.滑轮组的机械效率为80%13.如图所示,在“探究杠杆的平衡条件”实验中,已知杠杆上每个小格长度为2cm ,当弹簧测力计在A 点斜向上拉(与水平方向成30°角)杠杆,使杠杆在水平位置平衡时,下列说法正确的是()A.动力臂为0.08m B.此时为省力杠杆C.弹簧测力计的示数为4N D.钩码总重为2N14.在一次校运动会,小明骑一质量为m 的独轮车,以速度v 匀速通过一重为G、长为L 的水平独木桥,独木桥的两端由两根竖直支柱A、B 支撑着,如图所示.设独轮车骑上A 端支柱处为初始时刻(t=0),下面哪一个图正确地表示了B 端支柱所受压力F B与时间t的函数关系?(不考虑独木桥的形变)()A .B .C .D.﹣3 3 ﹣ 3 3 ﹣ 3 3 ﹣3 3 15.如图中 A O B 为一轻质杠杆,可绕悬点 O 转动.当 A 端用细线挂一空心铝球,在B 端悬挂质量为 1.35kg 物体时,杠杆恰好在水平位置平衡.若将铝球一半体积浸在水中,在 B 端悬挂重 3.5N 的物体时,杠杆重新平衡,此时铝球受到的浮力为 F已知:OA :OB=1:2,ρ 铝=2.7×103kg/m 3,g=10N/kg .设铝球实心部分的体积为 V实,铝球空心部分的体积为 V 空.则下列结果正确的是( )A .F 浮 =30N V 实 =1×10 mB .F 浮 =20N V 实 =1×10 mC .F 浮 =20N V 空 =2×10 mD .F 浮 =30N V 空 =3×10 m二.填空题(共 6 小题,满分 30 分)16.如图所示,F 、F ′到凸透镜的距离均等于焦距,P 、P ′到凸透镜的距离均为 2 倍焦距.那么,烛焰在光屏上成的应是倒立、 (填“放大”、“缩小”或“等大”)的实像;若把蜡烛移到 P 与 F 之间,调整光屏后,在光屏上得到的像将会 (填“变小”、“变大”或“不变”).17.如图所示,把两支完全相同的密度计分别放在甲、乙两种液体中,所受到的浮力为 F 甲和 F 乙,则 F 甲 F 乙;若它们的液面相平,则两液体对容器底部的压强关系是 P 甲 P 乙.18. 如图所示,物重 G 为 2000N ,斜面长 5m ,高 3m .斜面和滑轮组装置的总机械效率为 80%,若将重物沿斜面以 0.2m/s 的速度拉上来,则所需的拉力 F 为 N ,该装置的总功率是 W .19.将同一重物举高,如图所示,使用滑轮组的机械效率与使用斜面的机械效率之比为8:7,则分别使用这两种机械时的拉力之比F1:F2= .20.王波同学帮父母搬家,现有30 捆书籍.每捆书籍的质量都为5kg.王波想尽快将它们搬上10m 高处的新家.如图是王波可以提供的用于搬运物体的功率与被搬运物体质量之间的关系图象.由图可知,为了尽可能快地将这批书籍搬上新家,他每次应搬捆.若每次下楼时间是上楼时间的一半,则他最快完成搬运任务并返回原地,所用的总时间为s(g=10N/kg).21.甲、乙两人站在一堵光滑的墙壁前,两人之间相距102m,且距离墙壁均为68m,如图所示,甲开了一枪后,乙先后听到两声枪响的时间间隔为s.(已知空气中声音的传播速度为340m/s)三.解答题(共 3 小题,满分34 分)22.为了模拟水中物体被打捞的情境,同学们课外作如下探究:如图,用滑轮组将重200N 的物体从底面积为400cm2 的圆柱形容器中提起,容器中水面由90cm 降到70cm.已知每个滑轮重均为20N(不计绳重、水的阻力及滑轮与中心轴间的摩擦).求:(1)所提起物体的密度(2)物体完全出水后继续上升的过程中,滑轮组的机械效率.23.小明家的高压锅锅体直径为24mm,排气孔内径(孔内直径)为4mm.小明不慎丢失了锅的限压阀,当他到商店购买时售货员告诉他,生产这个锅的厂家提供的限压阀有两种,孔径相同,质量分别为100g 和60g.(1)请你根据说明书给出的数据,通过计算说明,小明应该买哪一种限压阀.(说明书标有:当大气压为105Pa 时,该锅最高温度可以达到120℃,已知:水的沸点与压强的关系如图所示,取g=10N/kg)(2)请你说明如果买另一种限压阀,使用时会出现什么问题.24.为了保护环境,治理水土流失,学校的环保小组设计并进行了河水含沙量的研究.第一阶段是理论分析:分别以 ρ 水、ρ 沙、ρ 泥水表示水、泥沙、泥沙水的密度,以 x 表示每立方米泥沙水中所含泥沙的质量(称做含沙量),导出了 ρ 泥水与 ρ 水、ρ 沙、x 的关系式;然后作出了泥沙水的密度 ρ 泥水随含沙量 x 变化的图象.第二阶段是实验验证:在一个量筒里放入一定量干燥的黄土,再倒入一定量的清水, 计算出含沙量 x ,并测出泥沙水的密度 ρ 泥水;接着再多次加入清水配制成不同密度的泥沙水,进行同样的计算和测量,由此得出 ρ 泥水与 x 的多组数据;然后根据这些数据作出了表示泥沙水的密度与含沙量关系的 ρ 泥水﹣x 图象.他们惊喜地发现,实验结果与理论分析是一致的.第三阶段是实际测量:在一次山洪冲刷地面时,他们采集了 40L 的水样,称出其总质量为 40.56kg .此前已经测出干燥的泥沙的密度 ρ 沙:2.4×103kg/m 3,于是求出了洪水中的平均含沙量.(1)请你参与环保小组第一阶段的工作,导出 ρ 泥水与 ρ 水、ρ 沙、x 的关系式.然后根据关系式作出泥沙水的密度 ρ 泥水随含沙量 x 变化图象的草图.(2)请你参与环保小组第三阶段的计算工作,求出洪水中的平均含沙量.。
第二届澄池杯比赛初赛数学试卷

∴∠BAE+∠CEH,∠B=∠EHC,∴△ABE∽△EHC
∴ABEH=AECE,∵AE =
AB2 ห้องสมุดไป่ตู้ BE2
= 10,
∴EH = 24
5
∴sin∠ECF=EHCE=4
5
5、C 由图象可知 A、B 两城市之间的距离为 300km,甲行驶的时间为 5 小时,
而乙是在甲出发 1 小时后出发的,且用时 3 小时,即比甲早到 1 小时,∴①②
a
b
∴a
=
1c,−
b
=
c+11,故x1
+
x2
=−
b c
=
c+c 1,x1 ·x2
=
c a
3、B x=0 时,y=-2,则点 C 的坐标为(0,-2),∴OC=2
y=0 时,x=2,则点 B 的坐标为(2,0),∴OB=2 ∴S△BOC=1x2x2=2
2
∴S△AOB: S△BOC=1:2, ∴S△AOB=1, ∴OB=2, ∴电 A 的坐标为 1
(2)己知距观测点 D 处 100 海里范围内有暗礁。若巡逻船 A 沿直线 AC 去营救 船 C,在去营救的途中有无触暗礁危险?(参考数据: 2 ≈ 1.41, 3 ≈ 1.73)
14. (10 分)某欢乐谷为回馈广大谷迷,在暑假期间退出学生个人门票优惠价,
各票价如下:
票价各类
(A)学生夜场票
(B)学生日通票
ABCD
∴S四边形 OEBF:S正方形 ABCD = 1:4,故正确;
(3)∴BE+BF=BF+CF=BC= 2OA;故正确; (4)∵∠EOG=∠BOE, ∠OEG=∠OBE=45°
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于2016年长郡第二届“澄池杯”竞赛问题汇总长郡系初中的同学们看过来,近日,长郡发出了最新的2016年长郡澄池杯竞赛的具体实施方案,方案中详细介绍了本次竞赛的参加办法,以及直升奖励加分情况。
(一)澄池杯是什么?
澄池杯是长郡针对集团内2016届初三学生设定的一项竞赛,第一次选拔是在2015年12月举行。
澄池杯的意义在于提前选拔尖子,给予直升方面的加分优惠,确保尖子能够直升而不外流。
第一届澄池杯举行的比较仓促,到今年,也就是面对集团内2017届初三的学生,长郡中学对于第二届澄池杯的举行也更有经验,把时间提前到了新初三开学前进行,同时,各种实施办法也更加成熟。
(二)第二届澄池杯怎么考?
根据长郡集团统一安排,竞赛分初赛和决赛。
初赛和决赛均由长郡中学本部命题、阅卷并依据竞赛成绩评奖。
初赛
时间:8月28日上午
地点:长郡双语和麓山国际,(双语、梅溪湖、芙蓉三校在双语考点,其余学校在麓山考点)长郡中学本部派出巡考员巡考;
参赛资格:长郡双语实验中学、麓山国际实验学校、长郡梅溪湖中学、长郡芙蓉中学、长郡雨花外国语学校、湘郡未来实验中学6校区初三年级综合排名前20%的学生。
复赛时间:待定
地点:长郡本部组考。
参赛资格:由长郡中学本部根据初赛结果确定各校区参赛学生名单。
(三)第二届澄池杯考什么?
考试科目:数学90分钟,英语60分钟,物理50分钟。
考试范围:数学——除九年级下以外的初中所有内容;英语——七年级和八年级的所有内容;物理——八年级的所有内容;初试侧重基础,复试侧重能力。
(四)澄池杯竞赛有什么奖励?
设立奖项:数学一等奖和特等奖共80人,英语一等奖80人,物理一等奖50人,数学、英语、物理设综合特等奖若干名。
奖励办法:数学特等奖或综合特等奖获奖学生可在初三直升中获得60分优惠加分,二项加分不累加。
说明:澄池杯获奖可以为孩子在选拔直升生的时候增添厚厚的筹码。
要知道,特等奖加60分是一个非常多的分数,而获得其他市级的竞赛只能加1-3分。
可以这么说,澄池杯获奖已经成为想直升长郡的关键。
在今年中考,就有一些平时成绩靠前但是澄池杯没获奖的孩子在竞争直升生名额的时候被挤下来。
所以2017年想直升的孩子,一定要特别重视这次竞赛。
另,这里没有介绍一等奖获奖是否能够加分,我们可以参考去年各校的直升生加分政策,如长郡双语2016年直升生中明确写道“参加长郡中学组织的“澄池杯”学科竞赛获特等奖加分60分,获一等奖加分15分”,我们可以推测,一等奖应该也可以获得加分的优惠。
至于,前面还听家长说过的“本次竞赛集团前十名,直接进入高一,不用参加初三的学习”,在这次方案中并没有体现,以后有最新消息再与大家分享!。
