初中几何基本模型
初中几何48个模型作业帮

初中几何是数学中的一个重要部分,它涉及到许多基本的几何概念和定理。
在学习初中几何时,了解和掌握一些常见的几何模型是非常有帮助的。
以下是48个初中几何模型:1. 等边三角形模型2. 等腰三角形模型3. 直角三角形模型4. 平行四边形模型5. 菱形模型6. 矩形模型7. 正方形模型8. 梯形模型9. 圆模型10. 扇形模型11. 弓形模型12. 切线模型13. 抛物线模型14. 双曲线模型15. 椭圆模型16. 角平分线定理模型17. 中线定理模型18. 弦长定理模型19. 勾股定理模型21. 外角和定理模型22. 线段比例定理模型23. 相似三角形判定定理模型24. 三角形内心定理模型25. 三角形外心定理模型26. 三角形重心定理模型27. 三角形垂心定理模型28. 四边形对角线性质定理模型29. 四边形面积公式模型30. 圆的周长公式模型31. 圆的面积公式模型32. 扇形面积公式模型33. 弓形面积公式模型34. 点到直线距离公式模型35. 两点间距离公式模型36. 角平分线性质定理模型37. 中位线定理模型38. 切线的性质定理模型39. 切线的判定定理模型40. 抛物线性质定理模型41. 双曲线性质定理模型43. 角的平分线性质定理的逆定理模型44. 三线合一的逆定理模型45. 线段垂直平分线的逆定理模型46. 余角、补角定理的逆定理模型47. 同位角、内错角、同旁内角定理的逆定理模型48. 正弦、余弦、正切的应用(三角函数的应用)这些几何模型可以帮助你更好地理解和掌握初中几何的知识点,并且能够让你更加熟练地解决各种几何问题。
希望这些信息对你有所帮助!。
初中几何48种数学模型系统讲解

初中几何48种数学模型系统讲解初中几何是数学中非常重要的一个分支,涉及到许多基础知识和技能。
在初中几何学习中,数学模型是非常重要的一环,它能够帮助学生更好地理解和掌握几何知识,并提高解题的能力。
下面我们就来介绍一下初中几何中常见的48种数学模型系统。
1. 平面几何模型:平面几何模型是研究平面上的图形和变换的数学模型,例如平移、旋转、对称等。
2. 立体几何模型:立体几何模型是研究空间中的图形和变换的数学模型,例如立体的投影、旋转、平移等。
3. 直线模型:直线模型是用来表示直线的数学模型,例如在平面几何中,可以使用坐标系来表示一条直线。
4. 线段模型:线段模型是用来表示线段的数学模型,例如在平面几何中,可以使用坐标系来表示一条线段。
5. 角度模型:角度模型是用来表示角度的数学模型,例如在平面几何中,可以使用角度制和弧度制来表示角度。
6. 相交模型:相交模型是用来表示图形相交的数学模型,例如在平面几何中,可以使用交点来表示两条直线相交的情况。
7. 平行模型:平行模型是用来表示平行线的数学模型,例如在平面几何中,可以使用平行线的定义来表示两条直线平行的情况。
8. 垂直模型:垂直模型是用来表示垂直线的数学模型,例如在平面几何中,可以使用垂直线的定义来表示两条直线垂直的情况。
9. 对称模型:对称模型是用来表示对称图形的数学模型,例如在平面几何中,可以使用对称轴来表示对称图形的情况。
10. 相似模型:相似模型是用来表示相似图形的数学模型,例如在平面几何中,可以使用相似比例来表示两个相似图形之间的关系。
11. 等比模型:等比模型是用来表示等比数列的数学模型,例如在几何中,可以使用等比数列来表示一些几何问题。
12. 等分模型:等分模型是用来表示等分线段的数学模型,例如在几何中,可以使用等分线段来表示将一个线段分成若干等分的情况。
13. 圆模型:圆模型是用来表示圆形的数学模型,例如在平面几何中,可以使用圆心、半径来表示一个圆。
初中数学63个几何模型

初中数学63个几何模型不同的几何模型在我们日常生活和学习中都有着广泛的应用。
通过学习这些几何模型,我们可以更好地理解和应用数学知识。
下面介绍63个几何模型的相关知识和应用。
第一类几何模型是平面图形。
平面图形包括三角形、四边形、五边形、六边形等。
三角形是最简单的平面图形,也是许多几何定理的基础,比如直角三角形的勾股定理。
四边形是指四条线段构成的图形,其中包括正方形、长方形、菱形等。
五边形和六边形则分别称为五边形和六边形。
这些平面图形在建筑、绘画、地图测量等方面都有广泛的应用。
第二类几何模型是立体图形。
立体图形包括长方体、正方体、圆柱、圆锥、球体等。
长方体和正方体是最常见的立体图形,它们具有稳定的立体结构,广泛应用于建筑、包装、设备、器具等领域。
圆柱和圆锥也有着广泛的应用,例如烟囱、钢管、饮水机等。
球体则广泛应用于科学、艺术、体育竞技等方面,例如地球仪、篮球、高尔夫球等。
第三类几何模型是曲面图形。
曲面图形包括椭球、双曲面、抛物面等。
椭球广泛应用于天文、地理和工程学等领域,例如地球表面的形状、汽车、飞机等的外形设计。
双曲面和抛物面则具有独特的形状和结构,广泛应用于建筑、航空航天、汽车等领域。
第四类几何模型是向量。
向量是表示大小和方向的量,具有几何意义。
向量广泛应用于物理学、工程学、计算机科学等领域,例如机器人运动控制、人工智能、网络传输等。
第五类几何模型是二次曲线。
二次曲线是由二次方程所定义的曲线,包括椭圆、超椭圆、双曲线等。
二次曲线具有丰富的形状和特征,在计算机图形学、通信工程、密码学等领域有着广泛应用。
总之,学习这些几何模型不仅可以帮助我们更好地理解和应用数学知识,还可以拓展我们的思维方式和解决问题的能力。
对于初中数学学习者而言,掌握这些几何模型是非常重要的,可以为以后的学习和工作打下坚实的基础。
初中几何基础模型赏析——初中生必会的48个模型结论

初中几何基础模型赏析——初中生必会的48个模型结论几何学是一门需要大量练习的学科,而熟练掌握几何模型结论是初中生学好几何学的前提。
以下是初中生必会的48个几何模型结论,希望能够帮助同学们更好地掌握几何学知识。
1. 垂线段定理:垂直于一条直线的所有线段长度相等。
2. 同位角定理:同位角相等。
3. 对顶角定理:对顶角相等。
4. 外角定理:一个三角形的外角等于其余两个内角之和。
5. 内角和定理:一个n边形的内角和为(n-2)×180°。
6. 直角三角形勾股定理:直角三角形两直角边上的平方和等于其斜边上的平方。
7. 等腰三角形底角定理:等腰三角形底角相等。
8. 等腰三角形高角定理:等腰三角形高角相等。
9. 等边三角形角定理:等边三角形三个角都是60°。
10. 等角三角形定理:等角三角形三个角相等。
11. 同弧角定理:在同一圆周上的两个弧所对应的圆心角相等。
12. 弧度制与度数制的转换:1弧度=180°/π。
13. 正弦定理:在任意三角形ABC中,有a/sinA=b/sinB=c/sinC。
14. 余弦定理:在任意三角形ABC中,有a=b+c-2bc cosA。
15. 正切定理:在任意三角形ABC中,有tanA=a/b。
16. 相似三角形定理:相似三角形对应角度相等,对应边比例相等。
17. 切线定理:切线与半径垂直。
18. 弦切角定理:弦切角等于弦所对的圆心角的一半。
19. 弧切角定理:弧切角等于弧所对的圆心角的一半。
20. 环形角定理:在同心圆中,对于同一条弦所对的两个角,小弧所对的角比大弧所对的角小一半。
21. 正多边形的内角定理:正n边形的每个内角大小为(n-2)×180°/n。
22. 正多边形的外角定理:正n边形的每个外角大小为360°/n。
23. 中线定理:三角形三条中线交于一点,且此点到三角形三个顶点距离的平均值等于三角形三个顶点到中点距离的平均值。
初中数学九大几何模型

【结论】:①△OAC^/XOB:):②ZAEB=60° : ®0E 平分NAED【结论】:①△OAC^/XOB:):②ZAEB=90° : ®OE 平分NAED初中数学九大几何模型【条件】:AOAB ^AOCD 均为等腰直角三角形:(3)顶角相等的两任意等腰三角形 【条件】:AOAB ^AOCD 均为等腰三角形; 且 ZCOD=ZAOB【结论】:①△OACq/XOB): ② ZAEB=ZAOB :®OE 平分 NAED模型二:手拉手模型——旋转型相似 (1) 一般情况【条件】:CD/7AB,将2X0CD 旋转至右图的位豈 将八。
旋转至右图的位【结论】:①右图中ZkOCDs△OABT t t AOAC^AOBD: ②延长AC 交BD 于点E,於有ZBEC=ZBQ/\ (2)特殊情况【条件】:CD/7AB, ZA03=90c 【结论】:①右图中ZkOCDs△OABT t t AOAC^AOBD : ② 延长AC 交BD 于点E,必有ZBEC=ZBOA : ③ BD = OD = OB =tanZ0C [):④BD 丄AC : AC OC OA =-ACxBD模型三、对角互补模型(1)全等型-90°【条件】:①ZA0B=ZDCE=90° :②0C 平分NAOB证明提示: ①作垂直,如图2,证明△ CDM^ACEN ②过点C 作CF 丄0C,如图3,证明△ ODC^ZXFEC 楽当ZDCE 的一边交A0的延长线于D 时(如图4)9 以上三个结论:©CD=CE: @0E-0D=j2 0C: S 4⑤连接 AD 、BC.必有AD?+BC2 = AB? +CD 2: 图3【结论】:®CD=CE:②OD+OE=JiOC:(1),皿 =S 场 + S* =三。
芒 ③膈(2)全等型-120°【条件】:®ZA0B=2ZDCE=120° :②OC 平分NA0B【结论】:©CD=CE:②0D+0E=0C:③S.好Sg +证明提示:①可参考“全等型-90° "证法一:②如右下图:在0B上取一点F,使0F=0C,证明ZX0CF为等边三角形。
初中数学九大几何模型
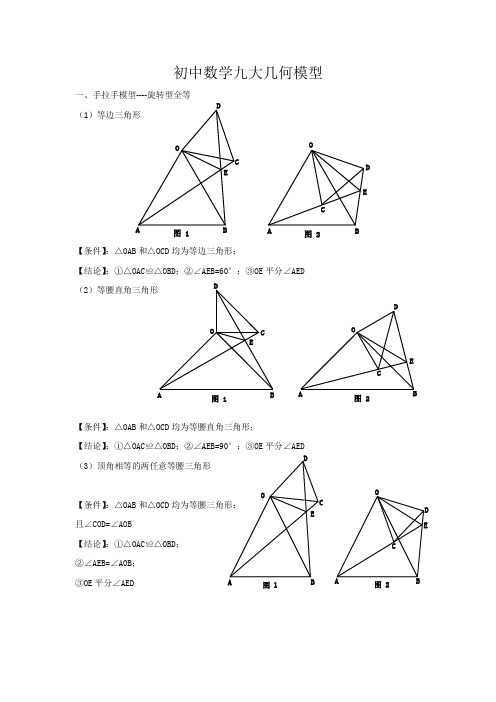
初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
初中几何60个模型总结
初中几何60个模型总结引言初中几何是数学学科中的核心内容之一,涵盖了平面几何和立体几何两个方面。
初中阶段的几何学习主要围绕几何图形的性质、变换以及模型的应用展开。
为了帮助初中生系统地掌握几何知识,本文总结了60个常见的初中几何模型,涵盖了平面几何和立体几何的相关内容。
平面几何模型1. 点•概念:点是几何图形中最基本的元素,没有长度、面积和体积。
•性质:点用大写字母表示,点之间的距离为0。
2. 线段•概念:两个不同点A和B之间的有限点的集合形成线段AB。
•性质:线段的长度可以测量。
3. 射线•概念:以一个端点A和通过A的一条射线确定一个射线。
•性质:射线上的点都在同一边。
4. 直线•概念:两个不同点之间的所有点的集合形成直线。
•性质:直线上的任意两点可以确定一条直线。
5. 角•概念:由两条射线共享一个公共端点形成的几何图形。
•性质:角以大写字母表示,可以通过度数来度量。
6. 三角形•概念:由三条线段连接形成的几何图形。
•性质:三角形的内角和为180度,包括等边三角形、等腰三角形等特殊类型。
7. 平行线•概念:在同一个平面上,不相交且不共面的两条直线。
•性质:平行线具有相同的斜率。
8. 直角•概念:两条互相垂直的直线或线段形成的角。
•性质:直角的度数为90度。
9. 平行四边形•概念:具有两对平行边的四边形。
•性质:平行四边形的对角线相互平分。
10. 梯形•概念:至少有一对平行边的四边形。
•性质:梯形的对角线不相等。
11. 正方形•概念:四条边相等且四个角为直角的四边形。
•性质:正方形的对角线相等且互相垂直。
12. 长方形•概念:四个角均为直角的四边形。
•性质:长方形的对角线相等但不垂直。
13. 菱形•概念:四条边相等且对角线相互垂直的四边形。
•性质:菱形的对角线互相平分。
14. 圆•概念:平面上所有到圆心距离相等的点的集合。
•性质:圆的半径为定值。
15. 扇形•概念:由圆心、圆上任意一点和该点到圆心的连线形成的图形。
初中几何46种模型大全
初中几何46种模型大全篇一:初中几何46种模型大全引言几何是初中数学的重要分支,其知识点涵盖了平面几何、立体几何、向量等多个方面。
在学习几何时,掌握各种几何模型是非常重要的,这些模型可以帮助我们理解和解决几何问题,提高解题能力。
本文将介绍初中几何中的46种常见的模型,包括它们的名称、定义、性质和应用。
正文1. 正方形模型正方形模型是几何中最基本的模型之一,它是一种边长相等的矩形。
正方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
正方形模型的性质有:- 正方形的四条边相等;- 正方形的对角线相等;- 正方形的面积等于其边长的平方。
2. 长方形模型长方形模型是有两个相等的长和两个不相等的宽的英雄。
长方形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和小于斜边的平方。
长方形模型的性质有:- 长方形的两条对角线相等;- 长方形的宽比长大,长比宽大;- 长方形的长和宽相等。
3. 平行线模型平行线模型是相互平行的直线。
平行线模型的定义如下:- 两直线平行,当且仅当它们的对应角相等且且它们的方向相同。
平行线模型的性质有:- 平行线之间有且仅有一个交点;- 平行线上的点的横坐标相等;- 平行线的方向相同。
4. 菱形模型菱形模型是具有四个相等的直角边的矩形。
菱形模型的定义如下:在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方,且任意两条边的长度小于第三条边的长度。
菱形模型的性质有:- 菱形的四条边相等;- 菱形的对角线相等;- 菱形的面积等于其四条边长度的平方和。
5. 等腰三角形模型等腰三角形模型是有一个相等的腰部的两个三角形。
等腰三角形模型的定义如下:- 在一个平面直角坐标系中,任意两条直角边的平方和等于斜边的平方。
等腰三角形模型的性质有:- 等腰三角形的两条直角边相等;- 等腰三角形的底角相等;- 等腰三角形的顶角平分线相等。
6. 等边三角形模型等边三角形模型是具有三个相等的边长的三角形。
初中数学30种模型汇总(最全几何知识点)
10.等面积模型:D是BC的中点
20.平移构造全等
30.二次函数中平行四边形存在性模型
01.三线八角
同位角:找F型
内错角:找Z型
同旁内角:找U型
02.拐角模型
一.锯齿型
1
1
3
2
2
3
4
∠1+∠3=∠2
∠1+∠2=∠3 +∠4
左和=右和
二.鹰嘴型
1
1
2
3
3
2
∠1+∠3=∠2
∠1+∠3=∠2
鹰嘴+小=大
一.大小等边三角形
虚线相等,且夹角为60°
(全等,八字形)
四.大小等腰三角形(顶角为α)
结论:虚线相等,且夹角为α
(全等,八字形)
三. 大小等腰直角三角形
结论:虚线相等,且夹角为90°
(全等,八字形)
二.大小正方形
结论:虚线相等,且夹角为90°
(全等,八字形)
15.半角模型
条件:正方形ABCD
∠EDF=45°
证:EF=AE+CF
条件:CD=AD,∠ADC=90°
∠EDF=45°
∠A+∠C=180°
证明:EF=AE+CF
条件:AB=AD
∠B+∠D=180°
∠EAF=1 ∠BAD
2
证明:EF=BE+DF
条件:AB=AC,∠BAC=90°
∠DAE=45°
证明:DE2=BD2+CE2
△CEF为直角三角形
初中数学30种模型汇总
(最全几何知识点)
01.三线八角
02.拐角模型
03.等积变换模型
初中数学必学48个几何模型
初中数学必学48个几何模型
1. 直线和线段
2. 射线
3. 角
4. 直角
5. 锐角和钝角
6. 平行线
7. 等腰三角形
8. 等边三角形
9. 直角三角形
10. 直角坐标系
11. 等比例线段
12. 外接圆和内切圆
13. 弧和扇形
14. 正方形
15. 长方形
16. 平行四边形
17. 梯形
18. 圆
19. 半圆
20. 圆周角
21. 正多边形
22. 立方体
23. 长方体
24. 正方体
25. 球体
26. 圆锥
27. 圆柱
28. 右锥和右圆锥
29. 高锥和高圆锥
30. 正棱柱
31. 正棱锥
32. 正六面体
33. 正八面体
34. 正十二面体
35. 菱形
36. 菱形组合
37. 等角三角形
38. 曲线
39. 等腰梯形
40. 对称图形
41. 平行四边形法则
42. 夹角
43. 三角形中位线定理
44. 三角形中心
45. 三角形外角和
46. 面积公式
47. 三分点
48. 垂线定理。
