八年级上册经典几何题分类训练
初二上几何证明题100题专题训练
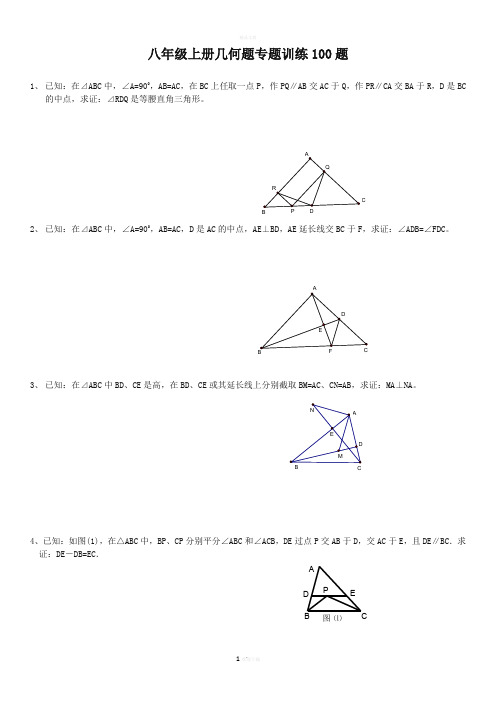
MN DEB C AA B C DE P 图 ⑴八年级上册几何题专题训练100题1、 已知:在⊿ABC 中,∠A=900,AB=AC ,在BC 上任取一点P ,作PQ ∥AB 交AC 于Q ,作PR ∥CA 交BA 于R ,D 是BC的中点,求证:⊿RDQ 是等腰直角三角形。
RQDCABP2、 已知:在⊿ABC 中,∠A=900,AB=AC ,D 是AC 的中点,AE ⊥BD ,AE 延长线交BC 于F ,求证:∠ADB=∠FDC 。
EFDCAB3、 已知:在⊿ABC 中BD 、CE 是高,在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ,求证:MA ⊥NA 。
4、已知:如图(1),在△ABC 中,BP 、CP 分别平分∠ABC 和∠ACB ,DE 过点P 交AB 于D ,交AC 于E ,且DE ∥BC .求证:DE -DB=EC .5、在Rt △ABC 中,AB =AC ,∠BAC =90°,O 为BC 的中点。
(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明);(2)如果点M 、N 分别在线段AB 、AC 上移动,在移动中保持AN =BM ,请判断△OMN 的形状,并证明你的结论。
6、如图,△ABC 为等边三角形,延长BC 到D ,延长BA 到E ,AE=BD , 连结EC 、ED ,求证:CE=DE7、如图,等腰三角形ABC 中,AB =AC ,∠A =90°,BD 平分∠ABC ,DE ⊥BC 且BC =10,求△DCE 的周长。
8. 如图,已知△EAB ≌△DCE ,AB ,EC 分别是两个三角形的最长边,∠A =∠C =35°,∠CDE =100°,∠DEB =10°,求∠AEC 的度数.A B COM NFO E DCB A9. 如图,点E 、A 、B 、F 在同一条直线上,AD 与BC 交于点O, 已知∠CAE=∠DBF,AC=BD.求证:∠C=∠D10.如图,OP平分∠AOB ,且OA=OB .(1)写出图中三对你认为全等的三角形(注:不添加任何辅助线); (2)从(1)中任选一个结论进行证明.11. 已知:如图,AB =AC ,DB =DC ,AD 的延长线交BC 于点E ,求证:BE =EC 。
初二上几何证明题50题专题训练好题汇编

八年级上册几何题专题训练50 题1. 如图,已知△EAB≌△D CE,AB ,EC 分别是两个三角形的最长边,∠A=∠C=35°,∠CDE=100 °,∠DEB=10 °,求∠AEC 的度数.2. 如图,点E、A、B、F 在同一条直线上,AD 与BC 交于点O, 已知∠CAE= ∠DBF,AC=BD. 求证:∠C= ∠DCDOE A B F3.如图,OP 平分∠AOB ,且OA=OB .线);(1)写出图中三对你认为全等的三角形(注:不添加任何辅助.明证(2)从(1)中任选一个结论进行4. 已知:如图,AB =AC,DB=DC ,AD 的延长线交BC 于点E,求证:BE=EC。
5. 如图,在△ABC 中,AB=AD=DC ,∠BAD=28 °,求∠B 和∠C 的度数。
6. 如图,B、D、C、E 在同一直线上,AB=AC ,AD=AE ,求证:BD=CE 。
7. 写出下列命题的逆命题,并判断逆命题的真假.如果是真命题,请给予证明;?如果是假命题,请举反例说明.命题:有两边上的高相等的三角形是等腰三角形.8. 如图,在△ABC 中,∠ACB=90o ,D 是AC 上的一点,且AD=BC ,DE AC 于D,∠EAB=90o .求证:AB=AE .9. 如图,等边△ABC 中,点P 在△ABC 内,点Q 在△ABC 外,B,P,Q 三点在一条直线上,且∠ABP= ∠ACQ,BP= CQ,问△APQ 是什么形状的三角形?试证明你的结论.10. 如图,△ABC 中,∠C=90 °,AB 的中垂线DE 交AB 于E,交BC 于D,若AB=13 ,AC=5 ,则△ACD 的周长为多少?11. 如图所示,AC⊥BC,AD ⊥BD ,AD =BC,CE⊥AB ,DF⊥AB ,垂足分别是E,F,求证:CE=DF.12. 如图,已知△ABC 中,∠ACB=90 °,AC=BC,BE⊥CE,垂足为E,AD ⊥CE,垂足为 D.(1) 判断直线BE 与AD 的位置关系是____;BE 与AD 之间的距离是线段____的长;(2) 若AD =6 cm ,BE=2 cm ,求BE 与AD 之间的距离及AB 的长.13. 如图,已知△ABC、△ADE 均为等边三角形,点 D 是BC 延长线上一点,连结CE,EA求证:BD=CEBC D14. 如图,△ABC 中,AB= AC,∠BAC=120 °,AD ⊥AC 交BC?于点D,求证:?BC=3 AD.15. 如图,四边形ABCD 中,∠DAB= ∠BCD=90 °,M 为BD 中点,N 为AC 中点,求证:M N ⊥AC .[来源:16 、已知:如图所示,在△ABC 中,∠ABC=45 °,CD ⊥AB 于点 D ,BE 平分∠ABC ,且BE⊥AC 于点E,与CD 相交于点F,H 是BC 边的中点,连接DH 与BE 相交于点G.(1 )求证:BF=A C;(2 )求证:DG=DF .16. 如图,点B,D 在射线AM 上,点C,E 在射线AN 上,且AB=BC=CD=DE ,已知∠EDM=84 °,求∠A 的度数.17. 如图所示,在△ABC 中,AB=AC ,BD ⊥AC 于点D,CE⊥AB 于点E,BD,CE 相交于 F.求证:AF 平分∠BAC.18. 如图所示,△ABC ≌△A DE,且∠CAD=10 °,∠B= ∠D=25 °,∠EAB=120 °,求∠DFB 和∠DGB 的度数.19. 已知:如图,在△ABC 中,AB=AC ,点 D 在边B C 上,DE⊥AB ,DF⊥AC,且DE=DF ,求证:△ABD ≌△A CD20. 如图,一张直角三角形的纸片ABC ,两直角边A C=6cm ,BC=8cm .现将直角边A C 沿直线A D 折叠,使它A B 上,且AC 与AE 重合,求CD 的长.落在斜边21. 已知:如图,在△ABC 中,AB=AC ,BD 平分∠ABC ,E 是底边BC 的延长A线上的一点且CD=CE.(1)求证:△BDE 是等腰三角形D(2)若∠A=36 °,求∠ADE 的度数.EB C22. 如图,在△ABC 中,AB=CB ,∠ABC=90 °,D 为AB 延长线上一点,点E 在BC 边上且BE=BD ,连结AE、DE、DC.(1)求证:AE=CD ;(2)若∠CAE=30 °,求∠BDC 的度数.23. 如图,在ABC 中,点D 在AC 边上,DB=BC ,点E 是CD 的中点,点 F 是AB 的中点,则可以得到结论:1EF AB,请说明理由.2AFDEB C24. 已知:如图,在ABC中, C ABC,点D 为边AC 上的一个动点,延长AB 至E,使BE=CD ,连结DE,交BC 于点P.(1)DP 与PE 相等吗?请说明理由.(2)若 C 60 ,AB=12 ,当DC=_________时,BEP是等腰三角形.(不必说明理由)25. 如图,C 为线段B D 上一点(不与点B,D 重合),在BD 同侧分别作正三角形ABC 和正三角形CDE,AD 与BE 交于一点F,AD 与CE 交于点H ,BE 与AC 交于点G。
八年级上册经典几何题分类训练

八年级上册经典几何题分类训练1.已知:如图1,点C 为线段AB 上一点,△ACM ,△CBN 都是等边三角形,AN 交MC 于点E ,BM 交CN 于点F . (1)求证:AN=BM ; (2)求证:△CEF 为等边三角形;(3)将△ACM 绕点C 按逆时针方向旋转90 O,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明).2.如图,△ABC 为等边三角形,AB=6cm ,O 为AB 上的任意一点(与B 点不重合),OD ⊥BC 于D ;DE ⊥AC 于E ;EP ⊥AB 于P 。
问:当OB 的长等于多少时,点P 与点O 重合?3、(2009年牡丹江)已知Rt ABC △中,90AC BC C D ==︒,∠,为AB 边的中点,90EDF ∠=°,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S +=△△△.当EDF ∠绕D 点旋转到DE AC 和不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEFS △、CEFS △、ABCS △又有怎样的数量关系?请写出你的猜想,不需证明.4、用两个全等的等边三角形△ABC 和△ACD 拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A 重合,两边分别与AB 、AC 重合.将三角尺绕点A 按逆时针方向旋转. (1)当三角尺的两边分别与菱形的两边BC 、CD 相交于点E 、F 时(如图所示),通过观察或测量BE 、CF 的长度,你能得出什么结论?并证明你的结论;(2)当三角尺的两边分别与菱形的两边BC 、CD 的延长线相交于点E 、F 时(如图所示),你在(1)中得到的结论还成立吗?说明理由。
八年级上册——《全等三角形》证明题题型归类训练

《全等三角形》证明题题型归类训练题型1:全等+等腰性质1、如图,在△ABE 中,AB =AE,AD =AC,∠BAD =∠EAC, BC 、DE 交于点O 。
求证:(1) △ABC ≌△AED ; (2) OB =OE 。
2、已知:如图,B 、E 、F 、C 四点在同一条直线上,AB =DC,BE =CF ,∠B =∠C . 求证:OA =OD .题型2:两次全等1、AB=AC ,DB=DC ,F 是AD 的延长线上的一点.求证:BF=CFFDCBA2、已知如图,E 、F 在BD 上,且AB =CD ,BF =DE ,AE =CF,求证:AC 与BD 互相平分O C E BDAA B E O F D C3、如图,在四边形ABCD 中,AD ∥BC,∠ABC=90°DE ⊥AC 于点F,交BC 于点G,交AB 的延长线于点E ,且AE=AC 。
求证:BG=FG题型3:直角三角形全等(余角性质)1、如图,在等腰Rt △ABC 中,∠C =90°,D 是斜边上AB 上任一点,AE ⊥CD 于E ,BF ⊥CD 交CD 的延长线于F ,CH ⊥AB 于H 点,交AE 于G . 求证:BD =CG .2、如图,将等腰直角三角形ABC 的直角顶点置于直线l 上,且过A ,B 两点分别作直线的垂线,垂足分别为D ,E ,请你在图中找出一对全等三角形,并写出证明它们全等的过程.3、如图,∠ABC =90°,AB =BC ,D 为AC 上一点,分别过A 、C 作BD 的垂线,垂足分别为E 、F 求证:EF =CF -AEAFCBDEGA BC FD E4、在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时, 求证: ①ADC ∆≌CEB ∆;②BE AD DE +=; (2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.5、如图:BE ⊥AC,CF ⊥AB ,BM=AC ,CN=AB.求证:(1)AM=AN ;(2)AM ⊥AN 。
初二上几何证明题100题专题训练

M N DEB CA八年级上册几何题专题训练100题之五兆芳芳创作1、 已知:在⊿ABC 中,∠A=900,AB=AC ,在BC 上任取一点P ,作PQ ∥AB 交AC 于Q ,作PR ∥CA 交BA 于R ,D 是BC 的中点,求证:⊿RDQ 是等腰直角三角形.2、 已知:在⊿ABC 中,∠A=900,AB=AC ,D 是AC 的中点,AE ⊥BD ,AE 延长线交BC 于F ,求证:∠ADB=∠FDC.3、 已知:在⊿ABC 中BD 、CE 是高,在BD 、CE 或其延长线上辨别截取BM=AC 、CN=AB ,求证:MA ⊥NA. 4、已知:如图(1),在△ABC 中,BP 、CP 辨别平分∠ABC 和∠ACB ,DE 过点P 交AB 于D ,交AC 于E ,且DE ∥BC .求证:DE -DB=EC . 5、在Rt △ABC 中,AB =AC ,∠BAC=90°,O 为BC 的中点.(1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明);(2)如果点M 、N 辨别在线段AB 、AC 上移动,在移动中保持AN =BM ,请判断△OMN 的形状,并证明你的结论.6、如图,△ABC 为等边三角形,延长BC 到D ,延长BA 到E ,AE=BD , 连结EC 、ED ,求证:CE=DE7、如图,等腰三角形ABC 中,AB =AC ,∠A =90°,BD 平分∠ABC ,DE ⊥BC 且BC =10,求△DCE 的周长.8. 如图,已知△EAB ≌△DCE ,AB ,EC 辨别是两个三角形的最长边,∠A =∠C =35°,∠CDE =100°,∠DEB =10°,求∠AEC 的度数.9. 如图,点E 、A 、B 、F 在同一条直线上,AD 与BC 交于点O,A BCO M N已知∠CAE=∠DBF,AC=BD.求证:∠C=∠D10.如图,OP平分∠AOB,且OA=OB.(1)写出图中三对你认为全等的三角形(注:不添加任何帮助线);(2)从(1)中任选一个结论进行证明.11. 已知:如图,AB=AC,DB=DC,AD的延长线交BC于点E,求证:BE=EC.12. 如图,在△ABC中,AB=AD=DC,∠BAD=28°,求∠B和∠C的度数.13. 如图,B、D、C、E在同一直线上,AB=AC,AD=AE,求证:BD=CE.14. 写出下列命题的逆命题,并判断逆命题的真假.如果是真命题,请赐与证明;•如果是假命题,请举反例说明.命题:有两边上的高相等的三角形是等腰三角形.15. 如图,在△ABC中,∠ACB=90º,D是AC上的一点,且AD=BC,DE AC 于D,∠EAB=90º.求证:AB=AE.16. 如图,等边△ABC中,点P在△ABC内,点Q在△ABC外,B,P,Q 三点在一条直线上,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.17. 如图,△ABC中,∠C=90°,AB的中垂线DE交AB于E,交BC于D,若AB=13,AC=5,则△ACD的周长为多少?18.如图所示,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足辨别是E,F,求证:CE=DF.19. 如图,已知△ABC 中,∠ACB =90°,AC =BC ,BE ⊥CE ,垂足为E ,AD ⊥CE ,垂足为D.(1)判断直线BE 与AD 的位置关系是____;BE 与AD 之间的距离是线段____的长;(2)若AD =6 cm ,BE =2 cm ,求BE 与AD 之间的距离及AB 的长.20. 如图,已知 △ABC 、△ADE 均为等边三角形,点D 是BC 延长线上一点,连结CE ,求证:BD=CE 21. 如图,△ABC 中,AB=AC ,∠BAC=120°,AD ⊥AC 交BC•于点D ,求证:•BC=3AD.22. 如图,四边形ABCD 中,∠DAB=∠BCD=90°,M 为BD 中点,N 为AC中点,求证:MN ⊥AC .23、已知:如图所示,在△ABC 中,∠ABC=45°,CD ⊥AB 于点D ,BE 平分∠ABC ,且BE ⊥AC 于点E ,与CD 相交于点F ,H 是BC 边的中点,连接DH 与BE 相交于点G .(1)求证:BF=AC ; (2)求证:DG=DF .24. 如图,点B ,D 在射线AM 上,点C ,E 在射线AN 上,且AB=BC=CD=DE ,已知∠EDM=84°,求∠A 的度数.25. 如图所示,在△ABC 中,AB=AC ,BD ⊥AC 于点D ,CE ⊥AB 于点E ,BD ,CE 相交于F.求证:AF 平分∠BAC.26. 如图所示,△ABC ≌△ADE ,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求 ∠DFB 和∠DGB 的度数.27. 已知:如图,在△ABC 中,AB=AC ,点D 在边BC 上,DE ⊥AB ,DF ⊥AC ,且DE=DF ,求证:△ABD ≌△ACDB AED C28. 如图,一张直角三角形的纸片ABC ,两直角边AC=6cm ,BC=8cm .现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且AC 与AE 重合,求CD 的长.29. 已知:如图,在△ABC 中,AB=AC ,BD 平分∠ABC ,E 是底边BC 的延长线上的一点且CD=CE.(1)求证:△BDE 是等腰三角形(2)若 ∠A=36°,求∠ADE 的度数. 30. 如图,在△ABC 中,AB=CB ,∠ABC=90°,D 为AB 延长线上一点,点E 在BC 边上且BE=BD ,连结AE 、DE 、DC .(1)求证:AE=CD ;(2)若∠CAE=30°,求∠BDC 的度数.31. 如图,在ABC ∆中,点D 在AC 边上,DB=BC ,点E 是CD 的中点,点F 是AB 的中点,则可以得到结论:12EF AB =,请说明理由. 32. 已知:如图,在ABC ∆中,C ABC ∠=∠,点D 为边AC 上的一个动点,延长AB 至E ,使BE=CD ,连结DE ,交BC 于点P.(1)DP 与PE 相等吗?请说明理由.(2)若60C ∠=︒,AB=12,当DC=_________时,BEP ∆是等腰三角形.(不必说明理由)33. 如图,C 为线段BD 上一点(不与点B ,D 重合),在BD 同侧辨别作正三角形ABC 和正三角形CDE ,AD 与BE 交于一点F ,AD 与CE 交于点H ,BE 与AC 交于点G .(1)求证:BE=AD ;(2)求∠AFG 的度数;A B C D E(3)求证:CG=CH34. 已知:如图,在△ABC 中,CD ⊥AB ,CD=BD ,BF 平分∠DBC ,与CD ,AC 辨别交与点E 、点F ,且DA=DE ,H 是BC 边的中点,连结DH 与BE 相交于点G .(1)求证:△EBD ≌△ACD ;(2)求证:点G 在∠DCB 的平分线上(3)试探索CF 、GF 和BG 之间的等量关系,并证明你的结论.35. 如图,在在△ABC 中,AB=CB ,∠ABC=90°,F 为AB 延长线上一单,点E 在BC 上,且AE=CF.(1)求证:CBF Rt ABE Rt ∆≅∆(2)若∠CAE=30°,求∠ACF 的度数36. 如图,△ACD 和△BCE 都是等腰直角三角形,∠ACD =∠BCE =90°,AE 交DC 于F ,BD 辨别交CE ,AE 于点G 、H. 试猜测线段AE 和BD 数量关系,并说明理由.37. 如图,在△ABC 中,AB =AC ,AD 和BE 是高,它们相交于点H ,且AE =BE .求证:AH =2BD .38. 如图,在ABC ∆中,32B ︒∠=,48C ︒∠=AE 平分BAC ∠交BC 于点E ,DF AE ⊥于点F ,求ADF ∠39. 如图所示,在△ABC 中,已知点D ,E ,,CE 的中点,AAM EG F D CB A 且ABC S ∆ =4,则BEF S ∆ 的值为多少.40. 如图,ABC ∆中,90ACB ∠=,CD BA ⊥于D ,AE 平分BAC ∠交CD 于F ,交BC 于E ,求证:CEF ∆是等腰三角形.41. 如图,在四边形ABCD 中,DC ∥AB , BD 平分∠ADC , ∠ADC=60°,过点B 作BE ⊥DC ,过点A 作AF ⊥BD ,垂足辨别为E 、F ,连接EF.判断△BEF 的形状,并说明理由.42. 如图,已知Rt △ABC ≌Rt △ADE ,∠ABC =∠ADE =90°,BC 与DE 相交于点F ,连接CD ,EB.(1)图中还有几对全等三角形,请你一一列举;(不必证明)(2)求证:CF =EF.43. 在ABC ∆中,BO 平分ABC ∠,点P 为直线AC 上一动点,PO BO ⊥于点O .(1)如图1,当40ABC ︒∠=,60BAC ︒∠=,点P 与点C 重应时,求APO ∠的度数;(2)如图2,当点P 在AC 延长线时,求证:()12APO ACB BAC ∠=∠-∠; (3)如图3,当点P 在边AC 所示位置时,请直接写出APO ∠与ACB∠,BAC ∠之间的数量关系式.44. 如图,在ABC ∆中,BAD DAC ∠=∠,DF AB ⊥,DM AC ⊥,AF=10cm , AC=14cm ,动点E 以2cm/s 的速度从A 点向F 点运动,动点G 以1cm/s 的速度从C 点向A 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t .(1) 求证:在运动进程中,不管取何值,都有2AED DGC S S ∆∆=; (2) 当取何值时,DFE ∆与DMG ∆全等.45. 如图,在Rt △ABC 中,∠B=90°,AB=3, D CBC=4,将△ABC折叠,使点B恰好落在边AC上,与点'B重合,AE为折痕,求'EB的长度46. 如图,已知ΔABC是等腰直角三角形,∠C=90°.(1)操纵并不雅察,如图,将三角板的45°角的顶点与点C重合,使这个角落在∠ACB的内部,两边辨别与斜边AB交于E、F两点,然后将这个角绕着点C在∠ACB的内部旋转,不雅察在点E、F的位置产生变更时,AE、EF、FB中最长线段是否始终是EF?写出不雅察结果.(2)探索:AE、EF、FB这三条线段能否组成以EF为斜边的直角三角形?如果能,试加以证明.47. 已知BD,CE是△ABC的两条高,M、N辨别为BC、DE的中点.(1)请写出线段MN与DE的位置有什么关系?请说明理由.(2)当∠A=45°时,请判断1△EMD为何种三角形,并说明理由48. 如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B,C在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.(1)求证:BD=DE+CE;(2)若直线AE绕点A旋转到如图(2)的位置(BD<CE)时,其余条件不变,问BD与DE,CE的关系如何?请赐与证明;(3)若直线AE绕点A旋转到如图(3)的位置(BD>CE)时,其余条件不变,问BD与DE,CE的关系如何?请直接写出结果,不需证明.49. 如图1,两个不全等的等腰直角三角形OAB和等腰直角三角形OCD叠放在一起,并且有公共的直角顶点O.(1)在图1中,你发明线段AC ,BD 的数量关系是________________ , 直线AC ,BD 相交成_________度角.(2)将图1中的△OAB 绕点O 顺时针旋转90°角,这时(1)中的两个结论是否成立?请做出判断并说明理由(3)将图1中的△OAB 绕点O 顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?请作出判断并说明理由.50.△BEC 是等腰直角三ABCD 的面积. 51. △O ,过点O 辨别作OD AB OE BC OF CA ⊥⊥⊥、、,垂足辨别为点D E F 、、. (1)如图1,若点O 是等边ABC △的三条高线的交点,请辨别说明下列两个结论成立的理由. 结论1.2OD OE OF ++=;结论2.32AD BE CF a ++=; (2)如图2,若点O 是等边ABC △内任意一点,则上述结论12、是否仍然成立?(写出说理进程).52. 已知两个共一个顶点的等腰Rt △ABC ,Rt △CEF ,∠ABC=∠CEF=90°,连接AF ,M 是AF 的中点,连接MB 、ME .(1)如图1,当CB 与CE 在同一直线上时,求证:MB ∥CF ;(2)如图1,若CB=a ,CE=2a ,求BM ,ME 的长;(3)如图2,当∠BCE=45°时,求证:BM=ME .53. 如图,已知ABC △中,∠B=∠C ,AB=AC=8厘米,BC=6厘米,点D 为AB 的中点.如果点P 在线段BC 上以每秒2厘米的速度由B 点向C 点运动,同时,点Q 在线段CA 上以每秒a 厘米的速度由C 点向A 点运动,设运动时间为t (秒).(1)用含t 的代数式暗示线段PC 的长度;O 图1 图2 图B(2)若点P 、Q 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由;(3)若点P 、Q 的运动速度不相等,当点Q 的运动速度a为多少时,能够使BPD △与CQP △全等?(4)若点Q 以(3)中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都顺时针沿ABC △三边运动,求经过量长时间点P 与点Q 第一次在ABC △的哪条边上相遇?54. 如图,在ABC ∆中,BAD DAC ∠=∠,DF AB ⊥,DM AC ⊥,AF=10cm ,AC=14cm ,动点E 以2cm/s 的速度从A 点向F 点运动,动点G 以1cm/s 的速度从C 点向A 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t .(1)求证:在运动进程中,不管t 取何值,都有2AED DGC S S ∆∆=;(2)当t 取何值时,DFE ∆与DMG ∆全等求(3)在(2)的前提下,若119126BD DC =,228AED S cm ∆=,BFD S ∆55. 已知等边△ABC 和点P ,设点P 到△ABC3边的AB 、AC 、BC•的距离辨别是h1,h2,h3,△ABC 的高为h ,若点P 在一边BC 上(图1),此时h=0,可得结论h1+h2+h3=h ,请你探索以下问题:当点P 在△ABC 内(图2)和点P 在△ABC 外(图3)这两种情况时,h1、h2、h3与h•之间有怎样的关系,请写出你的猜测,并扼要说明理由.(1) (2) (3)56.如图,△ABC 中,∠C=Rt ∠,AC=8cm ,BC=6cm ,若动点P 从点C 开始,按CABC 的路径运动,且速度为每秒2㎝,设运动的时间为t 秒.(1)求t为何值时,CP把△ABC的周长分红相等的两部分;(2)求t为何值时,CP把△ABC的面积分红相等的两部分;并求此时CP 的长;(3)求t为何值时,△BCP为等腰三角形?57. 已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A 出发,沿线段AB向点B运动.(1)如图1,设点P的运动时间为t(s),那么t=(s)时,△PBC是直角三角形;(2)如图2,若另一动点Q从点B出发,沿线段BC向点C运动,如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△PBQ是直角三角形?(3)如图3,若另一动点Q从点C出发,沿射线BC标的目的运动.连接PQ交AC于D.如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△DCQ是等腰三角形?(4)如图4,若另一动点Q从点C出发,沿射线BC标的目的运动.连接PQ交AC于D,连接PC.如果动点P、Q都以1cm/s的速度同时出发.请你猜测:在点P、Q的运动进程中,△PCD和△QCD的面积有什么关系?并说明理由.58.如图所示,已知AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,交AD于点E,连接AF,求证:∠B=∠CAF.59.如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足辨别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF.60.已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为_________.15.如图所示,已知点D是等边三角形ABC的边BC延长线上的一点,∠EBC=∠DAC ,CE ∥AB.求证:△CDE 是等边三角形.61.如图所示,在△ABC 中,AB=AC ,在AB 边上取点D ,在AC 的延长线上取点E ,使得BD=CE ,连接DE 交BC 于点G ,求证:DG=GE.62.一艘轮船以15海里/时的速度由南向北飞行,如图,在A 处望小岛P ,测得∠PAN=15°,两小时后,轮船到达B 处,测得∠PBN=30°,在小岛P 周围18海里的规模内有暗礁,若轮船持续向北飞行,有无触礁危险? 63.如图,公园内两条小河MO 、NO 在O处会合,两河形成的半岛上有一处奇迹P.现筹划在两条小河上各建一座小桥Q 和R ,并在半岛上修三段小路,连通两座小桥和奇迹.这两座小桥应建在何处,才干使修路费最少? 64. 三角形ABC 中,AB=AC ,∠BAC=120°,AB 的垂直平分线EF 交AB 于E ,交BC 于F .若FC=3cm ,则求BF 长度65. 在Rt △ABC 中,∠是斜边上的高.(1)请说明△的长.668cm ,•长BC•为10cm 痕为AE ).想一想,此时EC 67、如图一块四边形草坪求这块草坪的面积.68. 如图,A 、B 两个小集镇在河道CD 的同侧,辨别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河滨建一自来水厂,向A 、BN BA AB两镇供水,铺设水管的用度为每千米3万,请你在河道CD上选择水厂的位置M,使铺设水管的用度最节省,并求出总用度是多少?69.如图,A市气象站测得台风中心在A市正东标的目的300千米的B处,以107千米/时的速度向北偏西60°的BF标的目的移动,距台风中心200•千米规模内是受台风影响的区域.(1)A市是否会受到台风的影响?写出你的结论并赐与说明;(2)如果A市受这次台风影响,那么受台风影响的时间有多长?70、如图:在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD71、如图,AD是∠BAC的角平分线,DE⊥AB垂足为E,DF⊥AC,垂足为点F,且BD=CD 求证:BE=CF72、如图,点B和点C辨别为∠MAN两边上的点,AB=AC.(1)按下列语句画出图形:①AD⊥BC,垂足为D;②∠BCN的平分线CE与AD的延长线交于点E;③连结BE;(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:____≌____,____≌____;(3)并选择其中的一对全等三角形予以证明.73、已知:AB=AC,AD⊥BC,CE平分∠BCN,求证:△ADB≌△ADC;△BDE≌△CDE.AB D CM NE74、如图,PB、PC辨别是△ABC的外角平分线且相交于点P.求证:点P在∠A的平分线上AB CP75、如图,△ABC中,p是角平分线AD,BE的交点. 求证:点p在∠C的平分线上76、下列说法中,错误的是()A.三角形任意两个角的平分线的交点在三角形的内部B.三角形两个角的平分线的交点到三边的距离相等C.三角形两个角的平分线的交点在第三个角的平分线上D.三角形任意两个角的平分线的交点到三个顶点的距离相等77、如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM平分∠BAC78、如图,AP、CP辨别是△ABC外角∠MAC与∠NCA的平分线,它们相交于点P,PD⊥BM于点D,PF⊥BN于点F.求证:BP为∠MBN的平分线.79、如图,在∠AOB的两边OA,OB上辨别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB的平分线上.80、如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;(2)线段DM与AM有怎样的位置关系?请说明理由.81、八(1)班同学上数学勾当课,利用角尺平分一个角(如图所示).设计了如下筹划:(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA、OB之间,移动角尺使角尺两边相同的刻度与M、N重合,即PM=PN,过角尺顶点P的射线OP 就是∠AOB 的平分线.(Ⅱ)∠AOB 是一个任意角,在边OA 、OB 上辨别取OM=ON ,将角尺的直角顶点P 介于射线OA 、OB 之间,移动角尺使角尺两边相同的刻度与M 、N 重合,即PM=PN ,过角尺顶点P 的射线OP 就是∠AOB 的平分线.(1)筹划(Ⅰ)、筹划(Ⅱ)是否可行?若可行,请证明;若不成行,请说明理由;(2)在筹划(Ⅰ)PM=PN 的情况下,持续移动角尺,同时使PM ⊥OA ,PN ⊥OB .此筹划是否可行?请说明理由.内的一点,PE ⊥AB ,PF ⊥AC ,垂足辨别为点E ,F ,AE=AF.求证:(1)PE=PF ;(2)点P 在∠BAC 的角平分线上.83、如图,点D 、B 辨别在∠A 的两边上,C 是∠A 内一点,AB=AD ,BC=CD ,CE ⊥AD 于E ,CF ⊥AF 于F.求证:CE=CF84、已知三角形三边长为a ,b ,c ,且丨a+b+c 丨+丨a-b-c 丨=10,求b 的值.85、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC86、如图,△ABC 和△ADE 都是等腰直角三角形,CE与BD 相交于点M,BD 交AC 于点N ,证明:(1)BD=CE.(2)BD ⊥CE.87、如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD+BC=AB88、如图,△ABC 中BA=BC ,点D 是AB 延长线上一点,DF ⊥AC 于F 交B A C D F 2 1 EBC于E,求证:△DBE是等腰三角形.89、如图,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,AE⊥BD1BD.求证:BD是∠ABC的角平分线.交BD的延长线于E,且AE=290、如图,∠BAD=∠CAD,AD⊥BC,垂足为点D,BD=CD可知哪些线段是哪个三角形的角平分线、中线、高?91、如图所示,在△ABC中,已知AC=8,BC=6,AD⊥BC于D,AD=5,BE⊥AC于E,求BE的长92、如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,EF交AD于点O.请问:DO是△DEF的角平分线吗?请说明理由.(2)若将结论与AD是∠CAB的角平分线、DE∥AB、DF∥AC中的任一条件互换,所得命题正确吗?93、如图,△ABC中,∠ABC与∠ACB的平分线交于点I,按照下列条件,求∠BIC的度数.(1)若∠ABC=70°,∠ACB=50°,则∠BIC=°(2)若∠ABC+∠ACB=120°,则∠BIC=°(3)若∠A=90°,则∠BIC=°;(4)若∠A=n°则∠BIC=°(5)从上述计较中,我们能发明∠BIC与∠A的关系吗?AIB C94、如图,求证∠A+∠B+∠C+∠D+∠E=180°95、如图,不法则的五角星图案,求证:∠A+∠B+∠C+∠D+∠E=180°96、D为△ABC的边AB上一点,且∠ADC=∠ACD.求证:∠ACB>∠B97、如图,D是BC延长线上的一点,∠ABC.∠ACD的平分线交于点E,求证:∠E=1/2∠A98、如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的角平分线.(1)试求∠F与∠B,∠D的关系;(2)若∠B:∠D:∠F=2:4:x 求X的值99、如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=度.100.如图,在Rt△ABC中,已知∠ACB=90°,AC=BC,D为DC的中点,CE⊥AD于E,BF∥AC交CE的延长线于点F.求证:AB垂直平分DF.。
八年级的数学上册经典几何题集.doc
八年级上册经典几何题1、已知一个三角形有两边相等,其中两边长分别为5cm 和11cm ,则这个三角形的第三边长是 。
2、已知三角形的周长为9, 且三边长都是整数,则满足条件的三角形共有 个。
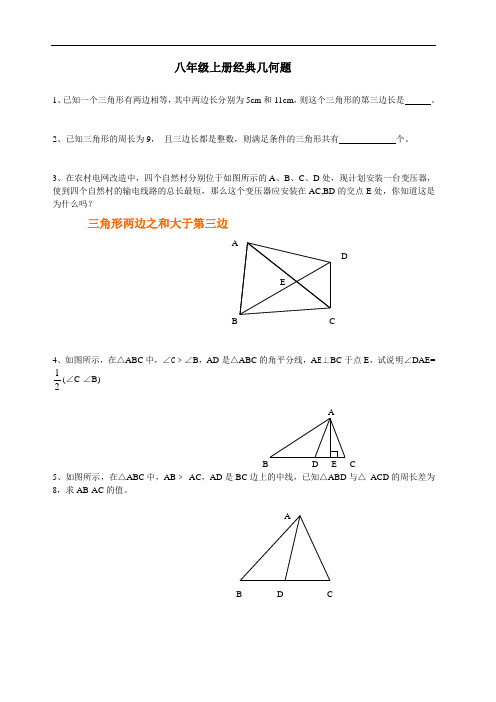
3、在农村电网改造中,四个自然村分别位于如图所示的A 、B 、C 、D 处,现计划安装一台变压器,使到四个自然村的输电线路的总长最短,那么这个变压器应安装在AC,BD 的交点E 处,你知道这是为什么吗?三角形两边之和大于第三边ADEB C4、如图所示,在△ABC 中,∠C ﹥∠B ,AD 是△ABC 的角平分线,A E ⊥BC 于点E ,试说明∠DAE=21(∠C-∠B)AB D E C5、如图所示,在△ABC 中,AB ﹥ AC ,AD 是BC 边上的中线,已知△ABD 与△ ACD 的周长差为8,求AB-AC 的值。
AB D C6、在学习完“三角形的中线”以 后,我们知道“三角形的一条中线将原三角形分成面积相等的两部分”,课后, 张老师给学生们布置了这样一个问题:有一块三角形蛋糕要平均分给6个小朋友,要求只切3刀,你有办法达到要求吗?试把你的方案画出来,并加以说明。
7、如图:在△ABC 中, D 为AC 的中点,E,F 为AB 上的两点,且AE=BF=41AB,求S △DEF :S △ABC 的值。
AEFB C8、如图所示,在△ABC 中,AD 是中线,你认为AD+BD 与21(AB+AC )有怎样的数量关系?请说明理由. 大于AB D C9、已知在△ABC 中,∠A =45°,高线BD 和高线CE 所在的直线交于点H ,求∠BHC 的度数.CDDHA E B10、在△ABC中,AB=AC,P点是BC上任意一点。
(1)如图,若P是BC边上任意一点,PF⊥AB于F点,PE⊥AC于点E ,BD为△ABC的高线,请探求PE,PF与BD之间的关系。
AF DEB PC (1)如图,若P是BC延长线上一点,PF⊥AB于F点,PE⊥AC于点E ,CD为△ABC的高线,请探求PE,PF与CD之间的关系。
初二上几何证明题题专题训练好题大全
八年级上册几何题专题训练50题1. 如图,已知△EAB ≌△DCE ,AB ,EC 分别是两个三角形的最长边,∠A =∠C =35°,∠CDE =100°,∠DEB =10°,求∠AEC 的度数.2. 如图,点E 、A 、B 、F 在同一条直线上,AD 与BC 交于点O, 已知∠CAE=∠DBF,AC=BD.求证:∠C=∠D3.如图,OP 平分∠AOB ,且OA=OB .(1)写出图中三对你认为全等的三角形(注:不添加任何辅助线);(2)从(1)中任选一个结论进行证明.4. 已知:如图,AB =AC ,DB =DC ,AD 的延长线交BC 于点E ,求证:BE =EC 。
5. 如图,在△ABC 中,AB=AD=DC ,∠BAD=28°,求∠B 和∠C 的度数。
7. 写出下列命题的逆命题,并判断逆命题的真假.如果是真命题,请给予证明;•如果是假命题,请举反例说明.命题:有两边上的高相等的三角形是等腰三角形.8. 如图,在△ABC 中,∠ACB=90o , D 是AC 上的一点,且AD=BC ,DE AC 于D , ∠EAB=90o .求证:AB=AE .9. 如图,等边△ABC 中,点P 在△ABC 内,点Q 在△ABC 外,B ,P ,Q 三点在一条直线上,且∠ABP =∠ACQ ,BP =CQ ,问△APQ 是什么形状的三角形?试证明你的结论.10. 如图,△ABC 中,∠C=90°,AB 的中垂线DE 交AB 于E ,交BC 于D ,若AB=13,AC=5,则△ACD 的周长为多少?11. 如图所示,AC ⊥BC ,AD ⊥BD ,AD =BC ,CE ⊥AB ,DF ⊥AB ,垂足分别是E ,F ,求证:CE =DF.12. 如图,已知△ABC 中,∠ACB =90°,AC =BC ,BE ⊥CE ,垂足为E ,AD ⊥CE ,垂足为D.(1)判断直线BE 与AD 的位置关系是____;BE 与AD 之间的距离是线段____的长;(2)若AD =6 cm ,BE =2 cm ,求BE 与AD 之间的距离及AB 的长.13. 如图,已知 △ABC 、△ADE 均为等边三角形,点D 是BC 延长线上一点,连结CE ,求证:BD=CE 14. 如图,△ABC 中,AB =AC ,∠BAC =120°,AD ⊥AC 交BC •于点D ,求证:•BC =3AD .15. 如图,四边形ABCD 中,∠DAB=∠BCD=90°,M 为BD 中点,N 为AC 中点,求证:MN ⊥AC .16、已知:如图所示,在△ABC 中,∠ABC=45°,CD ⊥AB 于点D ,BE 平分∠ABC ,且BE ⊥AC于点E ,与CD 相交于点F ,H 是BC 边的中点,连接DH 与BE 相交于点G .(1)求证:BF=A C ;?????(2)求证:DG=DF . 17. 如图,点B ,D 在射线AM 上,点C ,E 在射线AN 上,且AB=BC=CD=DE ,已知∠EDM=84°,求∠A 的度数.18. 如图所示,在△ABC 中,AB=AC ,BD ⊥AC 于点D ,CE ⊥AB 于点E ,BD ,CE 相交于F.求证:AF 平分∠BAC.6. 如图,B 、D 、C 、E 在同一直线上,AB=AC ,AD=AE ,求证:BD=CE 。
初二上几何证明题100题专题训练汇编
八年级上册几何题专题训练 100题1、已知:在"ABC 中,/ A=9C °, AB=AC 在BC 上任取一点 P,作PQ/ AB 交AC 于Q,作PR// CA 交BA 于R , D 是BC 的中点,求证:" RDQ 是等腰直角三角形。
2、已知:在"ABC 中,/ A=90°, AB=AC D 是 AC 的中点,AE ±BD, AE 延长线交 BC 于 F ,求证:/ADB2 FDC3、 已知:在"4、 已知:如图 // BC .求ABC 中BD CE 是高,在 BD CE 或其延长线上分别截取 BM=AC CN=AB 求证:MAL NA=(1),在△ ABC 中,BP 、CP 分别平分/ ABC 和/ACB , DE 过点 DE —DB=EC . P 交AB 于D ,交AC 于E ,且DEC5、在RtA ABC 中,AB= AC,/ BAC=90°, O 为BC 的中点。
⑴写出点O到厶ABC的三个顶点A、B、C的距离的大小关系(不要求证明);(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN= BM,请判断厶OMN的形状,并证明你的结论。
6、如图,△ ABC为等边三角形,延长BC到D,延长BA到E, AE=BD, 连结EC ED,求证:CE=DE7、如图,等腰三角形ABC中,AB= AC, / A= 90°, BD平分/ ABC, DE丄BC且BC= 10,求厶DCE的周长。
8.如图,已知△ EAB^A DCE AB, EC分别是两个三角形的最长边,求/ AEC的度数./ A=/ C= 35°, / CDE= 100°, / DEB= 10TT学习-----好资料9.如图,点E 、A 、B F 在同一条直线上,AD 与BC 交于点0,10.如图,0P 平分/ A0B 且0A=0B(1) 写出图中三对你认为全等的三角形(注:不添加任何辅助线) (2) 从(1)中任选一个结论进行证明.11. 已知:如图, AB= AC, DB= DC AD 的延长线交 BC 于点E ,求证:BE = EG已知/ CAE=Z DBF,AC=BD 求证:/C=Z D/ BAD=28,求/ B 和/C 的度数。
八年级数学上学期开学测试题分类之几何解答题(含解析)
2015-2016八年级数学上学期开学测试题分类之几何解答题1.如图,点O在直线AB上,OC平分∠DOB.若∠COB=36°.(1)求∠DOB的大小;(2)请你用量角器先画∠AOD的角平分线OE,再说明OE和OC的位置关系.【答案】(1)∠DOB=72°;(2)垂直.【解析】分析:根据角平分线的性质可得∠DOB=2∠COB进行求解;首先进行画图,然后计算.解:(1)∵OC平分∠DOB ∴∠DOB=2∠COB=2×36°=72°;(2)∵∠DOB=72°∴∠AOD=180°-72°=108°∵OE平分∠AOD ∴∠DOE=108°÷2=54°∴∠COE=∠DOE+∠COD=54°+36°=90°∴OE和OC互相垂直.【难度】一般2.如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.(1)求∠EDC的度数;(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.【答案】(1)35°;(2)(12n+35)°;(3)(215-12n)°.【解析】分析:(1)根据角平分线直接得出答案;(2)过点E作EF∥AB,然后根据平行线的性质和角平分线的性质求出角度;(3)首先根据题意画出图形,然后过点E作EF∥AB,按照第二小题同样的方法进行计算角度.解:(1)∵DE平分∠ADC,∠ADC=70°,∴∠EDC=12∠ADC=12×70°=35°;(2)过点E作EF∥AB,∵AB∥CD,∴AB∥CD∥EF,∴∠ABE=∠BEF,∠CDE=∠DEF,∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,∴∠A BE=12∠ABC=12n°,∠CDE=12∠ADC=35°,∴∠BED=∠BEF+∠DEF=12n°+35°;(3)过点E作EF∥AB∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°∴∠ABE=12∠ABC=12n°,∠CDE=12∠ADC=35°∵AB∥CD,∴AB∥CD∥EF,∴∠BEF=180°-∠ABE=180°-12n°,∠CDE=∠DEF=35°,∴∠BED=∠BEF+∠DEF=180°-12n°+35°=215°-12n°.故∠BED的度数发生了改为,改变为(215-12n)°.【难度】困难3.如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.(1)求线段MN 的长;(2)若C 为线段AB 上任意一点,满足AC+CB=acm ,其他条件不变,你能猜想MN 的长度吗?并说明理由。
八年级上册经典几何题分类训练
DACBNM GFHCE八年级上册经典几何题分类训练常见辅助线的作法有以下几种:1) 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”.2) 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”. 3) 遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.4) 过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”5) 截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.一、以等边三角形为基础1.△DAC, △EBC 均是等边三角形,AE,BD 分别与CD,CE 交于点M,N, 求证:(1)AE=BD (2)CM=CN (3) △CMN 为等边三角形(4)MN ∥BC 2.已知:如图1,点C 为线段AB 上一点,△ACM ,△CBN 都是等边三角形,AN 交MC 于点E ,BM 交CN 于点F . (1)求证:AN=BM ; (2)求证:△CEF 为等边三角形;(3)将△ACM 绕点C 按逆时针方向旋转90 O ,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明).3、如图所示,已知△ABC 和△BDE 都是等边三角形。
下列结论:① AE=CD ;②BF=BG ;③BH 平分∠AHD ;④∠AHC=600,⑤△BFG 是等边三角形;⑥ FG ∥AD 。
其中正确的有( )A 3个B 4个C 5个D 6个E图1 图2DCE A B (第22题) 4.如图,△ABC 为等边三角形,AB=6cm ,O 为AB 上的任意一点(与B点不重合),OD ⊥BC 于D ;DE ⊥AC 于E ;EP ⊥AB 于P 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级上册经典几何题分类训练
1.已知:如图1,点C 为线段AB 上一点,△ACM ,△CBN 都是等边三角形,AN 交MC 于点E ,BM 交CN 于点
F . (1)求证:AN=BM ; (2)求证:△CEF 为等边三角形;
(3)将△ACM 绕点C 按逆时针方向旋转90 O
,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明).
2.如图,△ABC 为等边三角形,AB=6cm ,O 为AB 上的任意一点(与B 点不重合),OD ⊥BC 于D ;DE ⊥AC 于E ;
EP ⊥AB 于P 。
问:当OB 的长等于多少时,点P 与点O 重合?
3、(2009年牡丹江)已知Rt ABC △中,90AC BC C D ==︒,∠,为AB 边的中点,90EDF ∠=°,
EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .
当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证
1
2DEF CEF ABC S S S +=
△△△.
当EDF ∠绕D 点旋转到DE AC 和不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF
S △、
CEF
S △、
ABC
S △又有怎样的数量关系?请写出你的猜想,不需证明.
4、用两个全等的等边三角形△ABC 和△ACD 拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A 重合,两边分别与AB 、AC 重合.将三角尺绕点A 按逆时针方向旋转. (1)当三角尺的两边分别与菱形的两边BC 、CD 相交于点E 、F 时(如图所示),通过观察或测量BE 、CF 的长度,你能得出什么结论?并证明你的结论;
(2)当三角尺的两边分别与菱形的两边BC 、CD 的延长线相交于点E 、F 时(如图所示),你在(1)中得到的结论还成立吗?说明理由。
9.如图,两个全等的含30°、60°角的三角板ADE 和三角板ABC 放置在一起,∠DEA=∠ACB=90°,∠DAE=∠ABC=30°,E 、A 、C 三点在一条直线上,连接BD ,取BD 中点M ,连接ME 、MC ,试判断△EMC 的形状,并说明理由.
5.已知:在△ABC 中,∠ACB 为锐角,点D 为射线BC 上一动点,连接AD ,以AD 为一边且在AD 的左侧作等腰直角△ADE ,解答下列各题:如果AB=AC ,∠BAC=90°. (i )当点D 在线段BC 上时(与点B 不重合),如图甲,线段BD ,CE 之间的位置关系为(ii )当点D 在线段BC 的延长线上时,如图乙,i )中的结论是否还成立?为什么?
A
E C
F B
D
图1
图3
A
D
F
E
C
B
A
D
B
C
E 图2
F
F
E
D C
B A
F E
D
C B
A
D
E
C
P O
B
A
6、在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
(1)写出点O 到△ABC的三个顶点A、B、C的距离的大小关系,并说明理由.
(2)若点M、N分别是AB、AC上的点,且BM=AN,试判断△OMN形状,并证明你的结论.
7.如图所示,已知在△AEC中,∠E=90°,AD平分∠EAC,DF⊥AC,垂足为F,DB=DC.
求证:BE=CF.
8、如图所示,已知D是等腰△ABC底边BC上的一点,它到两腰AB、AC的距离分别为DE、DF,CM⊥AB,垂足为M,请你探索一下线段DE、DF、CM三者之间的数量关系, 并给予证明.
11、已知:如图E在△ABC的边AC上,且∠AEB=∠ABC。
(3)求证:∠ABE=∠C;
(4)若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长。
12.已知:如图,ABC
△是等边三角形,过AB边上的点D作DG BC
∥,交AC于点G,在GD的延长线上取点E,使DE DB
=,连接AE CD
,.
(1)求证:AGE DAC
△≌△;
(2)过点E作EF DC
∥,交BC于点F,请你连接AF,并判断AEF
△
是怎样的三角形,试证明你的结论.
13.已知,如图①所示,在ABC
△和ADE
△中,AB AC
=,AD AE
=,BAC DAE
∠=∠,且点B A D
,,在一条直线上,连接BE CD M N
,,,分别为BE CD
,的中点.
(1)求证:①BE CD
=;②AN
AM=;
(2)在图①的基础上,将ADE
△绕点A按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立.
C
G
A
E
D
B F
C
E
N
D
A
B
M
图①
C
A
E
M
B
D
N
图②
A
B
F
C
D
E
E
D C
B
A
M
F
B
A
C
D
F
2
1
E
14、已知:△ABC边BC上的高AD所在的直线与AC上的高BE所在的直线相交于点F
(1)如图①,若△ABC为锐角三角形且∠ABC=45°过点F做FG∥BC,
交直线AB于点G,试探究线段FG,DC,AD三者之间满足怎样的
数量关系?并说明理由
(2)如图②,若∠ABC=135°,其他的条件不变,试探究(1)中三条
线段之间满足怎样的数量关系?并说明理由
15、如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.16、(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△A MN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
17、已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC
18、一节数学课后,老师布置了一道课后练习题:
如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点PD分别在AO和BC上,PB=PD,DE⊥AC 于点E,求证:△BPO≌△PDE.
(1)理清思路,完成解答(2)本题证明的思路可用下列框图表示:
根据上述思路,请你完整地书写本题的证明过程.
(2)特殊位置,证明结论
若PB平分∠ABO,其余条件不变.求证:AP=CD.。
