【信号与系统(郑君里)课后答案】第三章习题解答
信号与系统第三章答案2

y ''(t ) + 4 y '(t ) + 3 y (t ) = f (t )
(1)对上式两边取傅里叶变换得:
( jw ) 2 Y ( jw ) + 4( jw )Y ( jw ) + 3Y ( jw ) = F ( jw )
1 1 Y ( jw ) 1 1 2 2 H ( jw ) = = = = 2 F ( jw ) ( jw ) + 4( jw ) + 3 ( jw + 3)( jw + 1) ( jw + 1) ( jw + 3) 1 h(t ) = F -1[ H ( jw )] = (e- t - e-3t )U (t ) 2
jw =-2
= -1
d [Y ( jw )g( jw + 2) 2 ] =2 j w =2 dw
jw =-3
K 3 = Y ( jw )g( jw + 3)
即
= -2
Y ( jw ) =
-1 2 -2 + + ( jw + 2) 2 jw + 2 jw + 3
根据傅里叶变换的性质:
- jtf (t ) «
1 1 g jw + 2 ( jw + 3)( jw + 1) K3 K1 K2 = + + jw + 2 jw + 3 jw + 1
用部分分式展开法:
K1 = Y ( jw )g( jw + 2) K 2 = Y ( jw )g( jw + 3) K 3 = Y ( jw )g( jw + 1)
h(t ) = F -1[ H ( jw )] = (2e -3t - e -2t )U (t )
信号与系统习题答案第三章

第三章习题基础题3.1 证明cos t , cos(2)t , …, cos()nt (n 为正整数),在区间(0,2)π的正交集。
它是否是完备集?解:(积分???)此含数集在(0,2)π为正交集。
又有sin()nt 不属于此含数集02sin()cos()0nt mt dt π=⎰,对于所有的m 和n 。
由完备正交函数定义所以此函数集不完备。
3.2 上题的含数集在(0,)π是否为正交集?解:由此可知此含数集在区间(0,)π内是正交的。
3.3实周期信号()f t 在区间(,)22T T-内的能量定义为222()TT E f t dt -=⎰。
如有和信号12()()f t f t +(1)若1()f t 与2()f t 在区间(,)22T T-内相互正交,证明和信号的总能量等于各信号的能量之和;(2)若1()f t 与2()f t 不是相互正交的,求和信号的总能量。
解:(1)和信号f(t)的能量为[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2)由1()f t 与2()f t 在区间内正交可得2122()()0T T f t f t dt -=⎰则有 22221222()()T T T T E f t dt f t dt --=+⎰⎰即此时和信号的总能量等于各信号的能量之和。
和信号的能量为(2)[]222222222221212222()12()()()()()()T T T T T T T T T T E f t dt dtf t dt f t dt f t f t dtf t f t -----===+++⎰⎰⎰⎰⎰(少乘以2吧?)由1()f t 与2()f t 在区间(,)22T T-内不正交可得2122()()0T T f t f t dt K -=≠⎰则有2222222212122222()()()()T T T T T T T T E f t dt f t dt K f t dt f t dt ----=++≠+⎰⎰⎰⎰即此时和信号的总能量不等于各信号的能量之和。
郑君里《信号与系统》第3版笔记课后习题考研真题详解

郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解
攻重浩精研学习网提供资料
第1章绪论
1.1复习笔记
本章作为《信号与系统》的开篇章节,是整个信号与系统学习的基础。
本章介绍了有关信号与系统的基本概念和术语,给出几种典型的信号和系统的表现形式,讲述了各信号与系统的特点以及信号之间的运算和转换。
通过本章学习,读者应掌握:如何判断信号类型、不同信号之间的运算、信号的分解以及系统类型的判断。
一、信号概述
1信号的概念及分类(见表1-1-1)
表1-1-1信号的概念及分类
2典型的连续信号(见表1-1-2)
表1-1-2典型的信号及表示形式
3信号的运算(见表1-1-3)
表1-1-3信号的运算
4阶跃函数和冲激函数
阶跃信号和冲激信号是信号与系统中最基础的两种信号,许多复杂信号皆可由二者或二者的线性组合表示。
具体见表1-1-4及表1-1-5。
(1)单位阶跃信号u(t)
表1-1-4单位阶跃信号u(t)
(2)单位冲激信号δ(t)
表1-1-5单位冲激信号δ(t)表示形式及性质
5信号的分解
一个一般信号根据不同类型可分解为以下几种分量,具体见表1-1-6。
表1-1-6信号的分解
二、系统
1系统概念及分类(见表1-1-7)
表1-1-7系统的概念及分类
系统模型如下:
输入信号经过不同系统可得到不同输出信号,具体见表1-1-8。
表1-1-8不同系统特性。
郑君里《信号与系统》(第3版)(上册)(课后习题 傅里叶变换)【圣才出品】

第3章 傅里叶变换3-1 求图3-1所示对称周期矩形信号的傅里叶级数(三角形式与指数形式)。
图3-1解:(1)三角形式由图3-1可知,f(t)为奇函数,故有所以三角形式的傅里叶级数为。
(2)指数形式因所以指数形式的傅里叶级数为。
3-2 周期矩形信号如图3-2所示。
若:重复频率f=5kHz脉宽τ=20μs幅度E=10V求直流分量大小以及基波、二次和三次谐波的有效值。
图3-2解:由图3-2可知,f(x)为偶函数,且f=5kHz,得:所以直流分量为1V基波分量为1sin() 1.3910Vπ=≈二次谐波为2sin( 1.325Vπ=≈三次谐波为。
33sin() 1.2110V π=≈3-3 若周期矩形信号f 1(t )和f 2(t )波形如图3-2所示,f 1(t )的参数为τ=0.5μs,T=1μs,E=1V ;f 2(t )的参数为τ=1.5μs,T=3μs,E=3V ,分别求:(1)f 1(t )的谱线间隔和带宽(第一零点位置)频率单位以kHz 表示;(2)f 2(t )的谱线间隔和带宽;(3)f 1(t )与f 2(t )的基波幅度之比;(4)f 1(t )基波与f 2(t )三次谐波幅度之比。
解:由题3-2的结论可知,f(t)的傅里叶级数可表示为其中,。
(1)f 1(t )的谱线间隔,则带宽:。
(2)f 2(t )的谱线间隔带宽:。
(3)由题3-2可知,所以f 1(t )的基波幅度为:f 2(t )的基波幅度为:故。
(4)的三次谐波幅度为:故。
3-4 求图3-3所示周期三角信号的傅里叶级数并画出频谱图。
图3-3解:由图3-3可知,f(t)为偶函数,故。
bn所以的傅里叶级数可表示为()f t其幅度谱如图3-4所示。
图3-43-5 求图3-5所示半波余弦信号的傅里叶级数。
若E=10V ,f=10kHz ,大致画出幅度谱。
图3-5解:由图3-5可知,f(t)为偶函数,因而b n =0,();所以其傅里叶级数可表示为若E=10V ,,则幅度谱如图3-6所示。
《信号与系统》(郑君里)课后习题答案
(t )
2
非线性:设 r1 ( t ) = e1
( t ) 、 r2 ( t ) = e2 2 ( t ) ,
2 2 2 2
则⎡ ⎣ c1e1 ( t ) + c2 e2 ( t ) ⎤ ⎦ = c1 e1 ( t ) + c2 e2
2
( t ) + 2c1c2e1 ( t ) e2 ( t ) ≠ c1r1 ( t ) + c2 r2 ( t )
5
即 输 入 x1 ( t ) , x2 ( t ) 得 到 的 输 出 分 别 为 y1 ( t ) , y2 ( t ) , T ⎡ ⎣ x1 ( t ) ⎤ ⎦ = y1 ( t ) ,
T⎡ 。 ⎣ x2 ( t ) ⎤ ⎦ = y2 ( t ) ,则 T ⎡ ⎣ c1 x1 ( t ) + c2 x2 ( t ) ⎤ ⎦ = c1 y1 ( t ) + c2 y2 ( t ) ( c1 , c2 为常数)
解题过程:
(a-1)
(a-2)
(a-3)
4
(a-4)
(b) f ( t ) 为偶函数,故只有偶分量,为其本身
(c-1)
(c-2)
(c-3)
(c-4)
(d-1)
(d-2)
(d-3)
(d-4)
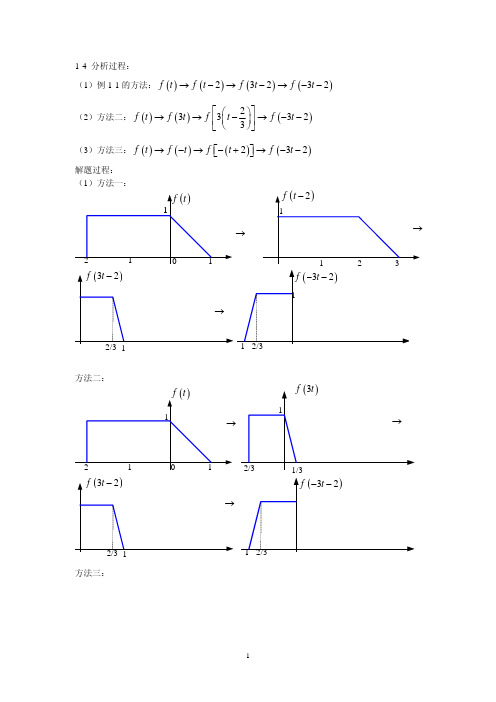
1-20 分析过程:本题为判断系统性质:线性、时不变性、因果性 (1)线性(Linearity) :基本含义为叠加性和均匀性
f (t )
1 1
f ( 3t )
→
→
-2
-1
0
1
-2/3
f ( 3t − 2 )
→
1/3
f ( −3t − 2 )
信号与系统第三章习题部分参考答案

(7) (1 − t) f (1 − t) ;
(2) [1 + m f (t)]cosω0 t
(4) (t + 2) f (t); ( ) (6) e− jω0 t df t
dt
(8) f (t)∗ f (t − 3);
t
(9) ∫τ f (τ )dτ −∞
1−t / 2
(11) ∫ f (τ )dτ −∞
2π (sin π t )2 ↔ 2π (1− ⎜w⎜)[ε(w + 2π ) − ε(w − 2π )]
πt
2π
即 (sin π t )2 ↔ (1− ⎜w⎜)[ε(ω + 2π ) − ε(w − 2π )]
πt
2π
(3)双边指数信号
∵ e−a⎜t⎜
↔
2a a2 + w2
(−∞
<
t
<
+∞)
∴ 2a a2 + w2
(13) f (t)∗ Sa(2t) (15) t df (1 − t)
dt
t+5
(10) ∫ f (τ )dτ −∞
(12) df (t) + f (3t ) − 2 e− jt ;
dt
(14) f (t) u(t)
(16) (t − 2) f (t)e j2(t−3)
解:(1) f 2 (t) + f (t) = f (t). f (t) + f (t) ↔ 1 [F (w}* F (w)] + F (w)
又 f (t) = 2 + cos⎜⎛ 2πt ⎟⎞ + 4sin⎜⎛ 5πt ⎟⎞
⎝3⎠
【信号与系统(郑君里)课后答案】第三章习题解答

【信号与系统(郑君⾥)课后答案】第三章习题解答3-1 解题过程:(1)三⾓形式的傅⽴叶级数(Fourier Series ,以下简称 FS )f ( t ) = a ++∞cos ( n ω t) + b sin ( n ω t ) a 0 ∑ n 1n 1 n =1式中ω1 =2π,n 为正整数,T 1 为信号周期T 11 t +T(a )直流分量a 0 = 0 ∫ 1 f ( t ) dtT1 t2 t +T(b )余弦分量的幅度a n = 0∫ 1f ( t ) cos ( n ω1t ) dtT1 t 02 t +T(c )正弦分量的幅度b n = 0 ∫ 1f ( t ) sin ( n ω1t ) dtT 1 t(2)指数形式的傅⽴叶级数+∞f ( t ) = ∑ F ( n ω1 )e jn ω1tn == F ( n ω1 ) = 1 ∫t 0 +T 1f ( t ) e ? jn ω1t dt T 1 t 0F n =1( a n ? jb n ) F ? n = 1 ( a n + jb n ) 2 2由图 3-1 可知, f ( t ) 为奇函数,因⽽a 0 = a n = 0 4 Tb n = T ∫02= 2Eπ n4TE2EEf (t ) sin ( n ω t ) dt =sin ( n ω t ) dt = cos ( n ω t = 1 ? cos ( n π2T 1 ∫0 2 1 n t 1 n ) 1n = 2, 4,n = 1, 3,所以,三⾓形式的 FS 为2 E1 12π f ( t ) =sin ( ω1t ) +sin ( 3ω1t ) +sin ( 5ω1t ) +ω1 =π 3 5Tn = 0, ±2, ±4,F n = ? jb n jE=2 n = 0,± 1, ±3,n π1所以,指数形式的 FS 为f ( t ) = ? jE π ej ω1t+ πjE e ? j ω1t ? 3jE π e j 3ω1t + 3jEπ e ? j 3ω1t +3-15 分析:半波余弦脉冲的表达式 f ( t ) =πτ E cos t u t+ τ 2求 f ( t ) 的傅⽴叶变换有如下两种⽅法。
信号与系统课后答案第三章作业答案

初始为 0, C2 -4
y f (t) -4e3tu(t) 4e2tu(t)
全响应= yx (t)+y f (t) 4e2tu(t)-2e3tu(t)
3-2 描述某 LTI 系统的微分方程为
d2 y(t) dt 2
3dy(t) dt来自2y(t)
df (t) dt
6
1
1
(2e1 e1 et ) u(t)
e1(2 et ) u(t)
(2)
f
(t)
a[u(t
s) 2
u(t
2)]
h(t) b[u(t 2) u(t 3)]
f
(t)
h(t)
ab[(t
1 2
)
u(t
1 2
)
(t
1 2
)
u(t
1) 2
tu(t)
1 4
(et
e3t
)u(t)
1 2
t
e3tu(t)
[
1 4
et
(
1 2
t
1 4
)e3t
]u
(t)
3-19 一 个 LTI 系 统 , 初 始 状 态 不 祥 。 当 激 励 为 f (t) 时 其 全 响 应 为
(2e3t sin 2t)u(t) ;当激励为 2 f (t) 时其全响应为 (e3t 2sin 2t)u(t) 。求
(1) 初始状态不变,当激励为 f (t 1) 时的全响应,并求出零输入相应、
零状态响应; (2) 初始状态是原来的两倍、激励为 2 f (t) 时系统的全响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-1 解题过程:
(1)三角形式的傅立叶级数(Fourier Series ,以下简称 FS )
f ( t ) = a +
+∞
cos ( n ω t
) + b sin ( n ω t ) a 0 ∑ n 1
n 1 n =1
式中ω1 =
2π
,n 为正整数,T 1 为信号周期
T 1
1 t +T
(a )直流分量
a 0 = 0 ∫ 1 f ( t ) dt
T
1 t
2 t +T
(b )余弦分量的幅度
a n = 0
∫ 1
f ( t ) cos ( n ω1t ) dt
T
1 t 0
2 t +T
(c )正弦分量的幅度
b n = 0 ∫ 1
f ( t ) sin ( n ω1t ) dt
T 1 t
(2)指数形式的傅立叶级数
+∞
f ( t ) = ∑ F ( n ω1 )e jn ω1t
n =
其中复数频谱
F n
= F ( n ω1 ) = 1 ∫t 0 +T 1
f ( t ) e − jn ω1
t dt T 1 t 0
F n =
1
( a n − jb n ) F − n = 1 ( a n + jb n ) 2 2
由图 3-1 可知, f ( t ) 为奇函数,因而a 0 = a n = 0
4 T
b n = T ∫02
= 2E
π n
4
T
E
−2E
E
f (
t ) sin ( n ω t ) dt =
sin ( n ω t ) dt = cos ( n ω t = 1 − cos ( n π
2T 1 ∫0 2 1 n t 1 n ) 1
n = 2, 4,
n = 1, 3,
所以,三角形式的 FS 为
2 E
1 1
2π f ( t ) =
sin ( ω1t ) +
sin ( 3ω1t ) +
sin ( 5ω1t ) +
ω1 =
π 3 5
T
指数形式的 FS 的系数为
1
n = 0, ±2, ±4,
F n = − jb n jE
=
2 n = 0,
−
± 1, ±3,
n π
1
所以,指数形式的 FS 为
f ( t ) = − jE π e
j ω1
t
+ πjE e − j ω1t − 3jE π e j 3ω1t + 3jE
π e − j 3ω1t +
3-15 分析:半波余弦脉冲的表达式 f ( t ) =
π
τ E cos t u t
+ τ 2
求 f ( t ) 的傅立叶变换有如下两种方法。
解题过程:
方法一:用定义
F ( ω ) =
τ
π
− j ωt
2
τ E cos
t e
dt
∫
− τ
2
=
E
τ π π
∫
e
+ e
dt
j
−ω t
− j +ω t
2
2
E π τ
π
τ
E
π j −ω − j
−ω
− j
=
e τ 2 − e τ 2
−
e τ π π
2 j τ − ω
2 j
τ + ω
τ
τ
E cos
ω
E cos
ω
2 2 =
+
π − ω
π + ω
τ
τ
τω
2 E τ cos
2 =
ωτ
2
π 1 −
π
ω = 2π
1
T
τ
− u t −
2
τ
π
τ
+ ω
j
+ω
2 − e τ 2
方法二:用 FT 的性质和典型的 FT 对
f ( t ) = E cos π t u t + τ − u t − τ
τ 2 2
F ( ω ) E π τ
τ = F cos t F u t + − u t −
2π 2 2 τ
π
π π
其中 F cos t
= π δ ω + + δ ω − , τ τ
τ
τ τ 2
ωτ
F u t + − u t − = sin 2 2
ω 2
代入 F ( ω ) = E
π
τ
τ
F cos
t
F u t +
− u t − 得
2π
τ
2
2
2
F (ω)=Eππ2ωτπ δω++ δω −sin
2πτω
τ2ω +
π
τω −
π
τ
ττ
sin sin
22
= E+
ππ
ω+ τω −τ
τω
2 Eτ cos
2
=π
ωτ 2 1 −
π
其频谱图如下图所示:
3-19 分析:本题意在说明:对于两频域信号,如果其幅频特性相同,但是相频特性不同则它们对应的时域信号是不一样的。
解题过程:
()(0 )(0 )()0(0 )(0 )(a)Fω= A uω +ω− uω −ω,ϕω=ω t uω +ω− uω−ω
(()(0 )(0 )
所以, Fω=Fωe jϕ(ω)=Ae jωt0uω +ω− uω −ω
先求 F1(ω)= u (ω+ω0)− u (ω−ω0)的FT: f1(t )
由 F Saωt=πuω +ω
c )− uω−ω
( c )ω
c
(( c )
3。
