第二节 常见离散型随机变量的分布
合集下载
第二节常见离散型随机变量的概率分布
例2.20 某种玻璃器皿在汽车运输中的破损率为2%，现 在一次运送1200件，试求，(1) 破损件数X的概率分布； (2) 最多破损30件的概率α．
解 (1) 为求破损件数X的概率分布，考虑n=1200次伯努 利试验，每次试验成功的概率为p=0.02，可见X的概率 分布是参数为的二项分布．由于n=1200和p=0.02显然满 足泊松定理的条件，可见近似服从参数为np=24的泊松 分布．
第二节、常见离散型随机变 量的概率分布
一、两点分布（0－1分布）
只有两个可能值的随机变量X的概率分布称做两点分布：
X
~
x1 q
x2 p
(q
1
p,
0
p
1)
特别，若x1 =0 , x2 =1,则称X服从参数为p的0-1分布，亦称伯
努利分布．只计“成功”和“失败”两种结局的试验称做伯
努利
试验．设X是试验成1功 , 的若次试数验：成功 ， X ~ 0 , 若试验失败 ,
n})
；
四、泊松分布、泊松定理和泊松流
称随机变量X服从参数为 0 的泊松分布，如果
PX k λ k eλ (k 0,1,2,)
k!
1、泊松定理 假设X服从二项分布，参数年n充分大，而 p充分小，且 n p 适中，则可以利用泊松分布概率近似计 算二项分布概率．
Ckn
pk (1
p)nk
(np)k k!
因此，至少需要安排3个人值班．
例2.15 假设一部设备在一个工作日因故停用的概率为0.2．一
周使用5个工作日可创利润10万元；使用4个工作日可创利润7
万元；使用3个工作日只创利润2万元；停用3个及多于3个工
作日亏损2万元．求所创利润的概率分布．
概率论与数理统计2.2.2 (0-1)分布
P{ X xk } pk , k 1, 2,
（2）列表法
X
x1 x2
xk
pk
p1 p2
pk
二、（0－1）分布：（也称两点分布）
引例1
射手每次射击的成绩在9.5环以上时被认为射击成功.
如果每次射击成功的概率为0.45，令
1, 当射击成功,
X 0,
当射击失败.
分布律为
X
0
1
P 0.55 0.45
则称X 服从（0-1）分布，
引例2
商店里有10张同类CD片，其中6张为一级品，3张为二级品， 1张为不合格品.顾客购买时任取其中一张，求取得合格品的概 率.
解
1, 取得合格品,
X 0, 否则.
分布律为X01 NhomakorabeaPk
0.1 0.6+0.3
则称X 服从（0-1）分布，取得合格品的概率为 PX 1 0.9.
的随机变量．
0,
X X () 1,
当 1, 当 2.
来描述这个随机试验的结果。
检查产品的质量是否合格，对新生婴儿的性别进行登记， 检验种子是否发芽以及“抛硬币”试验都可以用（0-1）
分布的随机变量来描述．
例1 在100件产品中,有95件正品,5件次品.现从中随机地取
一件,假如取到每件产品的机会都相等.
若定义随机变量X为
0, X 1,
当取到次品时 当取到正品时
则有 P{X=0}=0.05, P{X=1}=0.95
若定义随机变量Y为
1, Y 0,
当取到次品时 当取到正品时
则有 P{Y=0}=0.95, P{Y=1}=0.05
从中看到X,Y都服从(0-1)分布.
2离散型随机变量的分布列
X的所有可能取值是0,1,2,3.
P(X=0)=
C36 C130
=
20 120
=
1 6
,
P(X=1)=
C62C14 C130
=
60 120
=
1 2
,
P(X=2)=
C
2 4
C16
C130
=
36 120
=
3 10
,
P(X=3)=
C34 C130
=
4 120
=
1 30
.
∴X的分布列为
X
0
1
2
3
1
1
3
1
P
6
栏目索引
X
x1
x2
…
xi
…
xn
P
p1
p2
…
pi
…
pn
此表称为离散型随机变量X的概率分布列,简称为X的分布列,有时
也用等式P(X=xi)=pi,i=1,2,…,n表示X的分布列.
(2)分布列的性质
(i)pi③ ≥0 ,i=1,2,3,…,n;
n
(ii) pi 1. i 1
栏目索引
3.常见的离散型随机变量的概率分布
η
0
1
2
P
0.1
0.3
0.3
栏目索引
3 0.3
栏目索引
1-2 (2015北京朝阳一模改编)如图所示,某班一次数学测试成绩的茎叶 图和频率分布直方图都受到了不同程度的污损,其中,频率分布直方图 的分组区间分别为[50,60),[60,70),[70,80),[80,90),[90,100],据此解答以 下问题. (1)求全班人数及分数在[80,100]之间的频率; (2)现从分数在[80,100]之间的试卷中任取3份分析学生的失分情况,设 抽取的试卷分数在[90,100]的份数为X,求X的分布列.
概率论与数理统计 第二章 随机变量及其分布 第二节 离散型随机变量及其概率分布
以X记“第1人维护的20台中同一时刻发生故障的台 数”以Ai ( i 1,2,3,4)表示事件“第i人维护的20台中 ,
发生故障时不能及时维修”, 则知80台中发生故障
而不能及时维修的概率为
三、几种常见离散型随机变量的概率分布
P ( A1 A2 A3 A4 ) P ( A1 )
三、几种常见离散型随机变量的概率分布
3、独立重复试验与二项分布 （1）独立重复试验
三、几种常见离散型随机变量的概率分布
例5 某射手在一定条件下，独立地向目标连续射 击4次，如果每次击中目标的概率为0.8，求 ①恰好中三次的概率；②至少击中三次的概率。
三、几种常见离散型随机变量的概率分布
例5 某射手在一定条件下，独立地向目标连续射 击4次，如果每次击中目标的概率为0.8，求 ①恰好中三次的概率；②至少击中三次的概率。
三、几种常见离散型随机变量的概率分布
练习1 某类灯泡使用时数在1000小时以上 的概率是0.2，求三个灯泡在使用1000 小时以后最多只有一个坏了的概率.
解: 设X为三个灯泡在使用10ห้องสมุดไป่ตู้0小时已坏的灯泡数 . 把观察一个灯泡的使用 时数看作一次试验, “使用到1000小时已坏” P{X 1} =P{X=0}+P{X=1} 视为事件A .每次试验, A )3+3(0.8)(0.2)2 =(0.2出现的概率为0.8
本例中，n=20，p=0.2, 所以，(n+1)p=4.2, 故k0=4。
三、几种常见离散型随机变量的概率分布
练习3 设有80台同类型设备,各台工作是相互独立 的发生故障的概率都是 0.01,且一台设备的故障能 由一个人处理. 考虑两种配备维修工人的方法 , 其 一是由四人维护,每人负责20台; 其二是由3人共同 维护台80.试比较这两种方法在设备发生故障时不 能及时维修的概率的大小. 解 按第一种方法
2-2离散型随机变量及其分布律
松定理（第二章）和中心极限定理（第五章），利用这些定理
可以近似计算出它们的值．
3．泊松分布
定义 2.5 如果随机变量 X 的分布律为
P{X k} k e ， k 0,1, 2,L ， 0 ，
k!
就称 X 服从参数为 的泊松分布，记为 X ~ P() ．
【注 1】 P{X
k
k}
e
0 ， k 0,1, 2,L
一般地，在随机试验 E 中，如果样本空间 只包含两个
样本点
{1,2}，且
X
0, 1,
若 =1 , 若 =2 ,
则 X ~ B(1, p) ，其中 p P{X 1} P({2}) ．
在现实生活中，0 1两点分布有着广泛的应用．例如某产品 合格与不合格；某课程的考试及格与不及格；某事件 A 发生与 不发生等许多现象都能够刻划成 0 1两点分布．
§2 离散型随机变量及其分布律
一、离散型随机变量及其分布律的概念 定义 2.1 若随机变量 X 的取值为有限个或可列无限多个，就 称 X 为离散型随机变量．
定义 2.2 设 X 为离散型随机变量，其所有可能的取值为 x1, x2 ,L , xi ,L ，且
P{X xi} pi ， i 1, 2,L ．
的概率为 0.6 ，求该射手在 4 次射击中，命中目标次数 X 的
分布律，并问 X 取何值时的概率最大． 解 将每次射击看成一次随机试验，所需考查的试验结果只
有击中目标和没有击中目标，因此整个射击过程为 4 重的贝
努里试验．故由题意知， X ~ B(4, 0.6) ，即
P{X k} C4k 0.6k 0.44k ， k 0,1, 2,3, 4 ．
P{X
10}
2.5第2节离散型随机变量的分布律
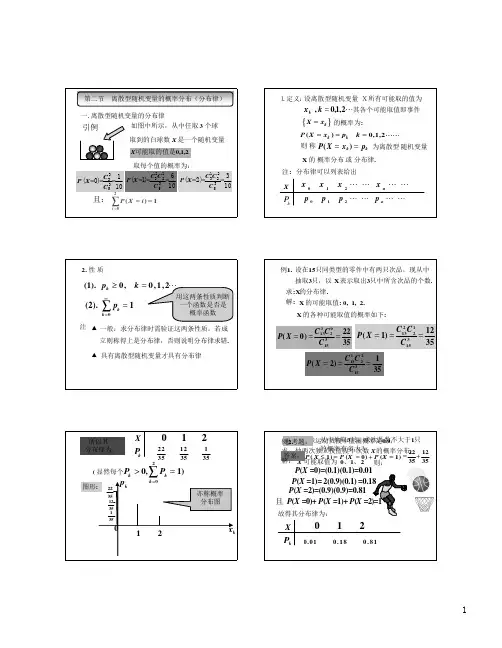
3
例６． 将一枚均匀骰子抛掷 ３ 次， 令:X 表示 3 次中出现“4”点的次数
求: X的概率函数
解: 显然，X的概率函数是：
P{
X
=
k
}
=
C
k 3
(
1 6
)k
(
5 6
)3− k
,
k = 0,1,2,3
3
0 .
定理
设一次试验中事件A发生的概率为 p , (0 < p < 1)
则在 n 次贝努利试验中事件A 恰发生 k 次概率为:
概 [(1
率− pP)+n (kp)x]就n 等的于展二开项式式中
xk
的系数， 这也是二项分布的名称
P(X = k) ≥ 0,
的由来 .
n
∑Cnk pk(1− p)n−k =( p +q)n =1
k=0
例7. 设某炮手射击的命中率为 0.8，为炸毁某个 目标， 经预测只要命中两发就够炸毁.
问 :希望发射5发炮弹就能炸毁目标的可能性有多大?
路 口3
路 口2
路 口1
P(X=2)=P(
A1
A2
A3
)
=
1⋅ 2
X表示该汽车首次遇到红灯前已通过的路口的个数
设 Ai={第i个路口遇红灯}, i=1,2,3
路 口3
路 口2
路 口1
P(X=3)=
P(
A1
A2
A3
)=
1 2
⋅
1 2
⋅
1 2
=1/8
于是得其分布律为：
X0 1 2 3
例5. 设生男孩的概率为 p， 生女孩的概率为 q=1-p， 令 X 表示随机抽查出生的4个婴儿 中“男孩”的个数.
第二节 离散型随机变量及其分布
说明： 1) 泊松分布与二项分布的关系：这两个分布的数学模 型都是Bernoulli概型。Poisson分布是二项分布当n很大 p 很小时的近似计算。 2) Poisson分布主要用于描述一些稀有事件，如地震、 火山爆发、特大洪水等等。
例3.1.3 (进货问题）由某商店过去的销售记录知
道，海尔彩电每月的销售数可用参数为λ =5的泊 松分布来描述，为了以95%以上的把握保证月底不 脱销，问商店在月底至少应进多少台？ 解：设每月的销售数为X，月底进N台，则
其概率分布为 P ( X 1) 3 10 即X服从两点分布。
7 P( X 0) 10
(2) 二项分布 B ( n, p )
背景：n 重Bernoulli 试验中，每次试验感兴 趣的事件A 在 n 次试验中发生的次数 —— X是一离散型随机变量
若P ( A ) = p , 则
Pn ( k ) P ( X k ) C p (1 p)
P{ X 1} 1 P{ X 0} =1 0.99
成功次数服从二项概率
400
0.9820
B(400, 0.01)
有百分之一的希望，就要做百分之百的努力!
(3) Poisson 分布 ( ) 或 P ( )
k! 其中 0 是常数，则称 X 服从参数为 的Poisson 分布，记作 ( ) 或 P ( )
k n k
n k
, k 0,1,, n
称 X 服从参数为n, p 的二项分布(也叫Bernolli 分布).记作
X ~ B( n, p)
0 – 1 分布是 n = 1 的二项分布.
例3.1.1 一大批产品的次品率为0.1，现从中取
出15件．试求下列事件的概率： B ={ 取出的15件产品中恰有2件次品 } C ={ 取出的15件产品中至少有2件次品 }
例3.1.3 (进货问题）由某商店过去的销售记录知
道，海尔彩电每月的销售数可用参数为λ =5的泊 松分布来描述，为了以95%以上的把握保证月底不 脱销，问商店在月底至少应进多少台？ 解：设每月的销售数为X，月底进N台，则
其概率分布为 P ( X 1) 3 10 即X服从两点分布。
7 P( X 0) 10
(2) 二项分布 B ( n, p )
背景：n 重Bernoulli 试验中，每次试验感兴 趣的事件A 在 n 次试验中发生的次数 —— X是一离散型随机变量
若P ( A ) = p , 则
Pn ( k ) P ( X k ) C p (1 p)
P{ X 1} 1 P{ X 0} =1 0.99
成功次数服从二项概率
400
0.9820
B(400, 0.01)
有百分之一的希望，就要做百分之百的努力!
(3) Poisson 分布 ( ) 或 P ( )
k! 其中 0 是常数，则称 X 服从参数为 的Poisson 分布，记作 ( ) 或 P ( )
k n k
n k
, k 0,1,, n
称 X 服从参数为n, p 的二项分布(也叫Bernolli 分布).记作
X ~ B( n, p)
0 – 1 分布是 n = 1 的二项分布.
例3.1.1 一大批产品的次品率为0.1，现从中取
出15件．试求下列事件的概率： B ={ 取出的15件产品中恰有2件次品 } C ={ 取出的15件产品中至少有2件次品 }
第二节 离散性随机变量及其分布
X 0 0.1 1 0.6
。 。 。
1
2 0.3
解： F ( x )＝P{ X x }
0, 0.1, ＝ 0.7, 1, x0 0 x1 1 x 2 x2
1
Pk
F ( x)
0
2
x
0, 0.1 , F ( x )＝ 0.7 , 1,
k!
,
k =0,1,2, …,
0
解: 依据概率分布的性质: P{X =k}≥0,
P{ X k } 1
k 0
这里用到了幂级数 展开式
欲使上述函数为概率分布
a≥0
a
k 0
k
k!
e
ae 1
k!
k 0
k
从中解得
ae
。
3. 利用分布律求事件概率 离散型随机变量的分布律不仅给出了{X=xk }
x0 0, F ( x )＝P{ X x }＝ x, 0 x 1 1, x1
1
x
0
1
用分布函数描述随机变量不如分布律直观， 对非离散型随机变量，是否有更直观的描述方法？
a
b
P{a X b} ?
的概率，而且通过它可以求事件{a X b}, a b 发生的概率。 由概率的有限可加性有
P{a X b}
a xk b
P{ X xk }
a xk b
pk
例2.3 设袋中有5只球，其中有2只白3只红。现从
中任取3只球(不放回)，求抽得的白球数X为k的概
注:
1. 这里分布函数的定义对任何随机变量都适用。 2. 分布函数F(x)＝P {Xx} 是一个普通的函数，它 的自变量是全体实数。掌握了X的分布函数就掌 握了X在(－∞, +∞)上的概率分布情况。
。 。 。
1
2 0.3
解： F ( x )＝P{ X x }
0, 0.1, ＝ 0.7, 1, x0 0 x1 1 x 2 x2
1
Pk
F ( x)
0
2
x
0, 0.1 , F ( x )＝ 0.7 , 1,
k!
,
k =0,1,2, …,
0
解: 依据概率分布的性质: P{X =k}≥0,
P{ X k } 1
k 0
这里用到了幂级数 展开式
欲使上述函数为概率分布
a≥0
a
k 0
k
k!
e
ae 1
k!
k 0
k
从中解得
ae
。
3. 利用分布律求事件概率 离散型随机变量的分布律不仅给出了{X=xk }
x0 0, F ( x )＝P{ X x }＝ x, 0 x 1 1, x1
1
x
0
1
用分布函数描述随机变量不如分布律直观， 对非离散型随机变量，是否有更直观的描述方法？
a
b
P{a X b} ?
的概率，而且通过它可以求事件{a X b}, a b 发生的概率。 由概率的有限可加性有
P{a X b}
a xk b
P{ X xk }
a xk b
pk
例2.3 设袋中有5只球，其中有2只白3只红。现从
中任取3只球(不放回)，求抽得的白球数X为k的概
注:
1. 这里分布函数的定义对任何随机变量都适用。 2. 分布函数F(x)＝P {Xx} 是一个普通的函数，它 的自变量是全体实数。掌握了X的分布函数就掌 握了X在(－∞, +∞)上的概率分布情况。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 第二节 常见离散型随机变量的分布
二、二项分布 （ 一 ） n 重 伯 努 利 试 验 (n-fold Bernoulli trials) 将伯努利试验独立地重复进行n 次就 称为 n 重伯努利试验。
第章 第二节 常见离散型随机变量的分布
n 重伯努利试验的特点： （1）只有两个结果，要么 A 发生， 要么 A 不发生； （2）每次试验事件 A 发生的概率都 等于p。 （3）n 次试验之间是相互独立的；
Pn (k ) C p q
k n k
nk
(k 0,1,, n)
第二章 第二节 常见离散型随机变量的分布
(二) 二项分布(binomial distribution) 若随机变量 X 的概率函数为
P( X k ) C p q
k n k nk
(k 0,1,, n)
第二章 第二节 常见离散型随机变量的分布
雅各 .伯努利(Bernoulli Jacob)瑞士 数学家，他在十七世纪末，在重复独立 试验概率模型研究方面，做了大量的工 作，以他命名的Bernoulli 分布是概率论 中最基本，也是最重要的分布，在它的 基础上，发展了 Poisson 分布，Normal 分布。
三、Poisson分布 四、超几何分布
第二章 第二节 常见离散型随机变量的分布
一、二点分布 （一）伯努利试验(Bernoulli trials) 进行一次试验，如果我们只关心某 事件A发生还是不发生，试验结果 只有两个，A和 A ，令
P( A) p, P( A) 1 p q,
这样的试验就称为伯努利试验。
第二章 第二节 常见离散型随机变量的分布
分布函数 设 X 是一随机变量，x 是 任意的一个实数，则函数 F(x)=P(Xx) 称为随机变量 X 的分布函数。 分布函数适用于离散型和连续型
第二章 第二节 常见离散型随机变量的分布
对离散型随机变量：
对于任意实数x1, x2 ( x1 < x2),
第二章 第二节 常见离散型随机变量的分布
第二章 第二节 常见离散型随机变量的分布
问题：在一次试验中，事件A发 生的概率为p,则在n次独立重复的 试验中，事件A恰好发生k次的概 率为多少？
答案：事件A恰好发生k次的概率
Pn (k ) C p q
k n k
nk
(k 0,1,, n)
第二章 第二节 常见离散型随机变量的分布
例 设随机变量X的分布律为： X P 3 4 5 1/10 3/10 6/10
求X的分布函数，并求P(X7/2)， P(3 <X9/2), P(3 X9/2)
第二章 第二节 常见离散型随机变量的分布
第二节 常见离散型 随机变量的分布
第二章 第二节 常见离散型随机变量的分布
一、二点分布
二、二项分布
第二章 第二节 常见离散型随机变量的分布
Poisson 定理 设 是一常数，n是任意正整数， 设npn ，则对于任意固定的非负整数
k，有
当n很大，且p很小时，令 np 则
(一般要求n≥10, p≤0.1)
第二章 第二节 常见离散型随机变量的分布
例 据以往经验，新生儿染色体异常 率为1%，试求100名新生儿中有0、 1、2个染色体异常的概率？
第二章 第二节 常见离散型随机变量的分布
(二)、二点分布(two point distribution)
在伯努利试验中，分别用0,1表示事 件A发生与不发生，这样X就是一个只能 取0或1的随机变量，其概率分布为： X P 0 1 p 1 p
其中0<p<1，则称 X 服从参数为 p 的二 点分布或0-1分布。
例 射击，n=3,k=2,用Ai表示“第i 次射中”，记B为射击3次恰好击 中2次，求P(B)
第二章 第二节 常见离散型随机变量的分布
n 重伯努利试验的计算公式 在 n 重伯努利试验中，事件 A 发生的概率为 p ，不发生的概率为 q=1p，则在 n 次独立重复试验中， 事件 A 恰好发生 k 次（0≤k≤n）的 概率为：
第二章 第二节 常见离散型随机变量的分布
解： 有反应的人数X服从二项分布
P( X k )
0
1
2
3
4
5
X k
0.59049 0.32805 0.72090 0.00810 0.00045 0.00001
第二章 第二节 常见离散型随机变量的分布
例 据以往经验，新生儿染色体异常率 为1%，试求100名新生儿中有0、1、2 个染色体异常的概率？ 解：n=100,p=0.01则100名新生儿中 发生染色体异常例数的概率为
k n k n k
0
n
（ 2） P ( X k ) C
k 0 k 0
k n
p q
k
nk
( p q) 1
第二章 第二节 常见离散型随机变量的分布
例 据报道，有10％的人对某药有 胃肠道反应。为考察某厂的产品质 量，现任选5人服用此药。试求： （1）k 个人有反应的概率 （k=0,1,2,3,4,5）； （2）不多于2人有反应的概率； （3）有人有反应的概率。
则称 X 服从参数为 n,p 的二项分布， 记为 X~B(n,p)。
第二章 第二节 常见离散型随机变量的分布
P( X k ) C p q
k n k
n k
n 恰好是二项展开式(p+q) 的通项
显然，二项分布满足离散型变量 分布律的条件：
（1）P ( X k ) C p q
解：n=100,p=0.01则100名新生儿 中发生染色体异常例数的概率为
第二章 第二节 常见离散型随机变量的分布
三.Poisson 分布(Poisson distribution) 若随机变量 X 的概率函数为 k P( X k ) e ( 0, k 0,1,2,) k! 则称 X 服从参数为 的 Poisson 分布， 记作 X~P()。
第二章 第二节 常见离散型随机变量的分布
显然，泊松分布满足离散型变量 分布律的条件：
（ 1） P ( X k )
k
P( X k ) （ 2） k 0 k 0