人教版高中数学【必修一】[知识点整理及重点题型梳理]_指数函数、对数函数、幂函数综合_提高
人教版高中数学必修一知识点梳理重点题型（常考知识点）巩固练习指数函数、对数函数、幂函数综合【学习目标】1．理解有理指数幂的含义，掌握幂的运算．2．理解指数函数的概念和意义，理解指数函数的单调性与特殊点． 3．理解对数的概念及其运算性质．4．重点理解指数函数、对数函数、幂函数的性质，熟练掌握指数、对数运算法则，明确算理，能对常见的指数型函数、对数型函数进行变形处理．5．会求以指数函数、对数函数、幂函数为载体的复合函数的定义域、单调性及值域等性质．6．知道指数函数x a y =与对数函数x y a log =互为反函数（a ＞0，a≠1）． 【知识框图】【要点梳理】要点一：指数及指数幂的运算 1．根式的概念a 的n 次方根的定义：一般地，如果n x a =，那么x 叫做a 的n 次方根，其中*1,n n N >∈当n 为奇数时，正数的n 次方根为正数，负数的n n 为偶数时，正数的n 次方根有两个，这两个数互为相反数可以表示为负数没有偶次方根，0的任何次方根都是0．n 叫做根指数，a 叫做被开方数． 2．n 次方根的性质：（1）当n a =；当n ,0,,0;a a a a a ≥⎧==⎨-<⎩（2）na =3．分数指数幂的意义：)0,,,1m na a m n N n =>∈>；()10,,,1m nm naa m n N n a-=>∈>要点诠释：0的正分数指数幂等于0，负分数指数幂没有意义． 4．有理数指数幂的运算性质：()0,0,,a b r s Q >>∈（1）rsr sa a a+= （2）()r srsa a = （3）()rr rab a b =要点二：指数函数及其性质 1．指数函数概念一般地，函数()0,1x y a a a =>≠且叫做指数函数，其中x 是自变量，函数的定义域为R ． 2要点三：对数与对数运算 1．对数的定义（1）若(0,1)xa N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数．（2）负数和零没有对数．（3）对数式与指数式的互化：log (0,1,0)xa x N a N a a N =⇔=>≠>．2．几个重要的对数恒等式log 10a =，log 1a a =，log b a a b =．3．常用对数与自然对数常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）． 4．对数的运算性质如果0,1,0,0a a M N >≠>>，那么 ①加法：log log log ()a a a M N MN += ②减法：log log log a a aMM N N-= ③数乘：log log ()na a n M M n R =∈④log a NaN =⑤log log (0,)b na a nM M b n R b=≠∈ ⑥换底公式：log log (0,1)log b a b NN b b a=>≠且要点四：对数函数及其性质 1．对数函数定义一般地，函数()log 0,1a y x a a =>≠且叫做对数函数，其中x 是自变量，函数的定义域()0,+∞． 2要点五：反函数 1．反函数的概念设函数()y f x =的定义域为A ，值域为C ，从式子()y f x =中解出x ，得式子()x y ϕ=．如果对于y 在C 中的任何一个值，通过式子()x y ϕ=，x 在A 中都有唯一确定的值和它对应，那么式子()x y ϕ=表示x 是y 的函数，函数()x y ϕ=叫做函数()y f x =的反函数，记作1()x f y -=，习惯上改写成1()y f x -=．2．反函数的性质（1）原函数()y f x =与反函数1()y fx -=的图象关于直线y x =对称．（2）函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域．（3）若(,)P a b 在原函数()y f x =的图象上，则'(,)P b a 在反函数1()y f x -=的图象上．（4）一般地，函数()y f x =要有反函数则它必须为单调函数．要点六：幂函数 1．幂函数概念形如()y x R αα=∈的函数，叫做幂函数，其中α为常数． 2．幂函数的性质（1）图象分布：幂函数图象分布在第一、二、三象限，第四象限无图象．幂函数是偶函数时，图象分布在第一、二象限（图象关于y 轴对称）；是奇函数时，图象分布在第一、三象限（图象关于原点对称）；是非奇非偶函数时，图象只分布在第一象限．（2）过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)．（3）单调性：如果0α>，则幂函数的图象过原点，并且在[0,)+∞上为增函数．如果0α<，则幂函数的图象在(0,)+∞上为减函数，在第一象限内，图象无限接近x 轴与y 轴．（4）奇偶性：当α为奇数时，幂函数为奇函数，当α为偶数时，幂函数为偶函数．当qpα=（其中,p q 互质，p 和q Z ∈），若p 为奇数q 为奇数时，则qpy x =是奇函数，若p 为奇数q 为偶数时，则q py x =是偶函数，若p 为偶数q 为奇数时，则qpy x =是非奇非偶函数．（5）图象特征：幂函数,(0,)y x x α=∈+∞，当1α>时，若01x <<，其图象在直线y x =下方，若1x >，其图象在直线y x =上方，当1α<时，若01x <<，其图象在直线y x =上方，若1x >，其图象在直线y x =下方．【典型例题】类型一：指数、对数运算 例1．计算（1） 2221log log 12log 422-； （2）33lg 2lg 53lg 2lg 5++； （3）222lg5lg8lg5lg 20lg 23+++；（4）lg0.7lg20172⎛⎫⋅ ⎪⎝⎭【思路点拨】运算时尽量把根式转化为分数指数幂，而小数也要化为分数为好． 【答案】（1）12-；（2）1；（3）3；（4）14．【解析】（1）原式=122221log 12log log 22-⎫===-； （2）原式=()()22lg 2lg5lg 2lg 2lg5lg 53lg 2lg5+-++=()2lg10lg 5lg 23lg 2lg 53lg 2lg 5⎡⎤⋅+-+⎣⎦=1-3lg 2lg5+3lg 2lg5=1（3）原式=()22lg52lg2lg51lg2lg 2++++ =()2lg5lg2lg5lg2(lg2lg5)++++ =2+lg5lg 2+=3；（4）令x =lg0.7lg20172⎛⎫⋅ ⎪⎝⎭，两边取常用对数得lg0.7lg 201lg lg 72x ⎡⎤⎛⎫=⋅⎢⎥ ⎪⎝⎭⎢⎥⎣⎦=()1lg2lg7(lg71)(lg2)++--=lg7lg 2lg7lg 2lg7lg 2+-+ =lg1414,x ∴=即lg0.7lg20172⎛⎫⋅ ⎪⎝⎭=14．【总结升华】这是一组很基本的对数运算的练习题，虽然在考试中这些运算要求并不高，但是数式运算是学习数学的基本功，通过这样的运算练习熟练掌握运算公式、法则，以及学习数式变换的各种技巧．举一反三：【变式1】552log 10log 0.25+=（ ）A ．0B ．1C ．2D ．4 【答案】C【解析】552log 10log 0.25+=25555log 10log 0.25log (1000.25)log 252+=⨯==．【变式2】（1）2(lg 2)lg 2lg 50lg 25+⋅+；（2）3948(log 2log 2)(log 3log 3)+⋅+． 【答案】（1）2；（2）54． 【解析】（1） 原式22(lg 2)(1lg5)lg 2lg5(lg 2lg51)lg 22lg5=+++=+++ (11)lg 22lg52(lg 2lg5)2=++=+=； （2） 原式lg 2lg 2lg3lg3lg 2lg 2lg3lg3()()()()lg3lg9lg 4lg8lg32lg32lg 23lg 2=+⋅+=+⋅+ 3lg 25lg 352lg 36lg 24=⋅=．类型二：指数函数、对数函数、幂函数的图象与性质例2．设偶函数()f x 满足3()8(0)f x x x =-≥，则{}|(2)0x f x ->= （ ）A ．{}|24x x x <->或B ． {}|04x x x <>或 C ． {}|06x x x <>或 D ． {}|24x x x <->或 【答案】 B 【解析】3()8(0)f x x x =-≥且()f x 是偶函数．338,0,()8,0,x x f x x x ⎧-≥⎪∴=⎨--<⎪⎩ ()320,280x x -≥⎧⎪∴⎨-->⎪⎩或()320,280x x -<⎧⎪⎨--->⎪⎩ ∴2,4,x x ≥⎧⎨>⎩或2,0.x x <⎧⎨<⎩ 解得4x >或0x <，故选B ．【总结升华】考查解不等式组及函数解析式，考查函数性质的综合运用． 举一反三：【变式1】已知函数123,0,()log ,0,x x f x x x +⎧≤=⎨>⎩若0()3f x >，则0x 的取值范围是（ ）．A ． 08x >B ． 00x <或08x >C ． 008x <<D ． 00x <或008x << 【答案】A 【解析】依题意0010,33x x +≤⎧⎨>⎩或0200,log 3x x >⎧⎨>⎩即000,11x x ≤⎧⎨+>⎩或02020,log log 8x x >⎧⎨>⎩，所以08x >，故选A ．例3．设函数212log ,0,()log (),0x x f x x x >⎧⎪=⎨-<⎪⎩ 若()()f a f a >-，则实数a 的取值范围是（ ） ．A ．()()1,00,1-B ．()(),11,-∞-+∞C ．()()1,01,-+∞ D ．()(),10,1-∞-【答案】C【解析】解法一：①若0a >，则0a -<，∴212log log a a >，得221log log a a >，得1a a>，解得1a >． ②若0,a <则0a ->，∴122log ()log ()a a ->-，221log ()log ()a a ∴->-解得()1,1a ∈- 由①②可知()()1,01,a ∈-+∞解法二：特殊值验证 令22,(2)log 21,a f ===(2)1f -=-，满足()()f a f a >-，故排除A 、D ．令2a =-，(2)1f -=-，(2)1f = 不满足()()f a f a >-，故排除B ．【总结升华】本题考查了分段函数的性质、分类思想的应用． 【幂指对函数综合377495 例1】例4．函数)86(log 231+-=x x y 的单调递增区间是（ ）A ．（3，+∞）B ．（－∞，3）C ．（4，+∞）D ．（－∞，2）【思路点拨】这是一个内层函数是二次函数，外层函数是对数函数的复合函数，其单调性由这两个函数的单调性共同决定，即“同增异减”．【答案】D【解析】函数)86(log 231+-=x x y 是由213log ,68y u u x x ==-+复合而成的，13log y u =是减函数，268u x x =-+在(),3-∞上单调递增，在()3,+∞上单调递减，由对数函数的真数必须大于零，即2680x x -+>，解得4x >或2x <，所以原函数的单调递增区间是(),2-∞，故选D ．例5．（2016 上海模拟）已知函数()xf x a =（a ＞0，a ≠1）在区间[―1，2]上的最大值为8，最小值为m ．若函数()(310g x m =-是单调增函数，则a =________．【思路点拨】根据题意求出m 的取值范围，再讨论a 的值，求出f （x ）的单调性，从而求出a 的值． 【答案】18 【解析】根据题意，得3－10m ＞0， 解得310m <；当a ＞1时，函数()xf x a =在区间[－1，2]上单调递增，最大值为28a =，解得a =13410m a -===>，不合题意，舍去； 当1＞a ＞0时，函数()xf x a =在区间[―1，2]上单调递减，最大值为18a -=，解得18a =，最小值为2136410m a ==<，满足题意； 综上，18a =．故答案为：18．【总结升华】本题主要考查指数函数的图象与性质的应用问题，通过讨论对数函数的底数确定函数的单调性是解决本题的关键．举一反三：【变式1】已知|1|()2x f x -=，该函数在区间[a ，b ]上的值域为[1，2]，记满足该条件的实数a 、b 所形成的实数对为点P （a ，b ），则由点P 构成的点集组成的图形为（ ）A ． 线段ADB ． 线段ABC ． 线段AD 与线段CD D ． 线段AB 与BC【思路点拨】由指数函数的图象和性质，我们易构造出满足条件函数|1|()2x f x -=在闭区间[a ，b ]上的值域为[1，2]的不等式组，画出函数的图象后与答案进行比照，即可得到答案．【答案】C【解析】∵函数|1|()2x f x -=的图象为开口方向朝上，以x =1为对称轴的曲线，如图．当x =1时，函数取最小值1， 若|1|22x y -==，则x =0，或x =1而函数|1|2x y -=|在闭区间[a ，b ]上的值域为[1，2]，则012a b =⎧⎨≤≤⎩或012a b <≤⎧⎨=⎩，则有序实数对（a ，b ）在坐标平面内所对应点组成图形为故选C ．【总结升华】本题考查的知识点是指数函数的性质，函数的值域，其中熟练掌指数函数在定区间上的值域问题，将已知转化为关于a ，b 的不等式组，是解答本题的关键．【变式2】已知函数|lg |,010,()16,10.2x x f x x x <≤⎧⎪=⎨-+>⎪⎩若,,a b c 互不相等，且()()()f a f b f c ==，则abc 的取值范围是（ ）．A ．（1，10）B ．（5，6）C ．（10，12）D ．（20，24） 【答案】C【解析】由,,a b c 互不相等，结合图象可知：这三个数分别在区间（0,1），（1,10），（10,12）上，不妨设(0,1),(1,10),(10,12)a b c ∈∈∈，由()()f a f b =得lg lg 0,a b +=即lg 0ab =，所以1ab =，所以()10,12abc ∈，故选C ．【总结升华】考查利用图象求解的能力和对数的运算，考查数形结合的思想方法． 类型三：综合问题例6．已知定义域为R 的函数12()2x x bf x a+-+=+是奇函数。
高一数学知识点梳理人教版
高一数学知识点梳理人教版数学是一门抽象而又实用的学科，对于高中生来说，数学的学习显得尤为重要。
本文将从人教版高一数学教材中梳理一些重要的知识点，帮助同学们更好地掌握数学。
一、函数与方程1. 一次函数：y=kx+b，其中k表示斜率，b表示截距。
掌握如何根据函数图像确定其函数关系式。
2. 二次函数：y=ax²+bx+c，其中a表示开口方向和开口大小，b 表示对称轴的位置，c表示平移。
要能够分析二次函数的图像特点，如顶点、对称轴等。
3. 指数与对数：掌握指数的运算规则，如幂的乘方、除方和零次幂。
对于对数，要理解对数的定义、性质和运算法则。
二、三角函数1. 基本概念：理解角度与弧度的转换关系，熟练掌握常用角的正弦、余弦和正切值。
2. 三角函数的图像：能够准确画出正弦、余弦和正切函数的图像，分析它们的周期和对称性。
3. 三角函数的性质：了解三角函数的周期性、奇偶性和单调性等性质，能够应用这些性质进行问题求解。
三、数列与数列的极限1. 数列的定义：理解数列的概念，知道如何写出数列的通项公式，并且能够计算数列中的任意项。
2. 等差数列与等比数列：掌握等差数列和等比数列的性质，能够求出等差数列或等比数列的前n项和。
3. 数列的极限：理解数列极限的定义，掌握收敛与发散的判定准则，能够求出数列的极限值。
四、三角方程与三角恒等式1. 三角方程的解法：掌握解三角方程的方法，如换元、化简等，能够解出常见的三角方程。
2. 三角恒等式：了解三角恒等式的基本形式，如和差角公式、倍角公式等。
能够灵活运用恒等式进行计算与证明。
五、几何1. 二维几何：熟练掌握平面图形的性质，在解题时能够巧妙地利用平面几何的知识。
2. 三维几何：了解空间几何的基本概念，理解平行关系、垂直关系和距离的计算方法。
3. 向量与坐标：掌握向量的概念和运算法则，熟练使用向量进行计算与证明。
了解坐标系的构建与应用。
六、概率与统计1. 概率的基本概念：了解事件、随机事件和样本空间的概念，掌握频率和概率之间的关系。
人教版高中数学必修一-第二章-基本初等函数知识点总结
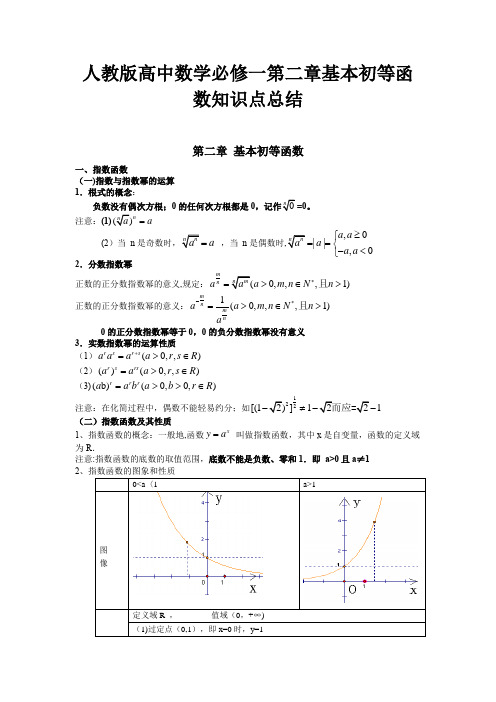
人教版高中数学必修一第二章基本初等函数知识点总结第二章 基本初等函数一、指数函数（一)指数与指数幂的运算 1．根式的概念：负数没有偶次方根；0的任何次方根都是0=0。
注意：(1)na =(2）当 n a = ，当 n 是偶数时,0||,0a a a a a ≥⎧==⎨-<⎩2．分数指数幂正数的正分数指数幂的意义,规定：0,,,1)m na a m n N n *=>∈>且正数的正分数指数幂的意义：_1(0,,,1)m nm naa m n N n a*=>∈>且0的正分数指数幂等于0，0的负分数指数幂没有意义 3．实数指数幂的运算性质 （1）(0,,)rsr s a a aa r s R +=>∈（2）()(0,,)r s rsa a a r s R =>∈ （3)(b)(0,0,)rrra ab a b r R =>>∈注意：在化简过程中，偶数不能轻易约分；如122[(1]11≠ （二）指数函数及其性质1、指数函数的概念：一般地,函数xy a = 叫做指数函数，其中x 是自变量，函数的定义域为R ．注意:指数函数的底数的取值范围，底数不能是负数、零和1．即 a>0且a ≠1 2a>1注意： 指数增长模型：y=N （1+p)指数型函数： y=ka 3 考点：(1)a b =N, 当b>0时，a,N 在1的同侧;当b 〈0时，a,N 在1的 异侧.（2）指数函数的单调性由底数决定的，底数不明确的时候要进行讨论。
掌握利用单调性比较幂的大小，同底找对应的指数函数,底数不同指数也不同插进1(=a 0）进行传递或者利用（1）的知识。
（3）求指数型函数的定义域可将底数去掉只看指数的式子，值域求法用单调性. （4)分辨不同底的指数函数图象利用a 1=a ，用x=1去截图象得到对应的底数。
(5）指数型函数：y=N （1+p)x 简写：y=ka x 二、对数函数 （一)对数1．对数的概念：一般地，如果x a N = ,那么数x 叫做以a 为底N 的对数，记作:log a x N = （ a - 底数， N — 真数，log a N — 对数式）说明：1。
最新人教版高中数学必修1第二章《指数函数和对数函数》知识搜索与探究归纳
2—6 指数函数和对数函数自助式复习板块知识搜索一、指数和对数 1.指数 (1)根式①根式的定义:一般地，如果x n=a ，那么x 叫做a 的n 次方根，其中n 为大于1的整数，n a 叫做根式，这里n 叫做根指数，a 叫做被开方数. ②根式的性质:(ⅰ)当n 为奇数时，有n n a = ; 当n 为偶数时，有n n a =|a |=⎩⎨⎧<-≥;0,,0,a a a a(ⅱ)负数没有偶次方根; (ⅲ)零的任何次方根为零. (2)幂的有关概念①正指数幂:)N (...*∈⋅⋅⋅=n a a a a n n个; ②零指数幂:a 0=1(a ≠0); ③负整数指数幂:a -p=p a1 (a ≠0,p ∈N *); ④正分数指数幂: nm a = (a >0,m,n ∈N *且n >1) ; ⑤负分数指数幂: nm nm aa1=(a >0，m,n ∈N *且n >1);⑥0的正分数指数幂为0，而0的负分数指数幂无意义. (3)有理数幂的性质 ①sr sraa a += (a >0,r,s ∈Q );②rs s r a a =)( (a >0,r,s ∈Q ); ③rrr b a ab =)( (a >0,b >0,r ∈Q ).答案：(1)a (2)n a m2.对数(1)对数的概念:如果a b=N(a >0,a ≠1),那么幂指数b 叫做以a 为底数N 的对数，记作 ，其中a 叫做底数，N 叫做 .(2)积、商、幂、方根的对数(M ，N 都是正数，a >0，且a ≠1,n ≠0). ①)(log N M a ⋅= ;②NMalog = ; ③n a M log = ;(3)对数的换底公式及对数恒等式(供选用). ①Na alog = (对数恒等式);②n a a log = ; ③aNN b b a log log log =(换底公式);④ab b a log 1log =;⑤n a a nN N log log =.答案：(1) N a log 真数 (2)①M a log +N a log ②M a log -N a log ③n M a log （3）①N ②n （4）二、指数函数和对数函数1.定义:函数y =a x叫做指数函数，它的 ，即y = 叫做对数函数(其中a >0，且a ≠1).答案：反函数 x a log2.性质:答案：（1）增 ［1,+∞) (0,1) 减 （0，1］ （1，+∞）（2）增 ［0，+∞） （-∞,0） 减 （-∞,0］ （0，+∞）3.画指数函数y =a x的图象，应抓住三个关键点:(1,a ),(0,1),(-1,a1).熟记指数函数y =10x ,y =(101)x ,y =2x和y = (21)x 在同一坐标系中的相对位置以及与底数的关系. 4.画对数函数y =log a x 的图象，应抓住三个关键点:(a ,1)，(1,0),( a1，-1).熟记对数函数y =log 2x ,x y 21log =,y =lg x 和x y 101log =在同一坐标系中的相对位置以及与底数的关系.探究归纳 要点1指数、对数的运算.【例1】 计算:(1)433333391624337+--; （2）;)3001()32(10])2[(])37(2[0625.05.013432041----+-⨯⨯--－）（（3）;25lg 50lg 2lg )2(lg 2+⋅+（4）);3log 3(log )2log 2(log 8493+⋅+（5）若,24log ,18log n m a a ==试用m 、n 表示5.1log a解析:在具体解题时应注意到要准确运用运算法则，正确地选择运算方式，熟练地进行各项运算.同时还要注意常用计算方法的应用，避免出现计算上的错误或多走弯路. （1）原式＝413131231331)33()3(32)23(337⨯+⨯⨯-⨯⨯-⨯-.03323)3(3322333731313134323131=+⨯-=+⨯⨯-⨯⨯-⨯=（2）原式＝21242414)103(3210)2()12(])5.0[(⨯--+-⨯⨯---.4220642310)32(102)21(61-=+-=-++-=- （3）原式＝2225lg ]52[lg(2lg )2(lg +⨯⋅+.210lg 25lg 22lg 25lg 2)5lg 2(lg 2lg 25lg 25lg 2lg 2)2(lg 25lg 2)5lg 2(lg 2lg )2(lg 22==+=++=+⋅+=+++=（4）原式＝)8lg 3lg 4lg 3lg )(9lg 2lg 3lg 2lg (++ .452lg 63lg 53lg 22lg 3)2lg 33lg 2lg 23lg )(3lg 22lg 3lg 2lg (=⋅=++= （5）⎩⎨⎧=+=+,3lg 2lg 3,3lg 22lg n m a aa a).34(51)2(512lg 3lg 5.1log ).3(513lg ),2(512lg n m m n n m m n a a a a a -=-=-=∴⎪⎪⎩⎪⎪⎨⎧-=-∴＝可以求出 归纳与迁移1.化为质因数的幂的形式，化根式为分数指数幂，化负指数幂为正指数幂等是指数运算的常用方法.2.对数的运算法则的使用既可从左到右，也可从右到左，换底公式可变通为1log log log ,log log =⋅⋅=a cb b nmb c b a a m na . 3.方程思想、化归思想在指、对数式的互化及计算中起着重要的作用，要在解题时自觉地加以运用.要点2 指数、对数的大小比较. 【例2】 比较下列各组数的大小.(1)3121)109()54(与;(2)9.01.17.01.19.0log ,8.0log 与;(3)m>n 时, log m 4与log n 4.解析:(1)由于这两个数底数与指数均不相同,可以用21)109(或31)54(作为中间量.因为54 <109,所以54 <109,即21)54(<21)109(.又0<109<1,21>31,所以由指数函数的单调性有21)109(<31)109(.故21)54(<31)109(.(2)根据对数函数的性质, log 0.70.8>0, log 1.10.9<0, 又由对数和指数函数的单调性, log 0.70.8<log 0.70.7=1,1.1 0.9>1.10=1,故1.1 0.9>log 0.70.8>log 1.10.9. (3)当m>1>n >0时, log m 4>0, log n 4<0, 所以log m 4>log n 4.当1>m>n >0时,由log 4m>log 4n >0,得log m 4<log n 4; 当m>n >1时,由0>log 4m>log 4n ,得log m 4<log n 4. 归纳与迁移1.比较两个指数幂或对数值大小的方法: (1)分清是底数相同还是指数(真数)相同;(2)利用指数、对数函数的单调性或图象比较大小;(3)当底数、指数(真数)均不相同时,可通过中间量过渡处理.2.多个指数幂或对数值比较大小时,可对它们先进行0,1分类,然后在每一类中比较大小.要点3 指数、对数函数的图象特征及应用.【例3】 根据下面四个指数函数的图象,说出a 、b 、c 、d 的大小关系.解析:从函数的单调性中可判断出a 、b 大于1,c 、d 小于1,但a 、b 的大小关系就要用别的方法.最好的方法是从直线 x =1 与四个指数函数的图象交点的上下中得到答案.令x =1,则a x =a ,b x =b ,c x =c ,d x=d. 由图象可得0<c <d<1<a <b .归纳与迁移1.取x =1,即特殊值法是解本类型问题的一种常用 方法.2.指数函数在第一象限部分图象的规律: 底数按从上到下逐渐减小; 在对数函数中有一类似规律; 底数按从上到下逐渐增大.3.可用上述结论来比较底不同、指数相同的两个幂的大小或底不同、真数相同的两个对数值的大小. 要点4 指数、对数函数性质、图象及与其他知识的综合应用. 【例4】(经典回放)已知函数f (x )=a ·b x的图象过点A (4,41)和B (5，1).(1)求函数f (x )的解析式.(2)记a n =log 2f (n ),n 是正整数，S n 是数列{a n }的前n 项和，解关于n 的不等式a n S n ≤0.(3)对于(2)中的a n 与S n ，整数104是否为数列{a n S n }中的项？若是，则求出相应的项数；若不是，请说明理由.解析:(1)由41=a ·b 4,1=a ·b 5,得b =4，a =10241, 故f (x ) =10241·4x.(2)由题意a n =log 2(10241·4n)=2n -10,S n =2n (a 1+a n )=n (n -9),a n S n =2n (n -5)(n -9),由a n S n ≤0，可得(n -5)(n -9)≤0,即5≤n ≤9.故n =5,6,7,8,9.(3)∵a 1S 1=64,a 2S 2=84,a 3S 3=72,a 4S 4=40.当5≤n ≤9时，a n S n ≤0;当10≤n ≤22时，a n S n ≤a 22S 22=9724<104;当n ≥23时，a n S n ≥a 23S 23=11 592>104.因此，104不是数列{a n S n }中的项.归纳与迁移 1.指数函数、对数函数是高考经常考查的内容,以指数、对数函数为载体,重点考查函数的单调性和奇偶性及函数图象的性质的运用.所以需加强函数思想、转化思想、数形结合思想的训练,要善于转化命题,要注意数形结合处理问题.2.对数与指数函数易于与其他知识相结合,是知识的交汇点,便于考查基础知识的能力,是高考命题的重点,因此应予以高度重视.。
高一数学人教版知识点梳理
高一数学人教版知识点梳理在高中数学学科中，数学人教版是一本具有权威性和广泛应用的教材。
在高一的数学学习中，学生们需要学习并掌握人教版数学中的多个知识点。
本文将对高一数学人教版知识点进行梳理，以帮助学生们更好地理解和应用这些知识。
1. 函数与方程1.1. 函数的概念和性质：了解函数的定义、自变量、函数值等概念，并掌握函数的奇偶性、单调性等性质。
1.2. 一次函数和二次函数：学习和应用一次函数和二次函数的性质、图像、方程等知识。
1.3. 指数函数和对数函数：掌握指数函数和对数函数的定义、性质以及与指数和对数相关的运算规则。
1.4. 三角函数：熟悉正弦函数、余弦函数、正切函数以及它们的图像、性质和运算规则。
2. 数列与数学归纳法2.1. 数列的概念和性质：了解数列的定义、通项公式、前n项和等概念，并能应用数列的性质解决实际问题。
2.2. 常见数列：学习和应用等差数列、等比数列、斐波那契数列等常见数列的性质和求和公式。
3. 平面解析几何3.1. 坐标系和平面方程：熟悉二维坐标系和坐标变换，学习平面直角坐标系和极坐标系的方程表示方法，并能根据方程判断图形和求解交点等问题。
3.2. 直线和圆：了解直线的斜率和方程、圆的方程及其性质，并能解决直线与直线、直线与圆、圆与圆的交点问题。
3.3. 曲线的方程：掌握抛物线、椭圆和双曲线的方程表示及其性质。
4. 解析几何与向量4.1. 向量的概念和运算：了解向量的定义、模长、方向以及加法、减法等运算规则，并能应用向量解决平面几何问题。
4.2. 平面向量的坐标表示：学习平面向量的坐标表示方法，掌握向量的数量积和向量积，能解决向量的垂直、平行、共线问题。
4.3. 位置向量与中点公式：熟悉位置向量的概念和性质，学习中点公式及其推广应用。
5. 三角函数的扩展与应用5.1. 三角函数的扩展：了解三角函数的定义域、值域、周期等性质，学习正弦、余弦、正切函数的图像和性质。
5.2. 三角函数的运算：学习和应用三角函数的和差化积、倍角公式、半角公式等运算规则。
人教版高中数学【必修一】[知识点整理及重点题型梳理]_指数函数、对数函数、幂函数综合_提高
![人教版高中数学【必修一】[知识点整理及重点题型梳理]_指数函数、对数函数、幂函数综合_提高](https://360docs-1393072327.cos.ap-beijing.myqcloud.com/f8e49588011ca300a7c390b2.webp)
人教版高中数学必修一知识点梳理重点题型(常考知识点)巩固练习指数函数、对数函数、哥函数综合【学习目标】1.理解有理指数哥的含义，掌握哥的运算.2.理解指数函数的概念和意义，理解指数函数的单调性与特殊点.3.理解对数的概念及其运算性质.4.重点理解指数函数、对数函数、哥函数的性质，熟练掌握指数、对数运算法则，明确算理，能对常见的指数型函数、对数型函数进行变形处理.5.会求以指数函数、对数函数、塞函数为载体的复合函数的定义域、单调性及值域等性质.6.知道指数函数y=a x与对数函数y=log a x互为反函数(a>0, awD.【知识框图】【要点梳理】要点一：指数及指数哥的运算1.根式的概念a的n次方根的定义：一般地，如果x n = a ,那么x叫做a的n次方根，其中n >1,n^ N*当n为奇数时，正数的n次方根为正数，负数的n次方根是负数，表示为V a ；当n为偶数时，正数的n次方根有两个，这两个数互为相反数可以表示为±V a .负数没有偶次方根，0的任何次方根都是0.式子垢叫做根式，n叫做根指数，a叫做被开方数.2. n次方根的性质：「LT a, a 之0,31)当n为奇数时，v a = a ；当n为偶数时，a a = a = 4[-a,a <0;-n22) (n/a ) = a3.分数指数哥的意义：m1n = —ma 0,m, n N ,n 1a n要点诠释：0的正分数指数哥等于 0,负分数指数哥没有意义. 4 .有理数指数哥的运算性质：a 0,b 0,r,s Qr s r sr 、srsrr r(1) a a =a(2) (a ) =a (3) (ab) =a b要点二：指数函数及其性质1.指数函数概念一般地，函数y =ax(a A0,且a =1 )叫做指数函数，其中 x 是自变量，函数的定义域为 R.2.指数函数函数性质：ma n = n /O m (a >0,m,n = N,n >1)； a1.对数的定义(1)若a x = N(a >0,且a =1),则x叫做以a为底N的对数，记作x =log a N ,其中a叫做底数,N叫做真数.(2)负数和零没有对数.(3)对数式与指数式的互化：x=log a Nu a x = N(a A0,a #1,N A0).2.几个重要的对数恒等式log a1=0, log a a =1, log a a b=b.3.常用对数与自然对数常用对数：lg N ,即iog10 N ；自然对数：lnN,即log e N (其中e = 2.71828…).4.对数的运算性质如果a >0, a#1,M >0,N >0,那么①加法：log a M log a N =log a(MN )②减法：log a M -log a N ^log a MN③数乘：nlog a M =log a M n(n R)④a log a N =N⑤log.b M n =nlog a M (b = 0,n R) a b⑥换底公式：log a N =l0gb N (b>0,且b#1) log b a要点四：对数函数及其性质1.对数函数定义一般地，函数y =log a x(a >0,且a 01 )叫做对数函数，其中x是自变量，函数的定义域(0,+“ ). 2.对数函数性质：1.反函数的概念设函数y = f (x)的定义域为A，值域为C ,从式子y = f (x)中解出x ,得式子x =平(y).如果对于y在C中的任何一个值，通过式子x=3(y),x在A中都有唯一确定的值和它对应，那么式子x=^(y)表示x是y的函数，函数x =?(y)叫做函数y = f (x)的反函数，记作x= f"( y),习惯上改写成y = f 0x).2.反函数的性质(1)原函数y = f(x)与反函数y = f」(x)的图象关于直线y = x对称.(2)函数y = f (x)的定义域、值域分别是其反函数y= f」(x)的值域、定义域.(3)若P(a,b)在原函数y = f(x)的图象上，则P'(b,a)在反函数y=f"(x)的图象上.(4)一般地，函数y = f (x)要有反函数则它必须为单调函数.要点六：哥函数1 .备函数概念形如y =x a(a w R)的函数，叫做哥函数，其中 a 为常数.2 .募函数的性质(1)图象分布：哥函数图象分布在第一、二、三象限，第四 象限无图象.募函数是偶函数时，图象分布在第一、二象限(图象 关于y 轴对称)；是奇函数时，图象分布在第一、三象限(图象关 于原点对称)；是非奇非偶函数时，图象只分布在第一象限.(2)过定点：所有的哥函数在(0, ~)都有定义，并且图象都通过点(1,1).(3)单调性：如果 a >0 ,则募函数的图象过原点，并且在 [0, +=)上为增函数.如果 0 <0,则募函数的图象在(0, +8)上为减函数，在第一象限内，图象无限接近 x 轴与y 轴.(4)奇偶性：当a 为奇数时，哥函数为奇函数，当 ”为偶数时,募函数为偶函数.当 a =9 (其中Pq_qp,q 互质，p 和q w Z ),若p 为奇数q 为奇数时，则y=x p是奇函数，若p 为奇数q 为偶数时，则y = x pq是偶函数，若p 为偶数q 为奇数时，则y=x p是非奇非偶函数.(5)图象特征：哥函数 y =xa, x w (0,十无)，当a >1时，若0<x<1,其图象在直线 y = x 下方，若x >1 ,其图象在直线y =x 上方，当a <1时，若0cx<1,其图象在直线y = x 上方，若x>1 ,其图 象在直线y=x 下方.【典型例题】类型一：指数、对数运算 例1 .计算(1)10g2^78+log 212—；10g 242；(2) lg 32+lg 35+3lg 2lg 5；o 21g52+—lg8 +lg51g 20 + lg 2 2； (4) 7lg20 3【思路点拨】运算时尽量把根式转化为分数指数骞，而小数也要化为分数为好.(1) -1; (2) 1 ; (3) 3; (4) 14.7 411、1 1 )用3 12不76「10g2H 2卜log 22(2)原式= (lg2+lg5 )Qg 2 2—lg 21g5 +lg 2 5 )+3lg 21g5= lg10 1(lg5+lg2 f —3lg 21g 51+31g 21g 5 =1-31g 21g5 +31g 21g5=1(3) (1 )原式=log 22 _(3)原式二21g5 21g2 1g5 1 1g2 1g 2=2 1g5 1g2 1g5 1g2(1g2 1g5)=2+ 1g5 +1g 2 =3;1 1g07(4)令x = 71g20J1 I ,两边取常用对数得21 lg0.71gx=1g 71g20|=(1+1g2 )1g7 十(1g7 -1)(-1g2)「⑶」= 1g7 1g 21g7 — 1g 21g7 1g 2=1g141g0.7, x =14，即71g201- i =14.2【总结升华】这是一组很基本的对数运算的练习题，虽然在考试中这些运算要求并不高，但是数式运算是学习数学的基本功，通过这样的运算练习熟练掌握运算公式、法则，以及学习数式变换的各种技巧. 举一反三：【变式1】210g 510+1og5 0.25 =( )A. 0B. 1C. 2D. 4【答案】C2 一一一一______________________ ___ ___ 一一一【解析】210g 5 10 + 1og5 0.25 = 1og510 + 1og5 0.25 = 1og 5(100 父0,25) = 1og5 25 =2 .【变式2】(1) (1g2)2+1g2 Jg50+1g25; (2) (1og3 2 + 1og9 2) <1og 4 3+ 1og g3).5【答案】(1) 2; (2)-.4【解析】(1)原式=(1g 2)2+(1+1g5)1g 2 + 1g5 2 =(1g 2 + 1g5+1)1g 2 + 21g5=(1+1)1g 2+21g5 =2(1g2+1g5) =2；1g 2 1g 2、,1g3 1g3、,1g 2 1g 2、, 1g3 1g3、(2)原式=(-^—) (-^―) =(-^— +-^-) (-^—十—^—)1g3 1g9 1g 4 1g8 1g3 21g3 21g 2 31g 231g 2 51g 3 521g 3 61g 2 4类型二：指数函数、对数函数、哥函数的图象与性质 例 2.设偶函数 f (x)满足 f (x) =x3—8(x 至 0),则{x| f (x —2) >0}=()A. {x|x <—2或 x >4}B. {x|x <0M £X >4}C. {x|x<0或x >6}D. {x|x 〈-减x >4}【答案】B【解析】'；f (x) =x 3 —8(x2 0)且f (x)是偶函数.3x 3 -8,x ,0, f(x) = 3 -x -8,x :: 0,x -2 _0,x -2 <0,3 或W3x -2 -8 0- x -2 -8 0x -2 x ：二2,\ i 或《x 4, x 二 0.解得x A 4或x < 0,故选B .【总结升华】考查解不等式组及函数解析式，考查函数性质的综合运用. 举一反三：3x1,x < 0, _【变式1】已知函数f(x)=4, ,若f (x 0) >3,则x 0的取值范围是().log 2x,x 0,B. x0<0 或 x 0>8C. 0 <x 0 <8D. x 0<0 或 0<x 0<8J_x 0 _ 0, _L x 0 0,W 或W ,所以x 0 >8,故选A.x 0 1 1 log 2 x 10g 2 8log 2 x, x 0,例3.设函数f(x)=$1ogi (_x )x <0若f (a) > f(—a)，则实数a 的取值范围是(),A.(-1,0 )1J (0,1)B. L ,-1)U(1*)C. (-1,0 )U(1, y )D, (-°0,T)U(0,1)【答案】C【解析】解法一：①若 a >0,则—a <0 ,1 ，, 1一 10g 2 a > log 1 a ,得 10g 2aA log 2—，得 a > 一，解得 a >1.A. x 0 >8【解析】依题意[%；0,或[% >0,3x0 1 3log 2 x 0②若a <0,则-a > 0 ,，log i (―a) >log2(—a),，log2(——)>log2(-a)2 a解得a三"1,1由①②可知a e ।1,0 (J 1, •二解法二：特殊值验证令a =2, f(2) -log2 2 =1,f(—2) = —1 ,满足f (a) > f (-a),故排除A、D.令a = -2, f(—2) = —1 , f(2)=1不满足f (a)> f(-a),故排除B.【总结升华】本题考查了分段函数的性质、分类思想的应用.【哥指对函数综合377495例1］2例4.函数y=log1(x —6x+8)的单倜递增区间是( )3A . (3, +00)B .(_ oo, 3) C. (4, +8) D. (―00, 2)【思路点拨】这是一个内层函数是二次函数，外层函数是对数函数的复合函数，其单调性由这两个函数的单调性共同决定，即同增异减”.【答案】D【解析】函数y =log1 (x2 -6x+8)是由y = l0g l u,u =x2 -6x+8复合而成的，y=log1u是减函 3 3 3 数，u=x2-6x+8在(-g,3)上单调递增，在(3,+s)上单调递减，由对数函数的真数必须大于零，即x2 -6x+8>0,解得乂>4或乂<2,所以原函数的单调递增区间是(-°0,2),故选D.例5. (2016上海模拟)已知函数f(x)=a x (a>0, aw1)在区间［—1, 2］上的最大值为8,最小值为m.若函数g(x) =(3 -10m) J x是单调增函数，则a=.【思路点拨】根据题意求出m的取值范围，再讨论a的值，求出f (x)的单调性，从而求出a的值.【答案】18【解析】根据题意，得3- 10m> 0,- 3解得m <—；10当a>1时，函数f(x)=a x 在区间［―1, 2］上单调递增，最大值为 a 2=8,解得a = 242,最小值为 、2 3— > —,不合题息，舍去;4 1011 当1>a>0时，函数f(x)=a 在区间［—1, 2］上单调递减，最大值为 a =8,解得a =—,最小值8一 213为m = a =— <—,满足题息；64 10… 1 综上，a = 一.8故答案为：1.8【总结升华】本题主要考查指数函数的图象与性质的应用问题，通过讨论对数函数的底数确定函数的 单调性是解决本题的关键.举一反三：【变式1】已知f(x)=2|x二|,该函数在区间［a, b ］上的值域为［1,足该条件的实数 a 、b 所形成的实数对为点 P (a, b),则由点P 构成 fA 组成的图形为( )A .线段AD B,线段AB口C.线段AD 与线段CDD.线段AB 与BC丁'''(【思路点拨】由指数函数的图象和性质，我们易构造出满足条件~天•］f(x)=2|x 口在闭区间［a, b ］上的值域为［1, 2］的不等式组，画出函数的与答案进行比照，即可得到答案.【解析】•.・函数f (x) =2|xj 的图象为开口方向朝上，以 x=1为对称轴的曲线，如图. 当x=1时，函数取最小值1, 若 y =2|xm = 2 ,贝U x=0,或 x=1而函数y=2|x=在闭区间［a, b ］上的值域为a = 0则a 或2.2 2］,记满的点集图象后1MbM 20 ：二a< 1b =2则有序实数对(a, b)在坐标平面内所对应点【解析】由a,b,c 互不相等，结合图象可知：这三个数分别在区间(设 aw(0,1),bw(1,10),cw(10,12),由 f(a)= f(b)得 lga+lgb=0,即 lgab = 0,所以 ab=1 ,所以 abcw(10,12),故选 C.【总结升华】考查利用图象求解的能力和对数的运算，考查数形结合的思想方法. 类型三：综合问题(I)求a, b 的值;(n)若对任意的t 三R,不等式f (2t 2—t) + f (t 2—t —k) < 0恒成立，求k 的取值范围【思路点拨】(i)利用奇函数的定义去解。
高中数学必修一指数函数对数函数知识点
高中数学必修一指数函数对数函数知识点高中数学必修一中，指数函数和对数函数是重要的知识点。
指数函数是一种以指数为自变量的函数，形式为y = a^x，其中a为底数，x为指数。
而对数函数是指数函数的逆运算，形式为y = loga(x)，其中a为底数，x为真数。
以下是关于指数函数和对数函数的具体知识点。
一、指数函数的图像和性质1.指数函数的基本形式：-y=a^x，其中a>0且a≠12.指数函数的基本性质：-当0<a<1时，指数函数呈现递减的图像；-当a>1时，指数函数呈现递增的图像；-当a=1时，指数函数为常数函数y=1二、对数函数的图像和性质1.对数函数的基本形式：- y = loga(x)，其中a > 0且a≠12.对数函数的基本性质：- 对数函数与指数函数互为反函数，即loga(a^x) = x，a^loga(x) = x；-对数函数的图像关于直线y=x对称；-对数函数的定义域为正实数集，值域为实数集。
三、指数函数和对数函数的运算性质1.指数函数的运算性质：-a^x*a^y=a^(x+y)；- (a^x)^y = a^(xy)；- (ab)^x = a^x * b^x；-a^0=1，其中a≠0。
2.对数函数的运算性质：- loga(xy) = loga(x) + loga(y)；- loga(x^y) = y * loga(x)；- loga(x/y) = loga(x) - loga(y)；- loga(1) = 0，其中a≠0。
四、指数函数和对数函数的应用1.指数函数在生活中的应用：-经济增长模型中的应用；-指数衰减与物质的半衰期计算；-大自然中的指数增长现象。
2.对数函数在生活中的应用：-pH值的计算；-放大器的功率增益计算；-数字音乐的音量计算。
综上所述，指数函数和对数函数是高中数学必修一中的重要知识点。
掌握了指数函数和对数函数的基本形式、性质以及运算规律，能够理解其图像特征和在实际问题中的应用。
人教版高中数学必修一知识点和重难点
人教版高中数学必修一————各章节知识点与重难点第一章集合与函数概念1.1 集合1.1.1集合的含义与表示【知识要点】1、集合的含义一般地，我们把研究对象统称为元素，把一些元素组成的总体叫做集合。
2、集合的中元素的三个特性（1）元素的确定性；（2）元素的互异性；（3）元素的无序性2、“属于”的概念我们通常用大写的拉丁字母A,B,C, ……表示集合，用小写拉丁字母a,b,c, ……表示元素如：如果a是集合A的元素，就说a属于集合A 记作a∈A，如果a不属于集合A 记作a∉A 3、常用数集及其记法非负整数集（即自然数集）记作：N；正整数集记作：N*或N+ ；整数集记作：Z；有理数集记作：Q；实数集记作：R4、集合的表示法（1）列举法：把集合中的元素一一列举出来，然后用一个大括号括上。
（2）描述法：用集合所含元素的公共特征表示集合的方法称为描述法。
①语言描述法：例：{不是直角三角形的三角形}②数学式子描述法：例：不等式x-3>2的解集是{x∈R| x-3>2}或{x| x-3>2}（3）图示法（Venn图）1.1.2 集合间的基本关系【知识要点】1、“包含”关系——子集一般地，对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，我们就说这两个集合有包含关系，称集合A为集合B的子集，记作A⊆B2、“相等”关系如果集合A的任何一个元素都是集合B的元素，同时,集合B的任何一个元素都是集合A的元素，我们就说集合A等于集合B，即：A=B A B B A且⇔⊆⊆3、真子集如果A⊆B,且A≠B那就说集合A是集合B的真子集，记作A⊂B(或B⊃A)4、空集不含任何元素的集合叫做空集，记为Φ规定: 空集是任何集合的子集，空集是任何非空集合的真子集.1.1.3 集合的基本运算【知识要点】1、交集的定义一般地，由所有属于A且属于B的元素所组成的集合,叫做A,B的交集．记作A∩B(读作“A 交B”)，即A∩B={x| x∈A，且x∈B}．2、并集的定义一般地，由所有属于集合A或属于集合B的元素所组成的集合，叫做A,B的并集。
人教版高一数学必修一精选知识点归纳5篇
人教版高一数学必修一精选知识点归纳5篇人教版高一数学必修一知识点1幂函数定义：形如y=x^a(a为常数)的函数，即以底数为自变量幂为因变量，指数为常量的函数称为幂函数。
定义域和值域：当a为不同的数值时，幂函数的定义域的不同情况如下：如果a为任意实数，则函数的定义域为大于0的所有实数;如果a 为负数，则x肯定不能为0，不过这时函数的定义域还必须根[据q的奇偶性来确定，即如果同时q为偶数，则x不能小于0，这时函数的定义域为大于0的所有实数;如果同时q为奇数，则函数的定义域为不等于0的所有实数。
当x为不同的数值时，幂函数的值域的不同情况如下：在x大于0时，函数的值域总是大于0的实数。
在x小于0时，则只有同时q为奇数，函数的值域为非零的实数。
而只有a为正数，0才进入函数的值域幂函数性质：对于a的取值为非零有理数，有必要分成几种情况来讨论各自的特性：首先我们知道如果a=p/q，q和p都是整数，则x^(p/q)=q 次根号(x的p次方)，如果q是奇数，函数的定义域是R，如果q是偶数，函数的定义域是[0，+∞)。
当指数n是负整数时，设a=-k，则x=1/(x^k)，显然x≠0，函数的定义域是(-∞，0)∪(0，+∞).因此可以看到x所受到的限制****于两点，一是有可能作为分母而不能是0，一是有可能在偶数次的根号下而不能为负数，那么我们就可以知道：排除了为0与负数两种可能，即对于x0，则a可以是任意实数;排除了为0这种可能，即对于x排除了为负数这种可能，即对于x为大于且等于0的所有实数，a就不能是负数。
总结起来，就可以得到当a为不同的数值时，幂函数的定义域的不同情况如下：如果a为任意实数，则函数的定义域为大于0的所有实数;如果a为负数，则x肯定不能为0，不过这时函数的定义域还必须根据q的奇偶性来确定，即如果同时q为偶数，则x不能小于0，这时函数的定义域为大于0的所有实数;如果同时q为奇数，则函数的定义域为不等于0的所有实数。
人教版高一数学必修一改版新教材重点知识总结——指数函数知识点总结
高中数学必修一重点知识总结指数函数部分1.指数函数和指数型函数的概念（1）函数x y a =（0a >且1a ≠）叫做指数函数。
其中，底数a 为常数，自变量x 在指数位置，定义域是R ，值域为()0,+∞。
【注意】幂函数：y x α=，自变量x 在底数位置，次数α为常数。
（2）形如x y ka b =+（0k ≠；0a >且1a ≠）的函数叫做指数型函数。
指数型函数是刻画指数增长或指数衰减变化规律的非常有用的函数模型。
2.指数函数图像3.指数函数图象的性质（1）图象都过()0,1点；定义域都为R ，值域都为()0,+∞。
（2）01a <<时在R 上单调递减;1a >时在R 上单调递增。
（3）当1a >时，底数越大，在y 轴右侧图象越靠近y 轴；当01a <<时，底数越小,在y 轴左侧图象越靠近y 轴。
4.指数函数的对称性（4）底数互为倒数的两个指数函数的图象关于y 轴对称。
即x y a =与1xy a ⎛⎫= ⎪⎝⎭图象关于于y 轴对称。
4.常见题型（1）根据指数函数解析式的特点（系数为1，次数只有一个x 等）求参数值。
（2）给几个指数函数的解析式找出它们分别对应的图象。
（3）根据几个指数函数的图象，判断它们底数的大小关系。
（4）根据指数函数恒过过定点（0,1）的性质，求指数型函数或相关复合函数中的参数值。
（5）构造指数函数后，利用指数函数的单调性比较两个形式复杂的实数的大小。
（6）求与指数函数复合后的函数的定义域、值域、单调区间、最值、奇偶性等。
（7）画出指数函数整体加绝对值、或是次数加绝对值后的函数图象，并结合图象的性质做题。
新教材 人教A版高中数学必修第一册 第四章 指数函数与对数函数 知识点考点汇总及解题方法规律提炼
第四章指数函数与对数函数4.1.1根式 (1)4.1.2指数幂及其运算 (4)4.2.1指数函数及其图象性质 (8)4.2.2指数函数的性质及其应用 (11)4.3.1对数的概念 (16)4.3.2对数的运算 (18)4.4.1对数函数及其图象 (22)4.4.2对数函数的性质及其应用 (26)4.4.3不同函数增长的差异 (30)4.5.1函数的零点与方程的解 (34)4.5.2用二分法求方程的近似解 (38)4.5.3函数模型的应用 (42)4.1.1根式要点整理1．根式的概念一般地，如果x n＝a，那么x叫做a的n次方根，其中n>1，且n∈N*. (1)当n是奇数时，正数的n次方根是一个正数，负数的n次方根是一个负数，这时，a的n次方根用符号na表示．(2)当n是偶数时，正数a的n次方根有两个，记为±na，负数没有偶次方根．(3)0的任何次方根都是0，记作n0＝0.式子na叫做根式，其中n(n>1，且n∈N*)叫做根指数，a叫做被开方数．2．根式的性质根据n次方根的意义，可以得到：(1)(na)n＝a.(2)当n是奇数时，na n＝a；当n是偶数时，na n＝|a|＝⎩⎨⎧a，a≥0，－a，a<0.温馨提示：(n a )n 中当n 为奇数时，a ∈R ；n 为偶数时，a ≥0，而(na n )中a ∈R .题型一根式的意义【典例1】 下列说法正确的个数是( )①16的4次方根是2；②416的运算结果是±2；③当n 为大于1的奇数时，na 对任意a ∈R 都有意义；④当n 为大于1的偶数时，na 只有当a ≥0时才有意义．A ．1B ．2C ．3D ．4(2)已知m 10＝2，则m 等于( ) A.102B ．－102 C.210D ．±102[思路导引] 利用n 次方根的概念求解．[解析] (1)①16的4次方根应是±2；②416＝2，所以正确的应为③④. (2)∵m 10＝2，∴m 是2的10次方根． ∴m ＝±102.[答案] (1)B (2)Dn (n >1)次方根的个数及符号的确定(1)正数的偶次方根有两个且互为相反数，任意实数的奇次方根只有一个． (2)根式na 的符号由根指数n 的奇偶性及被开方数a 的符号共同确定： ①当n 为偶数时，n a 为非负实数；②当n 为奇数时，na 的符号与a 的符号一致． 题型二简单根式的化简与求值【典例2】化简下列各式：(1) 5(－2)5；(2)4(－10)4；(3)4(－9)2；(4) 4(a－b)4.[思路导引] 利用na n的性质进行化简．[解] (1) 5(－2)5＝－2.(2) 4(－10)4＝|－10|＝10.(3) 4(－9)2＝434＝3.(4) 4(a－b)4＝|a－b|＝⎩⎨⎧a－b(a≥b)，b－a(a<b).根式的化简求值注意以下2点(1)首先要分清根式为奇次根式还是偶次根式，然后运用根式的性质进行化简或求值．(2)开偶次方时，先用绝对值表示开方的结果，再去掉绝对值符号化简，化简时要结合条件或分类讨论．题型三有限制条件的根式化简【典例3】设x∈[1,2]，化简(4x－1)4＋6(x2－4x＋4)3.[思路导引] 借助根式的性质去掉根号并化简．[解] (4x－1)4＋6(x2－4x＋4)3＝(4x－1)4＋6(x－2)6∵1≤x≤2，∴x－1≥0，x－2≤0.∴原式＝(x－1)＋|x－2|＝(x－1)＋(2－x)＝1.[变式] 若本例中的“x∈[1,2]”改为“x∈[2,3]”，其他条件不变，化简求值．[解] (4(x－1))4＋6(x2－4x＋4)3＝(4x－1)4＋6(x－2)6∵2≤x≤3，∴x－1>0，x－2≥0，∴原式＝(x－1)＋|x－2|＝x－1＋x－2＝2x－3.有限制条件根式的化简策略(1)有限制条件根式的化简问题，是指被开方数或被开方的表达式可以通过配方、拆分等方式进行化简．(2)有限制条件根式的化简经常用到配方的方法．当根指数为偶数时，在利用公式化简时，要考虑被开方数或被开方的表达式的正负．4.1.2指数幂及其运算要点整理1．分数指数幂的意义温馨提示：(1)分数指数幂a mn不可以理解为mn个a相乘．(2)对于正分数指数幂，规定其底数是正数．2．有理数指数幂的运算性质(1)a r a s＝a r＋s(a>0，r，s∈Q)；(2)(a r)s＝a rs(a>0，r，s∈Q)；(3)(ab)r＝a r b r(a>0，b>0，r∈Q)．3．无理数指数幂一般地，无理数指数幂a α(a >0，α是无理数)是一个确定的实数．有理数指数幂的运算性质同样适用于无理数指数幂．温馨提示：(1)对于无理指数幂，只需了解两点：①它是一个确定的实数；②它是有理数幂无限逼近的结果．(2)a －b ＝1ab (a >0，b 是正无理数)．(3)定义了无理数指数幂后，幂的指数由原来的有理数范围扩充到了实数范围．题型一根式与分数指数幂的互化【典例1】 用分数指数幂的形式表示下列各式(式中字母都是正数)： (1)13a 2；(2)a 3·3a 2；(3)3b －a 2.根式与分数指数幂互化的规律(2)在具体计算时，通常会把根式转化成分数指数幂的形式，然后利用有理数指数幂的运算性质解题．题型二指数幂的运算【典例2】 计算：[思路导引] 利用指数幂的运算性质化简求值．利用指数幂的运算性质化简求值的方法(1)进行指数幂的运算时，一般化负指数为正指数，化根式为分数指数幂，化小数为分数，同时兼顾运算的顺序．(2)在明确根指数的奇偶(或具体次数)时，若能明确被开方数的符号，则可以对根式进行化简运算．题型三条件求值问题[变式] (1)若本例条件不变，则a2－a－2＝________.[答案] (1)±3 5 (2)－3 3解决条件求值问题的一般方法——整体代入法对于条件求值问题，一般先化简代数式，再将字母取值代入求值．但有时字母的取值不知道或不易求出，这时可将所求代数式恰当地变形，构造出与已知条件相同或相似的结构，从而通过“整体代入法”巧妙地求出代数式的值．利用“整体代入法”求值常用的变形公式如下(a>0，b>0)：4.2.1指数函数及其图象性质要点整理1．指数函数的定义一般地，函数y ＝a x (a >0，且a ≠1)叫做指数函数，其中x 是自变量，函数的定义域为R .温馨提示：指数函数解析式的3个特征： (1)底数a 为大于0且不等于1的常数． (2)自变量x 的位置在指数上，且x 的系数是1. (3)a x 的系数是1. 2．指数函数的图象和性质温馨提示：(1)底数a 与1的大小关系决定了指数函数图象的“升”与“降”．当a >1时，指数函数的图象是“上升”的；当0<a <1时，指数函数的图象是“下降”的．(2)指数函数y ＝a x(a >0且a ≠1)的图象恒过点(0,1)，(1，a )，⎝⎛⎭⎪⎫－1，1a ，只要确定了这三个点的坐标，即可快速地画出指数函数y ＝a x (a >0且a ≠1)的大致图象．题型一指数函数的概念 【典例1】 (1)下列函数：①y ＝2·3x ；②y ＝3x ＋1；③y ＝3x ；④y ＝x 3. 其中，指数函数的个数是( ) A ．0 B ．1 C ．2D ．3(2)函数y ＝(a －2)2a x 是指数函数，则( ) A ．a ＝1或a ＝3 B ．a ＝1 C ．a ＝3D ．a >0且a ≠1[思路导引] 形如“y ＝a x (a >0，且a ≠1)”的函数为指数函数．[解析] (1)形如“y ＝a x(a >0，且a ≠1)”的函数为指数函数，只有③符合，选B.(2)由指数函数的概念可知，⎩⎨⎧(a －2)2＝1，a >0，a ≠1，得a ＝3.[答案] (1)B (2)C判断一个函数是指数函数的方法(1)看形式：只需判断其解析式是否符合y ＝a x (a >0，且a ≠1)这一结构特征． (2)明特征：看是否具备指数函数解析式具有的三个特征．只要有一个特征不具备，则该函数不是指数函数．题型二指数函数的图象【典例2】 (1)函数f (x )＝a x －b 的图象如图所示，其中a ，b 为常数，则下列结论正确的是( )A ．a >1，b <0B ．a >1，b >0C ．0<a <1，b >0D ．0<a <1，b <0(2)函数y＝a x－3＋3(a>0，且a≠1)的图象过定点________．[解析] (1)从曲线的变化趋势，可以得到函数f(x)为减函数，从而有0<a<1；从曲线位置看，是由函数y＝a x(0<a<1)的图象向左平移|－b|个单位长度得到，所以－b>0，即b<0.(2)因为指数函数y＝a x(a>0，且a≠1)的图象过定点(0,1)，所以在函数y ＝a x－3＋3中，令x－3＝0，得x＝3，此时y＝1＋3＝4，即函数y＝a x－3＋3的图象过定点(3,4)．[答案] (1)D (2)(3,4)处理指数函数图象问题的3个策略(1)抓住特殊点：指数函数的图象过定点(0,1)，求指数型函数图象所过的定点时，只要令指数为0，求出对应的y的值，即可得函数图象所过的定点．(2)巧用图象变换：函数图象的平移变换(左右平移、上下平移)．(3)利用函数的奇偶性与单调性：奇偶性确定函数图象的对称情况，单调性决定函数图象的走势．题型三指数函数的定义域与值域【典例3】求下列函数的定义域和值域：[思路导引] 利用整体换元的方法求解．[解] (1)要使函数式有意义，则1－3x≥0，即3x≤1＝30，因为函数y＝3x在R上是增函数，所以x≤0，故函数y＝1－3x的定义域为(－∞，0]．因为x≤0，所以0<3x≤1，所以0≤1－3x<1，所以1－3x∈[0,1)，即函数y＝1－3x的值域为[0,1)．“y＝a f(x)”型函数定义域、值域的求法(1)定义域是使f(x)有意义的x的取值范围，即函数y＝a f(x)的定义域与y＝f(x)的定义域相同．(2)值域问题，应分以下两步求解：①由定义域求出u＝f(x)的值域；②利用指数函数y＝a u的单调性求得此函数的值域．4.2.2指数函数的性质及其应用要点整理1．指数函数值与1的大小关系(1)a>1时，当x>0时，y>1；当x<0时，0<y<1.(2)0<a<1时，当x>0时，0<y<1；当x<0时，y>1.2．对称关系函数y＝a－x与y＝a x的图象关于y轴对称．3．图象位置关系底数a的大小决定了图象相对位置的高低．(1)在y轴右侧，图象从上到下相应的底数由大变小，“底大图高”．作出直线x＝1，与图象的交点从上至下即为底数从大到小的排列顺序．(2)在y轴左侧，图象正好相反．如图所示的指数函数的底数的大小关系为0<d<c<1<b<a.题型一利用指数函数的单调性比较大小【典例1】比较下列各组数的大小：(1)0.7－0.3与0.7－0.4；(2)2.51.4与1.21.4；(3)1.90.4与0.92.4.[思路导引] (1)利用指数函数的单调性比较；(2)利用指数函数的图象比较；(3)借助中间量1进行比较．[解] (1)∵y＝0.7x在R上为减函数，又∵－0.3>－0.4，∴0.7－0.3<0.7－0.4.(2)在同一坐标系中作出函数y＝2.5x与y＝1.2x的图象，如图所示．由图象可知2.51.4>1.21.4.(3)∵1.90.4>1.90＝1，0．92.4<0.90＝1， ∴1.90.4>0.92.4.比较幂的大小的3种类型及方法(1)对于底数相同但指数不同的两个幂的大小的比较，可以利用指数函数的单调性来判断．(2)对于底数不同，指数相同的两个幂的大小比较，可利用指数函数的图象的变化规律来判断．(3)对于底数不同且指数不同的幂的大小的比较，则应通过中间值(如0或1)来比较．题型二解简单的指数不等式【典例2】 (1)解不等式：⎝ ⎛⎭⎪⎫123x －1≤2；(2)已知ax 2－3x ＋1<a x ＋6(a >0，且a ≠1)，求x 的取值范围．[思路导引] (1)化为同底的指数不等式，再利用单调性求解；(2)分a >1与0<a <1两种情况解不等式．[解] (1)∵2＝⎝ ⎛⎭⎪⎫12－1，∴原不等式可以转化为⎝ ⎛⎭⎪⎫123x －1≤⎝ ⎛⎭⎪⎫12－1.∵y ＝⎝ ⎛⎭⎪⎫12x 在R 上是减函数，∴3x －1≥－1，∴x ≥0. 故原不等式的解集是{x |x ≥0}． (2)分情况讨论：①当0<a <1时，函数f (x )＝a x (a >0，且a ≠1)在R 上是减函数， ∴x 2－3x ＋1>x ＋6，∴x 2－4x －5>0，解得x <－1或x >5； ②当a >1时，函数f (x )＝a x (a >0，且a ≠1)在R 上是增函数， ∴x 2－3x ＋1<x ＋6，∴x 2－4x －5<0，解得－1<x <5. 综上所述，当0<a <1时，x <－1或x >5； 当a >1时，－1<x <5.指数不等式的求解策略(1)形如a x >a y 的不等式：可借助y ＝a x 的单调性求解．如果a 的值不确定，需分0<a <1和a >1两种情况讨论．(2)形如a x >b 的不等式：注意将b 化为以a 为底的指数幂的形式，再借助y ＝a x 的单调性求解．题型三指数型函数的单调性【典例3】 已知函数f (x )＝⎝ ⎛⎭⎪⎫13x 2－2x.(1)判断函数f (x )的单调性； (2)求函数f (x )的值域．[思路导引] 由函数u ＝x 2－2x 和函数y ＝⎝ ⎛⎭⎪⎫13u 的单调性判断．[解] (1)令u ＝x 2－2x ，则原函数变为y ＝⎝ ⎛⎭⎪⎫13u .∵u ＝x 2－2x ＝(x －1)2－1在(－∞，1]上单调递减，在[1，＋∞)上单调递增，又∵y ＝⎝ ⎛⎭⎪⎫13u在(－∞，＋∞)上单调递减，∴y ＝⎝ ⎛⎭⎪⎫13x 2－2x在(－∞，1]上单调递增，在[1，＋∞)上单调递减．(2)∵u ＝x 2－2x ＝(x －1)2－1≥－1， ∴y ＝⎝ ⎛⎭⎪⎫13u，u ∈[－1，＋∞)，∴0<⎝ ⎛⎭⎪⎫13u ≤⎝ ⎛⎭⎪⎫13－1＝3，∴原函数的值域为(0,3]．[变式] 若本例“f (x )＝⎝ ⎛⎭⎪⎫13x 2－2x ”改为“f (x )＝2|2x －1|”，其他条件不变，如何求解？[解] (1)设u ＝|2x －1|，由函数y ＝2u 和u ＝|2x －1|的定义域为R ，故函数y ＝2|2x －1|的定义域为R .∵u ＝|2x －1|在⎝ ⎛⎦⎥⎤－∞，12上单调递减，⎝ ⎛⎭⎪⎫12，＋∞上单调递增，而y ＝2u 是增函数，∴y ＝2|2x －1|在⎝ ⎛⎦⎥⎤－∞，12上单调递减，在⎝ ⎛⎭⎪⎫12，＋∞上单调递增．(2)∵u ＝|2x －1|≥0，∴2u ≥1. ∴原函数的值域为[1，＋∞)．指数型函数单调性的解题技巧(1)关于指数型函数y ＝a f (x )(a >0，且a ≠1)的单调性由两点决定，一是底数a >1还是0<a <1；二是f (x )的单调性．它由两个函数y ＝a u ，u ＝f (x )复合而成．(2)求复合函数的单调区间，首先求出函数的定义域，然后把函数分解成y ＝f (u )，u ＝φ(x )，通过f (u )和φ(x )的单调性，利用“同增异减”的原则，求出y ＝f [φ(x )]的单调性，即若y ＝f (u )与u ＝φ(x )的单调性相同(同增或同减)，则y ＝f [φ(x )]为增函数，若y ＝f (u )与u ＝φ(x )的单调性相反(一增一减)，则y ＝f [φ(x )]为减函数．题型四指数函数的实际应用【典例4】 某林区2016年木材蓄积量为200万立方米，由于采取了封山育林、严禁采伐等措施，使木材蓄积量的年平均增长率能达到5%.若经过x 年后，该林区的木材蓄积量为y 万立方米，求y ＝f (x )的表达式，并写出此函数的定义域．[解] 现有木材的蓄积量为200万立方米，经过1年后木材的蓄积量为200＋200×5%＝200(1＋5%)；经过2年后木材的蓄积量为200(1＋5%)＋200(1＋5%)×5%＝200×(1＋5%)2万立方米；…经过x 年后木材的蓄积量为200×(1＋5%)x 万立方米． 故y ＝f (x )＝200×(1＋5%)x ，x ∈N *.解决指数函数应用题的流程(1)审题：理解题意，弄清楚关键字词和字母的意义，从题意中提取信息． (2)建模：据已知条件，列出指数函数的关系式． (3)解模：运用数学知识解决问题．(4)回归：还原为实际问题，归纳得出结论．4.3.1对数的概念要点整理 1．对数的定义一般地，如果a x ＝N (a >0，且a ≠1)，那么数x 叫做以a 为底N 的对数，记作x ＝log a N ，其中a 叫做对数的底数，N 叫做真数．2．常用对数与自然对数通常我们将以10为底的对数叫做常用对数，记为lg N .在科学技术中常使用以无理数e ＝2.71828…为底的对数，以e 为底的对数称为自然对数，并记为ln N .3．指数与对数的互化当a >0，a ≠1时，a x ＝N ⇔x ＝log a N . 4．对数的性质 (1)log a 1＝0； (2)log a a ＝1；(3)零和负数没有对数． 题型一指数式与对数式的互化【典例1】 将下列指数式化为对数式，对数式化为指数式： (1)3－2＝19；(2)⎝ ⎛⎭⎪⎫14－2＝16；(3)log 1327＝－3；(4)log x64＝－6.[思路导引] 借助a b ＝N ⇔b ＝log a N (a >0，且a ≠1)转化． [解] (1)∵3－2＝19，∴log 319＝－2.(2)∵⎝ ⎛⎭⎪⎫14－2＝16，∴log 1416＝－2.(3)∵log13 27＝－3，∴⎝⎛⎭⎪⎫13－3＝27.(4)∵logx64＝－6，∴(x)－6＝64.指数式与对数式互化的方法(1)将指数式化为对数式，只需要将幂作为真数，指数当成对数值，底数不变，写出对数式；(2)将对数式化为指数式，只需将真数作为幂，对数作为指数，底数不变，写出指数式．题型二对数的计算【典例2】求下列各式中的x的值：(1)log64x＝－23；(2)log x8＝6；(3)lg100＝x；(4)－lne2＝x.[思路导引] 把对数式化为指数式求解．求对数值的3个步骤(1)设出所求对数值．(2)把对数式转化为指数式．(3)解有关方程，求得结果．题型三对数的性质[思路导引] 首先利用对数的基本性质化“繁”为“简”，再求值． [解] (1)由log (2x 2－1)(3x 2＋2x －1)＝1得⎩⎨⎧3x 2＋2x －1＝2x 2－1，3x 2＋2x －1>0，2x 2－1>0且2x 2－1≠1，解得x ＝－2.(2)由log 2[log 3(log 4x )]＝0可得log 3(log 4x )＝1，故log 4x ＝3，所以x ＝43＝64.对数性质的应用要点(1)使用对数的性质时，有时需要将底数或真数进行变形后才能运用；对于多重对数符号的，可以先把内层视为整体，逐层使用对数的性质．(2)对于指数中含有对数值的式子进行化简，应充分考虑对数恒等式的应用．这就要求首先要牢记对数恒等式a log a N ＝N 及其格式．4.3.2对数的运算要点整理 1．对数运算性质如果a>0，且a≠1，M>0，N>0，那么： (1)log a (M·N)＝log a M ＋log a N ； (2)log a MN ＝log a M －log a N ；(3)log a M n ＝nlog a M(n ∈R )．温馨提示：对数的这三条运算性质，都要注意只有当式子中所有的对数都有意义时，等式才成立．例如，log2[(－3)·(－5)]＝log2(－3)＋log2(－5)是错误的．2．对数换底公式若c>0，且c≠1，则loga b＝logcblogca(a>0，且a≠1，b>0)．3．由换底公式推导的重要结论(1)logan b n＝logab.(2)logan b m＝mnlogab.(3)loga b·logba＝1.(4)loga b·logbc·logcd＝logad.题型一对数运算性质的应用【典例1】求下列各式的值：(1)log345－log35；(2)log24·log28；(3)lg14－2lg 73＋lg7－lg18；(4)lg52＋23lg8＋lg5·lg20＋(lg2)2.[思路导引] 解题关键是弄清各式与对数运算积、商、幂中的哪种形式对应．[解](1)log345－log35＝log3455＝log39＝log332＝2.(2)log24·log28＝log222·log223＝2×3＝6.(3)原式＝lg2＋lg7－2(lg7－lg3)＋lg7－(lg2＋lg9) ＝lg2＋lg7－2lg7＋2lg3＋lg7－lg2－2lg3＝0.(4)原式＝2lg5＋23lg23＋lg5·lg(22×5)＋(lg2)2＝2lg5＋2lg2＋lg5·(2lg2＋lg5)＋(lg2)2＝2(lg5＋lg2)＋2lg5·lg2＋(lg5)2＋(lg2)2＝2lg10＋(lg5)2＋2lg5·lg2＋(lg2)2＝2＋(lg5＋lg2)2＝2＋(lg10)2＝2＋1＝3.对数式化简与求值的基本原则和方法(1)基本原则对数的化简求值一般是正用或逆用公式，对真数进行处理，选哪种策略化简，取决于问题的实际情况，一般本着便于真数化简的原则进行．(2)两种常用的方法①“收”，将同底的两对数的和(差)收成积(商)的对数； ②“拆”，将积(商)的对数拆成同底的两对数的和(差)． 题型二对数换底公式的应用【典例2】 (1)计算：①log 29·log 34； ②log 52×log 79log 513×log 734.(2)证明：①log a b·log b a ＝1(a>0，且a≠1；b>0，且b≠1)； ②log an b n ＝log a b(a>0，且a≠1，n≠0)． [思路导引] 利用换底公式计算、证明． [解] (1)①原式＝lg9lg2·lg4lg3＝lg32·lg22lg2·lg3＝2lg3·2lg2lg2·lg3＝4.②原式＝log 52log 513·log 79log 734＝log 132·log 349 ＝lg 2lg 13·lg9lg 34＝12lg2·2lg3－lg3·23lg2＝－32.(2)证明：①log a b·log b a ＝lgb lga ·lgalgb＝1. ②log an b n ＝lgb nlga n ＝nlgb nlga ＝lgblga＝log a b.[变式] (1)若本例(2)①改为“loga b·logbc·logcd＝logad”如何证明？(2)若本例(2)②改为“logan b m＝mnlogab”如何证明？[证明](1)loga b·logbc·logcd＝lgblga·lgclgb·lgdlgc＝lgdlga＝logad.(2)logan b m＝lgb mlga n＝mlgbnlga＝mnlogab.应用换底公式应注意的2个方面(1)化成同底的对数时，要注意换底公式的正用、逆用以及变形应用．(2)题目中有指数式和对数式时，要注意将指数式与对数式统一成一种形式．题型三对数的综合应用【典例3】(1)一种放射性物质不断变化为其他物质，每经过一年剩余的质量约是原来的75%，估计约经过多少年，该物质的剩余量是原来的13(结果保留1位有效数字)？(lg2≈0.3010，lg3≈0.4771)(2)已知log189＝a,18b＝5，用a、b表示log3645.[思路导引] 应用换底公式化简求值．[解](1)设最初的质量是1，经过x年，剩余量是y，则：经过1年，剩余量是y＝0.75；经过2年，剩余量是y＝0.752；…经过x年，剩余量是y＝0.75x；由题意得0.75x＝1 3，∴x＝log0.7513＝lg13lg34＝－lg3lg3－lg4≈4.∴估计经过4年，该物质的剩余量是原来的1 3 .(2)解法一：由18b＝5，得log185＝b，又log189＝a，所以log3645＝log1845log1836＝log18(9×5)log1818×2×99＝log189＋log185log18182－log189＝a＋b2－a.解法二：设log3645＝x，则36x＝45，即62x＝5×9，从而有182x＝5×9x＋1，对这个等式的两边都取以18为底的对数，得2x＝log185＋(x＋1)log189，又18b＝5，所以b＝log185. 所以2x＝b＋(x＋1)a，解得x＝a＋b2－a，即log3645＝a＋b2－a.解对数综合应用问题的3条策略(1)统一化：所求为对数式，条件转为对数式．(2)选底数：针对具体问题，选择恰当的底数．(3)会结合：学会换底公式与对数运算法则结合使用．4.4.1对数函数及其图象要点整理1．对数函数的概念函数y＝logax(a>0，且a≠1)叫做对数函数，其中x是自变量，函数的定义域是(0，＋∞)．温馨提示：(1)对数函数y＝logax是由指数函数y＝a x反解后将x、y互换得到的．(2)无论是指数函数还是对数函数，都有其底数a>0且a≠1.2．对数函数的图象及性质温馨提示：底数a与1的大小关系决定了对数函数图象的“升降”：当a>1时，对数函数的图象“上升”；当0<a<1时，对数函数的图象“下降”．3．当底数不同时对数函数图象的变化规律作直线y＝1与所给图象相交，交点的横坐标即为对数的底数，依据在第一象限内，自左向右，图象对应的对数函数的底数逐渐变大，可得b>a>1>d>c>0.题型一对数函数的概念【典例1】指出下列函数哪些是对数函数？(1)y＝3log2x；(2)y＝log6x；(3)y＝logx 3；(4)y＝log2x＋1.[思路导引] 紧扣对数函数的定义判断．[解](1)log2x的系数是3，不是1，不是对数函数．(2)符合对数函数的结构形式，是对数函数．(3)自变量在底数位置上，不是对数函数． (4)对数式log 2x 后又加1，不是对数函数．依据3个形式特点判断对数函数判断一个函数是对数函数必须是形如y ＝log a x(a>0且a≠1)的形式，即必须满足以下条件：(1)系数为1.(2)底数为大于0且不等于1的常数． (3)对数的真数仅有自变量x.题型二对数型函数的定义域 【典例2】 求下列函数的定义域． (1)y ＝3log 2x ；(2)y ＝log 0.5(4x －3)；(3)y ＝log 0.5(4x －3)－1；(4)y ＝log (x ＋1)(2－x)． [解] (1)定义域为(0，＋∞)． (2)由⎩⎨⎧4x －3>0，4x －3≤1，解得34<x≤1，∴定义域为⎝ ⎛⎦⎥⎤34，1.(3)由⎩⎨⎧4x －3>0，4x －3≤12，解得34<x≤78，∴定义域为⎝ ⎛⎦⎥⎤34，78.(4)由⎩⎨⎧x ＋1>0，x ＋1≠1，2－x>0，解得－1<x<0或0<x<2，∴定义域为(－1,0)∪(0,2)．求对数函数定义域的注意事项求与对数函数有关的函数定义域时，除遵循前面已学习过的求函数定义域的方法外，还要对这种函数自身有如下要求：一是要特别注意真数大于零；二是要注意对数的底数大于零且不等于1.题型三对数函数的图象【典例3】(1)已知a>0，且a≠1，则函数y＝a x与y＝loga(－x)的图象只能是( )(2)函数y＝loga(x＋1)－2(a>0，且a≠1)的图象恒过点________．[思路导引] 利用对数函数的图象特征求解．[解析](1)解法一：若0<a<1，则函数y＝a x的图象下降且过点(0,1)，而函数y＝loga(－x)的图象上升且过点(－1,0)，以上图象均不符合．若a>1，则函数y＝a x的图象上升且过点(0,1)，而函数y＝loga(－x)的图象下降且过点(－1,0)，只有B中图象符合．解法二：首先指数函数y＝a x的图象只可能在上半平面，函数y＝loga(－x)的图象只可能在左半平面，从而排除A、C；再看单调性，y＝a x与y＝loga(－x)的单调性正好相反，排除D.只有B中图象符合．(2)因为函数y＝logax (a>0，且a≠1)的图象恒过点(1,0)，则令x＋1＝1得x＝0，此时y＝loga (x＋1)－2＝－2，所以函数y＝loga(x＋1)－2(a>0，且a≠1)的图象恒过点(0，－2)．[答案](1)B (2)(0，－2)[变式] 若本例(2)的函数改为“y＝loga 2x＋1x－1＋2”，则图象恒过定点坐标是________．[解析]令2x＋1x－1＝1，得x＝－2，此时y＝2，∴函数y ＝log a2x ＋1x －1＋2过定点(－2,2)． [答案] (－2,2)处理对数函数图象问题的3个注意点(1)明确图象的分布区域．对数函数的图象在第一、四象限．当x 趋近于0时，函数图象会越来越靠近y 轴，但永远不会与y 轴相交．(2)建立分类讨论的思想．在画对数函数图象之前要先判断对数的底数a 的取值范围是a>1，还是0<a<1.(3)牢记特殊点．对数函数y ＝log a x(a>0，且a≠1)的图象经过点：(1,0)，(a,1)和⎝ ⎛⎭⎪⎫1a ，－1.4.4.2对数函数的性质及其应用要点整理1．对数函数值的符号规律(1)a>1时，当x>1时，y>0；当0<x<1时，y<0. (2)0<a<1时，当0<x<1时，y>0；当x>1时，y<0.可简记为“底真同，对数正；底真异，对数负”，“同”指同大于1或同小于1，“异”指一个大于1一个小于1.2．对称关系 (1)函数y ＝与y ＝log a x 的图象关于x 轴对称．(2)函数y ＝a x 与y ＝log a x 的图象关于直线y ＝x 对称． 3．反函数指数函数y ＝a x (a>0，且a≠1)和对数函数y ＝log a x(a>0，且a≠1)互为反函数．题型一比较对数值的大小【典例1】 比较下列各组中两个值的大小：(1)ln0.3，ln2；(2)log30.2，log40.2；(3)log3π，logπ3；(4)loga 3.1，loga5.2(a>0，且a≠1)．[思路导引] 利用对数单调性比较大小．[解](1)因为函数y＝lnx是增函数，且0.3<2，所以ln0.3<ln2.(2)解法一：因为0>log0.23>log0.24，所以1log0.23<1log0.24，即log30.2<log40.2.解法二：如图所示，由图可知log40.2>log30.2.(3)因为函数y＝log3x是增函数，且π>3，所以log3π>log33＝1.因为函数y＝logπx是增函数，且π>3，所以logπ3<logππ＝1.所以log3π>logπ3.(4)当a>1时，函数y＝logax在(0，＋∞)上是增函数，又3.1<5.2，所以loga 3.1<loga5.2；当0<a<1时，函数y＝logax在(0，＋∞)上是减函数，又3.1<5.2，所以loga 3.1>loga5.2.比较对数值大小时常用的4种方法(1)同底的利用对数函数的单调性，如典例1(1)．(2)同真的利用对数函数的图象或用换底公式转化，如典例1(2)．(3)底数和真数都不同，找中间量，如典例1(3)．(4)若底数为同一参数，则根据底数对对数函数单调性的影响，对底数进行分类讨论，如典例1(4)．题型二求解对数不等式【典例2】 (1)已知log a 12>1，求a 的取值范围；(2)已知log 0.7(2x)<log 0.7(x －1)，求x 的取值范围． [解] (1)由log a 12>1得log a 12>log a a.①当a>1时，有a<12，此时无解．②当0<a<1时，有12<a ，从而12<a<1.∴a 的取值范围是⎝ ⎛⎭⎪⎫12，1.(2)∵函数y ＝log 0.7x 在(0，＋∞)上为减函数， ∴由log 0.72x<log 0.7(x －1)得⎩⎨⎧2x>0，x －1>0，2x>x －1，解得x>1.∴x 的取值范围是(1，＋∞)．常见对数不等式的2种解法(1)形如log a x>log a b 的不等式，借助y ＝log a x 的单调性求解，如果a 的取值不确定，需分a>1与0<a<1两种情况讨论．(2)形如log a x>b 的不等式，应将b 化为以a 为底数的对数式的形式，再借助y ＝log a x 的单调性求解.题型三形如y ＝log a f(x)的函数的单调性【典例3】 求函数y ＝log 0.7(x 2－3x ＋2)的单调区间． [思路导引] 先求定义域，再根据复合函数的单调性求解．[解] 因为x 2－3x ＋2>0，所以x<1或x>2.所以函数的定义域为(－∞，1)∪(2，＋∞)，令t ＝x 2－3x ＋2，则y ＝log 0.7t ，显然y ＝log 0.7t 在(0，＋∞)上是单调递减的，而t ＝x 2－3x ＋2在(－∞，1)，(2，＋∞)上分别是单调递减和单调递增的，所以函数y ＝log 0.7(x 2－3x ＋2)的单调递增区间为(－∞，1)，单调递减区间为(2，＋∞)．求对数型函数单调区间的方法(1)求形如y ＝log a f(x)的函数的单调区间，一定树立定义域优先意识，即由f(x)>0，先求定义域．(2)求此类型函数单调区间的两种思路：①利用定义求解；②借助函数的性质，研究函数t ＝f(x)和y ＝log a t 在定义域上的单调性，利用“同增异减”的结论，从而判定y ＝log a f(x)的单调性．题型四与对数函数有关的值域问题 【典例4】 求下列函数的值域： (1)y ＝log 2(|x|＋4)；(2)f(x)＝log 2(－x 2－4x ＋12)．[思路导引] 求出真数的范围，利用对数函数的单调性求解．[解] (1)因为|x|＋4≥4，所以log 2(|x|＋4)≥log 24＝2，所以函数的值域为[2，＋∞)．(2)因为－x 2－4x ＋12＝－(x ＋2)2＋16≤16，所以0<－x 2－4x ＋12≤16，故log 2(－x 2－4x ＋12)≤log 216＝4，函数的值域为(－∞，4]．[变式] 若本例(2)函数改为“f(x)＝－3x ，x ∈[2,4]”，如何求解？[解] 令t ＝x ，则y ＝t 2－3t ＝⎝⎛⎭⎪⎫t －322－94， ∵2≤x≤4，即－2≤t≤－1.可知y ＝⎝ ⎛⎭⎪⎫t －322－94在[－2，－1]上单调递减．∴当t ＝－2时，y 取最大值为10； 当t ＝－1时，y 取最小值为4. ∴原函数的值域为[4,10]．对数型函数值域的求解技巧(1)求对数型函数的值域，一般需根据对数函数的单调性及真数的取值范围求解．(2)形如y ＝log a f(x)，y ＝a[f(x)]2＋bf(x)＋c 型的函数值域求解常用换元法、配方法等解题技巧．4.4.3不同函数增长的差异要点整理1．指数函数、对数函数、一次函数的性质2.指数函数、对数函数、一次函数的增长差异(1)在区间(0，＋∞)上，函数y ＝a x (a>1)，y ＝log a x(a>1)和y ＝kx(k>0)都是增函数，但它们的增长速度不同，且不在同一个“档次”上．(2)在区间(0，＋∞)上随着x 的增大，y ＝a x (a>1)增长速度越来越快，会超过并远远大于y ＝kx(k>0)的增长速度，而y ＝log a x(a>1)的增长速度则会越来越慢．(3)存在一个x 0，使得当x>x 0时，有log a x<kx<a x (a>1，k>0)．题型一不同函数增长的差异【典例1】 (1)当x 越来越大时，下列函数中，增长速度最快的应该是( ) A ．y ＝10000x B ．y ＝log 2x C ．y ＝x 1000 D ．y ＝⎝ ⎛⎭⎪⎫e 2x(2)四个变量y 1，y 2，y 3，y 4随变量x 变化的数据如下表：关于x 呈指数函数变化的变量是________．[思路导引] 借助指数函数、对数函数、一次函数的增长差异作出判断． [解析] (1)由于指数型函数的增长是爆炸式增长，则当x 越来越大时，函数y ＝⎝ ⎛⎭⎪⎫e 2x 增长速度最快．(2)以爆炸式增长的变量是呈指数函数变化的．从表格中可以看出，四个变量y 1，y 2，y 3，y 4均是从2开始变化，变量y 1，y 2，y 3，y 4都是越来越大，但是增长速度不同，其中变量y 2的增长速度最快，可知变量y 2关于x 呈指数函数变化．[答案] (1)D (2)y 2常见的函数模型及增长特点(1)线性函数模型线性函数模型y ＝kx ＋b(k>0)的增长特点是直线上升，其增长速度不变． (2)指数函数模型指数函数模型y ＝a x (a>1)的增长特点是随着自变量的增大，函数值增大的速度越来越快，即增长速度急剧，形象地称为“指数爆炸”．(3)对数函数模型对数函数模型y ＝log a x(a>1)的增长特点是随着自变量的增大，函数值增大的速度越来越慢，即增长速度平缓．(4)幂函数模型幂函数y ＝x n (n>0)的增长速度介于指数增长和对数增长之间．题型2函数模型的选择问题【典例2】 芦荟是一种经济作物，可以入药，有美容、保健的功效．某人准备栽培并销售芦荟，为了解行情，进行市场调研．从4月1日起，芦荟的种植成本Q(单位：元/千克)与上市时间t(单位：天)的数据情况如下表：(1)Q 与上市时间t 的变化关系的函数式：①Q ＝at ＋b ，②Q ＝at 2＋bt ＋c ，③Q ＝a·b t ，④Q ＝alog b t ；(2)利用你选择的函数，求芦荟种植成本最低时的上市时间及最低种植成本． [思路导引] 要选择最能反映芦荟种植成本与上市时间之间的变化关系的函数式，应该分析各函数的变化情况，通过研究这些函数的变化趋势与表格提供的实际数据是否相符来判断哪个函数是最优函数模型．[解] (1)由表中所提供的数据可知，反映芦荟种植成本Q 与上市时间t 的变化关系的函数不可能是常数函数，故用函数Q ＝at ＋b ，Q ＝a·b t ，Q ＝alog b t 中的任意一个来反映时都应有a≠0，而上面三个函数均为单调函数，这与表格提供的数据不符合，所以应选用二次函数Q ＝at 2＋bt ＋c 进行描述．将表格所提供的三组数据分别代入函数Q ＝at 2＋bt ＋c ，得⎩⎨⎧15.0＝2500a ＋50b ＋c ，10.8＝12100a ＋110b ＋c ，15.0＝62500a ＋250b ＋c ，解得⎩⎪⎨⎪⎧a ＝12000，b ＝－320，c ＝854.所以反映芦荟种植成本Q 与上市时间t 的变化关系的。