时间序列分析方法2
数据分析中的时间序列分析方法
数据分析中的时间序列分析方法时间序列分析是数据分析中常用的一种方法，通过对时间序列数据的分析，可以揭示出数据的趋势、周期性和随机变动等规律，从而为决策提供有力的支持。
本文将介绍几种常用的时间序列分析方法。
一、平滑法（Smoothing）平滑法是一种常见的时间序列分析方法，其主要目的是去除数据中的随机波动，揭示出数据的长期趋势。
平滑法最常用的方法包括简单移动平均法、加权移动平均法和指数平滑法等。
简单移动平均法将一段时间内的数据取平均值，加权移动平均法则对不同时间的数据进行加权计算，而指数平滑法则是根据数据的权重递推计算平滑值。
二、分解法（Decomposition）分解法是将时间序列数据分解为趋势、季节性和随机成分三个部分的方法。
通过分析趋势部分，可以了解数据的长期变化趋势；分析季节性部分，可以揭示出数据中的周期性变动；而随机成分则代表了不可预测的波动。
常用的分解法有加法分解和乘法分解两种方式。
加法分解是将时间序列数据减去趋势和季节性成分，得到的剩余部分就是随机成分；乘法分解则是将时间序列数据除以趋势和季节性成分，得到的结果同样是随机成分。
三、自回归移动平均模型（ARMA）自回归移动平均模型是一种常用的时间序列预测方法，通过对时间序列数据的自相关和移动平均相关进行建模，可以预测未来时间点的值。
ARMA模型是AR模型和MA模型的结合，AR模型用于描述数据的自相关关系，而MA模型则用于描述数据的移动平均相关关系。
ARMA模型的具体建模过程包括模型的阶数选择、参数估计和模型检验等。
四、季节性ARIMA模型（SARIMA）季节性ARIMA模型是在ARIMA模型的基础上加入季节性成分的一种模型。
季节性ARIMA模型主要用于处理具有明显季节性规律的时间序列数据。
与ARIMA模型类似，季节性ARIMA模型也包括模型阶数选择、参数估计和模型检验等步骤，不同的是在建模时需要考虑季节性的影响。
五、灰色系统模型（Grey Model）灰色系统模型是一种特殊的时间序列预测方法，主要适用于数据样本较少或者数据质量较差等情况。
管理数量方法与分析第三章_时间序列分析二
消费价格指数
110
80
消费价格指数 3 期移动平均预测 5期移动平均预测
50
86
88
90
92
94
96
98
00 20
年份
19
19
19
19
19
19
消费价格指数移动平均趋势
19
例题3.3.3
书上P92 例题3.7;
3.3.2
数学模型法
数学模型法 在对原有时间序列进行分析的基 础上,根据其发展变动的特点,寻找一个与之相匹配 的趋势曲线方程,并以此来测定长期趋势变动规律 的方法. 常用的趋势线数学模型 线性趋势与非线性趋势
年份 价格指数 1986 1987 1988 1989 118 1990 103.1 1991 103.4 1992 1993
106.3 107.3 118.8
106.4 114.7
年份
价格指数
1994
1995
1996
1997
102.8
1998
99.2
1999
98.6
2000
100.4
124.1 117.1 108.3
首先将移动平均数作为长期趋势值加以剔除， 再测定季节变动的方法.
具体方法如下
(1)计算移动平均趋势值 T(季度数据采用4项移动 平均 ,月份数据采用 12项移动平均 ),并将其结果进 行“中心化”处理.即将移动平均的结果再进行一 次二项的移动平均,即得出“中心化移动平均 值”(CMA) (2)计算移动平均的比值Y/T=SI，也称为修匀比率
具体做法
Y1 bt1 Y2 bt 2
Y1 Y2 b t1 t 2
Y1 , Y2 分别代表原时间序列实际观察中各部分 的平均数.
如何进行时间序列数据处理(二)
时间序列数据处理是一项重要的数据分析方法，它在各个领域都有广泛的应用。
通过对时间序列数据的处理，我们可以揭示出数据背后的趋势、周期和季节性等规律，从而为决策提供有力的支持。
下面将从数据预处理、趋势分析、周期分析和季节性分析四个方面来讨论如何进行时间序列数据处理。
一、数据预处理在进行时间序列数据处理之前，我们首先需要对数据进行预处理，以确保数据质量和完整性。
数据预处理的主要步骤包括数据清洗、数据平滑、缺失值处理和异常值处理。
数据清洗是指对原始数据进行去噪和去除异常值等处理，以消除数据中的噪声干扰。
数据平滑是指对数据进行平滑处理，以减少数据的波动性，使数据更加稳定。
缺失值处理是指对数据中的缺失值进行填补或删除，以确保数据的完整性。
异常值处理是指对数据中的异常值进行识别和处理，以排除异常数据对分析结果的干扰。
二、趋势分析趋势分析是指对时间序列数据的长期变化态势进行分析和预测。
通过趋势分析，我们可以揭示数据背后的基本发展趋势和方向。
常用的趋势分析方法包括移动平均法、指数平滑法和回归分析法等。
移动平均法是一种比较简单的趋势分析方法，它通过计算数据的平均值来剔除数据中的随机波动，从而揭示出数据的长期变化趋势。
指数平滑法是一种更为灵活和敏感的趋势分析方法，它通过对数据进行加权平均来揭示出数据的长期变化趋势。
回归分析法是一种基于数学模型的趋势分析方法，它通过建立变量之间的函数关系来描述数据的长期变化趋势。
三、周期分析周期分析是指对时间序列数据中周期性变动的规律性进行分析和预测。
通过周期分析，我们可以揭示数据背后的周期性波动和变动周期。
常用的周期分析方法包括傅里叶分析法、小波分析法和自相关分析法等。
傅里叶分析法是一种基于频谱分析的周期分析方法，它通过将时间序列数据转换到频域上进行分析，从而揭示出数据的周期性波动。
小波分析法是一种更为细致和精确的周期分析方法，它通过将时间序列数据分解为多个频率组成的子序列来揭示数据的周期性波动。
2-2第二章时间序列分析法
（1）简单平均法
例2：设某电网2001-2004年个季度的发电量如表2-5所示，试
用简易计算法列出发电量的一次线性趋势方程，再用简单平
均法计算出季节指数，并以次预测2005年该电网全年及各季
度的发电量。
表2-5
年次 季节
2001
2002
一 二 三 四 全年
(1) 1206030 1283687 1211133 1328247 5029097
n
4
b ty 3213072 160653.6
t2
20
y=a+bt=5459952+160653.6t
2005年t=5，代入公式，得到y=6263220 根据表2－5的调整后季节指数，2005年各季度 发电量为： 一季度：6263220×0.9666/4=1513507 二季度：6263220×1.0081/4=1578488 三季度：6263220×0.9768/4=1529478 四季度：6263220×1.0485/4=1641747
2、指数的分类 （1）个体指数：反映某一具体经济现象动态变动的相
对数
（2）综合指数：反映全部经济现象动态变动的相对数
（3）数量指标指数：它是表明经济活动结果数量 多少的指数。
（4）质量指标指数：它是表明经济工作质量好坏 的指数。
（5）定基指数：它是指各个指数都是以某一个固 定时期为基期而进行计算的一系列指数。
季别平均 季节指数
(6) 1319460 1375988 1333301 1431204 1364988
(7) 0.9666 1.0081 0.9768 1.0485 4.0000
调整后季 节指数 (8)
0.9666 1.0081 0.9768 1.0485 4.0000
时间序列分析-王燕-习题4答案
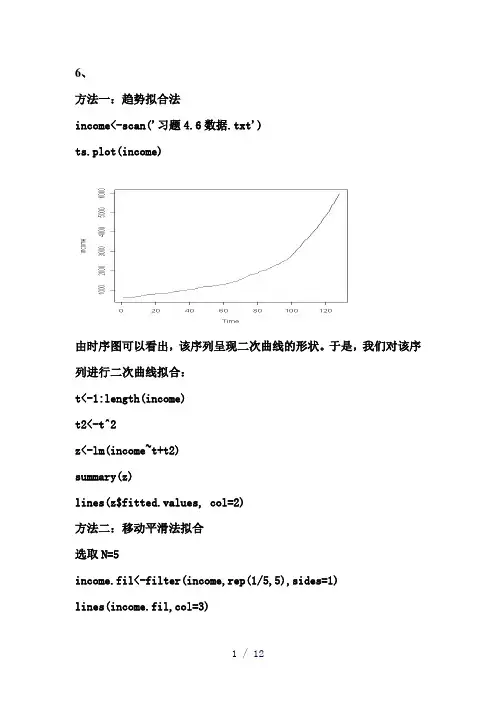
6、方法一：趋势拟合法income<-scan('习题4.6数据.txt')ts.plot(income)由时序图可以看出，该序列呈现二次曲线的形状。
于是，我们对该序列进行二次曲线拟合：t<-1:length(income)t2<-t^2z<-lm(income~t+t2)summary(z)lines(z$fitted.values, col=2)方法二：移动平滑法拟合选取N=5income.fil<-filter(income,rep(1/5,5),sides=1)lines(income.fil,col=3)7、（1）milk<-scan('习题4.7数据.txt')ts.plot(milk)从该序列的时序图中，我们看到长期递增趋势和以年为固定周期的季节波动同时作用于该序列,因此我们可以采用乘积模型和加法模型。
在这里以加法模型为例。
z<-scan('4.7.txt')ts.plot(z)z<-ts(z,start=c(1962,1),frequency=12)z.s<-decompose(z,type='additive') //运用加法模型进行分解z.1<-z-z.s$seas //提取其中的季节系数，并在z中减去（因为是加法模//型）该季节系数ts.plot(z.1)lines(z.s$trend,col=3)z.2<-ts(z.1)t<-1:length(z.2)t2<-t^2t3<-t^3r1<-lm(z.2~t)r2<-lm(z.2~t+t2)r3<-lm(z.2~t+t2+t3)summary(r1)summary(r2)summary(r3) ##发现3次拟合效果最佳，故选用三次拟合ts.plot(z.2)lines(r3$fitt,col=4)pt<-(length(z.2)+1) : (length(z.2)+12)pt1<-pt ##预测下一年序列pt2<-pt^2pt3<-pt^3pt<-matrix(c(pt1,pt2,pt3),byrow=T,nrow=3)/*为预测时间的矩阵。
时间序列分析方法
时间序列分析方法时间序列分析是一种常见的统计分析方法，它研究的是定量和定性的数据的动态变化情况，能反映系统潜在变化的趋势和规律，并且能通过预测技术预测未来趋势。
时间序列分析是研究随时间变化的数据可靠性和有效性的重要工具，能够发现其中的趋势和变化规律，从而帮助企业和投资者更全面地了解各种现象，更好地进行决策和行为分析。
时间序列分析可以通过应用不同的统计方法来完成，例如自相关分析、序列回归分析、协整和非线性统计分析等。
1.自相关分析自相关分析(AutoRegressive Analysis)是分析时间序列上延迟自身的统计方法，主要是描述时间序列动态变化趋势和长时间趋势。
它主要利用某一特定时刻以前t个时刻的数据来预测该时刻的值，并用一个具有时间序列模型来计算，如指数移动平均（EMA）和ARMA （Autoregressive Moving Average）等。
自相关分析的优点是简单容易，能够充分发挥时间序列的短期显著特征，缺点是只能反映短期的趋势，无法发现和分析长期的趋势。
2.序列回归序列回归（Sequence Regression）是一种统计学方法，它根据时间序列的趋势，建立一种回归关系，利用某一特定时刻以前n个时刻的数据，预测该时刻的数值，并以此来表示时间序列的趋势，如线性回归、非线性回归等。
序列回归的优点是能够表示时间序列上一些重要的长期特征，缺点是忽略了时间序列上短期的变化特征。
3.协整分析协整分析（Cointegration Analysis）是指时间序列上两个或多个序列的滞后值的长期关系。
它通过检验两个序列的相关度分析系统的同步变化，检测出两个长期运动不相关的非零均值，并利用协整分析模型来预测未来的发展趋势。
协整分析的优点是能够发现时间序列上的长期趋势，缺点是忽略了短期变化特征，而且模型拟合效果不太好。
4.非线性统计分析非线性统计分析（Nonlinear Statistical Analysis）是时间序列分析的一种方法，它可以用来描述一个序列的非线性变化特性，如分析非线性的自相关系数、分析变量的越界规律、预测变量系统整体特性，如混沌理论等。
时间序列数据分析的方法与应用
时间序列数据分析的方法与应用时间序列数据是指按照时间顺序记录的一系列数据，根据时间序列数据可以分析出数据的趋势、周期和季节性等特征。
时间序列数据分析是一种重要的统计方法，广泛应用于经济学、金融学、气象学、交通运输等领域。
时间序列数据的特点是有时间的先后顺序，时间上的变化会对数据产生影响。
时间序列数据分析一般包括两个主要步骤：模型识别与模型估计。
模型识别是指根据时间序列数据的特点来选择适当的模型，而模型估计是指利用已有的时间序列数据对模型中的参数进行估计。
下面主要介绍时间序列数据分析的方法和应用。
一、时间序列数据分析的方法1.时间序列图时间序列图是最简单、直观的分析方法，通过画出时间序列数据随时间的变化趋势，可以直观地观察到数据的趋势、季节性和周期性等信息。
2.平稳性检验平稳性是时间序列数据分析的基本假设，平稳时间序列具有恒定的均值和方差，不随时间而变化。
平稳性检验是为了验证时间序列数据是否平稳，常用的平稳性检验方法有ADF检验和KPSS检验等。
3.拟合ARIMA模型在时间序列数据分析中，ARIMA模型是一种常用的预测模型，它是自回归移动平均模型的组合，用来描述时间序列数据的自相关和滞后相关关系。
通过对已有的时间序列数据进行拟合ARIMA模型，可以得到时间序列数据的参数估计，从而进行未来的预测。
4.季节性调整时间序列数据中常常存在季节性变动，为了剔除季节性影响，可以进行季节性调整。
常用的季节性调整方法有季节性指数法和X-11法等。
5.平滑法平滑法是一种常用的时间序列数据分析方法，通过计算移动平均值或指数平滑法对数据进行平滑处理，可以减小数据的波动性，更好地观察到数据的趋势和周期性。
二、时间序列数据分析的应用1.经济学领域时间序列数据在宏观经济学和微观经济学中有广泛的应用。
例如，对GDP、通胀率、失业率等经济指标进行时间序列数据分析，可以发现经济的周期性波动和长期趋势，为经济政策的制定提供参考。
2.金融学领域金融市场中的价格、交易量等数据都是时间序列数据，通过时间序列数据分析可以揭示金融市场的规律。
应用时间序列分析sas (2)
应用时间序列分析 SAS什么是时间序列分析？时间序列分析是一种统计学方法，用于处理连续性的数据，这些数据是按照时间顺序收集的。
它的目的是通过分析过去的数据模式和趋势来预测的趋势。
时间序列分析可用于各种领域，如经济学、气象学、股票市场预测等。
时间序列数据通常具有以下特征：•趋势：随着时间的推移，数据的整体趋势可能会上升或下降。
•季节性：数据可能会显示出固定周期的重复模式，如每年的季节性变化。
•周期性：数据可能会显示出非固定周期的重复模式，如商业周期。
•随机性：数据可能会受到许多随机因素的影响，如市场波动或天气变化。
为什么要使用 SAS 进行时间序列分析？SAS（Statistical Analysis System）是一种功能强大的统计分析和数据管理软件。
它提供了丰富的数据分析和建模工具，特别适合应用于时间序列数据分析。
以下是使用 SAS 进行时间序列分析的一些主要优势：1.多种统计模型：SAS 提供了多种用于时间序列分析的统计模型，包括自回归移动平均模型（ARMA）、自回归积分移动平均模型（ARIMA）、季节性自回归移动平均模型（SARIMA）等。
这些模型可以帮助我们更好地理解时间序列数据的模式和趋势。
2.强大的数据处理能力：SAS 提供了丰富的数据处理功能，包括数据清洗、数据转换、变量选择等。
这些功能可以帮助我们对时间序列数据进行预处理，以便更好地应用统计模型进行分析。
3.可视化工具：SAS 提供了各种可视化工具，如图表和图形，可以帮助我们更直观地理解时间序列数据的模式和趋势。
这些可视化工具还可以帮助我们有效地呈现分析结果。
4.自动化分析：SAS 具有自动化分析的能力，可以帮助我们快速而准确地进行时间序列分析。
通过编写脚本和宏，可以自动化执行重复的分析任务，提高工作效率。
使用 SAS 进行时间序列分析的基本步骤以下是使用 SAS 进行时间序列分析的基本步骤：1.导入数据：，需要将时间序列数据导入 SAS 中。
时间序列分析：方法与应用(第二版)传统时间序列分析模型
型。
例1.1
9
例1.1
Y
3,000 2,500 2,000 1,500 1,000
500 0 1955 1960 1965 1970 1975 1980
社会商品零售总额时序图 10
例1.2
Y
9,000 8,000 7,000 6,000 5,000 4,000 3,000 2,000 1,000
10,000
9,000
8,000
7,000
6,000
5,000
4,000 1995
1996
1997
1998
1999
2000
Y
YY
37
为评价模型的预测效果，也可以象例1.12一样， 预留部分数据作为试测数据，评价模型的适用性。
38
fi 为季节指数
T为季节周期的长度，4或12
26
2. 适用条件：
既有季节变动，又有趋势变动 且波动幅度不断变化的时间序列
至少需要5年分月或分季的数据
3. 应用
例1.12 我国工业总产值序列
27
1）时序变化分析 绘制时序曲线图
明显的线性增长趋势、季节波动，且波动幅度随趋 势的增加而变大。
Y
6,000
3. 应用
例1.13 我国社会商品零售总额的分析预测
33
1）时序变化分析 绘制时序曲线图
明显的线性增长趋势、季节波动，且波动幅度随趋势 的增加基本不变。
Y
10,000
9,000
8,000
7,000
6,000
5,000
4,000
1995
1996
《时间序列分析》第二章 时间序列预处理习题解答[1]
![《时间序列分析》第二章 时间序列预处理习题解答[1]](https://img.taocdn.com/s3/m/afd770ef524de518964b7d1f.png)
97.0 105.4
proc print data=example2_3; proc arima data=example2_3; identify var=rain; run;
分析： （1） 如上图所示： （2） 根据样本时序图和样本自相关图可知，该序列平稳 （3） 根据白噪声检验，P 值都较大，可以判断该序列为白噪声序列，即该序列具有纯随 机性。
析： 分析 自相关图显示序列自 自相关系数 数长期位于零 零轴的一边 边， 这是具有 有单调趋势序 序列 的典 典型特征。
由下图可知 知，自相关系 系数长期位于 于零轴的一边 边，且自相关 关系数递减到 到零的速度较慢， 在 5 个延期中，自相关系数 数一直为正，说明这是一个 个有典型单调 调趋势的非平 平稳序列。
data example2; input ppm@@; time=intnx('month','01jan1975'd, _n_-1); format year year4.; cards; 330.45 331.90 331.63 333.05 332.81 334.65 334.66 336.25 335.89 337.41 337.81 339.25 330.97 330.05 332.46 330.87 333.23 332.41 335.07 334.39 336.44 335.71 338.16 337.19 331.64 328.58 333.36 329.24 334.55 331.32 336.33 332.44 337.63 333.68 339.88 335.49 332.87 328.31 334.45 328.87 335.82 330.73 337.39 332.25 338.54 333.69
时间序列分析(2)讲解
波动性模型
一、经济时间序列的典型事实
• 1. Most of the series contain a clear trend; • 2. Shocks to a series can display a high
degree of persistence; • 3. The volatility of many series is not
constant over time; • 4. Some series seem to meander; • 5. Some series share co-movements with
other series.
二、ARCH模型
• 1、预备知识 • （1）条件均值和无条件均值 • 对于平稳ARMA过程，如yt=a0+a1yt-1+εt，若要预测未
• 条称件 为均 条值 件预 方测 差的，误有差：为[yt+1-(a0+a1yt)]，其方差 Et[yt+1-(a0+a1yt)]2=Et (εt+1)2 =σ2
• 由件于 均|值a1|预<1测，优所于以无条条件件方均差值小预于测无。条件方差，条
二、ARCH模型
• 2、经济和金融时间序列中的异方差现象 • ① 观测变量序列的（条件）方差随某个
方差模型为： yt+1=εt+1xt
从而有： Var(yt+1|xt)=xt2σ2 可的xt序见条列，件相y方t+关差1的，也条则大件y；t方+若1的差x条依t2小件赖，方于则差xty的也t+实序1的现列条值相件。关方若。差x也t2大小，。则若y若t+1 • 一般地，可将方差模型设定为：
时间序列分析-王燕-习题4答案(2)
6、方法一：趋势拟合法income<-scan('习题4.6数据.txt')ts.plot(income)由时序图可以看出，该序列呈现二次曲线的形状。
于是，我们对该序列进行二次曲线拟合：t<-1:length(income)t2<-t^2z<-lm(income~t+t2)summary(z)lines(z$fitted.values, col=2)方法二：移动平滑法拟合选取N=5income.fil<-filter(income,rep(1/5,5),sides=1)lines(income.fil,col=3)7、（1）milk<-scan('习题4.7数据.txt')ts.plot(milk)从该序列的时序图中，我们看到长期递增趋势和以年为固定周期的季节波动同时作用于该序列,因此我们可以采用乘积模型和加法模型。
在这里以加法模型为例。
z<-scan('4.7.txt')ts.plot(z)z<-ts(z,start=c(1962,1),frequency=12)z.s<-decompose(z,type='additive') //运用加法模型进行分解z.1<-z-z.s$seas //提取其中的季节系数，并在z中减去（因为是加法模//型）该季节系数ts.plot(z.1)lines(z.s$trend,col=3)z.2<-ts(z.1)t<-1:length(z.2)t2<-t^2t3<-t^3r1<-lm(z.2~t)r2<-lm(z.2~t+t2)r3<-lm(z.2~t+t2+t3)summary(r1)summary(r2)summary(r3) ##发现3次拟合效果最佳，故选用三次拟合ts.plot(z.2)lines(r3$fitt,col=4)pt<-(length(z.2)+1) : (length(z.2)+12)pt1<-pt ##预测下一年序列pt2<-pt^2pt3<-pt^3pt<-matrix(c(pt1,pt2,pt3),byrow=T,nrow=3)/*为预测时间的矩阵。
第三章平稳时间序列分析-(2)
~
n
n
t
用迭代法，求得使其达最小的参数值。
最小二乘估计的特点
最小二乘估计充分应用了每一个观察值 所提供的信息，因而它的估计精度高； 不需总体分布，便于实现，所以条件最 小二乘估计方法使用率最高。
实际中，为便于计算，很多时候看作服从多元正态分 布
3、最小二乘估计
原理
使残差平方和达到最小的那组参数值即为最 小二乘估计值
n t 1 n
ˆ) 2 Q( t ( xt 1 xt 1 p xt p 1 t 1 q t q )2
c2 4 , c 2 ˆ2 1 12 2 2 , c ˆ1 1 c2 4 ,c 2 2
矩估计
c ˆ ˆ 2 , ˆ 1 1 ˆ 1 c
矩估计的特点：
优点 估计思想简单直观 不需要假设总体分布 计算量小（低阶模型场合） 缺点 信息浪费严重 只依赖p+q个样本自相关系数信息，其他信 息都被忽略 估计精度较差 通常矩估计方法被用作极大似然估计和最小二乘 估计迭代计算的初始值
【例3.7】考察ARMA模型的自相关性
ARMA(1,1): xt 0.5xt 1 t 0.8t 直观地考察该模型自相关系数和偏自相关系 数的性质。
样本自相关图
样本偏自相关图
显然，自相关系数和偏自相关系数拖尾
这也是直观选择拟合模型的 常用方法之一
ARMA模型相关性特征：
模型 自相关系数 偏自相关系数
1, , p ,1, ,q , ,
2
时间序列分析：方法与应用(第二版)两序列的协整和误差修正模型
Yt
0 1Yt 1 ...... kYt k t
H 01 ： 1 = … = k = 0
9
2. 第二个条件的检验 原假设：Y不是引起X变化的原因
无限制条件模型（UR）
Xt
0 1 X t 1 ...... k X t k
1Yt 1 ...... kY t k t
有限制条件模型（R）
Xt
0 1 X t 1 ...... k X t k t
x t+ t
+
、 的一致估计量 ˆ 、ˆ ，
构造一个线性组合，亦即计算残差
ˆ y x
t
t
t
第二步：残差序列单位根检验
残差序列 t 进行单位根检验
若
t ~ I（0）
表明两个序列是协整的，则（1，-b）为协整向量。 若残差序列存在单位根，则两个序列不是协整的。
例4.4
三、误差修正模型（ECM）
基于协整关系建立的误差修正模型（Error Correction
x 、 t 和、 yt 虽然是单位根过程，但它们存在一个线性组合
是平稳的。这是因为它们具有公共的I（1）因子 wt 。
16
（二）协整的含义及检验
1.概念
协整过程（co-integrated process）也有译为同积过程，
是一种特殊的向量单位根过程。
设{yt ，t = 1，2，......}为一n 维的向量单位根过程，它
b
xt
~I（1）。
13
2）两个零阶单整序列的线性组合
若两个序列是平稳序列，如 xt ~ I（0）， yt~ I（0），
则其线性组合也是平稳的，有a xt+ b yt~ I（0）；
统计学中的时间序列分析方法
统计学中的时间序列分析方法时间序列分析是一种重要的统计学方法，它研究同一现象在不同时间点上的观测值，并试图揭示其中的规律和趋势。
利用时间序列分析方法，我们可以对未来的趋势进行预测，辅助决策和规划。
本文将探讨几种常用的时间序列分析方法。
1. 移动平均法移动平均法是最简单也是最常用的时间序列分析方法之一。
它基于一个假设，即时间序列中的观测值受到随机误差的影响，但整体趋势是平稳的。
移动平均法通过计算一定时间窗口内的平均值，去除随机误差，揭示出时间序列的趋势。
2. 指数平滑法指数平滑法是另一种常用的时间序列分析方法。
它通过对时间序列的历史数据赋予不同的权重，预测未来的值。
指数平滑法的关键在于确定权重因子，通常使用最小二乘法或最大似然法进行估计。
该方法适用于数据波动频繁的情况，可以较好地揭示出趋势变化。
3. 自回归移动平均模型(ARMA)自回归移动平均模型是一种复杂且精确的时间序列分析方法。
它结合了自回归模型(AR)和移动平均模型(MA)的特点。
AR模型基于过去的观测值预测未来的值，而MA模型则基于过去的误差项预测未来的值。
ARMA模型可以较好地拟合包含趋势和周期性的时间序列数据。
4. 季节性差分法季节性差分法适用于存在明显季节性变化的时间序列数据。
它通过计算相邻时间点的差值，去除季节性因素，揭示出趋势和周期性变化。
该方法可以用于预测季节性销售数据、气候变化等。
5. 非参数方法除了上述方法，还有一些非参数方法可以用于时间序列分析。
这些方法不对数据的分布做出假设，更加灵活。
例如，核密度估计和小波分析等方法可以用于检测时间序列的异常值和突变。
总结起来，时间序列分析方法有很多种，每种方法都有其适用的领域和限制。
在实际应用中，我们需要根据具体情况选择合适的方法，并结合统计学原理和实践经验进行分析。
时间序列分析的结果可以帮助我们更好地理解数据的变化规律，为预测和决策提供科学依据。
因此，熟练掌握时间序列分析方法是每个统计学家和数据分析师的必备技能。
第三章平稳时间序列分析-2
例3.5 (1)xt 0.8xt1 t
理论偏自相关系数 样本偏自相关图
kk
0.8 0
,k 1 ,k 2
例3.5 (2)xt 0.8xt1 t
理论偏自相关系数 样本偏自相关图
kk
0.8 0
,k 1 ,k 2
例3.5 (3)xt xt1 0.5xt2 t
理论偏自相关系数 样本偏自相关图
三、平稳AR模型的统计性质
均值 方差 协方差 自相关系数 偏自相关系数
1、均值
如果AR(p)模型满足平稳性，则有 E(xt ) E(0 1xt1 p xt p t )
因平稳序列均值为常数，且{εt} 为白噪声序列，有
E(xt ) , E(t ) 0 ,t T
则
E(xt )
xt G j t j j0
两边求方差得
Var(xt )
G
2j
2
,
G j为Green函数
j0
特征根λ=φ1 平稳时，<1
【例3.2】求平稳AR(1)模型的方差
平稳AR(1)模型的传递形式为
xt
t 1 1B
i0
p
kjij ti
j1
(1B)i t
i0
1i ti
i0
Green函数为 Gj 1 j , j 0,1,
平稳AR(P)模型的自相关系数递推公式
k 1k1 2 k2 L p k p
可推得：常用平稳AR模型自相关系数递推公式
AR(1)模型
k 1k , k 0
AR(2)模型
1,
k
1
1 2
1k1 2 k2
k 0 k 1 k2
平稳AR模型自相关系数的拖尾性
时间序列分析
时间序列分析时间序列分析是一种统计学方法，用于分析时间序列数据的模式、趋势和周期性。
它可以帮助我们了解随着时间推移，数据如何变化，并预测未来的发展趋势。
本文将介绍时间序列分析的基本概念、常用方法和实际应用。
一、时间序列分析的基本概念时间序列是按照时间顺序排列的一系列数据点。
它可以是连续的，例如每天的股票价格，也可以是离散的，例如每个月的销售量。
时间序列分析旨在通过观察数据中的模式和趋势，揭示数据背后的规律和关系。
二、时间序列分析的常用方法1. 描述统计法描述统计法用于计算数据的统计指标，如平均值、标准差和相关系数。
这些指标可以帮助我们了解数据的分布情况和相关性。
2. 组件分析法组件分析法将时间序列分解为趋势、季节和随机成分。
趋势表示长期的变化趋势，季节表示重复出现的周期性变化，随机成分表示无法通过趋势和季节解释的随机波动。
通过对组成部分的分析，可以更好地理解时间序列的内在规律。
3. 平稳性检验法平稳性是时间序列分析的基本假设之一。
平稳时间序列的统计特性不随时间变化而改变。
平稳性检验可以通过观察时间序列的趋势、自相关图和单位根检验等方法进行。
4. 预测方法时间序列分析的一个重要应用是预测未来的数值。
常用的预测方法包括移动平均法、指数平滑法和ARIMA模型等。
这些方法基于过去的数据，通过建立模型来预测未来的趋势和周期性。
三、时间序列分析的实际应用时间序列分析在各个领域都有广泛的应用。
在金融领域，它可以用于股票价格的预测和风险管理；在经济学领域，它可以用于 GDP 的预测和经济政策制定；在气象学领域，它可以用于天气预报和气候变化研究。
除了上述领域外，时间序列分析还用于交通流量预测、销售预测、生态学研究等。
通过对历史数据的分析，我们可以更好地理解和预测未来的发展趋势，为决策提供依据。
结论时间序列分析是一种强大的工具，可以帮助我们理解时间序列数据中的模式和趋势。
通过对数据的描述统计、组件分析和预测，我们可以揭示数据背后的规律，并用于实际问题的解决。
第十章_时间序列分析法(二)
50＝a＋6b
解方程得：a ＝28，b＝3.667
＝ 则直线趋势预测模型为：ŶA 28＋3.667 t
根据此方程预测后两年的社会商品零售额为：
＝ Ŷ12 28＋3.667 ×12＝72.004（亿元）
＝ Ŷ13 28＋3.667 ×13＝75.671（亿元）
市场调查与预测
＝ Ŷ14 28＋3.667 ×14＝79.338（亿元）
……
＝ ＝ Ŷ11 341.99＋31.9 ×5 ＋0.66 ×5 2 518.04 (万台 )
……
对预测模型测算预测误差：
∑ |Yt- Ŷt|
MAE=
n
＝22.59/11＝2.054 (万台 )
误差很小，模型可用
市场调查与预测
87-27
§11.2 非线性趋势市场预测法
1. 二次曲线趋势市场预测模型
87-8
§11.1 直线趋势市场预测法
应用示例
2. 建立直线趋势预测模型——求出直线方程式中的a、b值
直观法比较简单，也比较节省。但穿过实际观察值点或不穿过散点， 都可以划出很多条直线，以哪条直线作为预测模型，是由预测者的 主管判断而定
若另一位预测者选定（4，43）和（7，53）两点，连成一条直线， 则得到另一个不同的预测模型：
市场调查与预测
87-19
§11.2 非线性趋势市场预测法
观察时间序列变动规律的方法有两种：
图形观察法
计算阶差判断法——通过计算市场现象时间序列实际观察值的 环比增减量（也称阶差），来判断现象变动的规律
一次差接近一个常数
直线趋势模型
二次差接近一个常数
二次曲线模型
三次差接近一个常数
三次曲线模型
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 个体表现为某个数值是随机的，但是，它们取得某个数 值的机会是不同的，即它们按一定的规律取值，即它们 的取值与确定的概率相对应。
样本和样本容量
• 总体中抽出若干个个体组成的集体称为样本。样本中 包含的个体的个数称为样本的容量，又称为样本的大 小。
Var(x+y)=Var(x )+Var(y )=Var(x-y) • Var(a+bx)=b2Var(x) • a,b为常数，x,y为两个相互独立的随机变量，则
(ax+by)=a2Var(x)+b2Var(y) • Var(x)=E(x2)-(E(x))2
数学期望与方差的图示
• 数学期望描述随机变量的集中程度，方差描述随机变 量的分散程度。
• 随机变量离均差平方的数学期望，叫随机变量的方差， 记作Var(x)。方差的算术平方根叫标准差。
若X为连续型随机变量，则X的方差以下式给出：
V X xEFra bibliotekx2
x
dx
2 V x Varx E x
xE x
2
E
x x 2
方差的意义
• 离均差和方差都是用来描述离散程度的，即描述X对于 它的期望的偏离程度，这种偏差越大，表明变量的取 值越分散。
• 如果了解总体的一般水平和离散程度，就已经对总体有 了粗略的了解；
• 在很多情况下，了解这两个数字特征还是求出总体分布 的基础和关键。
数学期望的性质
• 如果a、b为常数，则
•
E(aY+b)=aE(Y)+b
• 如果X、Y为两个随机变量，则
•
E(X+Y)=E(X)+E(Y)
• 如果g(x)和f(x)分别为X的两个函数，则
• 一般情况下，采用方差来描述离散程度。因为离均差 的和为0，无法体现随机变量的总离散程度。
• 事实上正偏差大亦或负偏差大，同样是离散程度大。 方差中由于有平方，从而消除了正负号的影响，并易 于加总，也易于强调大的偏离程度的突出作用。
方差的性质
• Var(c )=0 • Var(c+x)=Var(x ) • Var(cx)=c2Var(x) • x,y为相互独立的随机变量，则
•
E[g(X)+f(X)]=E[g(X)]+E[f(X)]
• 如果X、Y是两个独立的随机变量，则
•
E(X.Y)=E(X).E(Y)
方差
• 如果随机变量X的数学期望E(X)存在，称[X-E(X)]为随 机变量X的离均差。显然，随机变量离均差的数学期望 是0，即
E [ X-E(X) ] = 0
• 是连续型随机变量的方差
时间序列分析方法
确定型时间序列模型的参数估计
教学大纲
• 参数估计的基础知识 • 时间序列平滑方法 • 时间序列模型的回归方法
参数估计的基础知识
总体和个体
研究对象的全体称为总体，组成总体的每个基本单位称为个体。
• 按组成总体的个体的多寡分为：有限总体和无限总体；
• 总体具有同质性：每个个体具有共同的观察特征，而与 其它总体相区别；
• 每一次具体抽样所得的数据，就是n元随机变量的一 个观察值，记为（X1，……，Xn）。
• 通过总体的分布可以把总体和样本连接起来。
样本与所抽自的总体具有相同的分布
• 某一次具体的抽样的具体的数值（y1，……，yn）；
• 一次抽样的可能结果，它的每一次观察都是随机地从总体 中（每一个个体有同样的机会被选入）抽取一个，所以它 是一组随机变量（y1，y2，……，yn）
• 每一次抽样都来自同一总体（分布），也就是每一次抽样 都带来了与总体一样的分布信息。所以，样本与所来自的 总体分布相同。
统计量
• 设（y1，y2，……，yn）为一组样本观察值，函数 f（ y1，y2，……，yn ）若不含有未知参数，则称为 统计量。
• 统计量一般是连续函数。由于样本是随机变量，因而 它的函数也是随机变量，所以，统计量也是随机变量。
• 抽样是按随机原则选取的，即总体中每个个体有同样 的机会被选入样本。
随机变量
根据概率不同而取不同数值的变量称为随机变量RV
• 一个随机变量具有下列特性：可以取许多不同的数值， 取这些数值的概率为p，p满足：0 p 1
• 随机变量以一定的概率取到各种可能值，按其取值情 况随机变量可分为两类：离散型随机变量和连续型随 机变量
• 统计量一般用它来提取由样本带来的总体信息。
样本与总体之间的关系
• 样本是总体的一部分，是对总体随机抽样后得到的集 合
• 对观察者而言，总体是未知的，能够观测到的只是样 本的具体情况
• 我们所要做的就是通过对这些具体样本的情况的研究， 来推知整个总体的情况
对总体的描述——随机变量的数字特征
• 数学期望 • 方差 • 数学期望与方差的图示
研究数字特征的必要性
• 总体是一个随机变量。对总体的描述就是对随机变量的 描述。随机变量的分布是对随机变量最完整的描述
• 求出总体的分布往往不是一件容易的事情；
• 在很多情况下，我们并不需要全面考察随机变量的变化 情况，只需要了解总体的一些综合指标。一般说来，常 常需要了解总体的一般水平和它的离散程度；
– 离散型随机变量的取值是有限的，最多是可列多 个
– 连续型随机变量的取值充满整个数轴或某个区间
离散型随机变量与连续型随机变量
概
概
率
率
1.0 1.0
y 10 20 30 40 50
离散型随机变量
y 连续型随机变量
总体、随机变量、样本间的联系
• 总体就是一个随机变量，所谓样本就是n个（样本容 量n）相互独立且与总体有相同分布的随机变量 x1，……，xn。
1方差同、期望变大
2期望同、方差变小
5
5
10
5
样本分布的数字特征
• 样本分布函数 • 样本平均数 • 样本方差
样本平均数
• 总体的数字特征：是一个固定不变的数，称为参数； • 样本的数字特征：是随抽样而变化的数，是一个随机变量，称为
统计量。 • 样本平均数的定义
对于样本x1 , x2 , xn ，称
x 1 n
x
n i 1
i
为样本平均数。
• 样本平均数用来描述样本的平均水平。
样本方差和标准差
• 样本方差和标准差的定义
对于样本x1, x2 , xn，称
s x x 2 1 n n 1 i1
i
2
x x 以及s 1 n n 1 i1