实验 OpenGL几何变换
opengl实验报告

opengl实验报告OpenGL实验报告引言:OpenGL(Open Graphics Library)是一种跨平台的图形编程接口,被广泛应用于计算机图形学、游戏开发和科学可视化等领域。
本实验报告将介绍我对OpenGL的实验研究和学习成果。
一、实验目的本次实验的主要目的是掌握OpenGL的基本概念和使用方法,了解图形渲染的原理和过程,以及学习如何在OpenGL中创建和操作图形对象。
二、实验环境本次实验使用的是OpenGL的最新版本,并在Windows操作系统下进行开发。
使用的开发工具是Visual Studio和OpenGL的开发库。
三、实验过程1. 熟悉OpenGL的基本概念在开始实验之前,我先学习了OpenGL的基本概念,包括OpenGL的坐标系统、图形渲染管线、着色器等。
了解这些概念对于后续的实验非常重要。
2. 创建窗口和上下文在OpenGL中,我们需要先创建一个窗口和一个OpenGL上下文,以便进行图形渲染。
通过调用相关的OpenGL函数,我成功创建了一个窗口,并初始化了OpenGL的上下文。
3. 绘制基本图形接下来,我开始尝试绘制一些基本的图形,比如点、线和三角形。
通过设置顶点坐标和颜色,我成功绘制出了这些基本图形,并在窗口中显示出来。
4. 添加纹理为了使图形更加逼真和丰富,我学习了如何在OpenGL中添加纹理。
通过加载图片并设置纹理坐标,我成功将纹理贴在了绘制的图形上,使其具有了更加真实的效果。
5. 光照和阴影效果为了增加图形的立体感和真实感,我学习了如何在OpenGL中添加光照和阴影效果。
通过设置光源的位置和属性,以及材质的属性,我成功实现了光照和阴影的效果,使图形看起来更加逼真。
6. 动画效果为了使图形具有动态效果,我学习了如何在OpenGL中实现简单的动画效果。
通过每帧更新顶点的位置和纹理坐标,我成功实现了图形的旋转和平移动画,使其具有了动态的效果。
四、实验结果和分析通过以上的实验过程,我成功掌握了OpenGL的基本概念和使用方法,并实现了一些基本的图形渲染效果。
opengl 图形的变换与裁剪

12
0 1/ sx 1 1 S −1 = S ( , ) = 0 1/ s y sx s y 0 0
复合二维变换
复合二维平移
3
关于齐次坐标
用一个n+1维向量表示一个n维向量
二维点(x,y),用(X,Y,ω)表示: (2,3)的齐次坐标表示可 以是(4,6,2)、(3,4.5,1.5) ω可以任意选取
齐次坐标与普通坐标之间是一一对应关系
x=X/ω y=Y/ω
ω
P
齐次坐标表示点的优势
防止浮点数溢出 矩阵变换的统一表示
X ω=1 平面 Y
局部坐标系可以简化物体的定义 物体={标准体素,变换}
造型变换:
物体从局部坐标系到世界坐标系的变换 三维线性和非线性变换
28
三维模型变换:平移
三维平移T:三维点P(x,y,z)移动(tx,ty,tz)后, 得到点P'(x',y',z')
x′ 1 ′ y = 0 z′ 0 1 0 0 1 0 0 0 t x x 0 t y y 1 t z z 0 1 1
y
P
P'
x
z
32
三维模型变换
绕z轴逆时针旋转θ角的旋转变换Rz (注: θ可以是(x,y,z)的函数)
x′ cosθ ′ y = sin θ z′ 0 1 0 − sin θ cosθ 0 0 0 0 x 0 0 y 1 0 z 0 1 1
计算机图形学实验报告

计算机图形学实验报告
在计算机图形学课程中,实验是不可或缺的一部分。
通过实验,我们可以更好地理解课程中所学的知识,并且在实践中掌握这些
知识。
在本次实验中,我学习了如何使用OpenGL绘制三维图形,并了解了一些基本的图形变换和视图变换。
首先,我们需要通过OpenGL的基本命令来绘制基本图形,例
如线段、矩形、圆等。
这些基本的绘制命令需要首先设置OpenGL 的状态,例如绘制颜色、线段宽度等,才能正确地绘制出所需的
图形。
然后,在实验中我们学习了图形的变换。
变换是指通过一定的
规则将图形的形状、位置、大小等进行改变。
我们可以通过平移、旋转、缩放等变换来改变图形。
变换需要按照一定的顺序进行,
例如先进行旋转再进行平移等。
在OpenGL中,我们可以通过设
置变换矩阵来完成图形的变换。
变换矩阵包含了平移、旋转、缩
放等信息,通过矩阵乘法可以完成图形的复合变换。
最后,视图变换是指将三维场景中的图形投影到二维平面上,
成为我们所见到的图形。
在实验中,我们学习了透视投影和正交
投影两种方式。
透视投影是指将场景中的图形按照视点不同而产
生不同的远近缩放,使得图形呈现出三维感。
而正交投影则是简单地将场景中的图形按照平行投影的方式呈现在屏幕上。
在OpenGL中,我们可以通过设置视图矩阵和投影矩阵来完成视图变换。
通过本次实验,我对于计算机图形学有了更深入的了解,并掌握了一些基本的图形绘制和变换知识。
在今后的学习中,我将继续学习更高级的图形绘制技术,并应用于实际的项目中。
第四章OpenGL图形变换-gluLookAt用法
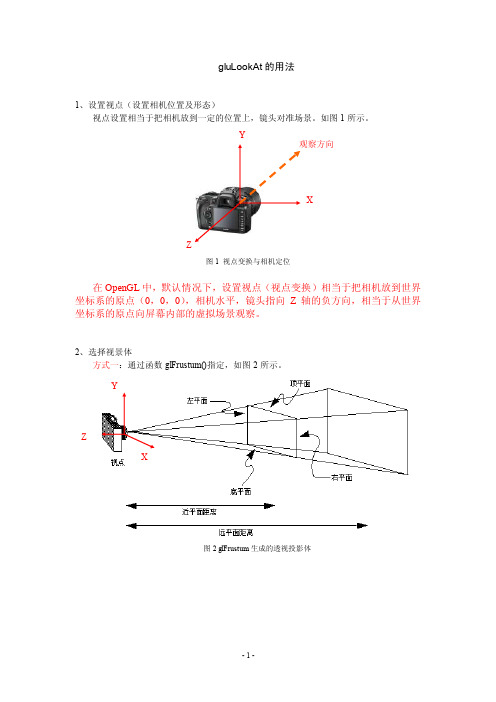
gluLookAt 的用法1、设置视点(设置相机位置及形态) 视点设置相当于把相机放到一定的位置上,镜头对准场景。
如图1所示。
图1 视点变换与相机定位在OpenGL 中,默认情况下,设置视点(视点变换)相当于把相机放到世界坐标系的原点(0,0,0),相机水平,镜头指向Z 轴的负方向,相当于从世界坐标系的原点向屏幕内部的虚拟场景观察。
2、选择视景体方式一:通过函数glFrustum()指定,如图2所示。
图2 glFrustum 生成的透视投影体YXZ Y YXZ观察方向方式二:通过函数gluPerspective 指定视景体,如图3所示。
图4-7 平行投影模型图图3 gluPerspective 生成的透视投影体YXZ Y3、移动景物(已实现)(借助于glTranslate 、glRotate 、glScale 等)移动前:图4 移动前物体移动后:图5 移动后物体(模型变换)XYX观察方向4、移动视点(移动相机)此处是我们要实现的功能。
用到的函数是:gluLookAt.函数原型:gluLookAt(GLdouble eyex, GLdouble eyey, Ldouble eyez,GLdouble centerx , GLdouble centery ,GLdouble centerz ,GLdouble upx , GLdouble upy ,GLdouble centerz );图6 gluLookAt示意图移动视点,就是调整相机的位置和形态,然后在新位置和方向处选择视景体,如下图所示。
图7 任意位置和形态的相机原始(默认)的相机位置可用如下语句来表述:gluLookAt(0, 0 , 0 ,0 , 0 , -1 ,0 , 1 ,0);简单的做法是:(1(2)在与Z轴负向平行的方向上选择观察中心点;也就是相机与观察中心点的连线形成的向量与X轴正向夹角为90度。
(3)移动相机假定此时,相机的位置为(eyex , eyey , eyez), 观察中心点的位置为(centerx , centery , centerz),R与X轴的夹角为90度。
第四章OpenGL图形变换(一)
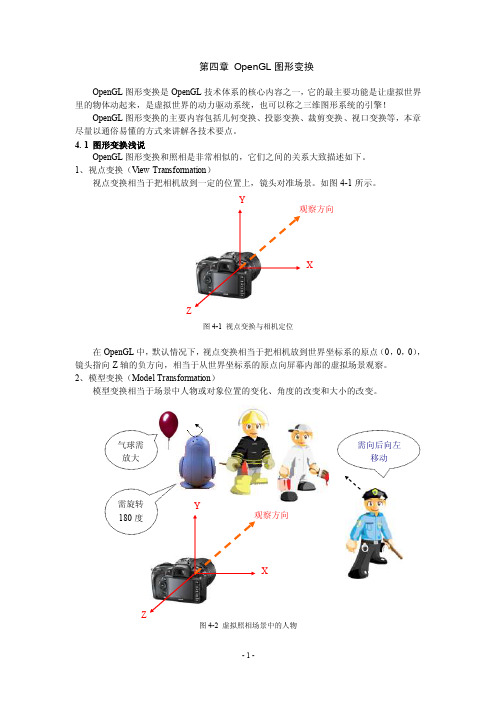
第四章 OpenGL 图形变换OpenGL 图形变换是OpenGL 技术体系的核心内容之一,它的最主要功能是让虚拟世界里的物体动起来,是虚拟世界的动力驱动系统,也可以称之三维图形系统的引擎!OpenGL 图形变换的主要内容包括几何变换、投影变换、裁剪变换、视口变换等,本章尽量以通俗易懂的方式来讲解各技术要点。
4. 1 图形变换浅说OpenGL 图形变换和照相是非常相似的,它们之间的关系大致描述如下。
1、视点变换(View Transformation ) 视点变换相当于把相机放到一定的位置上,镜头对准场景。
如图4-1所示。
图4-1 视点变换与相机定位在OpenGL中,默认情况下,视点变换相当于把相机放到世界坐标系的原点(0,0,0),镜头指向Z轴的负方向,相当于从世界坐标系的原点向屏幕内部的虚拟场景观察。
2、模型变换(Model Transformation)模型变换相当于场景中人物或对象位置的变化、角度的改变和大小的改变。
图4-2 虚拟照相场景中的人物YXZ观察方向X照相时场景中的人物或对象需要作调整,以便他们位于场景中合适的位置上。
有此时候人物不在视野范围内时,还要走动一下,进入镜头场景内,方向不对时,还要转动一下,眼睛转向镜头。
比如图4-2所示,照相时,警察不在镜头场景内,他需要向后向移动。
中间的企鹅背对镜头,他需要转过向来面向镜头。
企鹅向左边的气球中吹气,气球变大。
调整后的场景如图4-3所示。
图4-3 虚拟照相场景中的调整后人物或对象上述调整过程中的人员移动 和企鹅的转身动作 和气球充气变大 都属于模型变换。
3、投影变换(Projection Transformation ) 投影变换相当于调整相机镜头焦距,放大或缩小景物(如图4-4所示)。
图4-4 投影变换与相机焦距调整OpenGL 中投影变换的本质功能是定义一个视景体,使视景体外的多余部分被裁剪掉,再把景物变换到一个规则投影体(高、宽、深均为2个单位的立方体)。
基于OpenGL几何变换的虚拟漫游视点控制及应用

第2卷 8
Vo. 8 12
第2 4期
N O. 4 2
计算 机 工程 与设 计
Co mp t r g n e i g a d D e i n u e En i e rn n sg
20 年 1 月 07 2
D e .2 0 c 0 7
i c e t dt ee t o l in i a p id i o l iu l l t r u h b s d o a t l y tm n l . T ee e t f lt r u h h s i i s r a e d t c l so p l n s i v s a kh o g a e n p ri es se f al h f c k h o g a v d o c i s e wa c i y o wa v fe i g a d p e e a l e l i , wh c r v st a i t o a s a c f l n p l d v le t o x e t e l r f r b er a - me n n t i hp o e t h smeh d h s e e r h u d a p i a u s mee t n . h t r a e o K e r s wak h o g ; v e o n ; g o ti a s o ma i n ; Ocr e c l so e e to ; p ril se ywo d : ltru h iwp i t e merctn f r t s r o te ; o l i n d t ci n i atces tm y
T e iwp i t o to l g i l t r u h i c iv db s do r e dm e so a e me r a so a i n f e GL. T eOc e a h e o n n l n wak h o g a h e e a e nt e i nin l o ti tn f r t so Op n v c r i n s h g cr m o h t eht r t
计算机图形学OpenGL版实验1-4

实验1 OpenGL初识一、实验目的:熟悉编程环境;了解光栅图形显示器的特点;了解计算机绘图的特点;利用VC+OpenGL作为开发平台设计程序,以能够在屏幕上生成任意一个像素点为本实验的结束。
二、实验内容:(1)了解和使用VC的开发环境,理解简单的OpenGL程序结构。
(2)掌握OpenGL提供的基本图形函数,尤其是生成点的函数。
三、该程序的作用是在一个黑色的窗口中央画一个矩形、三角形和三个点,如图所示。
下面对各行语句进行说明:首先,需要包含头文件#include <GL/glut.h>,这是GLUT的头文件。
然后看main函数。
int main(int argc, char *argv[]),这个是带命令行参数的main函数。
这种以glut开头的函数都是GLUT工具包所提供的函数,下面对用到的几个函数进行介绍;1)glutInit,对GLUT进行初始化,这个函数必须在其它的GLUT使用之前调用一次。
其格式比较固定,一般都是glutInit(&argc, argv)就行;2) glutInitDisplayMode,设置显示方式,其中GLUT_RGB表示使用RGB颜色,与之对应的还有GLUT_INDEX(表示使用索引颜色)。
GLUT_SINGLE表示使用单缓冲,与之对应的还有GLUT_DOUBLE(使用双缓冲)。
更多信息,以后的实验教程会有讲解介绍;3) glutInitWindowPosition,设置窗口在屏幕中的位置;4) glutInitWindowSize,设置窗口的大小;5) glutCreateWindow,根据前述设置的信息创建窗口。
参数将被作为窗口的标题。
注意:窗口被创建后,并不立即显示到屏幕上。
需要调用glutMainLoop才能看到窗口;6) glutDisplayFunc,设置一个函数,当需要进行画图时,这个函数就会被调用。
(暂且这样理解);7) glutMainLoop,进行一个消息循环。
OpenGL空间(坐标系)变换

OpenGL空间(坐标系)变换⽹友的《3D图形学的学习策略》⼀⽂使我深受启发,在图形学以及openGL学习⽅⾯给了我很有价值的指导性意见,在此对前辈们的不吝赐教表⽰感激,谢谢你们的⽆私分享。
如⽂章所说,API是⼯具,不是本质,OpenGL/Direct3D的本质是图形学,⽽不是OpenGL/Direct3D的本⾝,API的本⾝只是⼀些Interface⽽已。
最重要的,最根本的是,你要明⽩这些API背后的图形学的原理---因为那才是根本中的根本。
其实很多事情,包括学习也涉及到⽣活,只有抓住了本质,才能体会到其中的真谛。
带着这种希望探究本质的学习⽅法,结合图形学原理,通过阅读书⽬和⽹友们的⽂章,我对OpenGL⼏何空间变换进⾏了总结性的学习。
OpenGL处理管线的⽬的是将对象的三维描述转换为可以显⽰的⼆维图像。
为了完成这个从三维到⼆维的转换,OpenGL 使⽤了多个空间(坐标系),每个空间完成特定的任务,从⼀个空间到另⼀个空间需要进⾏空间转换。
理解OpenGL所使⽤的各种空间以及它们间的变换是⾮常重要的。
如上图所⽰,openGL中使⽤的空间依次是:对象空间、世界空间、视点空间、裁剪空间、归⼀化设备空间、窗⼝空间、屏幕空间。
结合⾃⼰的理解,就每个空间完成的基本任务和空间的变换关系,总结如下。
对象空间。
对象空间中完成的最⼤任务是对象建模,三维对象的属性,包括顶点位置和表⾯法线等是在这个空间内指定的。
这个空间的坐标原点⼀般在对象上,有时候也在其他地⽅,主要是为了建模⽅便。
每⼀个对象都有⼀个⾃⼰的对象空间。
就openGL⽽⾔,我⽬前还没有接触到建⽴很复杂模型的应⽤,建模⼀般在其他地⽅如3DMAX中完成,然后读⼊openGL进⾏处理。
世界空间。
对象空间之后是世界空间,我理解为世界坐标系是固定不变的。
世界空间主要是对三维场景进⾏描述,就是把已经建⽴的各种对象摆放在三维空间中,空间的转换是通过模型变换完成的。
可以通过平移、旋转、⽐例缩放等把对象摆放在需要的位置,就好像买好家具以后设计房间布局⼀样。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验OpenGL几变换
1.实验目的:
理解掌握一个OpenGL程序平移、旋转、缩放变换的法。
2.实验容:
(1)阅读实验原理,运行示实验代码,掌握OpenGL程序平移、旋转、缩放变换的法;
(2)根据示代码,尝试完成实验作业;
3.实验原理:
(1)OpenGL下的几变换
在OpenGL的核心库中,每一种几变换都有一个独立的函数,所有变换都在三维空间中定义。
平移矩阵构造函数为glTranslate<f,d>(tx, ty, tz),作用是把当前矩阵和一个表示移动物体的矩阵相乘。
tx, ty,tz指定这个移动物体的矩阵,它们可以是任意的实数值,后缀为f(单精度浮点float)或d(双精度浮点double),对于二维应用来说,tz=0.0。
旋转矩阵构造函数为glRotate<f,d>(theta, vx, vy, vz),作用是把当前矩阵和一个表示旋转物体的矩阵相乘。
theta, vx, vy, vz指定这个旋转物体的矩阵,物体将绕着(0,0,0)到(x,y,z)的直线以逆时针旋转,参数theta表示旋转的角度。
向量v=(vx, vy,vz)的分量可以是任意的实数值,该向量用于定义通过坐标原点的旋转轴的向,后缀为f(单精度浮点float)或d(双精度浮点double),对于二维旋转来说,vx=0.0,vy=0.0,vz=1.0。
缩放矩阵构造函数为glScale<f,d>(sx, sy, sz),作用是把当前矩阵和一个表示缩放物体的矩阵相乘。
sx, sy,sz指定这个缩放物体的矩阵,分别表示在x,y,z向上的缩放比例,它们可以是任意的实数值,当缩放参数为负值时,该函数为反射矩阵,缩放相对于原点进行,后缀为f(单精度浮点float)或d(双精度浮点double)。
注意这里都是说“把当前矩阵和一个表示移动<旋转, 缩放>物体的矩阵相乘”,而不是直接说“这个函数就是旋转”或者“这个函数就是移动”,这是有原因的,马上就会讲到。
假设当前矩阵为单位矩阵,然后先乘以一个表示旋转的矩阵R,再乘以一个表示移动的矩阵T,最后得到的矩阵再乘上每一个顶点的坐标矩阵v。
那么,经过变换得到的顶点坐标就是((RT)v)。
由于矩阵乘法满足结合率,((RT)v) = R(Tv)),换句话说,实际上是先进行移动,然后进行旋转。
即:实际变换的顺序与代码中写的
顺序是相反的。
由于“先移动后旋转”和“先旋转后移动”得到的结果很可能不同,初学的时候需要特别注意这一点。
(2)OpenGL下的各种变换简介
我们生活在一个三维的世界——如果要观察一个物体,我们可以:
1、从不同的位置去观察它(人运动,选定某个位置去看)。
(视图变换)
2、移动或者旋转它,当然了,如果它只是计算机里面的物体,我们还可以放大或缩小它(物体运动,让人看它的不同部分)。
(模型变换)
3、如果把物体画下来,我们可以选择:是否需要一种“近大远小”的透视效果。
另外,我们可能只希望看到物体的一部分,而不是全部(指定看的围)。
(投影变换)
4、我们可能希望把整个看到的图形画下来,但它只占据纸的一部分,而不是全部(指定在显示器窗口的那个位置显示)。
(视口变换)
这些,都可以在OpenGL中实现。
从“相对移动”的观点来看,改变观察点的位置与向和改变物体本身的位置与向具有等效性。
在OpenGL中,实现这两种功能甚至使用的是同样的函数。
由于模型和视图的变换都通过矩阵运算来实现,在进行变换前,应先设置当前操作的矩阵为“模型视图矩阵”。
设置的法是以GL_MODELVIEW为参数调用glMatrixMode函数,像这样:
glMatrixMode(GL_MODELVIEW);
该语句指定一个4×4的建模矩阵作为当前矩阵。
通常,我们需要在进行变换前把当前矩阵设置为单位矩阵。
把当前矩阵设置为单位矩阵的函数为:glLoadIdentity();
我们在进行矩阵操作时,有可能需要先保存某个矩阵,过一段时间再恢复它。
当我们需要保存时,调用glPushMatrix()函数,它相当于把当前矩阵压入堆栈。
当需要恢复最近一次的保存时,调用glPopMatrix
()函数,它相当于从堆栈栈顶弹出一个矩阵为当前矩阵。
OpenGL规定堆栈的容量至少可以容纳32个矩阵,某些OpenGL实现中,堆栈的容量实际上超过了32个。
因此不必过于担心矩阵的容量问题。
通常,用这种先保存后恢复的措施,比先变换再逆变换要更便,更快速。
注意:模型视图矩阵和投影矩阵都有相应的堆栈。
使用glMatrixMode来指定当前操作的究竟是模型视图矩阵还是投影矩阵。
4.示代码:
(1)、Translate示例
生成图形:
注意理解:myDraw1()和myDraw2()生成的图形完全相同,为什么?
(2)、Rotate示例
生成图形:
注意理解:myDraw1()和myDraw2()生成的图形完全相同,为什么?
(3)、Scale示例
生成图形:
注意理解:myDraw1()和myDraw2()生成的图形完全相同,为什么?
(4)、综合示例
生成图形:
5. 实验作业:
绘制如下图形:
(2)用几变换绘制三个不同位置、旋转角度、颜色的菱形。
