逻辑代数的基本公式和常用公式
2逻辑代数公式定理+3逻辑代数的基本定理+4逻辑函数及其描述方法

2.5.2 逻辑函数的表示方法
• 真值表 • 逻辑式 • 逻辑图 • 波形图 • 卡诺图 • 计算机软件中的描述方式
• 各种表示方法之间可以相互转换
2.5.2 逻辑函数的表示方法
• 真值表
“或”真值表 A BL 0 00 0 11 1 01 1 11
5本继页续完
逻辑代数的基本公式和常用公式
一、基本公式 1.常量与变量间的运算规则: 或运算一定、律逻辑代数的基本定律 A+0=A;A+1=和1恒;等式 与运算定1律.常数间的运算定律 A•0=0;A •1=A;
令 A=0 和 1 , 代入逻辑加法各 式,然后参考 “或”真值表和 “与”真值表可 以证明各式成立。
“与”2真.基值本表可 以证明定各律式和成立。
恒等式 表律详是2.3见根.摩1课,据例 根本基逻: 定P本辑2定加4 、 乘、非三律种基本
运算法则,推导 出的逻辑运算的 一些基本定律。
9本继页续完
逻辑代数公式定理及公式化简法
基本定律和恒等式的证明
摩根定律的证明
基本定律和恒等式的证明最 有效的方法是检验等式左边的 函数与右边函数的真值表是否 吻合。
逻辑代数的基本公式和常用公式
一、基本公式 4.摩根定律 例:摩根定律(反演律)
(A·B·C···)’=A’+B’+C’+···
(A+B+C+···)’=A’·B’·C’····
利用摩根定律可以把“与”运算变 换为“或”运算,也可以把“或”运 算变换为“与”运算,其逻辑结果不 变。
令 A=0 和 1 , 代入逻辑加法各 式,然后参考 “或”真值表和
逻辑代数基础

所得到的图形叫n变量的卡诺图。
逻辑相邻的最小项:如果两个最小项只有一个变量互为反变 量,那么,就称这两个最小项在逻辑上相邻。 如最小项 m6=ABC、与
m7 =ABC 在逻辑上相邻 m7
m6
两变量卡诺图 AB 0 1 m0 m1 0 AB AB 1 mB AB A 2 m3 三变量卡诺图 B
四变量卡诺图 CD AB 00 01 11 10 00 m0 m1 m3 m2 01 m4 m5 m7 m6 A 11 m12 m13 m15 m14
b.去括号
ABC ABC AB
ABC ABC AB(C C )
ABC ABC ABC ABC
m3 m5 m7 m6 m(3,5,6,7)
三、 用卡诺图表示逻辑函数
1、卡诺图的引出 卡诺图:将n变量的全部最小项都填入小方格内,并使具有 逻辑相邻的最小项在几何位置上也相邻地排列起来,这样,
L CD 00 01 AB 00 1 1 01 11 10 1 0 1 0 0 0 11 10 1 0 1 1 1 0 1 1
例2 画出下式的卡诺图
L ( A, B, C , D) ( A B C D)( A B C D)( A B C D)
解
( A B C D)( A B C D) 1. 将逻辑函数化为最小项表达式
结合律:A + B + C = (A + B) + C
A · · = (A · · B C B) C
A 分配律: ( B + C ) = AB + AC
A + BC = ( A + B )( A + C )
2.3-2.5 逻辑代数的公式、定理、表示方法

0 1 2 3 4 5 6 7
m0 m1 m2 m3 m4 m5 m6 m7
④ 具有相邻性的两个最小项之和可以合 ① 在输入变量的任何取值下有一个最小 ③ 任意两个最小项的乘积为0。 ② 全体最小项和为1。 并成一项并消去一对因子。 项,而且仅有一个最小项的值为1。
二、最大项
在n变量逻辑函数中,若M为n个变量之 和,而且这n个变量均以原变量或反变 量的形式在M中出现一次,则称M为该 组变量的最大项。
?
思考: 2 个。 n个变量的最小项有多少个?
n
三变量(A、B、C)最小项的编号表:
相 邻
A' B ' C ' A' B ' C A' BC ' A' BC AB' C ' AB' C ABC' ABC
相 邻
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
证明: A A' B ( A A' )( A B)
A B
两个乘积项相加时,如果一项取反后是另一 项的因子,则此因子是多余的,可以消去。
(23) AB AB' A
当两个乘积项相加时,若它们分别包含B和B’ 两个因子而其他因子相同,则两项定能合并,且 可将B和B’消去。
(24) A( A B) A
小结: 掌握逻辑代数的基本公式和常用公式。
§ 2.4 逻辑代数的基本定理
2.4.1 代入定理
在任何一个包含A的逻辑等式中,若以另外
一个逻辑式代入式中A的位置,则等式依然成 立。
例如,已知 ( A B) A B (反演律),若用B+C代替 等式中的B,则可以得到适用于多变量的反演律, 即
「逻辑代数的基本公式和常用公式」

「逻辑代数的基本公式和常用公式」逻辑代数是研究逻辑运算的数学分支。
逻辑代数的基本公式和常用公式是逻辑代数中最常用的一些公式,它们用于简化和分析逻辑表达式,辅助求解逻辑问题。
以下是逻辑代数的基本公式和常用公式的详细介绍:一、基本公式:1. 同一律(Identity Law): A+0=A, A*1=A这个公式表示如果一个逻辑变量和零(逻辑或操作的恒等元素)进行逻辑或操作,或者和一(逻辑与操作的恒等元素)进行逻辑与操作,其结果仍然是这个变量本身。
2. 吸收律(Absorption Law): A+A*B = A, A*(A+B) = A吸收律表示在逻辑或操作中,如果一个变量和另外一个变量的逻辑与结果进行逻辑或操作,结果等于这个变量本身。
同样的,在逻辑与操作中,如果一个变量和一个逻辑或表达式的逻辑与结果进行逻辑与操作,结果也等于这个变量本身。
3. 同向性(Idempotent Law): A+A=A, A*A=A同向性表明在逻辑或操作或逻辑与操作中,对同一个变量连续进行这些操作多次,结果不变。
4. 零律(Zero Law): A+~A=1, A*~A=0零律表示对于任意逻辑变量,与其否定进行逻辑或操作的结果为真,与其否定进行逻辑与操作的结果为假。
5. 恒等律(Identity Law): A*~A=0, A+~A=1恒等律表示对于任意逻辑变量,与其否定进行逻辑与操作的结果为假,与其否定进行逻辑或操作的结果为真。
1. 分配律(Distribution Law): A*(B+C) = A*B + A*C, A+(B*C)= (A+B) * (A+C)分配律是逻辑代数中常用的一组公式,它们表示逻辑与操作和逻辑或操作之间的分配关系。
2. 德摩根定律(De Morgan's law):~(A+B) = ~A * ~B, ~(A*B) = ~A + ~B德摩根定律是逻辑代数中非常重要的定理,它们表示逻辑或操作和逻辑与操作之间的否定关系。
数字电路知识点总结(精华版)

数字电路知识点总结(精华版)数字电路知识点总结(精华版)第一章数字逻辑概论一、进位计数制1.十进制与二进制数的转换2.二进制数与十进制数的转换3.二进制数与十六进制数的转换二、基本逻辑门电路第二章逻辑代数逻辑函数的表示方法有:真值表、函数表达式、卡诺图、逻辑图和波形图等。
一、逻辑代数的基本公式和常用公式1.常量与变量的关系A + 0 = A,A × 1 = AA + 1 = 1,A × 0 = 02.与普通代数相运算规律a。
交换律:A + B = B + A,A × B = B × Ab。
结合律:(A + B) + C = A + (B + C),(A × B) × C = A ×(B × C)c。
分配律:A × (B + C) = A × B + A × C,A + B × C = (A + B) × (A + C)3.逻辑函数的特殊规律a。
同一律:A + A = Ab。
摩根定律:A + B = A × B,A × B = A + Bc。
关于否定的性质:A = A'二、逻辑函数的基本规则代入规则在任何一个逻辑等式中,如果将等式两边同时出现某一变量 A 的地方,都用一个函数 L 表示,则等式仍然成立,这个规则称为代入规则。
例如:A × B ⊕ C + A × B ⊕ C,可令 L = B ⊕ C,则上式变成 A × L + A × L = A ⊕ L = A ⊕ B ⊕ C。
三、逻辑函数的化简——公式化简法公式化简法就是利用逻辑函数的基本公式和常用公式化简逻辑函数,通常,我们将逻辑函数化简为最简的与或表达式。
1.合并项法利用 A + A' = 1 或 A × A' = 0,将二项合并为一项,合并时可消去一个变量。
数电期末总结基础知识要点

数电期末总结基础知识要点数字电路各章知识点第1章逻辑代数基础⼀、数制和码制1.⼆进制和⼗进制、⼗六进制的相互转换 2.补码的表⽰和计算 3.8421码表⽰⼆、逻辑代数的运算规则1.逻辑代数的三种基本运算:与、或、⾮ 2.逻辑代数的基本公式和常⽤公式逻辑代数的基本公式(P10)逻辑代数常⽤公式:吸收律:A AB A =+消去律:AB B A A =+ A B A AB =+ 多余项定律:C A AB BC C A AB +=++ 反演定律:B A AB += B A B A ?=+ B A AB B A B A +=+ 三、逻辑函数的三种表⽰⽅法及其互相转换★逻辑函数的三种表⽰⽅法为:真值表、函数式、逻辑图会从这三种中任⼀种推出其它⼆种,详见例1-6、例1-7 逻辑函数的最⼩项表⽰法四、逻辑函数的化简:★1、利⽤公式法对逻辑函数进⾏化简2、利⽤卡诺图队逻辑函数化简3、具有约束条件的逻辑函数化简例1.1利⽤公式法化简 BD C D A B A C B A ABCD F ++++=)(解:BD C D A B A C B A ABCD F ++++=)(BD C D A B A B A ++++= )(C B A C C B A +=+ BD C D A B +++= )(B B A B A =+ C D A D B +++= )(D B BD B +=+ C D B ++= )(D D A D =+ 例1.2 利⽤卡诺图化简逻辑函数 ∑=)107653()(、、、、m ABCD Y 约束条件为∑8)4210(、、、、m 解:函数Y 的卡诺图如下:00 01 11 1000011110AB CD111×11××××D B A Y +=第2章集成门电路⼀、三极管如开、关状态 1、饱和、截⽌条件:截⽌:beT VV < 饱和:CSBSB Ii Iβ>=2、反相器饱和、截⽌判断⼆、基本门电路及其逻辑符号★与门、或⾮门、⾮门、与⾮门、OC 门、三态门、异或、传输门(详见附表:电⽓图⽤图形符号 P321 )⼆、门电路的外特性★1、电阻特性:对TTL 门电路⽽⾔,输⼊端接电阻时,由于输⼊电流流过该电阻,会在电阻上产⽣压降,当电阻⼤于开门电阻时,相当于逻辑⾼电平。
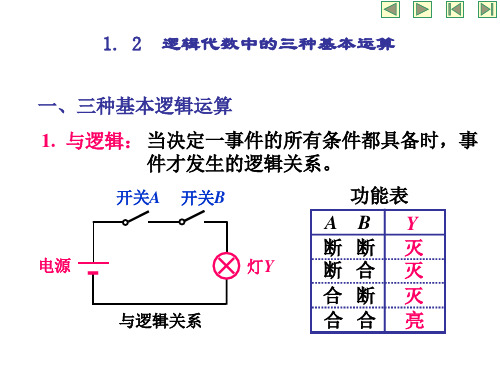
逻辑代数中的三种基本运算
& ≥1
Y3
(真值表略)
(4) 异或逻辑 A
=1
(Exclusive—OR) B
Y4 A B AB AB
(5) 同或逻辑 (异或非)
(Exclusive—NOR)
Y5 A B
A B
=1
AB AB
= A⊙B
Y4
A B Y4 00 0
01 1
10 1
11 0
A B Y5
) A
公式 (4) 证明: AB AC BC AB AC
左 AB AC ( A A) BC A AB A AB AC ABC ABC AB AC
推论
AB AC BCD AB AC
公式 (5) 证明: AB AB A B AB
左 AB AB ( A B) ( A B)
A A A B AB B B A B AB 即 A B = A⊙B 同理可证 A⊙B A B
六、关于异或运算的一些公式
异或 A B AB AB A B = A⊙B 同或 A⊙B AB A B A⊙B A B (1) 交换律 A B B A
(2) 结合律 ( A B) C A ( B C ) (3) 分配律 A ( B C) AB AC
(4) 常量和变量的异或运算 A 1 A A 0 A
(5) 因果互换律
如果 A B C
A A 0 A A 1
则有 A C B BC A
电源
开关B
灯Y
逻
或逻辑关系
辑A 符B
≥1
Y
号
或门(OR gate)
数电基础---逻辑代数

数电基础---逻辑代数介绍逻辑代数中基本的逻辑运算,基本公式,常⽤公式和基本定理。
逻辑门简单的逻辑门逻辑代数的基本运算有与(AND),或(OR),⾮(NOT)三种。
“与”门只有决定事物结果的全部条件同时具备时,结果才发⽣,这种因果关系称为逻辑与,或者称逻辑相乘。
逻辑真值表为A B Y000010100111其中A,B为输⼊,Y为输出。
在逻辑代数中,以“⋅”表⽰与运算。
A与B进⾏与逻辑运算时可以写成Y=A⋅B表⽰符号为为了简化书写,允许将A⋅B简写成AB,略去逻辑相乘的运算符号“⋅”。
"或"门在决定事物结果的诸条件中只要有任何⼀个满⾜,结果就会发⽣,这种因果关系称为逻辑或,或者称逻辑相加。
逻辑真值表为A B Y000011101111其中A,B为输⼊,Y为输出。
在逻辑代数中,以“+”表⽰或运算。
A与B进⾏或逻辑运算时可以写成Y=A+B表⽰符号为"⾮"门只要条件具备了,结果就不会发⽣,⽽条件不具备时,结果就⼀定发⽣,这种因果关系称为逻辑⾮,或者称逻辑相反。
逻辑真值表为A Y0110其中A为输⼊,Y为输出。
在逻辑代数中,以“′”表⽰⾮运算。
A进⾏⾮逻辑运算时可以写成Y=A′表⽰符号为复合逻辑门最常见的复合逻辑运算有与⾮(NAND),或⾮(NOR),与或⾮(AND-NOR),异或(EXCLUSIVE OR//XOR),同或(EXCLUSIVE NOR//XNOR )等。
“与⾮”门与⾮操作,将A,B先进⾏与运算,然后将结果求反,最后得到的即为A,B的与⾮运算结果。
(先与后⾮)逻辑真值表A B Y001011101110其中A,B为输⼊,Y为输出。
A与B进⾏与⾮逻辑运算时可以写成Y=(A⋅B)′表⽰符号为实际上可以把与⾮运算看作是与运算和⾮运算的组合,图形符号上的⼩圆圈表⽰⾮运算。
(后⾯会提到,可以将图像上的⼩圆圈看成⼀个⾮门) "或⾮"门或⾮操作,将A,B先进⾏或运算,然后将结果求反,最后得到的即为A,B的或⾮运算结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
逻辑代数的基本公式和常用公式
一.基本定义与运算
代数是以字母代替数,称因变量为自变量的函数,函数有定义域和值域。
——这些都是大家耳熟能详的概念。
如
或;
当自变量的取值(定义域)只有0和1(非0即1)函数的取值也只有0和1(非0即1)两个数——这种代数就是逻辑代数,这种变量就是逻辑变量,这种函数就是逻辑函数。
逻辑代数,亦称布尔代数,是英国数学家乔治布尔(George Boole)于1849年创立的。
在当时,这种代数纯粹是一种数学游戏,自然没有物理意义,也没有现实意义。
在其诞生100多年后才发现其应用和价值。
其规定:
1.所有可能出现的数只有0和1两个。
2.基本运算只有“与”、“或”、“非”三种。
与运算(逻辑与、逻辑乘)定义为(为与运算符,后用代替)
00=0 01=0 10=0 11=1 或
00=0 01=0 10=0 11=1
或运算(逻辑或、逻辑加)定义为(为或运算符,后用+代替)
00=0 01=1 10=1 11=1 或
0+0=0 0+1=1 1+0=1 1+1=1
非运算(取反)定义为:
至此布尔代数宣告诞生。
二、基本公式
如果用字母来代替数(字母的取值非0即1),根据布尔定义的三种基本运算,我们马上可推出下列基本公式:
A A=A A+A=A
A0=0 A+0=A
A1=A A+1=1
=+=
上述公式的证明可用穷举法。
如果对字母变量所有可能的取值,等式两边始终相等,该公
式即告成立。
现以=+为例进行证明。
对A、B两个逻辑变量,其所有可能的取值为00、01、10、11四种(不可能有第五种情况)列表如下:
由此可知:
=+
成立。
用上述方法读者很容易证明:
三、常用公式
1.
左边==右边
2.
左边==右边
例题:将下列函数化为最简与或表达式。
(公式1:)
= (公式2:)
()
练习题:
3.异或运算和同或运算(放到最小项卡诺图中讲)四、逻辑函数
1.定义:如果有若干个逻辑变量(如A、B、C、D)按与、或、非三种基本运算组合在一起,得到一个表达式L。
对逻辑变量的任意一组取值(如0000、0001、0010)L有唯一的值与之对应,则称L为逻辑函数。
逻辑变量A、B、C、D的逻辑函数记为:
L=f(A、B、C、D)
2.真值表:
在举重比赛中,通常设三名裁判:一名为主裁,另两名为副裁。
竞赛规则规定运动员每次试举必须获得主裁及至少一名副裁的认可,方算成功。
裁判员的态度只能同意和不同意两种;运动员的试举也只有成功与失败两种情况。
举重问题可用逻辑代数加以描述:
用A、B、C三个逻辑变量表示主副三裁判:取值1表示同意(成功),取值0表示不同意(失败—)。
举重运动员用L表示,取值1表示成功,0表示失败。
显然,L由A、B、C决定。
L为A、B、C 的逻辑函数。
列表如下:
该表称为逻辑函数L的真值表。
注意:真值表必须列出逻辑变量所有可能的取值所对应的函数值,不能有遗漏。
(二个变量有22=4,三个逻辑变量有23=8,四个变量有24=16种可能的取值……)
3.由真值表写出逻辑表达式:
从真值表可看出L取值为1只有三项,A、B、C的取值分别为101、110、和111三种情况L
才等于1。
、、三项与上述三种取值对应。
练习:1.已知函数Y=C(D+E)列出其真值表。
2.写出与下列真值表相对应的逻辑表达式并化简:
A B C Y
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 0
例:三个开关控制一个灯的电路如下图所示。
试用逻辑代数(数学)对该电路进行描述。
解:如果规定开关合上用1表示,断开用0表示;灯亮用1表示,灯灭用0表示。
显然该问题是一个逻辑问题。
L是K1、K2、K3三变量的逻辑函数,所以可以直接写出
L= K1(K2+K3)
我们也可以列出真值表:
显然这就是举重裁判的控制电路。
并联的开关可用或运算,串联的开关可用与运算来描述。
