学而思培优 2017-2018 一年级数学知识点第九讲
学而思初一数学春季班第9讲-目标满分班-教师版

三角形1级几何基础图形三角形的认识三角形2级三角形两大模型三角形3级三角形三大专题春季班第十一讲春季班第十讲色盲检测漫画释义满分晋级阶梯9几何基础图形——三角形的认识定 义示例剖析三角形的定义:由三条不在..同一条直线上的线段首尾顺次....连结组成的平面图形叫做三角形.三角形具有稳定性.... 表示法及读法:三角形用符号“△”表示,顶点是A 、B 、C 的三角形记作“ ABC △ ”,读作“三角形ABC ”.ABC △的三边有时也用a ,b ,c 表示.顶点A 的对边a (BC ) 顶点B 的对边b(AC ) 顶点C 的对边c (AB ) 三角形的内角:三角形的每两条边所组成的角叫做三角形的内角,简称三角形的角.,,A B C ∠∠∠是三角形的内角c b aCBA 思路导航知识互联网题型一:三角形的边A BC教师总结:根据三角形三边关系的相关考点考点一、已知两边求第三边的取值范围或边长例1、用三条绳子打结成三角形(不考虑结头长),已知两根分别为3cm,7cm,求第三根长度有什么限制.【解析】设第三根绳子长为xcm,有7-3<x<7+3,有4<x<10.例2、已知三角形两边长为3cm,6cm,且第三边为奇数,求第三边的长度.【解析】第三边为5cm或7cm考点二、判断三条线段能否构成三角形例3、以下列各组线段为边,能构成三角形的是()A.1cm,2cm,4cmB.8cm,6cm,4cmC.12cm,5cm,6cmD.8cm,6cm,2cm【解析】B考点三、确定三角形的个数问题例4、长度分别为2cm、3cm、4cm、5cm的木棒,从中任意取三根,能组成多少个三角形?【解析】从四根木棒中取三根,共有四种取法,分别是:①2cm、3cm、4cm;②2cm、3cm、5cm.③3cm、4cm、5cm;④2cm、4cm、5cm.其中①、③、④符合三角形三边关系,因此可以组成三个三角形.考点四、化简代数式问题如例2、⑶⑷考点五、三角形边的不等关系如思维拓展,训练2例题精讲【引例】一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长的最小值是()A.14 B.15 C.16 D.17【解析】根据三角形的第三边大于两边之差且小于两边之和,可得第三边的取值范围是410c<<,在这一范围内满足第三边是整数的点分别是5、6、7、8、9,而三角形的周长要取最小值,即当第三边5c=时,这个三角形周长最小,是3+5+7=15,故选B.典题精练【例1】 ⑴下列长度的三条线段能组成三角形的是( )A .1cm ,2cm ,5cmB .4cm ,5cm ,9cmC .5cm ,8cm ,15cmD .6cm ,8cm ,9cm⑵下列线段能组成三角形的是 .①123,, ②234,, ③222345,, ④222123(0)a a a a +++≠,,⑶已知三角形三边长分别为4,5,x ,则x 的取值范围是 。
学而思小学奥数个精彩讲座总汇全

第1讲计算综合(一)繁分数的运算,涉及分数与小数的定义新运算问题,综合性较强的计算问题.1.繁分数的运算必须注意多级分数的处理,如下所示:甚至可以简单地说:“先算短分数线的,后算长分数线的”.找到最长的分数线,将其上视为分子,其下视为分母.2.一般情况下进行分数的乘、除运算使用真分数或假分数,而不使用带分数.所以需将带分数化为假分数.3.某些时候将分数线视为除号,可使繁分数的运算更加直观.4.对于定义新运算,我们只需按题中的定义进行运算即可.5.本讲要求大家对分数运算有很好的掌握,可参阅《思维导引详解》五年级[第1讲循环小数与分数].1.计算:71147 18262 13581333416⨯+⨯-÷【分析与解】原式=7123723174612241488128131233+⨯=⨯=-2.计算:【分析与解】注意,作为被除数的这个繁分数的分子、分母均含有5199.于是,我们想到改变运算顺序,如果分子与分母在5199后的两个数字的运算结果一致,那么作为被除数的这个繁分数的值为1;如果不一致,也不会增加我们的计算量.所以我们决定改变作为被除数的繁分数的运算顺序.而作为除数的繁分数,我们注意两个加数的分母相似,于是统一通分为1995×.具体过程如下:原式=5919(3 5.22)19930.41.6910()52719950.5199519(6 5.22)950+-⨯÷+⨯-+=5191.3219930.440.40.59()519950.419950.5191.329-⨯⨯⨯÷+⨯⨯-=199320.41()19950.5+÷⨯=0.410.5÷=1143.计算:1111111987-+-【分析与解】原式=11198711986-+=198613973-=198739734.计算:已知=181111+12+1x+4=,则x等于多少【分析与解】方法一:1118x68114x112x7111+11148x62+214x1x+4+====+++++++交叉相乘有88x+66=96x+56,x=1.25.方法二:有11131118821x4+==+++,所以18222133x4+==++;所以13x42+=,那么x=.5.求944,43,443,...,44 (43)个这10个数的和.【分析与解】方法一:944+43+443...44 (43)++个=1044(441)(4441)...(44...41)+-+-++-个=104444444...44 (49)++++-个=1094(999999...999...9)99⨯++++-个=1004[(101)(1001)(10001)...(1000...01)]99⨯-+-+-++--个=914111.1009=49382715919⨯-个.方法二:先计算这10个数的个位数字和为39+4=31⨯;再计算这10个数的十位数字和为4×9=36,加上个位的进位的3,为36339+=;再计算这10个数的百位数字和为4×8=32,加上十位的进位的3,为32335+=;再计算这10个数的千位数字和为4×7=28,加上百位的进位的3,为28331+=;再计算这10个数的万位数字和为4×6=24,加上千位的进位的3,为24327+=;再计算这10个数的十万位数字和为4×5=20,加上万位的进位的2,为20222+=;再计算这10个数的百万位数字和为4×4=16,加上十万位的进位的2,为16218+=;再计算这10个数的千万位数字和为4×3=12,加上百万位的进位的1,为12113+=;再计算这10个数的亿位数字和为4×2=8,加上千万位的进位的1,为819+=;最后计算这10个数的十亿位数字和为4×1=4,加上亿位上没有进位,即为4.所以,这10个数的和为91.6.如图1-1,每一线段的端点上两数之和算作线段的长度,那么图中6条线段的长度之和是多少【分析与解】因为每个端点均有三条线段通过,所以这6条线段的长度之和为:1173(0.60.875)1+0.75+1.8+2.625=6.175=63440⨯+++=7.我们规定,符号“○”表示选择两数中较大数的运算,例如:3.5○=○=.符号“△”表示选择两数中较小数的运算,例如:△=△=.请计算:23155 (0.625)(0.4)33384 1235(0.3)( 2.25) 3104⨯+【分析与解】原式1550.6255155725384218384122562.253⨯=⨯÷=+8.规定(3)=2×3×4,(4)=3×4×5,(5)=4×5×6,(10)=9×10×11,….如果111(16)(17)(17)-=⨯,那么方框内应填的数是多少【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9.从和式11111124681012+++++中必须去掉哪两个分数,才能使得余下的分数之和等于1【分析与解】因为1116124+=,所以12,14,16,112的和为l,因此应去掉18与110.10.如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数,例如.那么在所有这种数中。
小学学而思奥数36个精彩讲座总汇

第1讲计算综合(一)繁分数的运算,涉及分数与小数的定义新运算问题,综合性较强的计算问题.1.繁分数的运算必须注意多级分数的处理,如下所示:甚至可以简单地说:“先算短分数线的,后算长分数线的”.找到最长的分数线,将其上视为分子,其下视为分母.2.一般情况下进行分数的乘、除运算使用真分数或假分数,而不使用带分数.所以需将带分数化为假分数.3.某些时候将分数线视为除号,可使繁分数的运算更加直观.4.对于定义新运算,我们只需按题中的定义进行运算即可.5.本讲要求大家对分数运算有很好的掌握,可参阅《思维导引详解》五年级[第1讲循环小数与分数].1.计算:71147 18262 13581333416⨯+⨯-÷【分析与解】原式=7123723174612241488128131233+⨯=⨯=-2.计算:【分析与解】注意,作为被除数的这个繁分数的分子、分母均含有5199.于是,我们想到改变运算顺序,如果分子与分母在5199后的两个数字的运算结果一致,那么作为被除数的这个繁分数的值为1;如果不一致,也不会增加我们的计算量.所以我们决定改变作为被除数的繁分数的运算顺序.而作为除数的繁分数,我们注意两个加数的分母相似,于是统一通分为1995×0.5.具体过程如下:原式=5919(3 5.22)19930.41.6 910()52719950.51995 19(6 5.22)950+-⨯÷+⨯-+=5 191.3219930.440.40.59()519950.419950.5191.329-⨯⨯⨯÷+⨯⨯-=199320.41()19950.5+÷⨯=0.410.5÷=1143.计算:1111111987-+-【分析与解】原式=11198711986-+=198613973-=198739734.计算:已知=181111+12+1x+4=,则x等于多少?【分析与解】方法一:1118x68114x112x7111+11148x62+214x1x+4+====+++++++交叉相乘有88x+66=96x+56,x=1.25.方法二:有11131118821x4+==+++,所以18222133x4+==++;所以13x42+=,那么x=1.25.5.求944,43,443,...,44 (43)个这10个数的和.【分析与解】方法一:944+43+443...44...43++个=1044(441)(4441)...(44...41)+-+-++-个=104444444...44...49++++-个=1094(999999...999...9)99⨯++++-个=1004[(101)(1001)(10001)...(1000...01)]99⨯-+-+-++--个 =914111.1009=49382715919⨯-个.方法二:先计算这10个数的个位数字和为39+4=31⨯;再计算这10个数的十位数字和为4×9=36,加上个位的进位的3,为36339+=; 再计算这10个数的百位数字和为4×8=32,加上十位的进位的3,为32335+=; 再计算这10个数的千位数字和为4×7=28,加上百位的进位的3,为28331+=; 再计算这10个数的万位数字和为4×6=24,加上千位的进位的3,为24327+=; 再计算这10个数的十万位数字和为4×5=20,加上万位的进位的2,为20222+=; 再计算这10个数的百万位数字和为4×4=16,加上十万位的进位的2,为16218+=; 再计算这10个数的千万位数字和为4×3=12,加上百万位的进位的1,为12113+=; 再计算这10个数的亿位数字和为4×2=8,加上千万位的进位的1,为819+=;最后计算这10个数的十亿位数字和为4×1=4,加上亿位上没有进位,即为4. 所以,这10个数的和为4938271591.6.如图1-1,每一线段的端点上两数之和算作线段的长度,那么图中6条线段的长度之和是多少?【分析与解】因为每个端点均有三条线段通过,所以这6条线段的长度之和为:1173(0.60.875)1+0.75+1.8+2.625=6.175=63440⨯+++=7.我们规定,符号“○”表示选择两数中较大数的运算,例如:3.5○2.9=2.9○3.5=3.5.符号“△”表示选择两数中较小数的运算,例如:3.5△2.9=2.9△3.5=2.9.请计算:23155(0.625)(0.4)333841235(0.3)( 2.25)3104⨯+【分析与解】原式1550.6255155725384218384122562.253⨯=⨯÷=+8.规定(3)=2×3×4,(4)=3×4×5,(5)=4×5×6,(10)=9×10×11,….如果111(16)(17)(17)-=⨯,那么方框内应填的数是多少?【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9.从和式11111124681012+++++中必须去掉哪两个分数,才能使得余下的分数之和等于1? 【分析与解】因为1116124+=,所以12,14,16,112的和为l,因此应去掉18与110.10.如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数,例如1.892915929.那么在所有这种数中。
学而思一级数学(精品收藏)
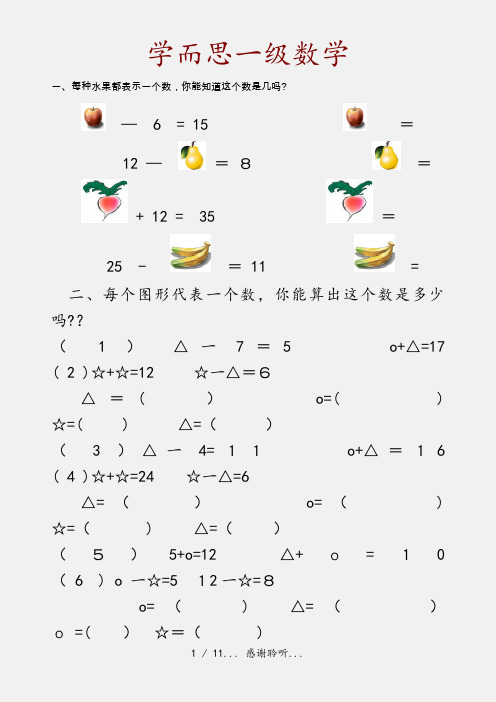
一、每种水果都表示一个数,你能知道这个数是几吗?— 6 = 15 =12 —=8=+ 12 = 35 =25 - = 11 =二、每个图形代表一个数,你能算出这个数是多少吗??( 1 )△一7=5o+△=17 ( 2 )☆+☆=12☆一△=6△=( )o=( ) ☆=( ) △=()( 3 )△一4=11o+△=1 6 ( 4 )☆+☆=24 ☆一△=6△=()o=()☆=() △=()(5)5+o=12 △+o=10 ( 6 ) o 一☆=512一☆=8o=() △=()o =( )☆=( )(7 )5+o=12△+o=10 ( 8 ) o 一☆=5 12一☆=8o=( )△=() o =()☆=( )(9)△+△=18△=( ) (10)口+口+△+△=14☆+o=13o =( )△+△+口=10△+o=15 ☆=( )△=( )口=( )三、每个图形代表一个数,你能算出这个数是多少吗?( 1 )△+□=9 ○—△=1 △+△+△=9△=()□=( )○=( )(2)△+ ○ = 12 ○+ ☆= 8 △+ ○+☆ = 21△=()○= ()☆=( )(3)你+我 = 7 你 + 他 = 18你+ 我+他 = 24你= ()我= ()他 = ()( 4 ) ○+□=10,□+△=12, ○+□+△=15。
○=(),□=(),△=()。
( 5 )△+○=9 △+△+○+○+○=25 ﻫ△=()○=()四、每个图形代表一个数,你能算出这个数是多少吗?(1) △+△+△+△=28△=( )△+△+□=20□=()(2)○+○+○=6 ○=( )△+△+△=12△=()(3)△-○=1 △=( )△+△—○=9 ○=()△+○-□=10 □=( )二、下图中每种水果各代表一个数,算一算,它们各代表几?+ = 7+ = 10+ = 9=( )=( ) =()已知:☆+☆+☆=6,△+△+△+△=20,则△-☆=( )已知:△+○=14 △-○=2 则△=( )○=( )已知:▲=●+●+●,▲+●=12,则●=(),▲=( )已知:△+ ○=5○+☆=9 △+○ + ☆ = 13△=()○= ()☆=()七、张老师把红、白、蓝各一个气球分别送给三位小朋友。
学而思讲义课件.doc

分数基本计算与比例初步内容提要:分数比例分数分数的概念把整体平均分成若干份,表示这样的一份或几份的数叫做分数如25表示把整体平均分成5份,占其中的2份分母表示把一个物体平均分成几份,分子是表示取其中的几份注意:分母不能为0分数的种类真分数:分子比分母小的分数,如2 3假分数:分子比分母大的分数,如3 2带分数:把假分数化成整数和真分数加在一起的分数,如32=1+21=112分数的性质1.分子和分母同时乘以或除以相同的数(0除外),分数的大小不变如246369==,8421005025==2.约分与通分约分:分子分母同时除以公因数,如425025=最简分数通分:把多个分数的分母变成一样,如224833412⨯⨯==比较大小333944312⨯⨯==注意:有时通分也可把分子变成一样3.分数的倒数倒数:乘积为1的两个数互为倒数分数:分子与分母的位置互换注意:0没有倒数分数和小数互化分数化小数:分子除以分母小数化分数:小数点后有1位数,2位数,3位数…,分母分别为10,100,1000…分子就是小数点后的数注意要化成最简分数如2250.4 5÷==0.012=123 1000250=分数的运算1.加减法同分母加减法:分母不变,分子相加减,结果化为最简分数异分母加减法:先通分,变为分母相同的分数,分子再相加减如:347888+=23342761 917153153153 +=+=2.乘除法乘法:分子乘分子,分母乘分母如3312311 88882243⨯4⨯4=⨯====1⨯133123 8884010 443⨯4⨯=⨯===55⨯5除法:除以一个数等于乘以这个数的倒数如33121 888242 343⨯4÷=⨯===43⨯3注意:分数的乘除法运算过程中可以先约分分数的四则混合运算的规律与整数一样特殊的约分连锁约分 整体约分连锁约分:4433221⨯⨯⨯=122⨯33⨯44⨯1=整体约分:3333123123246369123(123)13526103915135(123)⨯⨯⨯⨯+⨯⨯+⨯⨯⨯⨯⨯++⨯⨯+⨯⨯+⨯⨯⨯⨯⨯++==33(123)⨯++13⨯335(123)⨯⨯++25=我们来看看分数的乘除法 计算下列各式:28157549⨯=__________;315711÷=__________。
学而思小学奥数知识点梳理

学而思小学奥数知识点梳理学而思教材编写组侍春雷前言小学奥数知识点梳理,对于学而思的小学奥数大纲建设尤其必要,不过,对于知识点的概括很可能出现以偏概全挂一漏万的现象,为此,本人参考了单尊主编的《小学数学奥林匹克》、中国少年报社主编的《华杯赛教材》、《华杯赛集训指南》以及学而思的《寒假班系列教材》和华罗庚学校的教材共五套教材,力图打破原有体系,重新整合划分,构建十七块体系(其第十七为解题方法汇集,可补充相应杂题),原则上简明扼要,努力刻画小学奥数知识的主树干。
概述一、计算1.四则混合运算繁分数⑴运算顺序⑵分数、小数混合运算技巧一般而言:①加减运算中,能化成有限小数的统一以小数形式;②乘除运算中,统一以分数形式。
⑶带分数与假分数的互化⑷繁分数的化简2.简便计算⑴凑整思想⑵基准数思想⑶裂项与拆分⑷提取公因数⑸商不变性质⑹改变运算顺序①运算定律的综合运用②连减的性质③ 连除的性质④ 同级运算移项的性质⑤ 增减括号的性质⑥ 变式提取公因数形如:1212......(......)n n a b a b a b a a a b ÷±÷±±÷=±±±÷3. 估算求某式的整数部分:扩缩法4. 比较大小① 通分a. 通分母b. 通分子② 跟“中介”比③ 利用倒数性质 若111a b c >>,则c>b>a.。
形如:312123m m m n n n >>,则312123n n n m m m <<。
5. 定义新运算6. 特殊数列求和运用相关公式:①()21321+=++n n n②()()612121222++=+++n n n n③()21n a n n n n =+=+④()()412121222333+=++=+++n n n n ⑤131171001⨯⨯⨯=⨯=abc abc abcabc⑥()()b a b a b a -+=-22⑦1+2+3+4…(n-1)+n+(n-1)+…4+3+2+1=n 2二、 数论1. 奇偶性问题奇±奇=偶 奇×奇=奇奇±偶=奇奇×偶=偶偶±偶=偶偶×偶=偶2.位值原则形如:abc=100a+10b+c3.数的整除特征:4.整除性质①如果c|a、c|b,那么c|(a±b)。
学而思一年级数学

学而思一年级数学— 6 = 15 =12 —= 8 =+ 12 = 35 =25 —= 11 =学而思一年级数学( 1 ) △一7=5o+△=17 ( 2 )☆+☆=12 ☆一△=6 △=( ) o=( ) ☆=( ) △=( ) ( 3 )△一4=11 o+△=16 ( 4 )☆+☆=24 ☆一△=6 △=( ) o=( ) ☆=( ) △=( ) (5)5+o=12 △+o=10 ( 6 ) o 一☆=5 12一☆=8 o=( ) △=( ) o =( ) ☆=( ) ( 7 )5+o=12 △+o=10 ( 8 ) o 一☆=5 12一☆=8 o=( ) △=( ) o =( ) ☆=( ) (9 )△+△=18 △=( ) (10)口+口+△+△=14 ☆+ o =13 o =( ) △+△+口=10△+ o =15 ☆=( ) △=( ) 口=( )学而思一年级数学( 1 )△+□=9 ○-△=1 △+△+△=9△=()□=()○=()( 2 )△+ ○= 12 ○+ ☆= 8 △+ ○+ ☆= 21 △=( ) ○= ( ) ☆=( )( 3 )你+ 我= 7 你+ 他= 18 你+ 我+ 他= 24 你= ()我= ()他= ()( 4 )○+□=10;□+△=12;○+□+△=15。
○=();□=();△=()。
( 5 )△+○=9 △+△+○+○+○=25△=()○=()四、每个图形代表一个数;你能算出这个数是多少吗?(1)△+△+△+△=28 △=()△+△+□=20 □=()(2)○+○+○=6 ○=()△+△+△=12 △=()(3)△-○=1 △=()△+△-○=9 ○=()△+○-□=10 □=()二、下图中每种水果各代表一个数;算一算;它们各代表几?+= 7+= 10+= 9=()=()=()已知:☆+☆+☆=6;△+△+△+△=20;则△-☆=( )已知:△+○=14 △-○=2 则△=( ) ○=( )12;则●=();▲=()已知:▲=●+●+●;▲+●=已知:△+ ○= 5 ○+ ☆= 9 △+ ○+ ☆= 13△=( ) ○= ( ) ☆=( )七、张老师把红、白、蓝各一个气球分别送给三位小朋友。
学而思培优 一年级数学知识点

第一讲 孙行者有几个名字一、 枚举法有序思考目标:不重复,不漏掉二、 排列(有顺序 )1、 类型:名字、卡片、位置 魏雅楠老师2、方法:先固定开头,后交替位置三、 组合(无顺序)1、 类型:握手、击掌、打电话、搭配2、方法:连线法【例1】布莱克、树桩、简乐、石磊磊合照留念,树桩只能在从左往右的第二个位置,他们一共有多少种不同的排法呢?解析:首先四个人肯定有四个位置,先把四个位置写上。
看到树桩只能站在②号位置,给它一个特殊的符号,比如▲,布莱克用A 表示,简乐用B 来表示,石磊磊用C 来表示。
先确定树桩在②,接下来有序思考,先让A 站在一号位,两种;B 站在①号位,两种;C 站在①号位,两种。
一共六种。
具体如下:① ② ③ ④ A ▲ B CA ▲ CB B ▲ A CB ▲C A C ▲ A BC ▲ B A 2+2+2=6(种)答:一共有6种不同的站法。
【例3】四只猴子互相击掌庆祝胜利,想一想如果每两只猴子击一次掌(不能重复计数),他们一共需要几次击掌?解析:首先给四只猴子起个名字,A 、B 、C 、D ,第一个猴子A 先开始,分别找B 、C 、D 击掌;然后第二个猴子B ,已经跟A 击过掌了,那就不用再回去击掌了,只要往后面继续就行,所以找C 、D ;接下来是C ,还是只要往后继续,所以只有找D ,如下图:A B C D3+2+1=6(次)【例5】用下面的服装搭配一下,可以有几种不同的穿法?解析:首先上衣穿一件,下装穿一件,两两搭配,由于思考,先看第一件上衣可以搭配几种,连线连出来,再看第二件上衣,同样连线,如下图:答:可以有6种不同的搭配。
、共6题:前3题为自编题,后3题按课后作业改编(均需给出分析与解答)1、每两个人握手一次,请问6个小朋友需要握手几次?2、4个小朋友排队领奖品,其中有一个小朋友一定要在从左到右第二个位置,请问有几种排法?3、从森林到湖边有三条路,从湖边到帐篷有四条路,请问从森林经过湖边到帐蓬有几条不同的路可以走?4、有三个花瓶,分别为紫色和蓝色还有红色,还有两朵花,分别为玫瑰和百合,一个花瓶中插一朵花,请问有几种搭配方法5、有9个小朋友,每两个人要猜一次拳(不能重复计数),请问一共需要猜几次拳? 6、有三把椅子,分别为白色、蓝色、粉色,和四张桌子,分别为长方形、圆形、正方形和三角形,一张椅子搭配一张桌子,请问一共有几种不同的搭配方案?1、〔分析与解答〕:一共有5+4+3+2+1=15(种)2、〔分析与解答〕:首先4个人肯定有4个位置,先把4个位置写上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九讲 无敌的剪刀
一. 剪图形:用直线分割图形
1. 边到边(原来图形有几个角,剪完增加一个角)
2. 边到角(原来图形有几个角,剪完角的个数不变)
3. 角到角(原来图形有几个角,剪完减少一个角)
二. 剪绳子
1. 折成几段中间剪一刀 中间剪一刀后段数增加1
2. 对折几次中间剪一刀
先算出对折之后变成几段,中间剪一刀之后段数增加1
对折次数 对折成几段 剪一刀后变成几段
不对折 1段 +1 2段
对折一次 1+1=2段 +1 3段
对折两次 2+2=4段 +1 5段
对折三次 4+4=8段 +1 9段
•
•
•
三. 拼图形:照着目标补完整
方法:1、把最接近的补齐 2
、从好画的部分下手——王艳老师
例1:一张正方形的纸,剪去一个角,可能还有几个角?
解析:剪去一个角,其实就是用直线分割图形。
我们要考虑的就是剪刀是从
正方形的一条边剪到另外一条边,或者是从正方形的一条边剪到一个角,或
者是从一个角剪到另外一个角。
这样一共分别对应了三种情况。
①
③
①边到边(原来图形有4个角,剪完增加一个角变成5个角)
②边到角(原来图形有4个角,剪完角的个数不变还是4个角)
③角到角(原来图形有4个角,剪完减少一个角变成3个角)
例2:一根绳子折成3段(如下图)从中间剪一刀,可以剪成多少段?一根
绳子折成5段,从中间剪一刀,可以剪成多少段?折成10段呢?
① ②
③ ④
解析:将绳子折成3段,是指折完之后变成3段,沿着中间剪一刀,如上图红
色的线,将绳子分成了4段,我们列算式的时候可以写成3+1=4,表示剪后线
段增加1,所以将绳子折成5段的时候,从中间剪一刀,可以变成6段。
折成
10段的时候,可以变成11段。
例3:把一根绳子对折,然后从中间一刀剪开,这根绳子剪成了几段?一根绳子
对折2次,然后从中间一刀剪开,这根绳子剪成了几段?对折了三次呢?
解析:对折一次就是将一根绳子变成相等的两段,然后从中间剪一刀,剪成了几
段只需要拿对折后的段数加1就可以了; 将一根绳子对折两次,就是折成
2+2=4段,从中间剪一刀后,就是4+1=5段; 对折3次,就是折成4+4=8
段,从中间剪一刀后,就是8+1=9段。
共6题:前3题为自编题,后3题按课后作业改编(均需给
出分析与解答)
1、
一张梯形的纸剪一刀, 剪掉一个角后可以让它变成三角形?把它变成一个四边形?可以把它变成一个五边形?
解析:三角形有三个角,所以就是比梯形少一个角,我们如果要变成三角形,就
要从梯形的一个角剪到另外一个角;四边形有四个角,和梯形的角一样多,所以
我们要从梯形的一个角剪到一条边;五边形有五个角,所以比梯形多了一个角,
所以要从一条边剪到相邻的另外一条边。
2、一根绳子折成几段后,从中间剪一刀,可以剪成5段?’一根绳子折成几段后,从中间剪一刀,可以剪成20段?
解析:折成4段后,从中间剪开可以剪成5段;折成19段后,从中间剪开可以剪成20段。
3、一根绳子对折几次,然后从中间一刀剪开,可以把它剪成5段?一根绳子对折几次,然后从中间一刀剪开,可以把它剪成65段?
解析:从中间一刀剪开变成5段,那剪之前是5-1=4段,对折2次是4段;从中间一刀剪开变成65段,那剪之前是65-1=64段,对折6次是64段。
4、从下图右边的图形里各选出两个,把它们拼成左边的图形。
解析:要知道是哪两部分可以拼成给出的图形,我们要先让学生找与给出这个图形最相似的一部分,然后根据最相似的这部分来找缺少的那一块。
可以把最相似的这部分补起来找缺少的那一块,答案如下:正方形是由1和5拼成的,圆形是由1和3拼成的,三角形是由2和4拼成的。
5、在大森林里住着一群可爱的熊,它们是熊爸爸、熊妈妈,还有9只可爱的熊宝宝,9只熊宝宝住在一间正方形的卧室中,随着它们一天天地长大,都想自己单独住,熊爸爸、熊妈妈说:“只要在住的正方形卧室中再砌两个张方形墙,就能把你们的床位都分开,每只宝宝就有一间卧室了。
”小朋友,请你画一画,让9只熊宝宝都分别有自己的卧室。
解析:具体操作方法如下图所示。
6、请你在等号右边的答案中选择1个图形,使这个图形正好是左边两个图形相减的结果。
解析:我们可以在原图上先画出要减去的部分,然后再看剩下的图形与左边哪一个相同就可以找到答案了。
上面的题选B ,下面的题选D 。
1、〔分析与解答〕:
三角形,就要从梯形的一个角剪到另外一个角;四边形要从梯形的一个角剪到一条边;五边形,要从一条边剪到相邻的另外一条边。
2、〔分析与解答〕:
折成4段;折成19段。
3、〔分析与解答〕:
对折2次;对折6次
4、〔分析与解答〕:
正方形是由1和5拼成的,圆形是由1和3拼成的,三角形是由2和4拼成的。
5、〔分析与解答〕:
如题目解析所示。
6、〔分析与解答〕:
上面的题选B,下面的题选D。
