矩阵8
第8讲 分块矩阵、矩阵的秩.PPT

0 0 3 2
0
0
1
1
3
解:设
A
0
0
0
0 2 0 0
0 0 3 1
0 0 2 1
A1
A2
A3
A1 3 , A2 2 , A3 1
所以 A 3( 2)1 6
又
A11
1 3
,
A21
1 2
,
A31
1 1
2
3
1 3
0
0 0
故
A1
0
12 0
2
A3 A2 A 0
2 2
1 2 0
1
0 3
1 0
32 3
3 32
0
0
2 0 0
0
0
3
3.
(1)
3 B'
2A
1 3 0
0 2
3 1 0 2 0
0 2
0 1 1 0
0 2
3 2
0 1 1 0 0 1 0 3 1
1 0 6 1 0 0 0 0 6
同理可定义矩阵的初等列变换 (所用记号是 把“r”换成“c”).
三、 由 P 1AP B 有 P P1APP 1 P B P 1
A PBP 1 A2 AA PBP1PBP1 PBBP1 PB2P 1
A10 PB10P 1
P 1 1 1 4 3 1 1
B2 BB 1 0
0 1 2 0
0 2
(1)2 0
0 22
B3 B2B 1 0
Bs
A1 B1
0
L
0
0L A2 B2 L
LL 00
0
0
L
8阶离散余弦变换矩阵。

8阶离散余弦变换矩阵。
离散余弦变换(DCT)是一种常用的信号处理技术,广泛应用于图像和视频压缩、音频编码和解码等领域。
它通过将信号分解成一系列正弦基函数的加权和,实现信号在频域的表示和处理。
8阶离散余弦变换矩阵是一个8×8的矩阵,用于将8×8的图像块转换为频域表示。
这个矩阵是由一组正弦基函数构成,每个基函数在空域上是离散的,但在频域上是连续的。
通过对图像块进行离散余弦变换,可以得到图像块在频域上的系数,这些系数可以用于图像压缩和其他信号处理任务。
离散余弦变换的过程可以简单概括为以下几个步骤:
1. 将图像块进行预处理,例如减去均值或进行颜色转换等操作。
2. 将预处理后的图像块分成8×8的小块。
3. 对每个小块进行离散余弦变换,得到小块在频域上的系数。
4. 将频域系数进行量化,即将系数的精度降低,以减小数据量。
5. 对量化后的系数进行编码,以便于储存或传输。
离散余弦变换的主要优点是能够将图像数据在频域上进行压缩,使得图像可以更高效地储存和传输。
同时,它还具有一定的抗噪性能,可以减小图像信号受到噪声干扰的影响。
然而,离散余弦变换也有一些局限性。
它不能很好地处理图像中的边缘和纹理等高频信息,容易导致图像出现锯齿状的伪影。
为了克服这些问题,人们提出了一些改进的离散余弦变换方法,如离散小波变换等。
离散余弦变换作为一种常用的信号处理技术,在图像和视频编码等领域具有重要的应用价值。
通过合理地利用离散余弦变换,我们可以实现对图像和视频数据的高效处理和传输,为多媒体技术的发展做出贡献。
8-旋转矩阵

回想:R矩阵的性质
1、R是正交矩阵。即行、列、对角线元素平方和为 “1”,行列式的值是“1”。 1 T R R 2、正交矩阵的逆矩阵是它本身的转置即 。 3、R矩阵的9个元素中只有3个是独立的,是三个旋转 角的函数。 4、无论采用坐标系统如何(旋转参数不同),但R是不 变的。因为其转换关系是唯一确定的。所以有课本上 2-10的公式。 tan a3 / c3 tan ' b3 / c3 tan A a3 / b3 ' sin b3 sin a3 cos c3 ' tan b1 / b2 tan a / a tan c / c 2 1 1 2
2、若采用以X为主轴的坐标系统,R矩阵中的 九个元素为
a1 cos ' cos ' a 2 sin ' sin ' a3 sin ' b1 cos ' sin ' sin ' sin ' cos ' b2 cos ' cos ' sin ' sin ' sin ' b sin ' cos ' 3 c1 sin ' cos ' cos ' sin ' cos ' c 2 sin ' cos ' cos ' sin ' sin ' c3 cos ' cos '
b1
a1a3b3 a2 c3 2 1 a3
b2 1 b12 b32 c1 a2b3 a3b2 c2 a3b1 a1b3
矩阵位移法的计算步骤及示例

单元①②和③:
35
⎡ 500 0 0 − 500 0 0 ⎤
⎢ ⎢
0
12 24
0
− 12
24
⎥ ⎥
(1)
k
=
(2)
k
=
(3)
k
=
10
3
⎢ ⎢⎢−
0 500
24 0
64 0
0 − 24 32 ⎥
500 0
0
⎥ ⎥
⎢ 0 −12 − 24 0 12 − 24⎥
⎢ ⎢⎣ 0
24 32
0
− 24
⎥ 64 ⎥⎦
8-8 矩阵位移法的计算步骤及示例 1
矩阵位移法的计算步骤:(以后处理为例)
(1)对结点和单元进行编号,建立结构(整
体)坐标系和单元(局部)坐标系,并对结
点位移进行编号。
(2)计算各杆的单元刚度矩 k (e)、k (e) 。
(3)形成结构原始刚度矩阵K。
(4)计算固端力
F
(e) F
、等效结点荷载FE及综合
⎢⎣0.0 0.0 6.0 12.0⎥⎦
由于连续梁的单元刚度矩阵为非奇异矩阵, 由此组集而成的结构刚度矩阵K 也是非奇异 的,故无需再进行支座约束条件处理。
(4)计算固端力列阵及等效结点 15 荷载列阵。
②单元的固端力列阵
F (2) F
=
⎧ 300 ⎫ ⎩⎨− 300⎭⎬kN
⋅
m
等效结点荷载列阵:
k(3)
=
⎢ ⎢ ⎢
l(3) 2EI
⎢⎣ l ( 3 )
4
2EI l(3) 4EI l(3)
⎤ ⎥ ⎥ ⎥ ⎥⎦
3 4
(3)集成结构刚度矩阵K
八节点六面体单元 应变矩阵

在有限元分析中,应变矩阵是一个重要的概念,用于描述物体在受力后形状和尺寸的变化。
对于一个八节点六面体单元,应变矩阵的构建通常基于节点坐标和节点位移。
假设我们有一个六面体单元,其8个节点分别为N1到N8。
每个节点有三个自由度:x、y和z方向上的位移。
假设每个节点的位移分别为u、v和w。
首先,我们需要定义一个参考应变矩阵B。
对于一个六面体单元,B可以表示为:
B = [B1 B2 B3]
其中,B1、B2和B3是参考应变矩阵的三个子矩阵:
B1 = [0 0 0 0 0 0 0 0]
B2 = [0 0 0 0 0 0 0 0]
B3 = [0 0 0 0 0 0 0 0]
然后,我们可以根据节点的位移来更新B:
B1 = [∂u/∂x ∂u/∂y ∂u/∂z u/x u/y u/z u/x² u/y²]
B2 = [∂v/∂x ∂v/∂y ∂v/∂z v/x v/y v/z v/x² v/y²]
B3 = [∂w/∂x ∂w/∂y ∂w/∂z w/x w/y w/z w/x² w/y²]
其中,偏导数表示节点位移对坐标的偏导数,而其他项则基于偏导数和节点位移计算得出。
最后,我们可以将B与刚度矩阵K相乘,以得到节点力:
F = KB
注意,这只是一种常见的有限元分析方法,并且实际情况可能因具体的应用和需求而有所不同。
建议查阅相关文献或咨询专业人士以获取更准确的信息。
第八章 T矩阵

第八章 λ—矩阵一 内容概述 1 基本概念 1)λ— 矩阵 设p 是一个数域,λ是一个文字,则称以数域P 上λ的多项式作为元素的矩阵为λ—矩阵,记为 A (λ),B(λ)等。
2)λ—矩阵的运算:加法,减法,乘法,数乘和转置等,伴随矩阵,行列式,λ—矩阵的秩。
可逆λ—矩阵,λ—矩阵的初等变换,λ—矩阵的等价。
3)行列式因子:设m*n 的 —矩阵A(λ)的秩为r ,对于正整数k,1≤k ≤r 在A(λ)中所有k 级子式的首项系数为1的最大公因式称为 A(λ) 的K 级行列式因子。
记为D K (λ). 4)—矩阵的标准形,不变因子()()()⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛0...0...21x r x x d d d r ≥1,d i (λ)(i=1,2….r )是首项系数为1的多项式且d i (λ)|d 1+i (λ)(i=1,2,…r -1)称为A(λ) 的标准形。
d 1(λ),d 2(λ),…d r (λ)称为A(λ) 的不变因子。
5)行列式因子与不变因子的关系:D K (λ)=d 1(λ)…d k (λ)k=1,2,…r. d 1(λ)=D 1(λ)d k (λ)=()()λλ1-K K D D K=2,3…r6)初等因子,设 A 与 n*n 矩阵,把A 的每个次数大于0不变因子分解成互不相同的一次因式之方幂的乘积,所有这些一次因式的方幂(相同的按出现的次数计算)称为A 的初等因子。
A 的初等因子和不变因子相互唯一决定。
7)若当标准形⎪⎪⎪⎪⎪⎭⎫⎝⎛S J J J ...21 J i 为若当块 2. 矩阵等价的充分必要条件:设A ()λ与B ()λ都是s ⨯n 的λ--矩阵 则A ()λ≅B ()λ 〈=〉P ()λA ()λQ ()λ=B ()λ其中P ()λ和Q ()λ都是可逆矩阵A ()λ与B ()λ有相同的标准形 〈=〉A ()λ 与B ()λ有相同的行列式因子 〈=〉A ()λ与B ()λ有相同的不变因子3.矩阵相似的充分必要条件: 设A,B 都是n 阶方阵则 〈=〉λE-A ≅λE-B〈=〉A 与B 有相同的初等因子 〈=〉A 与B 有相同的不变因子〈=〉λE-A 与λE-B 有相同的标准形4矩阵A 与对角矩阵相似的充分必要条件: (1) 有个线性无关的特征向量 (2) 初等因子全是一次的 (3) 最小多项式无重根5如何求矩阵A 的若当标准形。
第8章 矩阵特征值计算

第八章 矩阵特征值计算1 特征值性质和估计工程实践中有许多种振动问题,如桥梁或建筑物的振动,机械机件的振动,飞机机翼的颤动等,这些问题的求解常常归纳为求矩阵的特征值问题。
另外,一些稳定分析问题及相关问题也可以转化为求矩阵特征值与特征向量的问题。
1.1 特征值问题及性质设矩阵n n ⨯∈A R (或n n ⨯C ),特征值问题是:求C λ∈和非零向量n R ∈x ,使λ=Ax x (1.1)其中x 是矩阵A 属于特征值λ的特征向量。
A 的全体特征值组成的集合记为sp()A 。
求A 的特征值问题(1.1)等价于求A 的特征方程()det()0p I λλ=-=A (1.2)的根。
因为一般不能通过有限次运算准确求解()0p λ=的根,所以特征值问题的数值方法只能是迭代法。
反之,有时为了求多项式111()n n n n q a a a λλλλ--=++++的零点,可以把()q λ看成矩阵123101010n a a a a ----⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦的特征多项式(除(1)n -因子不计)。
这是一个Hessenberg 矩阵,可用QR 方法求特征值,从而求出代数方程()0q λ=的根。
矩阵特征值和特征向量的计算问题可分为两类:一类是求矩阵A 的全部特征值及其对应的向量;另一类是求部分特征值(一个或几个、按模最大或最小)及其对应的特征向量。
本章介绍部分特征值和特征向量的幂法、内积法;求实对称矩阵全部特征值的雅可比法、Given 方法和Householder 方法;求任意矩阵全部特征值的QR 算法。
在第5章已给出特征值的一些重要性质,下面再补充一些基本性质。
定理1 设n n R ⨯∈A ,则(1) 设λ为A 的特征值,则λμ-为μ-A I 的特征值;(2) 设12,,,n λλλ是A 的特征值,()p x 是一多项式,则矩阵()p A 的特征值是12(),(),,()n p p p λλλ。
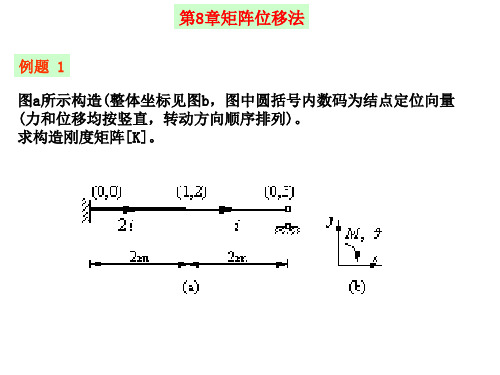
矩阵位移法例题
0
2 1 2
0
0
4 1 3
00 2 00 3
0
0
K③
41
3
0
0
0
00 3 000
5 集成总刚度矩阵
第8章矩阵位移法
4 2 2 2
0 1 8 4 0
K 2 2 4 2 4 1
21
2
4
12
2
0
2 1 4 1 4 1 3 0 2 8
1
2
3
6 形成荷载向量
P 60 190 62.5T
2 结点位移编号矩阵 3 各单元旳定位向量
0 0 0 C 0 0 1
0 0 2 0 0 0
2 3T
U1 0 0 0 0 0 1 U2 0 0 1 0 0 2 U3 0 0 2 0 0 0
-90 250
-250 187.5 -112.5
1
2
3
4
第8章矩阵位移法
4 各单元旳刚度矩阵
单元旳刚度矩阵与解法一相同
2 12i 2 BCx l2 Cy
12i (B l2 )CxC y
2 12i 2
BC Y
2 l
Cx
6i l Cy 6i l Cx
2 12i 2 BCx 2 C y
l 12i (B 2 )CxC y l
12i (B 2 )CxC y
l 2 12i 2 BCy 2 Cx
l
6i l Cy 6i l Cx
(e)
K
6i
4i
l Cy
6i l Cx
2i
2 12i 2 BCx 2 C y
l
12i (B 2 )CxC y
l
6i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定理8.2.1 存在, 定理8.2.1 设 A ∈ R m×n 且 A+存在,则
(1 ) A + ∈ A{1};
( 2 ) 若A是 n阶可逆矩阵,则 A + = A −1 ; 阶可逆矩阵,
( 3 ) 方程组 Ax = b 相容的充分必要条件是 AA + b = b;
( 4 ) 若方程组 Ax = b相容,则其通解是 相容, x = A + b + ( I − A + A) y , ∀y ∈ R n
第8章 广义逆矩阵
广义逆矩阵A 8.1 广义逆矩阵 -与线性方程组的解 广义逆矩阵A 8.2 广义逆矩阵 +与方程组的最小二乘解
广义逆矩阵A 8.1 广义逆矩阵 -与线性方程组的解
的解, 考虑线性方程组 Ax = b 的解,其中
x1 b1 x2 b2 m×n A = (aij ) ∈ R , x = , b = ∈ Rm M M x b n m
定理8.2.5 定理8.2.5
矩阵, 设A是 m×n矩阵,则 是 × 矩阵
(1) ( A+ ) + = A ;
( 2) ( A+ )T = ( AT )+ ; ( 3) A+ AAT = AT = AT AA + ;
(4) ( AT A) + = A+ ( AT ) + = A+ ( A+ )T ;
(1) 若方程组 Ax = b相容 , 则x = A + b是其极小范数解。 是其极小范数解。
( 2) 若方程组 Ax = b不相容 , 则其最小二乘解的通式 为 x = A + b + ( I − A + A) y , ∀ y ∈ R n .
ห้องสมุดไป่ตู้
( 3 ) 若方程组 Ax = b 不相容 , 则 x = A + b 是其极小最小二 乘解 .
定理8.2.2 存在并且唯一。 定理8.2.2 设 A ∈ R m×n 则 A+存在并且唯一。 ,
定理8.2.3 定理8.2.3 设A是秩为 r 的 m×n 矩阵,其满秩分解 是秩为 × 矩阵, 为 A=BC ,其中
B ∈ Rm×r , C ∈ Rr×n , rank( B) = rank(C ) = r,
(5) A + = ( AT A) + AT = AT ( AAT ) + ;
(6) rank( A) = rank( A+ ) = rank( AA+ ) = rank( A+ A) .
注
A-1的许多性质, A+并不具备,一般地 的许多性质, 并不具备,
(1) ( AB ) + ≠ B + A + ;
( 2) AA + ≠ A+ A;
( 3) ( A k )+ ≠ ( A + )k .
定义8.2.2 定义8.2.2 设 A ∈ R n 果存在 x ∈ R ,使
m ×n
不相容, 且方程组 AX=b 不相容,如
Ax − b 2 = min
的最小二乘解。 则称 x 是方程组 AX=b 的最小二乘解。
定理8.2.6 不相容, 定理8.2.6 设方程组 Ax=b 不相容,则 x 为其最小 二乘解的充分必要条件是 AT Ax = AT b . 定理8.2.7 定理8.2.7 设A是 m×n 矩阵, 是 × 矩阵,
Ir PAQ = 0 0 0
则 G ∈ A{1}的充分必要条件是
Ir G = Q L K P M
其中 K ∈ R r ×( m − r ) , L ∈ R ( n − r )× r 和 M ∈ R ( n − r )×( m − r )是任意矩阵 .
定理8.1.7 设 A是 m×n 矩阵, P 和 Q 分别是m 阶 定理8.1.7 是 × 矩阵, 分别是 – 阶非奇异方阵, 的减号逆, 和n 阶非奇异方阵,且B = PAQ,A 是A的减号逆,则 , 的减号逆
x = ( I − A − A) y , ∀y ∈ R n
定理8.1.4 定理8.1.4 设 A − 是A的任一减号逆且 b ∈ R(A) ,则 的任一减号逆且 线性方程组 Ax = b 的通解是
x = A − b + ( I − A − A) y , ∀y ∈ R n
定理8.1.5 定理8.1.5 设 A ∈ R m×n , B ∈ R p×q , C ∈ R m×q , (1)矩阵方程 (1)矩阵方程AXB=C有解的充分必要条件是 矩阵方程 有解的充分必要条件是
(1) rank ( A) ≤ rank ( A− ) ;
( 2) AA − 和 A − A是幂等矩阵 , 并且 rank ( AA − ) = rank ( A − A) = rank ( A) ;
( 3) Q −1 A − P −1 ∈ B{1} .
广义逆矩阵A 8.2 广义逆矩阵 +与方程组的最小二乘解
定义8.2.1 定义8.2.1 设 A ∈ R m×n,如果存在 n×m 矩阵 ,满 × 矩阵G, 足如下条件: 足如下条件:
(1)
AGA = A ;
( 2) GAG = G ;
( 3) ( AG ) = AG ;
T
(4) (GA)T = GA .
加号逆或 广义逆, 则称 G 是 A 的加号逆或 Moore-Penrose 广义逆,记为G =A+。
AA−CB− B = C
(2)如果 有解, (2)如果AXB=C有解,则其通解是 如果 有解
X = A−CB− + Y − A− AYBB− , ∀Y ∈ Rn× p
推论8.1.1 推论8.1.1 线性方程组 Ax=b 有解的充分必要条件 是 AA-b=b .
定理8.1.6 设A是m×n矩阵且 矩阵且rank(A) = r≥1,如果存 定理 是 × 矩阵且 , 在非奇异矩阵 P 和 Q 使得
则 A + = C T ( CC T ) −1 ( B T B ) −1 B T。
推论8.2.1 设A是m×n矩阵, 矩阵, 推论8.2.1 是 × 矩阵
(1) 若rank ( A) = n, 则 A + = ( AT A) −1 AT ;
( 2) 若rank ( A) = m , 则A+ = AT ( AAT ) −1 .
G ∈ A{1} 的充分必要条件是 AGA = A。
定理8.1.2 的任一减号逆, 定理8.1.2 设 A− 是A的任一减号逆,则 A{1} 的通 的任一减号逆 式为
A{1} = { A− + U − A− AUAA − | U ∈ R n×m }
定理8.1.3 定理8.1.3 设 A− 是A的任一减号逆,则齐次线性方 的任一减号逆, 程组 Ax = 0 的通解是
可解( 相容) 则方程组 Ax = b 可解(或相容)的充分必要条件是
b ∈ R ( A ) ≡ { Ay | y ∈ R n }
定义8.1.1 矩阵, 定义8.1.1 设 A 是 m×n 矩阵,如果存在 n×m 矩阵 G,使 ∀b ∈ R( A), x = Gb 是方程组 Ax = b 的解,则称G为 的解, , 为 A的一个减号逆,记为 G = A− 。 的一个减号逆 的一个减号逆, A的全体减号逆记为 A{1}。 的全体减号逆记为 定理8.1.1 定理8.1.1
1 1 ,求 A+ . 例8.2.1 设 A = 0 0
定理8.2.4 定理8.2.4 矩阵, 设A是 m×n矩阵, 是 × 矩阵
(1) 若 U , V 分别为 m , n 阶正交矩阵 , 则 (UAV ) + = V T A + U T ;
R 0 ( 2) 若 A = 0 0 且 R为 r阶可逆矩阵 , 则 R −1 0 A+ = 0 0 n× m
