matlab floyd最短路算法例题
matlab的floyd算法

matlab的floyd算法Floyd算法,是一种图论算法,用于在加权图中求解最短路径。
它是以发明者之一、罗伯特·弗洛伊德的名字命名的。
这个算法同样被用于对于任意两点之间的最长路径(所谓的最短路径问题)进行求解。
算法描述给定一个带权的有向图G=(V,E),其权值函数为w,下面我们定义从顶点i到顶点j的路径经过的最大权值为dist(i,j)。
特别地,当i=j时,dist(i,j)=0。
为了方便描述算法,我们用D(k,i,j)表示从顶点i到顶点j且路径中的所有顶点都在集合{1,2,⋯,k}中的所有路径中,最大边权值的最小值。
则从顶点i到顶点j的最短路径的边权值就是 D(n,i,j),其中n是图中顶点的数量。
算法思想:建立中间顶点集合算法是通过不断地扩充中间顶点集合S,来求解任意两点之间的最短路径。
具体来说,设S={1, 2, ⋯, k},其中k是整数。
Floyd算法的基本思想是,依次考察所有可能的中间顶点x(即所有S中的顶点),对于每个中间顶点x,若从i到x再到j的路径比已知的路径更短,则更新dist(i,j)为更小的值D(k,i,j)。
最终,在S={1, 2, ⋯, n}的情况下,所得到的D(n,i,j)就是顶点i到顶点j之间的最短路径的长度。
Floyd算法的核心是一个三重循环,在每一轮循环中,枚举S中所有的中间顶点x,通过动态规划计算出从i到j的最短路径长度D(k,i,j)。
这一过程可表述为:for k = 1 to nfor i = 1 to nfor j = 1 to nif D(k,i)+D(j,k) < D(k,i,j)D(k,i,j) = D(k,i)+D(j,k)其中D(0,i,j)即为dist(i,j),若i和j不连通,则D(0,i,j)=+Inf。
算法实现function D = Floyd(adjmat)% adjmat为邻接矩阵邻接矩阵adjmat的定义为:- 若两个顶点之间有边相连,则对应位置为该边的边权值;- 若两个顶点之间没有边相连,则对应位置为0。
最小费用最大流问题matlab程序

下面的最小费用最大流算法采用的是“基于Floyd最短路算法的Ford和Fulkerson迭加算法”,其基本思路为:把各条弧上单位流量的费用看成某种长度,用Floyd求最短路的方法确定一条自V1至Vn的最短路;再将这条最短路作为可扩充路,用求解最大流问题的方法将其上的流量增至最大可能值;而这条最短路上的流量增加后,其上各条弧的单位流量的费用要重新确定,如此多次迭代,最终得到最小费用最大流。
本源码由GreenSim团队原创,转载请注明function [f,MinCost,MaxFlow]=MinimumCostFlow(a,c,V,s,t)%%MinimumCostFlow.m% 最小费用最大流算法通用Matlab函数%% 基于Floyd最短路算法的Ford和Fulkerson迭加算法% GreenSim团队原创作品,转载请注明%% 输入参数列表% a 单位流量的费用矩阵% c 链路容量矩阵% V 最大流的预设值,可为无穷大% s 源节点% t 目的节点%% 输出参数列表% f 链路流量矩阵% MinCost 最小费用% MaxFlow 最大流量%% 第一步:初始化N=size(a,1);%节点数目f=zeros(N,N);%流量矩阵,初始时为零流MaxFlow=sum(f(s,:));%最大流量,初始时也为零flag=zeros(N,N);%真实的前向边应该被记住for i=1:Nfor j=1:Nif i~=j&&c(i,j)~=0flag(i,j)=1;%前向边标记flag(j,i)=-1;%反向边标记endif a(i,j)==infa(i,j)=BV;w(i,j)=BV;%为提高程序的稳健性,以一个有限大数取代无穷大endendendif L(end)<BVRE=1;%如果路径长度小于大数,说明路径存在elseRE=0;end%% 第二步:迭代过程while RE==1&&MaxFlow<=V%停止条件为达到最大流的预设值或者没有从s到t的最短路%以下为更新网络结构MinCost1=sum(sum(f.*a));MaxFlow1=sum(f(s,:));f1=f;TS=length(R)-1;%路径经过的跳数LY=zeros(1,TS);%流量裕度for i=1:TSLY(i)=c(R(i),R(i+1));endmaxLY=min(LY);%流量裕度的最小值,也即最大能够增加的流量for i=1:TSu=R(i);v=R(i+1);if flag(u,v)==1&&maxLY<c(u,v)%当这条边为前向边且是非饱和边时f(u,v)=f(u,v)+maxLY;%记录流量值w(u,v)=a(u,v);%更新权重值c(v,u)=c(v,u)+maxLY;%反向链路的流量裕度更新elseif flag(u,v)==1&&maxLY==c(u,v)%当这条边为前向边且是饱和边时 w(u,v)=BV;%更新权重值c(u,v)=c(u,v)-maxLY;%更新流量裕度值w(v,u)=-a(u,v);%反向链路权重更新elseif flag(u,v)==-1&&maxLY<c(u,v)%当这条边为反向边且是非饱和边时 w(v,u)=a(v,u);c(v,u)=c(v,u)+maxLY;w(u,v)=-a(v,u);elseif flag(u,v)==-1&&maxLY==c(u,v)%当这条边为反向边且是饱和边时 w(v,u)=a(v,u);c(u,v)=c(u,v)-maxLY;w(u,v)=BV;elseendendMaxFlow2=sum(f(s,:));MinCost2=sum(sum(f.*a));if MaxFlow2<=VMaxFlow=MaxFlow2;MinCost=MinCost2;[L,R]=FLOYD(w,s,t);elsef=f1+prop*(f-f1);MaxFlow=V;MinCost=MinCost1+prop*(MinCost2-MinCost1);returnendif L(end)<BVRE=1;%如果路径长度小于大数,说明路径存在elseRE=0;endendfunction [L,R]=FLOYD(w,s,t)n=size(w,1);D=w;path=zeros(n,n);%以下是标准floyd算法for i=1:nfor j=1:nif D(i,j)~=infpath(i,j)=j;endendendfor k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i,j)D(i,j)=D(i,k)+D(k,j);path(i,j)=path(i,k);endendendendL=zeros(0,0);R=s;while 1if s==tL=fliplr(L);L=[0,L];returnendL=[L,D(s,t)];R=[R,path(s,t)];s=path(s,t);end(此文档部分内容来源于网络,如有侵权请告知删除,文档可自行编辑修改内容,供参考,感谢您的支持)。
Floyd最短路算法的MATLAB程序

Floyd最短路算法的MATLAB程序Floyd最短路算法的MATLAB程序2006-08-17 20:14%floyd.m%采用floyd算法计算图a中每对顶点最短路 %d是矩离矩阵%r是路由矩阵function [d,r]=floyd(a)n=size(a,1);d=a;for i=1:nfor j=1:nr(i,j)=j;endendrfor k=1:nfor i=1:nfor j=1:nif d(i,k)+d(k,j)<d(i,j)< p="">d(i,j)=d(i,k)+d(k,j); r(i,j)=r(i,k)endendendkdrendvoid Dijkstral(int v0){int i;bool s[MAX_VEX];for(i=0;i<dim;i++)< p="">{d[v0][i]=map[v0][i];s[i]=false;if((i!=0)&&(d[v0][i]<inf))< p="">p[v0][i]=v0;elsep[v0][i]=-1;}s[v0]=true;d[v0][v0]=0;for(i=0;i<dim;i++)< p="">{double min=INF;int u=v0;for(int j=0;j<dim;j++)< p="">if(!s[j]&&d[v0][j]<min)< p="">{u=j;min=d[v0][j];}s[u]=true;for(int w=0;w<dim;w++)< p="">{if((!s[w])&&(d[v0][w]>d[v0][u]+map[u][w])) {d[v0][w]=d[v0][u]+map[u][w];p[v0][w]=u;}}}}Justin Hou介绍寻找最有价值路径(c语言)描述:从上(入口)往下行走,直到最下节点(出口)结束,将所经节点上的数值相加,要求找到一条最有价值路径(既是路径总数值最大)并输出总数值。
数学建模
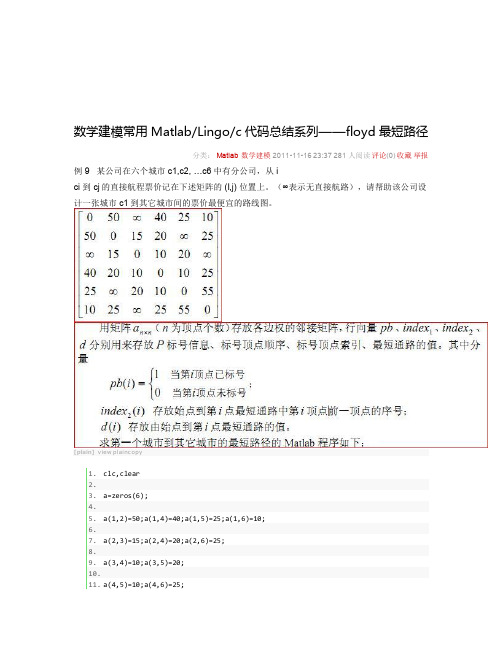
数学建模常用Matlab/Lingo/c代码总结系列——floyd最短路径分类:Matlab数学建模2011-11-16 23:37 281人阅读评论(0) 收藏举报例 9 某公司在六个城市c1,c2, …c6 中有分公司,从 ici 到 cj的直接航程票价记在下述矩阵的 (I,j) 位置上。
(∞表示无直接航路),请帮助该公司设计一张城市c1 到其它城市间的票价最便宜的路线图。
[plain]view plainc opy1.clc,clear2.3.a=zeros(6);4.5.a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;6.7.a(2,3)=15;a(2,4)=20;a(2,6)=25;8.9.a(3,4)=10;a(3,5)=20;10.11.a(4,5)=10;a(4,6)=25;12.13.a(5,6)=55;14.15.a=a+a';16.17.a(find(a==0))=inf;18.19.pb(1:length(a))=0;pb(1)=1;index1=1;index2=ones(1,length(a));20.21.d(1:length(a))=inf;d(1)=0;temp=1;22.23.while sum(pb)<length(a)24.25. tb=find(pb==0);26.27. d(tb)=min(d(tb),d(temp)+a(temp,tb));28.29. tmpb=find(d(tb)==min(d(tb)));30.31. temp=tb(tmpb(1));32.33. pb(temp)=1;34.35. index1=[index1,temp];36.37. temp2=find(d(index1)==d(temp)-a(temp,index1));38.39. index2(temp)=index1(temp2(1));40.41.end42.43.d, index1, index2编写 LINGO 程序如下:[plain]view plainc opy1.model:2.3.sets:4.5.cities/A,B1,B2,C1,C2,C3,D/;6.7.roads(cities,cities)/A B1,A B2,B1 C1,B1C2,B1 C3,B2 C1,8.9.B2 C2,B2 C3,C1 D,C2 D,C3 D/:w,x;10.11.endsets12.13.data:14.15.w=2 4 3 3 1 2 3 1 1 3 4;16.17.enddata18.19.n=@size(cities); !城市的个数;20.21.min=@sum(roads:w*x);22.23.@for(cities(i)|i #ne#1 #and# i #ne#n:24.25.@sum(roads(i,j):x(i,j))=@sum(roads(j,i):x(j,i)));26.27.@sum(roads(i,j)|i #eq#1:x(i,j))=1;28.29.@sum(roads(i,j)|j #eq#n:x(i,j))=1;31.end[plain]view plainc opy1.model:2.3.sets:4.5.cities/1..11/;6.7.roads(cities,cities):w,x;8.9.endsets10.11.data:12.13.w=0;14.15.enddata16.17.calc:18.19.w(1,2)=2;w(1,3)=8;w(1,4)=1;21.w(2,3)=6;w(2,5)=1;22.23.w(3,4)=7;w(3,5)=5;w(3,6)=1;w(3,7)=2;24.25.w(4,7)=9;26.27.w(5,6)=3;w(5,8)=2;w(5,9)=9;28.29.w(6,7)=4;w(6,9)=6;30.31.w(7,9)=3;w(7,10)=1;32.33.w(8,9)=7;w(8,11)=9;34.35.w(9,10)=1;w(9,11)=2;w(10,11)=4;36.37.@for(roads(i,j):w(i,j)=w(i,j)+w(j,i));38.39.@for(roads(i,j):w(i,j)=@if(w(i,j) #eq# 0,1000,w(i,j)));40.41.endcalc42.43.n=@size(cities); !城市的个数;44.45.min=@sum(roads:w*x);46.47.@for(cities(i)|i #ne#1 #and# i #ne#48.49.n:@sum(cities(j):x(i,j))=@sum(cities(j):x(j,i)));50.51.@sum(cities(j):x(1,j))=1;52.53.@sum(cities(j):x(j,1))=0; !不能回到顶点1;54.55.@sum(cities(j):x(j,n))=1;56.57.@for(roads:@bin(x));58.59.end60.61.例12 用Floyd算法求解例9。
matlab floyd最短路算法例题

matlab floyd最短路算法例题【原创版】目录一、引言二、Floyd 算法的原理与实现1.Floyd 算法的基本思想2.Floyd 算法的实现过程三、MATLAB 中 Floyd 算法的实现1.构建邻接矩阵2.实现 Floyd 算法3.显示最短路径四、Floyd 算法的应用案例1.案例描述2.案例分析五、总结正文一、引言在最短路径问题中,Floyd 算法是一种经典的动态规划算法。
它可以用于求解加权连通图(有向图、无向图)中所有顶点之间的最短路径长度。
本文将介绍 Floyd 算法的原理与实现,并在 MATLAB 中进行演示,最后通过一个实际案例来说明 Floyd 算法的应用。
二、Floyd 算法的原理与实现1.Floyd 算法的基本思想Floyd 算法的基本思想是:对于任意两个顶点 i 和 j,如果从顶点i 到顶点 j 的路径中有一个顶点 k,使得从顶点 i 到顶点 k 的路径长度加上从顶点 k 到顶点 j 的路径长度小于从顶点 i 直接到顶点 j 的路径长度,那么就将当前路径的长度更新为从顶点 i 到顶点 k 的路径长度加上从顶点 k 到顶点 j 的路径长度。
不断更新所有顶点之间的路径长度,直到所有顶点之间的路径长度都达到最短。
2.Floyd 算法的实现过程Floyd 算法的实现过程分为三个步骤:(1)构建邻接矩阵:邻接矩阵是一个二维数组,其中邻接矩阵的元素 a(i, j) 表示顶点 i 到顶点 j 的权值。
如果顶点 i 到顶点 j 之间没有边相连,则 a(i, j) 为无穷大(如 float("inf"))。
(2)初始化距离:将邻接矩阵中所有元素设置为无穷大,然后将主对角线上的元素设置为 0(表示从顶点 i 到顶点 i 的距离为 0)。
(3)迭代更新距离:遍历所有顶点 k,对于每个顶点 i 和 j,如果从顶点 i 到顶点 k 的距离加上从顶点 k 到顶点 j 的距离小于从顶点i 到顶点 j 的距离,那么就将当前距离更新为从顶点 i 到顶点 k 的距离加上从顶点 k 到顶点 j 的距离。
基于matlab的floyd算法 matlab计算最短路径

function [d,path]=floyd(a,sp,ep) % floyd % % Syntax: [d,path]=floyd(a,sp,ep) % % Inputs: % % % % % Outputs: % % % d - 最短路的距离 a sp ep - 距离矩阵是指 i 到 j 之间的距离,可以是有向的 - 起点的标号 - 终点的标号 - 最短路问题
试计算下图的最短路径, 1. 起点 C 点,终点 A 点。 2. 起点 A 点,终点 G 点。 3. 起点 D 点,终点 F 点。
试计算下图的最短路径, 1.起点 F 点,终点 A 点。 2. 起点 E 点,终点 C 点。
if D(i,j)~=inf path(i,j)=j; %j 是 i 的后续点 end end end for k=1:n for i=1:n for j=1:n if D(i,j)>D(i,k)+D(k,j)
D(i,j)=D(i,k)+D(k,j); path(i,j)=path(i,k); end end end end p=[sp]; mp=sp; for k=1:n if mp~=ep d=path(mp,ep); p=[p,d]; mp=d; end end d=D(sp,ep) path=p
path - 最短路的路径
பைடு நூலகம்
a =[ 0 50 Inf 50 0 15 inf; 15 ; 0 ];% a(i,j),从节点 i 到 j 之间的距离
% [d,path]=floyd(a,2,5) sp=3; ep=1; n=size(a,1); D=a; path=zeros(n,n); for i=1:n for j=1:n
matlab floyd最短路算法例题

感谢您为我指定了这个主题,让我有机会与您共享关于matlab floyd 最短路算法例题的深度和广度的文章。
在本文中,我将从浅入深地介绍这个主题,并给出相关的例题和解析,以便您能更好地理解这一算法。
1. matlab floyd最短路算法简介matlab floyd最短路算法是一种用于计算图中各顶点之间最短路径的算法。
它采用动态规划的思想,通过不断更新两点之间的最短距离来求解整个图中所有点之间的最短路径。
这个算法的时间复杂度为O(n^3),适用于有向图或者无向图。
2. 例题分析假设我们有一个有向图,包含5个点和7条边,我们需要使用matlab floyd算法来求解任意两点之间的最短路径。
- 我们首先需要构建图的邻接矩阵,表示各点之间的距离或者权值。
我们可以根据邻接矩阵使用matlab floyd算法来求解最短路径。
- 以图中任意两点之间的最短路径为例,假设我们需要求解点1到点4之间的最短路径。
我们可以在求解过程中使用动态规划的方法,通过不断更新点1到点4的最短距离来求解最终的最短路径。
3. 个人观点和理解对于matlab floyd最短路算法,我个人认为它是一种非常实用且高效的算法。
尤其是对于大规模的图,使用matlab floyd算法可以快速地求解各点之间的最短路径,为很多实际问题的求解提供了便利。
总结与回顾通过本文的介绍和例题分析,相信您对matlab floyd最短路算法已有了更深入的理解。
希望本文能够对您有所帮助,也欢迎您共享更多关于这个主题的想法和见解。
以上是本文对matlab floyd最短路算法的介绍和分析,希望能够带给您一些启发和帮助。
如果还有其他疑问或者需要进一步讨论,欢迎随时与我交流。
matlab floyd最短路算法是一种非常重要的图论算法,它能够在有向图或者无向图中高效地求解任意两点之间的最短路径。
在本文中,我们将更加深入地了解matlab floyd最短路算法的原理和实际应用,并通过详细的例题分析来加深对该算法的理解。
matlab floyd最短路算法例题

matlab floyd最短路算法例题摘要:一、简介二、Floyd 算法的原理三、MATLAB 实现Floyd 最短路算法的例题四、Floyd 算法的适用范围和局限性五、总结正文:一、简介Floyd 算法是一种经典的动态规划算法,用于求解加权连通图中所有顶点之间的最短路径。
它可以处理有向图和无向图,同时也可以处理带有负权边的图。
Floyd 算法的时间复杂度为O(n^3),其中n 为图的顶点数。
二、Floyd 算法的原理Floyd 算法的核心思想是:对于任意两个顶点i 和j,我们可以通过若干个中间顶点k 来进行路径传递。
也就是说,从顶点i 到顶点j 的最短路径可能经过顶点k,也可能直接从顶点i 到顶点j。
因此,我们需要遍历所有可能的中间顶点k,检查从顶点i 到顶点k 再到顶点j 的路径是否比直接从顶点i 到顶点j 的路径更短。
如果成立,我们就更新从顶点i 到顶点j 的路径长度。
三、MATLAB 实现Floyd 最短路算法的例题以下是一个简单的MATLAB 实现Floyd 算法的例题:```matlab% 创建一个邻接矩阵表示的图A = [0, 1, 0, 0, 0;1, 0, 1, 0, 0;0, 1, 0, 1, 0;0, 0, 1, 0, 1;0, 0, 0, 1, 0];% 使用Floyd 算法计算最短路径dist = floyd(A);% 输出最短路径距离矩阵disp(dist);```在这个例题中,我们创建了一个5x5 的邻接矩阵A 来表示一个简单的图。
然后我们使用MATLAB 内置的floyd 函数来计算该图的所有顶点之间的最短路径。
最后,我们输出最短路径距离矩阵。
四、Floyd 算法的适用范围和局限性Floyd 算法适用于求解加权连通图中所有顶点之间的最短路径问题。
它尤其适用于处理有向图和无向图,同时也可以处理带有负权边的图。
然而,Floyd 算法不能用于构造最短路径,也不能用于计算带有负权回路的最短路径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab floyd最短路算法例题
摘要:
一、Floyd 算法介绍
二、MATLAB 实现Floyd 最短路算法的例题
三、Floyd 算法的应用案例
四、总结
正文:
一、Floyd 算法介绍
Floyd 算法是一种经典的动态规划算法,用于求解加权连通图(有向图、无向图)中所有顶点之间最短路的长度。
该算法可以处理带有负权边的图,并且时间复杂度为O(n3)。
Floyd 算法的基本思想是:从任意节点i 到任意节点j 的最短路径不外乎2 种可能,1 是直接从i 到j,2 是从i 经过若干个节点k 到j。
所以,我们假设Dis(i,j) 为节点u 到节点v 的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) Dis(k,j) < Dis(i,j) 是否成立,如果成立,证明从i 到k 再到j 的路径比i 直接到j 的路径短,我们便设置
Dis(i,j) Dis(i,k) Dis(k,j)。
二、MATLAB 实现Floyd 最短路算法的例题
以下是一个使用MATLAB 实现Floyd 算法的例题:
```MATLAB
function [T,pred] = floyd(adj_matrix)
% 输入:邻接矩阵
% 输出:最短路径矩阵,预测矩阵
= size(adj_matrix, 1);
T = zeros(n, n);
pred = zeros(n, n);
for i = 1:n
for j = 1:n
for k = 1:n
if i ~= k && i ~= j && k ~= j
T(i, j) = min(T(i, j), T(i, k) + T(k, j));
pred(i, j) = T(i, k) + T(k, j);
end
end
end
end
end
```
三、Floyd 算法的应用案例
Floyd 算法在网络分析、社交网络、生物信息学等领域具有广泛的应用。
例如,在网络分析中,Floyd 算法可以用于寻找网络中的最短路径,以便快速传递信息或货物。
在社交网络中,Floyd 算法可以用于找到联系人之间的最短路径,以便在社交网络中快速传播信息。
在生物信息学中,Floyd 算法可以用于计算基因之间的最短路径,以便研究基因之间的功能关系。
四、总结
Floyd 算法是一种高效的最短路算法,可以用于求解加权连通图中所有顶点之间的最短路径。
该算法可以处理带有负权边的图,并且时间复杂度为
O(n3)。
