运筹学课程作业
运筹学作业题目

运筹学作业题目1. 题目描述某物流公司需要将货物从A地运送到B地,货物数量为N件。
已知A地和B 地之间有M个中转站,每个中转站都有一定的处理能力和储存能力。
现在需要你运用运筹学的方法,给出一个最优的货物运输方案。
2. 问题分析首先,我们需要确定以下几个问题:•货物从A地到B地的最短路径是什么?•每个中转站的处理能力和储存能力分别是多少?•每个中转站的位置以及与其他中转站的距离是多少?3. 数据收集为了解决这个问题,我们需要收集以下数据:•A地和B地之间的距离•每个中转站的处理能力和储存能力•每个中转站的位置以及与其他中转站的距离4. 模型建立我们可以将这个问题建模为一个网络图问题,其中A地和B地为源点和汇点,中转站为中间节点。
我们需要找到从源点到汇点的最短路径,并且满足各个中转站的处理能力和储存能力的限制。
我们可以使用最短路径算法(如Dijkstra算法或Floyd-Warshall算法)找到从源点到汇点的最短路径,并计算出该路径上各个中转站的处理能力和储存能力。
5. 求解与优化在求解过程中,我们需要考虑以下几个方面:•最短路径的选择:我们可以根据距离、处理能力和储存能力三个因素进行综合考虑,选择最优的路径。
•货物分配策略:根据中转站的处理能力和储存能力,我们需要制定合理的货物分配策略,使得所有中转站的资源利用率最大化。
•容量约束的处理:如果某个中转站的处理能力或储存能力不足,我们需要考虑如何调整货物的分配,以避免资源浪费或堆积。
6. 结果分析根据我们的模型和求解过程,我们可以得到一个最优的货物运输方案,并且可以得到以下几个结果:•最短路径:确定了从A地到B地的最短路径,方便后续货物的运输安排。
•中转站资源利用率:根据我们的货物分配策略,可以评估每个中转站资源的利用率,进一步优化中转站的运营效果。
•资源调配建议:如果存在处理能力或储存能力不足的中转站,我们可以提供资源调配建议,帮助公司优化资源分配。
运筹学作业(一)

《运筹学》作业(一)题1.某货轮分前、中、后三个舱位,结构参数见表1。
拟装运三种货物,性能参数见表2。
为了航运安全,要求舱位之间载重比例的偏差不超过10%,以保持船体的平衡。
问应如何制订货物的装运方案可使此运输的收益达到最大?建立该问题的LP 模型。
提示:用x ij 表示装运在第i 个舱位中的第j 种货物的重量,其中:i = 前, 中, 后; j = A, B, C ;故一共有9个变量。
目标是使总运费达到最大。
约束条件分为四组:每个舱位中货物的体积限制,重量限制,每种货物的数量限制,和舱位之间载重比例的偏差限制,故一共有12个约束条件。
题2.确定下列约束条件构成的可行域(1) ⎪⎩⎪⎨⎧≥≤+无约束 2121042x x x x (2)⎪⎩⎪⎨⎧≥-无约束无约束 21210x x x x (3) ⎪⎩⎪⎨⎧≥=≤+-05222121 x x x x (4) ⎪⎩⎪⎨⎧=≥≤+21422121 x x x x 题3.已知LP 问题: 0,,,844344243214213214321≥=++=++-++=x x x x x x x x x x x x x x Z s.t.max试确定⎪⎪⎭⎫ ⎝⎛-==-4/114/10,),(132B x x x B T 是否为最优解。
如果是,给出最优目标值;否则,确定新一轮的进、出变量。
提示 检验数 j j B j c p B c -=-1λ,j = 1, 4。
如果检验数的值大于或等于零,则为最优解;否则,令绝对值最大的负检验数对应的非基本变量进入,而令最小正比值对应的基本变量退出。
题4.给定LP 问题: 0,,42044602343025233212131321321≥≤+≤+≤++++=x x x x x x x x x x x x x Z s.t .m a x已知其最优解为:⎪⎪⎪⎭⎫ ⎝⎛--===-11202/1004/12/1,)20,230,100(),,(1632B x x x x T B T。
运筹学作业

图 17: 表9-9
把表的数据做成这些图,可以看出用电量,明显有季度性。在这六年中用电量逐年上升,当然也收到 不规则因素影响. 对于趋势投影和季度因素的预测问题, 用 T 表示趋势因素, S 表示季度因素, I 表示不确定因素。 这里在 做一个假设,就是不规则因素只在时间序列产生随机效应,而对季度没有影响。 对 于 这 样 的 时 间 序 列t时 期 的 函 数 Yt ,它 受 到t时 期 的 趋 势 因 素T,季 度 因 素Yt , 季 度 因 素St 和 不 确 定 因 素St 的影响,可以得到以下预测模型是你学生上传的作业,绝对原创 学号:6666888888 班级: 信息管理与信息系统
1
1
一:教材 P143
2
1
一:教材 P143
5.9某公司要生产2000件某种产品, 这种产品可以利用设备A,B,C,D任一种来加工, 但是要使用这三 种设备的任意一种,都需垫付相应的生产设备费(若不使用就不需要垫付)生产该产品的单位耗电量,成 本以及设备的生产准备费如表5-23所示。生产该产品的单位耗电量,成本以及各设备的生产准备费如表523所示。 如果生产总的用电量限制在2500度,请制定一个成本最低的生产方案。
图 15: 运价表三 故运输方案为 1分厂生产的50箱运往甲 250箱运往乙。 2分厂生产的 400箱运往甲。 3分厂生产的500箱运往丙。 运价最低,最低运价为 19300元。
5
第五题,教材P260,修改
10
图 16: 图ccc
5
(1) 预测下一年该校的用电量。
第五题,教材P260,修改
9.3 由于近几年高校扩大招生,某校近几年的用电量增加较快,表 9 − 9为该校6年来的用电情况。
图 6: 表4-26 解 确定决策变量。
运筹学作业

管理运筹学作业
第二章第七题
某公司正在制造两种产品,产品1和产品2,每天的产量分别是30个和120个,利润分别为500元/个,和400元/个,公司负责制造的副总经理希望了解是否可以通过改变这两种产品的数量而提高公司的利润。
公司各个车间的加工能力和制造单位产品所需要的加工工时,如下表所示:
车间产品1 产品2 车间的加工能力(每天
加工工时数)
1 2 0 300
2 0
3 540
3 2 2 440
4 1.2 1.
5 300
由上表可知:
(1)最优解为(150,70),目标函数最优值为103000。
(2)第一、第三车间的加工工时数用完,第二、第四车间的加工工时数没有用完,第二车间的松弛变量为330,第四车间的松弛变量为15。
(3)第一、第二、第三、第四车间加工工时的对偶价格分别为50、0、200、0。
对偶价格的定义为:在约束条件常数项中增加一个单位而使目标函数值得到改进的数量。
即:在第一车间中每增加一个工时,那么总利润将增加50元,第三车间每增加一个单位的工时,总利润增加200元;第二、第四车间增加工时,对总利润没有影响。
(4)目标函数中系数的灵敏度分析:
当目标函数的斜率小于等于—1时,此最优解不变。
当产品1的利润不变时,产品2的利润在【0,500】这个范围内变化时,此最优解不变;当产品2的利润不变时,产品1的利润大于等于400时,此最优解不变。
运筹学作业题

1运筹学作业题一、将下列线性规划问题化为标准型(1)、123123123123123 235567916..192513,0,Max z x x x x x x x x x s t x x x x x x =+++-≥-⎧⎪-+-=⎪⎨-+≤⎪⎪≥⎩符号不限(2)、123123123123 242+3=20..3+4=25,0,26Max z x x x x x x s t x x x x x x =+++⎧⎪+⎨⎪≥≤≤⎩ 二、求出下面线性规划问题的所有基解、基可行解和最优解12123412341234522+34=7..22++2=3,,,0Min z x x x x x x s t x x x x x x x x =-++⎧⎪+⎨⎪≥⎩三、用图解法求解下列线性规划问题,并说明解的类型(1)、121212212 501003002400..250,0Max z x x x x x x s t x x x =++≤⎧⎪+≤⎪⎨≤⎪⎪≥⎩ (2)、12121221212 393224..6250,0Max z x x x x x x s t x x x x x =++≤⎧⎪-+≤⎪⎪≤⎨⎪-≤⎪⎪≥⎩ 四、分别用图解法和单纯形法求解线性规划问题,并指出每一个单纯形表所对应的可行域的顶点122121212 25156224..5,0Max z x x x x x s t x x x x =+≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩ 五、分别用大M 法及两阶段法求解下列线性规划问题(1)、1231231231312332+114+23..2 1,,0Max z x x x x x x x x x s t x x x x x =---≤⎧⎪-+≥⎪⎨-=-⎪⎪≥⎩ (2)、121212123222..3412,0Max z x x x x s t x x x x =++≤⎧⎪+≥⎨⎪≥⎩2六、写出线性规划问题的对偶问题(1)、123123123123123 3526304320..40,0,Min z x x x x x x x x x s t x x x x x x =-+--+-≥⎧⎪+-≤⎪⎨-+=-⎪⎪≤≥⎩无约束(2)、123452345123413412345 37588 34162332 222 5..210525,0,Max z x x x x x x x x x x x x x x x x s t x x x x x =--++-+-=-⎧⎪+--≥⎪⎪-+-≤-⎪⎨-≤≤⎪⎪≤≤⎪≥⎪⎩无约束(3)、111111111 1,, 1,2,,..0 1,, 1,2,,nj jj nij j i j n ij j i j j j Max z c x a x b i m m a x b i m m m s t x j n n x j n n n====⎧≤=≤⎪⎪⎪⎪==++⎨⎪⎪≥=≤⎪=++⎪⎩∑∑∑无约束七、用对偶单纯形法求解线性规划问题123123123123524324..63510,,0Min z x x x x x x s t x x x x x x =++++≥⎧⎪++≥⎨⎪≥⎩ 八、灵敏度分析给出下列线性规划:12312312312362124+324..26+330,,0Max z x x x x x x s t x x x x x x =+++≤⎧⎪+≤⎨⎪≥⎩ 的最优单纯形表:3其中,s 1、s 2分别为第1、2约束方程的松弛变量。
运筹学作业(5)
运筹学作业(5)
习题1、清华大学运筹学(第三版)P112 4.2(2)
用图解法找出以下目标规划问题的满意解。
习题2、清华大学运筹学(第三版)P282 10.4(a)
用破圈法和避圈法求图中的最小树。
习题3、清华大学运筹学(第三版)P283 10.7图10-40
用课上介绍的逆推方法,求v1到v11的最短路径,标明路径,求出路长。
习题4:已知条件如表所示
p1:每周总利润不得低于10000元;
p2:因合同要求,A型机每周至少生产10台,B型机每周至少生产15台;
p3:希望工序Ⅰ的每周生产时间正好为150小时,工序Ⅱ的生产时间最好用足,甚至可适当加班。
试建立这个问题的目标规划模型并求解(可利用EXCEL求)。
思考题:在上题中,如果工序Ⅱ在加班时间内生产出来的产品,每台A型机减
少利润10元,每台B型机减少利润25元,并且工序Ⅱ的加班时间每周最多不超过30小时,这是p4级目标,试建立这个问题的目标规划模型并求解。
(此题下周四前会给出参考答案)。
运筹学作业题整理
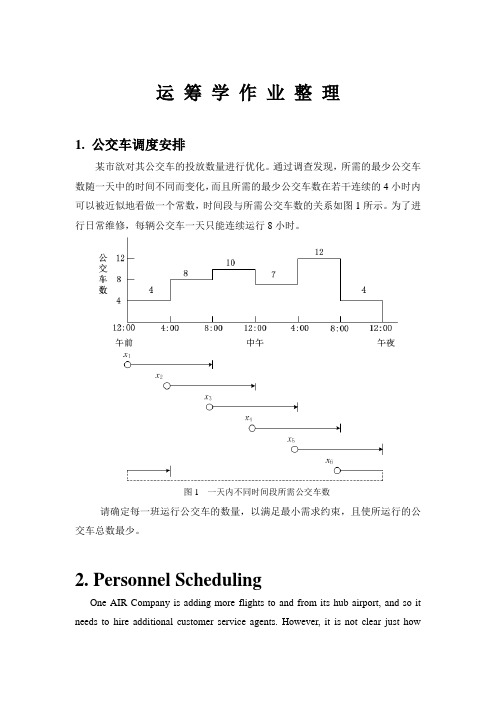
运筹学作业整理1. 公交车调度安排某市欲对其公交车的投放数量进行优化。
通过调查发现,所需的最少公交车数随一天中的时间不同而变化,而且所需的最少公交车数在若干连续的4小时内可以被近似地看做一个常数,时间段与所需公交车数的关系如图1所示。
为了进行日常维修,每辆公交车一天只能连续运行8小时。
图1 一天内不同时间段所需公交车数请确定每一班运行公交车的数量,以满足最小需求约束,且使所运行的公交车总数最少。
2. Personnel SchedulingOne AIR Company is adding more flights to and from its hub airport, and so it needs to hire additional customer service agents. However, it is not clear just howmany more should be hired. Management recognizes the need for cost control while also consistently providing a satisfactory level of service to customers. Therefore, an OR team is studying how to scheduling the agents to provide satisfactory service with the smallest personnel cost.Based on the new schedule of flights, an analysis has been made of the minimum number of customer service agents that need to be on duty at different times of the day to provide a satisfactory level of service. The right most column of the flowing table shows the number agents needs for the time periods given in the first column. The other entries in this table reflect one of the provisions in the company’s current contract with the union that the represents the customer service agents. The provision is that each agent works an 8-hour shift 5 days per week.The five authorized eight-hour shifts are–Shift 1: 6:00 AM to 2:00 PM–Shift 2: 8:00 AM to 4:00 PM–Shift 3: Noon to 8:00 PM–Shift 4: 4:00 PM to midnight-Shift 5: 10:00 PM to 6:00 AM.How many agents should be assigned to each shift? Please set up a LP model and solve it.3.已知某工厂计划生产I,II,III三种产品,各产品需要在A,B,C 设备上加工,有关数据见表4-24。
运筹学作业

运筹学作业数学0501班4-5(P177)某厂生产一种产品,该产品在未来四个月的销售量估计如表所示。
该产品的生产准备费用为每批500元,每件生产费用为1元,每个的存储费用每月1元。
假定1月初的存货为100解:根据生产一库存问题的一般解法以及题中所给条件,我们有4=n ,K k k k k B M d d d d x x h i C ,,2,3,5,4,0,1,1,1,5432151=========题中未给出,可认为仓库容量K M 与生产能力K B 均为无穷大,不受限制。
本问题中,,,K k k k M h l c K B 均不随k 而改变,据之求解如下,先求条件最优集合:当k=4时,由于0)(55≡x f 和04445=-+=d u x x⎩⎨⎧=≠-+=⎩⎨⎧=≠+=-=2,02,250,00,5)(44444344min 444x x x u u u x f x d u 其中,{}2,m in 04444==≤≤d d M x 即当24<x 时,有2444>-=x d u24=x 时,有0444=-=x d u⎩⎨⎧≤≤-==∴20,72,0)(44444x x x x f当k=3时,3333334-+=-+=u x d u x x {}5,m in 0434333=+=+≤≤d d d d M x{}{}{}3333333333433335,5,m in ,,m in 3,0m ax x d x M x B d x M x d d b u x +=+--=+--+≤≤-⎩⎨⎧=+-≠+-+++=0),(30),(35)(344334433333min 3u x f x u x f u x u x f u 若 03=x ,则533≤≤u ,13=x ,则423≤≤u23=x ,则313≤≤u ,33=x ,则203≤≤u 43=x ,则103≤≤u ,53=x ,则003≤≤u由此可计算()3f 结果如下表所示:当k=2时,5222223-+=-+=u x d u x x{}10,m in 043243222=++=++≤≤d d d d d d M x{}{}{}2222222432222105,10,m in ,,m in 5,0m ax x x M x B d x M x d d d B u x k k -=+--=+--++≤≤-⎩⎨⎧=+-≠+-+++=0),(0),(5)(23322233222222min 2u x f d x u x f d u x u x f u⎩⎨⎧=+-≠++=0),(50),(2233223322min 2u x f x u x f x u u若02=x ,则1052≤≤u ,12=x ,则442≤≤u22=x ,则832≤≤u ,32=x ,则722≤≤u42=x ,则612≤≤u ,52=x ,则502≤≤u 62=x ,则402≤≤u ,72=x ,则302≤≤u 82=x ,则202≤≤u ,92=x ,则102≤≤u 1102=x ,则002≤≤u由此可计算()2f ,结果如下表所示:当k=1时,有11=x ,4111112-+=-+=u x d u x x{}{}11114321111,,m in 4,0m ax d x M x d d d d B u x ---+++≤≤-即有1331≤≤u{}{})(22min )(45)(2212211111min 1x f u x f u x u x f u ++=+-+++=∴由此可计算()1f ,结果如下表所示:由于11=x 是唯一确定的,因此30)1(1=f 是整个问题的最优目标函数值,)1('1u 是最优决策,由以上计算过程可知最优决策有两个,于是可得最优策略如下:3*1=u5*2=u5*3=u0*4=u1*1=x0*2=x0*3=x2*4=x0*5=x或3*1=u10*2=u0*3=u0*4=u1*1=x0*2=x5*3=x2*4=x0*5=x即最优生产计划是1月份生产3百件,2月份生产5百件,3月份生产5百件,4月份不生产,或1月份生产3百件,2月份生产10百件,3月份不生产,4月份也不生产,总费用为30百元,两种最优方案中均利用适当的库存,节约了生产的固定费用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学课程作业
1. 某农场现有100hm2(公顷)土地及150000元资金可用于发展生产。
农场劳动力情况为秋冬季3500人日,春夏季4000人日,如劳动力本身用不了时可外出打工,春夏季收入为50元/人日,秋冬季为40元/人日。
该农场种植三种作物:大豆、玉米、小麦,并饲养奶牛和鸡。
种作物时不需要专门投资,而饲养动物时每头奶牛投资400元,每只鸡投资5元。
养奶牛时每头需拨出0.5 hm2(公顷)土地种饲草,并占用人工秋冬季为60人日,春秋季为30人日,年净收入为1000元/每头奶牛。
养鸡时不占用土地,需人工为每只鸡秋冬季需0.4人日,春夏季为0.2人日,年净收入为20元/每只鸡。
农场现有鸡舍允许最多养6000只鸡,牛栏允许最多养120头奶牛。
三种作物每年需要的人工及
试决定该农场的经营方案,使年净收入为最大。
建立线性规划模型
令种植大豆公顷数X1,玉米公顷数X2,小麦公顷数X3,X4只鸡,X5头牛,X6人秋冬去打工,X7人春夏去打工
所以可以设立条件带入
WinQSB
所以种100公顷小麦,多余的人力都去打工得到最大净收入220000元
2. 我国拟考虑某行业的投资布点问题,现已初步选择了七个投资项目,记作S1,S2……S,其中S~S处于东部地区,S~S处于西部地区,各项目的有关资料下表:
决策时,需考虑如下因素:
(1)投资总规模应控制在1000万元以内;
(2)西部地区无论选中的投资项目总数还是投资总量均不逊于东部地区;
(3)S1和S4是同类建设项目,应该避免重复建设;
(4)S7只有在S3上马的前提下方可上马;
(5)希望投资总效益最大。
为决策投资项目,试建立0—1整数规划模型。
所以上马S2,S3,S6,S7四个项目。
3.下表给出了一运输问题的产地、销地以及产量和销量,单位运费,求此运输问题的最优调运方案?
4. 某大学服务公司有一个鲜货店,每天以每斤6元的价格进鲜货,然后当天以每天8元的价格售出。
如果当天卖不出去,第二天就要以每斤3.5元的价格处理掉。
据此店以往的资料可知每天可售出10~15斤。
在100天的统计数据中,售出情况见下表:
试用期望收益法进行风险型决策。
最佳决策是alternative3 也就是每天进12斤
5. 实际工作和生活中面临大量的决策问题,请结合某一问题,阐述如何用运筹学方
法解决的?要求阐述所面临问题的背景、解决的思路。
