高中必修一指数和指数函数练习题及答案

合集下载

高中数学《指数函数》针对练习及答案

第二章函数2.4.2 指数函数（针对练习）针对练习针对练习一指数与指数幂的运算1．用分数指数幂的形式表示下列各式(a>0，b>0)．(1)a222．计算或化简下列各式：（1）(a－2)·(－4a－1)÷(12a－4)(a>0)；（2）213-233+0.0028-⎛⎫- ⎪⎝⎭－2)－1＋0. 3．计算：(1)1111242 114310.7562)164300---⎫⎛⎫⎛⎫⨯⨯+-++⎪ ⎪⎝⎭⎝⎭⎝⎭111133420,0)a ba b a b->>⎛⎫⎪⎝⎭4．计算：(1)10132114(2)924---⎛⎫⎛⎫-⨯-+-⎪ ⎪⎝⎭⎝⎭；(2)2932)-⨯5．(1)()2163278()[2]8---；(2)()())1213321()0040.1a b a b ---＞，＞.针对练习二指数函数的概念6．在①4x y =；①4y x =；①4x y =-；①()4xy =-；①()121,12xy a a a ⎛⎫=->≠ ⎪⎝⎭中，y 是关于x 的指数函数的个数是（） A ．1 B ．2 C ．3 D ．47．下列函数是指数函数的是（）A ．y ＝()2x πB ．y ＝(－9)xC ．y ＝2x －1D ．y ＝2×5x8．下列函数中为指数函数的是（） A ．23x y =⋅ B ．3x y =-C ．3x y -=D ．1x y =9．函数()244xy a a a =-+是指数函数，则有（）A ．a ＝1或a ＝3B ．a ＝1C ．a ＝3D ．a ＞0且a ≠110．若函数()x f x a =（a >0，且a ≠1）的图象经过(12,)3，则(1)f -=（） A．1 B ．2C D ．3针对练习三指数函数的图像11．函数2x y -=的图象大致是（）A ．B ．C ．D ．12．函数①x y a =；①x y b =；①x y c =；①x y d =的图象如图所示，a ，b ，c ，d 分别是下列四个数：5413，12中的一个，则a ，b ，c ，d 的值分别是（）A ．5413，12 B 54，12，13C ．12，1354D ．13，12，5413．若0a >且1a ≠，则函数()11x f x a -=+的图象一定过点（）A ．()0,2B ．()0,1-C ．()1,2D ．()1,1-14．已知函数f （x ）= ax +1的图象恒过定点P ，则P 点的坐标为（） A ．(0，1) B ．(0，2) C ．(1，2)D ．()1,1a +15．对任意实数01a <<，函数()11x f x a -=+的图象必过定点（）A ．()0,2B ．()1,2C ．()0,1D ．()1,1针对练习四指数函数的定义域16．函数y ） A ．(,3]-∞ B ．[3,)+∞ C ．(,2]-∞ D ．[2,)+∞17．函数()22f x x -的定义域为（） A ．[0,2) B ．(2,)+∞C ．()(),22,-∞+∞D ．[0,2)(2,)⋃+∞18．设函数f （x ），则函数f （x 4）的定义域为（） A ．(],4∞- B ．1,4∞⎛⎤- ⎥⎝⎦C ．(]0,4D ．10,4⎛⎤⎥⎝⎦19．已知函数()y f x =的定义域为()0,1，则函数()()21xF x f =-的定义域为（）A ．(),1-∞B ．()(),00,1-∞⋃C ．()0,∞+D ．[)0,120．函数y (－∞，0]，则a 的取值范围为( ) A ．a ＞0 B ．a ＜1 C ．0＜a ＜1 D ．a ≠1针对练习五指数函数的值域21．函数2212x xy -⎛⎫= ⎪⎝⎭的值域为（） A ．1,2⎡⎫+∞⎪⎢⎣⎭B ．1,2⎛⎤-∞ ⎥⎝⎦C ．10,2⎛⎤⎥⎝⎦D ．(]0,222．若23x ，则函数1()421x x f x +=-+的最小值为（） A ．4 B ．0 C ．5 D ．923．函数2121x x y -=+的值域是（）A ．()(),11,-∞--+∞B ．(),1-∞-C ．()1,1-D ．()(),11,-∞+∞24．已知函数()()1123,12,1x a x a x f x x -⎧-+<=⎨≥⎩的值域为R ，则实数a 的取值范围是（）A ．10,2⎡⎫⎪⎢⎣⎭B ．1,2⎛⎫-∞ ⎪⎝⎭C ．(),0-∞D ．[)0,225．函数2x y a =-（0a >且1a ≠，11x -≤≤）的值域是5,13⎡⎤-⎢⎥⎣⎦，则实数=a （）A ．3B ．13C ．3或13D ．23或32针对练习六指数函数的单调性26．函数2435x x y -+-=的单调递减区间是（） A ．[2,)+∞ B ．(,2]-∞ C ．(,1]-∞ D ．[1,)+∞27．函数223112x x y -+⎛⎫= ⎪⎝⎭的单调递减区间为（） A ．(1,)+∞ B ．3,4⎛⎤-∞ ⎥⎝C ．(),1-∞D ．3,4⎡⎫+∞⎪⎢⎣⎭28．若函数()215x axf x +⎛⎫= ⎪⎝⎭在[]1,2单调递减，则a 的取值范围（）A ．4a ≤-B ．2a ≤-C ．2a ≥-D ．4a ≥-29．若函数()(),1,513,13x a x f x a x x ⎧≥⎪=⎨-+<⎪⎩在R 上单调递减，则实数a 的取值范围是（） A ．12,33⎛⎤⎥⎝⎦B ．1,2C ．11,32⎡⎫⎪⎢⎣⎭D ．20,3⎛⎫⎪⎝⎭30．已知函数()()4211xa x x f x a x ⎧-≤=⎨>⎩，，是R 上的单调函数，那么实数a 的取值范围为（）A ．()01，B ．()13，C ．423⎡⎫⎪⎢⎣⎭，D ．312⎛⎤ ⎥⎝⎦，针对练习七比较大小与解不等式31．已知412a ⎛⎫= ⎪⎝⎭，124b =，122c =，则a ，b ，c 的大小关系是（） A ．a b c < ⎪⎪⎝⎭⎝⎭，则实数a 的取值范围是（） A ．(,1)-∞ B ．(1,)+∞C ．(3,)+∞D ．(3),-∞34．若x 满足不等式221139x x -+⎛⎫ ⎪⎝⎭，则函数2x y =的值域是（）A ．1,28⎡⎫⎪⎢⎣⎭B ．1,28⎡⎤⎢⎥⎣⎦C ．1,8⎛⎤-∞ ⎥⎝⎦D ．[2,)+∞35．若1133ab⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，则下列正确的是（）A ．33a b C ．11a b<D ．b c a c -<-针对练习八指数函数的应用36．专家对某地区新型流感爆发趋势进行研究发现，从确诊第一名患者开始累计时间t （单位：天）与病情爆发系数()f t 之间，满足函数模型：0.22(340)1()1t f t e --=+，当()0.1f t =时，标志着疫情将要局部爆发，则此时t 约为（参考数据： 1.13e ≈）（）A ．10B ．20C ．30D ．4037．基本再生数0R 与世代间隔T 是流行病学基本参数，基本再生数是指一个感染者传染的平均人数，世代间隔指两代间传染所需的平均时间，在α型病毒疫情初始阶段，可以用指数函数模型(e )rt I t =描述累计感染病例数()I t 随时间t （单位：天）的变化规律，指数增长率r 与0R 、T 近似满足01R rT =+，有学者基于已有数据估计出0 3.22R =，10T =.据此，在α型病毒疫情初始阶段，累计感染病例数增加至(0)I 的4倍，至少需要（）（参考数据：ln 20.69≈） A ．6天 B ．7天 C ．8天 D ．9天38．某灭活疫苗的有效保存时间T （单位：小时h ）与储藏的温度t （单位：①）满足的函数关系为e ht b T +=（k ，b 为常数，其中e 2.71828=⋅⋅⋅，是一个和π类似的无理数，叫自然对数的底数），超过有效保存时间，疫苗将不能使用.若在0①时的有效保存时间是1080h ，在10①时的有效保存时间是120h ，则该疫苗在15①时的有效保存时间为（） A ．15h B ．30h C ．40h D ．60h39．某食品的保鲜时间y （单位：小时）与储藏温度x （单位：C ︒）满足函数关系e kx b y +=（e 2.718=为自然对数的底数，,k b 为常数）．若该食品在0C ︒的保鲜时间是192小时，在33C ︒的保鲜时间是24小时，则该食品在22C ︒的保鲜时间是（） A ．20 小时 B ．24小时 C ．36小时 D ．48小时40．牛顿曾经提出了常温环境下的温度冷却模型：()100e ktθθθθ-=-+，其中为时间（单位：min ），0θ为环境温度，1θ为物体初始温度，θ为冷却后温度），假设在室内温度为20C 的情况下，一桶咖啡由100C 降低到60C 需要20min .则k 的值为（） A ．ln 220B ．ln 320C ．ln 210-D ．ln 310-第二章函数2.4.2 指数函数（针对练习）针对练习针对练习一指数与指数幂的运算1．用分数指数幂的形式表示下列各式(a >0，b >0)．(1)a2 2．【答案】(1)52a ； (2)136a ； (3)7362a b ； (4)76a . 【解析】【分析】由根式与有理数指数幂的关系，结合指数幂的运算性质化简求值即可. (1)原式＝11522222a a a a +⋅==. (2)原式＝22313333262a a a a +⋅==． (3)原式＝1221711333233332622222()()a ab a a b a b a b +⋅===.(4)原式＝55722666a a a a --⋅==． 2．计算或化简下列各式：（1）(a －2)·(－4a －1)÷(12a －4)(a >0)；（2）213-233+0.0028-⎛⎫- ⎪⎝⎭－2)－1＋0.【答案】（1）－13a ；（2）－1679.【解析】【分析】直接根据指数幂的运算性质计算即可. 【详解】(1)原式21434114(12)33a a a a ----+=-÷=-=-(2)原式213227118500--⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭213323()5002)12-⎡⎤=-+-+⎢⎥⎣⎦＝49＋20＋1＝－ 1679. 3．计算：(1)1111242114310.7562)164300---⎫⎛⎫⎛⎫⨯⨯+++ ⎪ ⎪⎝⎭⎝⎭⎝⎭111133420,0)a b a b a b ->>⎛⎫ ⎪⎝⎭【答案】(1)-16 (2)(0,0)a a b b>> 【解析】【分析】（1）根据分数指数幂的运算规则化简计算即可；（2）根据分数指数幂的运算规则化简得出结果. (1)原式=111222411010233-⎫⎫⎛⎫⨯⨯++⨯+ ⎪⎝⎭⎝⎭⎝⎭(12410223⎫=⨯-⨯+⎝⎭220216=-+=-(2)原式543311233(0,0)a baa b bab a b-==>> 4．计算：(1)1132114(2)924---⎛⎫⎛⎫-⨯-+- ⎪ ⎪⎝⎭⎝⎭；(2)2932)-⨯【答案】(1)196(2)【解析】【分析】（1）利用指数幂的运算性质即可求解.（2）利用根式与分数指数幂的互化以及指数幂的运算性质即可求解. (1)原式1111924()1218236=-⨯-+=++-=. (2)原式24119555636333222221[(8)](10)10(2)1010102---=⨯÷=⨯÷=⨯721102=⨯=== 5．(1)()21603278()[2]8---；(2)()())1213321()0040.1a b a b ---＞，＞.【答案】(1)8π+；(2)85. 【解析】【分析】(1)(2)均根据指数幂的运算性质即可计算；【详解】(1)原式233(2)=-1＋|3﹣π|162(2)+=4﹣1＋π﹣3＋23＝π＋8.(2)原式3332223322248510a b a b--⋅==.针对练习二指数函数的概念6．在①4x y =；①4y x =；①4x y =-；①()4xy =-；①()121,12xy a a a ⎛⎫=->≠ ⎪⎝⎭中，y 是关于x 的指数函数的个数是（） A ．1 B ．2 C ．3 D ．4【答案】B 【解析】【分析】直接根据指数函数的定义依次判断即可. 【详解】根据指数函数的定义，知①①中的函数是指数函数， ①中底数不是常数，指数不是自变量，所以不是指数函数； ①中4x 的系数是1-，所以不是指数函数； ①中底数40-<，所以不是指数函数．故选：B ．7．下列函数是指数函数的是（）A ．y ＝()2x πB ．y ＝(－9)xC ．y ＝2x －1D ．y ＝2×5x【答案】A 【解析】【分析】根据指数函数定义判断．【详解】B 中底数90-<，C 中指数是1x -，不是x ，D 中5x 前面系数不是1，根据指数函数定义，只有A 中函数是指数函数，故选：A.8．下列函数中为指数函数的是（）A ．23x y =⋅B ．3x y =-C ．3x y -=D ．1x y =【答案】C 【解析】【分析】根据指数函数的定义，逐项判定，即可求解. 【详解】根据指数函数的定义知，()0,1xy a a a =>≠，可得函数23x y =⋅不是指数函数；函数3x y =-不是指数函数；函数3x y -=是指数函数；函数1x y =不是指数函数. 故选：C.9．函数()244xy a a a =-+是指数函数，则有（）A ．a ＝1或a ＝3B ．a ＝1C ．a ＝3D ．a ＞0且a ≠1【答案】C 【解析】【分析】根据已知条件列不等式，由此求得正确选项. 【详解】由已知得244101a a a a ⎧-+=⎪>⎨⎪≠⎩，即2301a a a a ⎧+=⎪⎨⎪≠⎩，解得3a =．故选：C10．若函数()x f x a =（a >0，且a ≠1）的图象经过(12,)3，则(1)f -=（） A ．1 B ．2 CD ．3【答案】C 【解析】【分析】由指数函数所过的点求解析式，进而求(1)f -的值. 【详解】由题意，21(2)3f a ==，又a >0，则a =①()x f x =，故1(1)f --== 故选：C针对练习三指数函数的图像11．函数2x y -=的图象大致是（）A ．B ．C ．D ．【答案】D 【解析】【分析】根据函数的解析式可得函数2x y -=是以12为底数的指数函数，再根据指数函数的图像即可得出答案. 【详解】解：由122xxy -⎛⎫== ⎪⎝⎭，得函数2x y -=是以12为底数的指数函数，且函数为减函数，故D 选项符合题意. 故选：D.12．函数①x y a =；①x y b =；①x y c =；①x y d =的图象如图所示，a ，b ，c ，d 分别是下列四个数：5413，12中的一个，则a ，b ，c ，d 的值分别是（）A ．5413，12 B 54，12，13C ．12，1354D ．13，12，54【答案】C 【解析】【分析】由直线1x =与函数图象的交点的纵坐标从上到下依次为c ，d ，a ，b 即可求解. 【详解】解：直线1x =与函数图象的交点的纵坐标从上到下依次为c ，d ，a ，b ，511423>>，所以a ，b ，c ，d 的值分别是12，1354，故选：C.13．若0a >且1a ≠，则函数()11x f x a -=+的图象一定过点（）A ．()0,2B ．()0,1-C ．()1,2D ．()1,1-【答案】C 【解析】【分析】令10x -=求出定点的横坐标，即得解. 【详解】解：令10,1-=∴=x x .当1x =时，()1111=2f a -=+，所以函数()f x 的图象过点()1,2. 故选：C.14．已知函数f （x ）= ax +1的图象恒过定点P ，则P 点的坐标为（） A ．(0，1) B ．(0，2) C ．(1，2)D ．()1,1a +【答案】B 【解析】【分析】由指数函数过定点的性质进行求解. 【详解】()x f x a =的图象恒过定点()0,1，所以()1x f x a =+的图象恒过定点()0,2故选：B15．对任意实数01a <<，函数()11x f x a -=+的图象必过定点（）A ．()0,2B ．()1,2C ．()0,1D ．()1,1【答案】B 【解析】【分析】根据指数函数的知识确定正确选项. 【详解】当10x -=，即1x =时，()12f =，所以()f x 过定点()1,2. 故选：B针对练习四指数函数的定义域16．函数y ） A ．(,3]-∞ B ．[3,)+∞C ．(,2]-∞D ．[2,)+∞【答案】D 【解析】【分析】根据函数的定义域定义求解即可. 【详解】要使得函数y 则390x -≥，39x ≥，233x ≥，解得2x ≥.故函数y [2,)+∞. 故选：D.17．函数()22f x x -的定义域为（） A ．[0,2) B ．(2,)+∞C ．()(),22,-∞+∞D ．[0,2)(2,)⋃+∞【答案】D 【解析】求出使函数式有意义的自变量的范围即得、【详解】由21020x x ⎧-≥⎨-≠⎩得02x x ≥⎧⎨≠⎩，即[0,2)(2,)x ∈⋃+∞.故选：D.18．设函数f （x ），则函数f （x 4）的定义域为（） A ．(],4∞- B ．1,4∞⎛⎤- ⎥⎝⎦C ．(]0,4D ．10,4⎛⎤⎥⎝⎦【答案】A 【解析】【分析】求得4x f ⎛⎫= ⎪⎝⎭0，结合指数函数的性质求解即可．【详解】因为()f x =所以4x f ⎛⎫= ⎪⎝⎭因为44440,44,1,44x x x x -≥≤≤≤，所以4xf ⎛⎫⎪⎝⎭的定义域为(],4-∞，故选A ．【点睛】本题主要考查函数的定义域以及指数函数的单调性的应用，是基础题．定义域的三种类型及求法：(1)已知函数的解析式，则构造使解析式有意义的不等式(组)求解；(2) 对实际问题：由实际意义及使解析式有意义构成的不等式(组)求解；(3) 若已知函数()f x 的定义域为[],a b ，则函数()()f g x 的定义域由不等式()a g x b ≤≤求出.19．已知函数()y f x =的定义域为()0,1，则函数()()21xF x f =-的定义域为（）A ．(),1-∞B ．()(),00,1-∞⋃C ．()0,∞+D ．[)0,1【答案】B 【解析】【分析】抽象函数的定义域求解，要注意两点，一是定义域是x 的取值范围；二是同一对应法则下，取值范围一致. 【详解】()y f x =的定义域为()0,1，1021x-∴<<，即121121x x ⎧-<-<⎨≠⎩，10x x <⎧∴⎨≠⎩，解得：1x <且0x ≠， ()()21x F x f ∴=-的定义域为()(),00,1-∞⋃.故选：B .20．函数y (－∞，0]，则a 的取值范围为( ) A ．a ＞0 B ．a ＜1 C ．0＜a ＜1 D ．a ≠1【答案】C 【解析】【分析】由题意可得10x a -≥，对a 讨论，分1,01a a ><<,运用指数函数的单调性，列不等式即可得到a 的范围. 【详解】要使函数0y a >且1)a ≠有意义, 则10x a -≥, 即01x a a ≥=, 当1a >时，0x ≥；当01a <<时，0x ≤，因为y =的定义域为(],0-∞ 所以可得01a <<符合题意，a ∴的取值范围为01a <<，故选C.【点睛】本题考查函数的定义域以及指数函数的单调性，注意运用偶次根式被开方式非负，意在考查分类讨论思想与运算能力，属于中档题.针对练习五指数函数的值域21．函数2212x xy -⎛⎫= ⎪⎝⎭的值域为（） A ．1,2⎡⎫+∞⎪⎢⎣⎭B ．1,2⎛⎤-∞ ⎥⎝⎦C ．10,2⎛⎤⎥⎝⎦D ．(]0,2【答案】D 【解析】【分析】令22t x x =-，则12ty ⎛⎫= ⎪⎝⎭，转求二次函数与指数函数的值域即可.【详解】令22t x x =-，则12ty ⎛⎫= ⎪⎝⎭，①()222111t x x x =-=--≥-，①(],2120ty ⎛⎫⎪⎭∈= ⎝，①函数2212x xy -⎛⎫= ⎪⎝⎭的值域为(]0,2，故选：D22．若23x ，则函数1()421x x f x +=-+的最小值为（） A ．4 B ．0C ．5D ．9【答案】A 【解析】【分析】设23x t =，则2()21=-+f t t t 利用函数()f t 单调性可得答案. 【详解】设23x t =，则()22()211=-+=-f t t t t （3t ），对称轴为1t =，所以()f t 在[)3,+∞上单调递增，所以2min ()(3)32314f t f ==-⨯+=.故选：A.23．函数2121x x y -=+的值域是（）A ．()(),11,-∞--+∞B ．(),1-∞-C ．()1,1-D ．()(),11,-∞+∞【答案】C 【解析】【分析】将函数化为121xyy+=-，利用20x >列出关于y 的不等式，解出不等式即可. 【详解】设2121x x y -=+，由原式得121xy y +=-，20x >, 101yy+∴>-， ①11y -<<，即函数()f x 的值域为(1,1)-. 故选：C24．已知函数()()1123,12,1x a x a x f x x -⎧-+<=⎨≥⎩的值域为R ，则实数a 的取值范围是（） A ．10,2⎡⎫⎪⎢⎣⎭B ．1,2⎛⎫-∞ ⎪⎝⎭C ．(),0-∞D ．[)0,2【答案】A 【解析】【分析】先求出12x y -=在[)1,+∞上的取值范围，再利用分段函数的值域进行求解．【详解】因为12x y -=在[)1,+∞上单调递增，所以当1≥x 时，1022=1x y -=≥，若函数()f x 的值域为R ，则1201231a a a ->⎧⎨-+≥⎩，解得102a ≤<．故选：A.25．函数2x y a =-（0a >且1a ≠，11x -≤≤）的值域是5,13⎡⎤-⎢⎥⎣⎦，则实数=a （）A ．3B ．13C ．3或13D ．23或32【答案】C 【解析】当0a >且1a ≠时，函数为指数型函数，需要分情况进行讨论解决．当1a >时，函数2x y a =-是增函数；当01a <<时，函数2x y a =-是减函数，由此结合条件建立关于a的方程组，解之即可求得答案．【详解】当1a >时，2xy a =-在[]1,1-上为增函数， 211523a a-=⎧⎪∴⎨-=-⎪⎩，解得3a =；当01a <<时，2xy a =-在[]1,1-上为减函数，523121a a⎧-=-⎪⎪∴⎨⎪-=⎪⎩，解得13a =．综上可知：3a =或13．故选：C 【点睛】关键点点睛：本题主要考查了指数函数的单调性和值域，解题的关键是利用函数的单调性求解函数值域，但含有参数时往往需要讨论.针对练习六指数函数的单调性26．函数2435x x y -+-=的单调递减区间是（） A ．[2,)+∞ B ．(,2]-∞ C ．(,1]-∞ D ．[1,)+∞【答案】A 【解析】【分析】利用复合函数的单调性“同增异减”来解题. 【详解】设243x x μ=-+-，在(,2]-∞单调递增，在[2,)+∞单调递减，5y μ=在(,)-∞+∞单调递增，根据“同增异减”可得，函数2435x x y -+-=的单调递减区间是[2,)+∞. 故选：A.27．函数223112x x y -+⎛⎫= ⎪⎝⎭的单调递减区间为（） A ．(1,)+∞ B ．3,4⎛⎤-∞ ⎥⎝⎦C ．(),1-∞D ．3,4⎡⎫+∞⎪⎢⎣⎭【答案】D 【解析】【分析】根据复合函数单调性法则“同增异减”求解即可. 【详解】解：因为函数2231y x x =-+在区间3,4⎛⎫-∞ ⎪⎝⎭上单调递减，在3,4⎡⎫+∞⎪⎢⎣⎭上单调递增，函数12xy ⎛⎫= ⎪⎝⎭在定义域内是单调递减函数，所以，根据复合函数单调性法则“同增异减”得223112x x y -+⎛⎫= ⎪⎝⎭的单调递减区间为3,4⎡⎫+∞⎪⎢⎣⎭. 故选：D28．若函数()215x axf x +⎛⎫= ⎪⎝⎭在[]1,2单调递减，则a 的取值范围（）A ．4a ≤-B ．2a ≤-C ．2a ≥-D ．4a ≥-【答案】C 【解析】【分析】根据复合函数单调性来求得a 的取值范围. 【详解】依题意函数()215x axf x +⎛⎫= ⎪⎝⎭在[]1,2单调递减，15xy =在R 上递减， 2y x ax =+的开口向上，对称轴为2ax =-，根据复合函数单调性同增异减可知，122a a -≤⇒≥-. 故选：C29．若函数()(),1,513,13x a x f x a x x ⎧≥⎪=⎨-+<⎪⎩在R 上单调递减，则实数a 的取值范围是（） A ．12,33⎛⎤⎥⎝⎦B ．1,2C ．11,32⎡⎫⎪⎢⎣⎭D ．20,3⎛⎫⎪⎝⎭【答案】A 【解析】【分析】根据分段函数的性质，以及函数()f x 在R 上单调递减，结合指数函数的性质，可知011305133a a a a⎧⎪<<⎪-<⎨⎪⎪-+≥⎩，求解不等式，即可得到结果. 【详解】①函数()f x 在R 上单调递减，①011305133a a a a⎧⎪<<⎪-<⎨⎪⎪-+≥⎩，解得1233a <≤，实数a 的取值范围是12,33⎛⎤⎥⎝⎦. 故选：A.30．已知函数()()4211xa x x f x a x ⎧-≤=⎨>⎩，，是R 上的单调函数，那么实数a 的取值范围为（）A ．()01，B ．()13，C ．423⎡⎫⎪⎢⎣⎭，D ．312⎛⎤ ⎥⎝⎦，【答案】C 【解析】【分析】根据()f x 的单调性列不等式组，由此求得a 的取值范围. 【详解】函数()()4211xa x x f x a x ⎧-≤=⎨>⎩，，，若()f x 在R 上为单调递增函数，则()14201421a a a a ⎧->⎪>⎨⎪-⨯≤⎩，解得423a ≤<；若()f x 在R 上为单调递减函数，则()142001421a a a a ⎧-<⎪<<⎨⎪-⨯≥⎩，无解．综上所述，实数a 的取值范围为423⎡⎫⎪⎢⎣⎭，．故选：C针对练习七比较大小与解不等式31．已知412a ⎛⎫= ⎪⎝⎭，124b =，122c =，则a ，b ，c 的大小关系是（） A ．a b c << B ．c b a << C ．a c b << D ．b a c <<【答案】C 【解析】【分析】根据指数函数的单调性判断指数式的大小关系. 【详解】由题设，42a -=，2b =，122c =，又2x y =在定义域上递增， ①a c b <<. 故选：C.32．已知1313422,3,4a b c ===，则a ，b ，c 的大小关系为（） A ．a ⎪⎪⎝⎭⎝⎭，则实数a 的取值范围是（） A ．(,1)-∞ B ．(1,)+∞C ．(3,)+∞D ．(3),-∞【答案】A 【解析】【分析】根据指数函数的单调性，将函数不等式转化为自变量的不等式，解得即可；【详解】解：因为12xy ⎛⎫= ⎪⎝⎭在定义域上单调递减，所以2141122a a+-⎛⎫⎛⎫> ⎪⎪⎝⎭⎝⎭等价于214a a +<-，解得1a <，即原不等式的解集为(,1)-∞ 故选：A34．若x 满足不等式221139x x -+⎛⎫ ⎪⎝⎭，则函数2x y =的值域是（）A ．1,28⎡⎫⎪⎢⎣⎭B ．1,28⎡⎤⎢⎥⎣⎦C ．1,8⎛⎤-∞ ⎥⎝⎦D ．[2,)+∞【答案】B 【解析】【分析】利用指数函数的单调性得到自变量的范围，进而得到指数函数的值域. 【详解】由221139x x -+⎛⎫ ⎪⎝⎭可得2212(2)1339x x x -+--⎛⎫= ⎪⎝⎭，因为3x y =在R 上单调递增，所以2124x x +-+即x 2+2x -3≤0，解得：31x -≤≤ ，所以31222x y -=，即函数2x y =的值域是1,28⎡⎤⎢⎥⎣⎦，故选:B .35．若1133ab⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，则下列正确的是（）A ．33a b C ．11a b<D ．b c a c -<-【答案】D 【解析】【分析】先根据题干条件和函数13xy ⎛⎫= ⎪⎝⎭的单调性得到a b >，A 选项可以利用函数的单调性进行判断，BC 选项可以举出反例，D 选项用不等式的基本性质进行判断. 【详解】因为13xy ⎛⎫= ⎪⎝⎭在R 上单调递减，若1133a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭，则a b >，对于选项A ：若a b >，因为()3f x x =单调递增，所以33a b >，故A 错误；对于选项B ：当a b >时，若0c ，则ac bc =，故B 错误；对于选项C ：由a b >，不妨令1a =，2b =-，则此时11ab>，故C 错误；对于选项D ：由不等式性质，可知D 正确. 故选：D.针对练习八指数函数的应用36．专家对某地区新型流感爆发趋势进行研究发现，从确诊第一名患者开始累计时间t （单位：天）与病情爆发系数()f t 之间，满足函数模型：0.22(340)1()1t f t e--=+，当()0.1f t =时，标志着疫情将要局部爆发，则此时t 约为（参考数据： 1.13e ≈）（）A ．10B ．20C ．30D ．40【答案】A 【解析】【分析】根据()0.1f t =列式，并根据给出参考数据，结合指数函数的性质解相应的指数方程，即可得答案. 【详解】解：因为()0.1f t =，0.22(340)1()1t f t e--=+，所以0.22(340)10.11t e--=+，即0.22(340)011t e --=+，所以0.22(340)9t e --=，由于 1.13e ≈，故()21.12.29e e =≈，所以0.22(23).240t e e --≈，所以()0.22340 2.2t --≈，解得10t ≈. 故选：A.37．基本再生数0R 与世代间隔T 是流行病学基本参数，基本再生数是指一个感染者传染的平均人数，世代间隔指两代间传染所需的平均时间，在α型病毒疫情初始阶段，可以用指数函数模型(e )rt I t =描述累计感染病例数()I t 随时间t （单位：天）的变化规律，指数增长率r 与0R 、T 近似满足01R rT =+，有学者基于已有数据估计出0 3.22R =，10T =.据此，在α型病毒疫情初始阶段，累计感染病例数增加至(0)I 的4倍，至少需要（）（参考数据：ln 20.69≈） A ．6天 B ．7天 C ．8天 D ．9天【答案】B 【解析】【分析】根据题意将给出的数据代入公式即可计算出结果【详解】因为0 3.22R =，10T =，01R rT =+，所以可以得到01 3.2210.22210R r T --===0.2220(0)1I e ⨯==，由题意可知0.2224t e >，ln 42ln 220.696.20.2220.2220.222t ⨯>=≈≈ 所以至少需要7天，累计感染病例数增加至(0)I 的4倍故选：B38．某灭活疫苗的有效保存时间T （单位：小时h ）与储藏的温度t （单位：①）满足的函数关系为e ht b T +=（k ，b 为常数，其中e 2.71828=⋅⋅⋅，是一个和π类似的无理数，叫自然对数的底数），超过有效保存时间，疫苗将不能使用.若在0①时的有效保存时间是1080h ，在10①时的有效保存时间是120h ，则该疫苗在15①时的有效保存时间为（） A ．15h B ．30h C ．40h D ．60h【答案】C 【解析】【分析】根据已知的函数模型以及已知数据，待定系数即可求得结果. 【详解】由题意知1080e b =，1010120e e e k b k b +==⋅，所以()21051201ee 10809kk===，所以51e 3k =，所以151e 27k =，所以15151ee e 10804027k bk b +=⋅=⨯=. 故选：C ．39．某食品的保鲜时间y （单位：小时）与储藏温度x （单位：C ︒）满足函数关系e kx b y +=（e 2.718=为自然对数的底数，,k b 为常数）．若该食品在0C ︒的保鲜时间是192小时，在33C ︒的保鲜时间是24小时，则该食品在22C ︒的保鲜时间是（） A ．20 小时 B ．24小时 C ．36小时 D ．48小时【答案】D 【解析】【分析】根据题意建立方程组，进而解出11e ,e b k ，然后将22代入即可求得答案. 【详解】由题意，331133e 1922411e e 19282e24b k k k b+⎧=⇒==⇒=⎨=⎩，所以该食品在22C ︒的保鲜时间是2222e e e 1192484k b k b +=⋅=⨯=.故选：D.40．牛顿曾经提出了常温环境下的温度冷却模型：()100e ktθθθθ-=-+，其中为时间（单位：min ），0θ为环境温度，1θ为物体初始温度，θ为冷却后温度），假设在室内温度为20C 的情况下，一桶咖啡由100C 降低到60C 需要20min .则k 的值为（） A ．ln 220B ．ln 320C ．ln 210-D ．ln 310-【答案】A 【解析】【分析】把020θ=，1100θ=，60θ=，20t =代入()100e ktθθθθ-=-+可求得实数k 的值.【详解】由题意，把020θ=，1100θ=，60θ=，20t =代入()100e ktθθθθ-=-+中得2080e 2060k -+=，可得201e2k-=，所以，20ln 2k -=-，因此，ln 220k =. 故选：A.。

高一数学上册第二章--指数函数知识点及练习题(含答案)

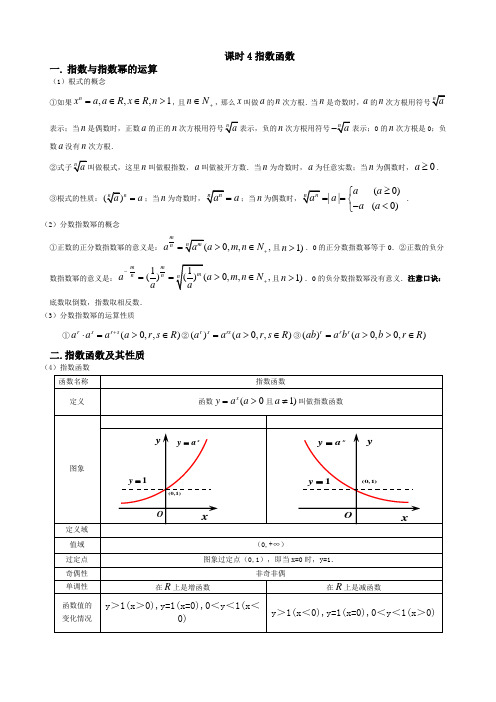
课时 4 指数函数一 . 指数与指数幂的运算（ 1）根式的观点①假如xna, a R, x R, n 1，且 nN ，那么 x 叫做 a 的 n 次方根．当 n 是奇数时， a 的 n 次方根用符号 na 表示；当 n 是偶数时，正数 a 的正的 n 次方根用符号na 表示，负的 n 次方根用符号na表示； 0 的 n 次方根是 0；负数 a 没有 n 次方根．②式子 n a 叫做根式，这里 n 叫做根指数， a 叫做被开方数．当n 为奇数时， a 为随意实数；当 n 为偶数时， a．③根式的性质： (na )n a ；当 n 为奇数时， n a n a ；当 n 为偶数时， n a n | a |a (a 0) ．a (a 0)（ 2）分数指数幂的观点mna m (a①正数的正分数指数幂的意义是：a n 0, m,n N , 且 n 1) ．0 的正分数指数幂等于0．②m(1m1 ) m( a正数的负分数指数幂的意义是：a n)n n (0, m, n N , 且 n1) ．0 的负分数指aa数幂没存心义．注意口诀：底数取倒数，指数取相反数．（ 3）分数指数幂的运算性质①a r a s a r s (a 0, r , s R)② (ar) sa rs (a 0, r , s R)③(ab)ra rb r (a0,b 0, rR)二 . 指数函数及其性质（ 4）指数函数函数名称指数函数定义函数 ya x (a 0 且 a1) 叫做指数函数a 1a 1yy a xya xy图象y1y1(0,1)(0,1)OxOx定义域 R值域（0,+ ∞）过定点图象过定点（0,1 ），即当 x=0 时， y=1．奇偶性非奇非偶单一性在 R 上是增函数在 R 上是减函数函数值的 y ＞ 1(x ＞ 0), y=1(x=0), 0＜ y ＜ 1(x ＜ 0)y ＞ 1(x ＜ 0), y=1(x=0), 0＜ y ＜ 1(x ＞ 0)变化状况a 变化对在第一象限内， a 越大图象越高，越凑近 y 轴；在第一象限内， a 越小图象越高，越凑近 y 轴；图象影响在第二象限内，a 越大图象越低，越凑近x 轴．在第二象限内，a 越小图象越低，越凑近x 轴．三 .例题剖析1.设 a 、 b 知足 0<a<b<1,以下不等式中正确的选项是 ( C)A.a a <a bB.b a 0 且 a ≠ 1),则以下等式中不正确的选项是 ( D )A.f(x+y)=f(x)f(y)f (x)B.f(x-y)=f ( y)C.f(nx)= ［ f(x) ］ nD.f ［ (xy) n ］ =［ f(x) ］ n ［ f(y) ］ n (n ∈ N * )分析：易知 A 、 B 、 C 都正确 .对于 D,f ［(xy)n］ =a (xy)n , 而［ f(x) ］ n ·［f(y) ］ n =(a x ) n ·(a y ) n =a nx+ny , 一般状况下 D 不建立 .11 34.设 a= ( 3) 3,b= ( 4)4,c= ( 3) 4,则 a 、b 、 c 的大小关系是 ( B )43 2A.c<a<b3分析： a= ( )B.c<b<aC.b<a<cD.b<c<a1 111(8133( 4)3 ( 4) 4=b, b=(4) 4)4(3) 4 =c.∴ a>b>c.3 332725.设 f(x)=4 x -2x+1,则 f -1 (0)=______1____________. 分析：令 f -1 (0)=a, 则 f(a)=0 即有 4a -2 · 2a =0.2a · (2 a -2)=0, 而 2a >0,∴ 2a =2 得 a=1.6.函数 y=a x-3 +4(a>0 且 a ≠ 1)的反函数的图象恒过定点 ______(5,3)____________.分析：因 y=a x 的图象恒过定点 (0,1), 向右平移 3 个单位 , 向上平移 4 个单位获得 y=a x-3 +4 的图象 , 易知恒过定点 (3,5).故其反函数过定点 (5,3).10 x 10 x.证明 f(x) 在 R 上是增函数 .7.已知函数 f(x)=x10 x10x1010x102x1,设 x 1<x 2∈ R,则f(x 1)-f(x2)=10x 1 1010x 1 10x 110x 210 x 2102 x 11 102 x 21 2(102 x 1102 x2).x 110x2 10x2 102 x1 1102 x21(102 x11)(102 x 2 1)∵ y=10 x是增函数 ,∴ 10 2x 1 10 2x 2 <0.而 10 2x 1 +1>0, 102 x 2 +1>0,故当 x <x 时 ,f(x)-f(x )<0,1212即 f(x 1)<f(x 2). 因此 f(x) 是增函数 .8.若定义运算 a b=b, ab,则函数 f(x)=3 x3-x 的值域为 ( A )a, a b,A.(0,1]B. ［ 1,+∞ )C.(0,+ ∞ )D.(- ∞ ,+∞ )分析：当 3x ≥3-x , 即 x ≥ 0 时 ,f(x)=3-x∈(0,1 ］ ;x-x, 即 x<0 时 ,f(x)=3x∈ (0,1).3 x , x 0, 当 3<3∴ f(x)=x值域为 (0,1).3x ,0,9.函数 y=a x 与 y=-a -x (a>0,a ≠1) 的图象 ( C )A. 对于 x 轴对称B.对于 y 轴对称C.对于原点对称D.对于直线 y=-x 对称分析：可利用函数图象的对称性来判断两图象的关系.10.当 x ∈［ -1,1］时 ,函数 f(x)=3 x-2 的值域为 _______［ -5,1 ］ ___________.3分析： f(x) 在［ -1,1 ］上单一递加 .11.设有两个命题 :(1)对于 x 的不等式 x 2+2ax+4>0对全部 x ∈ R 恒建立 ;(2) 函数 f(x)=-(5-2a) x是减函数 .若命题 (1)和 (2)中有且仅有一个是真命题 ,则实数 a 的取值范围是 _______(- ∞ ,-2)__________.分析： (1) 为真命题=(2a) 2-16<0-2<a<2. (2)为真命题 5-2a>1 a<2.若 (1) 假 (2) 真 , 则 a ∈ (- ∞ ,-2]. 若 (1) 真 (2) 假, 则 a ∈ (-2,2)∩［ 2,+ ∞］=.故 a 的取值范围为 (- ∞ ,-2).12.求函数 y=4 -x -2-x +1,x ∈［ -3,2］的最大值和最小值 .解：设 2-x=t, 由 x ∈［ -3,2 ］得 t ∈［ 1,8 ］ , 于是 y=t 2-t+1=(t-1)2+3. 当 t= 1时 ,y3 .424有最小值这时 x=1.当 t=8 时 ,y 有最大值57.这时 x=-3.2413.已知对于 x 的方程 2a2x-2-7a x-1 +3=0 有一个根是 2,求 a 的值和方程其他的根 . 解： ∵ 2 是方程 2a2x-2-9a x-1+4=0 的根 , 将 x=2 代入方程解得 a= 1或 a=4.2(1) 当 a= 1时 , 原方程化为 2· ( 1)2x-2-9(1) x-1 +4=0.①222x-1 2令 y=( 1) , 方程①变成 2y -9y+4=0,2解得 y 1=4,y 2= 1.∴ ( 1) x-1 =42x=-1,2( 1 ) x-1 = 1x=2.22(2) 当 a=4 时 , 原方程化为 2· 42x-2 -9 · 4x-1 +4=0. ②令 t=4 x-1 , 则方程②变成 2t 2-9t+4=0. 解得 t 1=4,t 2= 1.x-12=4x=2,∴44x-1 = 1x=- 1 .22故方程此外两根是当 a= 1时 ,x=-1;1 .2当 a=4 时 ,x=-214.函数 y= (1) 3 4xx 2的单一递加区间是 ( D )3A. ［ 1,2］B.［ 2,3］C.(-∞ ,2]D.［ 2,+∞ )分析：由于 y=3x2-4x+3 , 又 y=3t 单一递加 ,t=x 2-4x+3 在 x ∈［ 2,+ ∞ ) 上递加 , 故所求的递加区间为［ 2,+ ∞ ).15.已知 f(x)=3 x-b (2≤ x ≤ 4,b 为常数 ) 的图象经过点 (2,1), 则 F(x)=f 2(x)-2f(x) 的值域为 ( B )A. ［ -1,+∞ )B. ［ -1,63)C.［ 0,+∞ )D.(0,63 ］分析：由 f(2)=1, 得 32-b =1,b=2,f(x)=3 x-2.∴ F (x)= ［ f(x)-1 ］2-1=(3 x-2 -1) 2-1. 令 t=3 x-2 ,2 ≤x ≤4.2∴g(t)=(t-1) - 1,t ∈［ 1,9 ］.2.1 指数函数练习1．以下各式中建立的一项A ． ( n)71n 7 m 7B ．12 ( 3)433m3C ． 4 x 3y 3( x y) 4D ．393321111 1 52．化简 (a 3 b 2 )( 3a 2 b 3 ) ( a 6 b 6 ) 的结果3D ． 9a 2 A ． 6aB ． aC ． 9a3．设指数函数 f ( x)a x ( a 0, a1) ，则以下等式中不正确的选项是f (x) A ． f(x+y)=f(x) ·f(y)B ． f （ x y ）f ( y)C ． f (nx)[ f ( x)]n (nQ )D ． f ( xy) n [ f ( x)] n ·[f ( y)] n1 4．函数 y (x5) 0 ( x 2)2A ． { x | x 5, x 2}B ． { x | x 2}C ． { x | x 5}D ． { x | 2 x 5或 x 5}（）（）（）(n N )（）5．若指数函数 y a x 在 [－ 1,1]上的最大值与最小值的差是1，则底数 a 等于（）A ．15 B ．1 5 C ．15D ．5 122 226．当 a0 时，函数 y axb 和 yb ax 的图象只可能是（）7．函数 f ( x)2 |x| 的值域是（）A ． (0,1]B ． (0,1)C ． (0, )D ． R8．函数 f ( x)2 x 1, x 0，知足 f ( x)1的 x 的取值范围1x 2 , x（）A ． ( 1,1)B ． ( 1, )C ． { x | x 0或 x2}D ． { x | x 1或 x1}9．函数 y(1) x 2x2得单一递加区间是2（）A ．[ 1,1]B ． ( , 1]C ．[2,)D ．[ 1,2]2exe x210．已知 f ( x)（）2 ，则以下正确的选项是A ．奇函数，在 R 上为增函数B ．偶函数，在 R 上为增函数C ．奇函数，在 R 上为减函数D ．偶函数，在 R 上为减函数11．已知函数 f (x)的定义域是（1， 2），则函数 f (2 x ) 的定义域是.12．当 a ＞0 且 a ≠1 时，函数 f (x)=a x －2－ 3 必过定点.三、解答题：13．求函数 y1的定义域 .x5 x 1114．若 a ＞0， b ＞ 0，且 a+b=c ，求证： (1) 当r ＞1时， a r +b r ＜ c r ； (2) 当r ＜ 1时， a r +b r ＞ c r .a x 1 15．已知函数 f ( x)(a ＞1) .a x1（ 1）判断函数 f (x) 的奇偶性；（ 2）证明 f (x)在 (－∞， +∞ )上是增函数 .xa16．函数 f(x) ＝ a (a>0 ，且 a ≠1) 在区间 [1,2] 上的最大值比最小值大2，求 a 的值．参照答案一、 DCDDD AADDA二、 11． (0,1)；12． (2，－ 2) ；三、 13．解：要使函数存心义一定：x 1 0x 1x0 x 0x 1∴ 定义域为： x xR 且 x0, x 1a rrrb r此中a1,0b114．解：ba，c rcccc.r ＞1 ，a rb ra b 1，r r r当因此+b＜ c ；时c c c crrrrr当 r ＜ 1 时， aba b1，因此 a +b ＞c .ccc c15．解：(1)是奇函数 .(2) 设x ＜x ，则 f (x 1 )ax11 ax21 。

高中数学必修一《指数与指数函数》测试及答案2套

高中数学必修一《指数与指数函数》测试及答案2套单元测试卷一(时间：120分钟满分：150分) 第Ⅰ卷 (选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．若a <14，则化简44a －12的结果是( )A.1－4aB.4a －1 C ．－1－4aD ．－4a －12．某林区的森林蓄积量每年比上一年平均增加110.4%，那么经过x 年可增长到原来的y 倍，则函数y ＝f (x )的图象大致是( )3．设f (x )＝⎝ ⎛⎭⎪⎫12|x |，x ∈R ，那么f (x )是( )A ．奇函数且在(0，＋∞)上是增函数B ．偶函数且在(0，＋∞)上是增函数C ．奇函数且在(0，＋∞)上是减函数D ．偶函数且在(0，＋∞)上是减函数 4．若3a>1，则实数a 的取值范围为( )A ．(－∞，0)B ．(0,1)C ．(0，＋∞) D．(2，＋∞) 5．函数y ＝2x－12x ＋1是( )A ．奇函数B ．偶函数C ．非奇非偶函数D ．既是奇函数又是偶函数6．函数y ＝⎝ ⎛⎭⎪⎫12 x 2－2的单调递减区间为( )A ．(－∞，0]B ．0，＋∞)C ．(－∞，2]D ．2，＋∞)7．函数y＝⎝ ⎛⎭⎪⎫12－x 2＋2x 的值域是( ) A ．R B.⎣⎢⎡⎭⎪⎫12，＋∞ C ．(2，＋∞)D ．(0，＋∞)8．设f (x )是定义在实数集R 上的函数，满足条件：y ＝f (x ＋1)是偶函数，且当x ≥1时，f (x )＝5x，则f ⎝ ⎛⎭⎪⎫23，f ⎝ ⎛⎭⎪⎫32，f ⎝ ⎛⎭⎪⎫13的大小关系是( )A ．f ⎝ ⎛⎭⎪⎫13<f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫32B ．f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫13<f ⎝ ⎛⎭⎪⎫23C ．f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫13 D ．f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫13 9．函数y ＝|x |e－xx的图象的大致形状是( )10．下列函数中，与y ＝－3|x |的奇偶性相同，且在(－∞，0)上单调性也相同的是( ) A ．y ＝－1xB ．y ＝|x |－1|x |C ．y ＝－(2x ＋2－x)D ．y ＝x 3－111．已知函数f (x )＝⎩⎪⎨⎪⎧a xx <0，a －3x ＋4a x ≥0满足对任意x 1≠x 2，都有f x 1－f x 2x 1－x 2<0成立，则a 的取值范围是( )A.⎝ ⎛⎦⎥⎤0，14 B ．(0,1) C.⎣⎢⎡⎭⎪⎫14，1 D ．(0,3) 12．设函数f (x )＝2－x 2＋x ＋2 ，对于给定的正数K ，定义函数f K (x )＝⎩⎪⎨⎪⎧f x ，f x ≤K ，K ，f x >K ，若对于函数f (x )＝2－x 2＋x ＋2定义域内的任意x ，恒有f K (x )＝f (x )，则( )A ．K 的最大值为2 2B ．K 的最小值为2 2C ．K 的最大值为1D ．K 的最小值为1第Ⅱ卷 (非选择题共90分)二、填空题(本大题共4个小题，每小题5分，共20分，请把正确答案填在题中横线上) 13．2－12＋－42＋12－1－1－5＝________.14．函数f (x )＝2a x ＋1－3(a >0，且a ≠1)的图象经过的定点坐标是________．15．若函数f (x )＝⎩⎪⎨⎪⎧1x ，x <0，⎝ ⎛⎭⎪⎫13x，x ≥0，则不等式|f (x )|≥13的解集为________．16．设f (x )是定义在R 上的奇函数，且当x >0时，f (x )＝2x－3，则当x <0时，f (x )＝________.三、解答题(本大题共6个小题，共70分，解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分)函数f (x )＝k ·a －x(k ，a 为常数，a >0且a ≠1)的图象过点A (0,1)，B (3,8)． (1)求函数f (x )的解析式； (2)若函数g (x )＝f x －1f x ＋1，试判断函数g (x )的奇偶性并给出证明．18．(本小题满分12分) 已知函数f (x )＝2x－4x.(1)求y ＝f (x )在－1,1]上的值域； (2)解不等式f (x )>16－9×2x；(3)若关于x 的方程f (x )＋m －1＝0在－1,1]上有解，求m 的取值范围．19．(本小题满分12分)某医药研究所开发一种新药，如果成年人按规定的剂量服用，据监测，服药后每毫升血液中的含药量y (毫克)与时间t (小时)之间的关系近似满足如图所示的曲线．(1)写出服药后y 与t 之间的函数关系式y ＝f (t )；(2)进一步测定：每毫升血液中的含药量不少于0.25毫克时，药物对治疗疾病有效．求服药一次治疗疾病的有效时间．20．(本小题满分12分)已知函数f (x )＝a 2＋22x ＋1是奇函数．(1)求a 的值；(2)判断f (x )的单调性，并用定义加以证明； (3)求f (x )的值域．21．(本小题满分12分)已知函数f (x )＝⎝ ⎛⎭⎪⎫13x ，x ∈－1,1]，函数φ(x )＝f (x )]2－2af (x )＋3的最小值为h (a )．(1)求h (a )；(2)是否存在实数m >n >3，当h (a )的定义域为n ，m ]时，值域为n 2，m 2]？若存在，求出m ，n 的值；若不存在，请说明理由．22．(本小题满分12分)定义在D 上的函数f (x )，如果满足：对任意x ∈D ，存在常数M >0，都有|f (x )|≤M 成立，则称f (x )是D 上的有界函数，其中M 称为函数f (x )的上界．已知函数f (x )＝1＋a ·⎝ ⎛⎭⎪⎫13x ＋⎝ ⎛⎭⎪⎫19x.(1)当a ＝－12时，求函数f (x )在(－∞，0)上的值域，并判断函数f (x )在(－∞，0)上是否为有界函数，请说明理由；(2)若函数f (x )在0，＋∞)上是以4为上界的有界函数，求实数a 的取值范围．答案1．A 解析：∵a <14，∴4a －1<0，∴44a －12＝1－4a .2．D 解析：经过x 年后y ＝(1＋110.4%)x＝2.104x.3．D 解析：函数f (x )的定义域R 关于原点对称，且f (－x )＝⎝ ⎛⎭⎪⎫12|－x |＝⎝ ⎛⎭⎪⎫12|x |＝f (x )，所以f (x )是偶函数．又f (x )＝⎝ ⎛⎭⎪⎫12|x |＝⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫12x ，x ≥0，2x ，x <0，所以f (x )在(0，＋∞)上是减函数．4．C 解析：因为3a>1，所以3a>30,3>1，∴y ＝3a是增函数．∴a >0.5．A 解析：函数y ＝2x－12x ＋1的定义域(－∞，＋∞)关于原点对称，且f (－x )＝2－x－12－x ＋1＝12x －112x ＋1＝1－2x 1＋2x ＝－f (x )，所以该函数是奇函数． 6．B 解析：函数y ＝⎝ ⎛⎭⎪⎫12u为R 上的减函数，欲求函数y ＝⎝ ⎛⎭⎪⎫12x 2－2的单调递减区间，只需求函数u ＝x 2－2的单调递增区间，而函数u ＝x 2－2的单调递增区间为0，＋∞)．7．B 解析：令t ＝－x 2＋2x ，则t ＝－x 2＋2x 的值域为(－∞，1]，所以y ＝⎝ ⎛⎭⎪⎫12－x 2＋2x＝⎝ ⎛⎭⎪⎫12t 的值域为⎣⎢⎡⎭⎪⎫12，＋∞. 解题技巧：本题主要考查了指数型函数的值域，解决本题的关键是先求出指数t ＝－x 2＋2x 的值域，再根据复合函数的单调性求出指数型函数的值域．8．D 解析：∵y ＝f (x ＋1)是偶函数，∴y ＝f (x ＋1)的对称轴为x ＝0，∴y ＝f (x )的对称轴为x ＝1.又x ≥1时，f (x )＝5x，∴f (x )＝5x在1，＋∞)上是增函数，∴f (x )在(－∞，1]上是减函数．∵f ⎝ ⎛⎭⎪⎫32＝f ⎝ ⎛⎭⎪⎫12，且23>12>13，∴f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫12<f ⎝ ⎛⎭⎪⎫13，即f ⎝ ⎛⎭⎪⎫23<f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫13.9．C 解析：由函数的表达式知，x ≠0，y ＝e －x|x |x ＝⎩⎪⎨⎪⎧e －x，x >0，－e －x，x <0，所以它的图象是这样得到的：保留y ＝e －x，x ＞0的部分，将x ＜0的图象关于x 轴对称．故选D.10．C 解析：设函数f (x )＝y ＝－3|x |，x ∈R ，∴f (－x )＝－3|－x |.∵f (x )＝f (－x )，∴f (x )为偶函数．令t ＝|x |，∴t ＝|x |，x ∈(－∞，0)是减函数，由复合函数的单调性知，y＝－3|x |在x ∈(－∞，0)为增函数．选项A 为奇函数，∴A 错；选项B 为偶函数但是在x ∈(－∞，0)为减函数，∴B 错；选项C 令g (x )＝－(2x＋2－x)，g (－x )＝－(2－x＋2x)，∴g (x )＝g (－x )，∴g (x )为偶函数．由复合函数的单调性知，g (x )在x ∈(－∞，0)为增函数．故选C.11．A 解析：∵对任意x 1≠x 2，都有f x 1－f x 2x 1－x 2<0成立，∴f (x )是R 上的减函数．∴⎩⎪⎨⎪⎧0<a <1，a 0≥4a ，解得a ∈⎝ ⎛⎦⎥⎤0，14.故选A. 12．B 解析：∵函数f (x )＝2－x 2＋x ＋2的值域为1,22]，又∵对于给定的正数K ，定义函数f K (x )＝⎩⎪⎨⎪⎧f x ，f x ≤K ，K ，f x >K ，若对于函数f (x )＝2－x 2＋x ＋2定义域内的任意x ，恒有f K (x )＝f (x )，∴K ≥2 2.故选B.13．－22解析：2－ 12＋－42＋12－1－1－5＝12－42＋2＋11－1＝－32＋2＝－22.14．(－1，－1) 解析：由指数函数恒过定点(0,1)可知，函数f (x )＝2ax ＋1－3(a >0，且a ≠1)的图象恒过定点(－1，－1)．15．－3,1] 解析：当x <0时，|f (x )|≥13，即1x ≤－13，∴x ≥－3；当x ≥0时，|f (x )|≥13，即⎝ ⎛⎭⎪⎫13x ≥13，∴x ≤1.综上不等式的解集是x ∈－3,1]．解题技巧：本题主要考查了关于分段函数的不等式，解决本题的关键是分段求出不等式的解集，最后取并集．16．－2－x＋3 解析：当x <0时，－x >0.∵当x >0时，f (x )＝2x －3，∴f (－x )＝2－x－3.又f (x )是定义在R 上的奇函数，∴当x <0时，f (－x )＝2－x－3＝－f (x )，∴f (x )＝－2－x＋3.17．解：(1)由函数图案过点A (0,1)和B (3,8)知，⎩⎪⎨⎪⎧k ＝1，k ·a －3＝8，解得⎩⎪⎨⎪⎧k ＝1，a ＝12，∴f (x )＝2x.(2)函数g (x )＝2x－12x ＋1为奇函数．证明如下：函数g (x )定义域为R ，关于原点对称；且对于任意x ∈R ，都有g (－x )＝2－x－12－x ＋1＝1－2x 1＋2x ＝－2x－12x＋1＝－g (x )成立． ∴函数g (x )为奇函数．18．解：(1)设t ＝2x，因为x ∈－1,1]，∴t ∈⎣⎢⎡⎦⎥⎤12，2，y ＝t －t 2＝－⎝ ⎛⎭⎪⎫t －122＋14，∴t ＝12时，f (x )max ＝14，t ＝2时，f (x )min ＝－2.∴f (x )的值域为⎣⎢⎡⎦⎥⎤－2，14.(2)设t ＝2x ，由f (x )>16－9×2x 得t －t 2>16－9t ，即t 2－10t ＋16<0，∴2<t <8，即2<2x<8，∴1<x <3， ∴不等式的解集为(1,3)．(3)方程有解等价于m 在1－f (x )的值域内，∴m 的取值范围为⎣⎢⎡⎦⎥⎤34，3.19．解：(1)当t ∈0,1]时，设函数的解析式为y ＝kt ，将M (1,4)代入，得k ＝4，∴ y ＝4t .又当t ∈(1，＋∞)时，设函数的解析式为y ＝⎝ ⎛⎭⎪⎫12t －a，将点(3,1)代入得a ＝3，∴ y ＝⎝ ⎛⎭⎪⎫12t －3.综上，y ＝f (t )＝⎩⎪⎨⎪⎧4t ，0≤t ≤1，⎝ ⎛⎭⎪⎫12t －3，t >1.(2)由f (t )≥0.25，解得116≤t ≤5.所以服药一次治疗疾病的有效时间为5－116＝7916(小时)．解题技巧：解题时，先观察图形，将图形语言转化成符号语言．由图形可知这是一个一次函数、指数函数相结合的题目．根据条件设出解析式，结合图象中的已知点求出函数解析式，再利用分段函数的知识即可求解服药一次治疗疾病的有效时间．20．解：(1)由题知，f (x )的定义域是R ，∵f (x )是奇函数，∴f (0)＝0，即f (0)＝a 2＋220＋1＝0，解得a ＝－2.经验证可知，f (x )是奇函数， ∴a ＝－2.(3)f (x )＝－1＋22x ＋1，∵2x >0，∴2x＋1>1，∴0<22x ＋1<2，－1<－1＋22x ＋1<1，∴－1<y <1.故f (x )的值域为(－1,1)．21．解：(1)因为x ∈－1,1]，所以⎝ ⎛⎭⎪⎫13x ∈⎣⎢⎡⎦⎥⎤13，3.设t ＝⎝ ⎛⎭⎪⎫13x ，t ∈⎣⎢⎡⎦⎥⎤13，3，则φ(x )＝t 2－2at ＋3＝(t －a )2＋3－a 2.当a <13时，y min ＝h (a )＝φ⎝ ⎛⎭⎪⎫13＝289－2a 3；当13≤a ≤3时，y min ＝h (a )＝φ(a )＝3－a 2；当a >3时，y min ＝h (a )＝φ(3)＝12－6a .∴h (a )＝⎩⎪⎨⎪⎧289－2a 3⎝ ⎛⎭⎪⎫a <13，3－a 2⎝ ⎛⎭⎪⎫13≤a ≤3，12－6a a >3.(2)假设满足题意的m ，n 存在，∵m >n >3，∴h (a )＝12－6a 在(3，＋∞)上是减函数． ∵h (a )的定义域为n ，m ]，值域为n 2，m 2]，∴⎩⎪⎨⎪⎧12－6m ＝n 2，12－6n ＝m 2，两式相减，得6(m －n )＝(m －n )(m ＋n )．由m >n >3，∴m ＋n ＝6，但这与m >n >3矛盾，∴满足题意的m ，n 不存在．解题技巧：本题主要考查了指数型函数的值域、存在性问题；解决存在性问题的关键是先假设存在，把假设作为已知条件进行推理，若推理合理则存在，若推理不合理则不存在．22．解：(1)当a ＝－12时，f (x )＝1－12×⎝ ⎛⎭⎪⎫13x ＋⎝ ⎛⎭⎪⎫19x .令t ＝⎝ ⎛⎭⎪⎫13x，∵x <0，∴t >1，f (t )＝1－12t ＋t 2.∵f (t )＝1－12t ＋t 2在(1，＋∞)上单调递增，∴f (t )>32，即f (x )在(－∞，1)的值域为⎝ ⎛⎭⎪⎫32，＋∞. 故不存在常数M >0，使|f (x )|≤M 成立，∴函数f (x )在(－∞，0)上不是有界函数．(2)由题意知，|f (x )|≤4，即－4≤f (x )≤4对x ∈0，＋∞)恒成立．令t ＝⎝ ⎛⎭⎪⎫13x ，∵x ≥0，∴t ∈(0,1]，∴－⎝ ⎛⎭⎪⎫t ＋5t ≤a ≤3t－t 对t ∈(0,1]恒成立，∴⎣⎢⎡⎦⎥⎤－⎝⎛⎭⎪⎫t ＋5t max ≤a ≤⎝ ⎛⎭⎪⎫3t －t min . 设h (t )＝－⎝ ⎛⎭⎪⎫t ＋5t ，p (t )＝3t－t ，t ∈(0,1]．由于h (t )在t ∈(0,1]上递增，p (t )在t ∈(0,1]上递减，h (t )在t ∈(0,1]上的最大值为h (1)＝－6，p (t )在1，＋∞)上的最小值为p (1)＝2，则实数a 的取值范围为－6,2]．单元测试卷二(时间：120分钟满分：150分) 第Ⅰ卷 (选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．计算(－2)2] － 12 的结果是( ) A. 2 B ．－ 2 C.22D ．－222.⎝⎛⎭⎪⎫1120－(1－0.5－2)÷⎝⎛⎭⎪⎫27823的值为( )A．－13B.13C.43D.733．若a>1，则函数y＝a x与y＝(1－a)x2的图象可能是下列四个选项中的( )4．下列结论中正确的个数是( )①当a<0时，(a223＝a3；②na n＝|a|(n≥2，n∈N)；③函数y＝(x－2)12－(3x－7)0的定义域是2，＋∞)；④6－22＝32.A．1 B．2 C．3 D．45．指数函数y＝f(x)的图象经过点⎝⎛⎭⎪⎫－2，14，那么f(4)·f(2)等于( ) A．8 B．16 C．32 D．646．函数y＝21x的值域是( )A．(0，＋∞) B．(0,1)C．(0,1)∪(1，＋∞) D．(1，＋∞)7．函数y＝|2x－2|的图象是( )8．a ，b 满足0<a 0，a ≠1)的图象在第一、三、四象限内，则( ) A ．a >1B ．a >1，且m <0C ．0<a <1，且m >0D ．0<a <111．函数f (x )＝2x ＋2－4x，若x 2－x －6≤0，则f (x )的最大值和最小值分别是( ) A ．4，－32 B ．32，－4 C.23，0 D.43，1 12．若函数f (x )＝3x＋3－x与g (x )＝3x－3－x的定义域均为R ，则( ) A ．f (x )与g (x )均为偶函数 B ．f (x )为偶函数，g (x )为奇函数 C ．f (x )与g (x )均为奇函数 D ．f (x )为奇函数，g (x )为偶函数第Ⅱ卷 (非选择题共90分)二、填空题(本大题共4个小题，每小题5分，共20分，请把正确答案填在题中横线上) 13．已知a ＝0.80.7，b ＝0.80.9，c ＝1.20.8，则a ，b ，c 的大小关系为________．14．若方程⎝ ⎛⎭⎪⎫14x ＋⎝ ⎛⎭⎪⎫12x －1＋a ＝0有正数解，则实数a 的取值范围是________．15．已知函数f (x )＝⎝ ⎛⎭⎪⎫12|x －1|，则f (x )的单调递增区间是________．16．定义区间x 1，x 2](x 1<x 2)的长度为x 2－x 1，已知函数y ＝2|x |的定义域为a ，b ]，值域为1,2]，则区间a ，b ]的长度的最大值与最小值的差为________．三、解答题(本大题共6个小题，共70分，解答时应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分10分) 解不等式a 2x ＋7<a3x －2(a >0，a ≠1)．18．(本小题满分12分)已知函数f (x )＝3x，且f (a )＝2，g (x )＝3ax－4x. (1)求g (x )的解析式；(2)当x ∈－2,1]时，求g (x )的值域．19．(本小题满分12分)已知函数f (x )＝⎝ ⎛⎭⎪⎫12ax，a 为常数，且函数的图象过点(－1,2)．(1)求a 的值；(2)若g (x )＝4－x－2，且g (x )＝f (x )，求满足条件的x 的值．20．(本小题满分12分)已知函数f (x )＝a ·2x ＋b ·3x，其中常数a ，b 为实数． (1)当a >0，b >0时，判断并证明函数f (x )的单调性； (2)当ab <0时，求f (x ＋1)>f (x )时x 的取值范围．21．(本小题满分12分)设a ∈R ，f (x )＝a －22x ＋1(x ∈R )．(1)证明：对任意实数a ，f (x )为增函数； (2)试确定a 的值，使f (x )≤0恒成立．22．(本小题满分12分)已知定义域为R 的函数f (x )＝－2x＋b2x ＋1＋2是奇函数．(1)求b 的值；(2)判断函数f (x )的单调性；(3)若对任意的t ∈R ，不等式f (t 2－2t )＋f (2t 2－k )<0恒成立，求k 的取值范围．答案1．C 解析：(－2)2] － 12 ＝2－ 12 ＝12＝22.2．D 解析：原式＝1－(1－22)÷⎝ ⎛⎭⎪⎫322＝1－(－3)×49＝73.故选D.3．C 解析：a >1，∴y ＝a x在R 上单调递增且过(0,1)点，排除B ，D ，又∵1－a <0，∴y ＝(1－a )x 2的开口向下．4．A 解析：在①中，a <0时，(a 2) 32 >0，而a 3<0，∴①不成立．在②中，令a ＝－2，n ＝3，则3－23＝－2≠|－2|，∴②不成立．在③中，定义域应为⎣⎢⎡⎭⎪⎫2，73∪⎝ ⎛⎭⎪⎫73，＋∞，∴③不成立． ④式是正确的，∵6－22＝622＝32，∴④正确．5．D 解析：设f (x )＝a x(a >0且a ≠1)，由已知得14＝a －2，a 2＝4，所以a ＝2，于是f (x )＝2x，所以f (4)·f (2)＝24·22＝64.解题技巧：已知函数类型，求函数解析式，常用待定系数法，即先把函数设出来，再利用方程或方程组解出系数．6．C 解析：∵1x≠0，∴21x ≠1，∴函数y ＝21x的值域为(0,1)∪(1，＋∞)．7．B 解析：找两个特殊点，当x ＝0时，y ＝1，排除A ，C.当x ＝1时，y ＝0，排除D.故选B.8．C 解析：∵0<a a b ，故A 不成立，同理B 不成立，若a a <b a，则⎝ ⎛⎭⎪⎫a b a <1，∵0<a b<1,0<a <1， ∴⎝ ⎛⎭⎪⎫a ba <1成立，故选C. 9．D 解析：与曲线y ＝e x 关于y 轴对称的曲线为y ＝e －x ，函数y ＝e －x的图象向左平移一个单位长度即可得到函数f (x )的图象，即f (x )＝e－(x ＋1)＝e－x －1.解题技巧：函数图象的平移变换，要注意平移的方向和平移量．平移规律为：10．B 解析：由函数y ＝a x＋m －1(a >0，a ≠1)的图象在第一、三象限知，a >1.知函数在第四象限，∴a 0＋m －1<0，则有m <0.11．A 解析：f (x )＝2x ＋2－4x ＝－(2x )2＋4·2x ＝－(2x －2)2＋4，又∵x 2－x －6≤0，∴－2≤x ≤3，∴14≤2x≤8.当2x ＝2时，f (x )max ＝4，当2x＝8时，f (x )min ＝－32. 12．B 解析：因为f (－x )＝3－x＋3－(－x )＝3－x ＋3x＝f (x )，g (－x )＝3－x －3－(－x )＝3－x －3x ＝－g (x )，所以f (x )为偶函数，g (x )为奇函数．13．c >a >b 解析：由指数函数y ＝a x当0<a <1时为减函数知， 0．80.7>0.80.9，又1.20.8>1,0.80.7<1， ∴1.20.8>0.80.7>0.80.9，即c >a >b .14．(－3,0) 解析：令⎝ ⎛⎭⎪⎫12x＝t ，∵方程有正根，∴t ∈(0,1)．方程转化为t 2＋2t ＋a ＝0， ∴a ＝1－(t ＋1)2.∵t ∈(0,1)，∴a ∈(－3,0)．15．(－∞，1] 解析：解法一：由指数函数的性质可知，f (x )＝⎝ ⎛⎭⎪⎫12x在定义域上为减函数，故要求f (x )的单调递增区间，只需求y ＝|x －1|的单调递减区间．又y ＝|x －1|的单调递减区间为(－∞，1]，所以f (x )的单调递增区间为(－∞，1]．解法二：f (x )＝⎝ ⎛⎭⎪⎫12|x －1|＝⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫12x －1，x ≥1，2x －1，x <1.可画出f (x )的图象，并求其单调递增区间．解题技巧：既可以利用复合函数的“同增异减”法则求解，也可以去绝对值符号，转化为分段函数求解．16．1 解析：作出函数y ＝2|x |的图象(如图所示)．当x ＝0时，y ＝20＝1，当x ＝－1时，y ＝2|－1|＝2，当x ＝1时，y ＝21＝2，所以当值域为1,2]时，区间a ，b ]的长度的最大值为2，最小值为1，它们的差为1. 17．解：当a >1时，a 2x ＋7<a3x －2等价于2x ＋7<3x －2，∴x >9；当0<a <1时，a 2x ＋7<a3x －2等价于2x ＋7>3x －2.∴x <9.综上，当a >1时，不等式的解集为{x |x >9}；当0<a <1时，不等式的解集为{x |x <9}．解题技巧：注意按照底数进行分类讨论． 18．解：(1)由f (a )＝2，得3a＝2，a ＝log 32， ∴g (x )＝(3a )x－4x＝(3log 32)x －4x＝2x－4x＝－(2x )2＋2x. ∴g (x )＝－(2x )2＋2x. (2)设2x＝t ，∵x ∈－2,1]， ∴14≤t ≤2. g (t )＝－t 2＋t ＝－⎝⎛⎭⎪⎫t －122＋14，由g (t )在t ∈⎣⎢⎡⎦⎥⎤14，2上的图象可得，当t ＝12，即x ＝－1时，g (x )有最大值14；当t ＝2，即x ＝1时，g (x )有最小值－2. 故g (x )的值域是⎣⎢⎡⎦⎥⎤－2，14.19．解：(1)由已知得⎝ ⎛⎭⎪⎫12－a＝2，解得a ＝1.(2)由(1)知，f (x )＝⎝ ⎛⎭⎪⎫12x ，又g (x )＝f (x )，则4－x－2＝⎝ ⎛⎭⎪⎫12x ，即⎝ ⎛⎭⎪⎫14x －⎝ ⎛⎭⎪⎫12x －2＝0，即⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫12x 2－⎝ ⎛⎭⎪⎫12x－2＝0. 令⎝ ⎛⎭⎪⎫12x ＝t ，则t 2－t －2＝0，即(t －2)(t ＋1)＝0. 又t >0，故t ＝2，即⎝ ⎛⎭⎪⎫12x＝2，解得x ＝－1.20．解：(1)函数f (x )在R 上是增函数．证明如下：a >0，b >0，任取x 1，x 2∈R ，且x 1<x 2，(2)∵f (x ＋1)>f (x )， ∴f (x ＋1)－f (x )＝(a ·2x ＋1＋b ·3x ＋1)－(a ·2x＋b ·3x)＝a ·2x＋2b ·3x>0，当a <0，b >0时，⎝ ⎛⎭⎪⎫32x >－a 2b ，则x >log 1.5⎝ ⎛⎭⎪⎫－a 2b ，当a >0，b <0时，⎝ ⎛⎭⎪⎫32x <－a 2b ，则x <log 1.5⎝ ⎛⎭⎪⎫－a 2b . 综上，当a <0，b >0时，x 的取值范围是⎝ ⎛⎭⎪⎫log 1.5⎝ ⎛⎭⎪⎫－a 2b ，＋∞；当a >0，b <0时，x 的取值范围是⎝ ⎛⎭⎪⎫－∞，log 1.5⎝ ⎛⎭⎪⎫－a 2b . 21．(1)证明：任取x 1，x 2∈R ，且x 1<x 2，故对于任意实数a ，f (x )为增函数．(2)解：f (x )＝a －22x ＋1≤0恒成立，只要a ≤22x ＋1恒成立，问题转化为只要a 不大于22x＋1的最小值．∵x ∈R,2x>0恒成立，∴2x＋1>1. ∴0<12x ＋1<1,0<22x ＋1<2，∴a ≤0.故当a ∈(－∞，0]时，f (x )≤0恒成立．22．解：(1)因为f (x )是奇函数，所以f (0)＝0，即b －12＋2＝0，解得b ＝1.(3)因为f (x )是奇函数，f (t 2－2t )＋f (2t 2－k )<0，则f (t 2－2t )<－f (2t 2－k )＝f (k －2t 2)，因f (x )为减函数，由上式推得，t 2－2t >k －2t 2. 即对一切t ∈R 有3t 2－2t －k >0，从而判别式Δ＝4＋12k <0，解得k <－13.故k 的取值范围是⎝ ⎛⎭⎪⎫－∞，－13.。

高一数学指数运算及指数函数试题(有答案)

高一数学指数运算及指数函数试题一．选择题1．若xlog 23=1，则3x+9x的值为（B）A．3B．6C．2D．解：由题意x=，所以3x==2，所以9x=4，所以3x+9x=6故选B2．若非零实数a、b、c满足，则的值等于（B）A．1B．2C．3D．4解答：解：∵，∴设=m，a=log5m，b=log2m，c=2lgm，∴==2lgm（log m5+log m2）=2lgm•log m10=2．故选B．3．已知，则a等于（）A．B．C． 2 D． 4解：因为所以解得a=4故选D4．若a＞1，b＞1，p=，则a p等于（）A．1B．b C．l og b a D．a log b a解：由对数的换底公式可以得出p==log a（log b a），因此，a p等于log b a．故选C．5．已知lg2=a，10b=3，则log125可表示为（C）A．B．C．D．解：∵lg2=a，10b=3，∴lg3=b，∴log125===．故选C．6．若lgx﹣lgy=2a，则=（C）A．3a B．C．a D．解：∵lgx﹣lgy=2a，∴lg﹣lg=lg﹣lg=（lg﹣lg）=lg=（lgx﹣lgy）=•2a=a；故答案为C．7．已知函数，若实数a，b满足f（a）+f（b﹣2）=0，则a+b= A．﹣2 B．﹣1 C．0D．2解：f（x）+f（﹣x）=ln（x+）+ln（﹣x+=0∵f（a）+f（b﹣2）=0∴a+（b﹣2）=0∴a+b=2故选D．8．=（）A．1B．C．﹣2 D．解：原式=+2×lg2+lg5=+lg2+lg5=+1=，故选B．9．设，则=（）A．1B．2C．3D．4解：∵，∴==（）+（）+（）==3故选C10．，则实数a的取值区间应为（C）A．（1，2）B．（2，3）C．（3，4）D．（4，5）解：=log34+log37=log328∵3=log327＜log328＜log381=4∴实数a的取值区间应为（3，4）故选C．11．若lgx﹣lgy=a，则=（A）A．3a B．C．a D．解：=3（lgx﹣lg2）﹣3（lgy﹣lg2）=3（lgx﹣lgy）=3a故选A．12．设，则（）A．0＜P＜1 B．1＜P＜2 C．2＜P＜3 D．3＜P＜4 解：=log112+log113+log114+log115=log11（2×3×4×5）=log11120．∴log1111=1＜log11120＜log11121=2．故选B．13．已知a，b，c均为正数，且都不等于1，若实数x，y，z满足，则abc的值等于（A）A．1B．2C．3D．4解：∵a，b，c均为正数，且都不等于1，实数x，y，z满足，∴设a x=b y=c z=k（k＞0），则x=log a k，y=log b k，z=log c k，∴=log k a+log k b+log k c=log k abc=0，∴abc=1．故选A．14．化简a2•••的结果是（C）A．a B．C．a2D．a3解：∵a2•••=a2•••==a2，故选C15．若x，y∈R，且2x=18y=6xy，则x+y为（）A．0B．1C．1或2 D．0或2解：因为2x=18y=6xy，（1）当x=y=0时，等式成立，则x+y=0；（2）当x、y≠0时，由2x=18y=6xy得，xlg2=ylg18=xylg6，由xlg2=xylg6，得y=lg2/lg6，由ylg18=xylg6，得x=lg18/lg6，则x+y=lg18/lg6+lg2/lg6=（lg18+lg2）/lg6=lg36/lg6=2lg6/lg6=2．综上所述，x+y=0，或x+y=2．故选D．16．若32x+9=10•3x，那么x2+1的值为（D）A．1B．2C．5D．1或5解：令3x=t，（t＞0），原方程转化为：t2﹣10t+9=0，所以t=1或t=9，即3x=1或3x=9所以x=0或x=2，所以x2+1=1或5故选Dx x2A．﹣2＜a＜2 B．C．D．解；令t=2x，则t＞0若二次函数f（t）=t2﹣at+a2﹣3在（0，+∞）上有2个不同的零点，即0=t2﹣at+a2﹣3在（0，+∞）上有2个不同的根∴解可得，即故选D18．若关于x的方程=3﹣2a有解，则a的范围是（A）A．≤a＜B．a≥C．＜a＜D．a＞解：∵1﹣≤1，函数y=2x在R上是增函数，∴0＜≤21=2，故0＜3﹣2a≤2，解得≤a＜，故选A．二．填空题19．，则m=10．解：由已知，a=log2m，b=log5m．∴+=log m2+log m5=log m10=1∴m=10故答案为：10．20．已知x+y=12，xy=9，且x＜y，则=．解：由题设0＜x＜y∵xy=9，∴∴x+y﹣2==12﹣6=6x+y+2==12+6=18∴=，=∴=故答案为：21．化简：=（或或）．解：====．故答案为：（或或）．22．=1．解：===1．故答案为：1．23．函数在区间[﹣1，2]上的值域是[，8]．解：令g（x）=x2﹣2x=（x﹣1）2﹣1，对称轴为x=1，∴g（x）在[﹣1，1]上单调减，在[1，8]上单调递增，又f（x）=2g（x）为符合函数，∴f（x）=2g（x）在[﹣1，1]上单调减，在[1，，2]上单调递增，∴f（x）min=f（1）==；又f（﹣1）==23=8，f（2）==1，∴数在区间[﹣1，2]上的值域是[，8]．故答案为：[，8]．24．函数的值域为（0，8]．解：令t=x2+2|x|﹣3==结合二次函数的性质可得，t≥﹣3∴，且y＞0故答案为：（0，8]．25．函数（﹣3≤x≤1）的值域是[3﹣9，39]，单调递增区间是（﹣2，+∞）．．解：可以看做是由y=和t=﹣2x2﹣8x+1，两个函数符合而成，第一个函数是一个单调递减函数，要求原函数的值域，只要求出t=﹣2x2﹣8x+1，在[1，3]上的值域就可以，t∈[﹣9，9]此时y∈[3﹣9，39]函数的递增区间是（﹣∞，﹣2]，故答案为：[3﹣9，39]；（﹣2，+∞）三．解答题26．计算：（1）；（2）．解：（1）==（2）===2+2﹣lg3+lg2+lg3﹣lg2+2=627．（1）若，求的值；（2）化简（a＞0，b＞0）．解：（1）∵，∴x+x﹣1=9﹣2=7，x2+x﹣2=49﹣2=47，∴==3×6=18，∴==．（2）∵a ＞0，b ＞0，∴====．28．已知函数f （x ）=4x ﹣2x+1+3．（1）当f （x ）=11时，求x 的值；（2）当x ∈[﹣2，1]时，求f （x ）的最大值和最小值．解：（1）当f （x ）=11，即4x ﹣2x+1+3=11时，（2x ）2﹣2•2x ﹣8=0 ∴（2x ﹣4）（2x +2）=0 ∵2x ＞02x +2＞2，∴2x ﹣4=0，2x =4，故x=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）（2）f （x ）=（2x ）2﹣2•2x +3 （﹣2≤x ≤1）令∴f （x ）=（2x ﹣1）2+2当2x =1，即x=0时，函数的最小值f min （x ）=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）当2x =2，即x=1时，函数的最大值f max （x ）=3﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）29．已知函数||22)(x x x f -=. （1）若2)(=x f ，求x 的值；（2）若0)()2(2≥+t mf t f t 对于]2,1[∈t 恒成立，求实数m 的取值范围。

指数函数习题(经典含答案及详细解析)

指数函数习题一、选择题1．定义运算，则函数的图象大致为( )2．函数f(x)＝x2－bx＋c满足f(1＋x)＝f(1－x)且f(0)＝3，则f(b x)与f(c x)的大小关系是( )A．f(b x)≤f(c x)B．f(b x)≥f(c x)C．f(b x)>f(c x)D．大小关系随x的不同而不同3．函数y＝|2x－1|在区间(k－1，k＋1)内不单调，则k的取值范围是( )A．(－1，＋∞) B．(－∞，1)C．(－1,1) D．(0,2)4．设函数f(x)＝ln[(x－1)(2－x)]的定义域是A，函数g(x)＝lg(－1)的定义域是B，若A⊆B，则正数a的取值范围( )A．a>3 B．a≥3C．a> D．a≥5．已知函数，若数列{a n}满足a n＝f(n)(n∈N*)，且{a n}是递增数列，则实数a的取值范围是( )A．[，3) B．(，3)C．(2,3) D．(1,3)6．已知a>0且a≠1，f(x)＝x2－a x，当x∈(－1,1)时，均有f(x)<，则实数a 的取值范围是( )A．(0，]∪[2，＋∞) B．[，1)∪(1,4]C．[，1)∪(1,2] D．(0，)∪[4，＋∞)二、填空题7．函数y＝a x(a>0，且a≠1)在[1,2]上的最大值比最小值大，则a的值是________．8．若曲线|y|＝2x＋1与直线y＝b没有公共点，则b的取值范围是________．9．(2011·滨州模拟)定义：区间[x1，x2](x1<x2)的长度为x2－x1.已知函数y ＝2|x|的定义域为[a，b]，值域为[1,2]，则区间[a，b]的长度的最大值与最小值的差为________．三、解答题10．求函数y＝的定义域、值域和单调区间．11．(2011·银川模拟)若函数y＝a2x＋2a x－1(a>0且a≠1)在x∈[－1,1]上的最大值为14，求a的值．12．已知函数f(x)＝3x，f(a＋2)＝18，g(x)＝λ·3ax－4x的定义域为[0,1]．(1)求a的值；(2)若函数g(x)在区间[0,1]上是单调递减函数，求实数λ的取值范围．指数函数答案1.解析：由a⊗b＝得f(x)＝1⊗2x＝答案：A2. 解析：∵f(1＋x)＝f(1－x)，∴f(x)的对称轴为直线x＝1，由此得b ＝2.又f(0)＝3，∴c＝3.∴f(x)在(－∞，1)上递减，在(1，＋∞)上递增．若x≥0，则3x≥2x≥1，∴f(3x)≥f(2x)．若x<0，则3x<2x<1，∴f(3x)>f(2x)．∴f(3x)≥f(2x)．答案：A3.解析：由于函数y＝|2x－1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k－1，k＋1)内不单调，所以有k－1<0<k＋1，解得－1<k<1.答案：C4. 解析：由题意得：A＝(1,2)，a x－2x>1且a>2，由A⊆B知a x－2x>1在(1,2)上恒成立，即a x－2x－1>0在(1,2)上恒成立，令u(x)＝a x－2x－1，则u′(x)＝a x lna－2x ln2>0，所以函数u(x)在(1,2)上单调递增，则u(x)>u(1)＝a－3，即a≥3.答案：B5. 解析：数列{a n}满足a n＝f(n)(n∈N*)，则函数f(n)为增函数，注意a8－6>(3－a)×7－3，所以，解得2<a<3.答案：C6. 解析：f(x)<⇔x2－a x<⇔x2－<a x，考查函数y＝a x与y＝x2－的图象，当a>1时，必有a－1≥，即1<a≤2，当0<a<1时，必有a≥，即≤a<1，综上，≤a<1或1<a≤2.答案：C7. 解析：当a>1时，y＝a x在[1,2]上单调递增，故a2－a＝，得a＝.当0<a<1时，y＝a x在[1,2]上单调递减，故a－a2＝，得a＝.故a＝或.答案：或8. 解析：分别作出两个函数的图象，通过图象的交点个数来判断参数的取值范围．曲线|y|＝2x＋1与直线y＝b的图象如图所示，由图象可得：如果|y|＝2x＋1与直线y＝b没有公共点，则b应满足的条件是b∈[－1,1]．答案：[－1,1]9. 解析：如图满足条件的区间[a，b]，当a＝－1，b＝0或a＝0，b＝1时区间长度最小，最小值为1，当a＝－1，b＝1时区间长度最大，最大值为2，故其差为1.答案：110. 解：要使函数有意义，则只需－x2－3x＋4≥0，即x2＋3x－4≤0，解得－4≤x≤1.∴函数的定义域为{x|－4≤x≤1}．令t＝－x2－3x＋4，则t＝－x2－3x＋4＝－(x＋)2＋，∴当－4≤x≤1时，t max＝，此时x＝－，t min＝0，此时x＝－4或x＝1.∴0≤t≤.∴0≤≤.∴函数y＝的值域为[，1]．由t＝－x2－3x＋4＝－(x＋)2＋(－4≤x≤1)可知，当－4≤x≤－时，t是增函数，当－≤x≤1时，t是减函数．根据复合函数的单调性知：y＝在[－4，－]上是减函数，在[－，1]上是增函数．∴函数的单调增区间是[－，1]，单调减区间是[－4，－]．11. 解：令a x＝t，∴t>0，则y＝t2＋2t－1＝(t＋1)2－2，其对称轴为t ＝－1.该二次函数在[－1，＋∞)上是增函数．①若a>1，∵x∈[－1,1]，∴t＝a x∈[，a]，故当t＝a，即x＝1时，y max ＝a2＋2a－1＝14，解得a＝3(a＝－5舍去)．②若0<a<1，∵x∈[－1,1]，∴t＝a x∈[a，]，故当t＝，即x＝－1时，y max＝(＋1)2－2＝14.∴a＝或－(舍去)．综上可得a＝3或.12. 解：法一：(1)由已知得3a＋2＝18⇒3a＝2⇒a＝log32.(2)此时g(x)＝λ·2x－4x，设0≤x1<x2≤1，因为g(x)在区间[0,1]上是单调减函数，所以g(x1)－g(x2)＝(2x1－2x2)(λ－2x2－2x1)>0恒成立，即λ<2x2＋2x1恒成立．由于2x2＋2x1>20＋20＝2，所以实数λ的取值范围是λ≤2.法二：(1)同法一．(2)此时g(x)＝λ·2x－4x，因为g(x)在区间[0,1]上是单调减函数，所以有g′(x)＝λln2·2x－ln4·4x＝ln2[－2·(2x)2＋λ·2x]≤0成立．设2x＝u∈[1,2]，上式成立等价于－2u2＋λu≤0恒成立．因为u∈[1,2]，只需λ≤2u恒成立，所以实数λ的取值范围是λ≤2.。

高一数学上册指数函数知识点及练习题含答案

课时4指数函数一. 指数与指数幂的运算（1）根式的概念 ①如果,,,1nxa a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n表示；当n 是偶数时，正数a 的正的nn次方根用符号0的n 次方根是0；负数a 没有n 次方根．n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．③根式的性质：n a =；当na =；当n(0)|| (0)a a a a a ≥⎧==⎨-<⎩．（2）分数指数幂的概念①正数的正分数指数幂的意义是：0,,,m naa m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 1()0,,,m m nn aa m n N a -+==>∈且1)n >．0的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数．（3）分数指数幂的运算性质①(0,,)rs r s aa a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r ab a b a b r R =>>∈二.指数函数及其性质（4）指数函数a 变化对图象影响在第一象限内，a 越大图象越高，越靠近y 轴；在第二象限内，a 越大图象越低，越靠近x 轴．在第一象限内，a 越小图象越高，越靠近y 轴；在第二象限内，a 越小图象越低，越靠近x 轴．三.例题分析1.设a 、b 满足0<a<b<1,下列不等式中正确的是(C) A.a a <a b B.b a 0且a ≠1),则下列等式中不正确的是(D) A.f(x+y)=f(x)f(y)B.f(x-y)=)()(y f x f C.f(nx)=［f(x)］n D.f ［(xy)n ］=［f(x)］n ［f(y)］n (n ∈N *) 解析：易知A 、B 、C 都正确. 对于D,f ［(xy)n］=a(xy)n,而［f(x)］n·［f(y)］n=(a x )n·(a y)n=anx+ny,一般情况下D 不成立.4.设a=31)43(-,b=41)34(-,c=43)23(-,则a 、b 、c 的大小关系是(B)A.c<a<bB.c<b<aC.b<a<cD.b<c<a解析：a=413131)34()34()43(>=-=b,b=434141)23()278()34(-=>=c.∴a>b>c.5.设f(x)=4x -2x+1,则f -1(0)=______1____________. 解析：令f -1(0)=a,则f(a)=0即有4a-2·2a=0.2a·(2a-2)=0,而2a>0,∴2a=2得a=1.6.函数y=a x-3+4(a>0且a ≠1)的反函数的图象恒过定点______(5,3)____________.解析：因y=a x的图象恒过定点(0,1),向右平移3个单位,向上平移4个单位得到y=a x-3+4的图象,易知恒过定点(3,5).故其反函数过定点(5,3).7.已知函数f(x)=xx xx --+-10101010.证明f(x)在R 上是增函数.证明：∵f(x)=1101101010101022+-=+---x x xx x x , 设x 1<x 2∈R ,则f(x 1)-f(x 2)=)110)(110()1010(21101101101101010101010101010212122112222111122222222++-=+--+-=+--+-----x x x x x x x x x x x x x x x x . ∵y=10x 是增函数, ∴21221010x x -<0. 而1210x +1>0,2210x +1>0, 故当x 1<x 2时,f(x 1)-f(x 2)<0, 即f(x 1)<f(x 2). 所以f(x)是增函数.8.若定义运算a ⊗b=⎩⎨⎧<≥,,,,b a a b a b 则函数f(x)=3x ⊗3-x 的值域为(A)A.(0,1]B.［1,+∞)C.(0,+∞)D.(-∞,+∞)解析：当3x ≥3-x ,即x ≥0时,f(x)=3-x ∈(0,1］;当3x<3-x,即x<0时,f(x)=3x∈(0,1).∴f(x)=⎩⎨⎧<≥-,0,3,0,3x x x x 值域为(0,1).9.函数y=a x 与y=-a -x (a>0,a ≠1)的图象(C) A.关于x 轴对称B.关于y 轴对称 C.关于原点对称D.关于直线y=-x 对称解析：可利用函数图象的对称性来判断两图象的关系.10.当x ∈［-1,1］时,函数f(x)=3x -2的值域为_______［-35,1］___________. 解析：f(x)在［-1,1］上单调递增.11.设有两个命题:(1)关于x 的不等式x 2+2ax+4>0对一切x ∈R 恒成立;(2)函数f(x)=-(5-2a)x 是减函数.若命题(1)和(2)中有且仅有一个是真命题,则实数a 的取值范围是_______(-∞,-2)__________.解析：(1)为真命题⇔Δ=(2a)2-16<0⇔-2<a<2.(2)为真命题⇔5-2a>1⇔a<2.若(1)假(2)真,则a ∈(-∞,-2].若(1)真(2)假,则a ∈(-2,2)∩［2,+∞］=∅. 故a 的取值范围为(-∞,-2).12.求函数y=4-x -2-x +1,x ∈［-3,2］的最大值和最小值. 解：设2-x =t,由x ∈［-3,2］得t ∈［41,8］,于是y=t 2-t+1=(t-21)2+43.当t=21时,y 有最小值43.这时x=1.当t=8时,y 有最大值57.这时x=-3. 13.已知关于x 的方程2a 2x-2-7a x-1+3=0有一个根是2,求a 的值和方程其余的根. 解：∵2是方程2a 2x-2-9a x-1+4=0的根,将x=2代入方程解得a=21或a=4. (1)当a=21时,原方程化为2·(21)2x-2-9(21)x-1+4=0.① 令y=(21)x-1,方程①变为2y 2-9y+4=0, 解得y 1=4,y 2=21.∴(21)x-1=4⇒x=-1,(21)x-1=21⇒x=2. (2)当a=4时,原方程化为2·42x-2-9·4x-1+4=0.② 令t=4x-1,则方程②变为2t 2-9t+4=0.解得t 1=4,t 2=21. ∴4x-1=4⇒x=2, 4x-1=21⇒x=-21. 故方程另外两根是当a=21时,x=-1; 当a=4时,x=-21. 14.函数y=243)31(x x -+-的单调递增区间是(D) A.［1,2］B.［2,3］C.(-∞,2]D.［2,+∞)解析：因为y=3x2-4x+3,又y=3t 单调递增,t=x 2-4x+3在x∈［2,+∞)上递增,故所求的递增区间为［2,+∞).15.已知f(x)=3x-b (2≤x ≤4,b 为常数)的图象经过点(2,1),则F(x)=f 2(x)-2f(x)的值域为(B) A.［-1,+∞)B.［-1,63) C.［0,+∞)D.(0,63］解析：由f(2)=1,得32-b =1,b=2,f(x)=3x-2. ∴F(x)=［f(x)-1］2-1=(3x-2-1)2-1. 令t=3x-2,2≤x≤4.∴g(t)=(t -1)2-1,t∈［1,9］. ∴所求值域为［-1,63］.2.1指数函数练习1．下列各式中成立的一项（）A ．7177)(m n mn= B ．31243)3(-=-C ．43433)(y x y x +=+D ．3339=2．化简)31()3)((656131212132b a b a b a ÷-的结果（）A ．a 6B ．a -C ．a 9-D ．29a3．设指数函数)1,0()(≠>=a a a x f x ，则下列等式中不正确的是（） A ．f (x +y )=f(x )·f (y ) B ．)()(y f x f y x f =-）（ C ．)()]([)(Q n x f nx f n∈=D ．)()]([·)]([)(+∈=N n y f x f xy f n n n4．函数21)2()5(--+-=x x y（）A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或5．若指数函数x a y =在[－1,1]上的最大值与最小值的差是1，则底数a 等于（）A ．251+B ．251+- C ．251± D ．215± 6．当a ≠0时，函数y ax b =+和y b ax =的图象只可能是（）7．函数||2)(x x f -=的值域是（）A ．]1,0(B ．)1,0(C ．),0(+∞D ．R8．函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ，满足1)(>x f 的x 的取值范围（）A ．)1,1(-B ．),1(+∞-C ．}20|{-<>x x x 或D ．}11|{-<>x x x 或9．函数22)21(++-=x x y 得单调递增区间是（）A ．]21,1[-B ．]1,(--∞C ．),2[+∞D ．]2,21[10．已知2)(xx e e x f --=，则下列正确的是（）A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数 11．已知函数f (x )的定义域是（1，2），则函数)2(x f 的定义域是. 12．当a ＞0且a ≠1时，函数f (x )=a x －2－3必过定点. 三、解答题：13．求函数y x x =--1511的定义域.14．若a ＞0，b ＞0，且a +b =c ，求证：(1)当r ＞1时，a r +b r ＜c r ；(2)当r ＜1时，a r +b r ＞c r .15．已知函数11)(+-=x x a a x f (a ＞1).（1）判断函数f (x )的奇偶性；（2）证明f (x )在(－∞，+∞)上是增函数.16．函数f(x)＝a x(a>0，且a ≠1)在区间[1,2]上的最大值比最小值大，求a 的值．参考答案一、DCDDDAADDA二、11．(0,1)；12．(2，－2)；三、13．解：要使函数有意义必须：∴定义域为：{}x x R x x ∈≠≠且01,14．解：rrrrr c b c a c b a ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+，其中10,10<<<<cbc a . 当r ＞1时，1=+<⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr，所以a r +b r ＜c r；当r ＜1时，1=+>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛c b c a c b c a rr ，所以a r +b r ＞c r . 15．解：(1)是奇函数.(2)设x 1＜x 2，则1111)()(221121+--+-=-x x x x a a a a x f x f 。

高一数学必修指数函数试题及答案

高一数学必修1指数函数试题及答案1．已知集合M＝{－1,1}，N＝x12<2x＋1<4，x∈Z，则M∩N等于( ) A．{－1,1} B．{－1}C．{0} D．{－1,0}【解析】因为N＝{x|2－1<2x＋1<22，x∈Z}，又函数y＝2x在R上为增函数，∴N＝{x|－1<x＋1<2，x∈Z}＝{x|－2<x<1，x∈Z}＝{－1,0}．∴M∩N＝{－1,1}∩{－1,0}＝{－1}．故选B.【答案】 B2．设14<14b<14a<1，那么( )A．aa<ab<ba B．aa<ba<abC．ab<aa<ba D．ab<ba<aa【解析】由已知及函数y＝14x是R上的减函数，得0<a<b<1.由y＝ax(0<a<1)的单调性及a<b，得ab<aa.由0<a<b<1知0<ab<1.∵aba<ab0＝1.∴aa<ba.故选C.也可采用特殊值法，如取a＝13，b＝12.【答案】 C3．已知函数f(x)＝a－12x＋1，若f(x)为奇函数，则a＝________. 【解析】解法1：∵f(x)的定义域为R，又∵f(x)为奇函数，∴f(0)＝0，即a－120＋1＝0.∴a＝12.解法2：∵f(x)为奇函数，∴f(－x)＝－f(x)，即a－12－x＋1＝12x＋1－a，解得a＝12.【答案】124．函数y＝2－x2＋ax－1在区间(－∞，3)内递增，求a的取值范围．【解析】对u＝－x2＋ax－1＝－x－a22＋a24－1，增区间为－∞，a2，∴y的增区间为－∞，a2，由题意知3≤a2，∴a≥6.∴a的取值范围是a≥6.一、选择题(每小题5分，共20分)1．设y1＝40.9，y2＝80.48，y3＝(12)－1.5，则( )A．y3>y1>y2 B．y2>y1>y3C．y1>y2>y3 D．y1>y3>y2【解析】y1＝40.9＝21.8，y2＝80.48＝21.44，y3＝(12)－1.5＝21.5，∵y＝2x在定义域内为增函数，且1.8>1.5>1.44，∴y1>y3>y2.【答案】 D2．若142a＋1<143－2a，则实数a的取值范围是( )A.12，＋∞B.1，＋∞C．(－∞，1) D.－∞，12【解析】函数y＝14x在R上为减函数，∴2a＋1>3－2a，∴a>12.故选A.【答案】 A3．设函数f(x)定义在实数集上，它的图象关于直线x＝1对称，且当x≥1时，f(x)＝3x－1，则有( )A．f(13)<f(32)<f(23)B．f(23)<f(32)<f(13)C．f(23)<f(13)<f(32)D．f(32)<f(23)<f(13)【解析】因为f(x)的图象关于直线x＝1对称，所以f(13)＝f(53)，f(23)＝f(43)，因为函数f(x)＝3x－1在[1，＋∞)上是增函数，所以f(53)>f(32)>f(43)，即f(23)<f(32)<f(13)．故选B.【答案】 B4．如果函数f(x)＝(1－2a)x在实数集R上是减函数，那么实数a的取值范围是( ) A．(0，12) B．(12，＋∞)C．(－∞，12) D．(－12，12)【解析】根据指数函数的概念及性质求解．由已知得，实数a应满足1－2a>01－2a<1，解得a<12a>0，即a∈(0，12)．故选A.【答案】 A二、填空题(每小题5分，共10分)5．设a>0，f(x)＝exa＋aex(e>1)，是R上的偶函数，则a＝________.【解析】依题意，对一切x∈R，都有f(x)＝f(－x)，∴exa＋aex＝1aex＋aex，∴(a－1a)(ex－1ex)＝0.∴a－1a＝0，即a2＝1.又a>0，∴a＝1.【答案】 16．下列空格中填“>、<或＝”．(1)1.52.5________1.53.2，(2)0.5－1.2________0.5－1.5.【解析】(1)考察指数函数y＝1.5x.因为1.5>1，所以y＝1.5x在R上是单调增函数．又因为2.5<3.2，所以1.52.5<1.53.2.(2)考察指数函数y＝0.5x.因为0<0.5<1，所以y＝0.5x在R上是单调减函数．又因为－1.2>－1.5，所以0.5－1.2<0.5－1.5.【答案】<，<三、解答题(每小题10分，共20分)7．根据下列条件确定实数x的取值范围：a<1a1－2x(a>0且a≠1)．【解析】原不等式可以化为a2x－1>a12，因为函数y＝ax(a>0且a≠1)当底数a大于1时在R上是增函数；当底数a大于0小于1时在R上是减函数，所以当a>1时，由2x－1>12，解得x>34；当0<a<1时，由2x－1<12，解得x<34.综上可知：当a>1时，x>34；当0<a<1时，x<34.8．已知a>0且a≠1，讨论f(x)＝a－x2＋3x＋2的单调性．【解析】设u＝－x2＋3x＋2＝－x－322＋174，则当x≥32时，u是减函数，当x≤32时，u是增函数．又当a>1时，y＝au是增函数，当0<a<1时，y＝au是减函数，所以当a>1时，原函数f(x)＝a－x2＋3x＋2在32，＋∞上是减函数，在－∞，32上是增函数．当0<a<1时，原函数f(x)＝a－x2＋3x＋2在32，＋∞上是增函数，在－∞，32上是减函数．9．(10分)已知函数f(x)＝3x＋3－x.(1)判断函数的奇偶性；(2)求函数的单调增区间，并证明．【解析】(1)f(－x)＝3－x＋3－(－x)＝3－x＋3x＝f(x)且x∈R，∴函数f(x)＝3x＋3－x是偶函数．(2)由(1)知，函数的单调区间为(－∞，0]及[0，＋∞)，且[0，＋∞)是单调增区间．现证明如下：设0≤x1<x2，则f(x1)－f(x2)＝3x1＋3－x1－3x2－2－x2＝3x1－3x2＋13x1－13x2＝3x1－3x2＋3x2－3x13x13x2＝(3x2－3x1)?1－3x1＋x23x1＋x2.∵0≤x1<x2，∴3x2>3x1，3x1＋x2>1，∴f(x1)－f(x2)<0，即f(x1)<f(x2)，∴函数在[0，＋∞)上单调递增，即函数的单调增区间为[0，＋∞)．。

高一数学幂函数、指数函数和对数函数练习题(含答案)

高一数学幂函数、指数函数和对数函数练习题1、下列函数一定是指数函数的是（）Ａ、12+=x y B 、3x y = C 、x y -=3 D 、x y 23⋅=2、已知ab >0，下面四个等式中，正确命题的个数为（） ①lg （ab ）=lg a +lg b ②lg b a =lg a －lg b ③b a b a lg )lg(212= ④lg （ab ）=10log 1ab A ．0 B ．1 C ．2 D ．33、已知x =2+1，则lo g 4（x 3－x －6）等于（）A ．23 B ．45 C ．0 D ．21 4、已知m >0时10x =lg （10m ）+lg m 1，则x 的值为（） A ．2 B ．1 C ．0 D ．－15、下列图像正确的是（）A B C D6、若log a b ·log 3a =5，则b 等于（）A ．a 3B ．a 5C ．35D ．537、5、已知031log 31log >>b a ，则a 、b 的关系是（） A ．1＜b ＜a B ．1＜a ＜b C ．0＜a ＜b ＜1 D ．0＜b ＜a ＜1 8、若函数)1,0(1≠>-+=a a m a y x 的图象在第一、三、四象限内，则（）A 、1>aB 、1>a 且0<mC 、010><<m a 且D 、10<<a9、函数x y -=1)21(的单调递增区间是（） A 、),(+∞-∞ B 、),0(+∞ C 、),1(+∞ D 、)1,0(10、如图1—9所示，幂函数αx y =在第一象限的图象，比较1,,,,,04321αααα的大小（）A ．102431<<<<<ααααB ．104321<<<<<ααααC ．134210αααα<<<<<D ．142310αααα<<<<< 11、下列函数中既是偶函数又是（） A ． B ． C ． D ．12、函数R x x x y ∈=|,|，满足（）A ．奇函数是减函数B ．偶函数又是增函数C ．奇函数又是增函数D ．偶函数又是减函数13、若01<<-x ，则下列不等式中成立的是（）A 、 x x x 5.055<<-B 、 x x x -<<55.05C 、x x x 5.055<<-D 、 x x x 555.0<<-14、下列命题中正确的是（） A ．当0=α时函数αx y =的图象是一条直线B ．幂函数的图象都经过（0，0）和（1，1）点C ．若幂函数αx y =是奇函数，则αx y =是定义域上的增函数D ．幂函数的图象不可能出现在第四象限15、若2<x ，则|3|442x x x --+-的值是_____ _____.16、满足等式lg （x －1）+lg （x －2）=lg2的x 集合为______ _______。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

指数和指数函数一、选择题 1．（369a ）4（639a ）4等于（）（A ）a16（B ）a8（C ）a4（D ）a 22.若a>1,b<0,且a b+a -b=22,则a b-a -b的值等于（）（A ）6 （B ）±2 （C ）-2 （D ）23．函数f （x ）=(a 2-1)x在R 上是减函数，则a 的取值范围是（）（A ）1>a （B ）2<a （C ）a<2 （D ）1<2<a4.下列函数式中，满足f(x+1)=21f(x)的是( ) (A)21(x+1) (B)x+41 (C)2x (D)2-x5.下列f(x)=(1+a x )2xa-⋅是（）（A ）奇函数（B ）偶函数（C ）非奇非偶函数（D ）既奇且偶函数6．已知a>b,ab 0≠下列不等式（1）a 2>b 2,(2)2a>2b,(3)ba 11<,(4)a 31>b 31,(5)(31)a <(31)b中恒成立的有（）（A ）1个（B ）2个（C ）3个（D ）4个7．函数y=1212+-x x 是（）（A ）奇函数（B ）偶函数（C ）既奇又偶函数（D ）非奇非偶函数 8．函数y=121-x的值域是（）（A ）（-1,∞）（B ）（-,∞0）⋃（0，+∞）（C ）（-1，+∞）（D ）（-∞，-1）⋃（0，+∞）9．下列函数中，值域为R +的是（）（A ）y=5x-21 （B ）y=(31)1-x （C ）y=1)21(-x （D ）y=x 21- 10.函数y=2xx e e --的反函数是（）（A ）奇函数且在R +上是减函数（B ）偶函数且在R +上是减函数（C ）奇函数且在R +上是增函数（D ）偶函数且在R +上是增函数 11．下列关系中正确的是（）（A ）（21）32<（51）32<（21）31 （B ）（21）31<（21）32<（51）3212．若函数y=3+2x-1的反函数的图像经过P 点，则P 点坐标是（）（A ）（2，5）（B ）（1，3）（C ）（5，2）（D ）（3，1）13．函数f(x)=3x +5,则f -1(x)的定义域是（）（A ）（０，＋∞）（B ）（５，＋∞）（C ）（６，＋∞）（D ）（－∞，＋∞）14.若方程a x-x-a=0有两个根，则a 的取值范围是（）（A ）（1，+∞）（B ）（0，1）（C ）（0，+∞）（D ）φ15．已知函数f(x)=a x+k,它的图像经过点（1，7），又知其反函数的图像经过点（4，0），则函数f(x)的表达式是（）(A)f(x)=2x +5 (B)f(x)=5x +3 (C)f(x)=3x +4 (D)f(x)=4x+3 16.已知三个实数a,b=a a ,c=aaa ,其中0.9<a<1,则这三个数之间的大小关系是（）（A ）a<c<b （B ）a<b<c （C ）b<a<c （D ）c<a<b17．已知0<a<1,b<-1,则函数y=a x+b 的图像必定不经过（） (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限二、填空题 1．若a 23<a2,则a 的取值范围是。

2．若10x=3,10y=4,则10x-y= 。

3．化简⨯53xx 35xx×235xx = 。

4．函数y=1151--x x 的定义域是。

5．直线x=a(a>0)与函数y=(31)x ,y=(21)x ,y=2x ,y=10x的图像依次交于A 、B 、C 、D 四点，则这四点从上到下的排列次序是。

6．函数y=3232x -的单调递减区间是。

7．若f(52x-1)=x-2,则f(125)= .8．已知f(x)=2x,g(x)是一次函数，记F （x ）=f[g(x)],并且点（2，41）既在函数F （x ）的图像上，又在F -1（x ）的图像上，则F （x ）的解析式为 .三、解答题1．设0<a<1,解关于x 的不等式a1322+-x x >a522-+x x 。

2．设f(x)=2x ,g(x)=4x,g[g(x)]>g[f(x)]>f[g(x)]，求x 的取值范围。

3．已知x ∈[-3,2]，求f(x)=12141+-x x 的最小值与最大值。

4．设a ∈R,f(x)=)(1222R x a a x x ∈+-+⋅，试确定a 的值，使f(x)为奇函数。

5．已知函数y=(31)522++x x ，求其单调区间及值域。

6．若函数y=4x -3·2x+3的值域为[1，7]，试确定x 的取值范围。

7.已知函数f(x)=)1(11>+-a a a xx , (1)判断函数的奇偶性； (2)求该函数的值域；(3)证明f(x)是R 上的增函数。

第四单元指数与指数函数一、选择题1．0<a<1 2.433.14.(-∞,0)⋃(0,1) ⋃(1,+ ∞) ⎪⎩⎪⎨⎧≠-≠--015011x x x ,联立解得x ≠0,且x ≠1。

5．[（31）9，39] 令U=-2x 2-8x+1=-2(x+2)2+9,∵ -399,1≤≤-∴≤≤U x ,又∵y=(31)U 为减函数，∴（31）9≤y ≤39。

6。

D 、C 、B 、A 。

7．（0，+∞）令y=3U,U=2-3x 2, ∵y=3U为增函数，∴y=32323x -的单调递减区间为[0，+∞）。

8．0 f(125)=f(53)=f(52×2-1)=2-2=0。

9．31或3。

Y=m 2x+2m x-1=(mx+1)2-2, ∵它在区间[-1，1]上的最大值是14，∴（m -1+1）2-2=14或（m+1）2-2=14,解得m=31或3。

10．2710712+-x11．∵ g(x)是一次函数，∴可设g(x)=kx+b(k ≠0), ∵F(x)=f[g(x)]=2kx+b。

由已知有F （2）=41，F （41）=2，∴ ⎪⎩⎪⎨⎧=+-=+⎪⎩⎪⎨⎧==++1412222412412b k b k b k b k 即，∴ k=-712,b=710,∴f(x)=2-710712+x 三、解答题1．∵0<a<2,∴ y=a x在（-∞，+∞）上为减函数，∵ a 1322+-x x >a522-+x x , ∴2x 2-3x+1<x 2+2x-5,解得2<x<3,2.g[g(x)]=4x4=4x22=2122+x ,f[g(x)]=4x2=2x22,∵g[g(x)]>g[f(x)]>f[g(x)], ∴2122+x >212+x >2x22,∴22x+1>2x+1>22x,∴2x+1>x+1>2x,解得0<x<13.f(x)=43)212(12124121412+-=+=+-=+-----xx x x xx , ∵x ∈[-3,2], ∴8241≤≤-x .则当2-x =21,即x=1时,f(x)有最小值43；当2-x=8,即x=-3时，f(x)有最大值57。

4．要使f(x)为奇函数，∵ x ∈R,∴需f(x)+f(-x)=0, ∴f(x)=a-122)(,122+-=-+-x x a x f =a-1221++x x ,由1+x x x5．令y=(31)U ,U=x 2+2x+5,则y 是关于U 的减函数，而U 是(-∞,-1)上的减函数，[-1，+∞]上的增函数，∴ y=(31)522++x x 在（-∞，-1）上是增函数，而在[-1，+∞]上是减函数，又∵U=x 2+2x+5=(x+1)2+4≥4, ∴y=(31)522++x x 的值域为（0，（31）4）]。

6．Y=4x-33232322+⋅-=+⋅x xx ，依题意有⎪⎩⎪⎨⎧≥+⋅-≤+⋅-1323)2(7323)2(22x x x x 即⎪⎩⎪⎨⎧≤≥≤≤-1222421xx x 或，∴ 2,12042≤<≤≤xx 或由函数y=2x的单调性可得x ]2,1[]0,(⋃-∞∈。

7．（2x）2+a(2x)+a+1=0有实根，∵ 2x>0,∴相当于t 2+at+a+1=0有正根，则⎪⎩⎪⎨⎧>+>-≥∆⎩⎨⎧≤+=≥∆010001)0(0a a a f 或 8．（1）∵定义域为x R ∈,且f(-x)=)(),(1111x x f a a a a xxxx ∴-=+-=+---是奇函数；（2）f(x)=,2120,11,121121<+<∴>++-=+-+xxx x x a a a a a ∵即f(x)的值域为（-1，1）；（3）设x 1,x 2R ∈,且x 1<x 2,f(x 1)-f(x 2)=0)1)(1(2211112121221<++-=+--+-xx x x x x x x a a a a a a a a (∵分母大于零，且a 1x <a 2x ) ∴f(x)是R 上的增函数。