七年级找规律专题练习(精)
七年级初一常考找规律题目探索(精选汇总)

七年级常考找规律题目探索(精选汇总)类型一根据数据的排列找规律1.有一列数按5,4,3,2,1,5,4,3,2,1,……排列,第42个数字应该是()A、5B、4C、3D、22.在数列3,12,30,60,……中,请你观察数列的排列规律,则第5个数是()A.75B.90C.105D.1203.若下面每个表格中的4个数字所有相同的规律,则其中n的值为()A、105B、107C、109D、1114.按一定的规律排列的一列数依次为:…,按此规律排列下去,这列数中的第7个数是()A.B.C.D.5.把全体自然数按下面的方式进行排列:按照这样的规律推断,从2014到2016,箭头的方向应是()A.↓→B.→↑C.↑→D.→↓6.计算1﹣2+3﹣4+5﹣6+7﹣8+…+2009﹣2010的结果是()A.﹣1005B.﹣2010C.0D.﹣17.观察下列算式,用你所发现的规律得出22015的末位数字是()21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,….A.2B.4C.6D.88.等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和﹣1,若△ABC绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1;则翻转2012次后,点B所对应的数是()A.2013B.2010C.2011D.20129.任何实数a,可用[a]表示不超过a的最大整数,如:[4]=4,[]=1,现对36进行如下操作:36[]=6[]=2[]=1,这样对36只需进行3次操作后变为1,类似地,对99只需进行多少次操作后变为1?()A.1次B.2次C.3次D.4次10、如图所示,将圆的周长分为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数1所对应的点重合,再让圆沿着数轴按逆时针方向滚动,那么数轴上的数 2020将与圆周上的数字()重合.A.0B.1C.2D.312.填在下面各正方形中的四个数之间都有一定的规律,据此规律得出a+b+c=________13、如图,填在下面各正方形中的4个数之间都有相同的规律:根据这种规律,n的值应该等于.14.下面每个正方形中的五个数之间都有相同的规律,根据这种规律,则第4个正方形中间数字m为,第n个正方形的中间数字为.(用含n的代数式表示)17.如图,圆圈内分别标有0,1,2,3,4,…,11这12个数字.电子跳蚤每跳一次,可以从一个圆圈跳到相邻的圆圈,现在,一只电子跳蚤从标有数字“0”的圆圈开始,按逆时针方向跳了2011次后,落在一个圆圈中,该圆圈所标的数字是.18.有若干个数,第1个数记为a 1,第2个数记为a 2,第3个数记为a 3,···,第n 个数记为an ,若a 1=21,从第2个数起,每个数都等于“1与它前面的那个数的差的倒数”。
七年级数学找规律题习题汇总

找规律题一、数字排列规律题1、下面数列后两位应该填上什么数字呢? 2 3 5 8 12 17 __ __2、出下面横线上的数字。
1 123 5 8 ____ 213、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、…… 聪明的你猜猜第2016个( )4、有一串数字 3 6 10 15 21 ___ 第6个是什么数?5、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2016个数是( ).6、100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为 _________个.7、观察下列数据,按某种规律在横线上填上适当的数:1,,,,, ,……二、数、式计算规律题1、观察下列各算式1+3=4=,1+3+5=9=,1+3+5+7=16=…猜想:1+3+5+7+…+2019+2020=推广:1+3+5+7+9+…+(2n-1)+(2n+1)=2、已知下列等式:① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102 ; 由此规律知,第⑤个等式是 .3、观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____.43-95167-2592223244、1+2+3+ (100)经过研究,这个问题的一般性结论是 1+2+3+…+n= ,其中n是正整数.6、⑴ 第5、6排各有多少个座位? ⑵第n 排有多少个座位? 7、计算8、观察下列计算,,,…… 从计算结果中找规律,利用规律计算9、观察下列各式;①、1+1=1×2 ;②、2+2=2×3; ③、3+3=3×4 ;………请把你猜想到的规律用自然数n 表示出来 。
(完整)七年级数学专题规律探究题

七年级数学专题-----规律探究题题型一:数字变化类问题1 •观察下列按顺序排列的等式:引二1-*,2誌-書,巧€ 一+,4冷一+ 试猜想第n个等式(n为正整数):a n= ______________________ .2. 下表中的数字是按一定规律填写的,表中a的值应是____ .1 2 3 5 8 13 a-2 3 5 8 13 21 34 …3. ___ 观察下面的单项式:a,- 2a2, 4a3,- 8a4, ••根据你发现的规律,第8个式子是.4. 有一组等式:1222 3232,22326272,32 42 122132,4252202212……请观察它们的构成规律,用你发现的规律写出第8个等式为__________5. 把奇数列成下表,13113213L59152333111725h-itn! ■ b ■2737—39——根据表中数的排列规律,则上起第8行,左起第6列的数是5.在计数制中,通常我们使用的是“十进位制”,即“逢十进一”。
而计数制方法很多,如60进位制:60秒化为1分,60分化为1小时;24进位制:24小时化为1天;7进位制:7天化为1周等…而二进位制是计算机处理数据的依据。
已知二进十进位制0123456• • •请将二进制数10101010(二)写成十进制数为_______ .6 •观察下列各数,它们是按定规律排列的,则第n个数是15 3116?眈'7.观察一列单项式:1x, 3x2, 5x2, 7x, 9x2, 11x2,…,则第2013个单项式是8•有这样一组数据a i, a2, a3, •• a,满足以下规律:且I三・❻尸—-—3 勒二 ~-—j …,且—-------- (n多且n为正整数),贝U宠。
1312 1 _ J1 _a2n1 - a n_ L的值为________ (结果用数字表示).9. 观察下列各式的计算过程:5X 5=0X 1 X 100+25,15X 15=1X 2X 100+25,25X 25=2X 3X 100+25,35X 35=3X 4X 100+25,请猜测,第n个算式(n为正整数)应表示为_____________________________ 10. 如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是A. M=mnB. M=n(m+1)C. M=mn+1D. M=m(n+1)11. 观察下列等式:31=3, 32=9, 33=27, 34=81, 35=243, 36=729, 37=2187… 解答下列问题:3+32+33+3仃+32013的末位数字是()A. 0B. 1C. 3D. 712. ____________________________________________ 如下表,从左到右在每个小格中都填入一个整数,使得任意三个相邻格子所填整数之和都相等,则第2013个格子中的整数是_______________________________ .13. 将连续正整数按以下规律排列,则位于第 7行第7列的数x 是85篦一如邕二苑董三列策囚列篝三到邕七扪・・・第一行 136 10 1521 n 重二行 2 5 9 14 20 27 :第三行 413 15--- ■策四行712 1$25■・■11 17 2415 23 ■ ■•2215•电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个 方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数 字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,此WORD 中为方便大家识别与印刷,我还是把图乙中的0都标出来吧,以示与未掀开者的 区别),如图甲中的“ 3”表示它的周围八个方块中仅有 3个埋有雷.图乙第一行 从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有 ___________________________ .(请填入方块上的字母)16. 如图,在△ ABC 中,/ A=m°,/ ABC 和/ACD 的平分线交于点 A,得/ A;/ ABC 和/ACD 的平分线交于点 A ,得/ A;…/A2012BC 和/A 2012CD 的平分线交于 点 A ?013,贝 A 2013= ______ 度。
(word版)七年级数学找规律练习题和答案
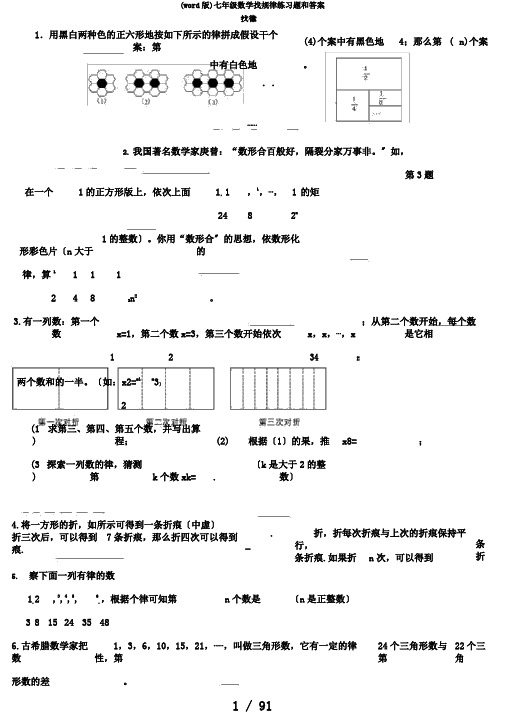
找律1.用黑白两种色的正六形地按如下所示的律拼成假设干个案:第(4)个案中有黑色地4;那么第(n)个案中有白色地。
..⋯⋯2.我国著名数学家庚曾:“数形合百般好,隔裂分家万事非。
〞如,在一个1的正方形版上,依次上面1,1,1,⋯,1的矩第3题2482n形彩色片〔n大于1的整数〕。
你用“数形合〞的思想,依数形化的律,算11112482n=。
3.有一列数:第一个数x=1,第二个数x=3,第三个数开始依次x,x,⋯,x ;从第二个数开始,每个数是它相1234n 两个数和的一半。
〔如:x2=x1x3〕2(1 )求第三、第四、第五个数,并写出算程;(2)根据〔1〕的果,推x8=;(3 )探索一列数的律,猜测第k个数xk=.〔k是大于2的整数〕4.将一方形的折,如所示可得到一条折痕〔中虚〕折三次后,可以得到7条折痕,那么折四次可以得到痕._.折,折每次折痕与上次的折痕保持平行,条折痕.如果折n次,可以得到条折5.察下面一列有律的数1,2,3,4,5,6,,根据个律可知第n个数是〔n是正整数〕38152435486.古希腊数学家把数1,3,6,10,15,21,⋯⋯,叫做三角形数,它有一定的律性,第24个三角形数与第22个三角形数的差。
按照一定序排列的一列数叫数列,一般用a1,a2,a3,⋯,an表示一个数列,可{an}.有数列{an}足一个关系式:a=an-n a,a,a的,然后行猜测n n的代数n+121234式表示〕8.察下面一列数:-1,2,-3,4,-5,6,-7,...,将列-12-34数排成以下形式10行从左第9个数是.-56-7-9按照上述律排下去,那么第10-1112-1314-1516......第8题1察以下等式9-1=816-4=1225-9=1636-16=20 ⋯⋯⋯⋯些等式反映自然数的某种律,n(n≥1)表示自然数,用关于n的等式表示个律.10.如是阳光广告公司某种商品的商案,中阴影局部色。
七年级数学找规律题(含答案)

七年级数学找规律题(含答案)1.观察下图,寻找规律,在“?”处填上的数字是( ). A.128 B.136 C.162 D.188 【答案】C2.寻找规律计算1 - 2+3 - 4+5 - 6+…+2015 - 2016等于 ( ) A.0 B.- 1 C.- 1008D.1008【答案】C3.找规律:21-20=20 ;22-21=21 ;23-22=2 2;………利用你的发现,求20+21+22+23+…+22018+22019的值是( ) A .22019 -1 B .22019 +1C .22020 -1D .22020 +1【答案】C4.先找规律,再填数:1111122+-=,111134212+-=,111156330+-=,111178456+-=,…,1120132014+-( )=()12014⨯.【答案】11007,2013. 5.找规律填上合适的数:﹣2,4,﹣8,16, ,64,… 【答案】﹣32.6.寻找规律,根据规律填空:31,152-,353,634-,995, ,…,第n 个数是 . 【答案】1436-14)1(21--+n n n (或:当n 时奇数时,142-n n;当n 时偶数时,142--n n )7.先找规律,再填数: 111111*********1,,,,122342125633078456............111+_______.2011201220112012+-=+-=+-=+-=-=⨯则 【答案】8.找规律填数:﹣1,2,﹣4,8,________ 【答案】﹣169.先找规律,再填数:11+12-1=12,13+14-12=112,15+16-13=130,17+18-14=156,12011+12012-________=120112012⨯ 【答案】10.已知C 32=3×21×2=3, C 53=5×4×31×2×3=10,C 64 =6×5×4×31×2×3×4=15,…观察以上计算过程,寻找规律计算C 85=_____. 【答案】56.11.已知:3212323=⨯⨯=C ,1032134535=⨯⨯⨯⨯=C ,154321345646=⨯⨯⨯⨯⨯⨯=C ,…,观察上面的计算过程,寻找规律并计算=610C .【答案】21012.观察下列各式并找规律,再猜想填空:()()()()223322332248a b a ab b a b x y x xy y x y +-+=++-+=+, ,则()()2223469a b a ab b +-+= ______ .【答案】33827a b + 13.观察下列计算:,,,……从计算结果中找规律,利用规律计算_______________ 【答案】14.已知: 233212C ⨯=⨯=3,35543123C ⨯⨯=⨯⨯=10,3565431234C ⨯⨯⨯=⨯⨯⨯=15,…,观察上面的计算过程,寻找规律并计算:34C =_____. 【答案】4. 15.已知:2332312C ⨯==⨯,3554310123C ⨯⨯==⨯⨯,466543151234⨯⨯⨯==⨯⨯⨯C ,…,观察上面的计算过程,寻找规律并计算C 106=_____. 【答案】21016.找规律:﹣12,2,﹣92,8,﹣252 ,18…,则第7个数为_____;第n 个数为_____(n 为正整数)【答案】﹣492 (﹣1)nn 22.17.观察烟花燃放图形,找规律:依此规律,第n 个图形中共有_________个★. 【答案】2+2n18.找规律,并按规律填上第五个数:,169,87,45,23-- . 【答案】-113219.观察下面的一列数,从中寻找规律,然后按规律填写接下去的3个数.12,34-,56,78-,910,________,________,________,… 【答案】1112-1314 1516- 20.观察表一,寻找规律,表二、表三、表四分别是从表一中截取的一部分,则a b m -+=_____.【答案】4321.观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a+b+c 的值为 .【答案】7622.观察下面的一列数,从中寻找规律,然后按规律写出接下去的三个数.12 ,-34 ,56 ,-78 ,910,… ________,…【答案】-1112;1314;−1516. 23.找规律.下列图中有大小不同的菱形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第n 幅图中共有________个.【答案】2n -124.观察下列各组勾股数,并寻找规律:①4,3,5; ②6,8,10; ③8,15,17; ④10,24,26 …… 请根据你发现的规律写出第⑦组勾股数:____________. 【答案】16,63,6525.用火柴棒按以下方式搭“小鱼” .…………搭1条“小鱼”需用8根火柴棒,搭2条“小鱼”需用14根火柴棒,搭3条“小鱼”需用20根火柴棒……观察并找规律,搭10条“小鱼”需用火柴棒的根数为 . 【答案】62 26.观察下列计算111122=-⨯ ,1112323=-⨯,1113434=-⨯,1114545=-⨯,……, (1)第n 个式子是_____________________________________; (2)从计算结果中找规律,利用规律计算:112⨯+123⨯+134⨯+145⨯+…+120092010⨯ 【答案】(1)()11111n n n n =-++;(2)20092010. 27.探究:()21112222122-=⨯-⨯=, () 3222? 2-==, ()4322? 2-==,……(1)请仔细观察,写出第4个等式; (2)请你找规律,写出第n 个等式;(3)计算:012201620172018222222+++⋅⋅⋅⋅⋅⋅++-. 【答案】(1)544442222122-=⨯-⨯=;(2)12222122n n n n n +-=⨯-⨯=;(3)-128.阅读下文,寻找规律:已知1x ≠时, ()()2111x x x -+=-,()()23111x x x x -++=-, ()()234111x x x x x -+++=-……(1)填空: ()1(x - 5)1x =-. (2)观察上式,并猜想:①()()211n x x x x -+++⋅⋅⋅+= . ②()()10911x x x x -++⋅⋅⋅++= . (3)根据你的猜想,计算:①()()234512122222-+++++= . ②23420161+3+3+3+33⋅⋅⋅⋅⋅⋅=_____________________【答案】(1)2341+x x x x +++(2)11n x+-; 111x -(3)612- (或 -63); 20173-1229.小明同学在一次找规律的游戏中发现如下的数字和规律,请你按照所给的式子,解答下列问题:21342+== 213593++== 21357164+++== 213579255++++==()1试猜想:135791129++++++⋯+=①______.()()135********n n ++++++⋯+-++=②______.()2用上述规律计算:2123255759+++⋯++=______.【答案】(1)①225;②(n+1)²(2)80030.找规律并解答问题.(1)按下图方式摆放黑色围棋子,填一填,每个图共需几枚棋子.(2)根据你发现的规律,算一算第13个图,共需要( )枚棋子.【答案】(1)详见解析;(2)40枚.31.观察表一,寻找规律.表二、表三分别是从表一中选取的一部分,则a=,ba+= .表一表二表三【答案】17=a2372=+ba32.细观察,找规律.下列各图中的1MA与nNA平行.()1图①中的12A A∠+∠=______ 度,图②中的123A A A∠+∠+∠=______ 度,图③中的1234A A A A ∠+∠+∠+∠=______ 度, 图④中的12345A A A A A ∠+∠+∠+∠+∠=______ 度,⋯,第⑩个图中的12311A A A A ∠+∠+∠+⋯+∠=______ 度()2第n 个图中的1231n A A A A +∠+∠+∠+⋯+∠=______ ()3请你证明图②的结论.【答案】(1)180;360;540;720;1800;(2)180n °;(3)详见解析. 33.找规律:(1)填空:41=________;42=______;43=______;44=______;45=________;46=________;…(2)你发现4的幂的个位数字有什么规律? (3)4250的个位数是什么数字?为什么?【答案】(1)4, 16, 64,256,1224,4896;(2)是循环数;(3)6. 34.观察等式找规律: ①第1个等式:22﹣1=1×3; ②第2个等式:42﹣1=3×5; ③第3个等式:62﹣1=5×7; ……(1)写出第5个等式: ; 第6个等式: ;(2)写出第n 个等式(用字母n 表示): ; (3)求111113355740254027++++⨯⨯⨯⨯的值.【答案】(1)102﹣1=9×11;122﹣1=11×13;(2)4n 2﹣1=(2n ﹣1)(2n+1);(3)2013402735.观察表l ,寻找规律.表2是从表l 中截取的一部分,其中a ,b ,c 的值分别为( )A.20,25,24B.25,20,24C.18,25,24D.20,30,25【答案】A36.阅读下文,寻找规律.计算:(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1﹣x3,(1﹣x)(1+x+x2+x3)=1﹣x4….(1)观察上式,并猜想:(1﹣x)(1+x+x2+…+x n)= .(2)根据你的猜想,计算:1+3+32+33…+3n= .(其中n是正整数)【答案】(1)1﹣x n+1,(2)﹣.37.如图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中:共有1个小立方体,其中1个看得见,0个看不见;如图②中:共有8个小立方体,其中7个看得见,1个看不见;如图③中:共有27个小立方体,其中19个看得见,8个看不见;…,则第⑥个图中,看得见的小立方体有_____个.【答案】9138.找规律.一张长方形桌子可坐6人,按下图方式讲桌子拼在一起。
(完整版)七年级找规律经典题汇总带答案

……一、数字排列规律题1、观察下列各算式: 1+3=4=22,1+3+5=9=23,1+3+5+7=16=24… 按此规律 (1)试猜想:1+3+5+7+…+2005+2007的值 ?(2)推广: 1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢? 2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个( )二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球 个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是 (填图形名称).三、数、式计算规律题 1、已知下列等式:① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102 ;由此规律知,第⑤个等式是 . 2、观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,… 根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____.3、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+ =+⨯=+b a aba b 则符合前面式子的规律,,若…21010 规律发现专题训练1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n )个图案中有白色..地砖 块。
七年级找规律经典题汇总带答案
一、数字排列规律题1、观察下列各算式: 1+3=4=22,1+3+5=9=23,1+3+5+7=16=24… 按此规律 (1)试猜想:1+3+5+7+…+2005+2007的值 ?(2)推广: 1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢? 2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个( )二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球 个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是 (填图形名称). 三、数、式计算规律题 1、已知下列等式:① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102 ; 由此规律知,第⑤个等式是 . 2、观察下面的几个算式:1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,… 根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____. 3、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+规律发现专题训练……1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n )个图案中有白色..地砖 块。
2.我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非。
(完整版)七年级找规律经典题汇总带答案
29、观察下列图形,根据变化规律推测第 100 个与第 个图形位置相同.
- 11 -
(完整版)七年级找规律经典题汇总带答案(word 版可编辑修改)
30、如图,用火柴棒按以下方式搭小鱼,搭 1 条小鱼用 8 根火柴棒,搭 2 条小鱼用 14
4、34 .考虑时,可以从第一个数开始,每 3 个数加一个括号(1,2,3)(,2,3,4)(,3,4,5),…… 一共加了 33 个括号,剩下的一个必是第 100 个。每个括号的第一个数分别是 1,2, 3,……因此第 100 个数必然是 34. 二、 1、602 2、圆 三、1、13 23 33 43 53 152
22、观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆)●□☆●●□☆
●□☆●●□☆●…若第一个图形是圆,则第 2008 个图形是 (填名 称). 23、下列图中有大小不同的菱形,第 1 幅图中有 1 个菱形,第 2 幅图中有 3 个菱形,第 3 幅图中有 5 个菱形,按照图示的规律摆下去,则第 n 幅图中有 个菱形.
a
a
规律发现专题训练
1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个
图案中有黑色地砖 4 块;那么第( n )个图案中有白色地砖
块.
……
2。我国著名数学家华罗庚曾说过:“数形结合百般好,
第3题
隔裂分家万事非。”如图,在一个边长为 1 的正方形纸版
上,依次贴上面积为 1 , 1 ,1 ,…, 1 的矩形彩色纸片(n 为大于 1 的整数)。请你
根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…
七年级数字找规律专题练习
初一数字找规律专题训练题1、已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:第1行 1第2行 -2 3第3行 -4 5 -6第4行 7 -8 9 -10第5行 11 -12 13 -14 15按照上述规律排下去,那么第10行从左边数第5个数等于 .2、观察下列算式:23451=+⨯ ,24462=+⨯,25473=+⨯,24846⨯+=,请你在察规律之后并用你得到的规律填空:250___________=+⨯, 第n 个式子呢? ___________________3、观察下列顺序排列的等式:9×0+1=19×1+2=119×2+3=219×3+4=319×4+5=41……猜想:第n 个等式(n 为正整数)应为 .4、观察下列各式,你会发现什么规律?3×5=15,而15=241-。
5×7=35,而35=261-……11×13=143,而143=2121-将你猜想到的规律用只含一个字母的式子表示出来:_______。
5、问题:你能比较20052006和20062005的大小吗?为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比较n n+1和(n+1)n 的大小(n 为正整数),我们从n=1,n=2,n=3……这些简单的情况入手,从中发现规律,经过归纳,猜出结论。
(1)通过计算,比较下列各组数字大小①12______22 ②23______32 ③ 34________43④45______54 ⑤54______65 ⑥67_________76(2)把第(1)题的结果经过归纳,你能得出什么结论?你能用只含有一个字母的式子表示吗?(3)根据上面的归纳猜想得到的结论,试比较两个数的大小20052006________20062005(填”>”,”<”, “=”)6、(1)3个球队进行单循环赛(参赛的每一个队都与其它所有各队比赛一场),总的比赛场数是多少?4个球队呢?m 个球队呢?(代数式表示出来)(2)当m=12时,总共比赛几场?7、按一定规律排列的一串数:112312345123,,,,,,,,,,,, (133355555777)------中,第98个数是_____________8、某仓库堆放一批圆木,一共20层,第一层3根,每往下一层多1根,问这堆圆木一共有多少根?9、观察下列数据,按某种规律在横线上填上适当的数:1,43-,95,167-,259, ,… 10、某月日历有一竖列四个日期,其中第二个日期与第四个日期的和是36,那么第三个日期是___________11、今年暑假,李老师一家三口人外出旅行一周,这一周各天的日期之和是91,那么李老师是_______号回家的12、如果这个月的5号是星期三,则20号是星期_________13、三个连续偶数中,n 是最小的一个,这三个数的和为_________。
初一数学上册找规律题型及真题练习题(含答案解析)
初一数学上册找规律题型及真题练习题(含答案解析)【找规律题目的类型】★设计类(1)用图形反映规律★数字类(1)与数阵有关的问题(2)等差型数列规律(3)等比型数列规律(4)含平方型数列规律(5)其它数列规律列举(6)循环型数列★计算类(1)根据已知等式探究规律(2)探究算式的计算规律★图形类(1)与视图、展开图有关的问题(2)几何图形变化规律题真题演练一、观察下列各算式:1+3=4=22,1+3+5=9=32,1+3+5+7=16=42按此规律(1)试猜想:1+3+5+7+…+2005+2007的值?(2)推广:1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少?答案:(1)1004的平方(2)n+1的平方二、下面数列后两位应该填上什么数字呢?2 3 5 8 12 17 __ __答案:23 30。
数列中每两个相邻数字间的差分别是1,2,3,4,5,6,7。
三、请填出下面横线上的数字。
1 123 5 8 ____ 21答案:13。
数列后面一个数是前面相邻两个数的和。
四、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么?答案:34 。
考虑时,可以从第一个数开始,每3个数加一个括号(1,2,3),(2,3,4),(3,4,5),……一共加了33个括号,剩下的一个必是第100个。
每个括号的第一个数分别是1,2,3,……因此第100个数必然是34。
五、有一串数字 3 6 10 15 21___ 第6个是什么数?答案:28。
3+3=6 6+4=10 10+5=15 15+6=21 21+7=28, 所以第6个是28。
其实一般这类的规律题无非就是在数的基础上加减乘除,有些麻烦点的就是一个数乘上倍数后在加1或减1。
六、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2005个数是( A )A.1 B.2 C.3 D.4七、100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为___个.答案:33八、观察排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球个答案:602、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是(填图形名称)答案:圆九、观察下面的几个算式:1+2+1=4, 1+2+3+2+1=9,1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1=____.答案:10000。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
找规律专题练习1、你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如下面草图所示。
这样捏合到第次后可拉出64根细面条。
第一次捏合第二次捏合第三次捏合2、如下图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去; (1填表:(2如果剪n 次,共剪出多少个小正方形? (3如果剪了100次,共剪出多少个小正方形? (4观察图形,你还能得出什么规律?3、小明写作业时不慎将墨水滴在数轴上,根据图中的数值,判定墨迹盖住部分的整数的和是 .4、填表并回答下列问题(2当x 非常大时,2100x的值接近于什么数? 5、现有黑色三角形“▲”和“△”共200个,按照一定规律排列如下: ▲ ▲△△▲△▲▲△△▲△▲▲……则黑色三角形有个,白色三角形有个。
6、仔细观察下列图形.当梯形的个数是n 时,图形的周长是 . 27、用火柴棒按如下方式搭三角形:(1 填写下表:(2 照这样的规律搭下去,搭n 个这样的三角形需要______根火柴棒8、把编号为1,2,3,4,…的若干盆花按右图所示摆放,花盆中的花按红、黄、蓝、紫的颜色依次循环排列,则第8行从左边数第6盆花的颜色为___________色. 9、已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:第1行 1第2行 -2 3第3行 -4 5 -6第4行 7 -8 9 -10第5行 11 -12 13 -14 15 … …按照上述规律排下去,那么第10行从左边数第5个数等于 . 10、观察下列算式:23451=+⨯ ,24462=+⨯,25473=+⨯,24846⨯+=,请你在察规律之后并用你得到的规律填空:250___________=+⨯, 第n 个式子呢? ___________________11、一张长方形桌子可坐6人,按下列方式讲桌子拼在一起。
①张桌子拼在一起可坐______人。
3张桌子拼在一起可坐____人,n 张桌子拼在一起可坐______人。
②一家餐厅有40张这样的长方形桌子,按照上图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐______人。
③若在②中,改成每8张桌子拼成1张大桌子,则共可坐_________人。
12、用计算器计算下列各式,并将结果填写在横线上。
① 1×7×15873= ② 2×7×15873= ③ 3×7×15873= ④ 4×7×15873=你发现了什么规律?把你发现的规律用简练的语言写出来; 13、观察下列顺序排列的等式:9×0+1=19×1+2=11 9×2+3=21 9×3+4=31 9×4+5=41 ……猜想:第n 个等式(n 为正整数应为 .14、一个两位数的个位数是a ,十位数字是b ,请用代数式表示这个两位数是__________________。
15、观察下列各式:31=3,32=9,33=27,34=81,35=243,36=729…你能从中发现底数为3的幂的个位数有什么规律吗?根据你发现的规律回答:32004的个位数字是 .16、观察下列各式,你会发现什么规律?3×5=15,而15=241-。
5×7=35,而35=261- ……11×13=143,而143=2121-将你猜想到的规律用只含一个字母的式子表示出来:_______。
17、问题:你能比较20052006和20062005的大小吗?为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比较nn+1和(n+1n 的大小(n 为正整数,我们从n=1,n=2,n=3……这些简单的情况入手,从中发现规律,经过归纳,猜出结论。
(1通过计算,比较下列各组数字大小①12______22 ②23______32 ③ 34________43④45______54 ⑤54______65 ⑥67_________76(2把第(1题的结果经过归纳,你能得出什么结论?你能用只含有一个字母的式子表示吗?(3根据上面的归纳猜想得到的结论,试比较两个数的大小(1分20052006________20062005(填”>”,”<”, “=”18、为了美化城市,某商场在门前的空地上用花盆按如图所示的方式搭正方形, (1 填写下表(2 按这个规律搭下去,搭第n 层正方形,需要________________盆花? 19、下面有三组数,请你填上合适的运算符号,使每一组数的结果都为10。
(1 1 5 59 =10; (2 3 3 3 3 =10 ; (3 1 1 9 9 =10 20、小红和小花在玩一种计算的游戏,计算的规则是dcb a =ad -bc 。
现在轮到小红计算4321 的值,请你帮忙算一算得多少?21、黑蚂蚁和红蚂蚁都认为自己跑得比对方快,刚好它们看到地上的几个半圆(图1,于是它们决定比一比。
黑蚂蚁沿着大半圆从甲处跑到乙处;红蚂蚁沿着两个小半圆也从甲处跑到乙处。
两只蚂蚁同时起跑,说也奇怪,两只蚂蚁同时到达了乙处。
(1 两只蚂蚁请你帮助判断:谁跑得快?(2两只蚂蚁对你的判断结果很不满意,决定再到(图2的几个半圆处再比赛一次,请你猜一猜,哪一只蚂蚁先从甲处跑到乙处?22.(13个球队进行单循环赛(参赛的每一个队都与其它所有各队比赛一场,总的比赛场数是多少?4个球队呢?m 个球队呢?(代数式表示出来(2当m=12时,总共比赛几场? 23.按一定规律排列的一串数:112312345123,,,,,,,,,,,, (133355555777------中,第98个数是_____________14.下面的算式里,符号○、△、和□分别代表三个不同的自然数,这三个数的和是________24.一群整数朋友按照一定的规律排成一排,可排在□位置的数跑掉了,请帮它们把跑掉的朋友找回来。
(15,8,11,14,□,20; (21,3,7,15,31,63,□; (31,1,2,3,5,8,□,21 25.下列两列数:2,4,6,8,10,12,……1994;6,13,20,27,34, (1994这两列数中,相同的数的个数是( A 、142 B 、143 C 、284 D 、28526.一串数字的排列规律是:第一个数是20,从第二个数起,每一个数比前一个数小8△ □○ 1111181=+++(1第10个数是多少?(2第n 个数是多少?(3第几个数是—6027.某仓库堆放一批圆木,一共20层,第一层3根,每往下一层多1根,问这堆圆木一共有多少根?28(1 从左下角到右上角的三个数字之和为45,那么这9个数的和是多少?这9个日期中最后一天是1月几日?(2 用这样的方框能否圈出总和为162的9个数?29.观察下列数据,按某种规律在横线上填上适当的数:1,43-,95,167-,259, , (30.如图,△ABC 中,D 是边BC上的中点, F 是线段CD 的中点,E 是边AC 的中点,则图中有_______条线段,有________个角,若△DEF 的面积是2,则△ABC 的面积是________31.平面内两两相交的6条直线,其交点个数最少为m 个,最多为n 个,则m+n 等于(A 、12B 、16C 、20D 、以上都不对32.如图,可以看成是边长为4的小正方形的巧克力糖,请你用尽可能多的不同方法把它分成形状、大小完全相同的四块,要求不把正方形糖块划破(至少五种方法33.在某月日历上一个竖列相邻的五个数之和为80,这五个数是______________________34.某月日历有一竖列四个日期,其中第二个日期与第四个日期的和是36,那么第三个日期是___________35.今年暑假,李老师一家三口人外出旅行一周,这一周各天的日期之和是91,那么李老师是_________号回家的36.如果这个月的5号是星期三,则20号是星期_________37.三个连续偶数中,n 是最小的一个,这三个数的和为_________。
38.下列图形中三角形的个数是(A.4个B.6个C. 9个D.10个 39、至少找出下列几何体的4个共同点A EFDB40、观察公式:公式1:3223333(a xa a x x a x +++=+公式2:4322344464(a xa a x a x x a x ++++=+ (1 这两个公式有什么特点? (2 利用公式计算: 21(21(2421(2621(24232234-+-⨯⨯+-⨯⨯+-⨯⨯+41、下面有三组数,请你填上合适的运算符号,使每一组数的结果都为10。
(1 1 5 5 9 =10 ; (2 3 3 3 3 =10 ; (3 1 1 9 9 =10 42.造一个含有字母p 和q 的代数式,使得不论p 、q 取何值,代数式的值永远不是正的。
43.图是2002年6月份的日历,现用一矩形在日历中任意框出4个数 a b ,请用一个等式表示,a 、b 、c 、d 之间的关系__________。
c d44.右图,是用火柴棒摆成的一个大三角形,它是由九个小三角形组成的,试将1、2、3、4、5、6、7、8、9分别填入这9个小三角形哪(每个小三角形内只填一个数,要求靠近大三角形每条边的每五个数相加的和相等,请想一想,怎样填45.王答应了大臣的一个要求:即在国际象棋棋盘上“第1格放一粒米,第二格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒……一直到64格”。
但是不久国王九发现国库里没有这么多米,然而国王的话不能不算数,国王又不好意思向别人借,怎么办呢?请你帮国王想一个好办法来解决这个问题。
(办法必须合乎情理,有创意者可适当多加分。
办法多者亦可多加分46. 如果连结多边形的一边上一点与其余各顶点可将某多边形分割成2004个三角形,求该多边形的边数.47. 如图1-26,在∆ABC 中,点D,E,F 分别是AB,BC,AC 三边中点,图中与∆BOD 面积相等的三角形有几个?E BC48. 观察图1-27中有几个三角形?由此你发现三角形的个数有什么规律呢?一个三角形 3个三角形 ______个三角形 ______个三角形_________个三角形(n 个点 49. 求个数① (1 将下表填写完整. 图形符号三角形个数 1 1 ②图 1-29 ③ 2 5 3 9 4 5 …….. …….. (1 (2 (2 在第 n 个图形中有几个三角形?(用含 n 的代数式表示 51、如图,哪些图形经过折叠可以围成一个长方体?(1)( 2)(3)(4) (1图 1-28(1中有多少个三角形? (2图 1-28(2中有多少个四边形? 50. 如图 1-29 所示,图①是一个三角形,分别连结这个三角形三边的中点(将这条边分为相等的两部分的点得到图②; 再分别连结图②中间的小三角形三边的中点,得到图③,按此方法继续下去,请你根据图中三角形个数的规律,完成下列问题(5)(6) 52、下列图形经过折叠能否围成一个正方体?A.1.5 小时 B.2 小时 D.4 小时 58、计算:1-2+3-4+ (2001)2002+2003= .。
