第二章 杆件的内力·截面法讲解
第二章 杆件的内力.截面法(第1、2、3节)
外 无外力段
力
q=0
均布载荷段
q>0
q<0
集中力
P C
集中力偶
m
C
水平直线
斜直线
自左向右突变 无变化
FS 图
FS
特
征
x
FS >0
FS
FS
x
x
FS <0 增函数
FS
FS FS1
C
x
FS2
x
降函数 FS1–FS2=P
FS
C x
M
斜直线
曲线
自左向右折角 自左向右突变
图M
M
M
M
M
与 M M1
特
x
x
x
x
xm
x
求:外力偶矩Me ( N·m)
解:PMe
n 30
P1000Me3n0
由此求得外力偶矩:
Me
Me
P103 00 P
M e
n
954 (N .9 m) n
若传递功率单位为马力(PS)时, 由于PS=735.5N·m/s
Me
702P4(N.m) n
杆件的内力.截面法
对称弯曲:工程中最常见的梁,其横截面一般至少有一根对称 轴,因而整个杆件有一个包含轴线的纵向对称面。 若所有外力都作用在该纵向对称面内时,梁弯曲变 形后的轴线将是位于该平面内的一条曲线,这种弯 曲形式称为对称弯曲。
注意 1、用截面法求轴力时,在切开的截面上建议假设正 的轴力,由平衡方程得出的FN值为正,说明轴力为正 (拉力); FN值为负,说明轴力为负(压力)。
2、在画轴力图时,填充为下画线或无填充,不要画剖 面线形式;并注上 符号 或 。
第二章内力与内力图详解

例:如左图,求n-n面的内力。 左半部分
Fx 0
FN FP
右半部分:
Fx 0 FN FP
左右两部分的力方向相反,但是同一内力, 因此规定内力由变形确定正负号,是标量。
§2-1 横截面上内力与内力分量
P2
P1
m
P4
P1
P2
m
P3 P2
P3
m P5
(a)
P1
y FR
m
M
C x
zm
(c)
P3
m
(b)
第二章 内力与内力图
§2-1 横截面上内力与内力分量 §2-2 轴向拉压杆的内力与内力图 §2-3 扭转圆轴的内力与内力图 §2-4 平面弯曲梁的内力与内力图 §2-5 平面刚架和曲杆的内力图
横截面上内力计算--截面法
截面法求内力步骤
❖ 将杆件在欲求内力的截面处假想的截断,取其中任一部分; ❖ 画出其受力图。所有外力,并在断面上画出相应内力; ❖ 由静平衡条件确定内力大小。
传动轴的扭矩图。
解:1)计算外力偶
MA
9549
PA n
9549 36 300
1146N.m
M B MC 350N.m;M D 446N.m
2)由外力偶分段,用截面法分别求每段
轴的扭矩即为1-,由
Mx 0
M B M x1 0 M x1 350N.m
B
C
A
350
700
446 x
D
扭矩图例2
10kN 30kN.m 20kN.m
A
2m B
10kN.m
D C
M x (kN.m)
10
A
B
20
C
02截面法求内力基本方法
0 -33 34.8
19
19
Y 0 YNAD 11 kN YNAD CD 0.5 X NAD AC 1.5 X NAD 3YNAD 33 kN
X 0 FNAC 33 kN
0 -33
-33
34.8 -8
19
19
0 -33
-33
34.8
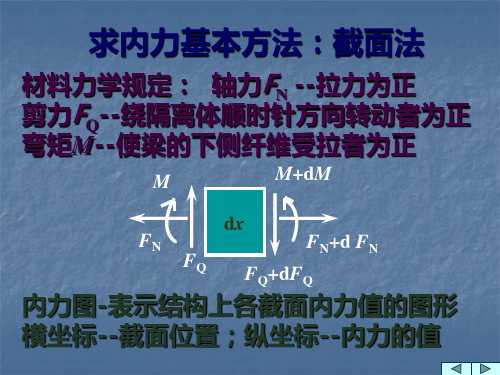
dM dx
FQ ,
dFQ q( x), dx
dFN p( x) dx
Mq
M+dM
dx
FN
dx
FN+d FN
FQ
FQ+dFQ
dM dx
FQ ,
dFQ q( x), dx
dFN p( x) dx
集中力
梁上 无外力 均布力作用 集中力作用 偶M作 铰处
情况
(q向下)
处(FP向下) 用处
斜直 剪力图 水平线 线(
)
为 零 处
有突 变(突 变值=
FP)
如 变 号
无 无变化 影
响
一般 抛物 有 有尖 有 有突变
弯矩图 为斜 线(
极 角(向 极 (突变 为零
直线 下凸) 值 下) 值 值=M)
曲杆微分关系
曲杆微段
dFN ds
=-qt+
FQ R
dFQ ds
=qn-
FN R
dM ds
=FQ-m
求内力基本方法:截面法
材料力学规定: 轴力FN --拉力为正 剪力FQ--绕隔离体顺时针方向转动者为正
弯矩M--使梁的下侧纤维受拉者为正
M
M+dM
试述求杆件横截面上内力的截面法步骤和方法

试述求杆件横截面上内力的截面法步骤和方法1. 了解截面法哎,说到工程力学里的截面法,别让这些名字吓坏了,其实就是一种找出杆件内部力量的简单方法。
咱们平常接触的建筑物、桥梁,或者一些机械构件,都是通过这种方法来确保它们的稳固和安全的。
这个方法简单来说就是用“剪刀”切一刀,把杆件“分尸”,然后分析切面上受力的情况。
好比是咱们剥苹果皮,剥开之后看里面的果肉,这样能更清楚地了解苹果的质量。
2. 截面法的步骤2.1 选取截面首先,挑选一个合适的截面,瞅准了方向之后,就下手了。
这个步骤就像在你脑子里画出一条切割线。
你得选择一个合适的位置,把杆件从中间“切开”。
这里要注意,选取的位置一定要使得切面上的力易于计算。
如果这个位置选错了,结果就像你在黑暗中找钥匙一样,费劲不讨好。
2.2 画出受力图接下来,别忘了给这片“切面”画上图。
要把杆件切开后,分离出的部分的受力情况画出来。
图上得标明各种内力,比如剪力、轴力和弯矩等等。
这些力就像是在打游戏时,你需要记录你的角色的状态和装备一样,你要准确记录这些力的情况,这样才能确保你计算的准确。
2.3 列出平衡方程然后,你就要写平衡方程了。
平衡方程是用来保证杆件在切开时的受力状态是平衡的,不会乱七八糟。
这些方程包括了力的平衡、力矩的平衡等。
就像你玩积木,如果要保持积木塔不倒,就得仔细计算每一块积木的放置位置。
2.4 解方程找内力最后,你要解这些方程,找出杆件内部的力量。
就像做数学题一样,把方程算出来,你就能得到具体的内力数值。
这个步骤可不能马虎,不然得到的结果就像是空话,没有实际意义。
3. 截面法的应用3.1 结构分析截面法在结构分析中的应用非常广泛。
无论是大桥、小楼,还是家里的门框,都是用这个方法来确保结构的安全性。
就像是大厨做菜,得先知道每种材料的用量和比例,才能做出美味的菜肴。
工程师用截面法就像是这个大厨,通过计算内力,确保建筑的稳定性和安全性。
3.2 机械设计在机械设计中,截面法也是必不可少的。
试述求杆件横截面上内力的截面法步骤和方法

试述求杆件横截面上内力的截面法步骤和方法哎呀,这可是个不简单的问题啊!不过别着急,我这个“知识小百科”可是见过世面的,一定能帮你解决。
今天我们就来聊聊:试述求杆件横截面上内力的截面法步骤和方法。
我们要知道杆件横截面上的内力是什么。
简单来说,就是杆件在受力时,由于各个部位的材料不同,所以产生的应力也不一样。
这些应力就会在杆件内部形成一种力量,我们称之为内力。
而求解这种内力的过程,就叫做截面法。
那么,截面法有哪些步骤呢?其实很简单,可以分为以下几步:
第一步:确定截面形状和尺寸。
这是非常重要的一步,因为不同的截面形状和尺寸会影响到内力的分布情况。
所以我们需要根据实际情况来选择合适的截面形状和尺寸。
第二步:建立坐标系。
这个步骤的目的是为了方便我们进行计算。
我们可以将杆件看作一个长方体,然后在这个长方体上建立一个坐标系,用来表示各个部位的位置和方向。
第三步:确定材料的性质和截面几何参数。
这一步也是非常关键的,因为不同的材料有着不同的弹性模量、泊松比等性质参数,而这些参数又会影响到内力的计算结果。
第四步:应用胡克定律和其他力学公式进行计算。
这一步需要我们掌握一定的力学知识和技巧,才能够正确地求解出内力的大小和方向。
好了,以上就是求解杆件横截面上内力的截面法步骤和方法了。
看起来有点复杂吧?但是只要认真学习,相信你也能轻松掌握哦!
希望我的回答对你有所帮助!如果你还有其他问题或者疑问,欢迎随时提出哦!。
截面法是求杆件内力的基本方法

一、概述截面法是工程力学中用于求解杆件内力的基本方法之一。
在工程结构分析和设计中,了解截面法的原理和应用是至关重要的。
本文将深入探讨截面法的基本概念、原理和应用,以帮助读者更好地理解和应用这一方法。
二、截面法的基本概念1.1 概念简介截面法是工程力学中用于分析杆件内力的一种方法,它基于杆件内力平衡的原理,通过考察杆件的截面上的内力分布情况来求解杆件的内力。
1.2 截面法的基本原理截面法基于力的平衡原理,即在杆件的截面上,杆件的内力必须满足横向平衡和转矩平衡的条件。
通过分析截面上的内力分布情况,可以确定杆件内的弯矩、剪力和轴力。
1.3 截面法的应用范围截面法适用于各种杆件的内力分析,包括梁、柱、桁架等结构中的杆件。
在工程实践中,截面法常常用于分析结构内部的受力情况,为结构设计和分析提供重要依据。
三、截面法的具体步骤2.1 确定截面在应用截面法时,首先需要确定分析的截面位置。
通常情况下,选择距离受力部位较近的位置作为截面。
2.2 绘制内力图在截面上绘制出杆件内的剪力图和弯矩图,根据平衡条件和力学原理,确定内力的方向和大小。
2.3 计算内力根据绘制的剪力图和弯矩图,可以直接求解出截面上的剪力、弯矩和轴力大小。
这些内力是杆件在该截面上的受力情况的表示。
2.4 检验平衡通过检验内力图的平衡条件,验证所得的内力是否符合力学平衡定律。
如果内力满足平衡条件,则认为截面法计算是正确的。
四、截面法的应用举例3.1 梁的截面力分析以简支梁为例,说明如何利用截面法分析梁的内力情况。
根据距离支座较近的位置选择截面,绘制剪力图和弯矩图,并计算出截面上的内力情况。
3.2 柱的截面力分析以等截面柱为例,说明如何利用截面法分析柱的内力情况。
通过选择适当位置的截面,绘制出内力图,计算出截面上的轴力和弯矩。
五、截面法的优缺点4.1 优点截面法简单直观,易于理解和应用。
通过截面法可以直接得到截面上的内力分布情况,为结构的受力分析提供了重要依据。
内力分析的基本方法-截面法

8kN 4kN E
4kN D C 4kN
C 4m n 1
A
D 4kN
N4
N1 N2 N3 N4
由结点E可知: N2 = -N3
取m-m截面以上为对象 由∑x= 0 得
解:取n-n截面以上为对象 ∑MD= 0 N1 ×6+8×3+4×4 = 0 得: N1 = -6.67 kN
N2=-6.67 kN
所以:
2、突变:在集中力作用处,剪力图有突变,弯矩图 有一尖角;在集中力偶作用处,弯矩图有突变,剪力 图无变化。 3、端值情况
详见教材p98表3-1
18
规律作图方法:
1、水平线图:段内任取截面求内力(一般取段端截面) 2、斜直线图:段内任取两截面求内力(一般取段两端 截面)
3、抛物线图:段内取两端截面及中间截面求弯矩
RA
RB 1、计算支座反力
得: QD= qL/2 Σmc= 0 MD–RA×L+qL×L/2 = 0 得: MD= qL2 取E--E截面右段为对象
ME
E
解得:RA=3qL/2 (竖直向上) RB=qL/2 (竖直向上)
2、取D--D截面左段为对象, 画出受力图 q D
MD
qL2
QE E
RA
D
ΣΎ= 0 Σmc= 0
2.5
=-2kNm(上拉) 静定平面刚架内力计算
一、刚架定义 刚架是由梁、柱等直杆组成的具有刚结点的结构, 其中全部或部分结点为刚结点。如图所示 D P C PC D
A
二、刚架的特点
B
A
B
1、结构内部空间较大,便于利用。 2、刚架的内力、变形峰值比用铰结点连接时小。
3、刚结点能传递力和力矩;而铰结点则只能传递力。
试述求杆件横截面上内力的截面法步骤和方法

试述求杆件横截面上内力的截面法步骤和方法哎呀,这可是个不小的题目啊!不过别着急,咱们一步一步来,就像吃冰激凌一样,先从最上面的一层开始。
咱们要明确一个概念:杆件横截面上内力的截面法步骤和方法。
简单来说,就是要知道在杆件的横截面上,有哪些力在作用,这些力是怎么分布的,以及如何计算这些力的合力。
好了,现在我们开始吧!1.1 第一步:确定杆件的形状和尺寸咱们要了解杆件的形状和尺寸。
这个就像是在点餐的时候,告诉服务员你要吃什么,多大份儿。
只有知道了这些信息,才能知道接下来要做什么。
所以呢,首先要搞清楚杆件是什么样子的,比如说是一个圆柱形还是一个方形,长度是多少,直径是多少等等。
1.2 第二步:分析杆件上的受力情况接下来,咱们要分析杆件上的受力情况。
这个就像是在吃饭的时候,要知道你吃了什么,哪些部位受到了压力,哪些部位受到了拉力等等。
只有知道了这些信息,才能知道接下来要怎么做。
所以呢,要仔细观察杆件上的各个部位,看看有哪些力在作用,比如说重力、支持力、摩擦力等等。
1.3 第三步:建立坐标系和截面图现在,咱们要建立一个坐标系和截面图。
这个就像是在看电影的时候,要把镜头定在一个合适的位置,方便观察。
只有建立了坐标系和截面图,才能更好地进行下一步的计算。
所以呢,要根据杆件的形状和尺寸,选择一个合适的坐标系和截面图。
2.1 第四步:求解内部各点的应力和位移有了坐标系和截面图之后,咱们就可以求解内部各点的应力和位移了。
这个就像是在做作业的时候,要把题目读懂了,才能找到正确的答案。
所以呢,要根据受力情况和材料性质,运用力学公式进行计算。
2.2 第五步:合成内部各点的合力和等效应力求解了内部各点的应力和位移之后,咱们就可以合成内部各点的合力和等效应力了。
这个就像是在玩游戏的时候,要把各个角色的力量加起来,才能打败敌人。
所以呢,要根据受力情况和材料性质,运用力学公式进行计算。
3.1 第六步:检查结果的合理性咱们要检查一下结果的合理性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
FN (+)FN
F
F
FN (-)FN
F
轴力图: 轴力沿轴线变化的图形
F
F
FN
轴力图的意义
+ x
① 直观反映轴力与截面位置变化关系; ② 确定出最大轴力的数值及其所在位置,即确定危险截面位置,为 强度计算提供依据。
例 图示杆的A、B、C、D点分别作用着大小为FA = 5 F、 FB = 8 F、 FC = 4 F、 FD= F 的力,方向如图,试求各段内力并画出杆 的轴力图。
应变
一、正应变(线应变)定义
av
Du Ds
棱边 ka 的平均正应变
lim
Du k点沿棱边 ka 方向的正应变
Ds0 Ds
正应变特点
1、 正应变是无量纲量 2、 过同一点不同方位的正应变一般不同
二、切应变定义 微体相邻棱边所夹直角的
改变量 g ,称为切应变
切应变量纲与单位
切应变为无量纲量 切应变单位为 弧度(rad)
BC
D
FN 2 FB FC FD 0
FB
FC
FD
FN2= –3F,
求BC段内力:
FN3
C
D
Fx 0 FN3 FC FD 0 FN3= 5F,
FC
FD
FN4
D
求CD段内力:
Fx 0 FN 4 FD 0
FN4= F
FD
FN1 2F, FN2= –3F, FN3= 5F, FN4= F
M
M
取左段为研究对象:
M 0, T M 0 M x
Tx
T M
取右段为研究对象:
M
x
M 0, M T 0 T x
T M
内力偶矩——扭矩 T
2、扭矩的符号规定:按右手螺旋法则判断。
右手的四指代表扭矩的旋转方向,大拇指代表其矢量方向,若 其矢量方向与截面的外法线方向相同,则扭矩规定为正值,反之为 负值。
宝剑锋从磨砺出
梅花香自苦寒来
第二章 杆件的内力·截面法
主要内容
1
基本概念-内力、截面法、应力、位移、变形与应变
2 轴向拉伸、压缩、扭转与弯曲的概念 3 剪力方程与弯矩方程-剪力图与弯矩图 4 载荷集度、剪力与弯矩之间的关系 5 平面刚架与平面曲杆的弯曲内力 6 杆件内力的普遍情况
1 基本概念-内力、截面法、应力、位移、变形与应变
内力和截面法
1 、内力的定义:在外力作用下,构件内部各部分之间因相对位置的
改变而引起的附加的相互作用力——附加内力。
2 、内力的特点:
①连续分布于截面上各处 ②随外力的变化而变化
3 、截面法:用以显示和求解内力的方法,其步骤为:
①截开:在待求内力的截面处假想地将构件截为两部分, 取其中一部分为研究对象—脱离体
②代替:用内力代替弃去部分对脱离体的作用—通常为 分布内力系
③平衡: 对脱离体列出平衡方程
应力
FN
FN 比较a、b图杆两杆
m
m
m
m
两杆的材料、长度均相同
(a)
(b)
所受的内力相同,为 FN
显然粗杆更为安全。
FF
F
应力的概念:
F
构杆的强度与内力在截面上的分 布和在某点处的聚集程度有关
① 应力定义: 截面上内力系在某一点处的聚集程度
2 轴向拉伸、压缩、扭转与弯曲的概念
轴向拉伸、压缩
一、轴向拉压的工程实例:
工程桁架
活塞杆
厂房的立柱 F
F
二、轴向拉压的概念:
(1)受力特点:外力合力作用线与杆轴线重合 (2)变形特点:杆沿轴线方向伸长或缩短
FN1
B
A
C
F
FN2
FN1 FN2
以轴向拉压为主要变形的杆件,称为拉压杆或轴向承载杆。
是反映一点处内力的强弱程度的基本量
F1
ΔFTy
⊿A面积上的内力合力 DF
DF DFN DFT
DFN⊥截面 DFT∥截面
DF
ΔFN
ΔFTz ΔA
F2
全应力
DF p lim
DA0 DA
正应力—垂直于截面的应力分量
全应力及应力分量
lim DFN dFN
DA0 DA dA
OA
BC
D
FA
FB
FC
FD
FN1 A
BC
D
FA
FB
FC
FD
解: 求OA段内力FN1:设截面如图
Fx 0 FD FC FB FA FN1 0
F 4F 8F 5F FN1 0
FN1 2F
OA
BC
D
FA
FB
FC
FD
求AB 段内力:
Fx 0
FN2
剪应力—切于截面的应力分量
lim DFT dFT
DA0 DA dA
应力的三要素: 截面、点、方向
受力物体内各截面上每点的应力,一般是不相同的,它随 着截面和截面上每点的位置而改变。 因此,在说明应力性质和数值时必须要说明它所在的位置。
应力的单位:
应力是一向量,其量纲是[力]/[长度]²。
例:已知外力 F,求:1-1截面的内力FN 。
代替,FN 代替。
③平衡, F
∑FX=0, FN - F = 0,
FN = F 以1-1截面的右段为研究对象:
FN
内力 FN 沿轴线方向,所以称为轴力。
F FN
F
轴力的符号规定:
拉伸—拉力,其轴力为正值。方向背离所在截面。 压缩—压力,其轴力为负值。方向指向所在截面。
FN1 2F, FN2= –3F, FN3= 5F, FN4= F
轴力图如下图示
OA FA
FN 2F
BC
D
FB
FC
FD
5F F x
3F
一、扭转的工程实例
扭转
1、螺丝刀杆工作时受扭。
阻抗力偶
Me
主动力偶
汽车方向盘的转动轴工作时受扭
机器中的传动轴工作时受扭
二、扭转的概念
受力特点:杆两端作用着大小相等、方向相反的力偶,且力 偶作用面垂直于杆的轴线。
+
T
-
3、内力图(扭矩图)表示构件各横截面扭矩沿轴线变化的图形。
扭矩图作法:同轴力图:
变形特点:杆任意两截面绕轴线发生相对转动。
Me
mA
主动力偶
阻抗力偶
me
主要发生扭转变形的杆——轴
圆轴受扭时其横截面上的内力偶矩称为扭矩,用符号T 表示。
扭矩大小可利用截面法来确定。
Me
1
Me
A Me
A
1 1
T
1 1
T
1
B
x
T Me
Me
B
扭转杆件的内力——扭矩及扭矩图
1、扭转杆件的内力(截面法)
应力的国际单位为牛顿/米²,称为帕斯卡,简称帕(Pa).
1Pa=1N/m2
1MPa=106Pa=1N/mm2
1GPa=109Pa
变形和位移
变形—构件受外力图作1.用3 后要发生形状和尺寸的改变 位移—变形后构件上的点、线、面发生的位置改变 变形和位移的关系—产生位移的原因是构件的变形, 构件变形
的结果引起构件上点、线、面的位移
