自动搜索平衡车的两种数学模型
平衡小车
平衡小车前言两轮自平衡小车是集成机械、电子、通信、自动化、嵌入式等技术于一体的小型智能机器人，涉及到传感器的驱动，数据的处理，角度的计算，电机的控制等，内容比较丰富。
原理篇一．任务分解假设维持车模直立、运行的动力都来自于车模的两个车轮。
车轮转动由两个直流电机驱动。
因此从控制角度来看，车模作为一个控制对象，它的控制输入量是两个电极的转动速度。
车模运动控制任务可以分解成以下三个基本控制任务：（1）控制车模平衡：通过控制两个电机正反向运动保持车模直立平衡状态；（2）控制车模速度：通过调节车模的倾角来实现车模速度控制，实际上最后还是演变成通过控制电机的转速来实现车轮速度的控制。
（3）控制车模方向：通过控制两个电机之间的转动差速实现车模转向控制。
车模直立和方向控制任务都是直接通过控制车模两个后轮驱动电机完成的。
假设车模电机可以虚拟地拆解成两个不同功能的驱动电机，它们同轴相连，分别控制车模的直立平衡、左右方向。
在实际控制中，是将控制车模直立和方向的控制信号叠加在一起加载电机上，只要电机处于线性状态就可以同时完成上面两个任务。
车模的速度是通过调节车模倾角来完成的。
车模不同的倾角会引起车模的加减速，从而达到对于速度的控制。
三个分解后的任务各自独立进行控制。
由于最终都是对同一个控制对象（车模的电机）进行控制，所以它们之间存在着耦合。
为了方便分析，在分析其中之一时假设其它控制对象都已经达到稳定。
比如在速度控制时，需要车模已经能够保持直立控制；在方向控制的时候，需要车模能够保持平衡和速度恒定；同样，在车模平衡控制时，也需要速度和方向控制也已经达到平稳。
这三个任务中保持车模平衡是关键。
由于车模同时受到三种控制的影响，从车模平衡控制的角度来看，其它两个控制就成为它的干扰。
因此对车模速度、方向的控制应该保持平滑，以减少对于平衡控制的干扰。
以速度调节为例，需要通过改变车模平衡控制中车模倾角设定值，从而改变车模实际倾斜角度。
为了避免影响车模平衡控制，这个车模倾角的改变需要非常缓慢的进行。
车辆的运动学模型和动力学模型
车辆的运动学模型和动⼒学模型系统建模是系统控制的前提和基础，对于⽆⼈车的横向控制（控制车辆转向，使其沿期望路径⾏驶），通过对车辆模型进⾏合理的简化和解耦，建⽴合适的车辆模型，对实现⽆⼈车的路径跟踪⾄关重要。
所谓车辆模型，即描述车辆运动状态的模型，⼀般可分为两类：运动学车辆模型；动⼒学车辆模型。
研究表明，在低速时，车辆的运动学特性较为突出；⽽在⾼速时，车辆的动⼒学特性对⾃⾝的运动状态影响较⼤。
1、运动学车辆模型车辆运动学模型如下图所⽰。
车辆运动学模型这⾥假定车辆是⼀个刚体，根据上图所⽰的⼏何关系，可以得到下⾯的车辆运动学数学模型。
运动学模型的数学公式其中，x0 和 y0 表⽰车辆质⼼的位置，v 为质⼼的纵向速度，r 为车辆的横摆⾓速度，Ψ为车辆的航向⾓，β为车辆的质⼼侧偏⾓。
在低速情况下，车辆在垂直⽅向的运动通常可以忽略，也即车辆的质⼼侧偏⾓为零，车辆的结构就像⾃⾏车⼀样，因此上述模型可以简化⼀个⾃⾏车模型，如下图所⽰：⾃⾏车模型整个模型的控制量可以简化为 v 和δ，即纵向车速和前轮偏⾓。
通常车辆的转向控制量为⽅向盘⾓度，因此需要根据转向传动⽐，将前轮偏⾓转化为⽅向盘⾓度。
上述的⾃⾏车车辆模型适⽤范围⾮常⼴，可以解决⼤部分问题。
但当车辆⾼速⾏驶时，使⽤简单的⼆⾃由度车辆模型通常⽆法满⾜横向控制的精确性和稳定性，这时就需要⽤到车辆的动⼒学模型。
2、动⼒学车辆模型汽车实际的动⼒学特性⾮常复杂，为精确描述车辆的运⾏状态，相关研究学者提出了多种多⾃由度的动⼒学模型。
不过，复杂的车辆动⼒学模型虽然较好的反映车辆的实际运动状态，但并不适⽤于⽆⼈车的横向控制。
其中，单轨模型是⼀个应⽤⽐较多的动⼒学车辆模型。
单轨模型是在忽略了空⽓动⼒学、车辆悬架系统、转向系统等的基础上，将前后轮分别⽤⼀个等效的前轮和后轮来代替，从⽽得到的车辆模型。
单轨模型的具体受⼒分析如下图所⽰。
单轨模型上图中的车⾝坐标系oxy，是以车辆质⼼为坐标原点，以沿车⾝向前的⽅向为x的正⽅向，以垂直于横轴的向左的⽅向为y的正⽅向。
自动跟随平衡小车的设计
自动跟随平衡小车的设计1 绪论1.1 研究背景与意义1.1.1 研究背景当今时代是产业智能化的时代，新兴的信息技术正在快速应用于各行各业，现代科学技术已经成为了产业变革最主要的推动力。
根据《中国制造2025》计划所述，我国将加大力度对智能自动化工程、智能交互机器人、智能交通管理、智能电器、智能家居控制等产业进行引领和推动。
此外，还应根据消费需求的动态感知，从研发、制造和产业组织模式等方面开发一系列新的制造模式。
2018年12月底，全国工业和信息化部部署2019年工作，其涉及智能制造、信息消费、5G等领域。
智能制造业的兴起和引起人们的重视，得益于人工智能的研究和发展，其可以理解为人工智能系统的前沿技术。
人机一体化智能系统是智能化技术早期的应用探索之一，正在逐步发展成为一种混合智能技术。
人机一体化智能系统的智能化应用主要体现在智能机械上，而对于人们的日常生活来说，智能化在在智能机器人的应用上体现得最为明显。
在工业生产上，很多领域通过智能化装置的应用，实现了手动控制与自动控制的结合，节省了人力，降低了物料损耗，提升了生产效率和经济性。
随着智能化在不同产业的生成过程中应用愈发广泛，其承担的作用也越来越重要。
1.1.2 研究意义1.推进双轮自平衡车的智能化研究自动跟随技术已经经历了很长时间的发展。
早在很多年以前，国内外的研究人员就开始了对自动跟随技术具体应用的探索，设计出了自主跟随四轮小车，自主跟随无人机等作品。
由于那个时期的自平衡车的相关技术还不成熟，导致很少有自动跟随技术在平衡车上应用。
在性质上，双轮自平衡车从属于智能机器人的发展范畴，在移动载具方面，它有所占空间小、驾驶灵活、容易停车且便于携带等特点，非常适合短距离的代步和应用于娱乐活动。
但由于自平衡车在交通复杂的环境下，其安全性能并不稳定，并且对驾驶者的安全防护措施比较欠缺，导致自平衡车的交通事故发生频繁，事故损伤普遍偏重，致使现阶段很多城市都出台法令限制平衡车通行；另一方面，在平衡车跟随功能方面，小米正在成为先驱者，虽然小米平衡车的性能和适用范围还有很多不足之处，但自动跟随相关研究方向的正确性已被证明，这也将成为未来服务型机器人种类中特殊的一面。
平衡车平衡原理 Arduino
（2）小车速度控制：使用PD（比例、微分）控制；
Outputs = ksi * (setp0 - positions) + ksp * (setp0 speeds_filter); //速度环控制 PI
（3）小车方向控制：使用PD（比例、微分）控制。
turnoutput = -turnout * ktp - Gyro_z * ktd;//旋转PD算法 控制 融合速度和Z轴旋转定位。
输出中，这样就会彻底消除速度控制误差。第二点，由于加入了速度 控制， 它可以补偿陀螺仪和重力加速度的漂移和误差。 所以此时重力 加速度传感器实际上没有必要了。 此时小车在控制启动的时候，需要保持小车的垂直状态。此时 陀螺仪的积分角度也初始化为0。当然如果电路中已经包括了重力加 速度传感器，也可以保留这部分，从而提高小车的稳定性。在后面的 最终给定的控制方案中，保留了这部分的控制回路。
图4 第二个问题可以通过角度控制给定值来解决。 给定小车直立控制 的设定值，在角度控制调节下，小车将会自动维持在一个角度。通过 前面小车直立控制算法可以知道，小车倾角最终是跟踪重力加速度Z 轴的角度。因此小车的倾角给定值与重力加速度Z轴角度相减，便可 以最终决定小车的倾角 第三个问题分析起来相对比较困难， 远比直观进行速度负反馈分 析复杂。首先对一个简单例子进行分析。假设小车开始保持静止，然 后增加给定速度， 为此需要小车往前倾斜以便获得加速度。 在小车直 立控制下，为了能够有一个往前的倾斜角度，车轮需要往后运动，这 样会引起车轮速度下降（因为车轮往负方向运动了）。由于负反馈， 使得小车往前倾角需要更大。如此循环，小车很快就会倾倒。原本利 用负反馈进行速度控制反而成了“正”反馈。 为什么负反馈控制在这儿失灵了呢？原来在直立控制下的小车
不同姿态解算在平衡车中的实现与应用
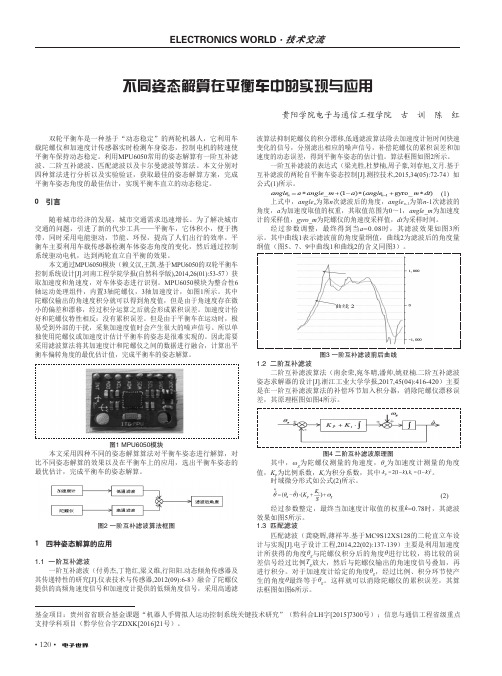
• 120•不同姿态解算在平衡车中的实现与应用贵阳学院电子与通信工程学院 古 训 陈 红双轮平衡车是一种基于“动态稳定”的两轮机器人，它利用车载陀螺仪和加速度计传感器实时检测车身姿态，控制电机的转速使平衡车保持动态稳定。
利用MPU6050常用的姿态解算有一阶互补滤波、二阶互补滤波、匹配滤波以及卡尔曼滤波等算法。
本文分别对四种算法进行分析以及实验验证，获取最佳的姿态解算方案，完成平衡车姿态角度的最佳估计，实现平衡车直立的动态稳定。
0 引言随着城市经济的发展，城市交通需求迅速增长。
为了解决城市交通的问题，引进了新的代步工具——平衡车，它体积小，便于携带，同时采用电能驱动，节能、环保，提高了人们出行的效率。
平衡车主要利用车载传感器检测车体姿态角度的变化，然后通过控制系统驱动电机，达到两轮直立自平衡的效果。
本文通过MPU6050模块（赖义汉,王凯.基于MPU6050的双轮平衡车控制系统设计[J].河南工程学院学报(自然科学版),2014,26(01):53-57）获取加速度和角速度，对车体姿态进行识别。
MPU6050模块为整合性6轴运动处理组件，内置3轴陀螺仪，3轴加速度计，如图1所示。
其中陀螺仪输出的角速度积分就可以得到角度值，但是由于角速度存在微小的偏差和漂移，经过积分运算之后就会形成累积误差。
加速度计恰好和陀螺仪特性相反：没有累积误差。
但是由于平衡车在运动时，极易受到外部的干扰，采集加速度值时会产生很大的噪声信号。
所以单独使用陀螺仪或加速度计估计平衡车的姿态是很难实现的。
因此需要采用滤波算法将其加速度计和陀螺仪之间的数据进行融合，计算出平衡车偏转角度的最优估计值，完成平衡车的姿态解算。
图1 MPU6050模块本文采用四种不同的姿态解算算法对平衡车姿态进行解算，对比不同姿态解算的效果以及在平衡车上的应用，选出平衡车姿态的最优估计，完成平衡车的姿态解算。
图2 一阶互补滤波算法框图1 四种姿态解算的应用1.1 一阶互补滤波一阶互补滤波（付勇杰,丁艳红,梁义维,行阳阳.动态倾角传感器及其传递特性的研究[J].仪表技术与传感器,2012(09):6-8）融合了陀螺仪提供的高频角速度信号和加速度计提供的低频角度信号，采用高通滤波算法抑制陀螺仪的积分漂移,低通滤波算法除去加速度计短时间快速变化的信号，分别滤出相应的噪声信号，补偿陀螺仪的累积误差和加速度的动态误差，得到平衡车姿态的估计值。
全自主移动双轮平衡车轨迹规划及平衡特性分析
全自主移动双轮平衡车轨迹规划及平衡特性分析全自主移动双轮平衡车是一种动态稳定的轮式移动机器人,其近年来己成为机器人研究的一个热点。
与传统的静态轮式移动机器人相比,其机械本体通常被设计成高重心、小占地面积。
由于全自主移动双轮平衡车以倒立摆原理为基础,故需要不断消耗能量来维持自身平衡。
稳定性是全自主移动双轮平衡车必须具备的首要性能,其不仅表现在前进/后退等简单运动中,还在转向等复杂运动中更为重要。
因为全自主移动双轮平衡车通过两个同轴的电机的协作来控制其运动。
本研究课题以全自主移动双轮平衡车的结构为基础,分析其动力学和运动学特点,创新的利用轨迹规划的方法提高全自主移动双轮平衡车转向运动过程中的稳定性,使其以一较快的速度匀速沿既定轨迹曲线运动且无碰撞。
本课题的主要研究内容分为以下四个部分:1.建立全自主双轮平衡车动力学和运动学数学模型,以动力学模型为基础分析其平衡特性,通过运动学模型分析其在转向过程中临界倾斜情况下曲率与速度的关系,确定其运动轨迹的最大曲率值。
2.根据A*路径搜索算法生成轨迹的不连续性,提出基于A*算法的三次B-spline曲线轨迹规划方法。
在原有A*路径搜索算法生成无碰撞路径的基础上,利用三次B-spline曲线平滑路径,使得轨迹曲线具有C2连续性,避免了全自主移动双轮平衡车不停地在路径点处启动、停止和原地转向。
3.考虑到生成轨迹曲线可能与障碍物发生碰撞,以及曲率并不一定满足全自主移动双轮平衡车运动轨迹曲率的要求,提出基于控制点修正的曲线曲率控制方法。
首先对轨迹曲线进行碰撞分析,然后结合A*路径搜索算法和三次B-spline 曲线的性质,确定控制点移动位置,最终实现对轨迹曲线曲率的控制。
4.验证移动控制点控制轨迹曲线曲率方法可行性。
根据上述分析过程编写算法,并在 matlab 软件上进行仿真。
仿真结果表明,该方法可以有效地控制轨迹曲线曲率,使其满足全自主移动双轮平衡车最大曲率要求。
一种采用双pid串级控制的双轮自平衡车的研制
摘 要一种采用双PID串级控制的双轮自平衡车的研制双轮自平衡车因其动力学系统同时具有多变量，非线性，不稳定，强耦合等特性，在研究各种控制方法等方面是较为领先的领域，所以双轮自平衡车的发展引起了人们广泛的关注。
双轮自平衡车可以用倒立摆模型进行分析，因其系统极其不稳定，务必要用强效巧妙的控制方法才能维持其稳定。
系统整体上主要由姿态传感子系统、CPU处理子系统、驱动子系统三部分构建而成，其中获取精确的姿态信息以及将获得数据进行融合和处理的算法决定了自平衡车的优劣。
其原理是自平衡车通过姿态传感器（MPU6050）高频率实时检测运行情况，将所采集的俯仰角和角度及加速度变化率传输给CPU，经由CPU融合处理并输出调整姿态的指令，从而驱动电动机使两个轮的转速发生相应的改变，实现车体平衡以及加速和减速的目的。
本文研制了一种采用双PID串级控制的双轮自平衡车，系统以STM32最小系统为核心板，采用运动处理传感器MPU6050实时检测角速度以及角度，并通过互补滤波的方式进行数据融合，用于减小传感信号温度漂移的影响，同时使自平衡车即使受到很大的外界干扰（如推拉、震动、颠簸等）也能够快速进行调整。
系统通过串级PID（Proportion Integration Differentiation）算法进行车体的控制，通过PD（Proportion Differentiation）控制使得车身能够直立运行，通过安装在直流电机上的测速码盘实时反馈电机转速和方向，并通过PI（Proportion Integration）控制来控制车身的速度。
该双轮自平衡车运用TB6612FNG电机驱动系统，调节PWM输出的占空比来改变电机的转速。
系统通过LM2940以及ASM1117子系统作为电源驱动，准确的转换电压并对STM32和电机供电。
最后对系统进行控制参数的调整和优化，最终实现让双轮自平衡车直立平衡运行的目标。
关键词：双轮平衡车,PID控制,互补滤波,姿态检测ABSTRACTDeveloping of a dual-wheel self-balancing vehicle using double PID cascade controlThe dual-wheeled self-balancing vehicle is a leading field in the research of various control methods because of its dynamic system of multi-variable, nonlinear, unstable and strong coupling, so the development of self-balancing two-wheeled vehicles has attracted widespread attention.The dual-wheel self-balancing vehicle can be analyzed by using inverted pendulum model. The system is extremely unstable, so it is important to use a effective method to maintain its stability. The system is mainly composed of three parts: attitude sensing subsystem, CPU processing subsystem and driving subsystem. The accurate attitude information and the algorithm which gets the data to be fused and processed determine the performance of self-balancing vehicle. The self-balancing vehicle detects operating conditions through the real-time high-frequency sensor (MPU6050), the collected pitch angle and acceleration rate of change is transmitted to the CPU, CPU fusion processing and output adjustment attitude commands, which drive the motor to make two wheels' speed change to achieve the purpose of acceleration, deceleration and balancing the body.In this paper, a dual-wheel self-balancing vehicle using double PID cascade control is developed. Using STM32 as the cord board and motion detection sensor(MPU6050)detects angular velocity and angle in real time. And performing data fusion by complement filter to reduce the influence of the temperature drift of the sensing signal. At the same time, even if the self-balancing vehicle suffers from great external interference (Push and pull, vibration, bump, etc.) can also be quickly adjusted. The system controls the vehicle body through the Proportion Integration Differentiation (PID) algorithm. By the control of PD (Proportion Differentiation), the vehicle body can be erected. The speed and direction of the motor are fed back in real time by the speed encoder installed on the DC motor. And using the control of Proportion Integration(PI) to control the body speed. The TB6612FNG driving system of motor is used in the self-balancing dual-wheel vehicle, and the motor speed is changed by adjusting the PWM output duty cycle. The system is powered by the LM2940 and the ASM1117 subsystem, which can convert voltage accurately, power theSTM32 and the motor. Finally, two-wheeled self-balancing vehicle upright balance operation is achieved by adjusting and optimizing the control parameters.Keywords:a auto-balancing vehicle with two wheels, PID control, Complementary filter, attitude detection目 录摘 要 (I)ABSTRACT (II)第一章 绪论 (1)1.1研究背景及意义 (1)1.2国内外研究现状 (1)1.2.1国外现状 (1)1.2.2国内现状 (5)1.3本文主要内容及章节内容 (6)第二章 平衡车系统原理分析 (7)2.1控制系统任务分析 (7)2.2平衡车数学模型 (8)2.2.1 平衡车的受力分析 (8)2.2.2平衡车的运动微分方程 (11)2.3 串级PID在平衡控制和速度控制中的应用 (12)2.3.1 PID算法简介 (12)2.3.2 PID算法在平衡控制中的应用原理 (14)2.3.3 PID算法在速度控制中的应用原理 (14)2.3.4 串级PID的原理及在系统中的应用 (15)2.4基于互补滤波的数据融合 (16)2.5本章小结 (16)第三章 系统硬件电路设计 (17)3.1 单片机最小系统STM32F103C8T6 (18)3.2系统电源模块 (19)3.3 运动处理传感器模块 (20)3.4电机驱动电路 (21)3.5编码器电路 (23)3.6底板综合设计 (24)3.7系统遥控电路设计 (26)3.7.1 单片机STC89C52 (26)3.7.2 无线收发器模块NRF24L01 (27)3.7.3 液晶显示模块12864 (28)3.8本章总结 (29)第四章 系统软件程序设计 (30)4.1主程序框架与初始化 (30)4.2 数据采集 (32)4.2.1.输入信号采集函数 (32)4.2.2.捕获电机脉冲函数 (32)4.3互补滤波数据融合算法 (33)4.4 串级PID控制 (33)4.4.1直立PD控制 (33)4.4.2速度PI控制 (34)4.5电机PWM输出 (36)4.6程序优化 (37)4.7本章小结 (37)第五章 系统调试 (38)5.1系统开发平台 (38)5.2姿态检测系统调试 (39)5.3控制系统PID参数的整定 (41)5.3.1直立PD控制参数调试 (41)5.3.2速度PI控制参数调试 (41)5.4本章小结 (42)第六章 总结与展望 (43)6.1总结 (43)6.2展望 (43)参考文献 (44)作者简介及攻读硕士期间发表的论文 (46)致 谢 (47)第一章 绪论1.1研究背景及意义近年来，双轮自平衡车的发展势头迅猛主要有以下两个原因，其一是它的实用性很强，可以应用到绝大多数领域，其二是支撑搭建双轮自平衡车的理论体系逐渐完善，技术手段日益先进，如数据获取更简单有效，数据处理更科学精确。
基于单片机的两轮自动平衡小车系统的设计
第30卷第12期2020年12月长春大学学报JOURNAL OF CHANGCHUN UNIVERSITYVol.30No.12Dec.2020基于单片机的两轮自动平衡小车系统的设计杜丽敏，王岩（长春大学电子信息工程学院，长春130022）摘要：通过对倒立摆模型的受力分析，使两轮小车保持自平衡运行状态。
硬件上采用STM32F103ZET6单片机为核心控制器，利用MPU6050检测小车的速度和加速度，选择L298N驱动两个两相直流电机，采用霍尔测速码盘获得电机的转速，通过电磁检测电路实现电磁轨迹跟踪。
软件上采用PI和PD构成串级控制算法,MPU6050采集到的小车姿态数据经卡尔曼滤波进行数据处理。
最终实现了平衡车的稳定控制，完成了小车直立和行走功能。
关键词：两轮自动平衡小车；STM32F103ZET6；MPU6050；串级控制器；卡尔曼滤波中图分类号:TP273文献标志码:A文章编号：1009-3907（2020）12-0019-06两轮自动平衡车凭借其运动灵活、体积小巧、经济环保等优点逐渐被人们喜欢，并且在人们的生产生活中起着越来越重要的作用。
两轮自动平衡小车采用倒立摆工作原理,使小车保持平衡状态，其系统具有非线性、强耦合、不稳定等特点⑴。
因此,两轮自平衡车不仅在市场中有很大的价值和前景，在验证或校验控制算法和控制理论上更有一个很好的实验平台［2］。
文献［3-4］设计了基于LQR的最优控制器,该控制算法具有较快的动态响应速度，对于干扰具有良好的鲁棒性;文献［5］针对和LQR两种控制方法进行了对比分析，证明了前者在欠驱动系统的控制中具有一定的参考价值;文献［6］针对两轮平衡小车给出了硬件设计方案，以及基于PID的控制算法，实验中验证了设计方案的可行性。
本文主要研究了PID控制算法在两轮自动平衡小车中的应用。
首先，构建以STM32F103ZET6单片机为核心的两轮直立小车控制系统;其次，对两轮自动平衡小车进行了数学建模,验证了PD控制算法可以使小车保持直立稳定状态，进而基于PID设计了串级控制算法;最后将所设计的控制算法应用在了实物中，实现了小车的直立和行走功能。
自平衡小车详解_陀螺仪和加速度详细介绍
4
电磁组直立行走任务分解 车模直立控制 车模速度控制
原理篇
车模方向控制 车模倾角测量 控制算法总框图 整体电路框图 DSC最小系统 倾角传感器电路
电路设计篇
电机驱动电路 速度传感器电路 电磁检测电路 车模简化与修改
机械设计篇
传感器安装 其它注意事项 软件功能框架 DSC资源配置
软件编写与调试篇
主要算法以及实现 程序调试与参数整定 运行测试
6
在上述三个任务中保持车模直立是关键。由于车模同时受到三种控制的影响，从车 模直立控制的角度，其它两个控制就成为它的干扰。因此在速度、方向控制的时候，应 该尽量平滑，以减少对于直立控制的干扰。三者之间的配合如图 2.1 所示。
图 1.2 参考设计方案内容
参考设计方案经过了实际验证测试，车模测试运行视频请在竞赛网站上下载。 参考设计方案最后附录中给出了用于下载资料的相关网站。
5
二、原理篇
2.1 直立行走任务分解
电磁组比赛要求车模在直立的状态下以两个轮子着地沿着赛道进行比赛，相比四轮 着地状态，车模控制任务更为复杂。为了能够方便找到解决问题的办法，首先将复杂的 问题分解成简单的问题进行讨论。 为了分析方便，根据比赛规则，假设维持车模直立、运行的动力都来自于车模的两 个后车轮，后轮转动由两个直流电机驱动。因此从控制角度来看，由控制车模两个电机 旋转方向及速度实现对车模的控制。车模运动控制任务可以分解成以下三个基本任务： （1） 控制车模直立：通过控制两个电机正反向运动保持车模直立状态； （2） 控制车模速度：通过控制两个电机转速速度实现车模行进控制； （3） 控制车模转向：通过控制两个电机之间的转动差速实现车模转向控制。 以上三个任务都是通过控制车模两个后轮驱动电机完成的。可以假设车模的电机可 以虚拟地被拆解成三个不同功能的驱动电机， 它们同轴相连， 分别控制车模的直立平衡、 前进行走、左右转向，如图 2.1 所示。
自平衡独轮车动力学模型的建立
2 自平衡独轮车动力学模型的建立2.1 自平衡的原理动态平衡原理即为自平衡独轮车的工作原理。
通过运动补偿算法，运用加速度传感器和陀螺仪对车体姿态测试，同时借助精密的伺服控制系统高敏地对电机进行驱动，并作适度的调节，从而使整个车体的平衡性以及稳定性得到确保。
由图 2.1能够得出，自平衡独轮车的车体摆动和它的转动是存在一定分离性的，驾驶人员的两腿将车身的两端夹紧，进而和车体产生了一个整体。
一旦其身体倾向后方，那么驱动车轮就会朝后转，从而防止车体倒向后方；反之，若是朝前，那么车轮就会朝钱转；若其身体处于竖直状态，那么则独轮车也就表现为动态平衡。
独轮车控制系统的重中之重就是平衡控制。
就自平衡独轮车加以建模并做深度分析，便能够对系统的特性产生更多的了解，这对于相应控制算法的设计规划甚为有益。
图2.12.2动力学建模2.2.1 物理模型化简自平衡独轮车不是平面机构，需要采用空间坐标的方式对其进行分析，坐标定义可详见图2.2，能够看出其自由度共有6个，其中平移、旋转各为3个。
俯仰角Ψ、横滚角γ、偏航角Φ均为其旋转姿态角。
因为独轮车的左右方向以驾驶者自身的调节为主，只能够控制前方和后方，故而把模型简单化至x o z平面，仅对这两个方向上的平衡控制进行探讨。
图2.2运动学是力学的一个分支，主要是站在几何的视角上来对物体位置伴随时间的波动规律进行阐述及探究的，刚体的运动学以对其自身的运动特性的研究为主，譬如转动经过、位移、角速度及其加速度等。
由于有部分难以测得的因素存在于独轮车的机械零件以及运动经过当中，因而必须对其做简化建模，因此作如下假设：1驾驶者和独轮车运动相同，可将二者看成一个整体，假定是刚体；2行走轮为质心在圆心的空心圆环；3在独轮车行驶期间，车轮和地面从始至终都处于彼此接触的状态，且一直是纯滚动；4忽略其他摩擦和外界干扰。
基于以上条件，我们进行独轮车物理模型化简如图 2.3，Φ为车轮转过的角度，θ为车体的倾角。
电动平衡车原理范文
电动平衡车原理范文电动平衡车是一种以自平衡为特点的电动交通工具。
它通过内置的陀螺仪和加速度传感器等设备，实时感知车身的倾斜角度，并控制电机以相应的力度和方向来平衡车身。
电动平衡车原理主要分为平衡控制和前进控制两个方面。
平衡控制是电动平衡车能够保持平衡的关键。
平衡控制主要依靠车身上的陀螺仪和加速度传感器。
陀螺仪可以感知车身在水平面上的转动变化，而加速度传感器可以感知车身的加速度变化。
陀螺仪和加速度传感器将采集到的数据传输给控制电路，控制电路根据这些数据来判断车身的倾斜角度，并通过控制电机的力度和转动方向来实现平衡。
当车身发生倾斜时，控制电路会相应地增加或减少电机的输出功率，使车身回到平衡状态，从而实现自动平衡。
前进控制是电动平衡车的主要控制方式。
前进控制主要依靠车身上的倾斜角度传感器和电机控制器。
倾斜角度传感器可以感知车身前倾的角度变化。
当车身前倾时，电机控制器会相应地增加电机的输出功率，使车身向前推进；当车身后倾时，电机控制器会相应地减少电机的输出功率，使车身向后移动。
电机控制器可以通过对电机的力度和转动方向进行控制，实现平衡车的前进和后退。
通过倾斜角度传感器和电机控制器的配合，电动平衡车可以实现前进、后退、原地转向等动作。
除了这些基本原理，电动平衡车还有一些其他的技术要点。
例如，电动平衡车可以通过脚部压力传感器来感知骑行者的意图，从而实现转向或刹车动作。
电动平衡车的控制系统还可以通过对电机的力度和方向进行微调，使骑行过程更加稳定和平滑。
此外，电动平衡车还可以通过对车身上方向控制杆的操作来实现转向和刹车，提高操控性和安全性。
总之，电动平衡车通过陀螺仪、加速度传感器、倾斜角度传感器等设备，实现对车身的实时感知和控制。
通过对电机的力度和方向进行控制，电动平衡车可以实现平衡、前进、后退、转向等动作，为骑行者提供便捷的出行工具。
两轮自平衡小车
式中， pwl ——左轮的轨迹(m)；
——左轮相对于机器人本体的转角(rad)；
——右轮相对于机器人本体的转角(rad)。
由机器人运动学模型可以看出，通过控制机器人左右两轮的速度，可以实现机器人沿着任意设定的轨 迹行走。 最大可控角度论证:（当驱动车轮的电机和减速机构选型确定后） 如下的平衡关系： g sin
（4-7）
因为两轮自平衡机器人平衡后，可假设车身倾角在 5 范围内。将式（4-7）在 =0（垂直于水平地面）附近展开并忽略高 次项（ sin 、 cos 1 ， 0 ） ，代入（4-2）式，得到车身前进运动模型：
J 1 （4-3）式中两相加，可适当： 2 m 2 v T H r r
右轮速度为：
xr R r cos yr 0 zr R r sin
2.车体的运动学模型
这里设定了一个小的时间间隔为 t ，对 t 时刻及 t t 时刻车体的运动进行分析。
Vb ——车体质心绕车轮轴转动的线速度(m/s)；
Vc 2 —— Vb 在 y ' 轴上的投影(m/s)；
X vC cos r cos L R 2 Y vC sin r sin L R 2
两轮自平衡机器人的角速度为：
r R L 2b 得 r R L 2b
于是可得到自平衡机器人的运动方程：
r cos X 2 Y r sin 2 r 2b r cos 2 r sin R L 2 r 2b
kmax cos rM
s2
代步平衡车原理
代步平衡车原理
代步平衡车是一种能够自动保持平衡的个人电动交通工具。
它的平衡原理主要基于三个关键部件：倾斜传感器、电机和控制系统。
首先，倾斜传感器是平衡车的核心部件之一。
它通常采用陀螺仪或加速度计等传感器来检测车身的倾斜角度。
当车身倾斜时，传感器会将这个信号发送给控制系统。
其次，电机也是平衡车的重要组成部分。
平衡车一般配备两个独立驱动的电机，一个位于车轮的前方，另一个位于后方。
这两个电机通过控制系统配合运作，实现车子的前进、后退以及转向等动作。
最后，控制系统是平衡车的大脑。
它接收来自倾斜传感器的倾斜角度信号，并根据这个信号来调整电机的转速和方向。
当车身前倾时，控制系统会使电机提高转速，使车辆前进；而当车身后倾时，控制系统则减少电机转速，使车辆后退。
通过持续不断地调整电机的转速和方向，控制系统能够保持车辆的平衡状态。
总结起来，代步平衡车的原理是通过倾斜传感器检测车身倾斜角度，并通过控制系统调整电机的转速和方向，从而保持车辆的平衡状态。
这种原理使得骑行者无需过多操作，只需要倾斜车身即可实现前进、后退和转向等动作。
不倒式平衡电动车模型设计
不倒式平衡电动车模型设计不倒式平衡电动车是一种以自平衡技术为核心的新型电动车，它能够通过内置的陀螺仪和加速度传感器实现自动平衡，使用户无需过多的驾驶技能就能够轻松驾驶。
这种电动车在城市出行、旅游观光、运输等领域具有广泛的应用前景。
为了更好地满足用户需求，设计一款优秀的不倒式平衡电动车模型至关重要。
在本文中，将就不倒式平衡电动车模型设计进行探讨，包括设计理念、技术参数、外观设计等内容。
1. 设计理念不倒式平衡电动车的设计理念是充分发挥自平衡技术的优势，提供给用户更加便捷、安全、舒适的出行体验。
设计理念应当注重安全性，确保电动车在行驶过程中能够始终保持平衡状态，避免倒车、翻车等情况的发生。
设计理念应当注重便捷性，电动车的操控应该简单易行，用户无需过多的训练和技能就能够熟练驾驶。
设计理念应当注重舒适性，在车辆的悬挂、座椅、操控系统等方面进行细致的设计，使用户在行驶过程中能够感受到舒适的驾驶体验。
2. 技术参数在不倒式平衡电动车的设计中，技术参数是至关重要的一环。
电动车的自平衡系统是设计的核心，它需要具备快速响应、高精度的特性，能够在瞬间感知车辆的倾斜状态并做出相应的调整。
电动车的动力系统也是设计的关键，需要具备足够的功率和续航能力，确保电动车在长时间行驶过程中能够保持良好的性能。
安全系统、悬挂系统、车身材料等方面的技术参数也需要进行综合考量，以确保不倒式平衡电动车在各个方面都能够达到优秀的水平。
3. 外观设计不倒式平衡电动车的外观设计也是十分重要的一环。
外观设计需要充分考虑到车辆的稳定性和舒适性，避免出现过于花哨或者过于简洁的设计，影响了车辆的使用感受。
外观设计需要考虑到用户的审美需求，力求做到时尚、个性、引人注目。
外观设计还需要考虑到车辆的实用性，合理设计车身结构和配件，使得车辆在实际使用中能够更加方便、实用。
不倒式平衡电动车模型设计需要充分考虑到安全性、便捷性、舒适性等方面的因素，运用先进的技术和创新的设计思路，才能够设计出一款优秀的不倒式平衡电动车模型。
两轮平衡车建模与系统设计
ＬＰＣＩ７６８系统程序算法设计……………………………………………………４１
两轮平衡车调试与实验数据分析………………………………………………４７
第５章
５．１两轮平衡车系统调试……………………………………………………………．．４７ ５．２无线串口数据……………………………………………………………………一４７ ５．３车子动态数据测试………………………………………………………………．．４７
１．１移动机器人的发展历程…………………………………………………………．．１
１．２两轮平衡车的研究意义…………………………………………………………．．３
１．３本论文研究内容…………………………………………………………………．．３ 第２章 两轮平衡车动力学模型分析……………………………………………………．．５
３．６编码器测速原理与应用设计……………………………………………………．．２６
３．６电机驱动原理与应用设计………………………………………………………．．２７
第４章
两轮平衡车测控软件系统设计…………………………………………………３０
４．１角度检测及滤波算法设计设计…………………………………………………．．３０ ４．１．１卡尔曼滤波算法……………………………………………………………３０ ４．１．２离散卡尔曼滤波算法………………………………………………………３２ ４．２平衡控制算法设计………………………………………………………………．．３４
ＴＷＯ．ＷＨＥＥＬＥＤ
ＳＥＬＦ．ＢＡＬＡＮＣＥＤ ＶＥＨＩＣＬＥ
ｏｆ ＭＯＤＥＬⅢＧ ＡＮＤ
ＳＹＳＴＥＭ ＤＥＳＩＧＮ
Ｇｒａｄｅ：２０１０ Ｃａｎｄｉｄａｔｅ：Ｚｈａｏ Ｌｅｉ
Ａｃａｄｅｍｉｃ Ｄｅｇｒｅｅ Ａｐｐｌｉｅｄ ｆｏｒ：Ｍａｓｔｅｒ Ｓｐｅｃｉａｌｉｔｙ：Ｔｅｓｔｉｎｇ Ｔｅｃｈｎｏｌｏｇｙ＆Ｉｎｓｔｒｕｍｅｎｔ
【原理分析】Google炫炸天的平衡自行车仅仅是概念吗？来看看惯性轮自行车吧
【原理分析】Google炫炸天的平衡⾃⾏车仅仅是概念吗？来看看惯性轮⾃⾏车吧1、聊⼀聊好了，今天为⼤家带来⼀些机器⼈制作的原理知识讲解，因为最近很多⼩伙伴问作者有什么可以锻炼⾃⼰的、⼜⾮常有意思的⼩项⽬吗?想来想去想了很久，⼤家感兴趣⼀⽅⾯就是GUI了，另⼀⽅⾯就是运动控制了，于是便有了今天的⽂章。
2、Google平衡⾃⾏车下⾯是从⾕歌平衡⾃⾏车宣传视频截图,⼤家可以欣赏⼀下⾕歌的⾃平衡车:分析分析：⼤伙看完应该会不禁惊叹，真的太厉害了，终于可以解放双⼿了，甚⾄还会想着什么时候普及上架，遗憾的是，最后⾕歌出了解释视频其实全是后期剪辑，⼤家认为是电影特效就好，仅仅是4⽉1⽇愚⼈节那天的⼀个玩笑。
其实作者在最初看到这个视频的时候特别惊讶，总是会考虑⾃⾏车的每个动作应该⽤什么样的理论去解释，也许这就是⼯科男的思维吧。
第2张可以通过调整车⾝重⼼使得其平衡，第3、4张也就是模拟⼈的⼀个正常骑⾏过程和⾃动导航功能，之前有百度⽆⼈车驾驶技术也就不奇怪了，原理上都说得通，然⽽第⼀张真的就有点夸张了吧。
那到底第⼀张这种⾃平衡效果能不能实现呢？3、Motor-Bike Robot下图来源于Motor-Bike Robot视频截图，该项⽬是⼀个国外学⽣竞赛的作品视频介绍:分析分析：这个视频中的⾃⾏车平衡效果与之前⾕歌第⼀张图的平衡效果⾮常接近了。
⼤家应该发现了该⾃⾏车有⼀个明显的特点就是其上⾯有⼀个轮盘随着车⾝⾓度在不断的来回转动，其实原理上该轮盘的转动就维系着⾃⾏车的⾃平衡，⾄于前后进退通过后轮驱动电机正反转实现，其转向是有对应的伺服电机进⾏转动。
下⾯我们就看看这个⼩车⾃平衡原理到底是怎样的。
4、惯性轮平衡⾃⾏车原理与控制分析我们⼀般叫该⾃⾏车上的那个轮盘叫惯性轮，电机对其进⾏驱动便会产⽣对应的⼒矩，有点类似于两个齿轮咬合进⾏转动的原理。
不过对于运动控制算法按照正常的开发流程⾸先我们应该对该⾃⾏车进⾏数学建模，使⽤的⼀般就是物理⼒学定理定律等等，所建⽴的现实模型都是强耦合、⾮线性的数学模型，这样就需要进⾏解耦和线性化从⽽简化物理模型来便于分析系统稳定性和控制器设计，然后获得初步整定参数，最后基本上就是优化参数和调节了，作者以后会再具体跟你们讲讲建模与控制的，这⾥就先不啰嗦。
平衡车运动方程
平衡车运动方程一、平衡车运动方程平衡车是一种无人驾驶的车辆，它通过电机、传感器和控制器来实现自动平衡和控制。
它的运动方程描述了平衡车的运动规律，是平衡车运动控制的基础。
1、动力学模型平衡车的动力学模型可以表示为：M（θ）*ddθ/dt^2 + C（θ，dθ/dt）*dθ/dt + G（θ） = T（t）其中，M（θ）是平衡车的转动惯量，C（θ，dθ/dt）是惯性阻尼系数，G（θ）是重力力矩，T（t）是电机的输出力矩。
2、状态空间模型由于平衡车的运动是非线性的，因此可以使用状态空间模型来描述它的运动规律：x′ = Ax + Bu其中，x′表示状态变量的导数，A是状态空间矩阵，B是输入矩阵，u是控制量。
3、控制方法控制平衡车的运动可以采用PID控制器，它能够根据设定的参数实现自动控制，从而达到自动平衡的目的。
PID控制器的运动方程为：u = Kp*e + Ki*∫e + Kd*(de/dt)其中，Kp、Ki和Kd是PID控制器的参数，e是误差，de/dt是误差的导数。
4、模型预测控制模型预测控制（Model Predictive Control，MPC）是一种基于模型的控制策略，它能够根据模型预测系统未来的状态，从而实现预测控制。
MPC的运动方程为：u = argmin (Kp*e + Ki*∫e + Kd*(de/dt))其中，Kp、Ki和Kd是MPC控制器的参数，e是误差，de/dt是误差的导数。
5、综合控制综合控制是将PID控制、模型预测控制和其他控制方法结合起来，使用多种控制策略实现自动控制的方法。
综合控制的运动方程为：u = f（Kp*e + Ki*∫e + Kd*(de/dt)，A，B）其中，Kp、Ki和Kd是PID控制器的参数，e是误差，de/dt是误差的导数，A和B是状态空间矩阵和输入矩阵。
二、总结以上就是平衡车运动方程的概述，它涉及到动力学模型、状态空间模型、PID控制、模型预测控制和综合控制等控制方法。
独轮平衡车原理
独轮平衡车原理独轮电动车是从独轮机器人演变而来其平衡问题的理论基础是移动的倒立摆,为高阶次、不稳定、非线性系统。
该系统的动力学模型复杂，属于欠驱动系统。
在静止状态下，车体受重力作用在车轮转动方向上不能维持平衡，必须通过运动调节才能实现平衡。
因此，它是一个动态平衡系统，具有较强的理论研究价值。
控制平衡：自平衡独轮电动车系统其实就是单级倒立摆和旋转式倒立摆的结合体,它由车身和一个由电机驱动的车轮组成，其实物图和简化的模型示意图如图1（a）和图1（b）所示，是一个典型的不稳定系统.独轮车前进的方向是x轴正方向,车体纵垂线为y轴,正方向向上。
当人和车体重心靠前，车身会向前倾斜，产生一个平衡角θ，为了保证人不摔倒，电机将驱动车轮向前运动,同理当人和车体重心靠后,电机将驱动车轮向后运动以保持平衡。
利用电机来加强改进平衡：在此基础上，自平衡电动独轮车加以改进，靠电机驱动的，采用陀螺仪与驱动电路控制保持不倒。
把身体向前倾斜就可以启动.速度则是由身体的倾斜程度来控制的，想要加速则向前倾，减速则向后倾.抛开人的主动操控，独轮平衡车保证正常工作一定离不开加速度传感器和角速度传感器(陀螺仪)。
加速度传感器：加速度传感器可以测量由地球引力作用或者物体运动所产生的加速度。
只需要测量其中一个方向上的加速度值，就可以计算出车倾角.比如使用X轴向上的加速度信号，车直立时，固定加速度器在X轴水平方向,此时输出信号为零偏电压信号。
当车发生倾斜时,重力加速度g便会在X轴方向形成加速度分量,从而引起该轴输出信号的变化。
但在实际车运行过程中，由于平衡车本身的运动所产生的加速度会产生很大的干扰信号叠加在上述测量信号上，使得输出信号无法准确反映真正的倾角.因此对于直立控制所需要的姿态信息不能完全由加速度传感器来获得角速度传感器：陀螺仪可以用来测量物体的旋转角速度。
平衡车上安装陀螺仪，可以测量车倾斜的角速度，将角速度信号进行积分处理便可以得到车的倾角.平衡车的核心部件: 谈到平衡我们就不得不说到陀螺仪,陀螺仪的原理就是，一个旋转物体的旋转轴所指的方向在不受外力影响时，是不会改变的。
自动平衡搜索车物理模型的控制系统分析以及对小偏差线性化方法的研究思考
自动平衡搜索车物理模型的控制系统分析以及对小偏差线性化方法的研究思考摘要：通过对自动平衡搜索车建立物理模型，建立物理方程式，在工作平衡点附近进行小偏差线性化。
然后通过求解特征方程以及劳斯判据进行系统稳定性分析。
结果发现系统是不稳定的。
但实际系统是稳定的，得出结论系统线性化后可能会导致稳定性变化。
但是该线性化系统在小偏差范围内是合理的。
进而对小偏差线性化方法进行学习研究。
关键词：自动平衡搜索车;稳定性分析;小偏差线性化1.自动平衡搜索车系统分析1.1自动平衡搜索车系统物理模型图1.2物理量M-小车的质量，kg;m-摆杆的质量，kg;u（t）-外作用力，N;z（t）-小车的移动距离，m;θ（t）-摆杆相对于直立方向的偏离角，rad。
1.3系统原理介绍1.4系统假设假设1：小车与摆杆仅作平面运动，摆杆质量，风力，摩擦等略去不计。
假设2：摆杆只在垂直位置附近作微小的摆动。
由于该系统的目的就是使摆杆保持直立不倒，因此该假设合理。
假设3：闭环系统反馈的作用是力图抑制或消除偏差，因此可以认为θ，dθ/dt接近于零，从而可以忽略微小的高次项，而保留θ，dθ/dt 项。
1.5系统分析1.5.1摆的运动可看作由牵引运动（小车平移）和相对运动（摆杆转动）的合成。
摆的水平运动为：。
1.5.2在垂直于摆杆的方向，摆的运动也由两部分合成;一部分为小车平移运动在该方向的投影;另一部分为摆的圆周运动。
1.6系统方程式1.6.1根据牛顿定律，沿水平方向：根据牛顿定律，沿摆杆转动方向：1.6.2在运动方程式中，有变量的乘积和三角函数，这是非线性方程，我们需要线性化方程由假设2可知，θ很小，那么三角函数就可以简化。
则微分方程可近似为：①②1.6.3由①②两式可得θ与u以及z与u的数学模型1.7系统稳定性分析1.7.1传递函数：1.7.2方法1：特征方程求解：分析：由于均存在一个大于0的特征根，因此系统均不稳定。
1.7.3方法2：劳斯判据劳斯阵列1劳斯阵列2分析：第一列的符号均发生了变化，系统均不稳定。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、研究背景及意义
自动搜索平衡车的两种数学模型。
它是用小车及车上倒置的摆模拟控制火箭垂直起飞的装置。
外力u(t)目的使摆保持与车身垂直。
火箭起飞阶段必须维持与地面垂直，待到达指定速度和高度后才开始转弯。
倘若火箭在起飞阶段受侧风干扰，火箭轴线偏离铅垂线一个小角度，则在重力作用下偏离角度会越来越大最终导致发射失败。
为防止失败．在火箭轴线刚偏离垂直位置时，应启动发动机产生横向力校正火箭位置使其与地面垂直。
为使问题简化，设车与摆只在平面内运动并忽略杆的质量，电机本身的惯性，摩擦，风力等因素，设摆球质量为m ，车质量为M ，摆长为l 。
二、建模机理
令H(t)和V(t)分别是小车通过铰链作用于杆也就是作用于摆球的水平分力和垂直分力。
当然杆通过铰链作用于车的反作用力为—H(t)和—V(t)。
应用牛顿定律得到：小车水平方向
)()()(y t H t u t M -=。
（2-1） 摆水平方向
2
..
..
..
22
)(sin cos )
sin ()(θθθθθml ml y m l y dt d m t H -+=+= （2-2）
摆垂直方向
)cos ()(22
θl dt
d m mg t V =- 2
...
)(cos sin θθθθml ml --= （2-3）
力的分解
θ
θ
cos sin )()(=t V t H （2-4） 将式（2）带入式（1）得到
)()(sin cos )(2.
....t u ml ml y m M =-++θθθθ
将式（2-2）、（2-3）代入式（2-4）得到
θ
θ
θθθθθθθθcos sin )(cos sin )(sin cos ..
2
.
....
2
.
..
=
---+l l g l l y 三、模型简化
上面两式均系非线性方程。
该系统目的在于控制摆与地面垂直，可以认为θ(t)和
)(t 。
θ都接近于零。
在此假设下，取sin θ(t)≈θ(t)，cos θ(t)≈l ，同时略去此θ(t)，)
(t 。
θ更高阶的无穷小量，经过如此线性化后得到
)(..
..t u ml y m M =++θ）
（ （2-5） 0..
..
=-+θθg l y （2-6）
对式（5）和式（6）等号两边分别取拉氏变换并令初始条件为零便求出由u （t ）到y(t)的传递函数)(g s yu 和由u(t)到θ(t)的传递函数
)(s g u
θ分别如下：
])([)(222g m M Mls s g ls s g yu +--= (2-7)
g
m M Mls s g u )(1
)(2+--=θ (2-8)
或者写为
)()()()()(s u s s s s y g g u yu ⎥⎥⎦
⎤⎢⎢⎣⎡=⎥
⎦⎤⎢⎣⎡θθ （2-9）
式（9）是系统频域中输入一输出描述式，为了推导它的动态方程式选取相变量作为状态变量，即 y x
=1
，。
y x
=2
，
θ=x
3
，。
θ=x 4 （2-10）
由式(5)和(6)导出
u M
M mg u M M mg y x x 1
132--=+-==θ。
u Ml
Ml g m M u Ml Ml g m M x x 1
)(1)(3
..
4.
-+=-+==θθ 得
)(1
010)()()()(0)(0
010*********
)()()()(4321.4.3.2.1t u M M t t t t g Ml m M g M
m t x t x t x t x x x x x ⎥⎥⎥⎥⎥⎦⎤
⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥
⎥⎦
⎤⎢⎢⎢⎢⎢⎣
⎡+-=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡（2-11) y=(1 0 0 0)x(t)
注意，本例得到的数学模型只适用θ(t)和)(t 。
θ很小的情况。
假设自动平衡车的参数为
2
/10,1,1,4s m g m l kg m kg M ====
则有
[]
00
0125.0-025.0005
.120
100005.2-00
0010=⎥⎥⎥⎥
⎦
⎤⎢⎢⎢
⎢⎣⎡=⎥⎥⎥⎥⎦
⎤⎢⎢⎢
⎢⎣⎡=C B A
所以系统的状态空间表达式为：
[]X
y u X X 000125.0025.0005.1200
0005.20000
10
.
=⎥⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢
⎢⎣⎡-=
4 系统能控性和能观性判别
控制系统的能控性和能观性是建立在状态空间描述的基础上的。
状态方程描述了输入()t u 引起状态()t x 变化的过程；输出方程则描述了由状态()t x 变化引起输出
()t y 变化的过程。
能控性和能观性正是利用状态方程和输出方程来分析输入()
t u 对状态()t x 的控制能力和输出()t y 对状态()t x 的反映能力。
若一个系统不能控、不能观，我们就无法对其控制、观测，因此，在分析和设计一个控制系统时，研究其能控性和能观性是非常有必要的。
4.1 能控性分析
用MA TLAB进行能控性判断程序如下：
A=[0 1 0 0;0 0 -2.5 0;0 0 0 1;0 0 12.5 0] B=[0 0.25 0 -0.25]'
C=[1 0 0 0]
d=ctrb(A,B)
r=Rank(d)
结果为：
d = 0 0.2500 0 0.6250
0.2500 0 0.6250 0
0 -0.2500 0 -3.1250
-0.2500 0 -3.1250 0
r = 4
由此得能控判别矩阵的秩为4等于n,因此该系统是。