离散时间信号分析
离散时间信号分析
实验一
学院:电气工程学院专业:测控技术与仪器班级:测仪101
实验二
学院:电气工程学院专业:测控技术与仪器班级:测仪101
实验三
学院:电气工程学院专业:测控技术与仪器班级:测仪101
实验四
学院:电气工程学院专业:测控技术与仪器班级:测仪101
实验五
学院:电气工程学院专业:测控技术与仪器班级:测仪101
%双线性变换法设计ButterWorth数字滤波器[n,Wn]=buttord(0.2,0.3,1,25,’s’);
[b,a]=butter(n,Wn,’s’);
freqs(b,a)
[bz,az]=bilinear(b,a,1);
通过本次实验,我基本掌握了双线性变换法及脉冲相应不变法设计
实验六
学院:电气工程学院专业:测控技术与仪器班级:测仪101。
Lecture 2_离散时间信号分析,华工数字信号处理课件,DSP

二、离散时间信号的运算
8
基本运算
相乘(product) 相加(addition)
wn xn yn wn xn yn wn Axn wn xn N wn x n
调制、加窗
集合平均
数乘(multiplication)
8 -6 -4 -2 0 2 4 6 10
Q: Can a sample of discrete-time signal take real (continuous) value?
4
离散信号是从哪里来的?
A discrete time sequence x[n] may be generated by periodically sampling a continuous-time signal at uniform intervals of time.
12
采样率的转换(1)
采样率转换:
从给定序列生成采样率高于或低于它的新序列的运算
设原采样率为 FT ,转换后的采样率为 FT
则采样率转换比:
FT R FT
R 1 :插值(Interpolation)
R 1
抽取(Decimation)
采样率的转换(2)
上采样(up-sampling)
序列
xn 的 Lp 范数定义:
x
L2 范数是 L1范数是
p
( x[n] )
p n
1
p
xn均方根;
xn平均绝对值; xn绝对值的峰值
L范数定义: x x max
有限长序列x的范数MATLAB计算
norm(x); norm(x,2); norm(x,1); norm(x,inf)
实验一 离散时间信号的时域分析
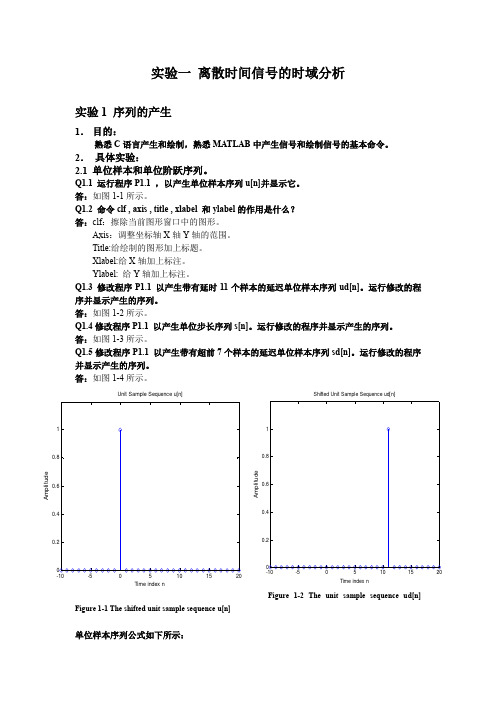
实验一 离散时间信号的时域分析实验1 序列的产生1. 目的:熟悉C 语言产生和绘制,熟悉MATLAB 中产生信号和绘制信号的基本命令。
2. 具体实验:2.1 单位样本和单位阶跃序列。
Q1.1 运行程序P1.1 ,以产生单位样本序列u[n]并显示它。
答:如图1-1所示。
Q1.2 命令clf , axis , title , xlabel 和ylabel 的作用是什么? 答:clf :擦除当前图形窗口中的图形。
Axis :调整坐标轴X 轴Y 轴的范围。
Title:给绘制的图形加上标题。
Xlabel:给X 轴加上标注。
Ylabel: 给Y 轴加上标注。
Q1.3 修改程序P1.1 以产生带有延时11个样本的延迟单位样本序列ud[n]。
运行修改的程序并显示产生的序列。
答:如图1-2所示。
Q1.4修改程序P1.1 以产生单位步长序列s[n]。
运行修改的程序并显示产生的序列。
答:如图1-3所示。
Q1.5修改程序P1.1 以产生带有超前7个样本的延迟单位样本序列sd[n]。
运行修改的程序并显示产生的序列。
答:如图1-4所示。
Figure 1-2 The unit sample sequence ud[n]Figure 1-1 The shifted unit sample sequence u[n]单位样本序列公式如下所示:Time index nA m p l i t u d eUnit Sample Sequence u[n]Time index nA m p l i t u d eShifted Unit Sample Sequence ud[n]1 , n=0 1 , n=k δ[n]= δ[n-k]=0 , 0≠0 0 , 0≠kFigure 1-3 The unit step sequence s[n] Figure 1-4 The shifted unit step sequence sd[n]单位阶跃序列公式如下所示:1 , n ≥0 1 , n ≥k μ[n]= μ[n-k]=0 , n <0 0 , n <k2.2 指数信号Q1.6 运行程序P1.2 ,以产生复数值的指数序列。
第三章 离散时间信号的频域分析_20111910119

-4-3-2-10123402468H(e j ω)的实部ω/π振幅-4-3-2-101234-4-2024H(e j ω)的虚部ω/π振幅-4-3-2-1123402468|H(e j ω)|幅度谱ω/π振幅-4-3-2-11234-2-1012相位谱[H(e j ω)]ω/π以弧度为单位的相位第三章 离散时间信号的频域分析学院:信息学院 专业:通信工程 姓名:马正智 学号:20111910119一、实验目的1、理解和掌握基于MATLAB 仿真研究离散时间傅里叶变换的时移性质;2、理解和掌握基于MATLAB 仿真研究离散时间傅里叶变换的频移性质;3、理解和掌握基于MATLAB 仿真研究离散时间傅里叶变换的卷积性质;4、理解和掌握基于MATLAB 仿真研究离散时间傅里叶变换的调制性质;5、理解和掌握基于MATLAB 仿真研究离散时间傅里叶变换的反转性质。
二、实验内容1、离散时间傅里叶变换Q3.1 在程序P3.1中,计算离散时间傅里叶变换的原始序列是什么?MATLAB 命令pause 的作用是什么?答:离散时间傅里叶变换的原始序列:ωωωj j j e e e H ---+=6.012)(;MATLAB 命令pause 的作用:程序执行到此命令时,图像显示到此停顿,点击键盘任意键,程序继续执行画出后面的图形。
Q3.2 运行程序P3.1,求离散时间傅里叶变换的实部、虚部以及幅度和相位普。
离散时间傅里叶变换是ω的周期函数吗?若是,周期是多少?描述这四个图形表示的对称性。
图Q3.2-1 图Q3.2-2答:离散时间傅里叶变换是ω的周期函数,周期为π2;四个图形表示偶—奇对称性。
Q3.3 修改程序P3.1,在范围πω≤≤0内计算如下序列的离散时间傅里叶变换:ωωωωωωω32327.05.03.013.05.07.0)(j j j j j j j e e e e e e e U ------+-+++-=0.10.20.30.40.50.60.70.80.911111|H(e j ω)|幅度谱ω/π振幅0.10.20.30.40.50.60.70.80.91-4-2024相位谱[H(e j ω)]ω/π以弧度为单位的相位0.10.20.30.40.50.60.70.80.91-1-0.500.51H(e j ω)的实部ω/π振幅0.10.20.30.40.50.60.70.80.91-1-0.500.51H(e j ω)的虚部ω/π振幅0.10.20.30.40.50.60.70.80.91-1-0.500.51H(e j ω)的实部ω/π振幅0.10.20.30.40.50.60.70.80.91-1-0.500.51H(e j ω)的虚部ω/π振幅0.10.20.30.40.50.60.70.80.911111|H(e j ω)|幅度谱ω/π振幅00.10.20.30.40.50.60.70.80.91-6-4-20相位谱[H(e j ω)]ω/π以弧度为单位的相位并重做习题Q3.2。
离散信号分析

下面我们来看2π/ω0与T及T0的关系,从而讨论上面所述正弦 型序列的周期性的条件意味着什么?
T0 1 1 1 = 2π = 2π = = 0T 2πf 0T f 0T T ω0
这表明,若要2π/ω0为整数,就表示连续正弦信号的周期T0应为采 样时间间隔T的整数倍;若要2π/ω0为有理数,就表示T0与T是互为 互素的整数,且有
式中, yk(n)就是系统对输入xk(n)的响应。 在证明一个系统是线性系统时,必须证明此系统同时满足可加 性和比例性,而且信号以及任何比例常数都可以是复数。
例1-1 以下系统是否为线性系统: y(n)=2x(n)+3 很容易证明这个系统不是线性的, 因为此系统不满足叠加原理。 证
T [a1 x1 (n) + a2 x2 (n)] = 2[a1 x1 (n) + a2 x2 (n)] + 3
x(n) = xa (nT )
然而,并不是所有的离散时间信号都是这样获得的。一些信号 可以认为是自然产生的离散时间序列,如每日股票市场价格、 人口统计数和仓库存量等。
1.1.1 序列的运算 1. 序列的移位 . 2. 序列的翻褶 . 3. 序列的和 . 4. 序列的乘积 . 5. 序列的标乘 . 6. 累加 .
2. 单位阶跃序列 . 单位阶跃序列u(n)
1 u ( n) = 0
n≥0 n<0
(1-2)
如图 1-5 所示。它很类似于连续时间信号与系统中的单位 阶跃函数u(t)。
u(n)
1
…
-5 -4
-3 -2
-1
0
1
2
3
4
5
6
n
图 1-5 u(n)序列
实验一离散时间信号的分析报告

工程大学信号分析与处理实验一专业:通信02班学生:瑶华学号:**********完成时间:2022年4月27日实验一: 离散时间信号的分析一、实验目的1.认识常用的各种信号,理解其数学表达式和波形表示。
2.掌握在计算机中生成及绘制数字信号波形的方法。
3.掌握序列的简单运算及计算机实现与作用。
4.理解离散时间傅立叶变换、Z 变换及它们的性质和信号的频域特性。
二、实验设备计算机,MATLAB 语言环境。
三、实验基础理论1.序列的相关概念2.常见序列● 单位取样序列⎩⎨⎧≠==0n 0,0n 1n ,)(δ ● 单位阶跃序列⎩⎨⎧<≥=0,00,1)(n n n u ● 单位矩形序列⎩⎨⎧-≤≤=其他,010,1)(N n n R N ● 实指数序列)()(n u a n x n =● 复指数序列n jw e n x )(0)(+=σ● 正弦型序列)n sin()(0ϕ+=w A n x3.序列的基本运算● 移位 y(n)=x(n-m)● 反褶 y(n)=x(-n)● 和 )()()(21n x n x n y +=● 积 )()()(21n x n x n y •=● 标乘 y(n)=mx(n)● 累加∑-∞==nm m x n y )()( ● 差分运算 ⎩⎨⎧--=∇-+=∆)1()()()()1()(x n x n x n x n x n x n 后相差分前向差分 4.离散傅里叶变换的相关概念● 定义 ∑+∞-∞=-=n jwn jwe n x e X )()(● 两个性质1) [])2()2()2()()(,2)(ππππ++∞-∞=+-+--===∑w j n nw j jw n w j jwn jw e X e n x e X e ew e X 故有。
由于的周期函数,周期为是 2) 当x (n )为实序列时,)(jw e X 的幅值)(jw e X 在π20≤≤w 区间是偶对称函数,相位)(arg jw e X 是奇对称函数。
6.离散时间信号与系统的时域分析

0, n 1 1 z ( n) x ( n) y ( n) , n 1 2 1 n 1 ( 2 )( n 1)( 2 ) , n 0
6 线性时不变离散系统的时域分析
5. 累加 设某一序列为x(n),则x(n)的累加序列 y(n)定义为
y ( n)
k
x(k ) x(n) * u(n)
n
根据上述性质可以推得以下结论:
f (n n1 ) * (n n2 ) f (n n1 n2 )
6 线性时不变离散系统的时域分析
例 已知 x1 (n) (n) 3 (n 1) 2 (n 2) x2 (n) u(n) u(n 3) 试求信号 x (n) ,它满足 x(n) x1 (n) x2 (n) 解:可利用上面讲述的性质求解。
1 1/ 2 1/4 -2 -1 0 1 1/8 ... 2
n
x(-n) 1 1/2 1/8 1/4 ... -2 -1 0
1
2
n
6 线性时不变离散系统的时域分析
3.序列的加减 两序列的加、减是指同序号(n)的序列值逐项对 应相加得一新序列。
6 线性时不变离散系统的时域分析
例:
x(n) 1 1/2 1/4 -2 -1 0 y(n) 2 1 1/4 1/2 1 2 n …
6 线性时不变离散系统的时域分析
2.单位阶跃序列
u(n)
1, u ( n) 0,
n0 n0
u(n)
...
-1 0 1 2 3 n
(n) u (n) u (n) u (n 1)
m 0
u (n) (n m) (n) (n 1) (n 2)
信号分析与处理第3章离散时间信号的分析_1-44

X (z) x(n)zn x(n)(re j )n [x(n)r n ]e j n
x
x
x
只有当 x(n)rn 符合绝对可和的收敛条件,即
x(n)r n
x=
时,x(n) 的 z 变换才有意义。对序列 x(n) ,其 z 变换 X (z)收
敛的所有 z 的集合称为 X (z)的收敛域,简记为 ROC
X (z) x(n)zn x(0) x(1)z1 x(2)z2 x0
上式是序列 x(n) 的单边 z 变换。
n<0 时样点均为零的序列称为因果序列,对因果序 列,其双边 z 变换与单边 z 变换相同。
单边 z 变换定义式表明,序列的单边 z 变换是复变 量 z 的负幂级数,该级数的系数即是序列 x(n) 本身。
1、 周期单位冲激串的傅里叶变换
周期单位冲激串,如图(a)所示。该函数在研
究信号的采样问题中经常用到,称为狄拉克梳状函数
或理想采样函数,用数学公式表示为
p(t) (t nT ) n
在 2.3 节中已得到,其傅里叶级数为 p(t) 1 ejkt
T k
上式表明,周期单位冲激串的傅里叶级数中,只包 含位于 0,0 ,20 ,…,k0 ,…处的频率分量, 每个频率分量的大小相等且都等于 1 。
两者进行相乘,如图(c) 所示,相乘结果 xS (t) x(t) p(t) 称为 x(t) 的采样信号(sampled signal),如 图(d)所示。xS (t) 中各分量的冲激强度构成的序列为 x(t) 的样本 x(n) 。
设采样间隔为TS ,采样角频率S
2
f
2 TS
。由采
样过程,有
xS (t) x(t) p(t)
为书写方便,对序列 x(n) 取 z 变换和对 X (z)取逆 z 变换常常记为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B 根据允许的过渡带宽度及阻带衰减确定所采用的窗函数和 N 值;
C 做 H d (e j ) 的逆傅里叶变换得 hd(n); D 对 hd(n)加窗处理得到有限长序列 h(n) hd (n) w(n) E 对 h(n)做傅里叶变换得到频率响应 H (e j ) ,用 H (e j ) 作为 H d (e j ) 的逼近,并用
3
离散时间系统分析
实验目的: 掌握线性卷积的计算机编程方法,利用卷积的方法观察、分析系统响应的时域特性。 验证卷积定理。 掌握循环卷积的计算机编程方法,并比较与线性卷积的差别。 实验原理 参考教材关于卷积的部分的论述。 实验内容: 1) MATLAB 提供卷积计算的函数有 CONV、CONV2 和 CONVN。 试用函数 CONV 计算如下图所示 x(n)和 y(n)序列的卷积。 MATLAB 参考代码 x=[1:10] y=[1:5] subplot(31 stem(x) xlabel('x(n)') subplot(312) stem(y) xlabel('y(n)') t=conv(x,y) subplot(313) stem(t) xlabel('x(n)*y(n)' 2)用 matlab 实现 conv 函数的相同功能。
C f s 和 N 确定后,即可确定所需相应模拟信号 x(t) 的长度
T N / f s NTs
(3)
分辨率 f 反比于 T,而不是 N,在给定的 T 的情况下,靠减小Ts 来增加 N 是不能提
高分辨率的,因为T NTs 为常数
2.谱分析步骤; A 数据准备
x(n) xa(t) tnT xa(nT )
表示,即它的系统函数,再利用 IIR 滤波器设计方案具体实现该滤波器。 2. 实验中用到的一些基本函数见教材第 6.2.2 节(与 IIR 数字滤波器设计相关 MATLAB 函 数)。
实验内容
已知通带截止频率 fp=5 kHz,通带最大衰减 p=2 dB,阻带截止频率 fs=12 kHz,阻带最小衰减 s=30 dB,按照以上技术指标设计巴特沃斯低通滤波器。
(4)
B 使用 FFT 计算信号的频谱
5
N 1
X (k ) x(n)WNkn
n0
(5)
X (k ) X r (k ) jX i (k )
(6)
C 由频谱计算幅度谱 X (k) 、相位谱 k 和功率谱 G(k)
X (k)
X
2 r
(k
)
X
2 i
(k
)
(7)
k
arctan
Xi (k ) Xr (k)
(8)
G(k)
X (k) 2XBiblioteka 2 r(k)
X
2 i
(k
)
(9)
3.实验中用到的一些基本函数简介
y=fft(x,n)
; 计算 n 点的 FFT。
abs(x)
; 取绝对值。
angle(z)
; 取相角。
[Pxx, f]= periodogram (xn, nfft, fs, window) ;%周期图谱估计
4
FFT 频谱分析
实验目的: MATLAB 函数编写信号傅利叶变换程序,观察不同参数设置条件下,信号傅立叶变 换的基本性质和特点。 实验原理 关于信号谱分析的步骤和方法参见教材第 3、4 章相关内容。为了解信号的特点,了 解信号频谱分布情况,应该对信号进行谱分析,计算出信号的幅度谱、相位谱和功率谱。 信号的谱分析可以用 FFT 实现,讨论如下: 1. 谱分析中的参数选择;
1)采用 matlab 自带函数设计; 2) 自己设计与 buttord 和 butter 功能相同的函数实现滤波器设计。
8
FIR 数字滤波器的设计
实验目的
1. 掌握 FIR 数字滤波器的设计方法与步骤; 2. 理解系统频率响应的概念,学习编写计算系统频率响应的方法。
实验原理
1. FIR 数字滤波器设计的详细内容见教材第 7 章。 窗函数法:设计 FIR 数字滤波器的步骤:
给定的技术指标来检验。 2. 实验中用到的一些基本函数见教材第 7.2.4 节(与 FIR 数字滤波器设计相关 MATLAB
函数)。
实验内容
设计例 7.2.1 所述的滤波器。
9
A 若已知信号的最高频率 f c ,为防止混叠,选定采样频率 f s :
fs 2 fc
(1)
B 根据实际需要,选定频率分辨 f ,一但选定后,即可确定 FFT 所需的点数 N
N f s / f
(2)
我们希望 f 越小越好,但 f 越小,N 越大,计算量、存储量也随之增大。一般取 N
为 2 的整次幂,以便用 FFT 计算,若已给定 N,可用补零方法便 N 为 2 的整次幂。
2
% n=m+n0; y=x; (5)反转 在这种运算中,序列 x(n)以 n=0 为中心翻转得到一个反转序列: y(n)=x(-n) 在 MATLAB 中,对序列值的翻转用 fliplr(x)实现,对序列各点位置的翻转用 -fliplr(n)实现,如下面的参考代码所示: MATLAB 参考代码 function[y,n]=sigfold(x,n) %implements y(n)=x(-n) %--------------------------------------------%[y,n]=sigfold(x,n) % y=fliplr(x); n=-fliplr(n);
7
IIR 数字巴特沃思滤波器的设计
实验目的
1. 掌握用模拟滤波器原型设计 IIR 滤波器的基本方法; 2. 掌握数字巴特沃思滤波器的设计方法与步骤;
3. 理解系统频率响应的概念,学习编写计算系统频率响应的方法。
实验原理
1.数字巴特沃思滤波器设计的详细内容见教材第 6 章,现将设计步骤归纳如下: A 根据给定的频带指标,由双线性变换的频率关系,确定相应的模拟滤波器原型频带 指标; B 利用原型低通滤波器,选择合适的参数,设计出符合指标的模拟低通滤波器; C 利用双线性变换,将所获得的模拟滤波器的 s 域表示转换为相应数字滤波器的 z 域
[Pxx, f]=pwelch (xn, nfft, fs, window, noverlap);%平均周期图法
Pxx=psd (xn)
;功率谱密度
实验内容 1. 已知序列 x(n)=2sin(0.48πn)+cos(0.52πn) 0≤n<100,试绘制 x(n)及它的频谱图。
clear all N=100; n=0:N-1; xn=2*sin(0.48*pi*n)+cos(0.52*pi*n); XK=fft(xn,N); magXK=abs(XK); phaXK=angle(XK);
1
下面的参考代码利用函数 sigmult 说明了这种运算,其验证将在后续实验中进行。 MATLAB 参考代码 function[y,n]=sigmult(x1,n1,x2,n2) %implements y(n)=x1(n)*x2(n) %--------------------------------------------%[y,n]=sigmult(x1,n1,x2,n2) %y=product sequence over n,which includes n1 and n2 %x1=first sequence over n1 %x2=second sequence over n2(n2 can be different from n1) % n=min(min(n1),min(n2)):max(max(n1),max(n2));%duration of y(n) y1=zeros(1,length(n)); y2=y1; y1(find((n>=min(n1))&(n<=max(n1))==1))=x1;%x1 with duration of y y2(find((n>=min(n2))&(n<=max(n2))==1))=x2;%x2 with duration of y y=y1.*y2;%sequence multiplication (3)加权 在这种运算中,每个样本均乘以标量 a: y(n)=ax(n) 在 MATLAB 中,算术运算符“*”用来实现加权运算。 (4)移位 在这种运算中,序列 x(n)总体进行 k 点的移位: y(n)=x(n-k) 下面的参考代码利用函数 sigshift 说明了这种运算,其验证将在后续实验中 进行。 MATLAB 参考代码 function[y,n]=sigshift(x,m,n0) %implements y(n)=x(n-n0) %--------------------------------------------%[y,n]=sigshift(x,m,n0)
6
subplot(1,2,1) plot(n,xn) xlabel('n');ylabel('x(n)'); title('x(n)N=100'); subplot(1,2,2) k=0:length(magXK)-1; stem(k,magXK,'.'); xlabel('k');ylabel('|X(K)|'); title('X(K)N=100');
离散时间信号分析
实验目的: 利用 MATLAB 进行离散时间序列的基本运算,掌握基本的 MATLAB 函 数的编写和调试方法。
实验内容: (1)信号相加 x(n)=x1(n)+x2(n) 当两个相加的序列长度不同时或位置不对应时,首先必须调整二者的位置对齐,然 后通过 zeros 函数左右补零使其长度相等后再相加。下面的参考代码利用函数 sigadd 说明 了这些运算,其验证将在后续实验中进行。 MATLAB 参考代码 function[y,n]=sigadd(x1,n1,x2,n2) %implements y(n)=x1(n)+x2(n) %--------------------------------------------%[y,n]=sigadd(x1,n1,x2,n2) %y=sum sequence over n,which includes n1 and n2 %x1=first sequence over n1 %x2=second sequence over n2(n2 can be different from n1) % n=min(min(n1),min(n2)):max(max(n1),max(n2));%duration of y(n) y1=zeros(1,length(n)); y2=y1; y1(find((n>=min(n1))&(n<=max(n1))==1))=x1;%x1 with duration of y y2(find((n>=min(n2))&(n<=max(n2))==1))=x2;%x2 with duration of y y=y1+y2;%sequence addition (2)信号相乘 信号相乘,即两个序列的乘积(或称“点乘”),表达式为: x(n)=x1(n)?x2(n) 在 MATLAB 中,用运算符“.*”实现。
